0 引　言

应用于船舶的载流管道具有较高长细比，整个管道之中并不设定约束设施，不具备较高固定频率，受到较为规律的阻力与升力影响，导致船舶载流管道出现比较显著的涡激振动^[1-3]，所以载流管道的涡流振动检测工作就显得尤为重要。有学者对错列的海洋列管开展涡激振动的数值模拟，该方法的计算过程更加稳定，借助有限元软件计算涡激振动^[4]。还有学者提出三维流体动力学模拟不同材料海洋立管的涡激振动情况，并使用弹性模量等方法计算流动力学，证明优化后的纤维复合材料管的性能更佳^[5]。该方法虽然计算过程较为复杂，但是结果具有较大借鉴意义，进一步研究后将影响深远^[6]。

本文主要研究船舶载流管道涡激振动数值模拟方法，借助流体力学软件计算并模拟出载流管道涡激振动，为未来船舶管道优化提供数据支持。

1 基于CFD的船舶载流管道涡激振动数值模拟 1.1 边界条件确定与网格划分

利用流体动力学计算软件(CFD)对常见船舶所搭载的载流管道涡激振动问题开展三维数值模拟，模型构建需要先确定模型边界条件，并正确划分网格^[7]。本文研究船舶所处区域入口与出口分别是速度入口与自由出流。使用软件中的网格划分功能将所研究区域划分成由六面体结构组成的网格，在网格上划分研究区域，靠近载流管道壁面的位置将网格加密，其他位置的网格则可以稀疏处理。模型中载流管道的参数为：管道长度9.74 m，管道外径与管壁厚度分别为0.03 m与0.56 mm，管道长径比为493，顶部预紧力与弹性模量分别为828 N与1.036*10¹¹/(N/m²)。网格划分与模型构建结果见图1。

表示流体流动的无量纲数被称为雷诺数。由于雷诺数自身存在差异，所以模型构架时还需要考虑网格尺度差异，本文所构建模型沿着载流管道的第一层网格高度符合 $ {y^ + } \approx 1 $ ，为了确保边界层节点分布足够充分，设定1.3作为靠近管壁位置的网格增长率。管道里面第1层网格高度 $ {y^ + } $ 使用下式计算获得：

$ {y^ + } = 0.173*R{e^{0.9}}\left( {\Delta y/D} \right)。$

(1)

式中： $ \Delta y $ 与 $ D $ 分别表示网格在 $ y $ 方向的尺寸和载流管道的直径； $ Re $ 表示雷诺数。

式(2)为约化速度 $ Ur $ 计算式，根据该式能够计算出1～10约化速度下雷诺数与流体速度：

$ Ur = U/\left( {{f_s}*D} \right)。$

(2)

通过式(2)计算得到的雷诺数与流体速度 $ U $ ，f_s表示量程范围。

1.2 数值计算

模型构建时已经确定所研究船舶周围海洋环境范围，经过估算该区域的长度与宽度分别为载流管道之间的30倍与20倍，区域高度则为管道尺寸的10倍， $ D $ 也表示特征尺度，长宽比确定是为了能够充分获取载流管道后部尾流特性^[11-12]。载流管道所处区域上游来流与下游尾流区的长度分别为特征尺度的10倍和20倍，左右两侧长度均为特征尺度的10倍^[8]。载流管道上承受的力主要包括阻力与升力，利用湍流模型，通过计算确定阻力系数C_D与升力系数C_L就能获得载流管道所承受力。

1.3 流体场与固体场控制方程计算

1)流体场控制方程计算

所研究的流场海洋环境也可以看作是具有黏性但是压缩性较差的流体。通过Adams-Bashforth格式(二阶事件精度)描述事件离散，公式为：

$ \begin{gathered} {u^{n + 1}} = {u^n} + t\left( {1.5{h^n} - 0.5{h^{n - 1}} - 1.5\nabla {p^n} + 0.5\nabla {p^{n - 1}}} \right) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {f^{n + 0.5}}t 。\\ \end{gathered} $

(6)

式中： $ u $ 与 $ h $ 分别表示速度张量与压强， $h = \nabla * $ [ $- u*u + $ ${ \left( {\nabla u + \nabla u'} \right)}$ ]； $ p $ 与 $ \nabla $ 分别用于描述压强与Hamilton算子，用于描述矩阵转置； $ n $ ， $ n - 1 $ ， $ n + 1 $ 和 $ n + 0.5 $ 均代表时间步。附加于正交网格的体积力，浸入边界点与正交网格点之间的映射关系需要经分布函数与插值函数共同构建。

2)固体场控制方程计算

通过三维实体单元有限元法模拟船舶载流管道的动力详情，为获得有限元方程，载流管道结构空间离散通过三维二结点梁单元实现，无论何种位置的结点都具备6个自由度。由于Newmark-β法具有较无条件稳定特点，同时能够实现流场时间步长一致，二阶时间精度较高，可以应用求解动力方程。

1.4 流固耦合模拟

从整个载流管道上随机选取一小截作为研究对象，待稳定该截管道振动后，能够确定该截管道上、下张力能够限制管道竖向位移。如果横向位置的载流管道失去平衡，载流管道上、下两端的作用会帮助载流管道重新回到平衡位置^[9]。由此可以确定载流管道的边界条件：无论是顺流方向还是竖直方向，载流管道上下2个环面的位移均为0，而横流方向载流管道可以任何方向自由移动，在管道的外面布置弹性约束，该约束值设定为2000 N/m³。模态分析载流管道，确定2.71 Hz作为载流管道的一阶固有频率，该数值也比较接近实际载流管道的振动频率。涡激振动实际上是较具代表性的流固耦合问题，运用CFD软件中包含的流固耦合分析技术，在软件中利用专门的CFX模块与Mechanical模块结合流固耦合算法实现流体与固体双向耦合计算。使用CFD软件中增强版多长求解器(MFX)实现数据在CFX模块与Mechanical模块中的传递。

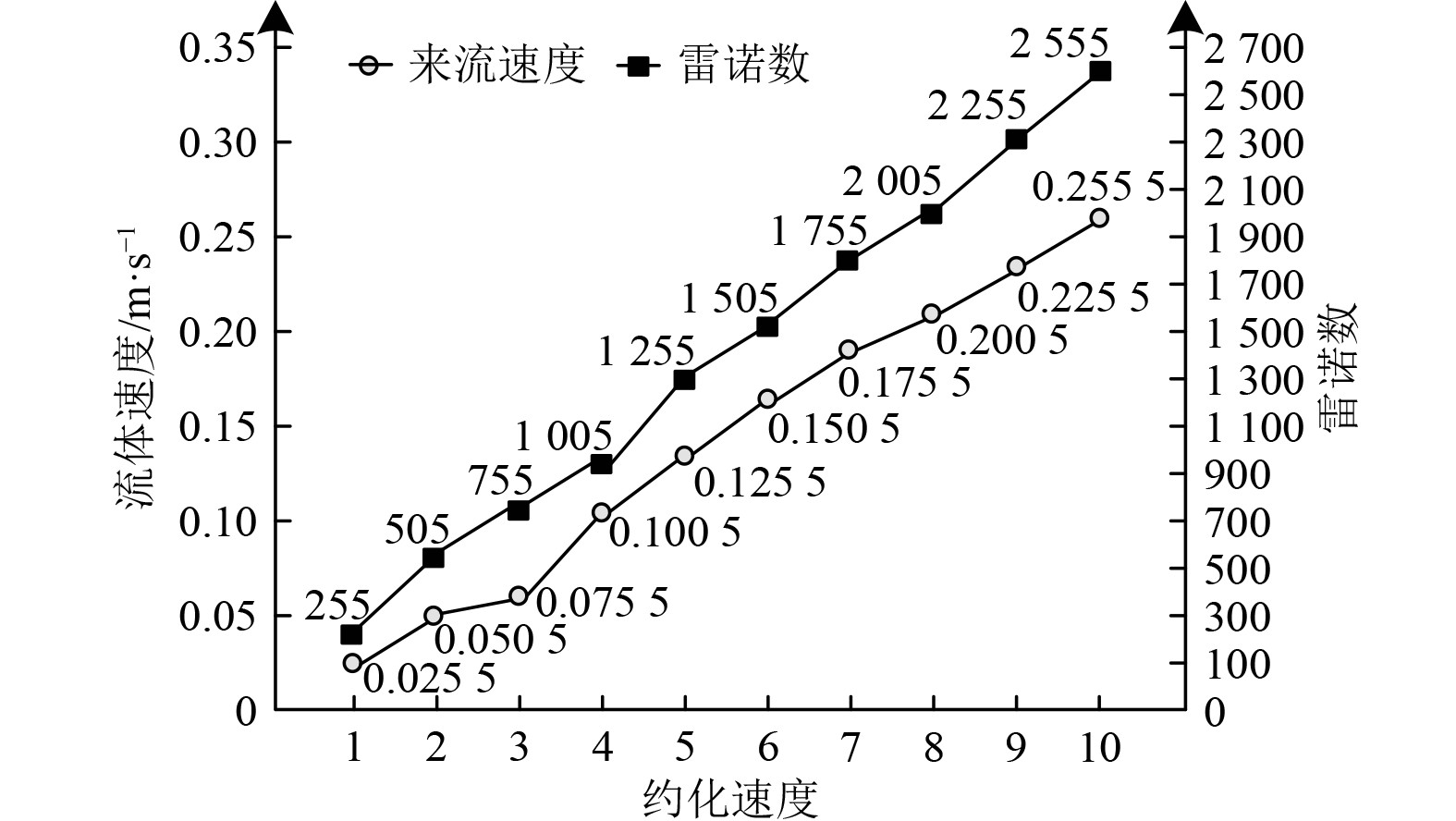
2 算例分析 2.1 升力与阻力计算

根据式(2)计算出各约化速度所对应的雷诺数与流体速度，数值结果见图2。

根据图2的计算结果，结合式(3)与式(4)，计算得出升力系数与阻力系数，计算结果见表1。从表1可知，随着雷诺系数的升高，载流管道的阻力系数基本没有发生改变，而升力系数呈现出上升趋势。雷诺系数越大，漩涡脱落的时间越少，同时漩涡脱落的频率也随着雷诺系数的升高而增长。

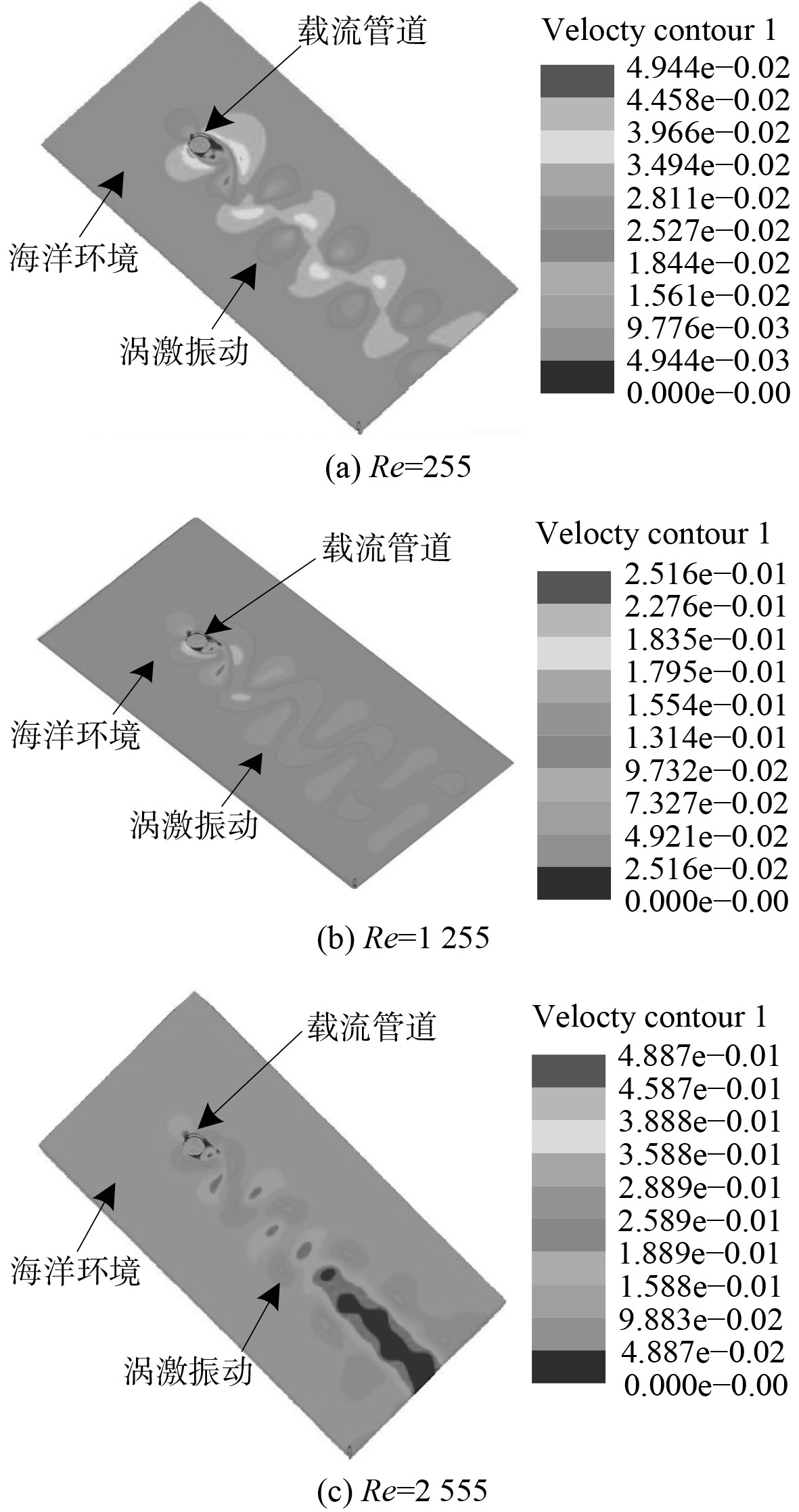
选择最低、最高以及中间3个具有代表性的雷诺数，使用CFD软件生成涡激振动速度场，结果见图3。从图3可知，3个具有代表性的雷诺数下，载流管道的后部位置均出现较为显著的漩涡脱落情况，脱落频率约为2.5 s 次。雷诺数保持上升趋势，漩涡持续时间缩短，由此证明，雷诺数增大，缩短层流过渡到湍流的时间。

2.2 载流管道振型分析

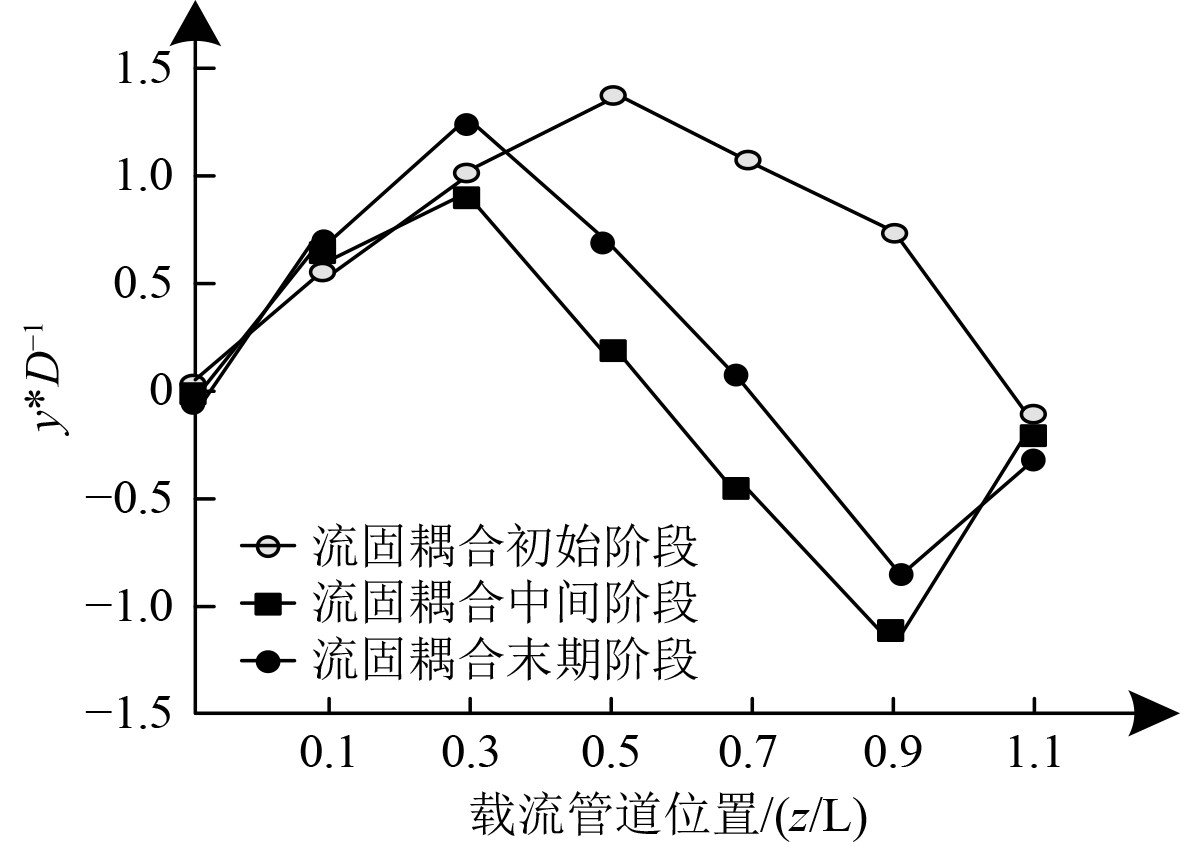
载流管道在海洋环境中会受到来自横向和竖向2个方向的涡激振动影响，本文研究竖向涡激振动下载流管道的振动情况，结果见图4。由图4可知，流固耦合初始阶段下，载流管道振动的振型呈现出一阶模态，随着耦合时间推移，涡激振动能量不断释放，待到达耦合中间阶段，振型转变为二阶模态，这种状态表示载流管道涡激振动的模态振动特性，这也符合以往研究者得出的实际实验结果。流固耦合持续到末期阶段载流管道的振动依旧保持二阶模态，结合图4，漩涡脱落此时也锁定在二阶模态之中，由此可以判断，本文所使用的数值模拟方法可以完全模拟出锁定现象。

3 结　语

本文使用CFD软件研究船舶载流管道涡激振动数值模拟方法，通过流固耦合等模型实现涡激振动的三维数值模拟。经过实验分析发现，本文的数值模拟方法能够有效研究船舶载流管道的涡激振动情况。受到涡激振动影响，船舶载流管道会出现较为显著的扰动情况，漩涡脱落与漩涡强度均呈现出显著三维特征。通过计算获得不同雷诺数下阻力系数与升力系数的计算结果，确定流固耦合会造成锁定现象，这种锁定现象会严重影响载流管道的涡激振动。尽管海洋中的水流速度是均匀的，但是涡激振动对于载流管道的振动影响却是不均匀的，长期受到涡激振动影响，载流管道将发生严重变形与损坏。