0 引　言

船舶壳体结构具有线型复杂、耦合严重等特点，导致其塑性性能在外界作用下会发生显著的非线性变化^[1-3]。塑性损伤指的是船体在受到外力的影响下，其发生的弹性形变，当超过承受的极限数值后，船舶壳体会形成无法恢复的形变情况^[4]。针对船舶壳体结构塑性损伤计算问题，甄春博等^[5]和唐首祺等^[6]分别对船结构疲劳强度影响因素和结构的疲劳程度展开相关分析，但是在上述分析过程中，对于线性和非线性2种冲击下的船舶壳体的塑性变化结果，仍需深入研究和验证。

精细积分算法是一种用于求解一阶常微分方程的高精度算法，其在结构动力学分析等多个领域中被大量应用。因此，本文利用精细积分算法计算精度较高的优势，计算船舶壳体结构受到的冲击力，依据该计算结果，分析船舶壳体的疲劳强度，并通过有限元模型分析其塑性损伤情况。

1 船舶壳体结构塑性损伤计算 1.1 船舶壳体结构计算试验模型

由于船舶壳体结构塑性损伤发生在冲击和爆炸等情况下，因此，试验采用近水场爆炸方式进行，为保证塑性损伤计算结果的可靠性，保证有限元软件模拟的精准性，本文针对当下船舶的实际情况，采用双壳体结构船舶作为试验模型，该模型长1.2 m、宽0.75 m，环肋间距和高度分别为0.2 m和0.15 m。

1.2 基于精细积分的冲击力计算

发生冲击和爆炸等情况下，船舶壳体结构会直接受到冲击，为精准分析在该冲击下船舶壳体结构的塑性损伤情况，需精准掌握冲击力的强度^[7]，本文采用精细积分算法进行冲击力的精装计算。船舶壳体结构的自由度数量用 $ n $ 表示，在冲击作用下，船舶壳体结构的运动方程为：

$ {\boldsymbol{D}}f\left( t \right) = {\boldsymbol{M}}x\left( t \right) + {\boldsymbol{C}}x\left( t \right) + {\boldsymbol{K}}x\left( t \right)。$

(1)

式中： $ {\boldsymbol{D}} $ 表示载荷分布矩阵，即冲击力分布矩阵；f(t)表示其向量； $ {\boldsymbol{M}} $ ， $ {\boldsymbol{C}} $ ， $ {\boldsymbol{K}} $ 分别为对应船舶壳体结构质量、阻尼和刚度；x(t)表示广义情况下的位移向量。

将船舶壳体结构转移至状态空间内得到：

$ Z = {\boldsymbol{A}}Z\left( t \right) + {\boldsymbol{B}}f\left( t \right)。$

(2)

式中： ${\boldsymbol{A}}$ 表示状态空间内的结构系统矩阵， ${\boldsymbol{B}}$ 表示惯性矩阵； $ Z\left( t \right) = \left\{ {\begin{array}{*{20}{c}} {x\left( t \right)} \\ {x'\left( t \right)} \end{array}} \right. $ ，其中 $ x'\left( t \right) $ 表示冲击下的位移向量，求解公式(2)可得出：

$ \begin{gathered} Z\left( t \right) \approx {e^{A\Delta t}}Z\left( {t - \Delta t} \right)+ \\ \frac{1}{2}\Delta t\left[ {{e^{A\Delta t}}{\boldsymbol{B}}f\left( {t - \Delta t} \right) + {\boldsymbol{B}}f\left( t \right)} \right] 。\\ \end{gathered} $

(3)

式中： $ \Delta t $ 表示时间步长； $ {e^{A\Delta t}} $ 为计算该算子。

利用精细积分求解原理^[8]，对概算子中的 $ \Delta t $ 实行细分处理，形成数量为 $ m = {2^N} $ 的等分；设 $ f = {2^N}\Delta t $ ，其中， $ N $ 表示模态阶数，则可得出 $ {e^{A\Delta t}} $ 的求解，则该结果即为精确解，可得出冲击力计算结果。

1.3 船舶壳体结构疲劳损失计算

船舶壳体结构受到的冲击类别不同，冲击程度分为线性和非线性2种，基于计算得出的冲击力计算结果，衡量冲击下船舶壳体结构的疲劳情况。为保证计算结果的精准性，采用计及冲击力的频谱分析计算方法完成。该方法能够分析冲击下^[9]船舶壳体结构的应力-时力，同时计算冲击作用下，壳体结构的各个点损伤情况以及疲劳损伤的贡献度、影响系数，并对相应传递函数实行修正和计算，获取应力谱，以此得出冲击下船舶壳体结构的疲劳损伤结果。以计算的冲击力结果为基础，计算冲击力结果下船舶的冲击非线性贡献度和影响系数，在冲击作用下，由于波浪弯矩和应力之间呈现线性关联，则采用影响系数修正船舶壳体结构垂向冲击弯矩，以此实现应力响应传递函数的修正，完成应力谱的计算，得出冲击作用下船舶壳体结构的疲劳损伤情况。

1.4 船舶壳体结构塑性损伤计算

为直观呈现船舶壳体结构在冲击情况下的塑性损伤结果，采用MSC/PATRAN有限元模型对试验模型实行模拟，模拟结果如图1所示。

采用有限元软件中板壳单元完成船舶模型的网格划分，划分的单元总数量为82206，坐标系采用右手坐标系，X轴表示船首，Y轴表示左舷，Z轴表示垂直向上。模拟冲击过程中，在模型的两侧和底部进行冲击模拟，并且对船舶底部壳体结构的冲击载荷施加进行约束，并且沿着船舶底部壳体结构船长方向最大应力区域，完成边界条件的设定。边界条件设定时，应考虑非线性冲击作用下，非线性有限元分析时，边界条件对船舶壳体结构的承载力存在直接影响，因此，在设定边界条件时，需结合船舶壳体结构在冲击情况下的受力情况，完成边界条件的设定。以船舶底部壳体结构长度方向为依据，在底部两侧边上完成X和Z方向的位移和转角的固定；在船舶底部宽度方向上，固定底部两边Y和Z方向上的转角以及X方向的位移。船舶壳体结构在冲击作用下，弹性损伤与结构的屈曲强度存在直接关联，因此，在计算船舶壳体结构塑性损伤时，需充分衡量结构的几何刚度矩阵，该矩阵与划分的单元几何形状和单元承受的轴向力以及面力之间存在直接关联，因此，依划分的网格单元，形成船舶壳体结构的弹性刚度矩阵K_E，同时结合与中面力存在关联的几何刚度矩阵K_G，以此得出船舶壳体平衡方程，其公式为：

$ F = \left( {{{\boldsymbol{K}}_E} + {{\boldsymbol{K}}_G}} \right){D_b}。$

(4)

式中：D_b为位移向量； $ F $ 为整体冲击载荷向量。

K_G和面内的压力 $ P $ 之间为正比关系，如果比例因子采用 $ \lambda $ 表示，以此为依据完成 $ P $ 的增加，即p=λP^*，P^*表示参考值。依据该方式对K_G实行线性增加处理后，得到新的结果 $ \lambda \left( {{{\boldsymbol{K}}_G}^ * } \right) $ ；在 $ P = {P^ * } $ 的情况下， $ {{\boldsymbol{K}}_G}^ * $ 表示此时的几何刚度矩阵。当面内的 $ P $ 值较小时， $ {{\boldsymbol{K}}_G}^ * $ 最大程度接近常量，当面内的 $ P $ 值接近极限时，面内压力公式为：

$ {P_{cr}} = {\lambda _{cr}}{P^ * }，$

(5)

当船舶壳体结构发生塑性损伤后， $ F = 0 $ ，则壳体结构可在极小的弯曲状态下保持平衡，此时的平衡状态即为屈服状态，因此得出：

$ \left[ {{{\boldsymbol{K}}_E} + \lambda \left( {{{\boldsymbol{K}}_G}^ * } \right)} \right]{D_b} = 0 ，$

(6)

在此情况下，该公式的系数矩阵行列结果需为0，其公式为：

$ \left| {{{\boldsymbol{K}}_E} + \lambda \left( {{{\boldsymbol{K}}_G}^ * } \right)} \right| = 0 。$

(7)

对式(7)求解后，可获取船舶壳体结构的数个特征结果λ₁，将该结果中的最小值代入式(5)，即可得出船舶壳体结构的临界冲击载荷应力结果，通过有限元模型进行屈曲模态分析。

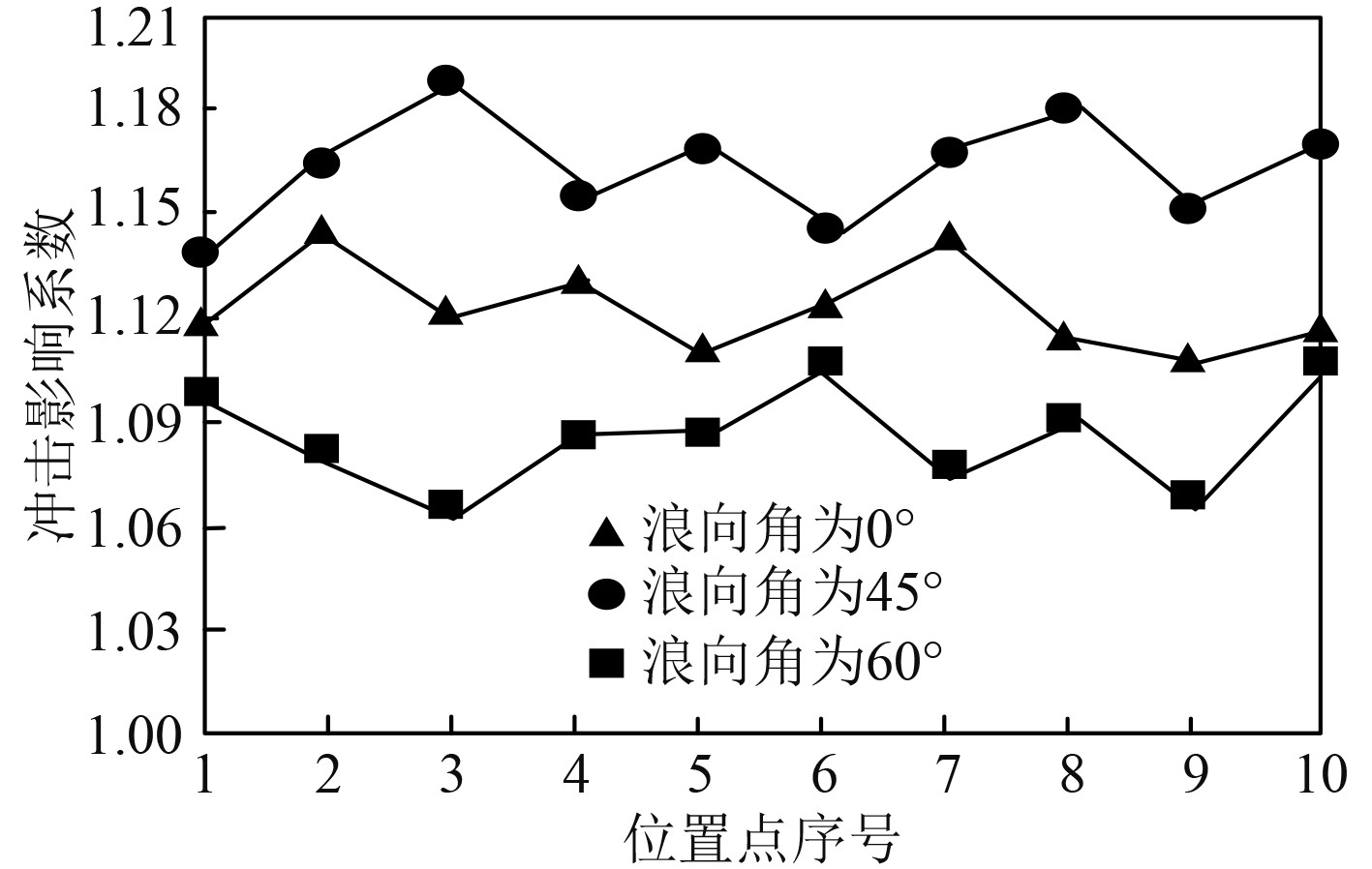
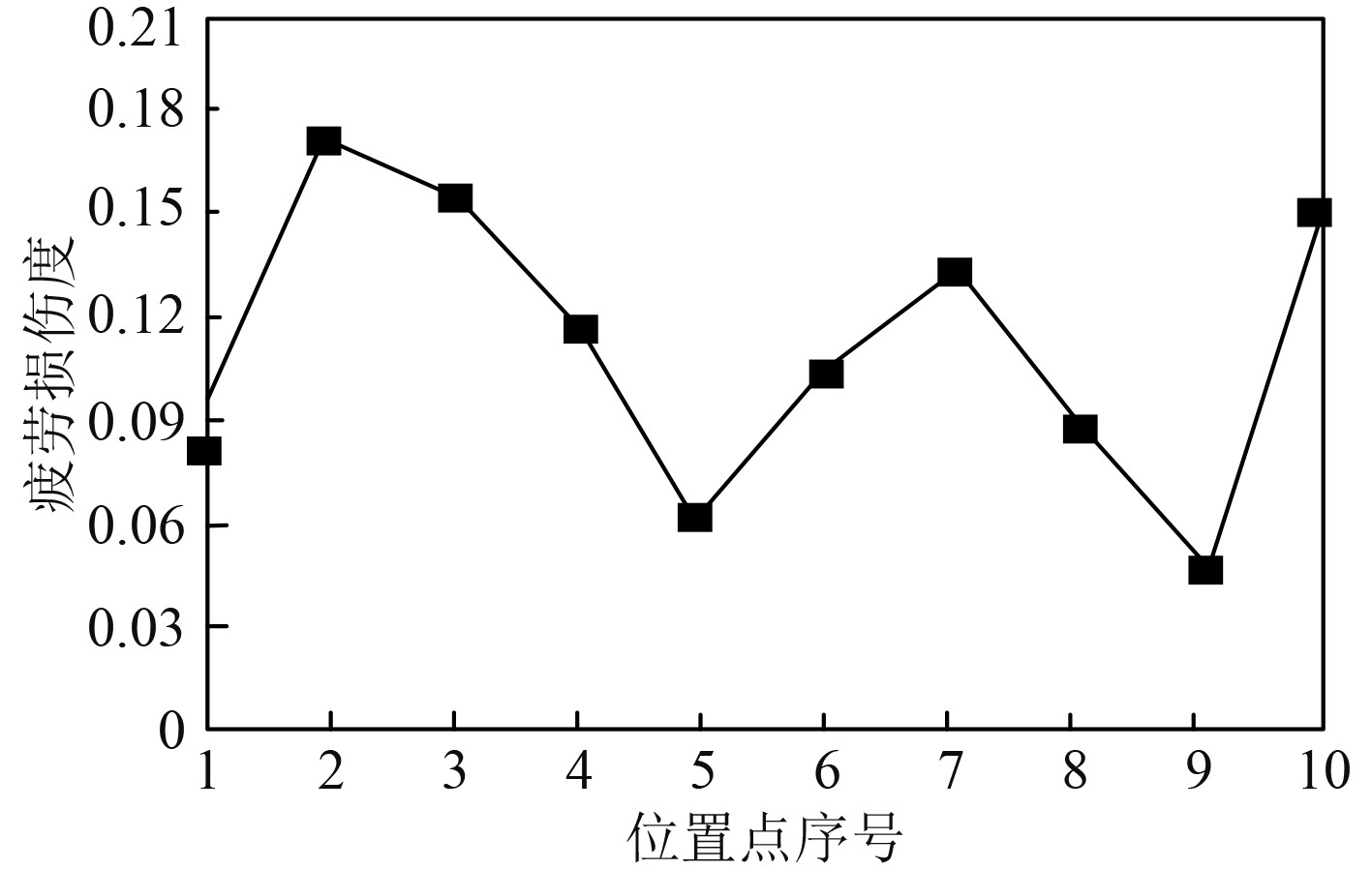
2 结果与分析 2.1 船舶壳体结构疲劳损失计算结果分析

获取爆炸位于船舶壳体结构15 m的近水场距离下，壳体结构在不同的浪向角下，爆炸侧的船舶壳体结构10处随机位置的冲击影响系数的结果，如图2所示。同时，随机抽取爆炸侧船舶客体结构的10处位置总损伤度结果，如图3所示。由图2和图3的测试结果得出：在不同的浪向角下，爆炸侧的船舶壳体结构10处随机位置的冲击影响系数结果存在一定差异，其中，浪向角为45°时的冲击影响系数值最高，表示该角度下，船舶壳体结构位置受到的冲击较大；壳体结构两端的冲击影响系数结果相对较低。除此之外，浪向角的继续增加，冲击影响系数的结果则逐渐减小。在该爆炸距离下，船舶壳体结构不同位置点发生的疲劳损伤结果也存在差异，表示不同位置的壳体结构，在同一冲击作用下的疲劳损伤程度存在差异。

2.2 船舶底部冲击应变结果

获取舰船壳体侧向结构受到冲击时，其底部应变结果如图4所示。由图4的测试结果得出：在船舶壳体结构侧面发生爆炸后，船舶底部在爆炸冲击的影响下，其产生的应力从冲击侧开始向另一侧传播，并且距离冲击处越近，则应变越明显，表示该位置的塑性形变越明显。

2.3 船舶壳体结构冲击应力分布结果

在壳体结构的正下方进行爆炸模拟，整个船舶壳体结构塑性分布结果如图5所示。可知，在壳体结构的正下方形成冲击力后，整个船舶壳体结构发生明显的塑性损伤分布，并且中间位置的塑性损伤程度严重，达到其极限载荷，其他位置的损伤程度相对较小。

2.4 塑性损伤结果计算

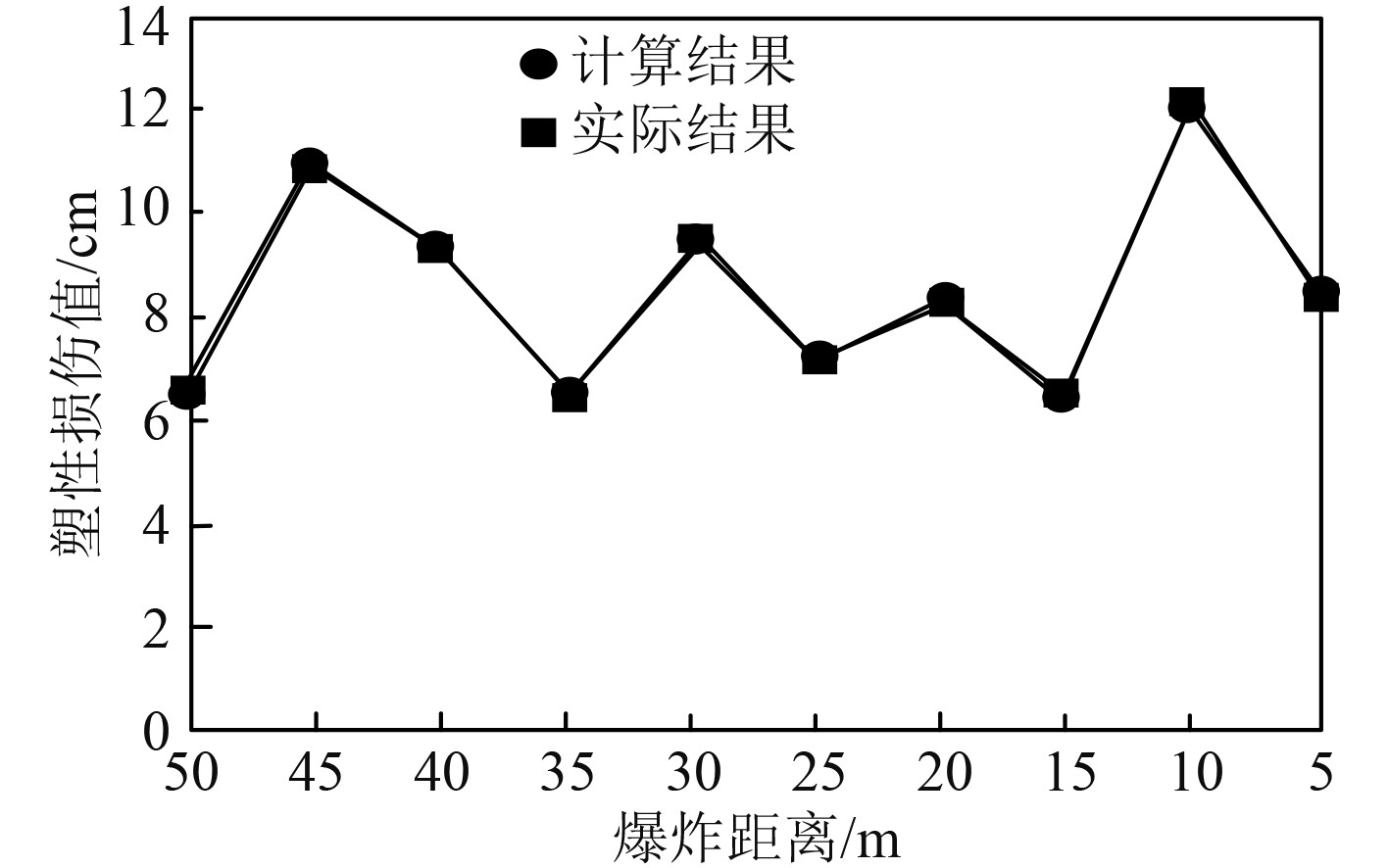
依据有限元模型获取船舶壳体结构在不同爆炸距离下，塑性损伤计算结果，如图6所示。可知，船舶壳体结构在不同的爆炸距离下，其发生的塑性损伤值也发生不同的变化，距离越近，损伤值越高；当爆炸冲击距离为10 m时，塑性损伤结果值最大，为12.75 cm，并且损伤计算结果与理论实际结果一致。

3 结　语

船舶壳体结构是船舶整体结构中的重要部分，其承载船舶的大部分冲击力，为精准分析船舶壳体结构在冲击作用下的塑性损伤情况，并获取损伤计算结果，本文研究应用精细分析的船舶壳体结构塑性损伤计算方法，并以某船舶壳体结构为例，展开试验。结果表明，船舶壳体在冲击下，不同位置受到的冲击程度存在差异，并且疲劳损伤程度也存在差异；在不同的冲击状态下，船舶壳体结构发生的应力也存在明显差异，船舶不同壳体位置的应变船舶情况也不同，塑性损伤结果和冲击发生距离，存在直接影响。