因为舰船结构的特殊性,所以既需减轻舰船结构质量,加快其速度,还需确保其抗爆性能,抵抗不同爆炸物的冲击[1-3]。为降低舰船结构质量,加快其航行速度,需研究舰船轮廓CAD模型参数优化方法,依据优化后的CAD模型,制造质量较轻、航行速度较快的舰船。王一镜等[4]以结构质量为目标函数,建立船体结构优化模型,通过自适应变异粒子群算法求解该模型,获取船体结构优化结果,该方法可有效优化船体结构,降低船体结构质量,为船体结构优化提供帮助。罗文俊等[5]人通过序贯优化方法建立船体结构优化的兴趣子域空间,通过信息熵函数缩减该空间,通过Kriging动态代理模型拟合缩减后的空间,获取船体结构优化结果,该方法可有效优化船体结构,降低船体结构质量,该方法具备一定高效性与适用性。但这2种方法均存在早熟收敛、无法跳出局部极值等缺陷。GA-PSO融合算法,融合了GA算法较优的全局搜索效果,PSO算法较优的局部搜索效果,可快速跳出局部极值[6],加快收敛效率。为此研究基于GA-PSO融合算法的舰船轮廓CAD模型参数优化方法,提升舰船轮廓CAD模型参数优化效果,降低舰船结构质量。
1 舰船轮廓CAD模型参数优化 1.1 舰船轮廓CAD模型参数优化模型以舰船抗爆性能不变为前提,以最轻舰船结构质量为目标函数,建立舰船轮廓CAD模型参数优化模型,公式如下:
| $ \min F\left( X \right) = M + \sum\limits_{i = 1}^n {{\rho _i}{S_i}{b_i}}。$ | (1) |
其中:M为舰船中固定设备与人员等质量;ρi、Si、bi为第i个舰船构件密度、面积、厚度;n为舰船构件数量。
舰船轮廓CAD模型参数优化约束条件包含几何、总纵弯曲与应力约束,外板几何约束为:
| $ {b}_{船底板}\geqslant 6.57,{b}_{舭列板}\geqslant {b}_{船底板},{b}_{外板}\geqslant 0.8{b}_{船底板};$ | (2) |
甲板几何约束为:
| $ {S}_{货仓甲板半剖}\geqslant 98,{b}_{货仓甲板}\geqslant 8.1;$ | (3) |
船底部骨架几何约束为:
| $ \begin{split}&{O}_{实肋板}\geqslant 392.4,{b}_{中内龙骨}\geqslant {b}_{实肋板},\\ &{h}_{中内龙骨}\geqslant {h}_{实肋板},{b}_{旁内龙骨}\geqslant {b}_{实肋板},\\ &{h}_{旁内龙骨}\geqslant {h}_{实肋板};\end{split} $ | (4) |
舷侧骨架几何约束为:
| $ {O}_{强肋骨}\geqslant 128.9,{b}_{舭肘板}\geqslant {b}_{实肋板} ;$ | (5) |
甲板骨架几何约束为:
| $ \begin{split}&{O}_{机舱区横梁}\geqslant 152.87,{O}_{非机舱区横梁}\geqslant 11.55,\\ &{O}_{机舱区纵桁}\geqslant 213.5,{O}_{非机舱区纵桁}\geqslant 234;\end{split} $ | (6) |
舱壁与扶强材几何约束为:
| $ {b}_{普通舱壁}\geqslant 3.7,{O}_{扶强材}\geqslant 20.3 ;$ | (7) |
舱口几何约束为:
| $ \begin{split}&{b}_{舱口围板}\geqslant 7.7,{h}_{舱口围板}\geqslant 1989.9,\\ &{S}_{围板水平纵桁半剖}\geqslant 0.4{S}_{舱口围板};\end{split}$ | (8) |
甲板室几何约束为:
| $ \begin{split}&{b}_{上层建筑舱壁}\geqslant 3,{O}_{甲板室扶强材}\geqslant 7.37,\\ &{O}_{甲板横梁}\geqslant 5.4,{O}_{甲板纵桁}\geqslant 34.4。\end{split} $ | (9) |
总纵弯曲约束包含最小剖面模数与最小惯性矩约束,舰船中部最小剖面模数约束为:
| $ O \geqslant \gamma K{O_0} 。$ | (10) |
其中:O0为符合标准的最小中剖面模数;γ为修正系数;K为材料换算系数。
最小惯性矩约束为:
| $ g\left( x \right) = 2\left( \displaystyle{\sum {{A_i}U_i^2} - \frac{{{{\left( \displaystyle{\sum {{A_i}U_i^{}} } \right)}^2}}}{\displaystyle{\sum {{A_i}} }}} \right) - 56890.26 \geqslant 0 。$ | (11) |
其中:Ai为第i个舰船构件的剖面积;
应力约束包含静水弯曲应力、合成弯曲应力与剪切力约束[7,8],静水弯曲应力约束为:
| $ \frac{{10K\left| {{G_s}} \right|}}{{{W_b}}} \leqslant {\sigma _s} 。$ | (12) |
其中:Gs为静水弯矩;Ob为剖面计算点位置的剖面模数;σs为静水弯曲应力。
合成弯曲应力约束为:
| $ \frac{{10K\left| {{G_s} + {M_a}} \right|}}{{{O_b}}} \leqslant {\sigma _b}。$ | (13) |
其中:Ma为波浪附加弯矩;σb为合成弯曲应力。
剪切力约束为:
| $ {\tau _i} = \gamma \frac{{\left| {{F_e}} \right|Z}}{\displaystyle{I\sum b }} \leqslant \left| \tau \right|。$ | (14) |
其中:
GA-PSO融合算法可充分利用GA算法与PSO算法的优势,获取最轻舰船结构质量对应的舰船轮廓CAD模型优化参数,求解流程如图1所示。
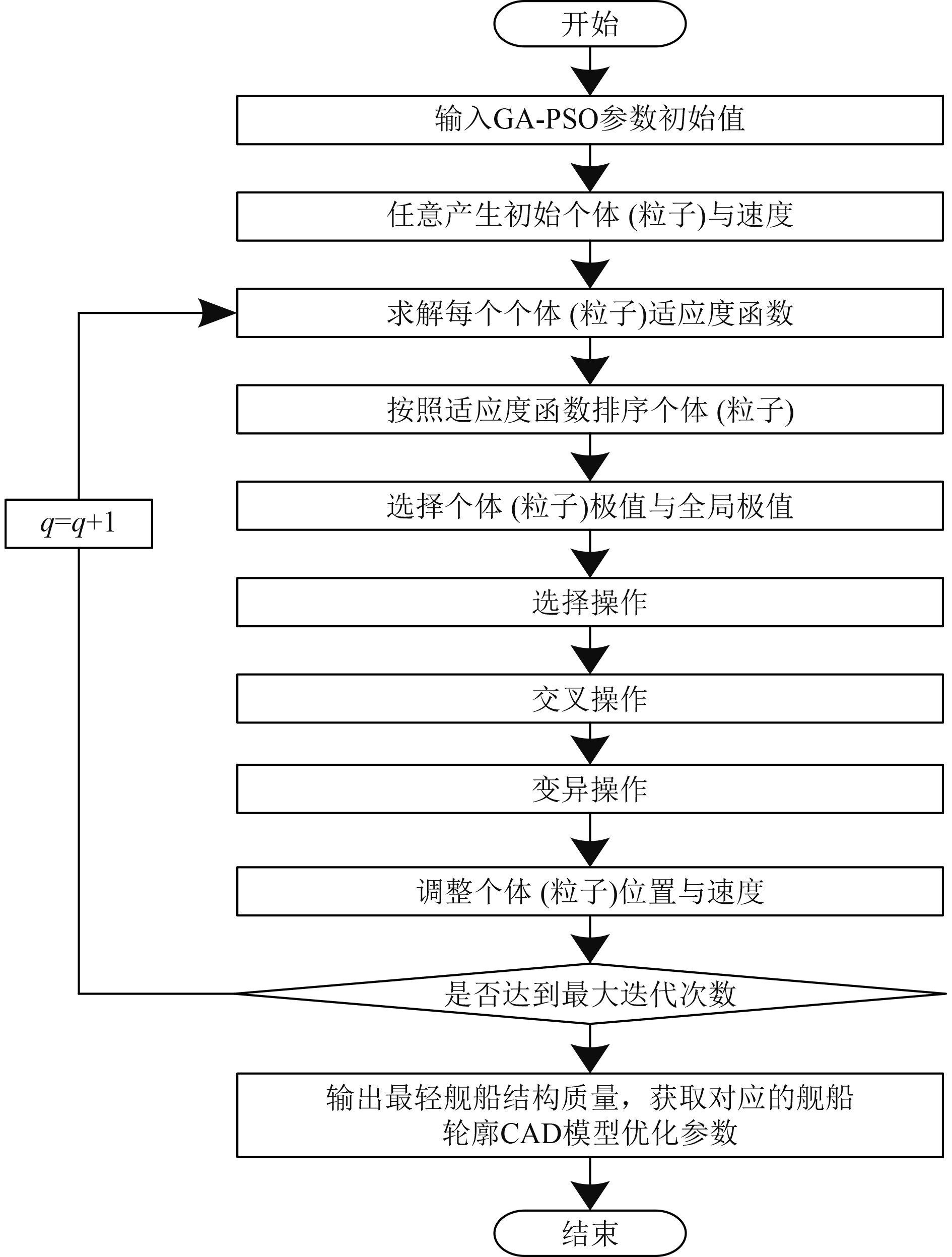
|
图 1 求解流程 Fig. 1 Solution process |
舰船轮廓CAD模型参数优化模型求解步骤如下:
步骤1 GA-PSO参数初始化,各个体代表一个舰船轮廓CAD模型参数优化模型的解,任意产生舰船轮廓CAD模型参数优化模型求解的个体(粒子)及对应的速度;
步骤2 按照式(1)的舰船轮廓CAD模型参数优化的目标函数,求解当下种群内个体的f值;
步骤3 依据f值升序排列当下种群内的个体,寻找个体极值
步骤4 选择操作,任意选取种群内的个体为选择算子,展开交叉操作;
步骤5 展开交叉操作,获取新个体,实施变异操作;
步骤6 利开变异操作,获取新个体;
步骤7 PSO算法通调整新个体速度与位置;
步骤8 达到qmax时,结束算法,输出舰船轮廓CAD模型参数优化模型的最佳解,即最轻舰船结构质量以及对应的舰船轮廓CAD模型优化参数,反之,令迭代次数增加,返回步骤2。
2 实验结果与分析利用本文方法对某船进行轮廓CAD模型参数优化,该船为不对称双尾船型,设计双桨、双机与双舵,最大承重量约7698 t。
在随机选择一艘舰船,利用本文方法优化该艘舰船轮廓CAD模型参数,绘制舰船轮廓CAD模型,结果如图2所示。从图2可知,本文方法可有效优化舰船轮廓CAD模型参数,大部分舰船CAD模型参数值均低于初始值,可有效优化舰船轮廓CAD模型参数,降低舰船轮廓质量。

|
图 2 部分舰船轮廓CAD模型 Fig. 2 CAD model of ship contour |
以本文方法优化后的舰船轮廓CAD模型参数中舱口围板为例,利用有限元模型分析本文方法优化前后舰船舱口围板的应力云图,舱口围板允许的规范最大应力值是200 N/mm2,分析结果如图3所示。可知,本文方法优化后的舰船舱口围板,其应力值明显高于优化前,虽然本文方法优化后的舰船舱口围板应力值有所增长,但依旧未超过舰船舱口围板允许的最大应力值。实验证明,本文方法可在规范应力允许范围内,最大程度地降低舰船结构质量,具备较优的舰船轮廓CAD模型参数优化效果。

|
图 3 优化前后舰船舱口围板的应力云图 Fig. 3 Stress cloud diagram of ship hatch coaming before and after optimization |
舰船内板吸能越大,其抗爆性能越佳,为此分析不同载荷工况时,本文方法优化前后舰船的内板吸能,载荷工况分别是400 kgTNT距舰船外板6 m,7 m,8 m,9 m的爆炸载荷,对应的最低内板吸能分别是1×1010 J,1.2×1010 J,1.5×1010 J,2.0×1010 J,分析结果如图4所示。由图4可知,随着爆炸载荷距离的增加,舰船内板吸能逐渐降低。当时间达到0.10s时,各荷载工况下,舰船内板吸能均趋于稳定,各荷载工况下,本文方法优化后的内板吸能均明显高于最低内板吸能,说明本文方法优化舰船轮廓CAD模型参数后,所设计的舰船抗爆性能较优。
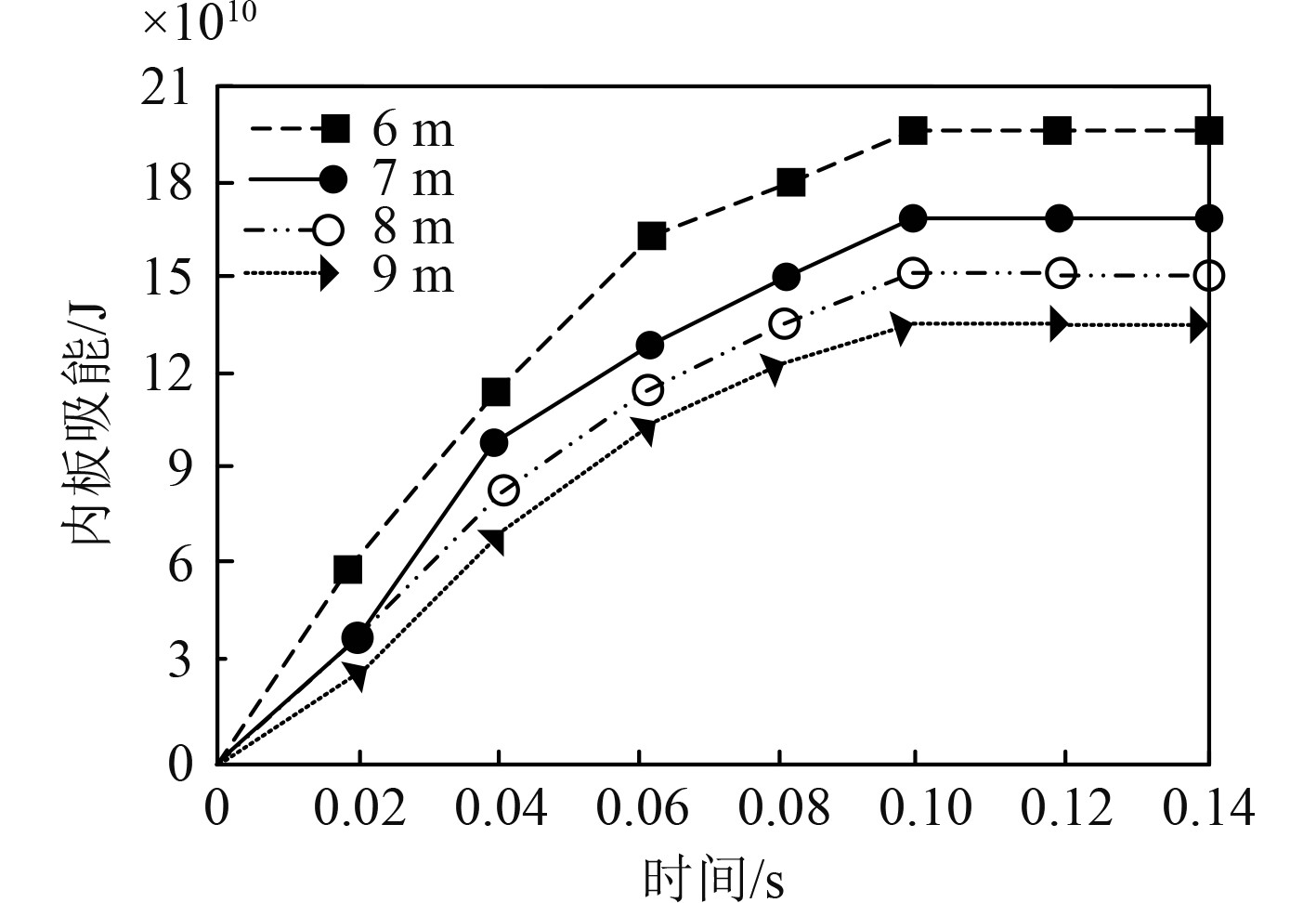
|
图 4 舰船内板吸能分析结果 Fig. 4 Analysis results of energy absorption of ship inner plate |
优化舰船轮廓CAD模型参数,可加快舰船制造效率,降低能源消耗,减少二氧化碳排放量,促进舰船制造的可持续健康发展。为此研究基于GA-PSO融合算法的舰船轮廓CAD模型参数优化方法,降低舰船结构质量,达到舰船节能减排的目的。本文方法仅考虑了舰船构件自身的参数,并未考虑构件间的安装距离与布置方案等参数,日后还需考虑构件安装距离与布置方案等参数,进一步提升舰船轮廓CAD模型参数优化效果。
| [1] |
卢雨, 顾朱浩, 王瑞宇. 基于CAD与CATIA二次开发的船体快速建模方法[J]. 中国舰船研究, 2020, 15(6): 121-127. LU Yu, GU Zhuhao, WANG Ruiyu. Rapid hull modeling methodology based on CAD and CATIA secondary development[J]. Chinese Journal of Ship Research, 2020, 15(6): 121-127. |
| [2] |
徐思豪, 杜文磊, 彭亚康, 等. 基于CATIA V6的船舶结构有限元网格方法[J]. 船舶工程, 2019, 41(8): 26-30. XU Sihao, DU Wenlei, PENG Yakang, et al. Method for Generating Ship Structure Finite Element Mesh Based on CATIA V6[J]. Ship Engineering, 2019, 41(8): 26-30. |
| [3] |
焦甲龙, 卿川东, 任慧龙, 等. 基于FEM-BEM法考虑弹振效应的超大型船舶结构疲劳损伤分析[J]. 中国造船, 2019, 60(2): 117-130. JIAO Jialong, QING Chuandong, REN Huilong, et al. A Hybrid FEM-BEM Approach to Structural Fatigue Damage Analysis of Ultra-large Ship Considering Springing Effects[J]. Shipbuilding of China, 2019, 60(2): 117-130. DOI:10.3969/j.issn.1000-4882.2019.02.012 |
| [4] |
王一镜, 罗广恩, 王陈阳, 等. 基于自适应变异粒子群算法的船舶结构优化方法[J]. 中国舰船研究, 2022, 17(2): 156-164. WANG Yijing, LUO Guangen, WANG Chenyang, et al. Ship structural optimization method based on daptive mutation particle swarm algorithm[J]. Chinese Journal of Ship Research, 2022, 17(2): 156-164. DOI:10.19693/j.issn.1673-3185.02306 |
| [5] |
周凤杰. 船舶避碰的粒子群-遗传(PSO-GA)的混合优化算法研究[J]. 船舶力学, 2021, 25(07): 909-916. ZHOU Fengjie. Research on hybrid optimization algorithm of particle swarm-genetic (PSO-GA) for ship collision avoidance[J]. Journal of Ship Mechanics, 2021, 25(07): 909-916. DOI:10.3969/j.issn.1007-7294.2021.07.008 |
| [6] |
郭天奇, 夏益美, 王福花, 等. 基于混合动态罚函数改进协同优化算法的船舶结构静动力学优化设计[J]. 振动与冲击, 2019, 38(20): 70-76. GUO Tianqi, XIA Yimei, WANG Fuhua, et al. An improved collaborative optimization algorithm of ship structures' static and dynamic subject based on the mixed and dynamic penalty function[J]. Journal of Vibration and Shock, 2019, 38(20): 70-76. |
| [7] |
朱俊侠, 吴嘉蒙, 蔡诗剑, 等. 基于拓扑优化方法的船体支柱布局优化设计[J]. 海洋工程, 2019, 37(4): 70-79. ZHU Junxia, WU Jiameng, CAI Shijian, et al. Optimal arrangement of ship pillars based on topology optimization method[J]. The Ocean Engineering, 2019, 37(4): 70-79. |
| [8] |
苏绍娟, 张祥, 王天霖, 等. 多工况应力约束下多用途船货舱结构优化[J]. 船海工程, 2020, 49(1): 52-55+60. SU Shaojuan, ZHANG Xiang, WANG Tianlin, et al. Optimization of Cargo Hold Structure of a Multipurpose Ship under Multiple Load Conditions Stress Constraints[J]. Ship & Ocean Engineering, 2020, 49(1): 52-55+60. DOI:10.3963/j.issn.1671-7953.2020.01.013 |
| [9] |
马寒阳, 董金善. 冲击载荷作用下LNG燃料罐防波板参数多目标优化[J]. 船舶力学, 2021, 25(9): 1251-1259. MA Hanyang, DONG Jinshan. Multi-objective optimization of baffle structural parameters in LNG fuel tank under impact load[J]. Journal of Ship Mechanics, 2021, 25(9): 1251-1259. DOI:10.3969/j.issn.1007-7294.2021.09.013 |
 2022, Vol. 44
2022, Vol. 44
