海上运动的大型平台结构物,通常需要抵抗较为恶劣的海况。在恶劣的风浪条件下,航行或静止阶段,会产生剧烈的摇荡。在运动过程中,波浪会对船体外壳产生猛烈的抨击,特别是具有大外飘以及舷侧船体的结构物,如半潜平台、半潜船、大件货物运输船,这种抨击会更为剧烈,从而对结构产生较大的载荷,影响结构安全[1-2]。在设计阶段对平台可能遭受到的波浪抨击压力进行计算分析,针对船体外飘壳体或其突出结构进行加强设计,保证其具有足够的结构强度,是大型外飘型平台设计的关键点之一。
在设计初期,如果能对浮体的运动进行提前预报,根据预报的结果,可对实船在风浪中的操控提供有效的方案。通常可以进行理论分析或者数值仿真的手段,估算船体受到的抨击压力结果。文献[2]通过理论研究的方式利用动量定理得出了经典的砰击压力计算公式。文献[3]计算船体在规则波或者不规则波下的波浪抨击压力;文献[4]基于理论计算的方法,得到波浪载荷短期预报的极值计算的经验公式,分析了半潜平台在砰击载荷作用下产生的影响。本文从规范校核的角度[5-6]出发,结合规范的校核要求,利用Hydrostar软件开展基于线性频域理论下的波浪砰击短期预报研究,利用理论与经验结合的方式,采用直接计算的方式为结构校核提供砰击载荷结果。
1 计算方法 1.1 耐波性计算方法本文耐波性理论计算采用法国BV船级社成熟的水动力学商用软件HydroStar,该软件基于三维线性频域势流理论进行计算[7]。
频域理论认为波浪与平台(船体)间相互作用已持续了相当长时间,入射波的初始扰动和平台初始摇荡的瞬态影响已消失,流场运动已经达到稳态程度。如入射波为简谐的,则浮体的运动亦是简谐的,两者仅存在相位差,平台运动频率为波浪频率,进而可在频域内求解稳态场。频域方法的优点是计算速度快,计算结果也令人满意,在工程上应用非常广泛[7]。
本文考虑粘性对横摇的影响,计算模型考虑了线性和二次横摇阻尼系数,采用经典ITH半经验公式进行横摇阻尼计算。此外,为计算方便,本文计算未考虑减摇鳍等减摇设备的影响。
1.2 抨击压力计算方法考虑ABS和DNV的规范要求。ABS规范中,可通过选取典型计算点在对应海况下运动响应得到响应的垂向速度幅值,抨击压力PS可以通过下式计算得到:
| $ {P_S} = \frac{1}{2}k{C_S}{C_{3D}}{C_P}{v^n}。$ | (1) |
其中:
| $ {C_p} = \frac{{2.5}}{{{{(\tan \beta )}^{1.1}}}} 。$ | (2) |
式中:
| $ v = \sqrt {2\sigma _v^2\left( {{{\rm{In}}} \frac{t}{{{T_2}}}} \right)} 。$ | (3) |
式中:
最具有大外飘型甲板特点的船型即航母、半潜平台以及大件货物运输船,其中以航母的外飘特点最为突出。为了研究此类结构特点,选取突出较为明显的航母线型进行研究。根据国外部分公开航母数据[10-13]的外形特征,初步设计了具有大外飘型甲板的线型。
在线型设计时,将左右舷设计为不对称型(下文中称为线型1),可简化分析工作。通过不对称线型的左右舷计算,研究抨击压力受突出物的延伸程度的影响。

|
图 1 线型1模型 Fig. 1 Model of hull 1 |
由于本线型为参考设计,根据常见的半潜运输船以及大件货物甲板运输船型,初步确定本船的部分参数以及计算工况。
总体尺度如表1所示。
|
|
表 1 线型1总体尺度 Tab.1 Main dimension of test platform |
为分析不同吃水下抨击压力的影响,计算初步选取2个吃水作为计算输入,如表2所示。
|
|
表 2 线型1计算工况 Tab.2 Calculation condition of test platform |
|
图 2 计算船体平均湿表面网格模型 Fig. 2 Wet surface mesh of hull |
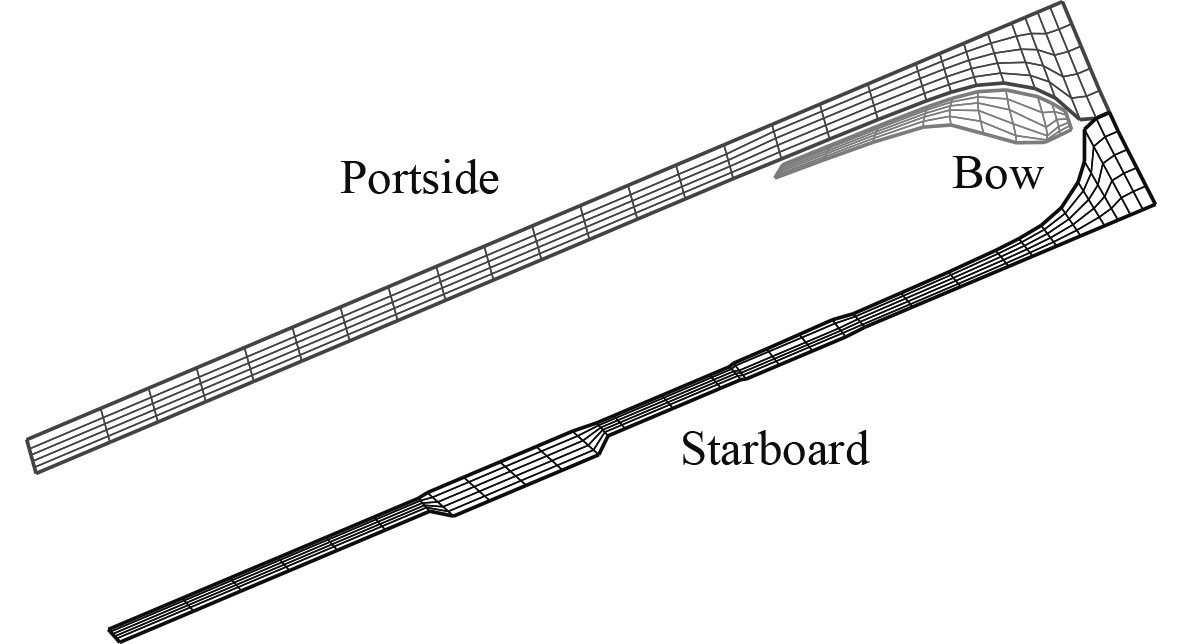
|
图 3 抨击压力计算区域坐标点示意图 Fig. 3 Positions of wave impact loading pressure |
由于本线型为参考设计,根据目前业内常见的海工作业船工作海况确定计算海况条件。通常海工作业船可在比较恶劣的海况下工作,部分可在6级以上的海况下进行作业。
为提供恶劣海况下结构设计参考,计算海况初步确定为7级海况,海况资料如表3所示。
|
|
表 3 海况资料 Tab.3 Sea state information |
针对海况资料选择不同的波浪谱进行分析。
不规则波浪谱采用两参数Bretschneider谱,方向扩散函数采用cos平方形式。海浪谱密度公式如下:
| $ {S_h}(\omega ) = \frac{{5\omega _p^4H_s^2}}{{16{\omega ^5}}}\exp \left[ { - 1.25{{\left( {{{{\omega _p}} \mathord{\left/ {\vphantom {{{\omega _p}} \omega }} \right. } \omega }} \right)}^4}} \right]。$ | (4) |
其中:
方向扩散函数采用cos平方形式,公式如下:
| $ \varPhi (\mu ) = \frac{2}{\text{π} }{\cos ^2}\mu \;\;\;\;\;\; \mu \in \left[ - \frac{{\text{π} } }{2},\frac{{\text{π} } }{2}\right] 。$ | (5) |
式中:
线型1抨击压力计算所选取环境条件如表4所示。
|
|
表 4 抨击压力计算海况列表 Tab.4 Sea state of wave impact loading pressure calculation |
初步估算时,左舷舷侧突出物底部选取162个计算点,右舷舷侧突出物底部选取198个计算点。主船体首部左舷外飘选取60个计算点,图3为计算区域坐标点示意图。
根据耐波性计算得到上述选点的垂向相对运动速度最大值和抨击压力最大值,如图5和图6所示。

|
图 4 垂向相对运动速度最大值包络云图 Fig. 4 Maximum envelope cloud of vertical relative velocity |
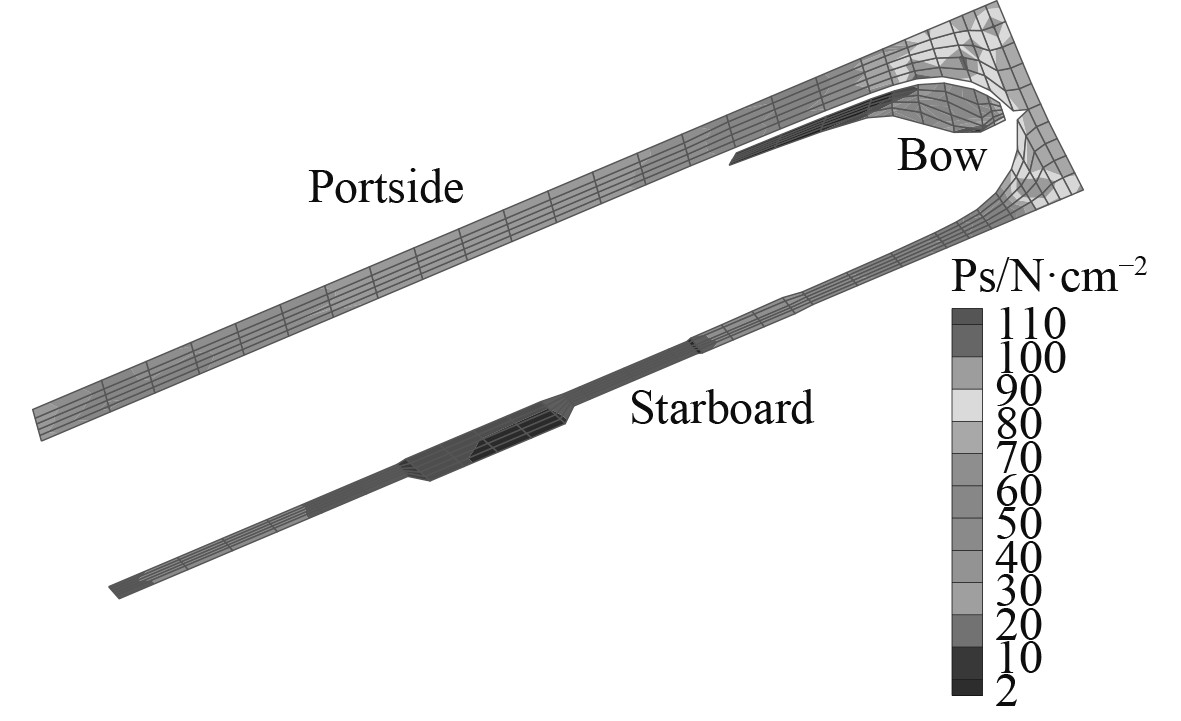
|
图 5 抨击压力最大值包络云图 Fig. 5 Maximum envelope cloud of wave impact loading pressure |
选取计算值较大的点(抨击压力>85 N/cm2)进行后续的计算分析,主要集中于首部首垂线以前,计算点如表5所示。
|
|
表 5 首部左舷舷侧突出物底部抨击压力计算坐标点列表 Tab.5 Wave impact loading pressure calculation points of fore side protrusion at portside |
鉴于计算数据较多,以所选位置中抨击压力最大者进行列表比较。
4.1 T=5 m的计算结果|
|
表 6 T=5 m各航速下抨击压力最大值 Tab.6 T=5 m wave impact loading pressure at different velocity |
根据上述结果可得到不同航速不同吃水在有义波高为7m时,船体外板(或外飘结构)受到的抨击压力分布情况,其结论如下:
1))吃水越大,产生抨击压力较大的区域会逐渐向上偏移;
2))吃水越大,在同样的航速下抨击压力的最大值会有所减小;
(3) 抨击压力会随航速的增加而逐渐增大;
4) 出现抨击压力最大的位置大多位于首部,并且为顺浪航行时,即浪向角0/360°时;
5) 出现抨击压力最大的波浪周期约为13 s,可以通过规避恶劣海况的方式,减小抨击压力的风险;
6)抨击压力最大值出现位置,在不同吃水下、不同航速下有所不同。吃水较小时,航速变化时,最大值出现位置较为固定;而吃水较大时,由于不同位置的垂向速度分布不均匀,导致最大值出现位置有所不同;
7)从结果可以看出,抨击压力最大值出现位置基本处于水线上6~7 m处,为1个有义波高的位置,可通过型线优化调整外飘结构的位置,适当增大外飘结构的高度,来有效减小抨击风险。
为了更直观反映外飘型浮体所受抨击压力随航速以及吃水的变化,对上述结果进行整理,做出抨击压力随航速变化分析曲线。如图6所示。
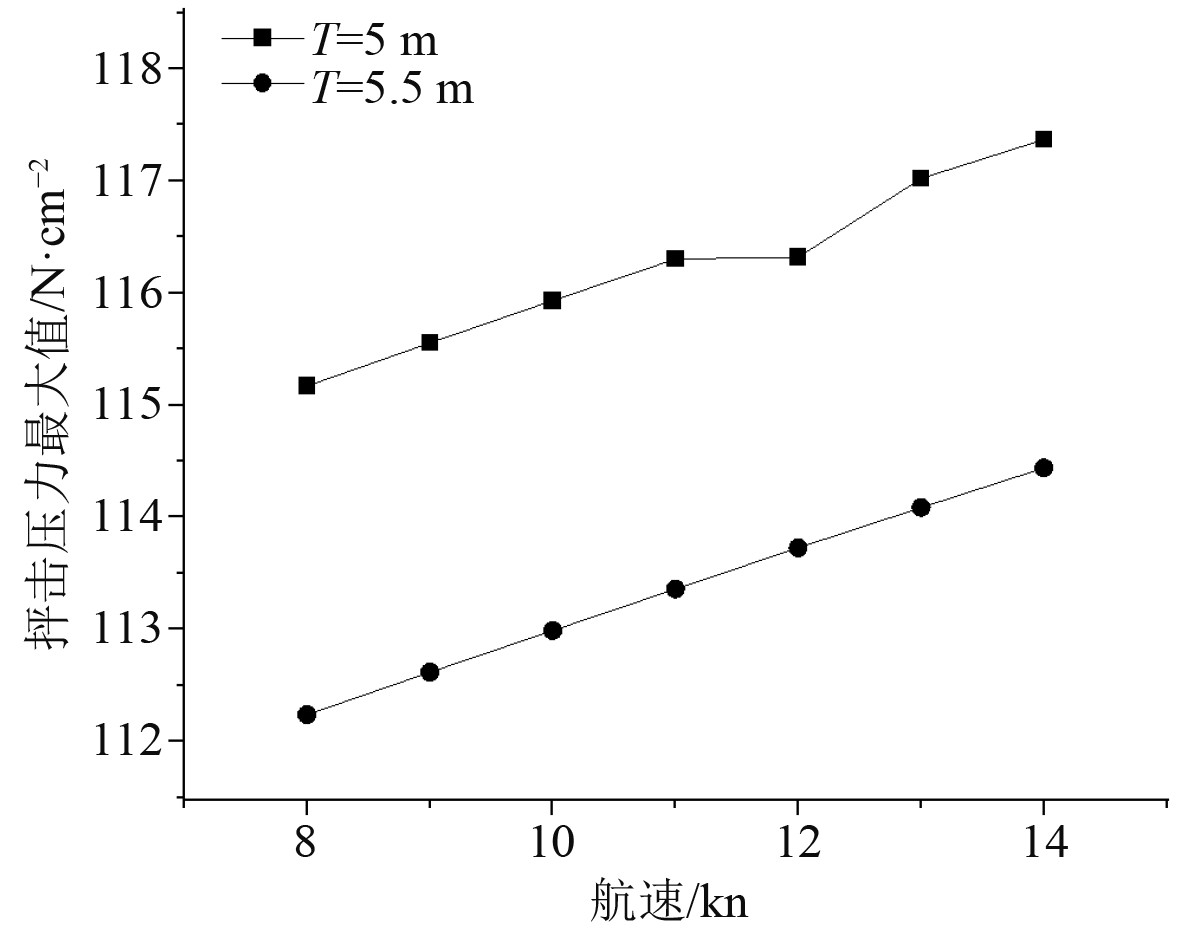
|
图 6 不同吃水抨击压力最大值随航速分布 Fig. 6 Wave impact loading pressure distribution with speed at different draught |
本文参考ABS及DNV规范要求,从理论计算方法入手,针对大型具有外飘甲板的线型在高海况下运动,根据不同海况下的海浪统计结果,计算不规则波作用下,船体或突出结构受到波浪作用产生的抨击压力的短期预报结果。分析不同吃水,不同航速下,产生最大抨击压力的位置,以此得到不同航速与不同吃水对产生抨击压力位置的一般规律。
在进行上述计算分析后,得到抨击压力与航速、吃水以及线型的关系。
得到以下结论:
1)同一型船,在航速相同的条件下,吃水越小,水上结构受到的抨击压力越小,
2)针对相同海况,相同吃水,抨击压力会随航速增加而增大;
3)可以通过选择有利海况以及有利首向角的方式,尽量避免顺浪航行,降低抨击压力的风险;
4)针对同样的线型而言,抨击压力最大值通常位于首部,可通过采用线型优化的方式,通过降低外飘结构高度,避免抨击压力带来的风险。
本文采用的计算方法为理论计算方法,在方案初期即可通过计算的方式横向比较不同线型,不同航速下,大型外飘结构在高海况下可能遇到抨击压力的风险,在设计 初期为结构设计提供较为可靠的设计依据。
| [1] |
戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M]. 北京: 国防工业出版社, 2007.
|
| [2] |
汪雪良, 杨鹏, 顾学康, 等. 船体结构砰击总体载荷理论研究综述[J]. 中国舰船研究, 2015, 10(1): 7-18. WANG Xueliang, YANG Peng, GU Xuekang, et al. Review of the theoretical investigation of slamming of global wave loads on ship structures[J]. Chinese Journal of Ship Research, 2015, 10(1): 7-18. DOI:10.3969/j.issn.1673-3185.2015.01.002 |
| [3] |
李远鹤, 罗广恩, 王一镜, 等. 规则波作用下船首外飘波浪砰击载荷研究[J]. 舰船科学技术, 2021, 43(21): 39-46+51. LI Yuan-he, LUO Guang-en, WANG Yi-jing, et al. Research on the slamming load of the outgoing wave of ship bow under the action of regular wave[J]. SHIP SCIENCE AND TECHNOLOGY, 2021, 43(21): 39-46+51. |
| [4] |
贺俊松, 彭文科. 船舶波浪载荷短期极值的经验公式[J]. 中国造船, 2011, 52(2): 74-86. HE Junsong, PENG Wenke. Empirical formula for ships’ short-term wave induced loads[J]. Shipbuilding of China, 2011, 52(2): 74-86. DOI:10.3969/j.issn.1000-4882.2011.02.010 |
| [5] |
高畅, 田其磊, 李红涛. 半潜式平台波浪砰击分析与应用[J]. 中国海洋平台, 2021, 36(6): 50-53+78. GAO Chang, TIAN Qilei, LI Hongtao. Wave slamming analysis and application for semi-submersible platform[J]. China Offshore Platform, 2021, 36(6): 50-53+78. DOI:10.12226/j.issn.1001-4500.2021.06.20210610 |
| [6] |
高畅, 田其磊, 初同林. 波浪砰击分析在半潜式平台的应用[J]. 石油工程建设, 2020, 46(S1): 18-21. GAO Chang, TIAN Qilei, CHU Tonglin. Application of wave impact analysis for column stabilized unit[J]. petroleum Engineering Construstion, 2020, 46(S1): 18-21. |
| [7] |
李积德. 船舶耐波性[M]. 哈尔滨: 哈尔滨工程大学出版社, 2007.
|
| [8] |
ABS, Guide for slamming loads and strength assessment for vessels[S] 2013.
|
| [9] |
DNV-RP-C205, Environmental conditions and environmental loads[S]. DNV, 2010.
|
| [10] |
孙守鹏. “尼米兹”级航母战斗群的发展过程①[J]. 舰载武器, 2003(11): 4-8+93. |
| [11] |
孙守鹏. “尼米兹”级航母战斗群的发展过程(2)[J]. 舰载武器, 2003(12): 4-8+93. |
| [12] |
佚名. 美国海军尼米兹级航母[J]. 军事记者, 2014(4): 76. |
| [13] |
施征. 苏联85型常规航母发展计划[J]. 舰载武器, 2010(4): 56-62. |
| [14] |
MALENICA S, CHEN Xiao-Bo. On then irregular frequencies appearing in wave diffraction-radiation solutions[J]. International Journal of Offshore and Polar Engineering, 1998. Vol 8 : 110–114
|
| [15] |
李积德, 《船舶耐波性》, 哈尔滨工程大学出版社, 2007-10.
|
| [16] |
方钟圣. 西北太平洋波浪统计集[M]. 北京: 国防工业出版社, 1996.
|
| [17] |
李远鹤. 艏外飘型船舶波浪砰击载荷预报[D]. 镇江: 江苏科技大学, 2020. Li Yuanhe, Research on Bow Flare Slamming Load Forecast Induced by Wave[D] Zhenjiang: Jiangsu University of Science and Technology, 2020. |
 2022, Vol. 44
2022, Vol. 44
