2. 福建省船舶与海洋工程重点实验室,福建 厦门 361021
2. Key Laboratory of Ship and Ocean Engineering of Fujian province, Xiamen 361021, China
电动船舶因为采用电动机推进,在航行过程中不产生废气和含油废水,符合国家的环保要求。电力驱动在小型船舶上就有更高的可行性,小型船舶发动机功率更小,容易搭配合适的电动机和电池组。电动船舶受电池容量的限制,比传统燃油船更需要进行阻力优化来提升续航里程,所以需要对小型电动船舶阻力优化进行研究。
调整纵倾可以改变船舶水线以下船体与水作用面的几何形状,进而可以改变阻力大小。在纵倾优化方面,Hafizul Islam等[1]通过开源原件OpenFOAM对KCS船不同航速时不同纵倾角对应的阻力值进行了数值计算,对纵倾带来的阻力变化给出了具体的数值,并提出航速不同时阻力最小纵倾角也不同。Xujian Lv等[2]提出一种船舶阻力的预报方法,通过Wigley船和HUST船进行了验证,并计算了不同配平状态下的阻力。宋磊等[3]计算了180000 DWT散货船不同纵倾的阻力,并通过实验进行了验证,得出改变纵倾角可以改变船舶阻力,证明数值计算的准确性。童骏等[4]计算了LPG船不同吃水、不同速度、不同纵倾角的阻力,并有试验验证,证明CFD方法计算船舶纵倾值是可行的。随着计算机技术的迅速发展以及CFD方法在船舶领域的广泛应用,为纵倾优化提供了更多的计算方法[5-7]。
本文以1艘5.2 m小型船舶为例进行纵倾优化,对实船进行静态推力试验获取电机功率与推力的关系。再进行实船动态航行试验获得稳定航速下的电机功率,得到功率与航速的关系。将船舶稳定航行时电机功率,代入到功率与推力关系式中求得该航速下的螺旋桨推力,从而建立起推力与航速关系。因船舶较小且航速较低,所以螺旋桨推力近似等于船舶阻力。以该船的稳定航速进行CFD阻力性能计算,将阻力仿真计算数据与试验获得的阻力数据进行对比,证明数值计算方法可靠。通过CFD方法计算相同航速、相同吃水条件下各个纵倾角对应的阻力,获得该航速和吃水条件下阻力最小的纵倾角。通过纵倾优化调整压载位置减小航行阻力,具有实际应用价值,对其他小型船舶也具有借鉴意义。
1 实船试验与船体阻力数值计算 1.1 实船试验选取1艘电动铝合金船作为研究对象,搭载锂电池和电动舷外挂机。
|
|
表 1 船舶主尺度 Tab.1 Ship main dimension |
1) 试验方案
实船试验选在一处水面平静的人工湖进行,试验方案如下:
① 通过2条长度相同绳索绳索,一段系在船上,另一端系在拉力计S型传感器上。
② 将S型传感器系在缆桩上,并保证2条绳索加上拉力计S型传感器的长度相同。
③ 测量绳索与码头的夹角。
④ 将船系泊在2个码头之间的水域内,将船牵引至2条绳索拉直状态。
⑤ 启动舷外机,逐渐增大油门,待拉力计示数稳定时记录下推力与功率的关系。

|
图 1 试验方案示意图 Fig. 1 Experimental scheme Figure |
2) 试验结果
试验中电机最大功率达到了9 603 W,最大推力对应的功率是8 720 W
测得绳索与码头夹角
| $ {{F}}_{{T}}={{F}}_{{y}},$ | (1) |
| $ {{F}}_{{y}}{=F\mathrm{cos}(\theta)},$ | (2) |
电机功率P与螺旋桨推力
|
|
表 2 功率与推力关系 Tab.2 Relationship between power and thrust |

|
图 2 功率与推力曲线 Fig. 2 Power and thrust curve |
对功率与推力关系进行回归分析得到三次多项式回归方程:
| $ {P=-}{{10}}^{{-9}}{{{F}}_{{T}}}^{{3}}{+9\times}{{10}}^{{-6}}{{{F}}_{{T}}}^{{2}}{+0.140\;9}{{F}}_{{T}}{+154.17}。$ | (3) |
回归方程的
在风速较小的天气条件下航行,记录下船舶达到稳定航速时电动机达到的功率。采用的电机可以采集速度和功率信息。
|
|
表 3 航速与对应功率 Tab.3 Speed and corresponding power |
CFD技术的基本原理是满足质量守恒、能量守恒和动量守恒[8]。船舶外流场计算中,流体是作为不可压缩的流体的水,故可以不考虑能量守恒方程。
1) 连续性方程
当计算满足连续性方程时可以保证计算满足质量守恒方程,即单位时间内流入控制体和流出控制体的流体质量相等。将水看作不可压缩流体,则密度恒定,连续性方程微分形式可简化为如下式:
| $ \frac{{\partial \rho}}{{\partial t}}+\frac{{\partial}\left({\rho}{{u}}_{{x}}\right)}{{\partial x}}+\frac{{\partial}\left({\rho}{{u}}_{{y}}\right)}{{\partial y}}+\frac{{\partial}\left({\rho}{{u}}_{{z}}\right)}{{\partial z}}{=0}。$ | (4) |
式中:
2) Navier-Stokes方程
N-S(Navier-Stokes)方程描述的是控制体所受外力的总和等于控制体中流体动量对时间的变化率,表达式如下:
| $ \frac{\partial{{u}}_{{x}}}{{\partial t}}+{{u}}_{{x}}\frac{\partial{{u}}_{{x}}}{{\partial x}}+{{u}}_{{y}}\frac{{\partial}{{u}}_{{x}}}{{\partial y}}+ {{u}}_{{z}}\frac{\partial{{u}}_{{x}}}{\partial{z}}{=X-}\frac{{1}}{\rho}\frac{{\partial \rho}}{{\partial x}}{+ν}{{\nabla}}^{{2}}{{u}}_{{x}}, $ | (5) |
| $ \frac{{\partial}{{u}}_{{y}}}{{\partial\textit{t}}}+{{u}}_{{x}}\frac{{\partial}{{u}}_{{y}}}{{\partial{x}}}+{{u}}_{{y}}\frac{{\partial}{{u}}_{{y}}}{{\partial{y}}}+{{u}}_{{z}}\frac{{\partial}{{u}}_{{y}}}{{\partial{z}}}{=X-}\frac{\text{1}}{{ρ}}\frac{{\partial{ρ}}}{{\partial{y}}}\text{+ν}{{\nabla}}^{\text{2}}{{u}}_{{y}},$ | (6) |
| $ \frac{{\partial}{{u}}_{{z}}}{{\partial{t}}}+{{u}}_{{x}}\frac{{\partial}{{u}}_{{z}}}{{\partial{x}}}+{{u}}_{{y}}\frac{{\partial}{{u}}_{{z}}}{{\partial{y}}}+{{u}}_{{z}}\frac{{\partial}{{u}}_{{z}}}{{\partial{z}}}{=X-}\frac{\text{1}}{{ρ}}\frac{{\partial{ρ}}}{{\partial{z}}}\text{+ν}{\nabla}^{\text{2}}{{u}}_{{x}}。$ | (7) |
3) 雷诺平均方程
湍流是流体中普遍存在的现象,船舶外流场中也不例外。湍流运动复杂,具有很大的随机性,CFD很难对其进行准确模拟。可以从工程的角度对湍流造成的平均运动情况进行模拟,通过雷诺平均方程将控制方程进行时均化处理进行模拟,方程表达式如下:
| $ \frac{\text{∂ρ}}{\text{∂\textit{t}}}\text+\frac{\text{∂}}{\text{∂\textit{xi}}}\left(\text{ρ}{\textit{u}}_{\textit{i}}\right)\text{=0},$ | (8) |
| $ \begin{split} &\frac{{\partial}}{{\partial{t}}}\left(\text{ρ}{{u}}_{{i}}\right)+\frac{{\partial}}{{\partial}{{x}}_{{j}}}\left(\text{ρ}{{u}}_{{i}}{{u}}_{{j}}\right)=-\frac{{\partial{p}}}{{\partial{xi}}}+\\ &\frac{{\partial}}{{\partial}}\left[{μ} \left(\frac{{\partial}{{u}}_{{i}}}{{\partial}{{x}}_{{j}}}+\frac{{\partial}{{u}}_{{j}}}{{\partial}{{x}}_{{i}}}- \frac{\text{2}}{\text{3}}{{\delta}}_{{ij}}\frac{{\partial}{{u}}_{{l}}}{{\partial}{{x}}_{{l}}}\right) - \text{ρ}\stackrel-{{{u}}_{{i}}^{'}{{u}}_{{j}}^{'}}\right]。\end{split} $ | (9) |
式中:t为时间;μ为流体的动力粘性系数;ρ为流体密度;
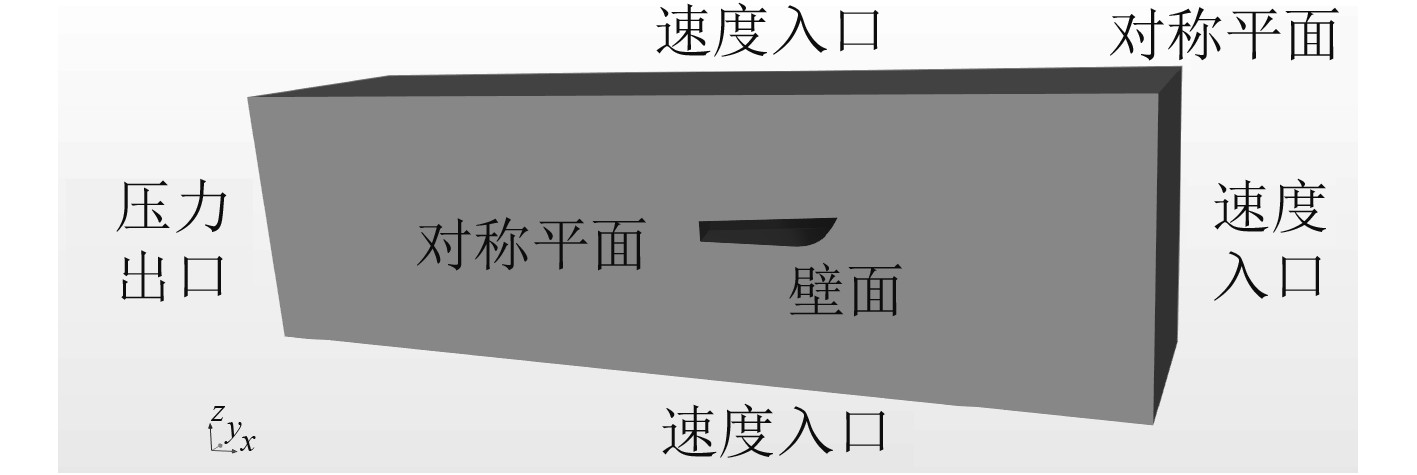
根据实船设计数据通过三维建模软件进行建模,如图3 所示。采用商业CFD软件STAR-CCM+进行流体力学仿真。建立尺寸7Lpp×2Lpp×2Lpp的流体计算域,流域入口设置在船首上游2Lpp处,出口设置在船尾下游4Lpp处,因为船舶航行中以船舶中纵剖面为界左右两侧流场对称,为减少网格数量取半个流场作为研究对象。流体计算域设置情况如图4所示。

|
图 3 三维模型 Fig. 3 Three-dimensional model |
|
图 4 计算域边界设置 Fig. 4 Calculation domain boundary setting |
本研究使用商业CFD(计算流体力学)软件STAR-CCM+对该船进行流体力学数值计算,计算该船稳定航速时航行的阻力。
1.2.3 网格划分采用切割体网格对流场进行网格划分,在船体表面设置棱柱层网格作为边界层,边界层数为6,网格增长率取1.3,边界层总厚度为0.02 m。网格最大尺寸为1 m最小尺寸为0.05 m,体网格增长率和面网格增长率均设置为慢。船体表面较为复杂,为提高仿真精度对船体表面网格进行加密,大小为0.05 m。为了更准确地捕捉到自由液面的开尔文波,对自由液面处网格进行了加密,网格大小为0.1 m。网格总数175万个,网格划分效果如图5网格划分情况。

|
图 5 网格划分情况 Fig. 5 Grid division |
采用三维粘性不可压RANS方程进行求解。物理模型选择隐式非定常、欧拉多相流、VOF方法和k-ε湍流模型,并加入VOF波和重力模型。欧拉相设置为水和空气,VOF波模型选择静水,速度设置为X方向−4.1 m/s吃水设置0.3 m。物理模型初始条件体积分数设置为复合,各个相的体积分数选择场函数,在函数库中选择对应的函数,速度入口和压力出口的体积分数设置与初始条件相同。最大内部迭代10,取消勾选最大步数。时间步长度为0.025 s,最大内部迭代步数10,最大物理时间130 s。
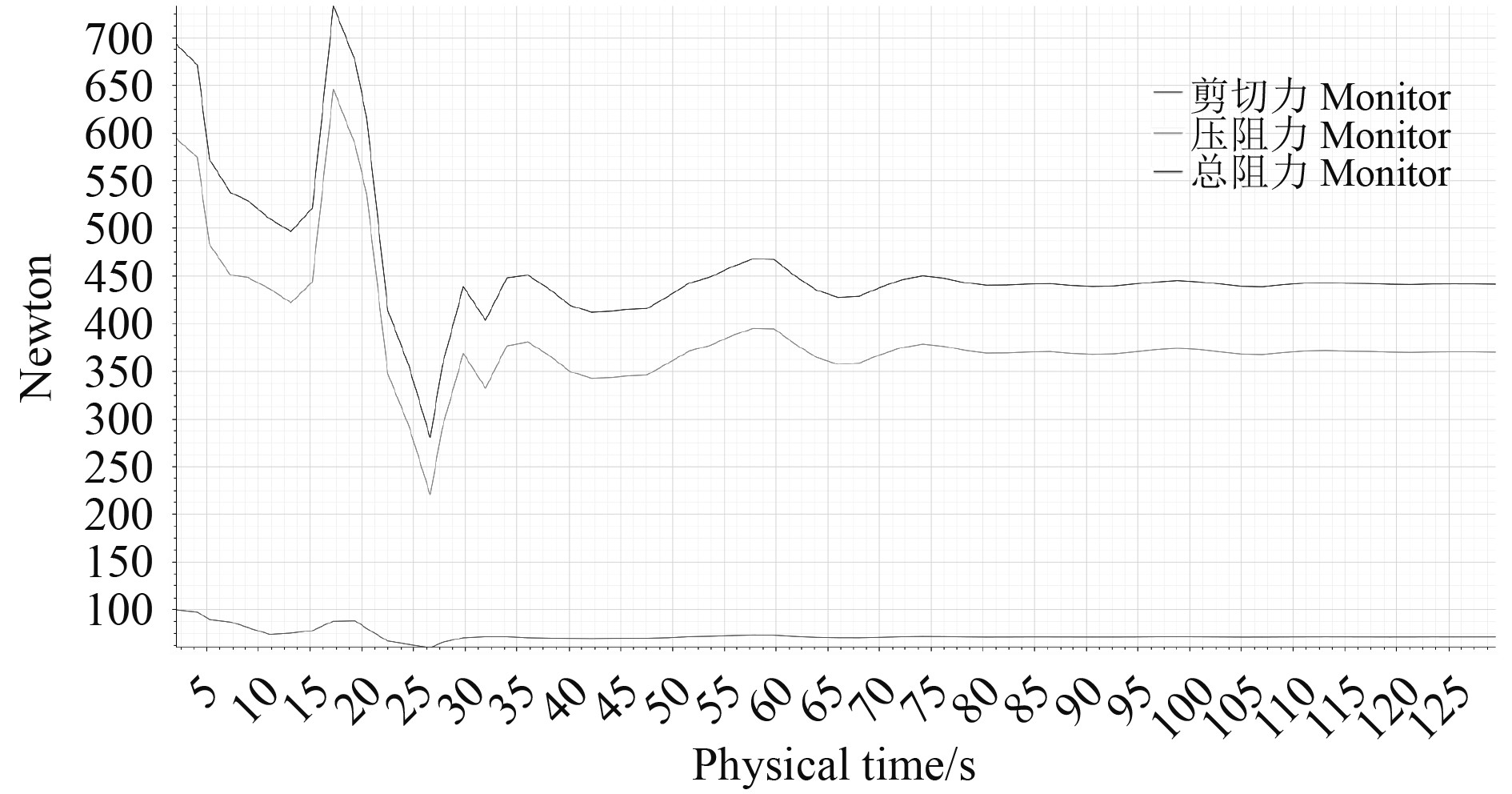
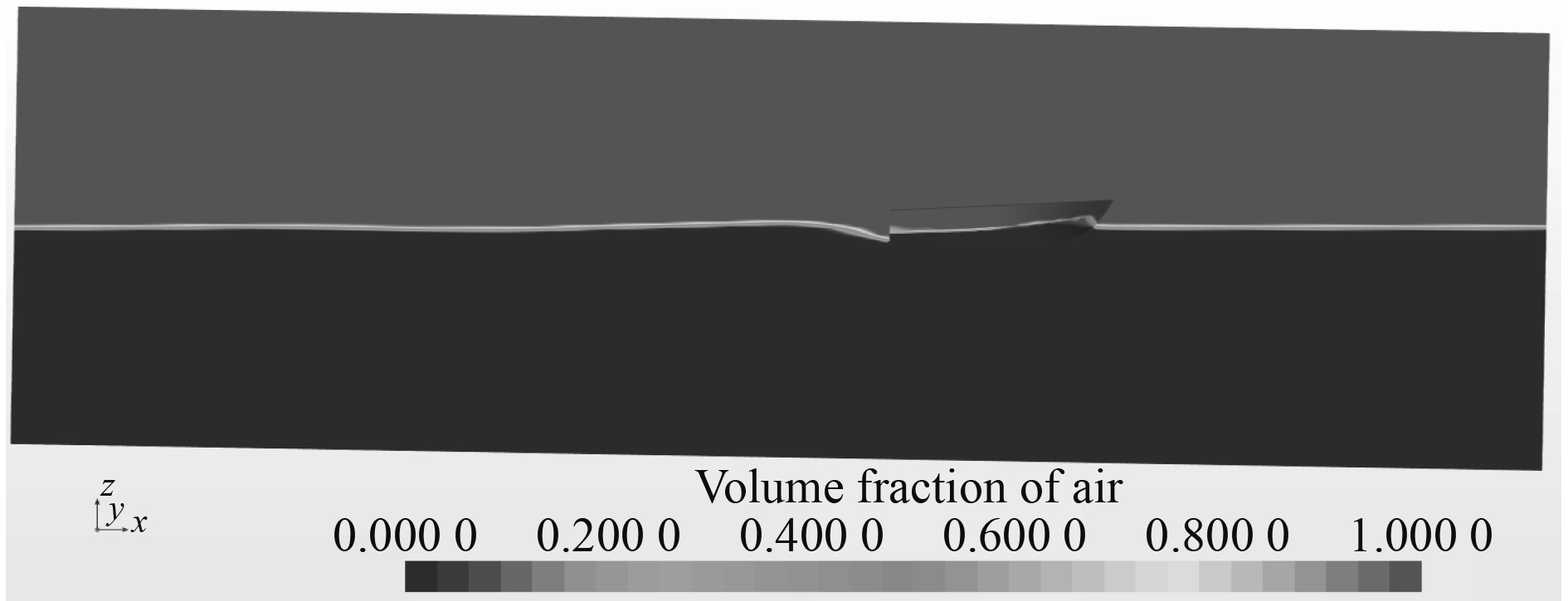
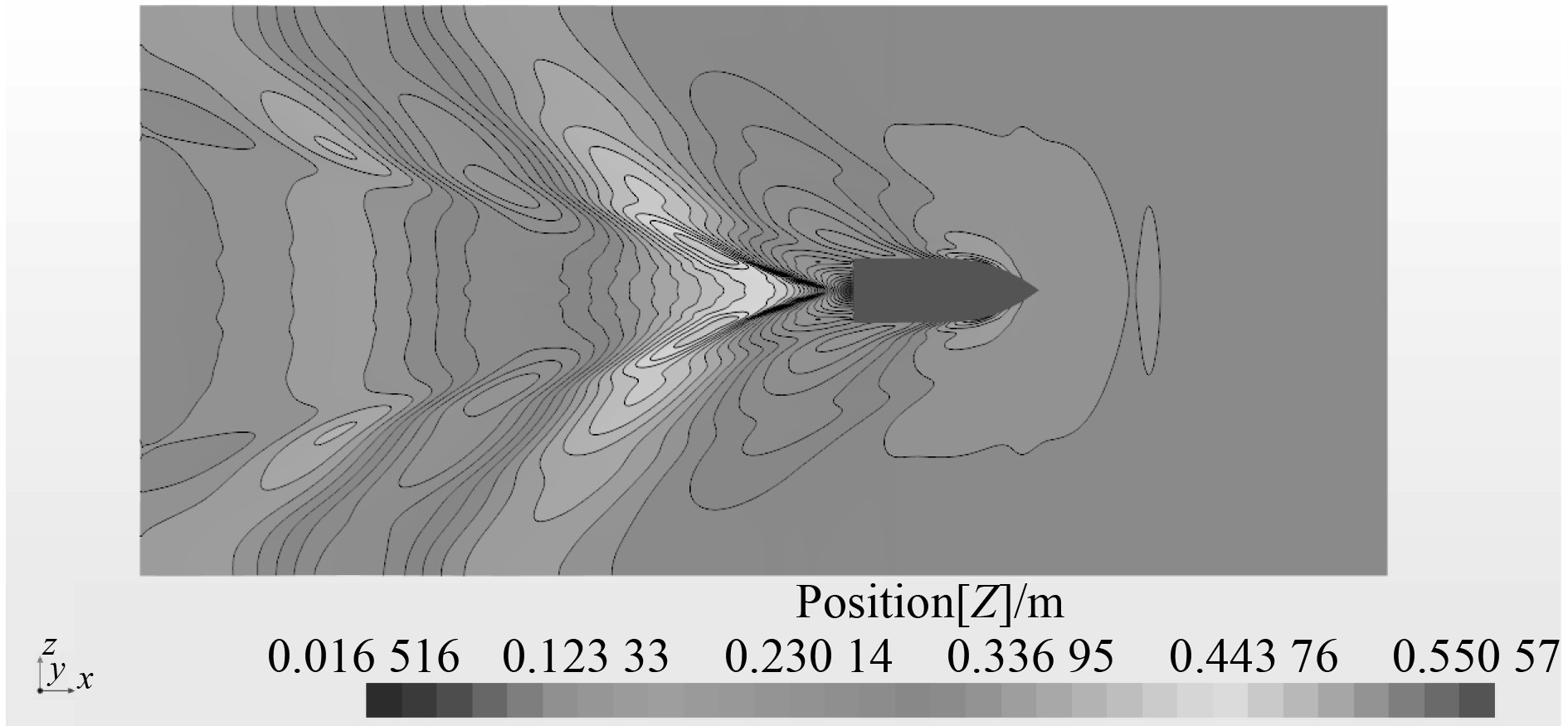
1.2.5 CFD计算结果通过CFD计算航速为8.1 kn时阻力波动情况如图6 所示。可以看出,在75 s后阻力值趋于收敛。通过图7自由液面位置可以直观查看船舶纵倾状况以及自由液面与船的位置关系,通过图8波形图可以看出与船舶航行时产生的实际波形较为接近。
|
图 6 阻力值 Fig. 6 Resistance value |
|
图 7 自由液面位置 Fig. 7 Free surface position |
|
图 8 波形图 Fig. 8 Wave making picture |
通过静态推力实验获得功率与推力的关系,通过实船动态航行试验获得航速与功率的关系,将每个航速对应的功率代入功率与推力关系式(3)中求得每个航速下螺旋桨推力。因为船体较小并且航速较低,8 kn时傅汝德数为0.58,因此螺旋桨推力近似等于船舶受到的阻力。
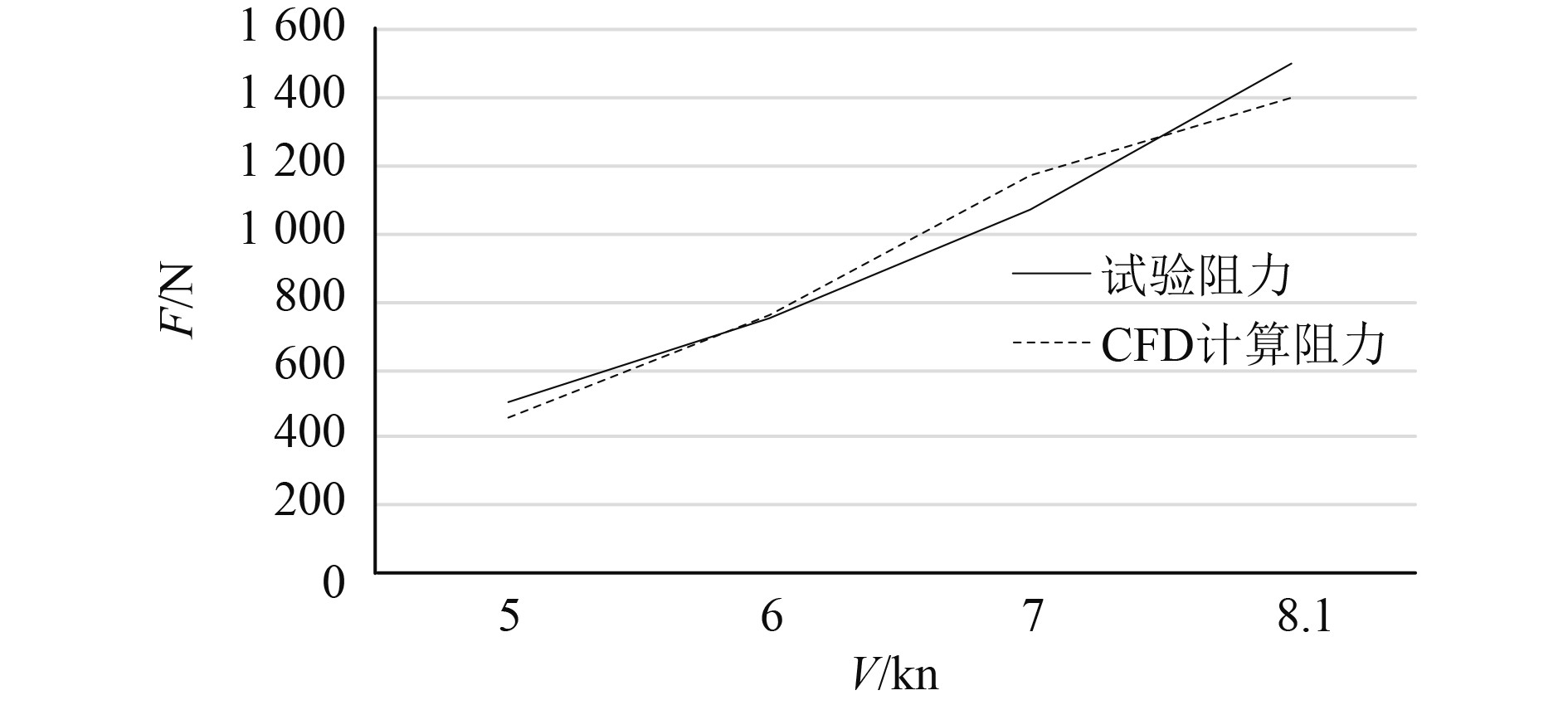
实船航行中最大功率达到了9999 W,最大航速达到了8.1 kn。选取5 kn,6 kn,7 kn和8.1 kn这4个稳定状态下的航速与CFD计算数据进行对比,可以看出阻力变化趋势试验结果与CFD计算结果大体一致,如图9所示。试验阻力与CFD计算阻力最大误差为9.19%,差额来源有实船推力试验误差、船体表面伴流和螺旋桨带来的阻力增额以及建模误差等。从计算结果看,使用STAR-CCM+进行上述设置计算船舶阻力比较可靠,计算准确度可以用来进行纵倾优化。
|
图 9 阻力对比曲线 Fig. 9 Resistance comparison curve |
根据静止时船舶的吃水线与龙骨和尾封板的交点,通过三维建模软件计算出设计载况时船舶重心纵向位置为距船尾2.2 m。在设计载况下,通过水平尺量出船舶静止时甲板与水平面夹角为0.55°,以下纵倾角均为甲板与水平面夹角。
在DFBI选项调整船舶重心位置实现不同的纵倾角。DFBI可以保持船舶总重量不变,改变重心位置来改变纵倾值,可以保证船舶排水体积不变,实现等容倾斜,较直接设定纵倾值有更高的计算精度。纵倾角以尾倾为正,首倾为负表示。重量设为700 kg分别计算8 kn时重心纵向位置x1=1.8 m,x2=2 m,x3=2.1 m,x4=2.16 m,x5=2.2 m,x6=2.4 m这6个浮态的阻力。
|
|
表 4 阻力试验结果 Tab.4 Resistance experiment results |
|
|
表 5 阻力计算结果 Tab.5 Resistance calculation results |
船舶在排水不变时,改变纵倾会导致船舶水线以下几何形状发生改变,进一步影响到船体的湿表面积、水线面形状、船首来流和船尾去流。这些变化必然导致船舶兴波阻力、摩擦阻力和粘压阻力的变化,总阻力也会随着相应改变。
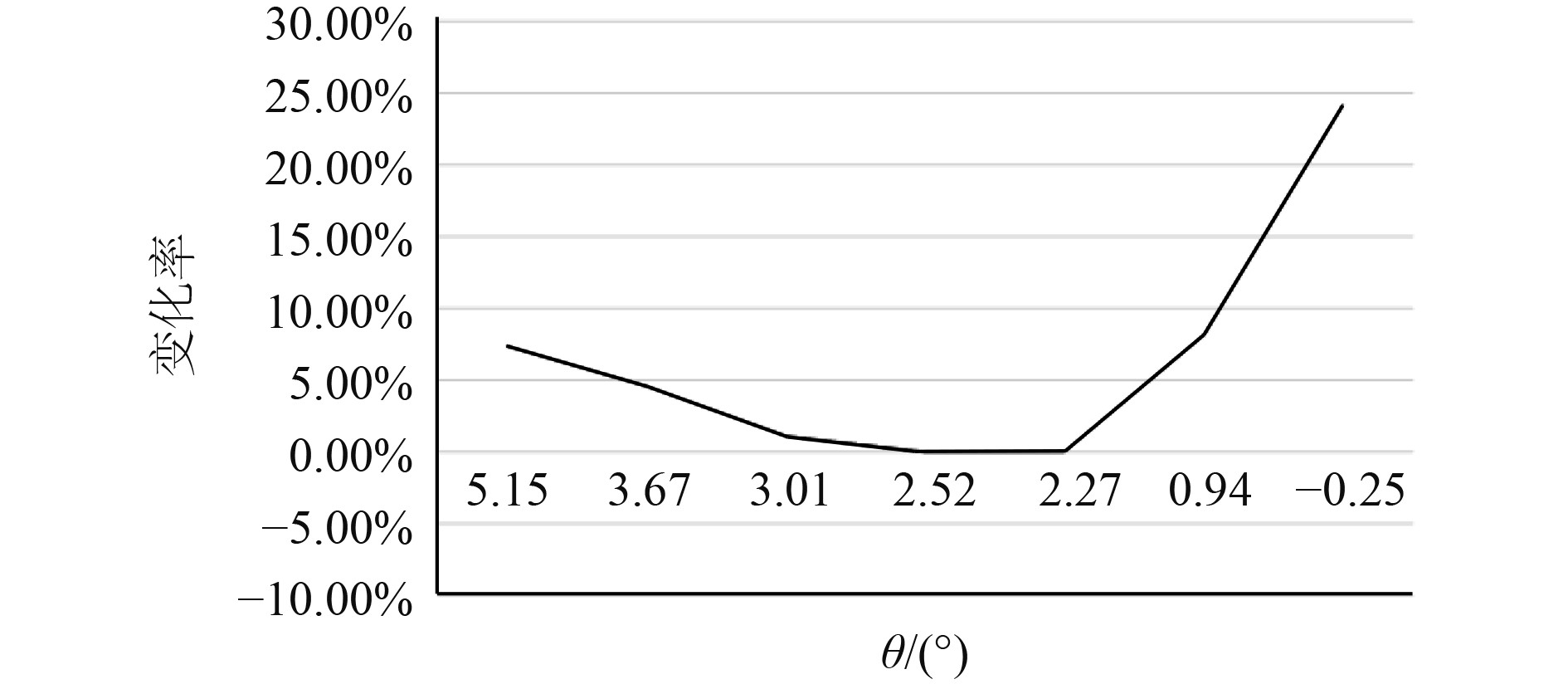
从图10和图11CFD计算结果可以看出,阻力最小的纵倾值是θ=2.52°时阻力最小,对应的重心位置是θ=2.16 m。增大尾倾或者增大首倾都会导致船舶阻力的增加,首倾阻力增加更为明显。阻力最大值比最小值高出了24.15%。随着首倾或者尾倾的增加,压阻力变化更为明显,在总阻力中的占比逐渐上升。

|
图 10 阻力曲线图 Fig. 10 Resistance curve diagram |
|
图 11 阻力变化 Fig. 11 changes in resistance |
本文利用改变纵倾值可以改变船舶阻力的原理,对一艘小型船舶进行螺旋桨静态推力试验和实船航行试验。建立小型船舶的3D模型,通过CFD软件STAR-CCM+对模型进行CFD仿真计算,并与实船航行试验结果进行对比。对不同纵倾时的阻力值进行仿真计算,根据结果可以得到以下结论:
1)使用商业CFD软件STAR-CCM+中
2)阻力大小受纵倾影响较大,阻力最小值的纵倾角为尾倾2.52°,最大值纵倾角首倾0.25°,阻力最大值较最小值高出24.15%;
3)电动船舶在实际应用中通过改变纵倾的方式减小船舶航行阻力,在不改变航速、吃水的情况下达到最小阻力,进而延长续航里程,减少充电次数。
| [1] |
ISLAM H, SOARES CG. Effect of trim on container ship resistance at different ship speeds and drafts[J]. Ocean Engineering, 2019, 183. |
| [2] |
LV X, WU X, SUN J, et al. Trim optimization of ship by a potential-based panel method[J]. Advances in Mechanical Engineering, 2013, 2013. |
| [3] |
宋磊, 涂海文, 谢文雄, 等. 散货船纵倾阻力研究[J]. 舰船科学技术, 2016, 38(23): 48-52. |
| [4] |
童骏, 涂海文, 孙江龙. 船舶纵倾优化减阻数值模拟研究[J]. 中国海洋大学学报(自然科学版), 2018, 48(7): 123-129. |
| [5] |
郭春雨, 王恋舟, 赵庆新, 等. 一种计及姿态变化的船舶阻力预报方法[J]. 船舶工程, 2015, 37(1): 31-34. |
| [6] |
杨其雷, 朱鹏飞, 艾万政. 集装箱船纵倾优化数值模拟[J]. 舰船科学技术, 2021, 43(7): 60-63. |
| [7] |
王英第, 陈彦臻, 周伟健, 等. 船体阻力数值预报研究及黏性流场计算[J]. 舰船科学技术, 2020, 42(1): 17-22. DOI:10.3404/j.issn.1672-7649.2020.01.004 |
| [8] |
周帅. 最小阻力参数化船型自动优化设计方法研究[D]. 大连: 大连理工大学, 2019.
|
 2022, Vol. 44
2022, Vol. 44
