在过去的几十年间,欠驱动水面船舶在海洋工程领域发挥了重要作用,如海洋运输、海洋勘探、海上救援和海图绘制[1]。在这些应用中,欠驱动船舶的航迹控制对于完成任务的质量与效率至关重要[2]。此外,航迹控制问题是欠驱动船舶实现自主控制需要解决的基本问题,因此得到了国内外学者的广泛关注[3]。航迹控制作为典型的欠驱动船舶运动控制问题,具体是通过控制律的设计使船舶沿期望航迹运动。船舶航行过程中一般考虑纵荡、横荡及首摇3个自由度的运动,且各自由度之间存在非线性耦合。此外,船舶操纵条件,船舶运动特性与所面对的海洋环境扰动均存在不确定性。这些非线性与不确定性因素都给船舶航迹控制带来了严峻的挑战[4]。因此,研究欠驱动船舶的航迹控制具有重要意义。
任何水面船舶都会受到模型不确定性、未知参数、风、波浪、载荷和洋流变化引起的内外干扰的影响[5]。因此,在船舶运动控制中需要设计高可靠性控制系统。沈智鹏等[6]针对三自由度船舶航迹跟踪控制问题,考虑环境扰动信息未知,设计了一种带非线性观测器的动态面自适应输出反馈控制方法。该方法利用模型坐标变换设计非线性观测器估计船舶速度,采用自适应律估计海洋环境干扰界值,避免了参数漂移。李世正等[7]研究了船舶航迹控制方法,基于神经网络算法实现航迹跟踪控制,并进行了Matlab仿真验证。Xu等[8]针对非线性船舶轨迹跟踪控制问题,基于Backstepping和Lyapunov稳定性理论,设计了虚拟控制变量和Lyapunov函数。提出一种非线性轨迹跟踪控制算法,并基于该算法和LOS制导律,设计了一种非线性轨迹跟踪控制器。Liu等[9]考虑执行器饱和度和状态约束等问题设计了滑模控制器,有效提升了系统鲁棒性。Wang等[10]针对船舶易受风等干扰影响航向偏差的问题,提出一种模糊自适应迭代滑模控制方法。通过将估计功能引入模糊控制方案,在线估计和调整设计参数,可以提升控制速度,有效地消除了抖振现象。
以上研究都是基于船舶模型的控制器设计方法,相比于其他控制对象,船舶建模工作尤其复杂,精准的模型信息带来精确的控制效果,但船舶是一种强非线性、强耦合性的控制对象,对这类模型复杂、模型参数不确定的系统,精确的模型信息难以获得。实际研究中需要通过缩比模型进行大量水池试验,工作量繁重,且模型的准确性难以保证。此外,由于环境变化、船体生长附着物等情况导致船舶模型信息失效,基于模型的控制方法将不再适用。另一方面,无模型自适应控制是一种在线的数据驱动控制方法,其主要思想是,在每个工作点处,任何一般非线性系统都可以被等效为一个动态线性化数据模型。然后,利用系统输入输出数据估计伪雅克比参数。MFAC已经在很多领域得到应用,如过程控制[11-12]、能量控制[13]等。因此,研究一种不需要任何模型信息的船舶航迹控制方法具有重要意义。
1 船舶三自由度运动数学模型船舶在海上航行时应考虑沿
| $ \begin{split} & m(\dot u - rv) = {X_H} + {X_P} + {X_R} + {X_W},\\ & m(\dot v + ru) = {Y_H} + {Y_P} + {Y_R} + {Y_W} ,\\ & {I_{ZZ}}\dot r = {N_H} + {N_P} + {N_R} + {N_W} 。\end{split} $ | (1) |
其中:
欠驱动船舶的执行机构只提供了前向推力和转首力矩,对于侧向移动无法控制。对于此类控制对象,采用视线导航法可以实现精准的航迹控制。通过前视向量及前视点的设定,将船舶路径控制中的位置控制转化为航向控制[15]。
2.1 直线视线导航法在进行直线段航迹控制时,首先设置起始点
在大地坐标系下,首先确定当前时刻船舶的位置为
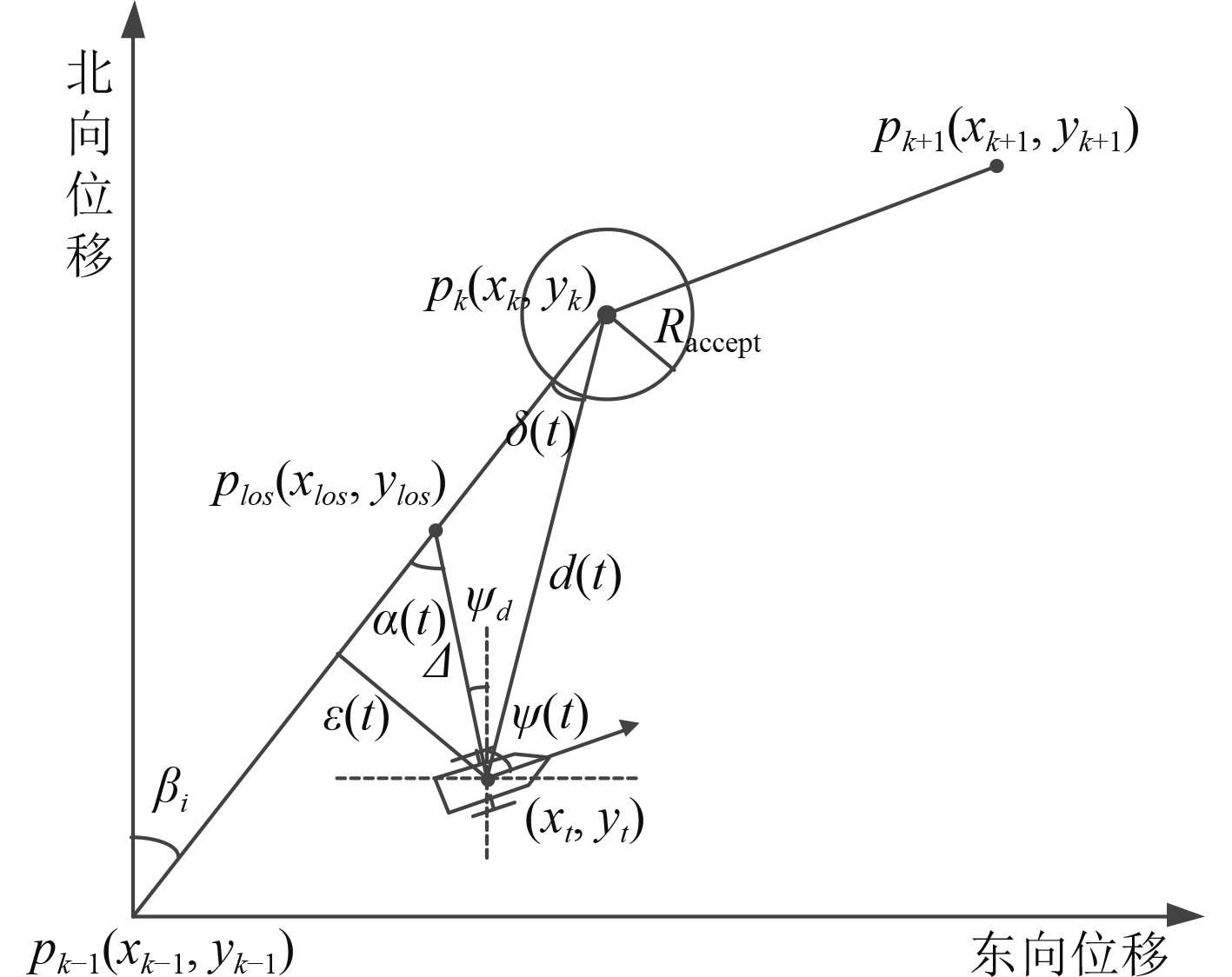
|
图 1 直线段视线导航法原理 Fig. 1 Schematic diagram of straight LOS |
通过几何关系分析可以得到:
| $ {\beta _i} = {\rm{arctan}}(({y_k} - {y_{k - 1}})/({x_k} - {x_{k - 1}})) ,$ | (2) |
| $ \delta (t) = {\beta _i} - {\rm{arctan}}(({y_k} - {y_t})/({x_k} - {x_t})) ,$ | (3) |
| $ d(t) = \sqrt {{{({x_k} - {x_t})}^2} + {{({y_k} - {y_t})}^2}} ,$ | (4) |
| $ \varepsilon (t) = d(t){\text{sin}}(\delta (t)) 。$ | (5) |
当船舶距离目标点较远时
| $ \alpha (t) = \left\{ \begin{gathered} {\text{arcsin}}(\varepsilon (t)/\Delta ),{\text{ }}\left| {\varepsilon (t)} \right| \leqslant \Delta ,\\ \text{π} /2 \cdot {\text{sign}}(\varepsilon (t)),{\text{ }}\left| {\varepsilon (t)} \right| > \Delta 。\\ \end{gathered} \right. $ | (6) |
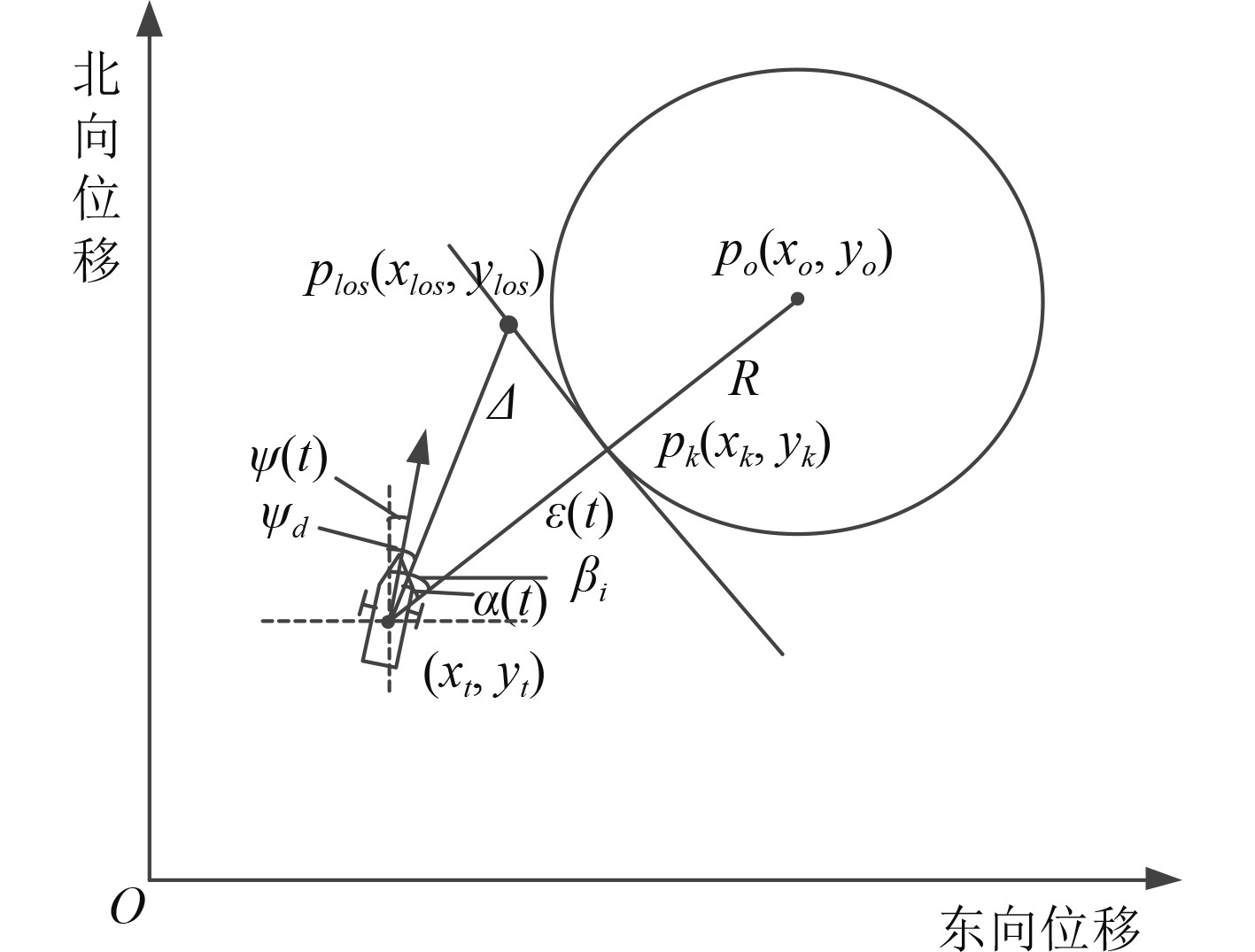
|
图 2 圆弧视线导航法 Fig. 2 Schematic diagram of circle LOS |
通过几何分析可得:
| $ {\beta _i} = \arctan (({y_0} - {y_t})/({x_0} - {x_t})) ,$ | (7) |
| $ \varepsilon (t) = \sqrt {{{({x_0} - {x_t})}^2} + {{({y_0} - {y_t})}^2}} - R ,$ | (8) |
| $ {{\varPsi }_d} = {\beta _i} - \alpha (t)。$ | (9) |
传统的动态线性化方法基本都是从数学角度进行分析,采用任意的线性、非线性函数动态线性化方法。这些线性化方法有的对模型精度要求很高,有的会在不同程度上忽略非线性函数在线性化过程中对控制器设计或系统分析的影响。
对于一般的多输入多输出离散时间非线性系统可以描述如下:
| $ \begin{split} q(k + 1) = &f(q(k),q(k - 1),{\mkern 1mu} \cdots ,{\mkern 1mu} q(k - {n_q}),{\mkern 1mu} u(k), \\ &u(k - 1),{\mkern 1mu} \cdots ,{\mkern 1mu} u(k - {n_u}))。\end{split} $ | (10) |
其中:
假设1 除有限时间点外,
假设2 除有限时间点外,系统(3)满足广义李普希兹条件,即对任意
| $ \left| {q({k_1} + 1) - q({k_2} + 1)} \right| \leqslant b\left| {u({k_1}) - u({k_2})} \right| 。$ | (11) |
其中
从实际角度出发,上述对控制对象的假设是合理的。假设1是对控制系统中一般非线性系统的常见约束。假设2从能量角度解释为系统有界输入对应有界输出。
定理1 对满足假设1与假设2的非线性系统式(10)当
| $ \Delta q(k + 1) = {\phi _c}(k)\Delta u(k) ,$ | (12) |
并且在所有的时刻k,
由定理1可知,当非线性系统式(10)满足假设1与假设2,并且对于所有时刻k有
| $ q(k + 1) = q(k) + {\phi _c}(k)\Delta u(k) 。$ | (13) |
其中,
考虑如下估计准则函数:
| $ \begin{split} J({\phi _c}(k)) = &{\left| {q(k) - q(k - 1) - {\phi _c}(k)\Delta u(k - 1)} \right|^2} + \\ &\mu {\left| {{\phi _c}(k) - {{\hat \phi }_c}(k - 1)} \right|^2} ,\end{split} $ | (14) |
其中,
| $ \begin{split} {{\hat \phi }_c}(k) = &{{\hat \phi }_c}(k - 1) + \\ &\frac{{\eta \Delta u(k - 1)}}{{\mu + \Delta u{{(k - 1)}^2}}}(\Delta q(k) - {{\hat \phi }_c}(k - 1)\Delta u(k - 1)) 。\end{split} $ | (15) |
其中,
考虑如下控制输入准则函数
| $ J(u(k)) = {\left\| {{q^*}(k + 1) - q(k + 1)} \right\|^2} + \lambda {\left\| {u(k) - u(k - 1)} \right\|^2} ,$ | (16) |
其中
| $ u(k) = u(k - 1) + \frac{{\rho {\phi _c}(k)}}{{\lambda + {{\left| {{\phi _c}(k)} \right|}^2}}}({q^*}(k + 1) - q(k)) ,$ | (17) |
其中,
以上是一般形式的基于CFDL的MFAC方法,直接用于船舶航迹控制存在误差收敛速度慢、控制误差大且不断波动的问题,因此引入PD控制可以得到改进的无模型自适应PD控制算法为:
| $ \begin{split} u(k) = &u(k - 1) + \frac{{\rho {\phi _c}(k)}}{{\lambda + {{\left| {{\phi _c}(k)} \right|}^2}}}({k_p}({q^*}(k + 1) - q(k))+ \\ & {k_d}(\Delta {q^*}(k + 1) - \Delta q(k)))。\end{split} $ | (18) |
其中:
通过计算机仿真来验证本文所提控制系统的有效性,仿真软件采用Matlab R2017b,PC机处理器为Intel Corei3-7100,3.9 GHz处理器,操作系统为Windows7旗舰版。
由于PID控制方法在工业制造中具有广泛的应用,原理简单、实用性强且不需要任何模型信息。因此,为验证本文所提无模型控制方法的有效性,将不需要任何模型信息的船舶无模型控制方法增量式PID控制加入对比研究。
仿真中控制船舶跟踪圆形轨迹为圆心位于
从图3可以看出,2种控制方法都可以实现轨迹跟踪控制,但是PID的控制效果较差,在整个跟踪过程中存在明显误差,相比之下无模型自适应PD控制几乎与参考轨迹相重合,控制精度更高,证明了本文所提控制算法无模型自适应PD控制的有效性。为进一步分析控制效果,绘制三自由度航迹控制响应曲线如图4所示。
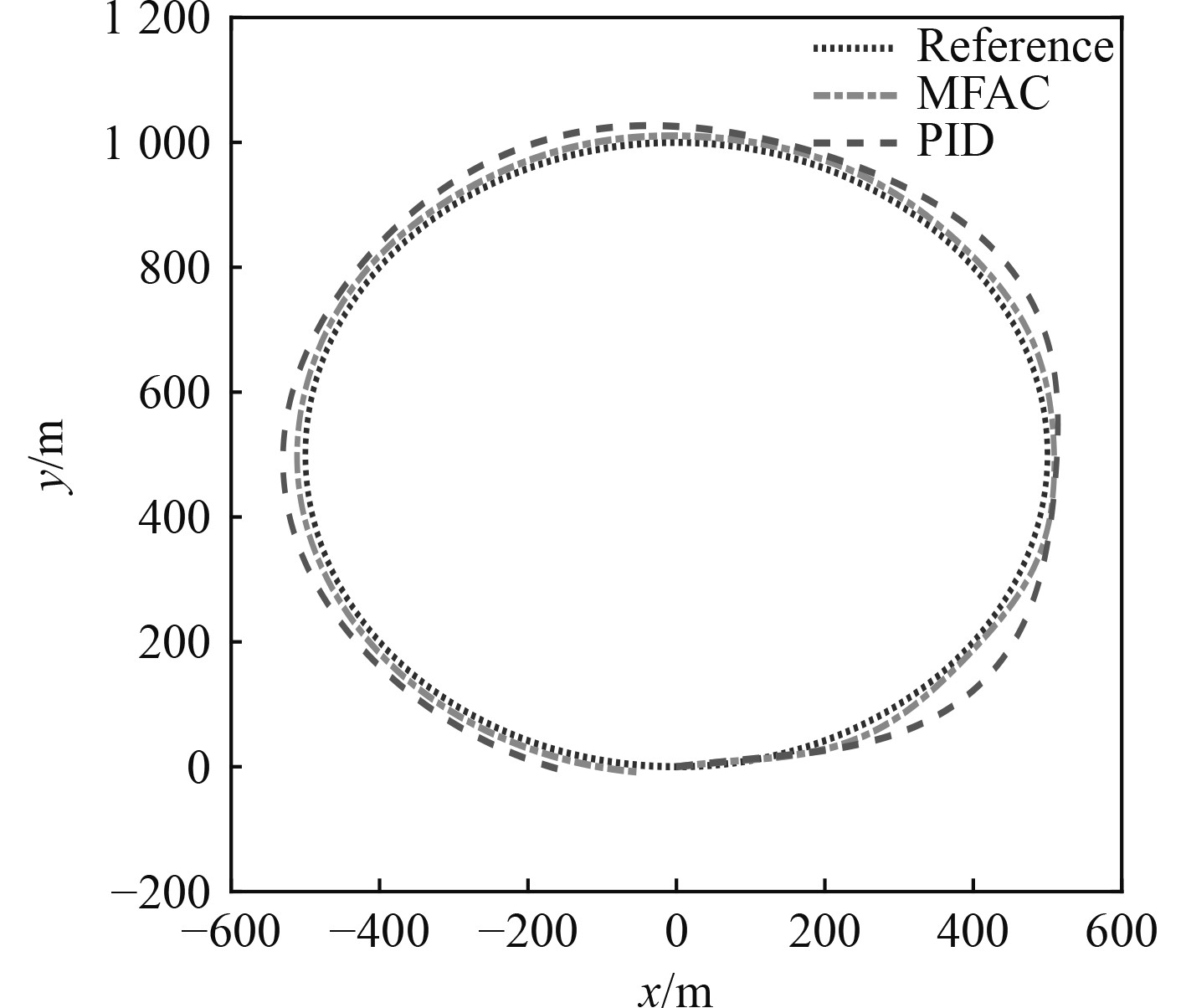
|
图 3 船舶航迹控制响应曲线 Fig. 3 Tracking control response curve |
从图4可以看出,在3个控制自由度上,无模型自适应PD控制的效果都明显好于PID,此外PID控制误差存在波动现象,收敛速度较慢。
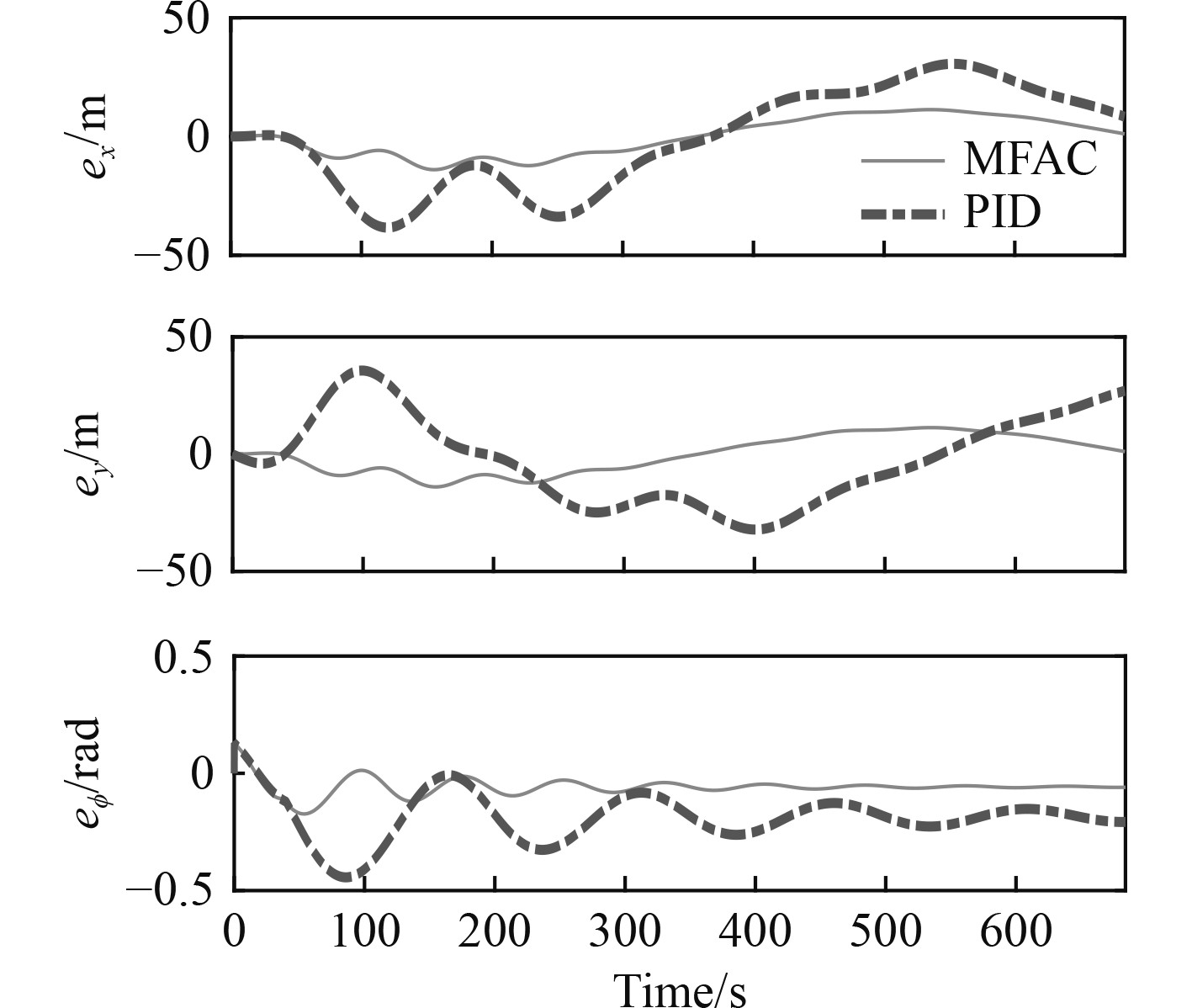
|
图 4 各自由度航迹控制误差 Fig. 4 Tracking control error of each degree |
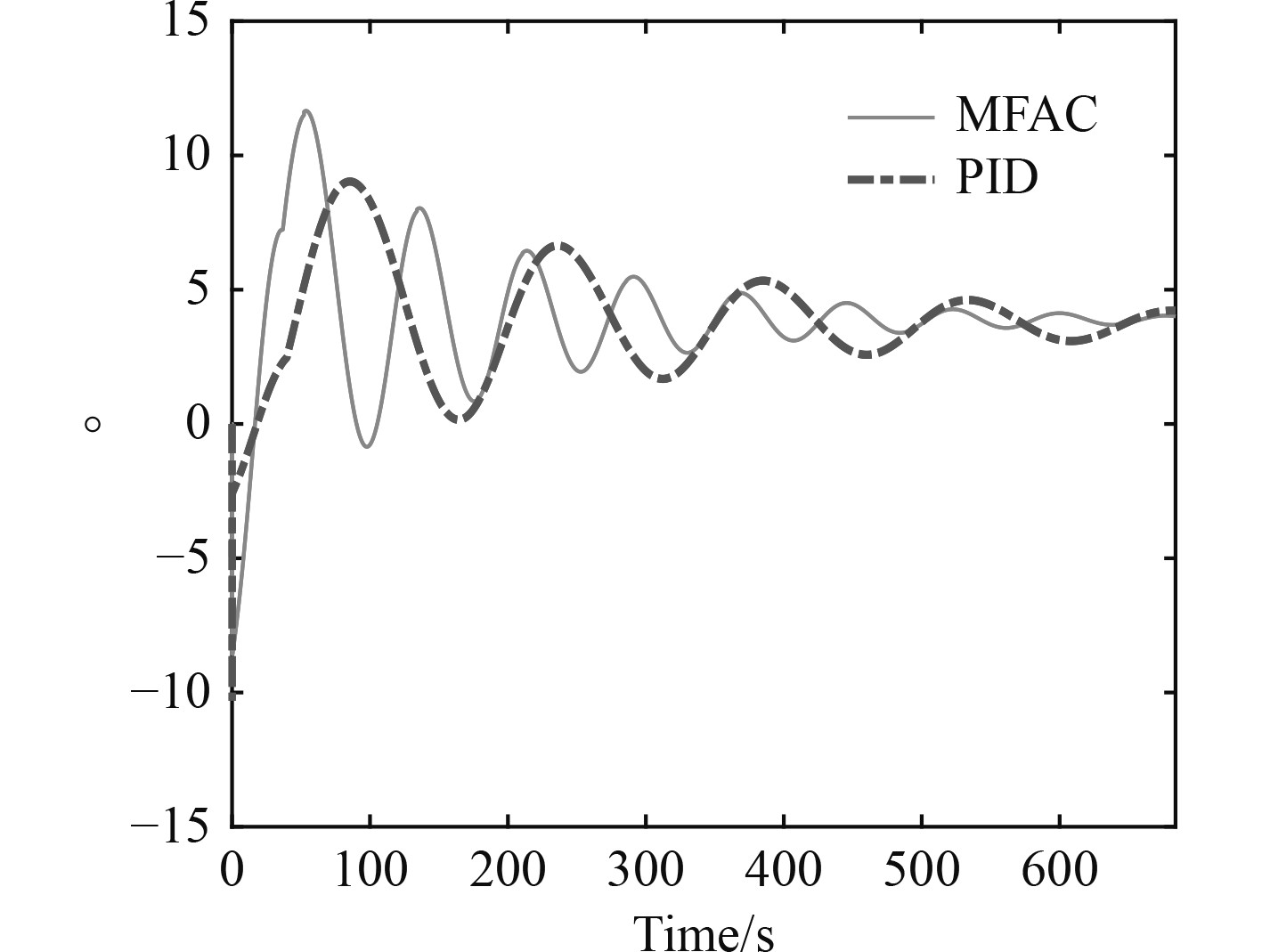
|
图 5 舵角输出曲线 Fig. 5 Rudder angle curve |
为定量分析算法的控制性能,定义控制器的性能评价指标:绝对误差积分(integral absolute error, IAE),其中
| $ \begin{split} & IA{E_{xy}}[m] = \int_0^T {(\left| {{e_x}} \right| + \left| {{e_y}} \right|)} {\rm{d}}t ,\\ & IA{E_\varphi }[rad] = \int_0^T {\left| {{e_\varphi }} \right|} {\rm{d}}t。\end{split} $ | (19) |
从表1可以看出,在整个航迹控制过程中,无论是xy方向的误差累积,还是
|
|
表 1 绝对误差积分 Tab.1 The integral of absolute error |
本文研究欠驱动船舶在模型信息无法获取情况下的航迹控制问题,基于紧格式动态线性化方法进行无模型自适应控制器设计。针对一般形式的无模型自适应控制器在船舶航迹控制中存在的误差收敛速度慢、控制精度低的问题,设计了改进的无模型自适应PD控制方法。为了验证本文所提控制方法的有效性将传统的无模型控制方法增量式PID加入对比研究,仿真结果表明,相比于增量式PID控制方法,本文所设计的MFAC-PD具有更高的控制精度,且调参简单使用方便。
| [1] |
HASSANI V, SORENSE A J, PASCOAL A M, et al. Robust dynamic positioning of offshore vessels using mixed-μsynthesis modeling, design, and practice[J]. Ocean Engineering, 2017, 129: 389-400. DOI:10.1016/j.oceaneng.2016.10.041 |
| [2] |
HU C, WANG R, YAN F, et al. Robust composite nonlinear feedback path-following control for under-actuated surface vessels with desired heading amendment[J]. IEEE Transactions on Industrial Electronics. 2016, 63(10): 6386-6394.
|
| [3] |
TANG Y, XING X. KARIMI H R, et al. Tracking control of networked multi-agent systems under new characterizations of impulses and its applications in robotic systems[J]. IEEE Transactions on Industrial Electronics, 2016, 62(2): 1299-1307. |
| [4] |
邱峰, 李伟, 宁君. 基于线性自抗扰控制的船舶航迹积分滑模控制器[J]. 上海海事大学学报, 2017, 38(3): 12-17+51. QIU F, LI W, NING J. Integral sliding-mode controller of ship tracking based on linear active disturbance rejection control[J]. Journal of Shanghai Maritime University, 2017, 38(3): 12-17+51. |
| [5] |
QU Y, XIAO B, FU Z, et al. Trajectory exponential tracking control of unmanned surface ships with external disturbance and system uncertainties[J]. ISA Transactions, 2018, 78: 47-55. DOI:10.1016/j.isatra.2017.12.020 |
| [6] |
沈智鹏, 毕艳楠, 郭坦坦, 等. 带非线性观测器的欠驱动船舶自适应动态面输出反馈轨迹跟踪控制[J]. 系统工程与电子技术, 2009, 17(6): 710-717. SHEN Z, BI Y, GUO T, et al. SINS/GPS integrated navigation method based on vector tracking[J]. Journal of Chinese Inertial Technology, 2009, 17(6): 710-717. |
| [7] |
李世正, 崔兰超. 非线性控制技术在船舶航迹跟踪控制器开发的应用[J]. 舰船科学技术, 2019, 41(04): 31-33. |
| [8] |
XU Hai-jun, LIU Yong, ZHA Zhi-qiang. Design of trajectory tracking control of under-actuated ship[C]//20174th International Conference on Information, Cybernetics and Computational Social System(ICCSS). 2017.
|
| [9] |
LIU Y, NIU Y, ZOU Y, et al. Adaptive sliding mode reliable control for switched systems with actuator degradation[J]. IET Control Theory and applications, 2015, 9(8): 1197-1204. |
| [10] |
WANG R, SHEN Z. Fuzzy adaptive iterative sliding mode control for sail-assisted ship trajectory tracking[C]//2017 4th International Conference on Information, Cybernetics and Computational Social Systems(ICCSS), IEEE, 2017: 105–110.
|
| [11] |
贾欣乐, 杨盐生. 船舶运动数学模型-机理建模与辨识建模[M]. 大连: 连海事大学出版社, 1997.
|
| [12] |
HOU Z, ZHU Y, Controller-dynamic-linearization-based model free adaptive control for discrete-time nonlinear systems[J]. IEEE Transactions on Industrial Informatics, 2013, 9(4): 2301–2309.
|
| [13] |
WENG Y, GAO X. Data-driven robust output tracking control for gas collector pressure system of coke ovens[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5): 4187–4198.
|
| [14] |
ZHANG H, ZHOU J, SUN Q, et al, Data-driven control for interlinked AC/DC microgrids via model-free adaptive control and dual-droop control[J]. IEEE Transactions on Smart Grid, 2017, 8(2): 557–571.
|
| [15] |
于立新. 基于LOS法的USV滑模控制与路径跟踪研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
 2022, Vol. 44
2022, Vol. 44

