潮流能是潮汐现象引起的海洋水流具有的动能,由于具有可预测性强、能量转换效率高、对海洋环境影响较小等特点而受到关注。潮流能水轮机作为主要的潮流能捕获装置,可以分为垂直轴水轮机和水平轴水轮机。
近年来,随着计算流体力学的发展和计算机水平的提高,国内外学者对水轮机的水动力性能进行了研究。张继生等[1]研究了并排双水平轴水轮机的横向间距及安装高度,发现随着横向间距增大,来流方向相同的最大水流作用力和尾流场中最大流速均有所减小,相对安装高度对其影响也十分显著。刘恒等[2]对不同桨距角下,水轮机支撑结构的周围流场和叶片的应力变化情况进行探讨。宋科[3]通过CFD技术,测试所设计水平轴水轮机导管的剖面拱度、攻角及多导管组的水轮机水动力学性能影响。随后,又在前面基础上,对组合式导管进一步研究[4]。骆锐东[5]针对叶轮效率不高以及制造运行成本高,基于导流罩的设计原则和风力扩散器原理,设计了一种双边对称式折线型导流罩。通过水槽实验,验证了叶轮能够较好地捕获双向来流能量。Prasetyo A等[6]针对Savonius水轮机效率低的问题,在水轮机上安装导流板引导水流,增加其工作力矩。对比相同排量下,不带导流板的涡轮,输出功率提升显著。Prasetyo H等[7]将水轮机的叶片数、叶片曲率角、攻角和阻塞系统倾斜角等4种参数组合后进行数值模拟。Yasuyuki N[8]对下冲式横流水轮机采用直叶片及弯曲叶片的区别感兴趣,通过实验和数值分析对其性能和流场进行研究,证实了直叶转轮的输出功率确实比弯曲叶片高。
国内外学者针对水平轴轴潮流能水轮机进行了大量的研究,研究思路大多是通过改善流场提高其获能效率。本文结合仿生鲸鱼鳍的结构特点,设计具有前缘结节的水平轴潮流能水轮机仿生叶片,利用STAR-CCM++软件进行实尺度数值模拟,并与传统水平轴潮流能水轮机的水动力性能进行比较,所得结论可为仿生学应用于潮流能水轮机的后续研究提供一定参考
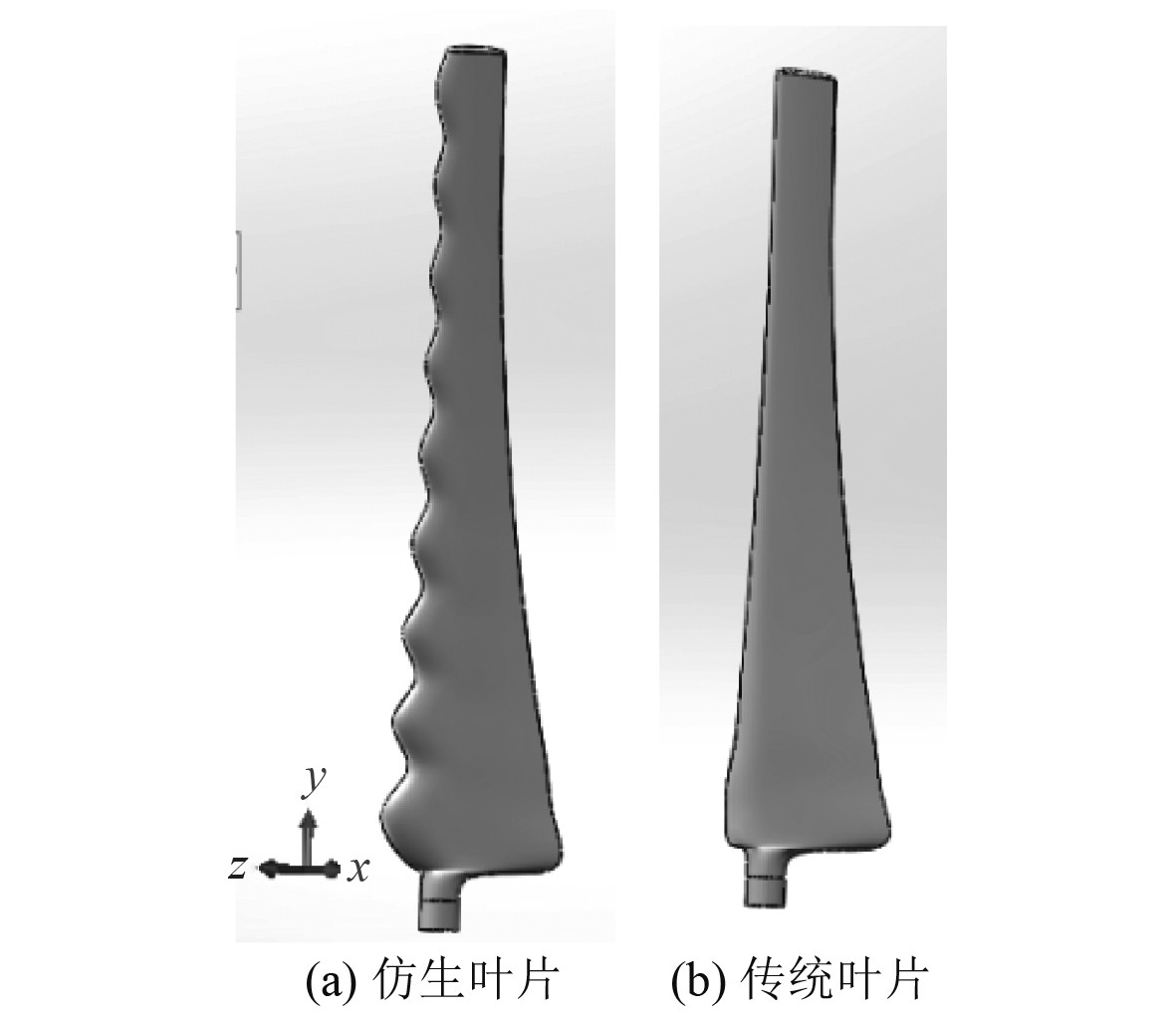
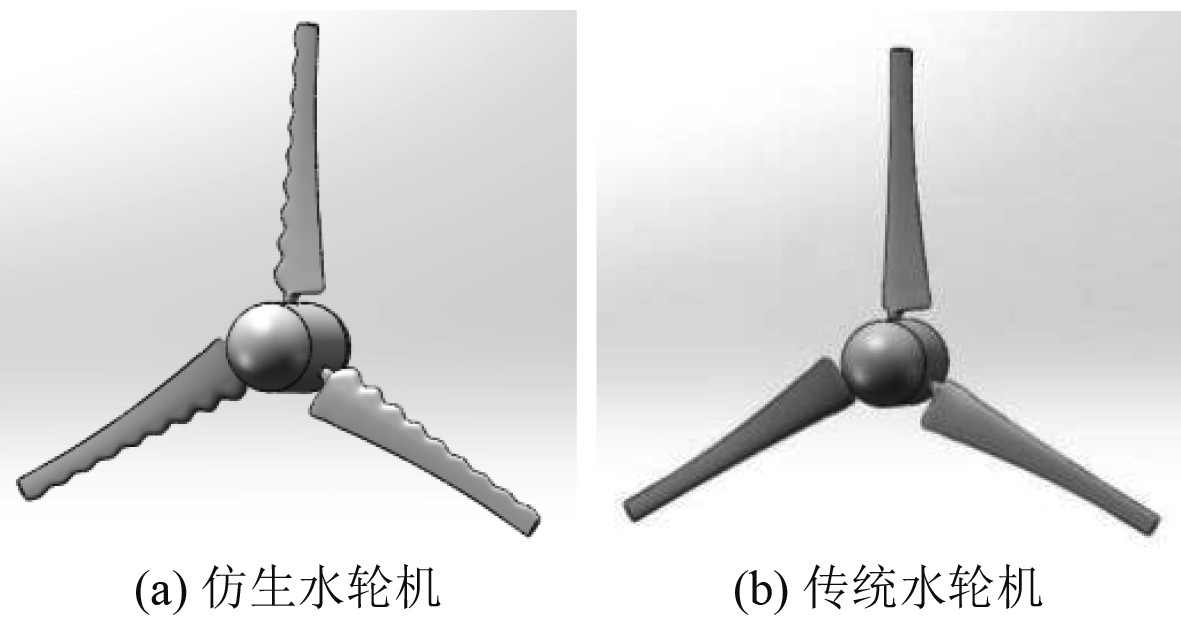
1 数值模型 1.1 几何模型的建立本文叶片截面翼型选用NACA0018,仿生叶片的前缘曲线为标准的正弦曲线,如图1(a)所示。传统叶片前缘则为一条光滑曲线,即沿展长方向为均匀截面,如图1(b)所示。结节形状如图2所示,H和W分别为正弦结节的波高和波长,结节波高为传统叶片同展长处弦长的0.1倍,为了保持叶片的厚度,所有截面的结节都从最大厚度点向前延伸。结节波长为500 mm,结节个数为9。表1列出了不同展长位置处传统叶片弦长(C0)和仿生叶片弦长(C)。图3为仿生水轮机和传统水轮机图。
|
图 1 仿生叶片和传统叶片 Fig. 1 Standard blade and Bionic blade |

|
图 2 结节图 Fig. 2 Nodules figure |
|
|
表 1 叶片外形参数 Tab.1 Blade profile parameters |
|
图 3 仿生水轮机及传统水轮机 Fig. 3 Standard turbine and bionic turbine |
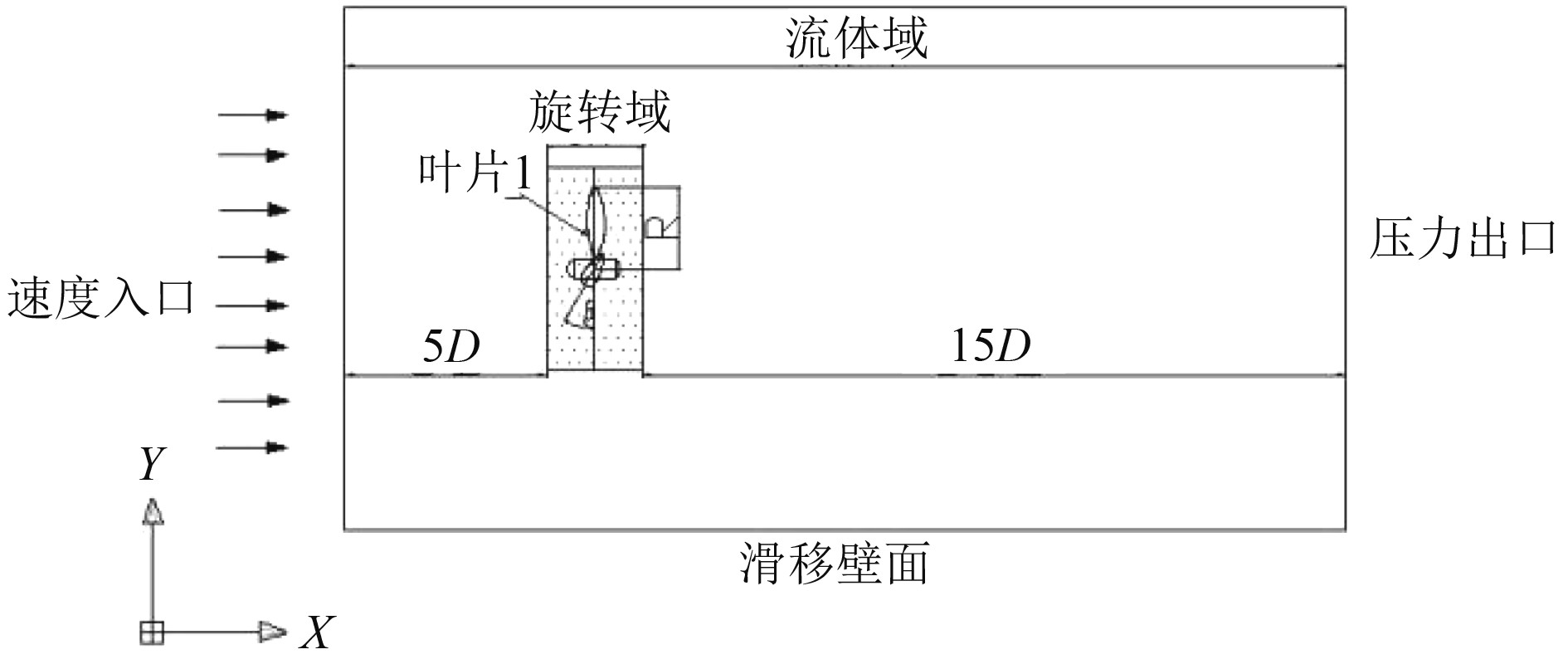
运用STAR-CCM+软件建立计算模型,计算域分为流体域和旋转域(阴影部分)两部分,如图4所示。计算域长180 m,宽90 m,深90 m,轮毂的中心位置为(45 m, 45 m和45 m),水轮机上游区域长45 m,下游区域长135 m,圆柱型旋转域半径为7 m,高7 m。应用滑移网格技术进行网格划分,旋转域的外表面设为交界面。为了保证计算精度同时提高运算效率,采用六面体网格,对旋转区域网格进行加密处理,网格总数为258万。入口边界条件设置为速度入口,出口边界条件设置为压力出口,旋转域表面设置为交界面,其余边界设置为滑移壁面。
|
图 4 计算域图 Fig. 4 Computational domain diagram |
假设流体是不可压的,流场的连续方程和动量方程[9] 为:
连续方程
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0,$ | (1) |
动量方程
| $ \frac{{\partial \left( {\rho {u_j}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_j}}} = - \frac{{\partial P}}{{\partial {x_j}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right]。$ | (2) |
式中:
采用SST k-
参照图4,建立水轮机整体坐标系O-XYZ,选取水轮机转轴中心为坐标原点O,来流方向沿X轴正向,垂直于来流的方向为Y轴。假设在均匀来流中,水轮机以恒定的旋转角速度ω绕转轴中心O旋转,其半径为R;X轴正方向背向于水轮机转轴中心,水轮机迎流面朝向X轴负向。叶片1的起始位置在Y轴正方向。为了方便分析,定义无量纲参数包括水轮机的能量利用率CP、扭矩系数CT和轴向力系数CF,表达式分别为:
| $ {C_P} = \frac{P}{{0.5\rho {V^3}{\text{π}} {R^2}}},$ | (3) |
| $ {C_T} = \frac{T}{{0.5\rho {V^2}{\text{π}} {R^2}}},$ | (4) |
| $ {C_F} = \frac{F}{{0.5\rho {V^2}{\text{π}} {R^2}}},$ | (5) |
| $ \lambda = \frac{{n{\text{π}} R}}{{30V}}。$ | (6) |
式中:P为水轮机发电功率;T为水轮机主轴转矩,中心转轴为x轴;F为轴向力;V为水流速度,沿x轴正方向流动;ρ为介质密度;R为水轮机半径,
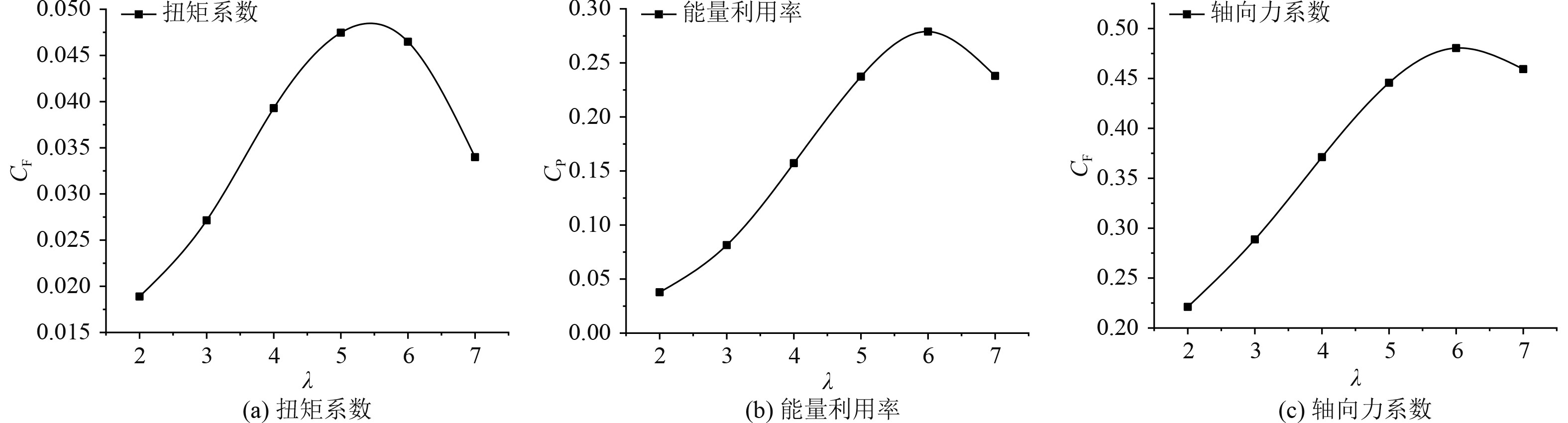
对潮流能水轮机的额定流速为1.5 m/s、桨距角为5°时的6种工况进行数值模拟,得到了潮流能水轮机在不同尖速比下的扭矩系数、轴向力系数和能量利用率,如图5所示。
|
图 5 各工况下潮流能水轮机数值模拟结果 Fig. 5 Numerical simulation results of tidal current turbine under various working conditions |
由图5可知,桨距角为5°时,扭矩系数起初随着尖速比增大而迅速上升,当尖速比达到6时取得最佳值0.474,随后开始呈现下降趋势。能量利用率影响水轮机的发电效率,其移动趋势与扭矩系数近似,最大值在尖速比6处取得,为0.28。轴向力系数也是随着尖速比不断提高,至尖速比6处取得最大值0.48。
2.2 仿生水轮机与传统水轮机水动力性能比较对传统水轮机进行数值模拟,模拟的工况与仿生水轮机完全相同,并将计算结果进行对比分析,如图6所示。
|
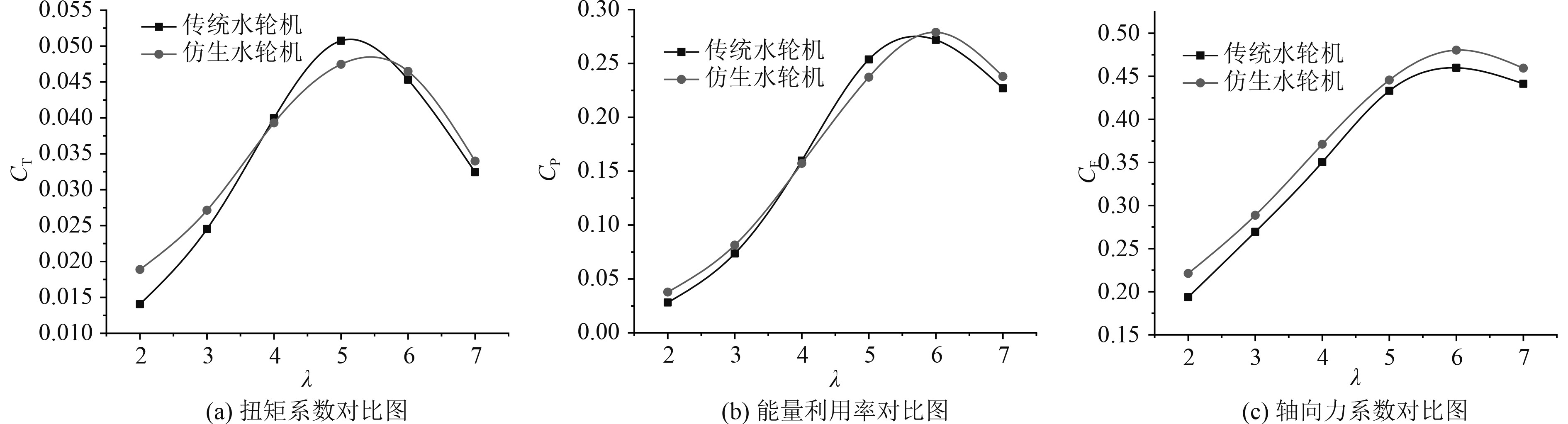
图 6 传统水轮机与仿生水轮机数值结果对比 Fig. 6 Comparison of numerical results between standard turbine and bionic turbine |
图6(a)为仿生水轮机与传统水轮机的扭矩系数对比图。扭矩系数影响了水轮机的启动和发电机的选用。水轮机在启动阶段,若扭矩大,则水轮机容易启动,开始发电的流速也越低。桨距角为5°时,在尖速比低于4和大于6时,仿生水轮机的扭矩系数相比传统水轮机均有所提升,低尖速比区最高提高24%左右,高尖速比区提高6%左右。
图6(b)为仿生水轮机与传统水轮机的能量利用率变化趋势图。桨距角为5°时,在低尖速比时,仿生水轮机能量利用率相比传统水轮机最高可提高34.3%。尖速比大于5.5以后,仿生水轮机的能量利用率略高于传统水轮机。仿生水轮机在尖速比λ为6时取得最佳能量利用率,相比传统水轮机,提高了2.6%。
轴向力系数主要影响水轮机支撑结构设计。较小的轴向力,不需要庞大的支撑结构,从而达到可以减少生产制造成本目的。图6(c)中仿生水轮机的轴向力系数始终大于传统水轮机,表明在5°桨距角下,仿生水轮机可能对支撑结构要求更高。
2.3 不同桨距角下仿生水轮机与传统水轮机的水动力性能比较桨距角是指叶片顶端翼型弦线与旋转平面的夹角,为研究桨距角对潮流能水轮机的性能影响,选取4个桨距角,分别为3°,5°,8°和10°,设定流速为1.5 m/s,不同桨距角下仿生水轮机与传统水轮机的数值结果对比如图7~图9所示。
|
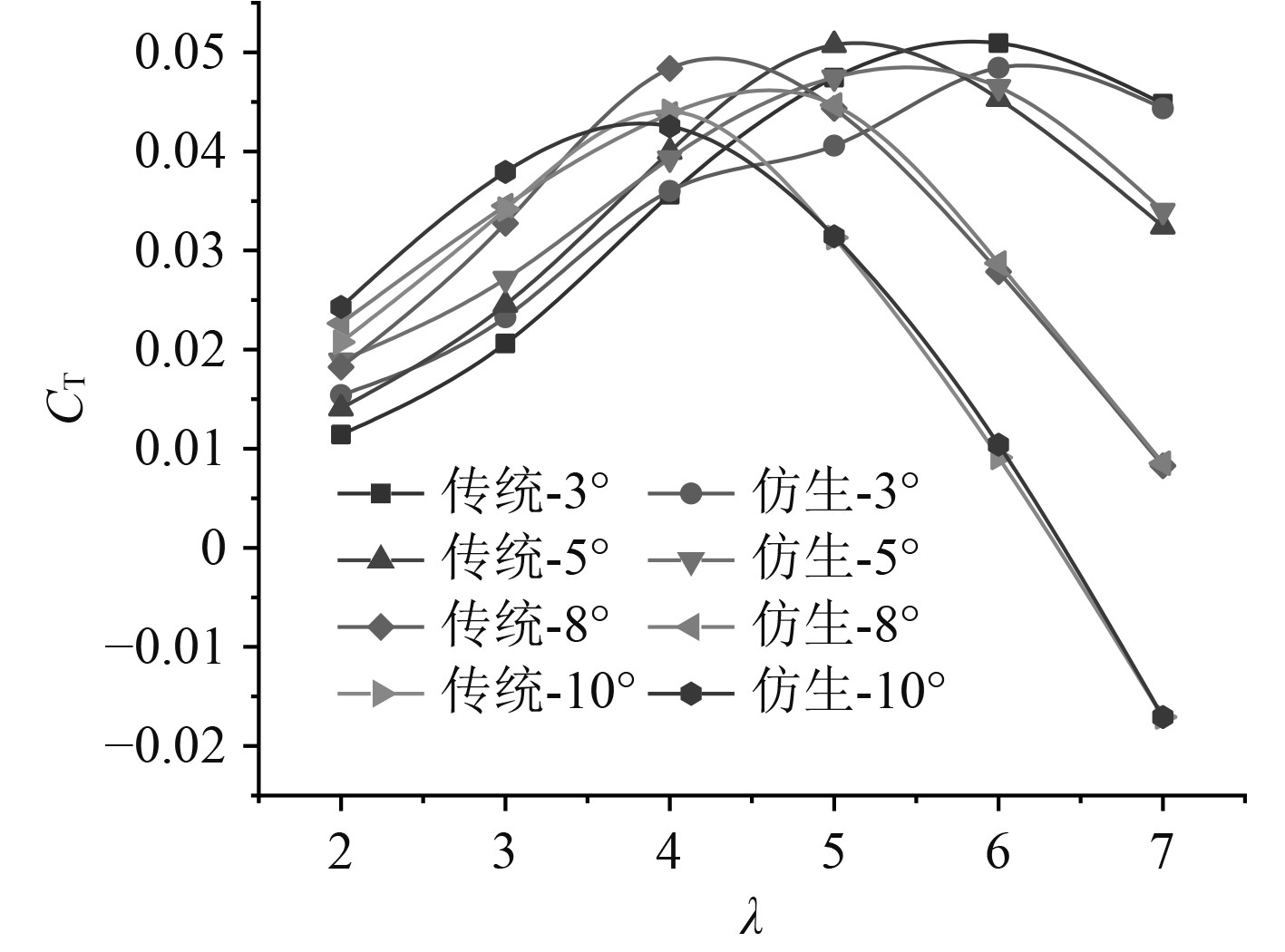
图 7 不同桨距角下的扭矩系数 Fig. 7 Torque coefficient at different pitch angles |
|
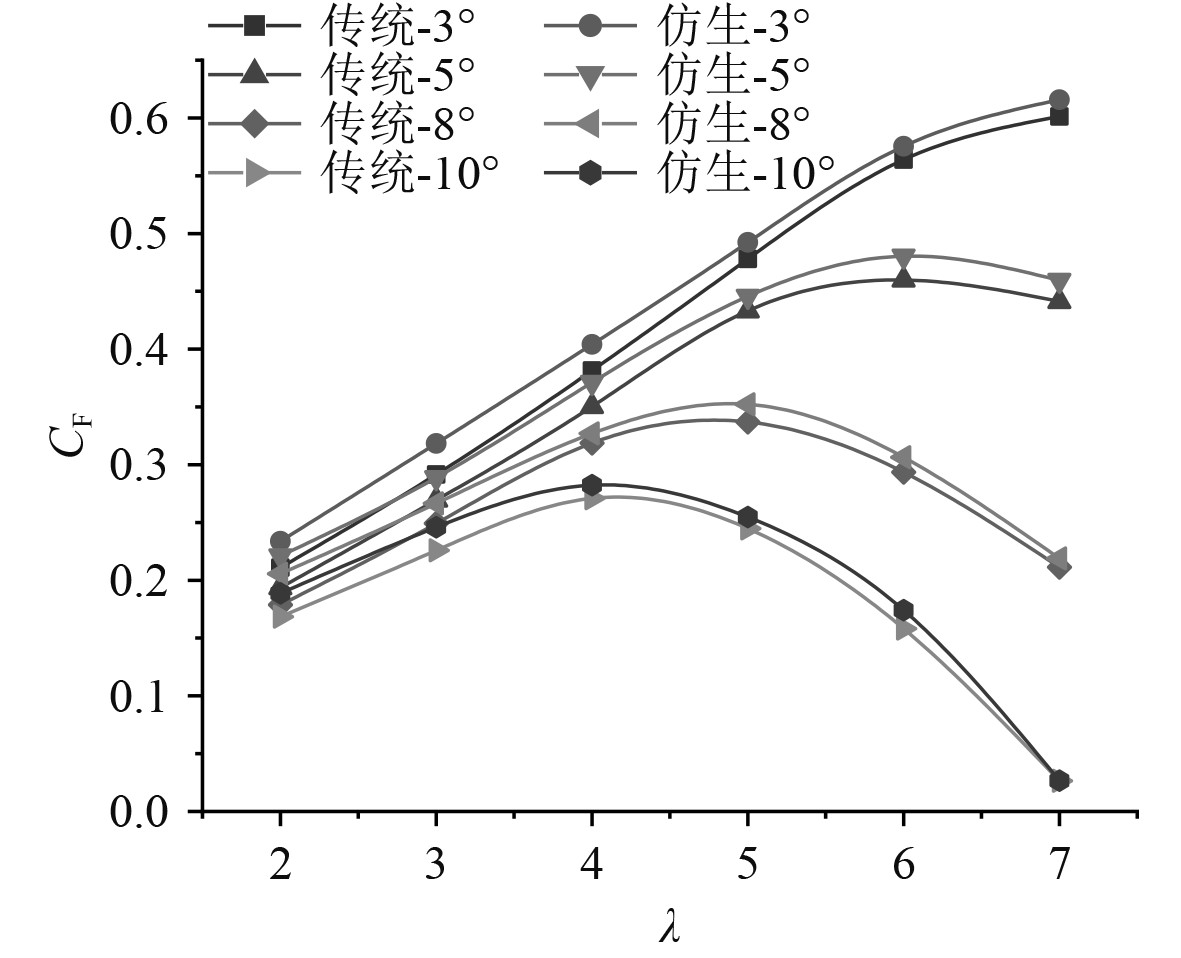
图 9 不同桨距角下的轴向力系数 Fig. 9 Axial force coefficient under different pitch angles |
由图7可知,各个桨距角下的扭矩系数变化趋势近似,前期均随着尖速比增大而增大。在桨距角为3°时,仿生水轮机在尖速比低于4范围内,扭矩系数均比传统水轮机高,最大提高了34.1%左右;桨距角为5°时,仿生水轮机的扭矩系数相比传统水轮机进一步提升,低尖速比区最高提高了24%左右,高尖速比区提高了6%左右;至桨距角为8°时,仿生水轮机扭矩系数较优异区域开始向低尖速比区移动,低尖速比区扭矩系数最高提高17%左右,高尖速比区提高1%左右;桨距角为10°时,其在尖速比为2处比传统水轮机提高16%左右。说明额定流速下,仿生水轮机低尖速比时产生的转矩更高,相比传统水轮机需要的启动流速较低,高尖速比区的扭矩改善较小。
由图8可知,相比较传统水轮机:当桨距角为3°时,仿生水轮机在尖速比低于4范围内的CP略高,在尖速比为2时最高提高34.9%,两者均在同一尖速比λ为7时取得最佳能量利用率;当桨距角为5°时,仿生水轮机的能量利用率在低尖速比区最大提高34.3%。在高尖速比区,最大提高了2.6%。最佳能量利用率在尖速比λ为6时取得。对比桨距角3°的工况,取得最佳能量利用率的尖速比在减小;当桨距角为8°时,在低尖速比时最大提高24.3%,在高尖速比区,最大提高了3.1%。仿生水轮机在尖速比λ为5时取得最佳能量利用率;当桨距角为10°时,在低尖速比工况下,仿生水轮机的能量利用率依旧比传统水轮机提升29.1%。综上,仿生叶片主要作用在低尖速比范围内,并且随着桨距角的增大,最佳能量利用率取得的尖速比也在向低尖速比区移动。

|
图 8 不同桨距角下的能量利用率 Fig. 8 Energy efficiency at different pitch angles |
由图9可知,随着桨距角的增大,挡水面积的减小,轴向力系数总体来说不断减小。仿生水轮机的轴向力系数在各个桨距角下均大于传统水轮机,表明仿生水轮机对于支撑结构的要求更高。
3 流场特性对比 3.1 不同尖速比下仿生水轮机与传统水轮机约束流线分析选取额定流速1.5 m/s,桨距角为5°的流线图加以分析。仿生水轮机以bi表示(bio-mimetic),传统水轮机以tr表示(traditional)。图片以水轮机类型-桨距角度-尖速比命名,例如bi-5-2。
由图10 可以看出,叶片流线沿展长方向流动代表出现边界层分离。速比越小,叶片的实际攻角越大,边界层分离越剧烈。尖速比为2时,2种叶片背流面均发生完全的流动分离。仿生叶片在靠近叶根处和前缘波峰处维持附着流动,相比传统水轮机流动分离趋势略缓,因此,仿生水轮机性能相比传统水轮机会有所提升;当尖速比为5时,传统水轮机距离叶尖1/5远的尾缘处率先出现流动分离。仿生水轮机背流面2/3区域流线出现扭曲,围绕在尾缘处流动;当尖速比为6时,仿生叶片仅靠近叶根尾缘1/4区间内,波谷处流动有小范围扭曲,传统水轮机靠近叶根处尾缘区域有流动分离现象。

|
图 10 桨距角5°的背流面约束流线图 Fig. 10 Backflow surface constrained flow diagram with pitch angle of 5° |
由于来流影响,叶片迎流面受到冲击,表现为正压,背流面由于挡水效应,表现为负压,在叶片的尖端容易出现叶尖涡,所以针对背流面进行压力分析。在桨距角为5°时,低尖速比下,仿生水轮机产生的扭矩更大,整体性能更为优越,当尖速处于4~5之间,传统水轮机获能更多,当尖速比大于6以后,仿生水轮机扭矩又高于传统水轮机。所以现针对尖速比2和取得最佳能量利用率的尖速比5及尖速比6的工况进行分析。
由图11可以看出,尖速比为2时,仿生叶片背流面在正弦前缘波谷弦向处,出现低压区,相比传统叶片,低压区域更大。尖速比为5时,仿生水轮机背流面在前缘波峰处的压力相比传统水轮机同位置要高。仿生水轮机压差小于传统水轮机,因此尖速比为5时,仿生水轮机的性能不如传统水轮机。图11(c)中尖速比为6时,仿生水轮机背流面波峰处的压力相比传统水轮机同位置要高,但靠近叶根处的波谷,由于分流作用加剧两侧波峰的流线向波谷扩散,在波谷处形成对流,产生负压区,而传统水轮机同位置处,对比压力略高于仿生水轮机。因此尖速比为6时,仿生水轮机的性能不如传统水轮机。

|
图 11 桨距角为5距时叶片背流面压力图 Fig. 11 Pressure diagram of blade backflow surface when pitch Angle is 5° |
扭矩系数及能量利用率在各个桨距角下的低尖速比区均提升显著,因此选择尖速比为2的工况观察各个桨距角下叶片背流面流线分布。
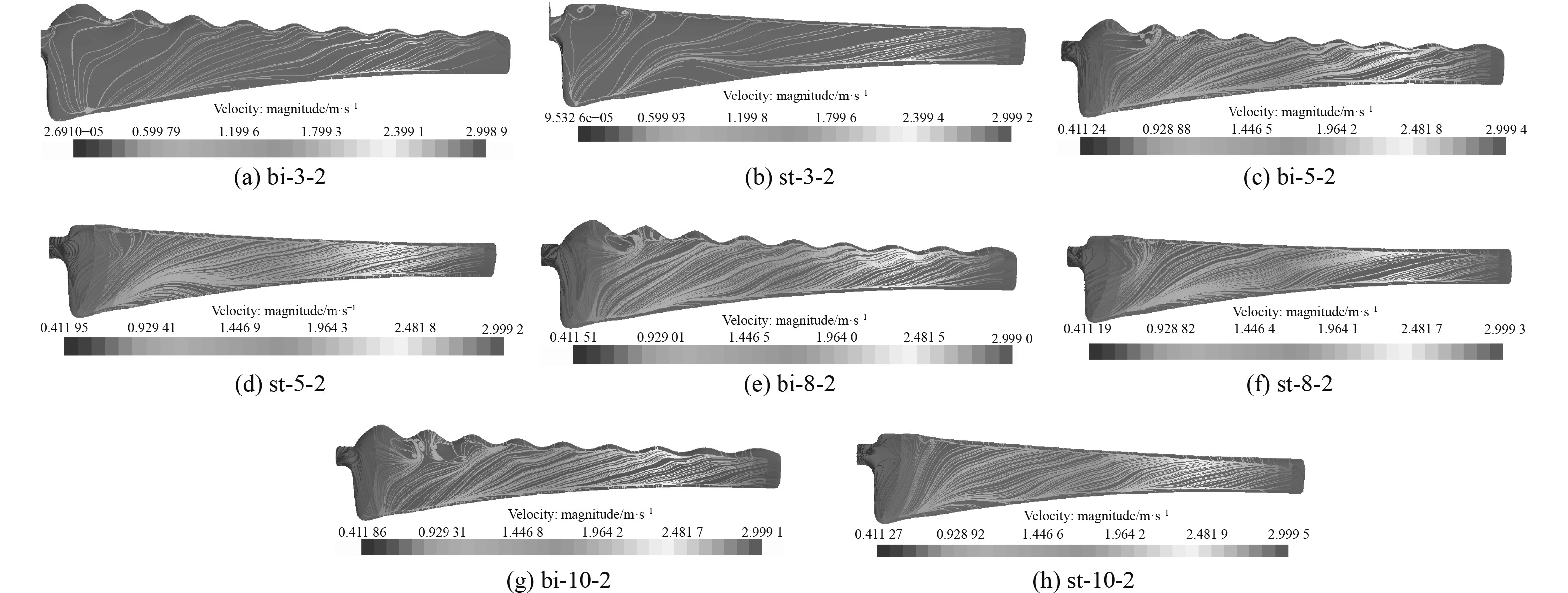
由图12可以看出,尖速比越小,叶片实际攻角越大,边界层分离越剧烈。尖速比为2时,各个桨距角下2种叶片背流面均发生大幅度流动分离。桨距角为3°时,传统叶片流动完全分离,仿生叶片由于仿生前缘波峰的分流,在靠近叶根处与叶尖前缘波峰极小区域还维持着附着流动。仿生叶片附着流动区域相比传统水轮机略大。随着桨距角增大至10°,传统叶片的叶根处和叶尖尾端都出现附着流动。但同桨距角下的仿生叶片,靠近展向一个波长区域内弦向附着流动明显,前缘处也可以明显看到流动分离的控制效果更好。因此此尖速比下,仿生水轮机表现整体来说更加优异。
|
图 12 不同桨距角下叶片背流面流线图 Fig. 12 Motion pattern of blade backflow surface at different pitch angles |
本文在STAR-CCM+中对仿生水平轴潮流能水轮机进行数值模拟,与传统水平轴潮流能水轮机的水动力性能进行对比后,所得结论如下:
1)在额定流速为1.5 m/s时,带有正弦前缘结节的仿生叶片的影响主要是在较低尖速比范围(2~4)内,而叶片失速的情况下。仿生叶片可以使水轮机产生较大的转矩和推力,相比传统水轮机所需的启动流速更低。能量利用率方面,仿生水轮机在低尖速比区最高可以提升约34%,在高尖速比区也有一定提升,但作用不如低尖速比区显著。
2)在所选取的3°,5°,8°及10°四个不同桨距角中,对于较低的桨距角,仿生叶片所带来的改善要大于较高的桨距角。
3)对比不同尖速比下的水轮机背流面压力云图可知,尖速比增大,转速增大,背流面的负压由翼型弦向前缘向后缘延伸,从叶尖向水轮机叶片的中部发展,选择合适的尖速比可以减少叶片的强度破坏和叶尖涡的产生。
| [1] |
张继生, 曹运修, 吴修广, 等. 并排水平轴潮流能水轮机组水动力特性研究[J]. 河海大学学报(自然科学版), 2017(3).
|
| [2] |
刘恒, 王文全, 闫妍. 变桨距角下水平轴海流能水轮机水动力特性及结构性能[J]. 排灌机械工程学报, 2017, 35(5): 393-397. |
| [3] |
宋科. 导管水轮机发电装置水动力学性能研究[C]// 第十届全国流体力学学术会议论文摘要集, 2018.
|
| [4] |
宋科, 王文全, 闫妍. 新型组合式导管水轮机水动力性能研究[J]. 水力发电学报, 2019(6): 113-120. DOI:10.11660/slfdxb.20190612 |
| [5] |
骆锐东. 悬浮式水平轴潮流能水轮机及其导流罩的设计与水动力分析[D]. 上海: 上海海洋大学, 2020.
|
| [6] |
PRASETYO A, KRISTIAWAN B, DANARDONO D, et al. The effect of deflector angle in savonius water turbine with horizontal axis on the power output of water flow in pipe[J]. Journal of Physics Conference, 2018, 979: 12043. DOI:10.1088/1742-6596/979/1/012043 |
| [7] |
PRASETYO H, BUDIANA E P, DDDP T, et al. The simulation study of horizontal axis water turbine using flow simulation solidworks application[J]. IOP Conference Series:Materials Science and Engineering, 2018, 308: 12022. DOI:10.1088/1757-899X/308/1/012022 |
| [8] |
YASUYUKI N, TERUMI I, YANRONG L, et al. Study on an undershot cross-flow water turbine with straight blades[J]. International Journal of Rotating Machinery, 2016, 2015: 1-10. |
| [9] |
刘恒, 王文全, 闫妍. 变桨距角下水平轴海流能水轮机水动力特性及结构性能[J]. 排灌机械工程学报, 2017(5).
|
| [10] |
于晓丽, 王树杰, 袁鹏, 等. 两种湍流模型在潮流能水轮机数值模拟中的适用性研究[J]. 中国海洋大学学报(自然科学版), 2019, 49(2): 114-120. |
 2022, Vol. 44
2022, Vol. 44

