0 引　言

深海运载平台能够将人员输送到几千米的海底深处，被广泛应用于资源勘探、海底科考、打捞搜救等领域。目前，针对深海运载平台的研究主要朝着下潜深度更深、作业时间更长、续航时间更久等方面发展，国内外积极开展新型多耐压体深海运载平台研究。针对多耐压体之间固连结构的研究也成为整个深海运载平台设计研究的关键^[1]。多个耐压体结构与固连结构一般通过焊接连接在一起^[2]，固连结构主要由板架组成，不仅承担耐压体之间的固定和连接作用，同时可以作为其他结构的主要安装基础。对于大型深海运载平台，在水面状态下，固连结构是平台结构所受周期性波浪动压力、波浪抨击力、拖曳力、惯性力的主传力通道。固连结构的疲劳破坏将会导致深海运载平台整体结构散架，同时，当固连结构上的疲劳发展到耐压结构上时，亦会对耐压结构整体强度造成较大的影响，影响耐压结构的极限承载能力，从而导致灾难性后果。因此确保多体固连结构的疲劳强度对深海运载平台在长期服役过程中结构完整性和作业能力的实现具有重要意义。

谱分析方法^[3-6]是一种直接计算方法，相比其他计算方法，谱分析方法能够较为直观并且准确地进行疲劳评估。谱分析方法通过对船体进行水动力分析得到结构所受波浪载荷及其运动响应，得到应力响应函数，并结合海浪谱得到结构的应力响应谱和应力范围分布，最后根据S-N曲线计算结构疲劳累积损伤和疲劳寿命。万松林等^[5]对某型舰船局部热点部位进行了谱分析计算，得到较为精确和符合实际作业的计算结果，从而合理地完成结构强度的分析和评估。谱分析方法的重点和难点在于复杂工况下结构应力响应谱的计算，杨鹏和官腾等^[7-8]运用三维水弹性理论，计算得到波浪载荷下船体热点部位载荷响应情况，其计算结果对危险工况下的结构应力响应校核具有一定指导意义。

本文针对水面工况，利用中国船舶科学研究中心开发的三维水弹性软ICS-TAHFTS^[9]，基于模态叠加原理对深海运载平台的水弹性响应进行计算，采用谱分析方法对固连结构热点应力部位疲劳损伤和疲劳寿命进行预报，为运载平台设计和疲劳损伤评估提供参考。

1 三维水弹性理论

对于水面结构，相对平衡位置的运动和弹性变形可以表示为：

$ \vec u = \sum\limits_{r = 1}^m {{{\vec u}_r}{p_r}} = \sum\limits_{r = 1}^m {\left( {{u_r},{v_r},{w_r}} \right){p_r}}。$

(1)

式中：p_r (r = 1, 2, …, m)表示相对于第r阶干模态位移的主坐标分量。

广义线性水弹性力学的运动方程为：

$ \left( {\left[ {\boldsymbol{a}} \right] + \left[ {\boldsymbol{A}} \right]} \right)\left\{ {\ddot P} \right\} + \left( {\left[ {\boldsymbol{b}} \right] + \left[ {\boldsymbol{B}} \right]} \right)\left\{ {\dot P} \right\} + \left( {\left[ {\boldsymbol{c}} \right] + \left[ {\boldsymbol{C}} \right]} \right)\left\{ P \right\} = \left\{ {\boldsymbol{F}} \right\}，$

(2)

式中：[A]，[B]，[C]分别代表广义的流体附加质量矩阵、辐射阻尼矩阵以及恢复力系数矩阵；[a]，[b]，[c]分别代表船体结构广义的质量矩阵、阻尼矩阵以及刚度矩阵，[a]和c]一般可由系统质量阵和刚度阵的正交性求得，而[b]中的元素一般通过试验或经验公式确定；{F}表示广义的波浪激励力；{P}表示广义的向量坐标^[10]。

由于三维水弹性是基于线性响应系统，因此在获得结构的主坐标响应函数后，规则波下的船体结构上任一点的弯矩、剪力、位移和应力均可以使用模态叠加法求取^[7]。

2 结构主要参数和模态

深海运载平台主体结构由5个耐压体、固连结构、轻外壳构成，如图1和图2所示。

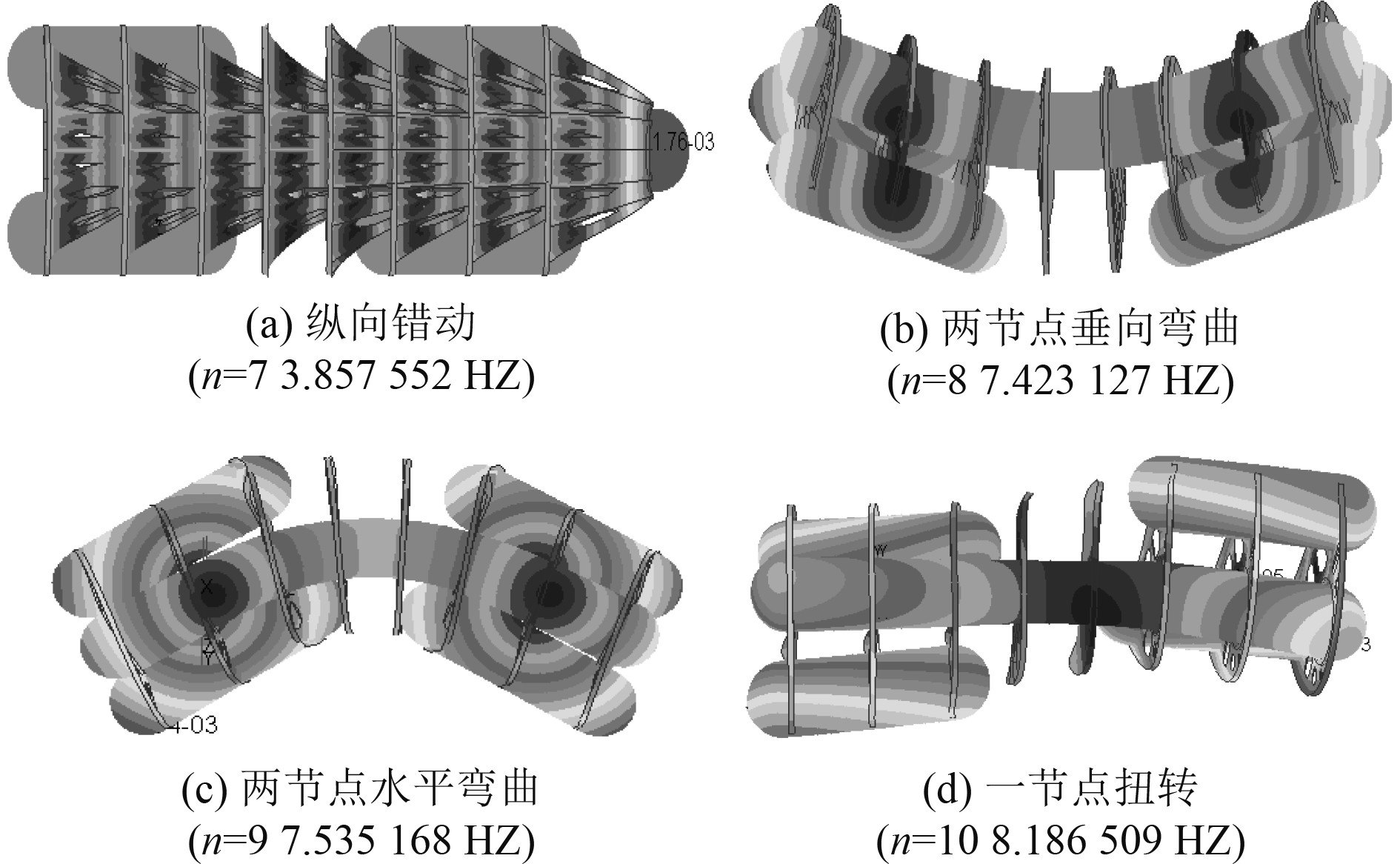
通过有限元模型计算结构在真空中的干模态和相应振型，结构典型振型7～10阶结果如图3所示。

3 频域水弹性分析

计算波浪频率范围为0.05～3 rad/s（步长0.05rad/s）下7个浪向角（0°，30°，60°，90°，120°，150°，180°）作用下的结构水弹性响应，对前6阶模态添加4%的人工粘性阻尼，其余模态添加2%的人工粘性阻尼进行水弹性分析。利用下式对波浪激励力进行无量纲化^[8]：

$ F/\left( {\rho g\nabla {S _F}} \right)。$

(3)

式中： $\rho $ 为水密度； $\nabla $ 为排水体积；当 $I \geqslant 7$ 或 $I \leqslant 3$ 时， ${S _F} = 1.0$ ；当 $4 \leqslant I \leqslant 6$ 时， ${S _F} = {L_{BP}}$ ， ${L_{BP}}$ 为两柱间长。

图4为30°浪向时前10阶模态下结构所受波浪激励力和主坐标响应的计算结果。

结果表明，P₃，P₅，P₇在低频区域的主坐标响应峰值由刚体运动引起，P₆，P₈，P₉，P₁₀在1.5 rad/s附近的主坐标响应峰值由波浪激励力引起，P₃，P₄，P₅，P₇，P₈在0.8 rad/s附近的主坐标响应峰值则是由刚体运动和波浪激励力共同作用引起的。

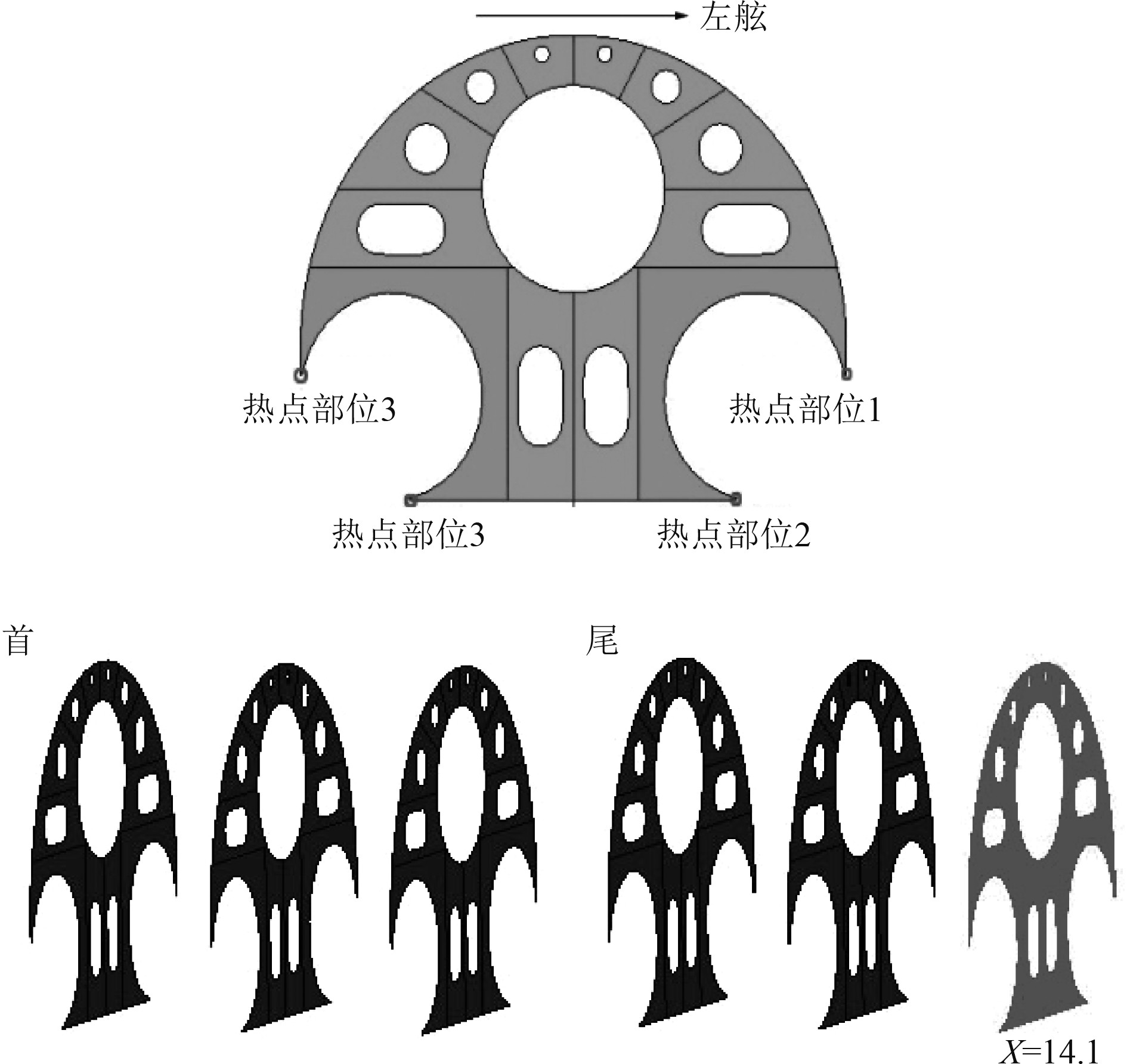
4 结构应力响应

对6道固连结构（X=8.1，11.1，14.1，21.6，24.6，27.6）进行静力分析后发现，固连结构与下耐压体连接处存在较大的应力集中，且应力集中值远大于板上其他部位，因此仅对该部位进行分析。根据结构应力云图选取应力最大位置（X=14.1）的固连结构进行分析计算，如图5所示。

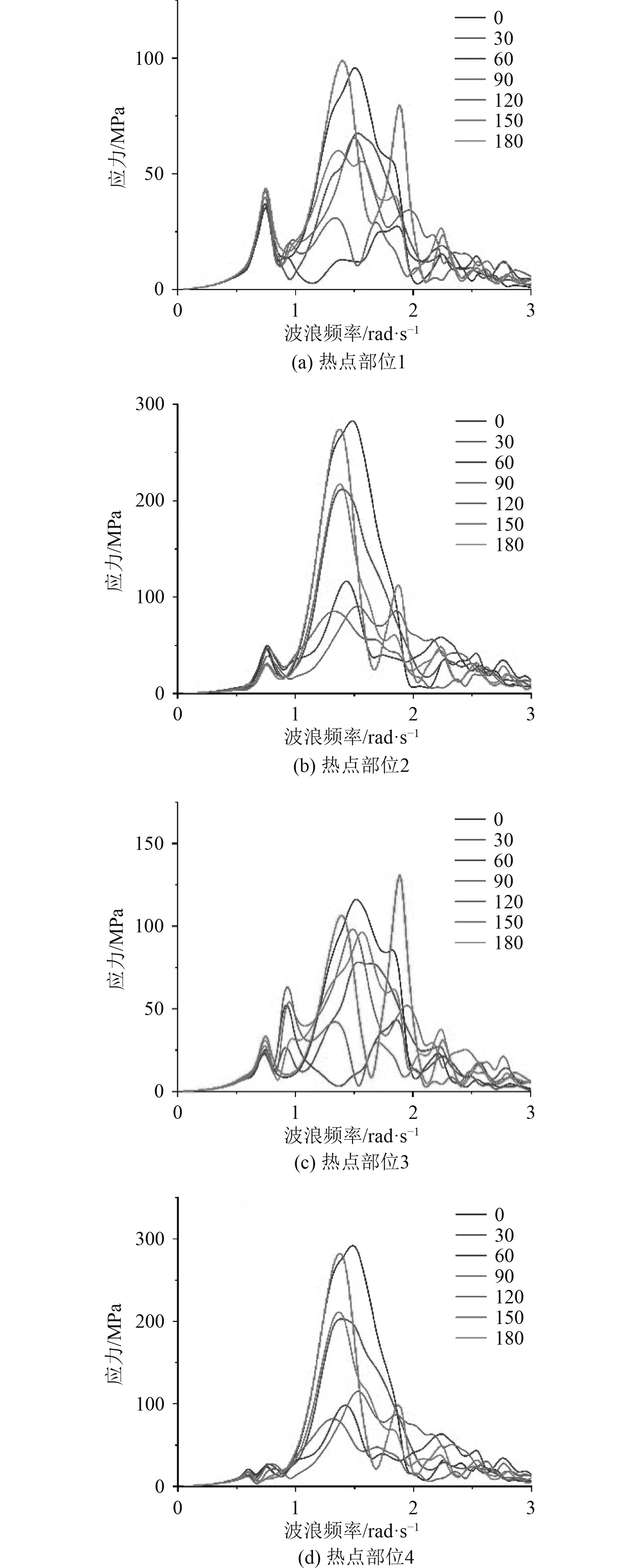
根据各个热点节点在波浪载荷下的不同浪向应力响应计算结果，叠加不同模态的主坐标响应和对应的结构应力分析得到各单元的直接应力（ ${\sigma _x}$ 、 ${\sigma _y}$ 、 ${\tau _{xy}}$ ）的传递函数，并进行插值计算，得到热点节点处直接应力的传递函数。根据热点节点处插值计算得到的直接应力结果计算热点处的主应力，结构热点部位应力传递函数如图6所示。

5 疲劳累积损伤计算

选用IACS^[11]推荐的北大西洋波浪谱，从中选取出现波高在4.5 m以下（包含4.5 m）、概率在1%以上的海况，这些海况约占全部海况的80％。

波浪功率谱密度选用ISSC推荐的P-M双参数谱，其定义如下：

$ {S_\zeta }\left( \omega \right) = 124H_S^2T_z^{ - 4}{\omega ^{ - 5}}\exp \left[ { - \frac{{496}}{{T_z^4{\omega ^4}}}} \right]。$

(4)

式中： $ {H_S} $ 为有义波高； $ {T_Z} $ 为平均跨零周期。

谱分析法利用传递函数由海洋波浪谱来预测结构中的波浪诱导应力谱，通过应力传递函数 ${H_\sigma }\left( {\omega \left| \theta \right.} \right)$ 和波浪谱 ${S_\eta }\left( {\omega \left| {{H_s},{T_s}} \right.} \right)$ 就可得到应力能量谱为：

$ {S}_{\sigma }\left(\omega |{H}_{s},{T}_{s},\theta \right)={\left|{H}_{\sigma }\left(\omega |\theta \right)\right|}^{2}\cdot {S}_{\eta }\left(\omega |{H}_{s},{T}_{s}\right) ，$

(5)

假定风浪是平稳正态随机过程时，由此而引起的结构物的运动、构件应力等也都是正态随机过程，其幅值符合Rayleigh分布，这一假定相应的应力过程是零均值的窄带高斯过程，概率密度为：

$ g\left( S \right) = \frac{S}{{4{\sigma ^2}}}\exp \left[ { - {{\left( {\frac{S}{{2\sqrt 2 \sigma }}} \right)}^2}} \right]。$

(6)

式中：S为应力范围； $\sigma $ 为 $\sqrt {m_0}$ ， $\sqrt {m_0} $ 为应力谱的0次矩。

应力能量谱的第n阶谱矩为：

$ {m_n} = \int_0^\infty {{\omega ^n}} {S_\sigma }\left( {\omega \left| {{H_s},{T_s},\theta } \right.} \right)\text d \omega，$

(7)

则平均作用频率和谱宽参数为：

$ {f_{0i}} = \frac{1}{{2\pi }}\sqrt {\frac{{{m_{2i}}}}{{{m_{0i}}}}}，$

(8)

$ {\varepsilon _i} = \sqrt {1 - \frac{{{m_{2i}}^2}}{{{m_{0i}}{m_{4i}}}}}。$

(9)

式中： ${m_{4i}}$ ， ${m_{2i}}$ 和 ${m_{0i}}$ 分别为第i短期海况的应力谱的4阶矩、2阶矩和0阶矩。

根据Miner准则，对于所有单斜率S-N曲线，疲劳累积损伤表达式可以表示为：

$ D = \frac{T}{K}{\left( {2\sqrt 2 } \right)^m}\Gamma \left( {\frac{m}{2} + 1} \right)\sum\limits_{i = 1}^M {\lambda \left( {m,{\varepsilon _i}} \right){f_{0i}}{p_i}{{\left( {{\sigma _i}} \right)}^m}}。$

(10)

式中： ${\sigma _i}$ 为所计算的第i个短期海况的0阶谱矩的平方根；m和K为S-N曲线参数。

$\Gamma$ 为伽马函数，定义如下：

$ \Gamma \left( x \right) = \int_0^\infty {{t^{x - 1}}{e^{ - t}}} \text dt，$

(11)

$ \lambda $ 为Wirsching雨流修正因子，计算如下：

$ \lambda \left( {m,{\varepsilon _i}} \right){\text{ = }}a\left( m \right) + \left[ {1 - a\left( m \right)} \right]{\left[ {1 - {\varepsilon _i}} \right]^{b\left( m \right)}} 。$

(12)

式中： $a\left( m \right){\text{ = }}0.926 - 0.033m$ ， $ b\left( m \right){\text{ = }}1.587m - 2.323 $ ； ${\varepsilon _i}$ 为第i个短期海况的谱宽。

大型深海运载平台设计使用寿命为30年，由于水面工况仅占全寿命周期的5％，因此假设固连结构水面工况下实际寿命为1.5年，且结构受到的各个浪向的波浪载荷等概率，选择计算S-N曲线为： ${S^{ - 7.71656}} \cdot 4.02778 \times {10^{23}} = N$ ，热点部位疲劳寿命计算结果如表1所示。

结果表明，热点部位1和热点部位3疲劳累积损伤值较小，可以认为其不发生疲劳损伤；热点部位2和热点部位4疲劳损伤较大，2个部位均符合疲劳寿命使用要求。表1结果也表明，0°和180°浪向对热点部位2和热点部位4处疲劳损伤有比较大的贡献，60°，90°和120°浪向对结构疲劳损伤的贡献度较小，可以认为在60°，90°和120°下几乎不发生疲劳损伤。

6 结　语

本文采用三维频域水弹性软件ICS-TAHFTS计算了大型深海运载平台在波浪作用下的频域水弹性响应。针对耐压体之间的固连结构选取4个典型结构热点部位，利用谱分析方法计算热点部位在波浪载荷下的疲劳累积损伤和疲劳寿命。

利用三维水弹性理论能够较为准确反映结构的水动力响应情况，ICS-TAHFTS软件可以方便计算出结构所受波浪激励力、主坐标响应和应力传递函数等。虽然谱分析方法涉及计算的工况较多，过程复杂，但能够直观并且准确反映结构受环境载荷影响的响应情况，计算结果相对准确。

本文计算结果表明固连结构在与耐压体连接部分位置存在较为明显的应力集中现象，在热点部位2和热点部位4处，固连结构与耐压体连接热点部位存在较大的疲劳损伤。在顶浪和随浪状态时，固连结构应力明显增大，较容易产生疲劳损伤，在后续设计中需重点考虑。