0 引　言

潜器近水面低速运动受到波浪力和近水面效应的影响，是一项技术难度较大的操纵工况。为了确保潜器完成各种作业任务，运动过程中潜器的运动参数变化须尽量微小和平缓，即潜器的深度和姿态角及其随时间的变化率，都要控制在较小范围内，这对潜器低速航行于有波浪作用近水面时的运动控制提出了更高要求。因此，探索潜器近水面低速运动的数学模型和仿真预报显得尤为重要。

1 近水面操纵运动模型

对标准的水下操纵运动模型公式进行简化，得到潜器六自由度线性运动微分方程^[1]：

$ \left\{ \begin{gathered} {{m (\dot u + }}{{{z}}_{{G}}}{{\dot q - }}{{\textit{x}}_{\textit{G}}}({{\textit{q}}^{\rm{2}}} + {{\textit{r}}^{\rm{2}}}{{)) = }}\frac{{\rm{1}}}{{\rm{2}}}{\rho}{{\textit{L}}^{\rm{4}}}{{(}}{{{\textit{X}\,'}}_{{\textit{qq}}}}{{\textit{q}}^{\rm{2}}}{\rm{ + }}{{{\textit{X}\,'}}_{{\textit{rr}}}}{{\textit{r}}^{\rm{2}}}) + \\ \frac{{\rm{1}}}{{\rm{2}}}{\rho}{{\textit{L}}^{\rm{3}}}{{{\textit{X}\,'}}_{{{\dot u}}}}{{\dot u}}+ \frac{{\rm{1}}}{{\rm{2}}}{\rho}{{\textit{L}}^{\rm{2}}}{{(}}{{{\textit{X}\,'}}_{{\textit{uu}}}}{{\textit{u}}^{\rm{2}}}{{ + }}{{{\textit{X}\,'}}_{{\textit{vv}}}}{{\textit{v}}^{\rm{2}}}{{ + }}{{{\textit{X}\,'}}_{{\textit{ww}}}}{{\textit{w}}^{\rm{2}}} \\ {{ + }}{{{\textit{X}\,'}}_{{{\delta}_{{b}}}{{\delta}_{{b}}}}}{\delta}_{{b}}^{\rm{2}}{{ + }}{{{{X}\,'}}_{{{\delta}_{{s}}}{{\delta}_{{s}}}}}{\delta}_{{s}}^{\rm{2}}{{ + }}{{{{X}\,'}}_{{{\delta}_{{r}}}{{\delta}_{{r}}}}}{\delta}_{{r}}^{\rm{2}}{{)}} +{{\textit{X}}_{\textit{L}}}{{ + }}{{\textit{X}}_{\textit{P}}}{{ + }}{{\textit{X}}_{\textit{t}}}，\\ {{m(\dot v + \textit{ur} + }}{{{x}}_{{G}}}{{\dot r - }}{{\textit{z}}_{\textit{G}}}{{\dot p) = }}{{\textit{Y}}_{\textit{H}}}{{ + }}{{\textit{Y}}_{\textit{W}}}{{ + }}{{\textit{Y}}_{\textit{P}}}，\\ {{m(\dot w - \textit{uq} - }}{{{x}}_{{G}}}{{\dot q) = }}{{\textit{Z}}_{\textit{H}}}{{ + }}{{\textit{Z}}_{\textit{W}}}{{ + }}{{\textit{Z}}_{\textit{P}}}，\\ {{{J}}_{{x}}}{{\dot p - \textit{m}}}{{{z}}_{{G}}}{{(\dot v + \textit{ur}) = }}{{{K}}_{{H}}}{{ + }}{{{K}}_{{W}}}{{ + }}{{{K}}_{{P}}}{{ - mghsin\theta }}，\\ {{{J}}_{{y}}}{{\dot q + \textit{m}}}{{\textit{z}}_{\textit{G}}}{{\dot u - \textit{m}}}{{\textit{x}}_{\textit{G}}}{{(\dot w - \textit{uq}) = }}{{\textit{M}}_{\textit{H}}}{{ + }}{{\textit{M}}_{\textit{W}}}{{ + }}{{\textit{M}}_{\textit{P}}}{{ - \textit{mghsin}\theta }}，\\ {{{J}}_{{z}}}{{\dot r + \textit{m}}}{{\textit{x}}_{\textit{G}}}{{(\dot v + \textit{ur}) = }}{{\textit{N}}_{\textit{H}}}{{ + }}{{\textit{N}}_{\textit{W}}}{{ + }}{{\textit{N}}_{\textit{P}}}。\\ \end{gathered} \right. $

(1)

式中：m为潜器水下状态的质量，kg；u，v，w为潜器坐标系原点的线速度在Ox，Oy，Oz轴方向的分量，m/s；p，q，r为角速度在Ox，Oy，Oz轴方向的分量，rad/s；x，y，z为潜器受到的作用力在Ox，Oy，Oz轴方向的分量；K，M，N为潜器受到的作用力矩在Ox，Oy，Oz轴方向的分量，N·m；Xt为螺旋桨推力，N；h为潜器水下状态的稳心高，m； $\textit{φ}，\textit{θ}，\textit{ψ}$ 为横摇角、纵摇角和艏向角，rad；本文的坐标系、名词术语和符号规则均采用国际水池会议(ITTC)推荐和GJB-符号与术语体系。下角标H为表示潜器受到的水动力和水动力矩；下角标W为表示潜器受到的波浪力和力矩；下角标P为表示浮力控制措施产生的力和力矩。

2 近水面力学环境分析及建模

低速航行于有波浪作用的近水面环境中，潜器面临的操纵条件非常苛刻。潜器在近水面复杂力学环境中，受到自由液面和波浪的作用，对主要力学分项进行数学分析和建模。

2.1 水动力与波浪力

波浪中近水面影响包括静水中近水面自由表面影响和平均波浪力及力矩的影响，计算式如下：

$ \left\{ \begin{gathered} {F_{{U^2}}} = {{Z'}_s}\frac{1}{2}\rho {U^2}{L^2} + {{\tilde F}_w}，\\ {M_{{U^2}}} = {{M'}_s}\frac{1}{2}\rho {U^2}{L^3} + {{\tilde M}_w}。\\ \end{gathered} \right. $

(2)

式中： $ {F_{{U^2}}} $ 和 $ {M_{{U^2}}} $ 为波浪中近水面影响的力和力矩， $ {\tilde{F}}_{w}\text{和}{\tilde{M}}_{w} $ 为平均波浪力和力矩。

潜器近水面的运动可分解为与外力变化频率相应的低频和波频运动。由于潜器具有巨大的惯性，对于高于波频范围的外力，潜器的运动响应很小，因此忽略高频作用力引起的运动。对于潜器的低频运动，近水面运动的低频成分是在垂直面运动受到的二阶平均波浪力、舵力和其他低频力作用下产生的运动。因此在潜器近水面低速航行的运动计算中，忽略运动的高频成分，潜器的运动由低频运动和波频运动两部分组成，并用上述方法分别计算然后叠加，得到潜器的整个运动^[2-3]。潜器在近水面航行时受到的一阶波浪力采用STF流体运动切片理论^[4]和Frank源分布——紧密拟合法相结合的方法求得，垂直面内的二阶平均波浪力（垂向力和俯仰力矩），采用J.N.Newman和C.M.Lee提出的细长体平均波浪力公式及波浪力三维近似修正方法求得。

给定航行状态下作用在潜器上总的波浪力瞬时值按下式计算：

$ F(t) = \sum\limits_{i = 1}^{30} \left[\begin{split} &{{(2{S_w}({\omega _{0i}})\Delta {\omega _0})}^{1/2}}\cos ({\omega _{ei}}t + {\varepsilon _i} + {\varepsilon _j}){F^{(1)}}/{\zeta _a}+ \\ & (2{S_w}({\omega _{0i}})\Delta {\omega _0}){F^{(2)}}/\zeta _a^2。\end{split} \right] $

(3)

式中： $ F(t) $ 为波浪力瞬时值，N； $ {S_w} $ 为海浪谱密度， $ {{\text{m}}^{{2}}} \cdot {\text{s}} $ ； $ {\omega _{0i}} $ 为波浪圆频率， $ {\text{rad}} \cdot {{\text{s}}^{{{ - 1}}}} $ ； $ {\omega _{ei}} $ 为遭遇圆频率， $ {\text{rad}} \cdot {{\text{s}}^{{{ - 1}}}} $ ； $ t $ 为时间，s； $ {\varepsilon _i} $ 为线性叠加波浪力元的随机相位，rad； $ {\varepsilon _j} $ 为一阶波浪力响应的相位角，rad； $ \Delta {\omega _0} $ 为圆频率间距， $ {\text{rad}} \cdot {{\text{s}}^{{{ - 1}}}} $ ； $ {F}^{(1)}/{\zeta }_{a}，{F}^{(2)}/{\zeta }_{a}^{2} $ 为一阶、二阶波浪力响应， $\text{N}\cdot {\text{m}}^{{-1}}，\text{N}\cdot {\text{m}}^{{-2}}$ 。

2.2 操纵控制力模型

潜器近水面低速航行时，通常操纵首、尾升降舵控制运动和姿态^[5-6]。升降舵和方向舵的操纵采用基于深度、纵倾和航向反馈的PID控制算法^[7-8]。输出操舵指令，运动计算中使用的指令舵角表达式为：

$ \left\{ \begin{array}{l} {{\delta}_{{{b}}\,{{d}}}}= {{{a}}_{\rm{1}}}{{\Delta \zeta + }}{{{a}}_{\rm{2}}}{\rm{\dot \zeta }}，\\ {{\delta}_{{{s}}\,{{d}}}}{{ = }}{{{b}}_{\rm{1}}}{\theta}{{{b}}_{\rm{2}}}{\rm{\dot \theta + }}{{{b}}_{\rm{3}}}{{\delta}_{{b}}}，\\ {{\delta}_{{{r}}\,{{d}}}}{{ = }}{{{c}}_{\rm{1}}}{\rm{\psi + }}{{{c}}_{\rm{2}}}{\rm{\dot \psi }}。\end{array} \right. $

(4)

式中： ${\text{δ}}_{{bd}},\;{\text{δ}}_{{sd}},\;{\text{δ}}_{{rd}}$ 为首舵、尾升降舵、方向舵指令舵角，rad； ${{a}}_{{1}},\;{{a}}_{{2}},\;{{b}}_{{1}},\;{{b}}_{{2}},\;{{b}}_{{3}},\;{{c}}_{{1}},\;{{c}}_{{2}}$ 为指令舵角系数。

在低速航行状态下，作为主要控制力的升降舵舵力就显得不足，仅操舵很难控制住潜器的深度，必须采取其他辅助措施配合控制。在本文运动控制模型中，采用基于操舵和动态均衡的潜器低速运动协同控制，通过对潜器内水舱注排水的方法，弥补舵力的不足。由于浮力控制措施引起深度变化响应较慢，且需要处理随机干扰作用，因此控制模型在处理潜器的运动反馈时采用当前时刻若干采样数据的时均值，其产生的控制力和力矩以时间函数形式表达。

注排水流量的变化过程用一阶惯性环节模拟，数学表达式为：

$ {{T\dot Q + Q = }}{{{Q}}_{{t}}}。$

(5)

式中： ${{Q}}$ 为注排水流量， $ {{\text{m}}^{\text{3}}}{\text{/s}} $ ； ${{T}}$ 为 时间常数，s； ${{{Q}}_{{t}}}$ 为注排水流量指令值， $ {{\text{m}}^{\text{3}}}{\text{/s}} $ 。

在运动过程中，根据潜器的静不均衡量、深度变化量、垂速和首舵舵角，计算需要由注排水产生的作用力的指令值，然后与实际注排水产生的作用力比较，确定注排水流量的指令值 ${{{Q}}_{{t}}}$ 。其中 ${{{Q}}_{{t}}}$ 包括定量调控量 ${{{Q}}_{{e}}}$ 和动态调控量 ${{{Q}}_{{d}}}$ ，具体计算公式如下：

$ {Q_t} = {Q_d} + {Q_e}，$

(6)

定量调控水量的变化规律如下：

$ \left\{ \begin{gathered} {Q_e} = {Q_{e0}}(t)/{T_c}{\text{ }}0 \leqslant t < ({T_c})，\\ {Q_e} = {Q_{e0}}{\text{ t}} \geqslant {\text{(}}{T_c}{\text{)}}。\\ \end{gathered} \right. $

(7)

式中： $ {Q_e} $ 为定量调控水量，t； $ {Q_{e0}} $ 为定量调控水量指令值，t； $ t $ 为时间，s； $ {T_c} $ 为调控时间常数，s；基于深度和操舵反馈的动态调控量的变化规律如下：

$ \left\{ \begin{gathered} {Q_d} = {Q_{WD}}，\quad \;\,\quad \quad \,{P_{TZd}} - {P_{TZ}} > {P_{TZMK}}，\\ {Q_d} = 0，\quad \quad \;\; - {P_{TZMK}} \leqslant {P_{TZd}} - {P_{TZ}} \leqslant {P_{TZMK}}，\\ {Q_d} = - {Q_{WD}}，\quad \quad \quad {P_{TZd}} - {P_{TZ}} < - {P_{TZMK}}。\\ \end{gathered} \right. $

(8)

式中： $ {Q_{WD}} $ 为注排水流量的稳态值， $ {{\text{m}}^{\text{3}}}{\text{/min}} $ ； $ {P_{TZMK}} $ 为注排水控制门槛值，N； $ {P_{TZd}} $ 为动态调控的指令值，N。

$ {P_{TZd}} = - \rho g({A_1}\Delta \zeta + {A_2}\dot \zeta + {A_3}{\delta _b})。$

(9)

式中： $ \Delta \zeta $ 为深度相对初始深度的变化量，m； $ \dot \zeta $ 为深度变化速度，m/s； $ {A}_{1},\;{A}_{2},\;{A}_{3} $ 为控制参数。

3 潜器近水面力学环境与协同控制仿真预报

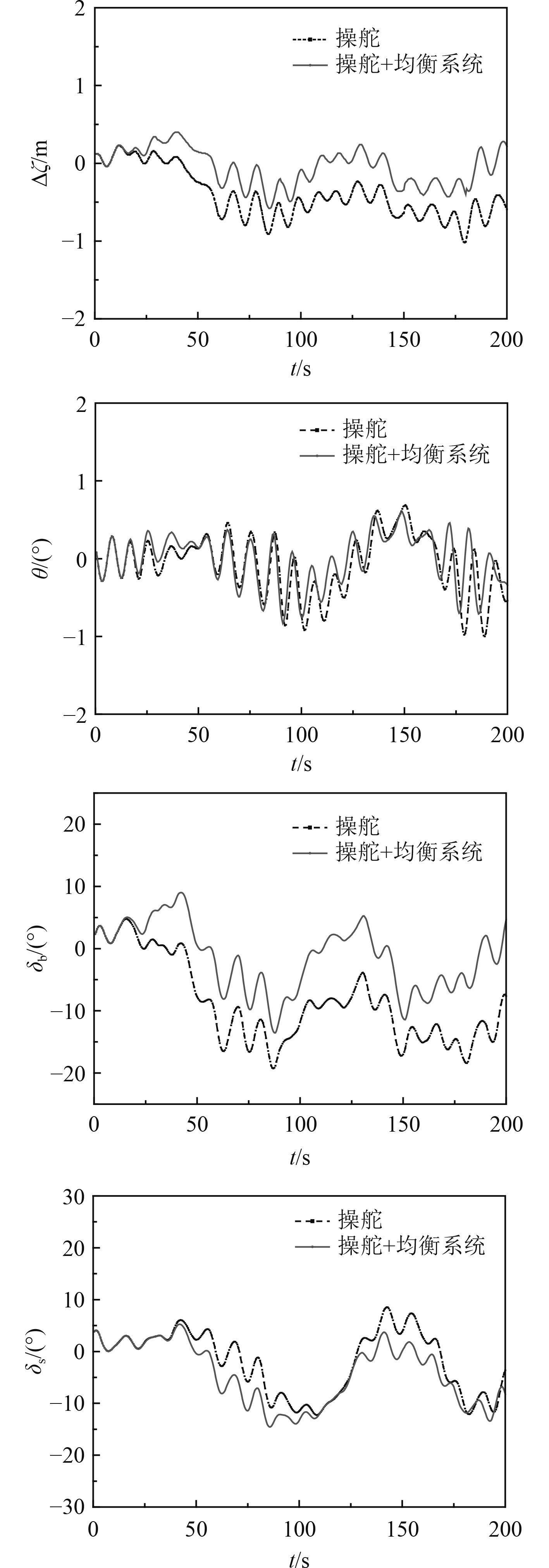
在5级海况波浪环境中，对潜器近水面低速运动过程进行仿真。在航速为10%和15%最大航速、以定深定向航行为控制目标，对仅采用升降舵和采用升降舵与均衡系统协调控制2种控制方式分别进行仿真计算。潜器运动姿态、升降舵角仿真结果曲线如图1所示。

分析仿真计算结果，由于低航速带来的舵效较低，控制效果相对较差。从图1可以清晰看出，10%Umax时深度、纵倾变化范围较大，在自动算法控制下，升降舵角相对较大，以更多弥补舵效的不足。对于潜器定深定向航行操纵控制，仿真结果显示，深度和纵倾均在随机海浪的波浪力作用下出现不规则振荡，控制模型中对控制反馈的运动参数进行了时均滤波处理，仿真结果收敛速度较快，规律匹配较好。

由计算结果看出，采取协同操纵控制方法后，可以使潜器深度控制在较小的深度范围内，比不使用协同控制时的深度变化有显著减小。

4 结　语

本文对潜器运动数学模型、复杂海洋环境条件下波浪力的数学处理和表达方式及各种控制措施产生的作用力等进行系统研究。在控制方式方面，研究了操舵系统和均衡系统协同参与运动控制的问题等。结果表明，波浪力及近水面效应对运动有较显著影响，通过操舵和均衡系统注排水的调节，可以对潜器的运动进行较满意的控制。