炮弹受到装药量的限制对舰船的毁伤能力要比导弹小得多,尤其是当炮弹无法穿透舰船外壳实现内爆时,爆炸威力的利用率将大打折扣。半穿甲弹是一种利用动能穿透进入舰艇等目标内部进而发生爆炸,依靠爆炸冲击波、自然破片等对目标实现毁伤的弹药。由于半穿甲弹在外形、材料、引信等方面经过特殊设计,因此具有较强的穿甲能力。目前,半穿甲弹主要配备在各型中大口径舰炮上,用于打击敌方舰船以及岸上坚固目标等。事实表明,半穿甲弹相比传统杀伤爆破弹更适合用于打击具有较强外部防护的舰船等目标,因此在中大口径舰炮上得到越来越广泛的应用。
加筋板结构由于具有较好的力学特性,因此在舰船中得到了广泛应用。近年来,国内外学者对靶板在弹丸/破片侵彻作用下的动态响应以及破坏过程进行了大量的研究[1-4],其中大部分学者都是针对均值板的穿甲问题进行研究[5-6],针对加筋板穿甲问题研究还比较少,已有的部分针对加筋板穿甲问题的研究中,一般也是采用等效均质板的方式进行[7-10],这并不能很好地反映加强筋对穿甲过程的影响。
针对上述问题,采用理论分析和数值模拟相结合的方法,研究半穿甲弹的穿甲过程和毁伤机理,分析加强筋对弹体穿甲能力的影响,确定半穿甲弹对靶板的穿甲剩余速度等数据。研究成果可为加强舰船结构的防护设计提供参考,为半穿甲弹打击敌方舰船目标时的战斗能力计算和毁伤效能评估等提供依据。
1 有限元模型的建立 1.1 模型设计利用Ls-dyna数值模拟软件研究半穿甲弹对加筋板的穿甲过程。首先建立弹丸和加筋板的仿真模型,弹丸总长60 mm,直径130 mm,弹头锥度

|
图 1 弹丸模型 Fig. 1 The projectile model |

|
图 2 加筋板结构模型 Fig. 2 The stiffened plate model |
舰船舷侧板架结构的加强筋往往设计在钢板内侧,仿真过程中弹丸也应从钢板的无筋一侧进行攻击,如图3所示。对模型进行网格划分,有限元模型共包括70875个单元,加强筋与壁板相接处采用共节点方式建模。

|
图 3 弹丸与加筋板有限元模型 Fig. 3 The projectile and stiffened plate finite element models |
美国军用舰船的钢材主要采用HY系列,如HY80,HY100,HY130等,新型的HSLA系列船舶用钢也得到越来越广泛的使用,表1列举了几种美军典型舰船用钢的力学性能[11]。
|
|
表 1 HY系列与HSLA系列钢的力学性能 Tab.1 Mechanical properties of HY and HSLA series steel |
美国常规潜艇、驱护舰以及航母钢板主要采用了HY80,HY100这2种材料,HY100钢主要用于舰艇的外壳等对材料强度要求较高的部位,HY80主要用于舰艇内部结构,强度最高的HY130通常用于核潜艇外壳以及航母甲板等对材料要求更高的部位。另外美国最新研制出的HSLA系列钢材,具有成本低,强度高,韧性好等优点,也得到了广泛应用。
加筋板结构采用HY100钢,该型钢材在美国大中型水面舰艇中得到大量应用,具有较强的代表性,其材料参数如表2所示[12]。
|
|
表 2 HY100钢材料参数 Tab.2 Material parameter of HY100 steel |
在数值模拟过程中,采用Johnson-Cook(简称J-C模型)本构模型对材料进行表征,其本构模型方程式为:
| $ \mathrm{\sigma }=\left(A+B{\varepsilon }^{n}\right)\left[1+C{\rm{ln}}\left(1+\frac{\dot{\varepsilon }}{{\dot{\varepsilon }}_{0}}\right)\right]\left(1-{T}^{*m}\right)。$ | (1) |
式中:
|
|
表 3 HY100钢材料参数 Tab.3 Material parameter of HY100 steel |
材料的失效准则也可以通过J-C模型来定义,其失效参数表达式为:
| $ D=\sum \frac{\Delta \varepsilon }{{\varepsilon }^{f}},$ | (2) |
| $ {\varepsilon }^{f}=\left[{D}_{1}+{D}_{2}{e}^{{D}_{3}{\sigma }^{*}}\right]\left[1+{D}_{4}{\rm{ln}}{\dot{\varepsilon }}^{*}\right]\left[1+{D}_{5}{T}^{*}\right]。$ | (3) |
式中:
|
|
表 4 材料失效参数 Tab.4 Material failure parameter |
为了节省计算资源,半穿甲弹按照刚体进行建模,穿甲过程中可认为弹体不发生任何变形,因此不需要选择具体的材料,只需要根据相应口径弹丸的实际质量设置弹丸模型的材料密度即可,以保证在相应的初始速度条件下,弹丸模型具有与真实弹丸同样的动能。
1.3 单元类型、接触方式及算法选择弹丸、加筋板均采用六面体单元进行精细化网格划分,为消除沙漏效应和避免零能模式,采用全积分单元和沙漏控制,采用Lagrange算法,对于材料大变形等非线性问题的模拟效果较好,弹丸与加筋板之间采用ERODING_SURFACE_TO_SURFACE接触算法。为了使板架结构在穿甲过程中不发生位移,在其边界处设置了位移约束条件,弹丸根据不同情况沿轴向赋予不同的初速。
2 数值模拟分析利用上述有限元模型对半穿甲弹对加筋板穿甲过程进行模拟,分析加筋板在弹丸穿甲作用下的力学性能和毁伤机理,并从弹丸穿甲速度变化以及能量吸收的角度分析加强筋对板架结构抗穿甲特性的影响。
2.1 弹丸对加筋板的侵彻过程分析对弹丸赋予500 m/s的初速度,以90°垂直侵彻加筋板无筋部位,由于弹丸速度较高,动能较大,当弹丸接触加筋板时,加筋板局部因压力突变而发生塑性变形,如图4(a)所示。随着弹丸进一步侵彻,加筋板局压力进一步增大导致钢板材料失效,弹头处钢板出现破口,如图4(b)所示。破口在弹丸挤进过程中呈现扩孔效应,如图4(c)所示。随着弹丸进一步挤进,破口随之增大,并出现花瓣毁伤模式,如图4(d)所示。
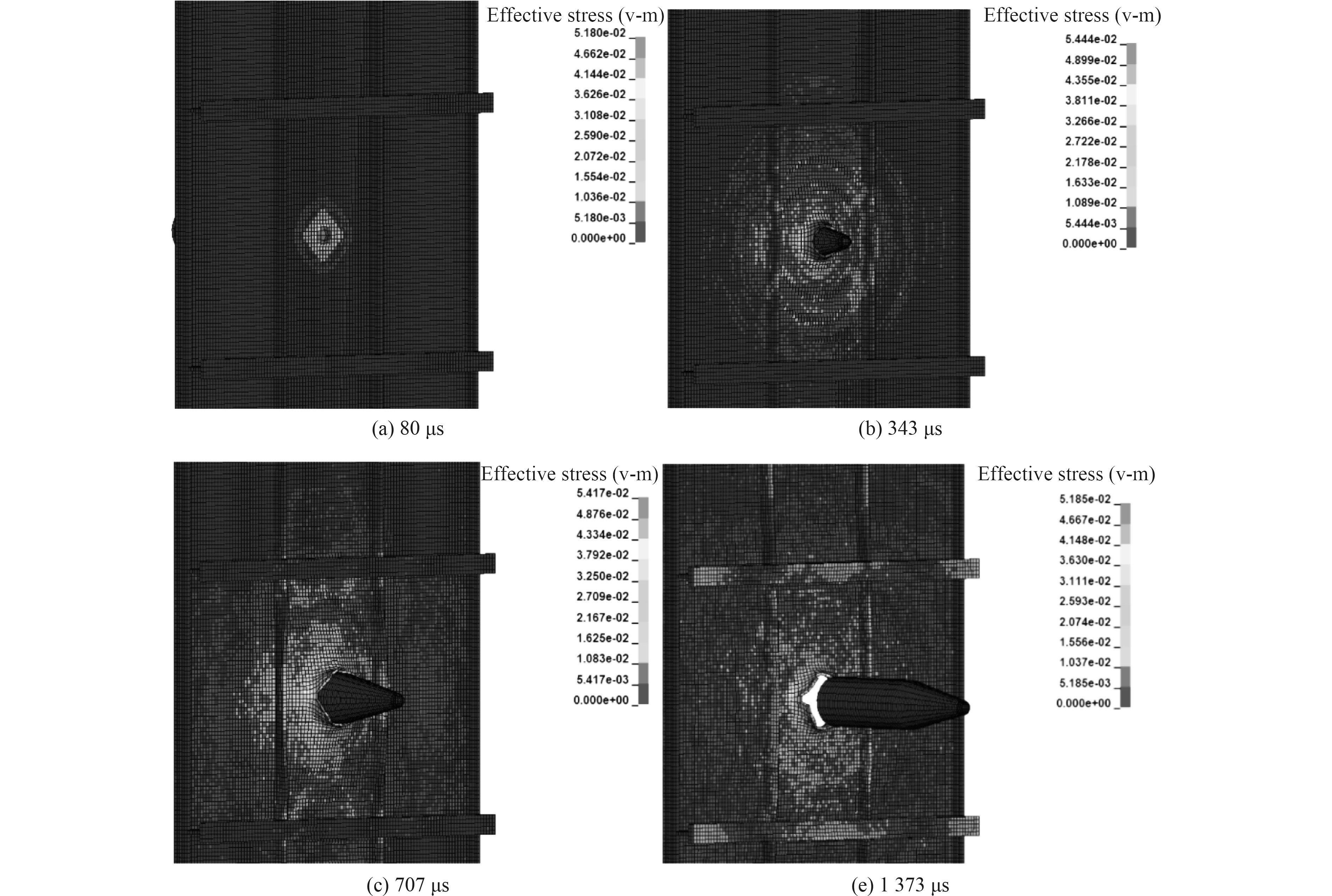
|
图 4 弹丸穿甲过程von mises应力云图(对无筋部位) Fig. 4 Von mises stress cloud image of projectile armor piercing process(on the unreinforced part) |
当弹丸以同样的初速撞击加筋板纵横筋相交部位时,其穿甲过程与对无筋部位的穿甲有着明显区别。随着弹丸撞击能力的传播,加强筋承受较大的应力,并沿着筋的方向传播,如图5(a)所示。随着弹丸的侵彻,钢板出现破口,弱筋首先断裂,如图5(b)所示。强筋在弹丸侵彻过程中出现了偏移变形,但并未发生断裂,如图5(c)所示。受加强筋的影响,破口呈现不规则形状,如图5(d)所示。

|
图 5 弹丸穿甲过程von mises应力云图(对有筋部位) Fig. 5 Von mises stress cloud image of projectile armor piercing process(on the stiffened part) |
当弹丸在侵彻加筋板无筋部位时,其速度曲线整体呈非线性,弹丸从接触钢板到破口出现期间速度下降较快,钢板约在运行至120 μs左右钢板出现破口,部分压力得到释放,此时弹丸速度下降出现明显变缓,至160 μs往后,弹丸处于扩孔过程,速度变化较稳定,整体呈线性,直至完全贯穿,弹丸总体速度下降了约23 m/s,如图6(a)所示。
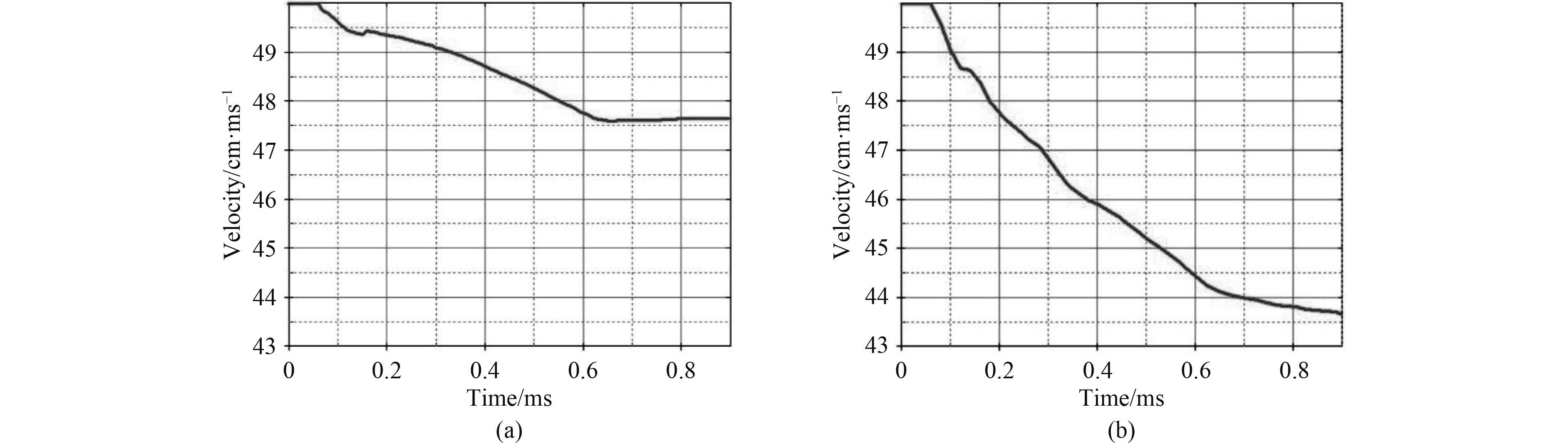
|
图 6 弹丸穿甲过程速度历程 Fig. 6 Velocity history of projectile armor-piercing process |
当弹丸在侵彻加筋板纵横筋相交处时,其速度曲线与侵彻无筋部位时有明显区别。弹丸在侵彻过程中,其速度曲线整体呈下降逐渐减缓的趋势,期间未因出现破口而出现明显变化,主要原因是强筋始终未断裂,对弹丸速度变化起到较大影响。弹丸总体速度下降了约63 m/s,如图6(b)所示。
当弹丸在侵彻加筋板无筋部位时,钢板吸收了主要的能量,而加强筋由于未与弹丸直接接触,所吸收的能量也十分有限,因此对抵抗弹丸的侵彻效果不明显,如图7(a)所示。当弹丸在侵彻加筋板纵横筋相交处时,钢板和加强筋均吸收了较大能量,如图7(b)所示。可以看出,钢板单独吸收的能量也要比侵彻无筋部位时要大,总体能量吸收大小顺序依次为钢板、强筋、弱筋,可见加强筋对于提高整个加筋板的强度发挥着重要作用。
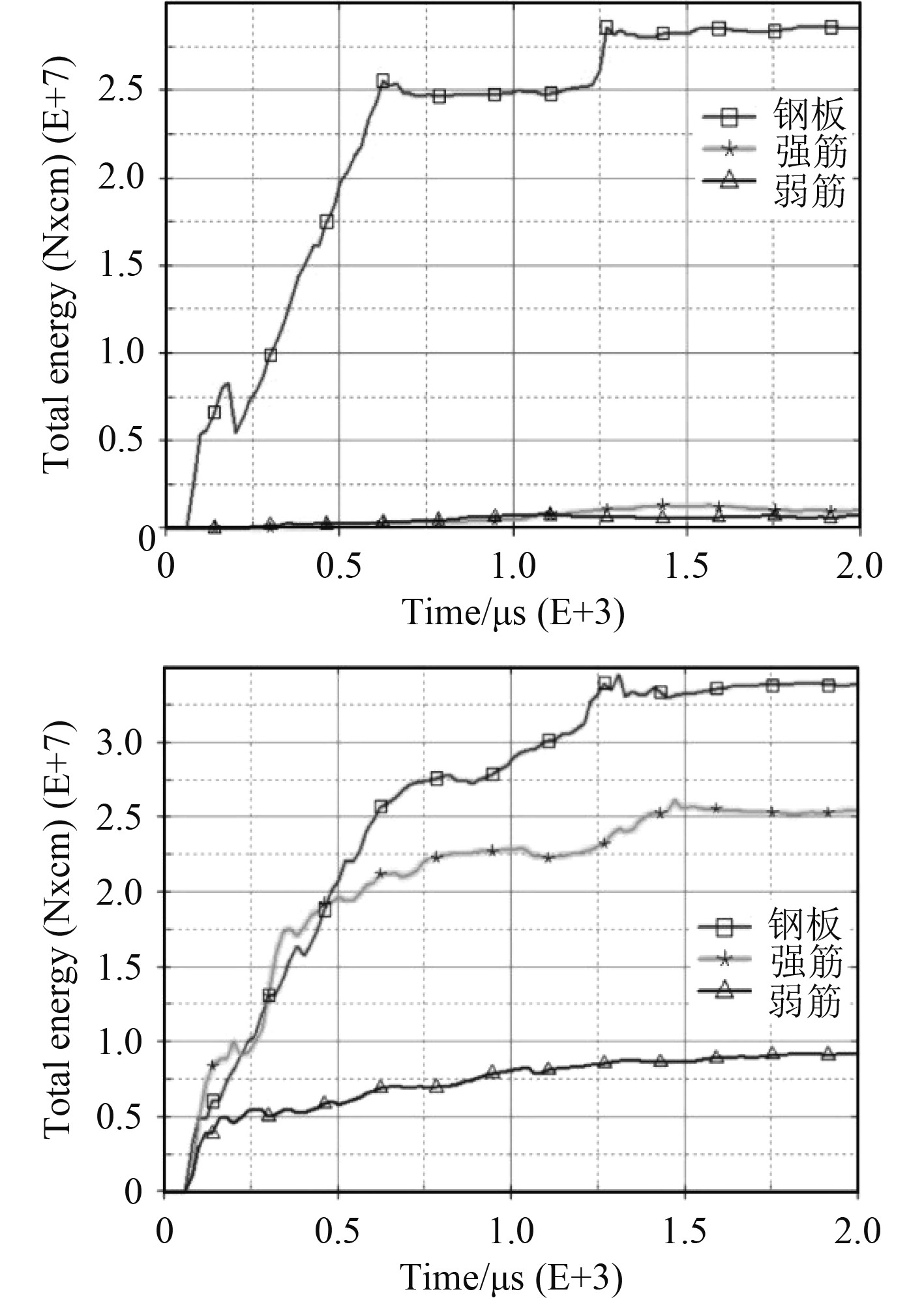
|
图 7 加筋板总能量变化过程 Fig. 7 Change process of total energy of stiffened plate |
弹丸以不同初速垂直侵彻加筋板无筋部位时,弹丸剩余速度与初速之间的关系如图8所示。可以看出,弹丸在低速侵彻阶段的剩余速度与初速的变化曲率较高速阶段要稍微偏大一些,随着弹丸初速的增大,弹丸剩余速度与初速之间近似呈线性关系。
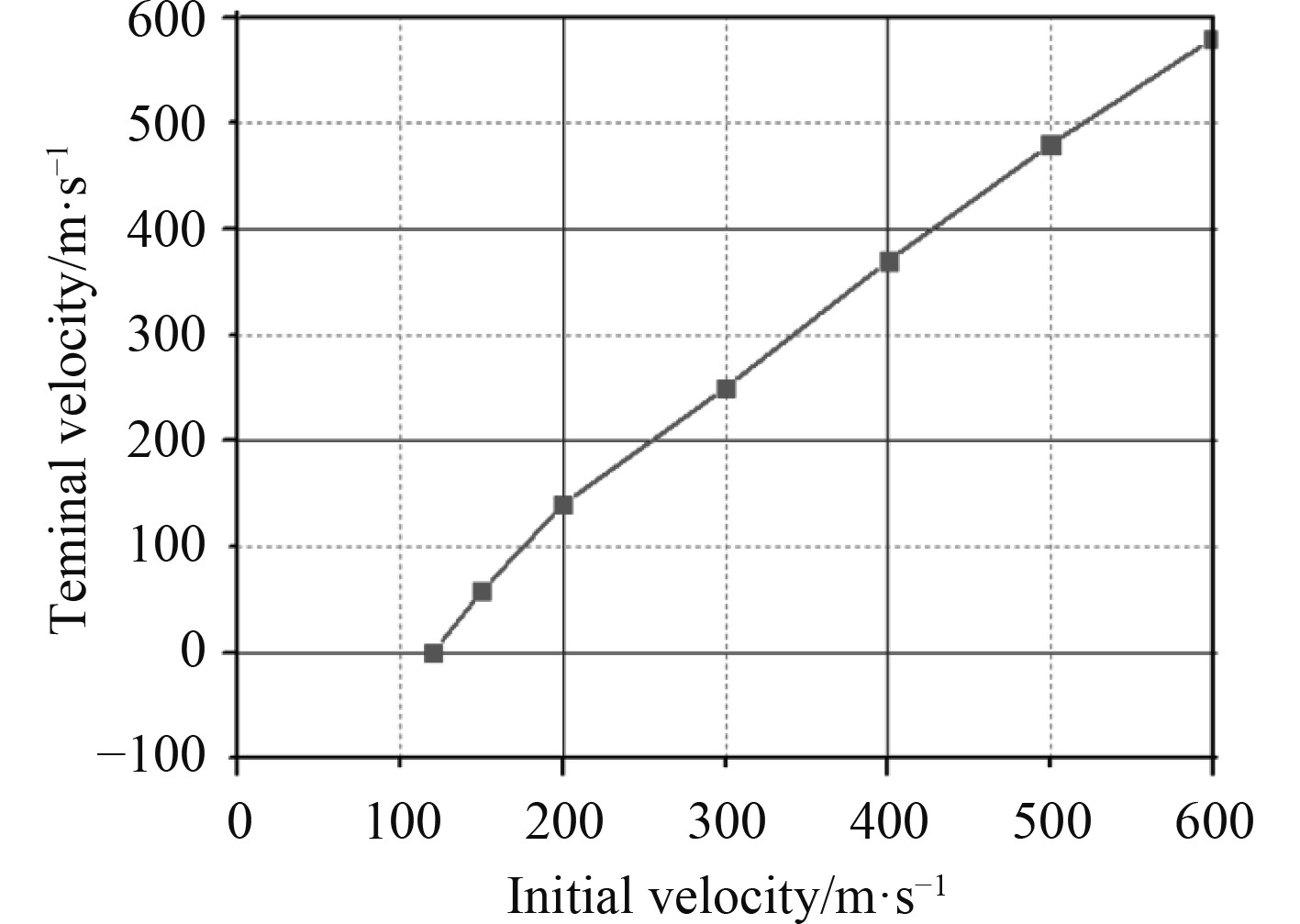
|
图 8 不同初速条件下弹丸垂直侵彻加筋板剩余速度 Fig. 8 Residual velocity of vertical penetration of projectile into stiffened plate at different initial velocities |
当弹丸侵彻加筋板的无筋部位时,可以看作是弹丸对均质板的侵彻过程,因此可以采用文献[3]的剩余速度模型进行计算。假设弹丸击穿钢板所需能量的大小正好是弹丸极限穿甲时的动能大小,根据能量原理可得:
| $ \frac{1}{2}M{v}_{0}^{2}=\frac{1}{2}M{v}_{c}^{2}+\frac{1}{2}M{v}_{f}^{2}+\frac{1}{2}m{v}_{f}^{2}。$ | (4) |
式中:M为弹丸的质量;m为塞块的质量;
| $ {v}_{f}=\sqrt{\frac{M({v}_{0}^{2}-{v}_{c}^{2})}{M+m}}。$ | (5) |
对于均质钢板的极限穿甲速度采用K.A.贝尔金公式求解,其表达式为:
| $ {v}_{c}=6060\sqrt{k{\delta }_{s}\left(1+\phi \right)}{D}^{0.75}{H}^{0.7}/\left({M}^{0.5}\mathrm{cos}\alpha \right)。$ | (6) |
式中:
| $ k=\left(2\sqrt{2}/3\right){C}_{e}^{0.5}[0.2245i/(1+\phi )+0.0034],$ | (7) |
其中,i为弹丸头部形状系数,计算公式为:
| $ i=\left[\left(8-5{n}_{2}\right)/15{n}_{1}\right]\sqrt{\left(1-{n}_{1}\right)\left(2{n}_{1}+{n}_{2}-1\right)}+{n}_{2}^{2}。$ | (8) |
式中:
假设弹丸穿甲过程中,破扣处崩落的塞块质量为m,其表达式为:
| $ m=K(\text{π} {D}^{2}/4)(H/\mathrm{c}\mathrm{o}\mathrm{s}\alpha ){\rho }_{1}。$ | (9) |
式中:
利用Ls-dyna有限元仿真软件模拟弹丸在5种不同初速条件下对加筋板无筋部位垂直穿甲的过程,取不同工况下弹丸穿甲后的剩余速度。同时,利用穿甲剩余速度理论求解相同工况下弹丸的剩余速度,将数值仿真结果与理论计算结果做对比,如表5所示。
|
|
表 5 弹丸剩余速度数值仿真结果与理论计算结果的对比 Tab.5 Comparison between numerical simulation and theoretical calculation of residual velocity of the projectile |
可以看出,在相同弹丸初速、侵彻角度等条件下,弹丸的穿甲剩余速度数值仿真结果与理论计算结果基本一致,最大误差不超过6.5%,说明数值仿真结果可信。
4 结 语通过利用数值模拟和理论计算相结合的方法,分析半穿甲弹对加筋板结构穿甲过程中的结构响应、毁伤机理以及弹丸穿甲剩余速度,得到了弹丸对加筋板有筋部位和无筋部位穿甲时,加筋板的破口形态、能量吸收以及弹丸的速度变化情况,并分析了弹丸在不同初速条件下对加筋板的穿甲剩余速度。研究表明,弹丸在极限穿甲速度附近,其穿甲剩余速度与初速的之间曲率较大,且呈非线性关系,随着弹丸初速的增大,弹丸剩余速度与初速之间近似呈线性关系。当弹丸对加筋板有筋部位穿甲时,加强筋能够有效吸收弹丸冲击的能力,弹丸穿甲速度下降较明显;当弹丸对加筋板无筋部位穿甲时,加强筋对于抵抗弹丸的侵彻作用不明显。可见,分析弹丸对加筋板的穿甲问题,需要首先明确弹丸的着靶部位。
| [1] |
陈长海, 朱锡, 侯海量. 加筋板架抗动能穿甲的等效防护厚度研究[J]. 海军工程大学学报, 2010, 22(1): 31-38. CHEN C H, ZHU X, HOU H L. Equivalent protection thickness of stiffened plate against kinetic piercing[J]. Journal of Naval University of Engineering, 2010, 22(1): 31-38. |
| [2] |
张宁. 半穿甲弹对舰船钢的穿甲弹道特性研究[D]. 南京: 南京理工大学, 2016.
|
| [3] |
段卓平. 半穿甲弹丸对加筋靶板侵彻的终点弹道的实验和理论研究[J]. 爆炸与冲击, 2005, 25(6): 547-552. DUAN Z P. The experimental and theoretical research for end-point trajectory of warhead penetrating ribbings structural target[J]. Explosion and Shock Waves, 2005, 25(6): 547-552. DOI:10.3321/j.issn:1001-1455.2005.06.011 |
| [4] |
屈科佛, 姚勇, 邓勇军, 等. 多层靶板抗不同形状高速破片侵彻性能研究[J]. 兵器装备工程学报, 2020, 41(2): 6-9. QU K, YAO Y, DENG Y J, et al. Numerical study on effect of fragment shape on penetration resistance of multi-layered target[J]. Journal of Ordnance Equipment Engineering, 2020, 41(2): 6-9. DOI:10.11809/bqzbgcxb2020.02.002 |
| [5] |
董三强, 蔡星会, 王国亮, 等. 攻角对半穿甲战斗部侵彻航母双层靶板的效应研究[J]. 舰船科学术, 2017, 39(11): 33-37. DONG S Q, CAI X H, WANG Guoliang, et al. Numerical simulation research on effect of warhead penetrating double-layer aircraft carrier targets[J]. Ship Science and Technology, 2017, 39(11): 33-37. |
| [6] |
刘润华, 陈国光, 侯飞, 等. 弹丸侵彻陶瓷/钢复合靶板数值研究[J]. 兵器装备工程学报, 2020, 41(3): 183-188. LIU R H, CHEN G G, HOU F, et al. Numerical study of projectile penetration into ceramic/steel composite target plate[J]. Journal of Ordnance Equipment Engineering, 2020, 41(3): 183-188. DOI:10.11809/bqzbgcxb2020.03.037 |
| [7] |
熊飞, 石全, 王广彦, 等. 不同侵彻速度下陶瓷复合装甲等效均质钢靶板的建立[J]. 火力与指挥控制, 2014, 40(4): 72-75. XIONG F, SHI Q, WANG G Y, et al. Establishment of equivalent steel target of ceramic compound armor at different projectile’s velocity[J]. Fire Control & Command Control, 2014, 40(4): 72-75. |
| [8] |
宋卫东, 宁建国, 张中国, 等. 多层加筋靶板的侵彻模型与等效方法[J]. 弹道学报, 2004, 16(3): 54-59. SONG W D, NING J G, ZHANG Z G, et al. Penetration model and equivalence method of multi-layered stiffener plates[J]. Journal of Ballistics, 2004, 16(3): 54-59. |
| [9] |
展婷变, 吕淑芳, 黄德雨. 截卵形弹体正侵彻加强筋结构靶的理论分析[J]. 弹道学报, 2012, 24(1): 52-57. ZHAN T B, LV S F, HUANG D Y. Theoretical analysis on normal penetration of truncated oval-nosed projectile into stiffened plate[J]. Journal of Ballistics, 2012, 24(1): 52-57. DOI:10.3969/j.issn.1004-499X.2012.01.011 |
| [10] |
张宁. 均质靶板和加筋靶板抗弹性能的数值模拟研究[J]. 兵器装备工程学报, 2016, 37(2): 30-33. ZHANG N. Numerical simulation for effect of homogeneous and stiffened plates on resisting projectile penetration[J]. Journal of Ordnance Equipment Engineering, 2016, 37(2): 30-33. DOI:10.11809/scbgxb2016.02.008 |
| [11] |
王文杰. 高性能先进舰船用合金材料的应用现状及展望[J]. 材料导报, 2013, 6(7): 98-105. WAND W J. The application status and perspective of alloys for high performance and advanced naval vessels[J]. Materials Reports, 2013, 6(7): 98-105. DOI:10.3969/j.issn.1005-023X.2013.07.022 |
| [12] |
辛春亮, 薛再清, 涂建, 等. 有限元分析常用材料参数手册[M]. 北京: 机械工业出版社, 2020: 77–78.
|
 2022, Vol. 44
2022, Vol. 44
