现有诱饵发射装置多采用舷侧发射形式,发射时存在较大侧滑角,在侧力及力矩作用下,为保证诱饵安全离艇,对其出管速度具有较高要求,但过高的出管速度同时也会带来较大的发射噪声。究竟以多大的速度出管,需采用适当的方法对其出管安全性进行验证。首先对诱饵出管外弹道进行研究,并得到艇速对诱饵出管安全性的影响规律,从而为诱饵智能发射提供输出依据。以某气动不平衡式发射装置为例,建立“高压气瓶-控制阀-诱饵发射管”系统内弹道模型。基于安全离艇的出管速度和发射深度作为研究变量,通过控制阀芯运动速度来实现对其内弹道的调节以满足所需的出管速度,并对上述结果构建样本数据,通过多元拟合的方法得到程控阀芯运动速度与发射深度和出管速度的关系式,从而为内弹道智能控制提供输入依据。
本文为武器智能发射及控制提供一种高效的研究方法,在保证器材安全离艇的同时,实现较低的发射噪声及最优的能量利用率。基于刚体运动六自由度模型进行理论计算,并实现了诱饵出管过程仿真,可实时观察诱饵与发射管的相对位置,为判断其出管安全性提供有效方法。采用多元拟合的方法,得到了基于安全离艇出管速度和发射深度的控制阀芯运动速度规律,从而为内弹道智能控制提供决策依据。
1 诱饵运动六自由度模型计算理论 1.1 控制方程[1-2]诱饵运动的六自由度控制方程形式如下:
| $ m\frac{{{{\rm{d}}^2}x}}{{{\rm{d}}{t^2}}} = {[{F_x}]_{ground}},$ | (1) |
| $ m\frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{t^2}}} = {[{F_y}]_{ground}},$ | (2) |
| $ m\frac{{{{\rm{d}}^2}{\textit{z}}}}{{{\rm{d}}{t^2}}} = {[{F_{\textit{z}}}]_{ground}},$ | (3) |
| $ {J_x}\frac{{{\rm{d}}{\omega _x}}}{{{\rm{d}}t}} = \sum {{M_x}},$ | (4) |
| $ {J_y}\frac{{{\rm{d}}{\omega _y}}}{{{\rm{d}}t}} = \sum {{M_y}},$ | (5) |
| $ {J_{\textit{z}}}\frac{{{\rm{d}}{\omega _{\textit{z}}}}}{{{\rm{d}}t}} = \sum {{M_{\textit{z}}}}。$ | (6) |
式(1)~式(3)为地面坐标系下建立的平动微分方程,用于求解诱饵运动轨迹(x, y, z)。其中,
诱饵运动过程中受到螺旋桨产生的推力T,阻力D、升力L、侧力Z,重浮力
由于诱饵受到的力定义方式表现在不同坐标系下,因此需要通过旋转矩阵将其统一到同一坐标系下建立运动微分方程。
地面坐标系和雷体坐标系之间存在着俯仰角
| $ \begin{split} \left[ {\begin{array}{*{20}{c}} x \\ y \\ {\textit{z}} \end{array}} \right] =& {L_x}(\varphi ){L_{\textit{z}}}(\theta ){L_y}(\psi )\left[ {\begin{array}{*{20}{c}} {{x_0}} \\ {{y_0}} \\ {{{\textit{z}}_0}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \varphi }&{\sin \varphi } \\ 0&{ - \sin \varphi }&{\cos \varphi } \end{array}} \right]\times\\ &\left[ {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta }&0 \\ { - \sin \theta }&{\cos \theta }&0 \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \psi }&0&{ - \sin \psi } \\ 0&1&0 \\ {\sin \psi }&0&{\cos \psi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_0}} \\ {{y_0}} \\ {{{\textit{z}}_0}} \end{array}} \right],\hfill \\ \end{split} $ | (7) |
| $ \begin{split} \left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{y_1}} \\ {{{\textit{z}}_1}} \end{array}} \right] =& {L_{\textit{z}}}(\alpha ){L_y}(\beta )\left[ {\begin{array}{*{20}{c}} x \\ y \\ {\textit{z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{\sin \alpha }&0 \\ { - \sin \alpha }&{\cos \alpha }&0 \\ 0&0&1 \end{array}} \right]\times\\ &\left[ {\begin{array}{*{20}{c}} {\cos \beta }&0&{ - \sin \beta } \\ 0&1&0 \\ {\sin \beta }&0&{\cos \beta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x \\ y \\ {\textit{z}} \end{array}} \right]。\end{split} $ | (8) |
建立诱饵运动六自由度方程的旋转关系。将速度坐标系下的阻力D、升力L、侧力Z以及阻尼力旋转到雷体坐标系下,如下式:
| $ {\left[ {\begin{array}{*{20}{c}} {{F_x}} \\ {{F_y}} \\ {{F_{\textit{z}}}} \end{array}} \right]_{body}} = {L_{\textit{z}}}(\alpha ){L_y}(\beta )\left[ {\begin{array}{*{20}{c}} {D + {X_d}} \\ {L + {Y_d}} \\ {Z + {Z_d}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} T \\ 0 \\ 0 \end{array}} \right] ,$ | (9) |
将转化后的上述各力旋转到地面坐标系下,如下式:
| $ {\left[ {\begin{array}{*{20}{c}} {{F_x}} \\ {{F_y}} \\ {{F_{\textit{z}}}} \end{array}} \right]_{ground}} = {L_x}(\varphi ){L_{\textit{z}}}(\theta ){L_y}(\psi ){\left[ {\begin{array}{*{20}{c}} {{F_x}} \\ {{F_y}} \\ {{F_{\textit{z}}}} \end{array}} \right]_{body}} + \left[ {\begin{array}{*{20}{c}} 0 \\ {\Delta G} \\ 0 \end{array}} \right]。$ | (10) |
阻力:
| $ D = {C_{xS}}\frac{1}{2}\rho {V^2}S ,$ | (11) |
其中,
升力:
| $ L = C_y^\alpha \alpha \frac{1}{2}\rho {V^2}S + C_y^{{\delta _e}}{\delta _e}\frac{1}{2}\rho {V^2}S。$ | (12) |
其中,第1项为攻角
侧力:
| $ Z = C_{\textit{z}}^\beta \beta \frac{1}{2}\rho {V^2}S + C_{\textit{z}}^{{\delta _r}}{\delta _r}\frac{1}{2}\rho {V^2}S。$ | (13) |
其中,第1项为侧滑角
阻尼力:
由于
| $ {Y_d} = C_y^{{\omega _{\textit{z}}}}\frac{1}{2}\rho VSl{\omega _{\textit{z}}},$ | (14) |
| $ {Z_d} = C_{\textit{z}}^{{\omega _y}}\frac{1}{2}\rho VSl{\omega _y} 。$ | (15) |
式中:
俯仰力矩:
| $ \begin{split}\sum {M_{\textit{z}}} =& (m_{\textit{z}}^\alpha \alpha + m_{\textit{z}}^{{\delta _e}}{\delta _e})\frac{1}{2}\rho {V^2}Sl + m_{\textit{z}}^{{\omega _z}}\times\\ &\frac{1}{2}\rho VS{l^2}{\omega _{\textit{z}}} + G \cdot \Delta L \cdot \cos \theta \cos \varphi。\end{split}$ | (16) |
其中,
偏航力矩:
| $\begin{split} \sum {M_y} = & (m_y^\beta \beta + m_y^{{\delta _r}}{\delta _r})\frac{1}{2}\rho {V^2}Sl +\\ & m_y^{{\omega _y}}\frac{1}{2}\rho VS{l^2}{\omega _y} + G \cdot \Delta L \cdot \cos \theta \sin \varphi。\end{split}$ | (17) |
其中,
滚转力矩:
| $ \sum {{M_x} = m_x^\beta \beta \frac{1}{2}\rho {V^2}Sl} + \Delta {M_p} 。$ | (18) |
其中,
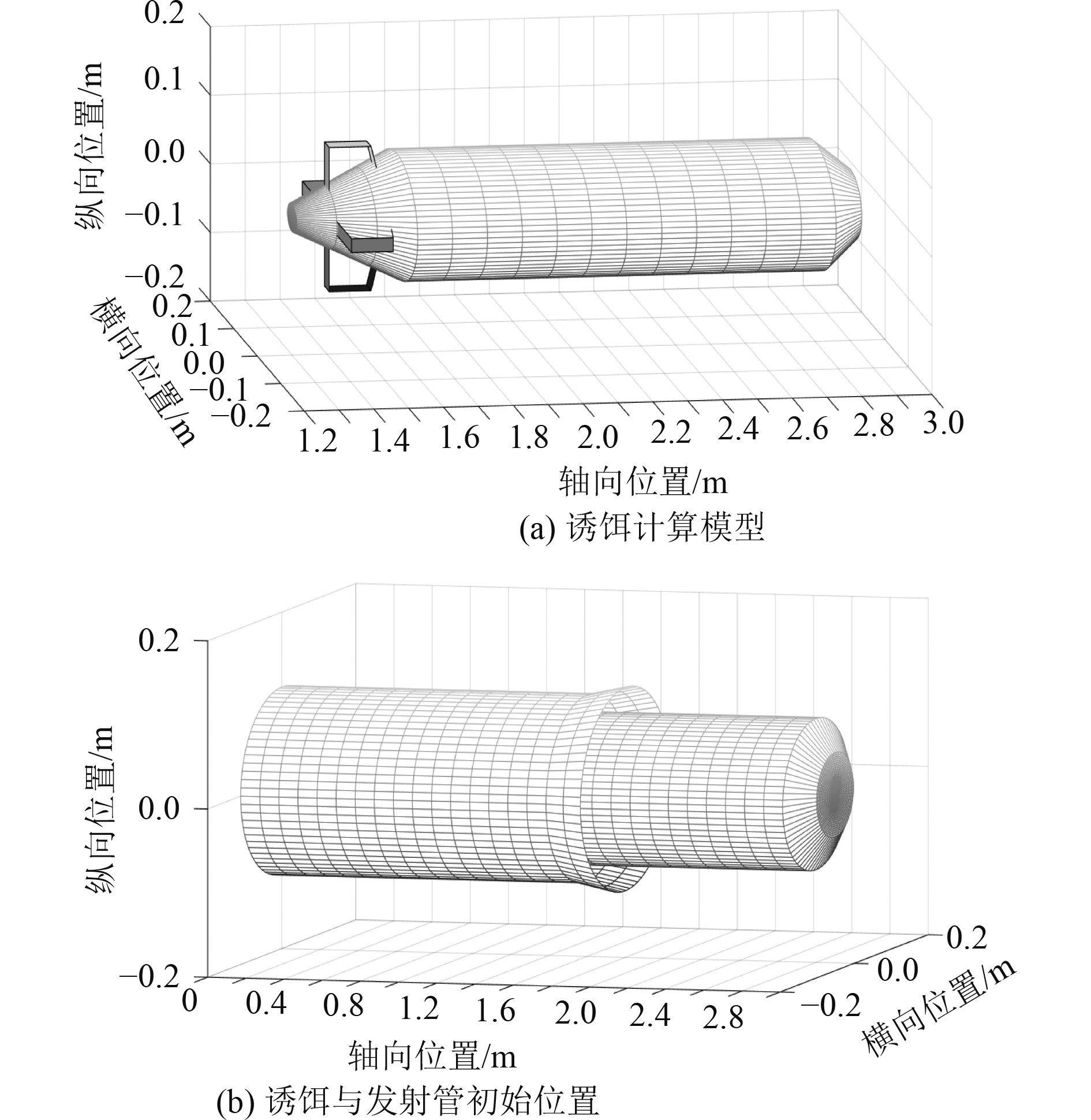
发射管口通常按某锥度设计成喇叭口状,诱饵采用某通信浮标参数,在Matlab中绘制诱饵和喇叭口计算模型如图1所示。
|
图 1 诱饵及发射管计算模型 Fig. 1 Models of the decoy and the tube |
以某40 N左右正浮力诱饵为例进行计算,根据文献[3],参考其诱饵升力系数、俯仰力矩系数如下:
当攻角在−35°~+35°之间时,
| $ {C_y}(\alpha ) = C_y^\alpha \alpha = 2.837\;4\alpha + 16.155\;3{\alpha ^3} - 20.856\;8{\alpha ^5} ,$ | (19) |
| $ {m_{\textit{z}}}(\alpha ) = m_{\textit{z}}^\alpha \alpha = 0.799\;1\alpha - 3.793\;5{\alpha ^3} + 5.234\;5{\alpha ^5} 。$ | (20) |
式中攻角均需转为弧度单位。
当攻角大于
对于侧力系数和偏航力矩系数,当
由文献[3]可知,阻尼力和阻尼力矩对角速度的旋转导数:
| $ C_y^{{\omega _{\textit{z}}}} = - C_{\textit{z}}^{{\omega _y}} = 0.797\;6 \text{,} m_{\textit{z}}^{{\omega _{\textit{z}}}} = m_y^{{\omega _y}} = - 0.376\;0 。$ | (21) |
数值计算中,为方便观察离艇过程,不考虑滚转运动,并且在非自航发射中,中间弹道过程不启动螺旋桨,也不对舵面进行操纵,即在计算中作如下简化:
| $ \varphi = 0;{\text{ }}{\omega _x} = 0;{\text{ }}{\delta _e} = 0;{\text{ }}{\delta _r} = 0 。$ | (22) |
以诱饵圆柱段末端面进入发射管与喇叭口交界处为0时刻进行计算,结果如下:
1)艇速3 m/s工况
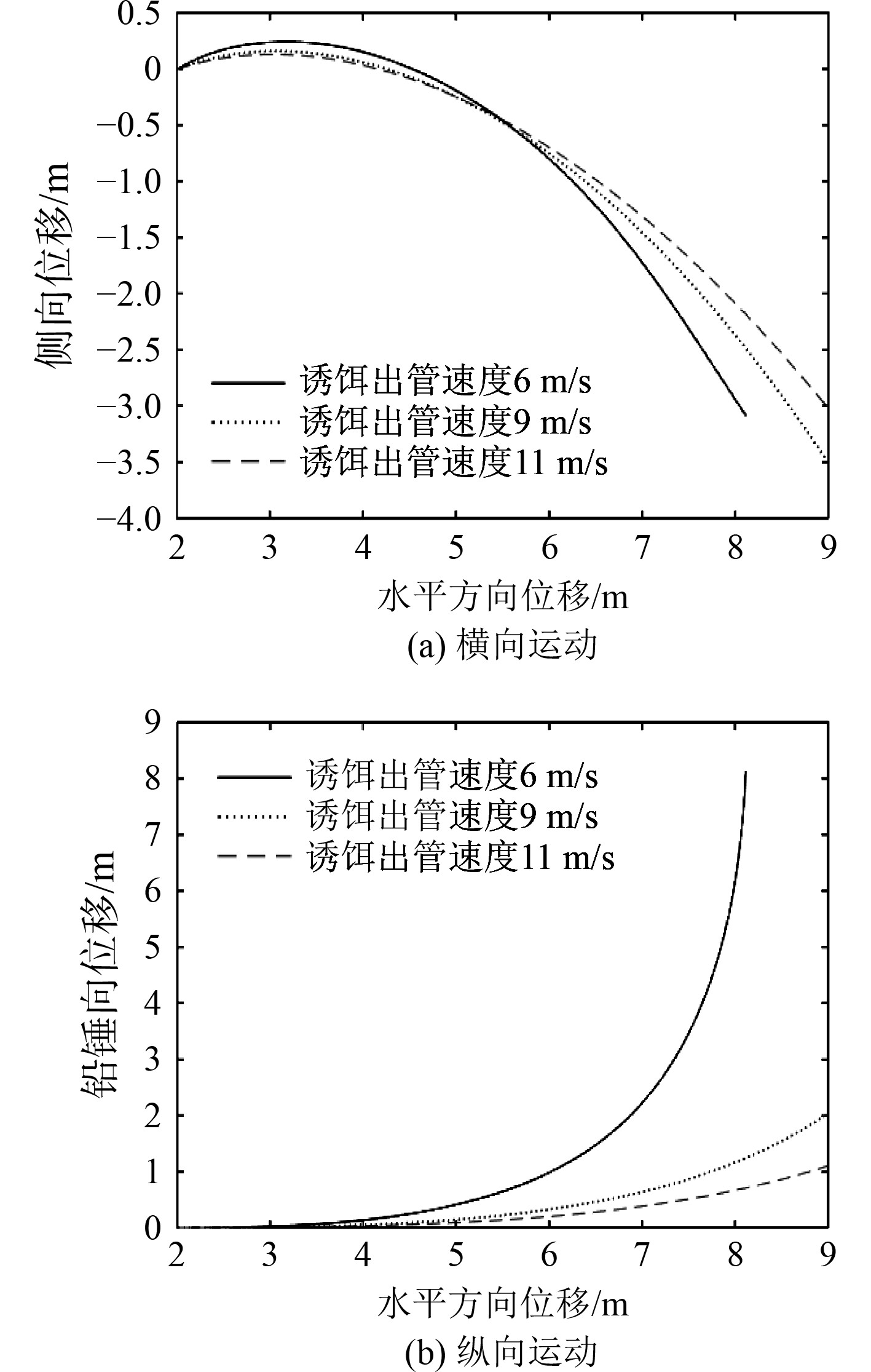
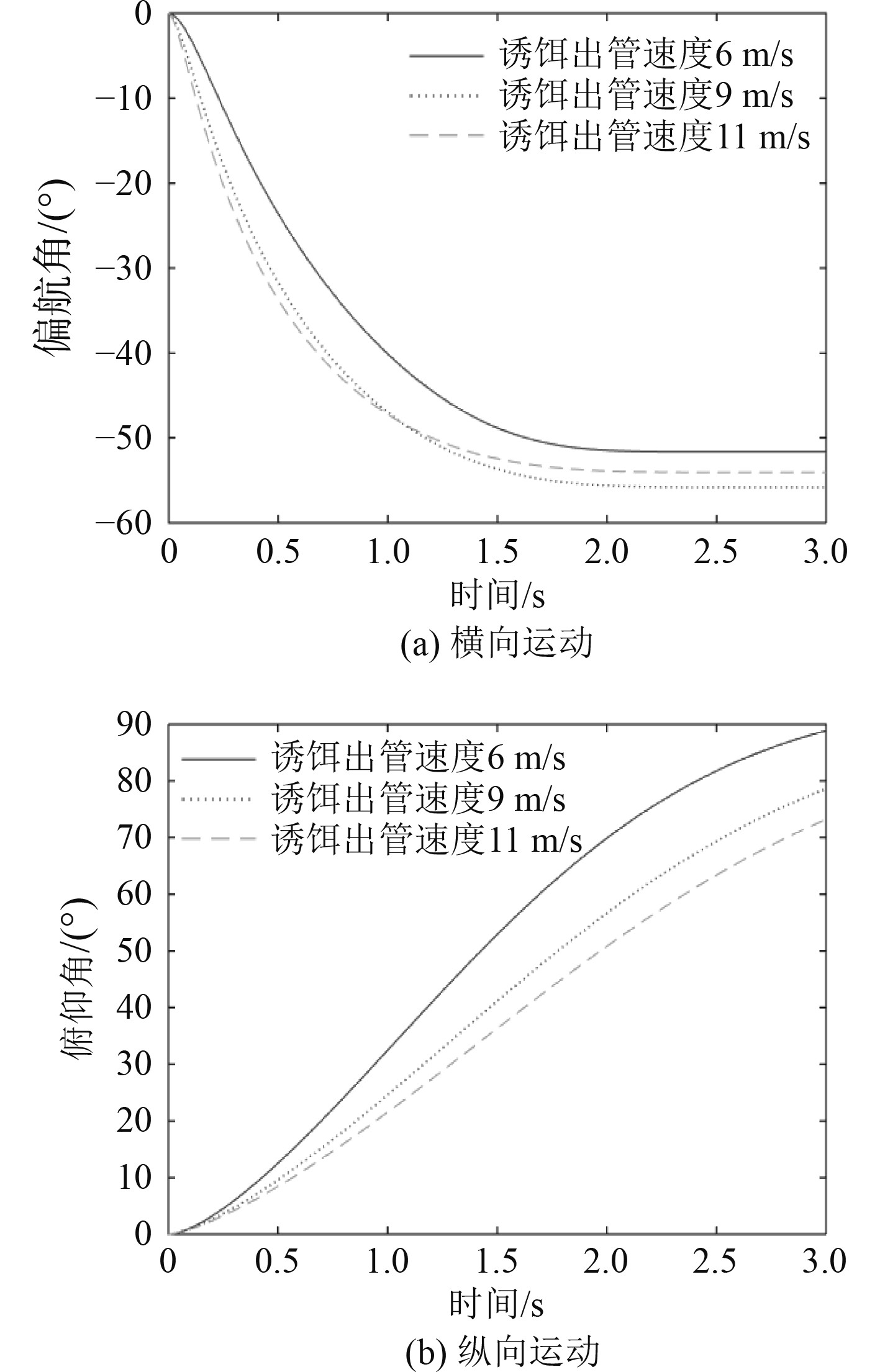
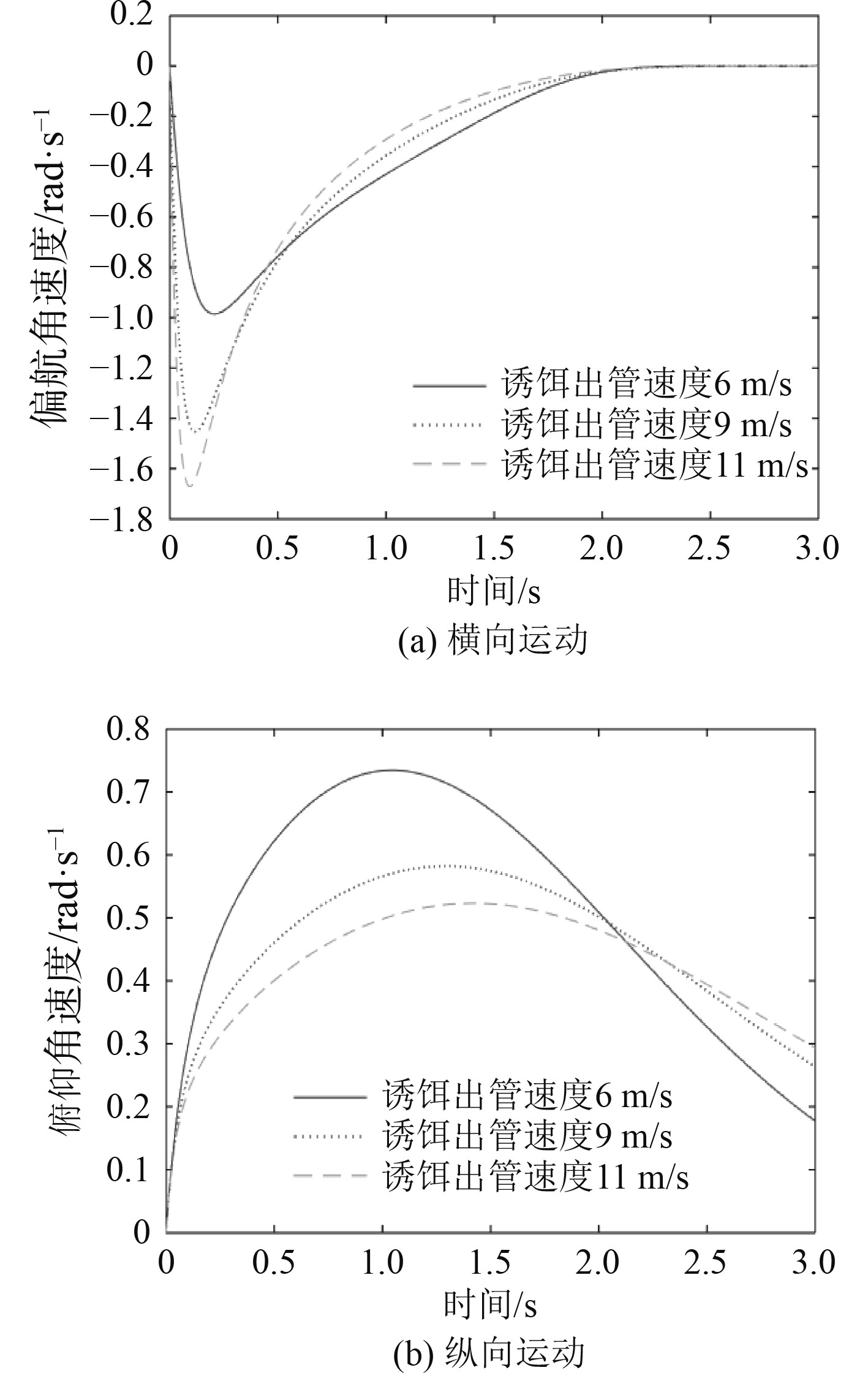
对于横向运动,通过图2和图3可以看出,诱饵发射以后,由于初始较大侧滑角的存在,因此在侧力和侧力矩作用下,其横向运动轨迹会发生回转[6],且诱饵作偏航运动。由图4和图5可知,当旋转角速度较大时,出现较大的横向阻尼力矩,与侧滑角引起的偏航力矩相互抵消,此时旋转角速度又逐渐减小。由图3和图4可知,当偏航角速度减小至0时,对于诱饵不同出管速度的工况(6 m/s,9 m/s,11 m/s),其最终分别保持相应固定的偏航角52°,56°,54°进行运动。侧力亦是如此,由于阻尼力的存在与侧力相互抵消,当侧向合力减小至0时,横向速度方向也不再发生旋转,所以横向运动曲线后续不再回转。
|
图 2 不同出管速度下,诱饵重心运动轨迹 Fig. 2 The trajectory of the gravity center of the decoy at different terminal velocity |
|
图 3 不同出管速度下,诱饵绕浮心旋转角度 Fig. 3 The rotation of the decoy around the center of buoyancy at different terminal velocity |
|
图 4 不同出管速度下,诱饵旋转角速度 Fig. 4 The angular velocity of the decoy at different terminal velocity |
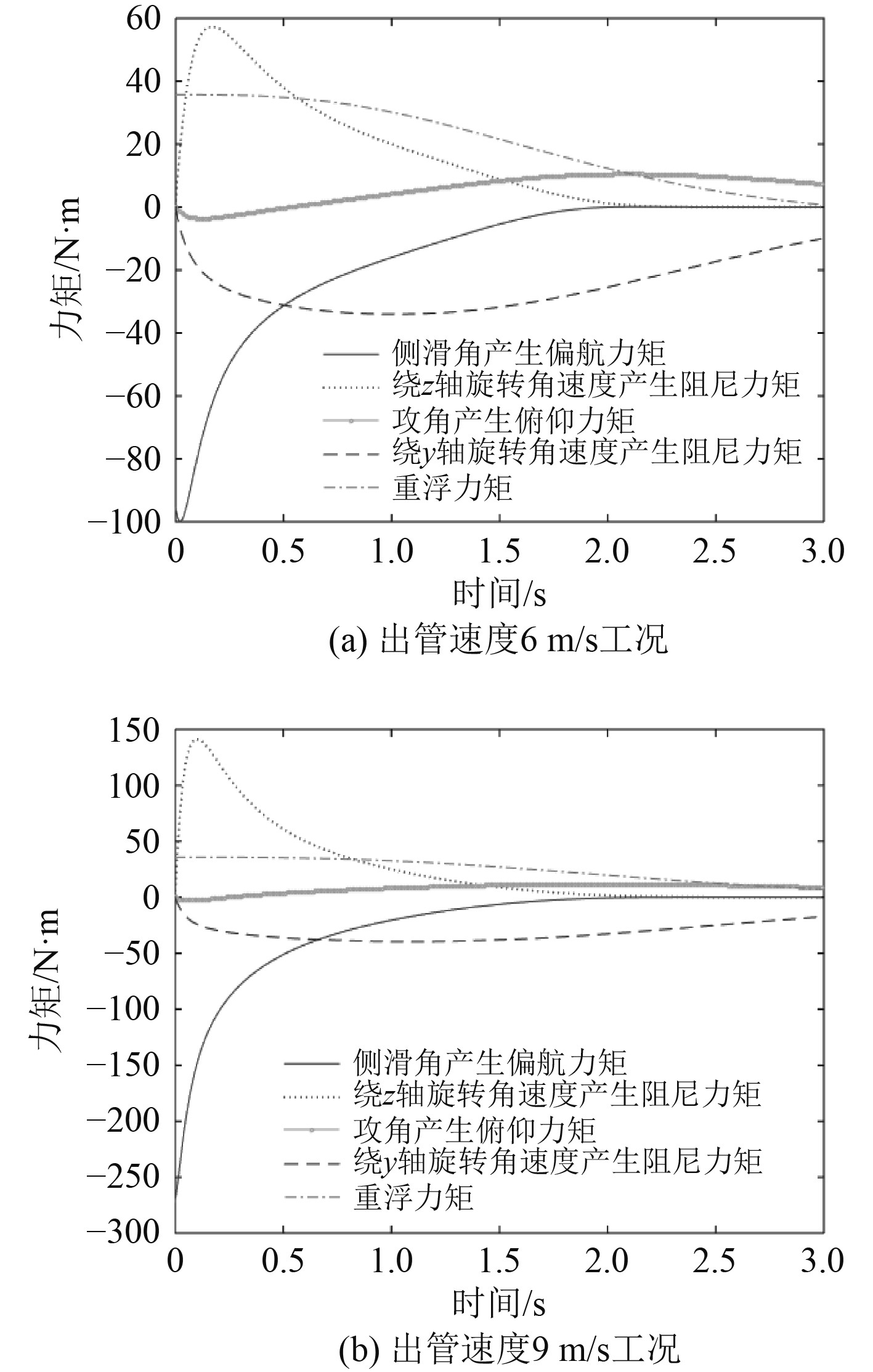
|
图 5 诱饵运动所受力矩(前2项为横向力矩,后3项为纵向力矩) Fig. 5 Moments applied to the decoy (The first two terms are lateral moments, the rest terms are longitudinal moments) |
对于纵向运动,在正浮力作用下,诱饵向上运动,初始阶段为负攻角运动。由图4和图5可知,重力和浮力共同作用产生较大的抬头力矩,因此加快了诱饵抬头速率,逐渐转为正攻角运动。随着俯仰角速度的变化,相应地纵向阻尼力矩也随之变化。由图3可知,出管3 s左右,对于诱饵不同出管速度的工况(6 m/s,9 m/s,11 m/s),其分别可相应抬头约90°,80°,73°。
相比于纵向运动而言,由于横向运动中初始较大侧滑角的存在,因此横向运动出管安全条件比纵向要苛刻,所以出管安全仅需考虑横向运动即可。
从图6可以看出,在3 m/s艇速下,当诱饵以4 m/s速度出管时,诱饵右鳍舵很明显与发射管口发生碰撞。当诱饵以5 m/s速度出管时,诱饵右鳍舵不与喇叭口发生碰撞,能够保证出管安全性。
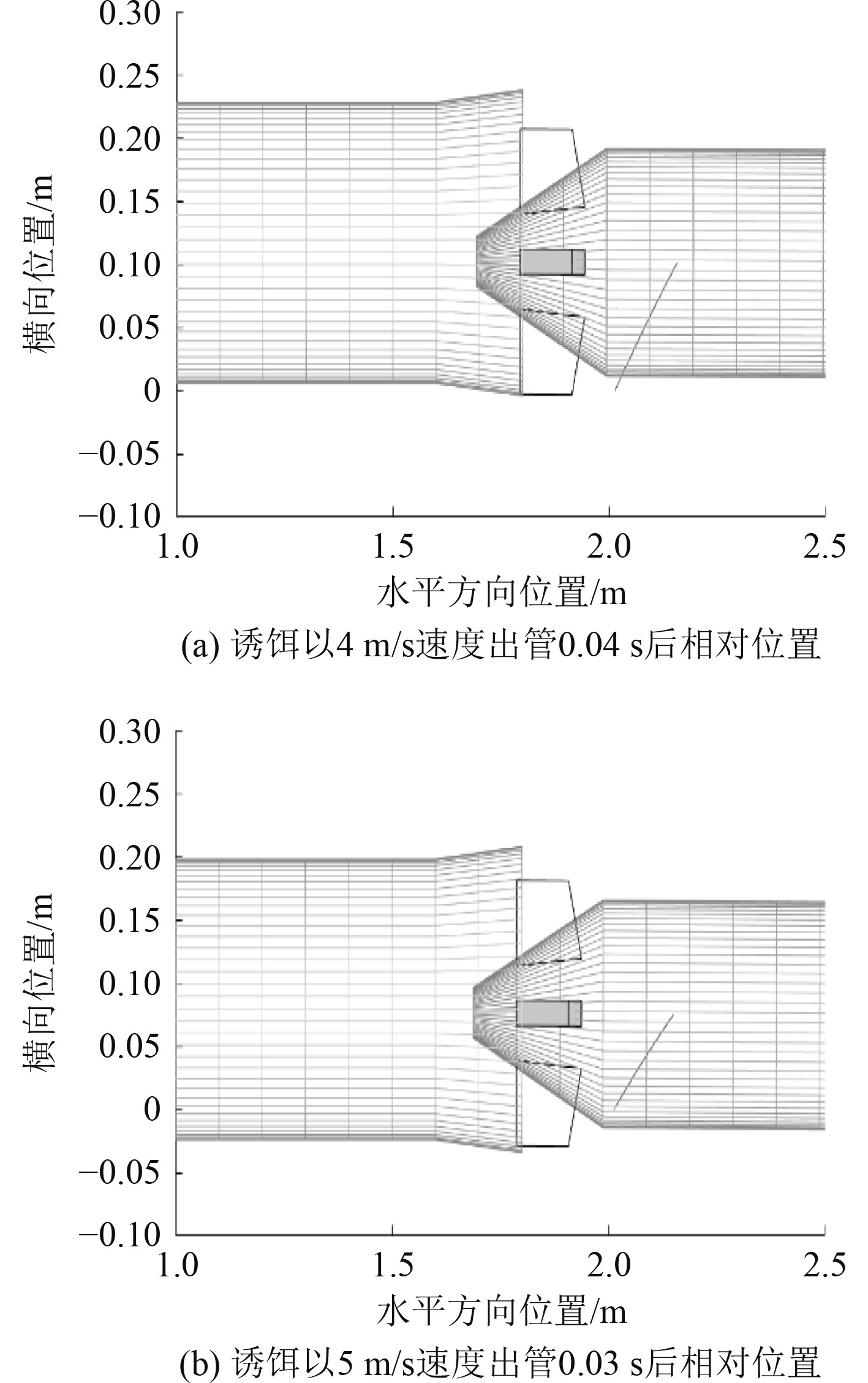
|
图 6 艇速3 m/s时,诱饵不同速度出管的离艇安全性(横向视角) Fig. 6 Launch safety at different terminal velocity of the decoy when the velocity of submarine is 3 m/s (Lateral perspective) |
由于本文重点关注出管安全性的问题,因此后续不再对诱饵离艇后的位移、姿态角、角速度、力矩等外弹道特性进行展开,仅关注诱饵尾锥段出管时的相对位置。
2)艇速4 m/s工况
从图7可以看出,在4 m/s艇速下,当诱饵以5 m/s或6 m/s速度出管时,诱饵右鳍舵会与发射管口发生碰撞,存在安全隐患。当诱饵以7 m/s速度出管时,诱饵右鳍舵出管后距喇叭口段边界仍有一定的安全裕量,因此对于4 m/s艇速时,7 m/s的诱饵出管速度能够保证安全性。
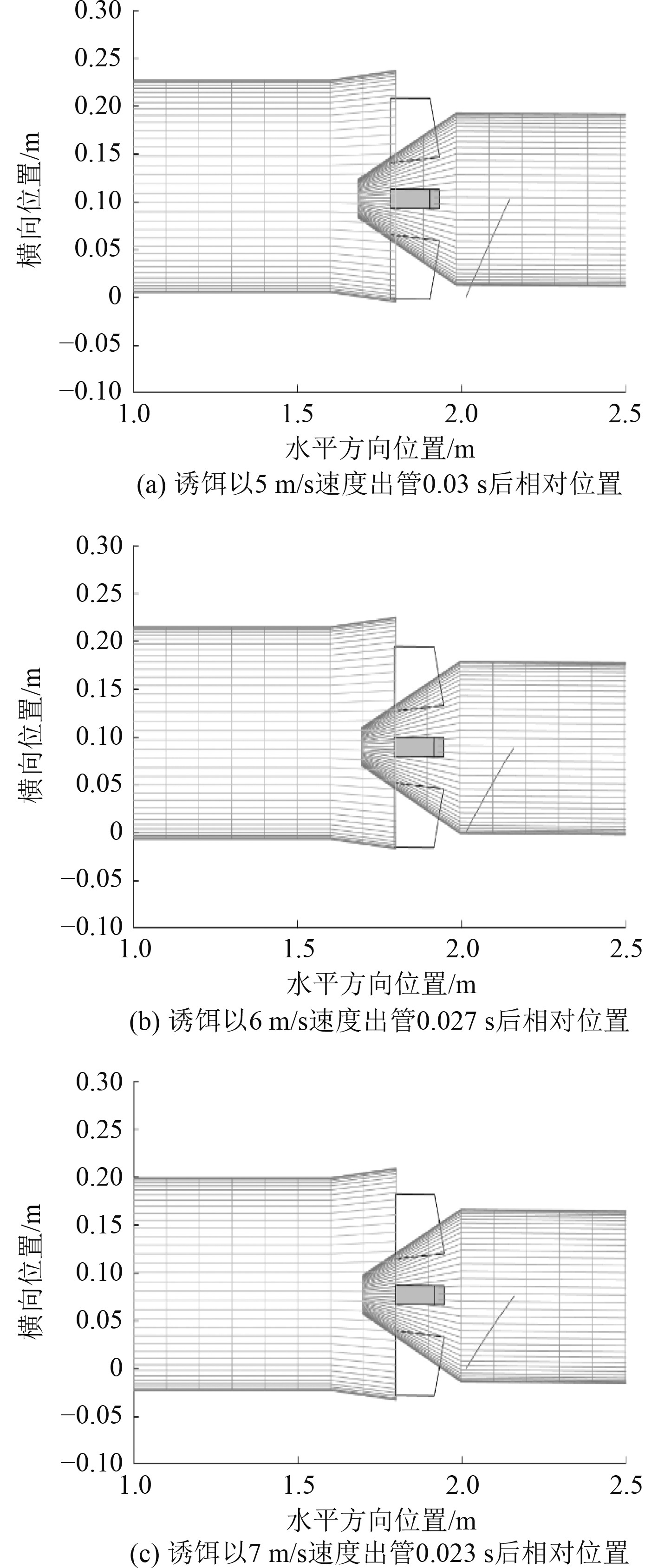
|
图 7 艇速4 m/s时,诱饵不同速度出管的离艇安全性(横向视角) Fig. 7 Launch safety at different terminal velocity of the decoy when the velocity of submarine is 4 m/s (Lateral perspective) |
3)艇速3~7.5 m/s工况
对于艇速3~7.5 m/s工况下,诱饵安全离艇出管速度计算结果如表1所示。
|
|
表 1 不同艇速时,诱饵安全离艇所需出管速度 Tab.1 Terminal velocity of the decoy required for launch safety at different velocity of submarine |
基于表1数值计算结果,采用数据拟合的方法构建诱饵安全离艇出管速度关于艇速的多项表达式,经拟合发现,采用6次多项式即具有较好地拟合结果,其关系式如下式:
| $ \begin{split}{V_{\min }} =& 0.017\;8{V_T}^6 - 0.514\;9{V_T}^5 + 6.034\;2{V_T}^4 - \\ &36.558\;7{V_T}^3 +120.511\;3{V_T}^2 - 202.745\;4{V_T} +\\ &139.094\;4 。\end{split}$ | (23) |
式中:
以某气动不平衡式发射装置为例,简化示意图[7-11]如图8所示。基于安全离艇所需出管速度,通过控制阀系统可调节阀芯运动规律,从而控制特型孔面积开度[8,9,11,12],从而对其内弹道特性进行控制以满足诱饵安全离艇所需出管速度。研究控制阀芯运动速度与安全离艇所需出管速度和发射深度之间的关系表达式,从而为内弹道智能控制提供依据。首先建立“高压气瓶-控制阀-诱饵发射管”系统内弹道计算模型,选定特形孔结构形式,并针对不同出管速度和发射深度作为研究变量,通过智能算法匹配相应的阀芯速度。最后,对上述步骤计算结果构建样本数据,并通过多元拟合的方法[13]得到阀芯速度关于出管速度和发射深度的多项表达式,从而为智能控制提供依据。
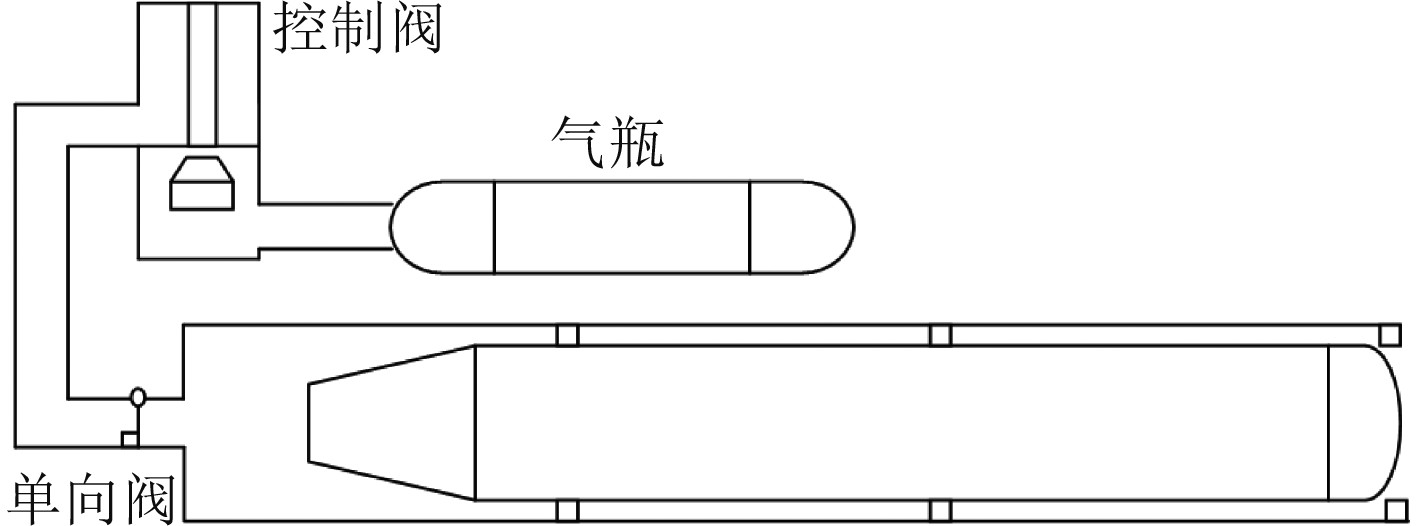
|
图 8 “高压气瓶-控制阀-诱饵发射管”系统简化示意图 Fig. 8 Diagram of system of high pressure gas bottle-control valve-tube |
发射气瓶内,理想气体状态方程为:
| $ {P_f}{V_f} = {m_f}R{T_f},$ | (24) |
发射气瓶内气体压力变化微分方程为:
| $ \frac{{{\rm{d}}{P_f}}}{{{\rm{d}}t}} = - \frac{{k{P_f}}}{{{m_f}}} \cdot {Q_{mv}} ,$ | (25) |
发射气瓶内气体质量变化微分方程为:
| $ \frac{{{\rm{d}}{m_f}}}{{{\rm{d}}t}} = - {Q_{mv}}。$ | (26) |
式中:
当
| $ {Q_{mv}} = \varphi {S_v}{P_f}\sqrt {\frac{k}{{R{T_f}}}} {\left( {\frac{2}{{k + 1}}} \right)^{\tfrac{{k + 1}}{{2(k - 1)}}}}。$ | (27) |
当
| $ {Q_{mv}} = \varphi {S_v}{P_f}\sqrt {\frac{{2k}}{{R{T_f}(k - 1)}}\left[ {{{\left( {\frac{{{P_b}}}{{{P_f}}}} \right)}^{\tfrac{2}{k}}} - {{\left( {\frac{{{P_b}}}{{{P_f}}}} \right)}^{\tfrac{{k + 1}}{k}}}} \right]} 。$ | (28) |
式中:
3)诱饵发射管
发射管后腔内气体压力变化微分方程为[14]:
| $ \frac{{{\rm{d}}{P_b}}}{{{\rm{d}}t}} = - \frac{{{P_b}k{A_b}}}{{{V_{b0}} + {A_b} \cdot x}} \cdot \frac{{{\rm{d}}x}}{{{\rm{d}}t}} + \frac{{k{P_f}{V_f}}}{{{m_f}({V_{b0}} + {A_b} \cdot x)}}{Q_{mv}}。$ | (29) |
| $ \frac{{{\rm{d}}{m_b}}}{{{\rm{d}}t}} = {Q_{mv}}。$ | (30) |
式中:
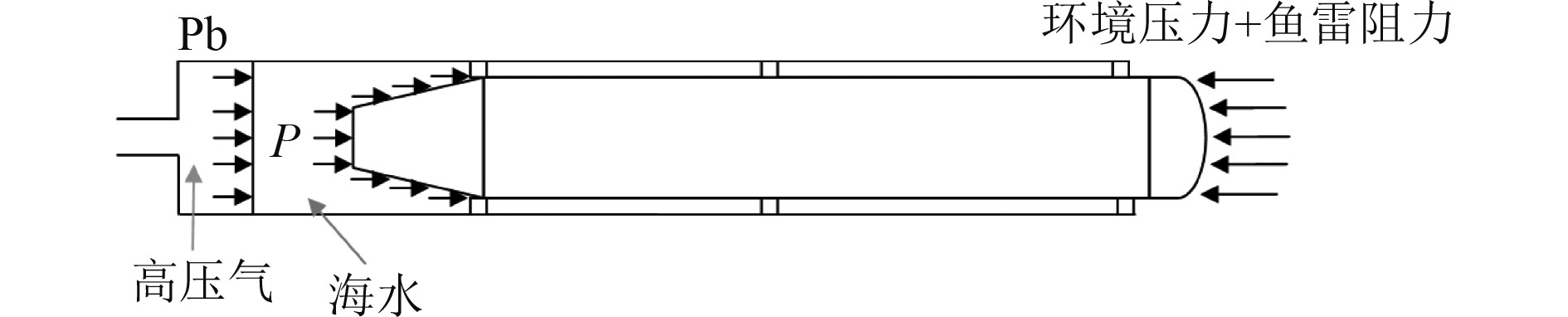
|
图 9 诱饵运动水平方向受力分析[15] Fig. 9 Analysis of horizontal force of the decoy |
根据连续性方程,并以海水作不可压处理,诱饵与后腔海水之间满足如下关系:
| $ {V_w}{A_b} = {V_t}{A_t} ,$ | (31) |
| $ {a_w}{A_b} = {a_t}{A_t} ,$ | (32) |
| $ ({P_b} - P){A_b} = {m_w}{a_w},$ | (33) |
| $ (P - Pa){A_t} - {F_D} = {m_t}{a_t} 、$ | (34) |
式中:
由式(31)~式(34)可得发射管后腔海水压力方程为:
| $ P = \left({P_a}{A_t} + {F_D} + \frac{{{m_t}A_b^2}}{{{m_w}{A_t}}}{P_b}\right)\left/\left({A_t} + \frac{{{m_t}A_b^2}}{{{m_w}{A_t}}}\right) \right.,$ | (35) |
| $ {F_D} = \frac{1}{2}\rho {A_t}V_t^2{C_D} 。$ | (36) |
式中:
经文献[12]可计算所需气瓶规格及压力,控制阀特形孔形状为梯形+矩形的组合。以5~11 m/s诱饵出管速度为例作为输出条件进行迭代计算,得到不同发射深度下满足该出管速度的相应阀芯速度控制规律。
发射深度10 m时弹道特性如图10所示,发射深度200 m时弹道特性如图11所示。
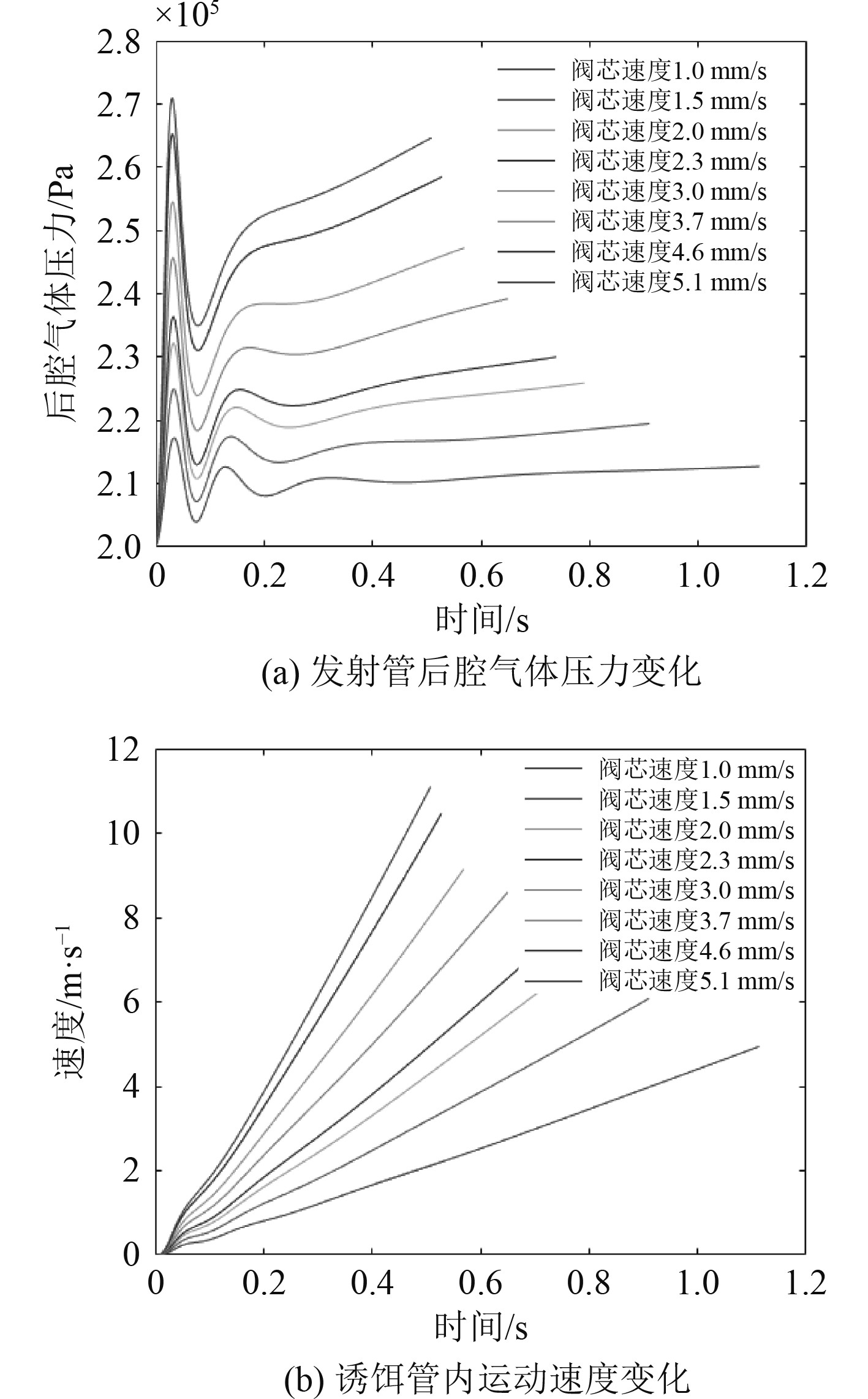
|
图 10 发射深度10 m时,不同阀芯速度下,发射诱饵内弹道特性 Fig. 10 The characteristics of internal ballistic for different velocity of spool at the launch depth of 10 m |
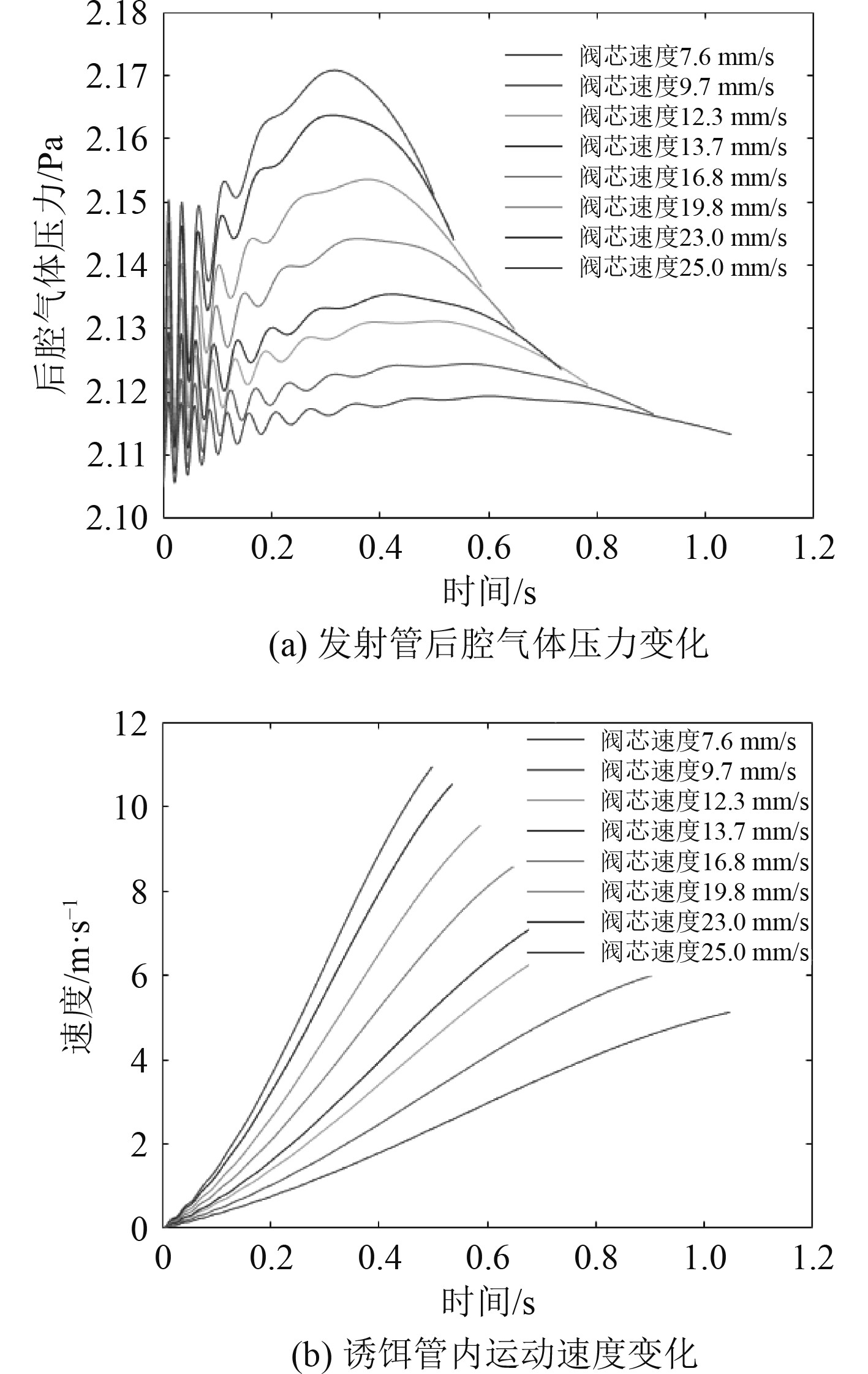
|
图 11 发射深度200 m时,不同阀芯速度下,发射诱饵内弹道特性 Fig. 11 The characteristics of internal ballistic for different velocity of spool at the launch depth of 200 m |
以5~11 m/s诱饵出管速度为例,针对发射深度10~200 m范围内,每大约加深50 m计算一组阀芯所需速度,并构建如表2所示样本数据库。
|
|
表 2 不同发射深度下,满足所需出管速度的控制阀芯速度控制规律 Tab.2 Required motion law of spool to realize needed terminal velocity of the decoy at different launch depth |
基于所计算的样本数据库,采用Matlab多元拟合函数nlinfit进行多项式拟合,根据经验,通过对多项式构成优化,采用下式具有较小的残差。
| $ \begin{split} {V_{fx}} = & - 55.039\;7 - 2.199\;7H - 2.953{H^2} + 2.291\;1{H^3} -\\ &0.502\;3{H^4} + 28.027\;9{V_{\min }} - 1.417\;9{V_{\min }}^2 -\\ &1.775{V_{\min }}^3 + 0.485\;8{V_{\min }}^4 - 0.055\;2{V_{\min }}^5 +\\ &0.003{V_{\min }}^6 - 6.377\;1 \times {10^{ - 5}}{V_{\min }}^7 + 1.454H{V_{\min }} -\\& 0.026\;7{H^2}{V_{\min }}^2 + 7.428 \times {10^{ - 4}}{H^3}{V_{\min }}^3 。\\[-10pt] \end{split} $ | (37) |
式中:
其中,拟合结果最大正残差为0.236 m/s,最大负残差为−0.141 m/s,拟合结果与样本数据对比如图12所示,由于某些工况下,拟合阀芯速度比样本数据最多低了0.141 m/s,同时可知阀芯速度越快,出管速度越快,因此可对阀芯速度拟合结果式(37)+0.141 m/s,即可保障所有工况安全出管,并且对大部分工况具有一定安全裕量。至此,即可根据式(37)对控制阀进行控制,从而实现对内弹道的智能控制。
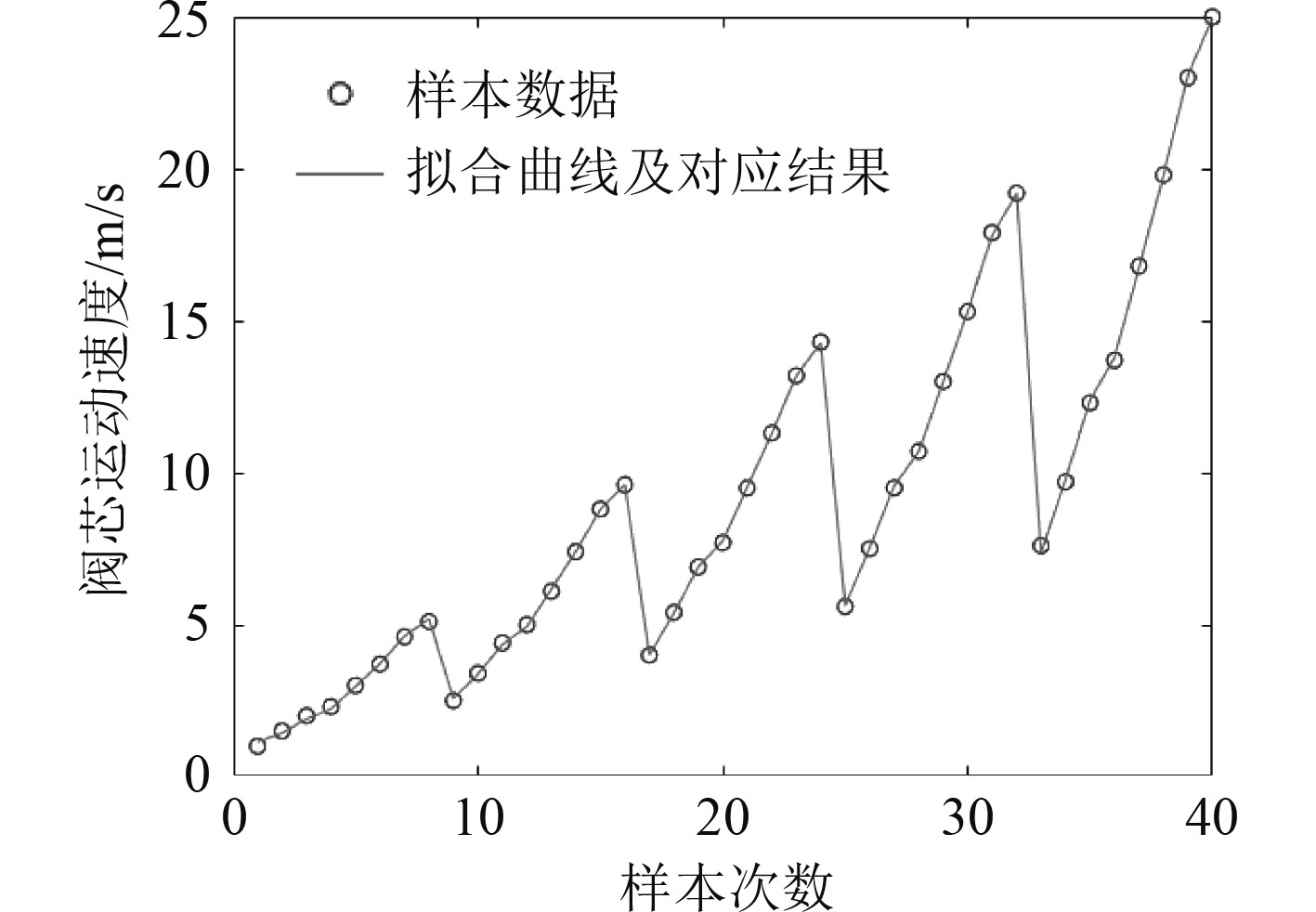
|
图 12 拟合结果与原始样本数据对比 Fig. 12 Comparisons between fitting results and original sample data |
1)基于诱饵运动六自由度模型进行数值计算,对发射诱饵外弹道特性进行分析,得到了诱饵出管后纵向运动和横向运动的位移、姿态角、角速度变化规律及所受力矩情况;
2)针对不同艇速,对诱饵出管安全性进行分析,在Matlab中实现出管过程模拟演示;
3)得到诱饵安全出管速度关于艇速的多项表达式,艇速越快,安全出管所需速度越高;
4)基于某型气动不平衡式发射装置,建立了“高压气瓶-控制阀-诱饵发射管”系统内弹道计算模型;
5)针对不同深度,得到了满足所需出管速度的控制阀芯运动速度规律,并构建样本数据库;基于样本数据库,采用多元拟合的方法,得到了阀芯运动速度关于发射深度和安全出管速度的关系式,并具有较好拟合结果,从而为内弹道智能控制提供决策依据。
上述过程提供了一种智能发射及控制的高效研究方法,可在保证器材安全出管的同时,实现较低的发射噪声及最优的能量利用率。由于上述计算仅采用了某型诱饵及发射管参数,最终得到的多项式仅用于相应模型的发射控制,至于其他参数的诱饵及发射装置需具体问题具体分析,但研究方法都一致适用。
| [1] |
潘光. 鱼雷力学[M]. 陕西: 陕西师范大学出版社, 2013.
|
| [2] |
WANG Z, WU Z. Six-DOF trajectory optimization for reusable launch vehicles via Gauss pseudospectral method[J]. Journal of Systems Engineering and Electronics, 2016, 27(2): 434-441. DOI:10.1109/JSEE.2016.00044 |
| [3] |
宣建明. 水声对抗器材发射安全性研究[A]. 发射技术论文集, 七〇五所昆明分部, 2000, 371–381.
|
| [4] |
华琦, 段浩, 等. 鱼雷水下发射的6-DOF运动仿真[J]. 舰船科学技术, 2019, 41(4): 137-141. |
| [5] |
MA D L, WANG S Q, YANG M Q, et al. Dynamic simulation of aerial towed decoy system based on tension recurrence algorithm[J]. Chinese Journal of Aeronautics, 2016, 29(6): 1484-1495. DOI:10.1016/j.cja.2016.09.003 |
| [6] |
LI Z H, ZHANG Z H, WANG S Z. The safety measure for the torpedo decoy after launching [C]// Proceedings of the 2002 International Symposium on Safety Science and Technology (2002 ISSST), 2002, 7.
|
| [7] |
段浩. 鱼雷发射技术[M]. 北京: 国防工业出版社, 2015.
|
| [8] |
李忠杰, 王树宗, 等. 气动式水下发射装置的可调节发射阀仿真研究[J]. 系统仿真学报, 2005, 17(12): 3074-3075+3080. DOI:10.3969/j.issn.1004-731X.2005.12.061 |
| [9] |
练永庆, 王树宗, 等. 气动式水下发射器的发射阀仿真设计研究[J]. 兵工学报, 2003, 24(3): 354-358. DOI:10.3321/j.issn:1000-1093.2003.03.016 |
| [10] |
黄苏和, 王凯帅, 刘星. 潜用AUV自航发射弹道建模与仿真[J]. 水下无人系统学报, 2018, 26(2): 129-132. |
| [11] |
练永庆, 周厚成, 吴开锋, 等. 气动不平衡式发射装置气水回收过程仿真与分析[J]. 鱼雷技术, 2012, 20(3): 220-224. |
| [12] |
唐树辉. 潜用气动鱼雷发射装置大深度发射技术研究[A]. 发射技术论文集, 七〇五所昆明分部, 2000, 93–98.
|
| [13] |
李继刚, 陈华秋, 等. 浅述多元数据处理的一种简化拟合形式及算法剖析[J]. 海洋技术, 2002, 21(3): 1-4. DOI:10.3969/j.issn.1003-2029.2002.03.001 |
| [14] |
鲁子双, 丁福康. 水面舰艇鱼雷发射装置气动发射内弹道微分解法[A]. 发射技术论文集, 七〇五所昆明分部, 2000, 237–240.
|
| [15] |
秦楠, 马亮, 秦庚申. 液压平衡式发射装置自航发射内弹道模型与仿真[J]. 火力与指挥控制, 2014, 39(9): 87–90.
|
 2022, Vol. 44
2022, Vol. 44

