0 引　言

惯性导航系统的工作原理是经典力学理论，系统在工作时采集的参数包括陀螺仪信号、加速度计信号等，通过惯性敏感器件的时间和空间转换，并结合相应的信号处理技术，最终确定导航物体的运动方位、姿态和航迹等参数。

陀螺仪是惯性导航系统的角位移或角速度测量器件，也是系统的核心部件，陀螺仪技术的先进性直接影响惯性导航系统的发展。20世纪初期，导航系统使用的陀螺仪多为机械转子陀螺仪，目标角位移和角速度信息采集的精度较低，20世纪50年代后，气动、液压陀螺仪获得了迅速发展，陀螺仪的精度得到明显提高。光纤陀螺仪是目前精度等级最高的一种陀螺仪，是本文的主要研究对象。

本文研究惯性捷联导航系统的标定和数据对准，数据标定和对准的目的是将导航系统陀螺仪和加速度计2种元件的信息进行融合，过滤惯性导航系统的误差，从而提高惯性捷联导航系统的精度。

1 惯性捷联导航系统的工作原理和坐标建立

惯性捷联导航系统以惯性元件的采集信号为基础，通过导航信息循环往复的更新，获得目标物体的位置、速度、方向等信息。

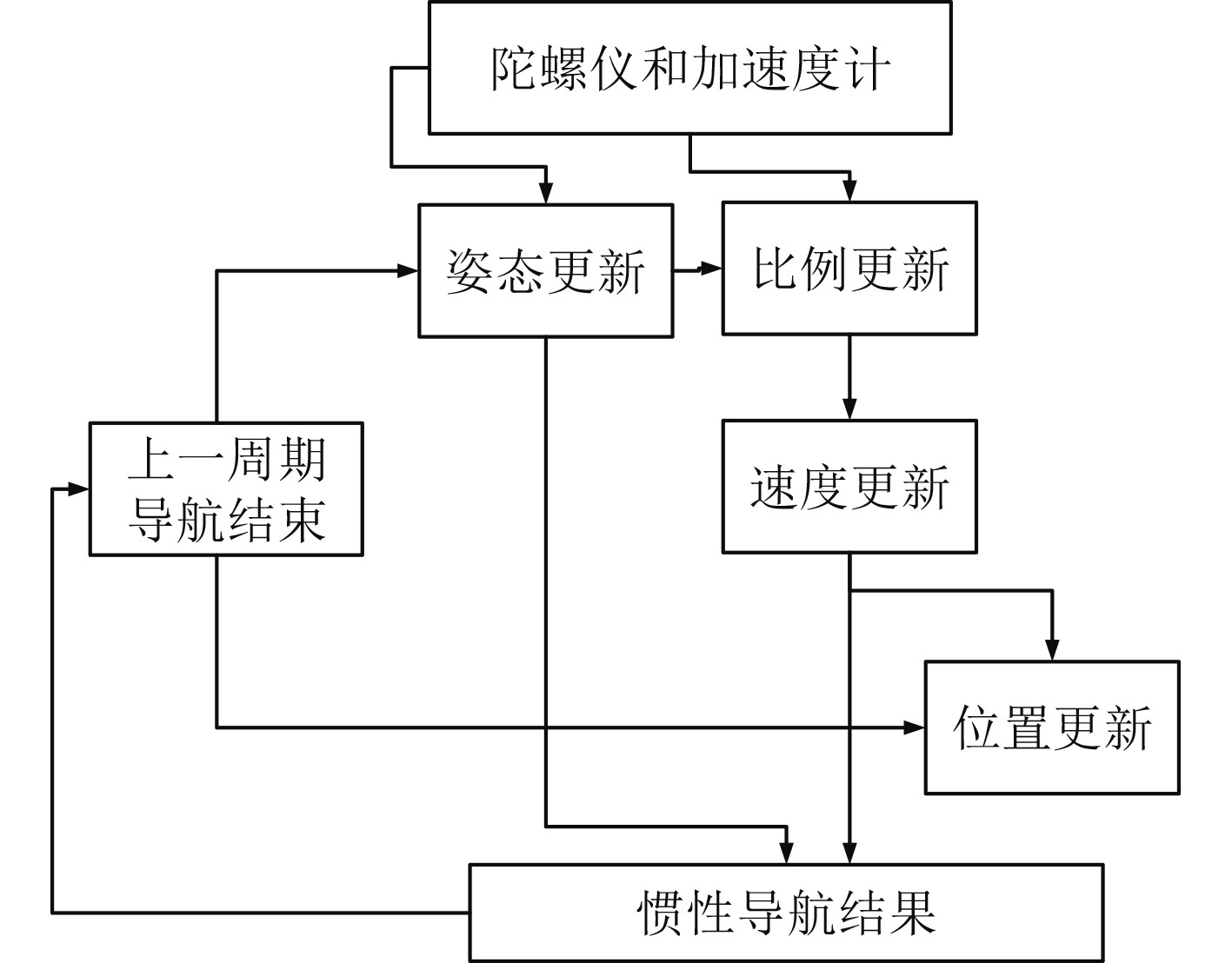
惯性捷联导航系统的工作原理如图1所示。

惯性捷联导航系统常用的坐标系有地心惯性坐标系、地球坐标系、载体坐标系、导航坐标系等，分别如下：

1）地心惯性坐标系

地心惯性坐标系以地球的质心为坐标原点，oz轴指向北极，ox轴和oy轴在赤道平面内，ox轴指向地面的春分点，oy轴由右手正交定则确定，地心惯性坐标系不随地球自转。

2）地球坐标系

地球坐标系与地心惯性坐标系不同，地球坐标系的原点为地球中心，oz轴指向北极，ox轴指向本初子午线，oy轴指向赤道，并与本初子午线垂直。地球坐标系与地球的自转运动固联，以地球坐标系为参考，描述目标物体与地球的相对位置关系。

3）载体坐标系

载体坐标系固定于目标载体上，坐标系原点为载体中心，ox轴指向载体的右侧90°方向，oy轴竖直向上，oz轴由右手正交定则确定。

4）导航坐标系

导航坐标系是惯性捷联导航系统在进行目标参数解算时采用的参考坐标系，惯性捷联导航系统多采用当地水平坐标系作为参考，将高度设置为固定值，只进行水平定位解算。本文选取的导航坐标系oz轴垂直于大地指向天空，ox轴和oy分别指向东方和北方，这种坐标系适用于除极区外的导航场景^[1]。

为了分析惯性捷联导航系统的坐标转换关系，文中将载体坐标系建为 $o - {x_1}{y_1}{z_1}$ ，导航坐标系建为 $o - {x_2}{y_2}{z_2}$ ，地球坐标系建为 $o - {x_3}{y_3}{z_3}$ ，坐标系的转换示意图如图2所示。

1）载体坐标系 $o - {x_1}{y_1}{z_1}$ 和导航坐标系 $o - {x_2}{y_2}{z_2}$ 的转换方式为：

$ \left[ A \right] = C_n^1C_1^2{\mathbf{C}}_2^b\left[ B \right]，$

转换矩阵分别如下：

$ C_n^1 = \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi }&0 \\ {\sin \psi }&{\cos \psi }&0 \\ 0&0&1 \end{array}} \right]，$

$ C_1^2 = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \theta }&{\sin \theta } \\ 0&{ - \sin \theta }&{\cos \theta } \end{array}} \right]，$

$ {\boldsymbol{C}}_2^b = \left[ {\begin{array}{*{20}{c}} {\cos \phi }&0&{ - \sin \phi } \\ 0&1&0 \\ {\sin \phi }&0&{\cos \phi } \end{array}} \right]。$

式中： $\psi $ 为俯仰角， $\theta $ 为航向角， $\phi $ 为翻滚角。

2）载体坐标系 $o - {x_1}{y_1}{z_1}$ 和地球坐标系 $o - {x_3}{y_3}{z_3}$ 转换矩阵为：

$ {\boldsymbol{C}}_i^e = \left[ {\begin{array}{*{20}{c}} {\cos \left( {{\omega _{ie}}t} \right)}&{\sin \left( {{\omega _{ie}}t} \right)}&0 \\ { - \sin \left( {{\omega _{ie}}t} \right)}&{\cos \left( {{\omega _{ie}}t} \right)}&0 \\ 0&0&1 \end{array}} \right]，$

式中， ${\omega _{ie}}$ 为旋转角度。

3）导航坐标系 $o - {x_2}{y_2}{z_2}$ 和地球坐标系 $o - {x_3}{y_3}{z_3}$ 的转换矩阵为：

$ {\boldsymbol{C}}_e^n = \left[ {\begin{array}{*{20}{c}} 0&{ - \sin L}&{\cos L} \\ 1&0&0 \\ 0&{\cos L}&{\sin L} \end{array}} \right]。$

式中， $L$ 为旋转角度。

2 船舶惯性捷联导航系统的标定和数据对准 2.1 光纤陀螺仪原理与建模

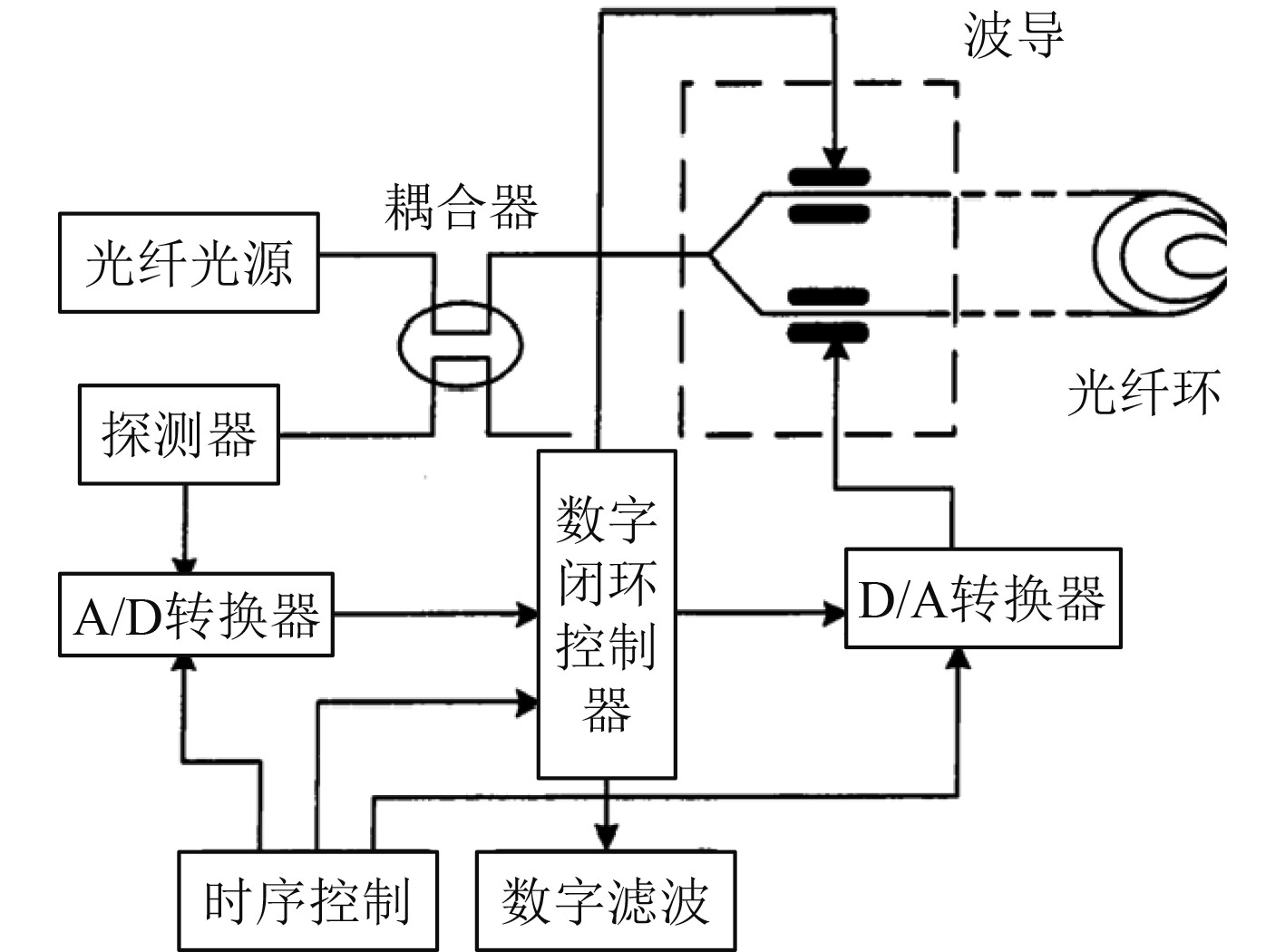
光纤陀螺仪是基于Sagnac效应^[2]研发的一种新型角速率传感器，信号采集精度非常高，光纤陀螺仪主要由耦合器、光纤光源、波导、光纤环、数字闭环控制器、A/D和D/A转换等部件构成。

图3为光纤陀螺仪工作原理图。

光纤陀螺仪使用光纤构成一个环形光路，材料为石英，折射率约为1.5，光在真空中的传播速度为c，可得光在光纤回路中的顺、逆时针的传播速度分别为：

$ {c_a} = \frac{{c/n + R\omega }}{{1 + R\omega /nc}}，$

$ {c_b} = \frac{{c/n - R\omega }}{{1 - R\omega /nc}}。$

式中： ${c_a}$ 为顺时针的光传播速度， $R$ 为光纤闭环的半径， $\omega $ 为光路转动的角速度， $n$ 为光纤的折射率， ${c_b}$ 为逆时针的光传播速度。

光在光纤回路中绕行一周的时间应满足：

$ {t_a} = \frac{{2{\text{π}} R + R\omega {t_a}}}{{{c_a}}}\text{，} $

$ {t_b} = \frac{{2{\text{π}} R - Ra{t_b}}}{{{c_b}}}\text{，} $

合并时间与速度公式，可得：

$ {t_a} = \frac{{2{\text{π}} R(nc + R\omega )}}{{{c^2} - {{(R\omega )}^2}}}\text{，} $

$ {t_b} = \frac{{2{\text{π}} R(nc - R\omega )}}{{{c^2} - {{(R\omega )}^2}}}。$

由于光在真空中的光速为3×10⁸ m/s，可求得2束光在光纤中绕行一周的时间与光程差^[3]为：

$ \Delta t = \frac{{4{\text{π}} {R^2}}}{{{c^2}}}\omega = \frac{{4A}}{{{c^2}}}\text{，} $

$ \Delta L = \frac{{4{\text{π}}{R^2}}}{c}\omega = \frac{{4A}}{c}\text{，} $

其中，A为环形管路的面积。

进而可以由光程差获得顺时针和逆时针光的相位差：

$ \Delta \Phi = \frac{{2{\text{π}} \Delta L}}{\lambda } = \frac{{8{\text{π}} NA}}{{\lambda c}}\omega \text{。} $

式中： $L$ 为光纤长度， $\lambda $ 为光波长。

图4为光纤陀螺仪在一段时间内采集的船舶加速度信号。

2.2 船舶惯性捷联导航系统的噪声信号建模

与数字导航系统不同，惯性捷联导航系统直接安装在船舶载体上，船舶在工作场景下的冲击、振动和运动都会对捷联惯性仪器带来动态噪声，包括光纤陀螺测量噪声、随机噪声、零偏噪声等。

1）光纤陀螺测量噪声

首先建立测量方程：

$ N = K\left( {\theta + {\omega _\beta }t} \right)\text{，} $

对测量方程求导可得测量误差：

$ \Delta N = \Delta K\left( {\theta + {\omega _\beta }t} \right) + K\left( {\Delta \omega t + \Delta \theta } \right) + K{\omega _\beta }\Delta t \text{，} $

式中： $N$ 为脉冲个数， $K$ 为光纤陀螺标定因数， $\theta $ 为空间转角， $ {\omega _\beta } $ 为陀螺的零漂^[4]。

2）随机噪声

光纤陀螺仪和加速度计都会产生随机噪声，可用高斯白噪声近似代替，记为：

$ {f_d} = \left[ {{\delta _e}^x\;\;{\delta _e}^y\;\;{\delta _e}^z} \right] 。$

3）零偏噪声

指陀螺仪和加速度计输入信号为零时的偏差，记为：

$ {f_0} = \left[ {{\chi _e}^x\;\;{\chi _e}^y\;\;{\chi _e}^z} \right] 。$

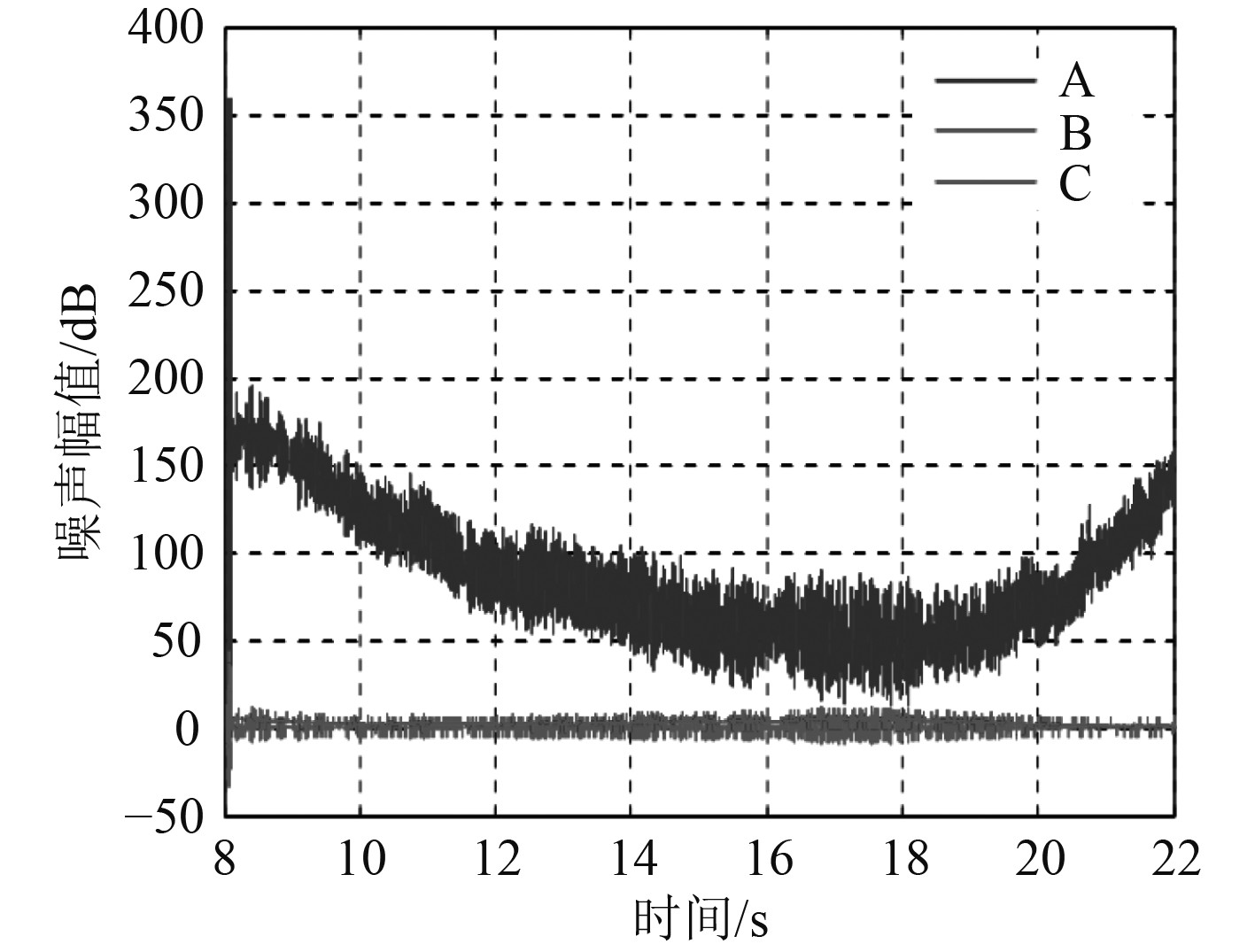
图5为惯性捷联导航系统的3种噪声信号的曲线。图中，A，B，C分别为光纤陀螺测量噪声、随机噪声、零偏噪声。

2.3 船舶惯性捷联导航系统的标定和数据对准方案设计

捷联惯性导航系统主要有2种数据标定方法，分别是系统级标定方法和分立标定法，其中，分立标定法是目前最常用的方法。

在进行导航系统数据标定时，在导航系统的工作状态下，将系统的误差信号作为观测量，包括速度误差、位置误差等，标定系统的观测方程为：

$ \widehat Z = C\widehat X + \widehat w + \delta \widehat V \text{。} $

式中： $ C $ 为观测矩阵， $ \widehat w $ 为观测噪声， $ \widehat X $ 为陀螺仪的误差信号， $ \widehat V $ 为加速度计的误差信号^[5]。

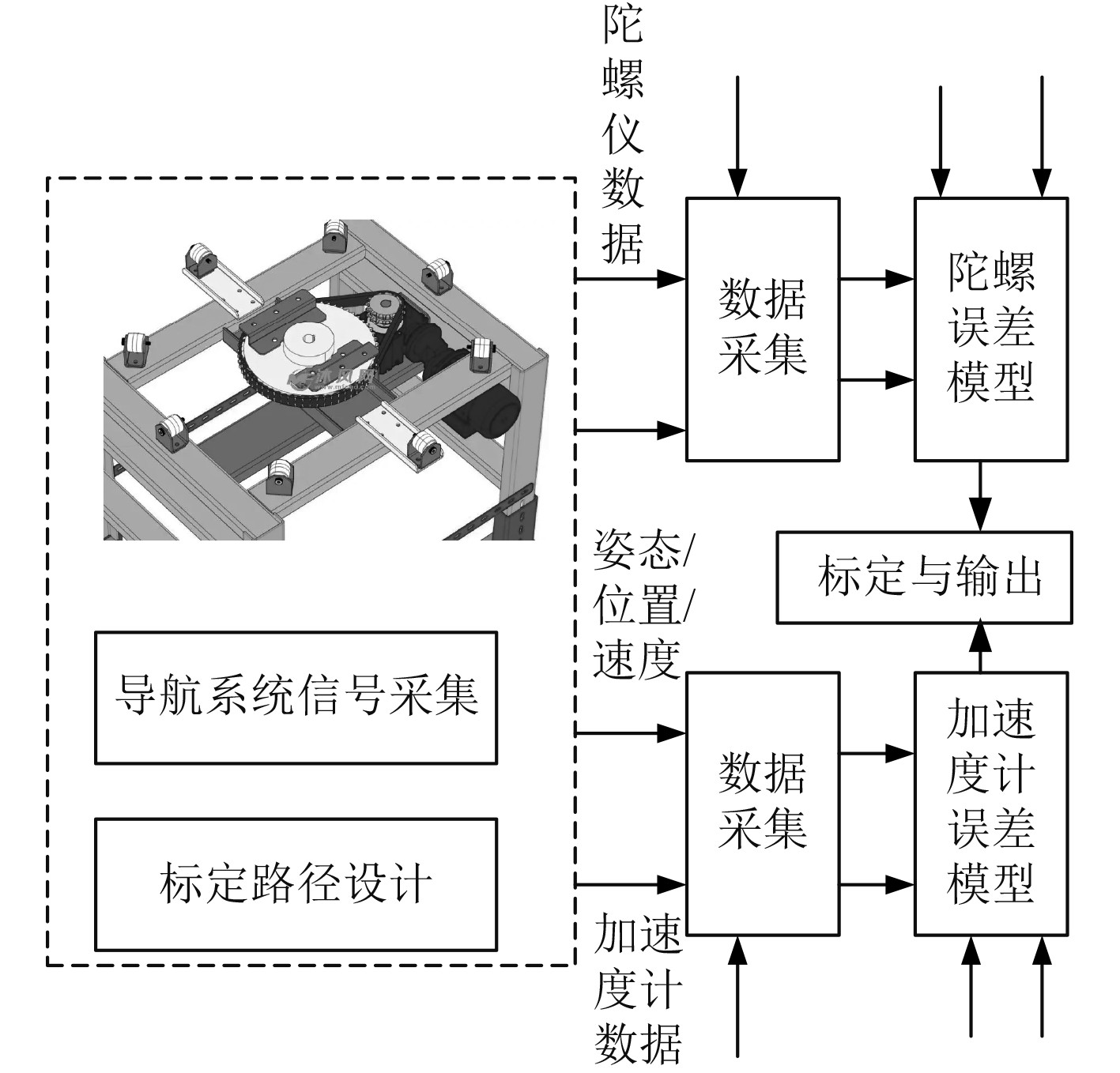
惯性捷联导航系统的标定方案原理图如图6所示。

2.4 船舶惯性捷联导航系统的标定和数据对准仿真

仿真平台采用Matlab中的Simulink软件包，支持线性、非线性系统的数据采样。

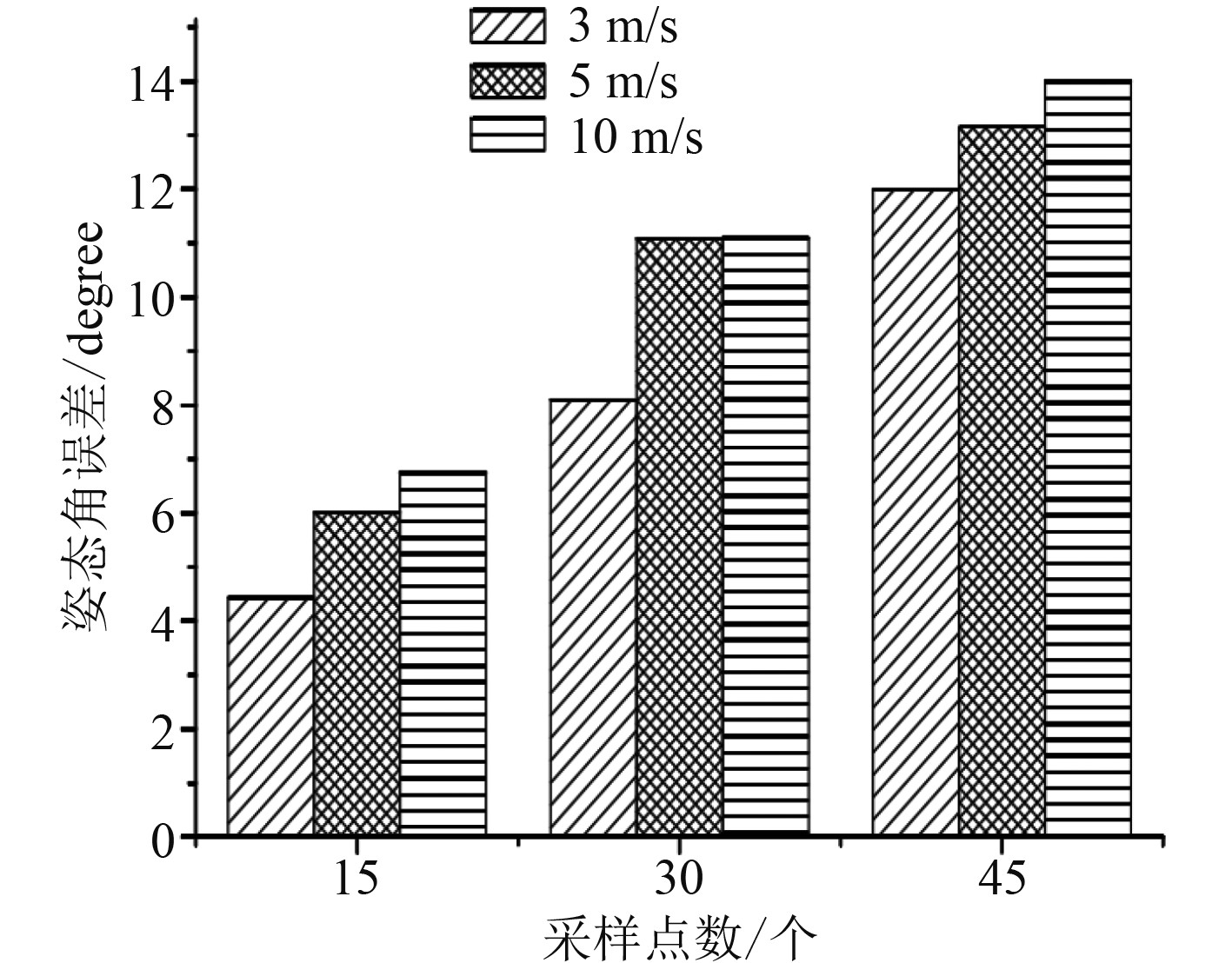
将陀螺仪、加速度计和导航系统的噪声信号作为输入，进行不同航行速度下的姿态角误差信号仿真，采样周期为0.1 s，得到图7所示的姿态角误差柱形图。

3 结　语

惯性捷联导航系统的关键部件是陀螺仪和加速度计，本文针对惯性捷联导航系统的误差特性与数据标定进行研究，设计数据标定和对准方案，建立导航系统的噪声模型，能够有效提高惯性捷联导航系统的信号精度。