船舶在螺旋桨推进力和风、浪、流干扰作用下会产生非线性运动,由于非线性运动无法通过导航系统进行预测,因此可能会导致船舶发生偏航、船体碰撞等事故。为了提高船舶在靠岸、系泊过程的安全性,必须要对船舶的非线性运动进行控制。
本文研究非线性船舶模型的运动控制,采用的控制原理为鲁棒神经网络控制算法,从非线性船舶的运动建模、动力系统螺旋桨建模、鲁棒神经网络控制器的原理等方面进行详细的研究。
1 非线性船舶模型的运动建模及边界条件建模建立非线性船舶运动坐标系如图1所示。
可知,静坐标系O-XYZ的OX方向指向东方,OY指向北方,OZ指向地心。船体坐标系o-xyz固定在船舶上,ox轴方向指向船首,oy指向侧舷,oz指向甲板垂直方向。

|
图 1 非线性船舶运动坐标系 Fig. 1 Nonlinear ship motion coordinate system |
建立船舶的运动学模型:
| $ \left\{ {\begin{array}{*{20}{c}} {{F_X} = m\ddot x = m{a_X}} ,\\ {{F_Y} = m\ddot y = m{a_Y}} ,\\ {{F_Z} = m\ddot {\textit{z}} = m{a_Z}} 。\end{array}} \right. $ | (1) |
式中:m为船舶的质量;aX,aY,aZ为沿3个坐标轴方向的加速度。
船舶在运动坐标系o-xyz中的位置记为(x0,y0,z0),船舶运动参数的坐标转换公式为:
| $ \left\{ {\begin{aligned} &{{{\dot x}_0} = {V_x}\cos \gamma \cos \beta + {V_y}\cos \gamma \sin \beta } ,\\ &{{{\dot y}_0} = {V_x}\sin \gamma \cos \beta + {V_ {\textit{z}}}\cos \gamma \cos \alpha } ,\\ &{{{\dot {\textit{z}}}_0} = - {V_x}\sin \beta + {V_y}\cos \beta \sin \alpha - {V_ {\textit{z}}}\cos \beta } ,\\ &{\dot \alpha = {w_x} + {w_y}\tan \beta \sin \lambda },\\ &\dot \beta = {w_x}\cos \alpha - {w_ {\textit{z}}}\sin \alpha ,\\ &\dot \gamma = {w_y}\sin \alpha /\cos \beta 。\end{aligned}} \right. $ | (2) |
式中:
船舶非线性运动的边界条件包括螺旋桨及船舵作用力、船舶受到的海风作用力和海浪作用力[1]。
1)海浪作用力
海浪的波形函数为:
| $ \xi(t)=\sum_{i=1}^{n} \xi \cos \left(k \psi \pm \omega t+\varepsilon_{i}\right)。$ | (3) |
式中:
海浪波形图如图2所示。

|
图 2 海浪波形图 Fig. 2 Wave waveform |
海浪的干扰力方程为:
| $ F(t) = \sum\limits_{i = 1}^n {{m} {a_x}\cos \left( {{w_i}t + {\varepsilon _i}} \right) + } \sum\limits_{i = 1}^n {{m} {a_y}\cos \left( {{w_i}t + {\varepsilon _i}} \right)}。$ | (4) |
式中:
2)海风作用力
将海风作用力沿3个坐标轴分解,可得模型如下:
| $ \left\{ {\begin{aligned} &{{F_{{x_0}}} = \frac{1}{2}\rho {V_x}C{a_x}{A_0}} ,\\ &{{F_{{y_0}}} = \frac{1}{2}\rho {V_y}C{a_y}{A_1}},\\ &{{F_{{z_0}}} = \frac{1}{2}\rho {V_z}C{a_z}{A_2}} 。\end{aligned}} \right. $ | (5) |
式中:
当船舶发生非线性运动时,往往处于欠驱动的状态,这时螺旋桨和船舵作用力达不到额定输出,故在建立螺旋桨和船舵作用力时,采用面元法进行其流体动力学分析。
建立船舶螺旋桨桨叶剖面的坐标系,如图3所示。
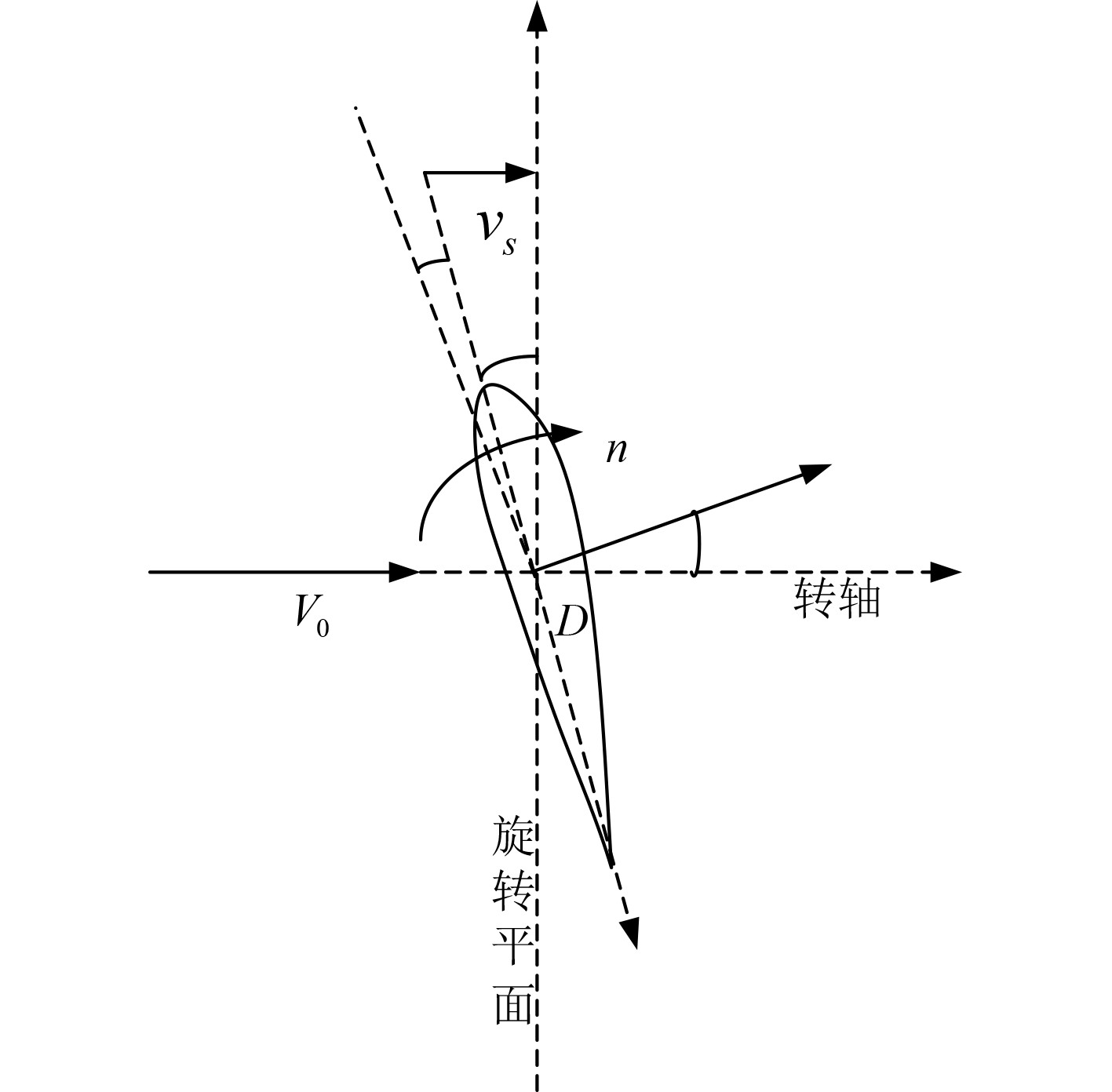
|
图 3 船舶螺旋桨的桨叶剖面坐标系 Fig. 3 Coordinate system of blade profile of ship propeller |
假设船舵相对于海水的速度为
| $ {h_s} = {v_s} \cdot n 。$ | (6) |
螺旋桨的进速比[2]为:
| $ {J_0} = \frac{{{v_s}}}{{nD}} 。$ | (7) |
式中:
螺旋桨的推进效率为:
| $ {\eta _0} = \frac{{{P_V}}}{{{T_L}2{\text{π}} n}} 。$ | (8) |
式中:
| $ \begin{array}{*{20}{l}} {{F_L} = {K_P}\rho {n^2}{D^4}} ,\\ {{T_L} = {K_m}\rho {n^2}{D^5}}。\end{array} $ | (9) |
式中:
船舶非线性运动过程需要考虑船体与海水的伴流效应,定义海水的流速为
| $ \xi = 1 - \frac{{{v_s}}}{{{v_c}}}。$ | (10) |

|
图 4 伴流系数与船舶长度和宽度关系图 Fig. 4 Relationship between wake coefficient and ship length and width |
在求解船舵作用力时,首先建立在该运动速度下的海水基本控制方程,分别如下:
1)连续性方程
| $ \frac{{{\rm{d}}{\rho _{}}}}{{{\rm{d}}t}} + {\rho _{}}\Delta \cdot {v_c} = 0 。$ | (11) |
式中:
2)动量方程
| $ {\rho _{}}\frac{{{\rm{d}}{v_c}}}{{{\rm{d}}t}} = {\rho _{}}f + \Delta \cdot \sigma。$ | (12) |
式中:
3)能量方程
| $ \rho \frac{{{\rm{d}}E}}{{{\rm{d}}t}} = - \rho \Delta \cdot {v_c} + Q - \Delta q 。$ | (13) |
式中:
4)雷诺方程
| $ \left\{ {\begin{aligned} &{\rho \frac{{{\rm{d}}{v_c}}}{{{\rm{d}}t}} = \frac{{\partial \sigma }}{{\partial t}} + \rho f} ,\\ &{\frac{{\rho \partial {v_c}}}{{\partial t}} + \frac{{{\partial ^2}(P)}}{{\partial t}} = \frac{\partial }{{\partial {t^2}}}(\xi \frac{{\partial {v_c}}}{{\partial t}}) - Q}。\end{aligned}} \right. $ | (14) |
式中:
船舵的作用力方程为:
| $ \frac{{\partial \left( {\rho {v_c}} \right)}}{{\partial t}} + div\left( {\rho {v_c}} \right) = - \frac{{\partial P}}{{\partial t}} + \frac{{\partial {F_{\tau x}}}}{{\partial x}} + \frac{{\partial {F_{\tau y}}}}{{\partial y}} + \frac{{\partial {F_{\tau z}}}}{{\partial z}} 。$ | (15) |
式中:
神经网络不仅具有非线性变换的特征,而且在复杂系统的并行运算、动态系统的辨识方面具有明显优势。
在建立非线性船舶运动控制器时,采用了一种鲁棒神经网络算法,该算法的拓扑结构如图5所示。

|
图 5 鲁棒神经网络的结构原理图 Fig. 5 Structure principle diagram of robust neural network |
鲁棒神经网络的权值矢量为
| $ e_K^{} = {y_k} - f 。$ | (16) |
控制器的目标函数为:
| $ E = \frac{1}{N}\sum\limits_{K = 1}^N {e_K^2} = \frac{1}{N}\sum\limits_{K = 1}^N {{{\left( {{y_K} - f} \right)}^2}} 。$ | (17) |
将该式展开可得:
| $ \begin{split} E = &\frac{1}{N}\sum\limits_{K = 1}^N {{{\left( {{y_k} - W_A^{\rm{T}}{b_k}} \right)}^2}} = \hfill \\ &\frac{1}{N}\sum\limits_{K = 1}^N {{{\left( {f_k^2 - 2{y_k}b_k^{\rm{T}}{W_A} + W_A^{\rm{T}}{b_k}b_k^{\rm{T}}{W_A}} \right)}^2}} 。\\ \end{split} $ | (18) |
令
可得:
| $ E = \frac{1}{N}\sum\limits_{K = 1}^N {y_k^2} - 2{P^{\rm{T}}}{W_A} + W_A^{\rm{T}}R{W_A}。$ | (19) |
将上式作为鲁棒神经网络的显函数[5],求导可得:
| $ \frac{{\partial E}}{{\partial {W_A}}} = {\left( {\frac{{\partial E}}{{\partial {W_A}}},\frac{{\partial E}}{{\partial {W_{A2}}}},\frac{{\partial E}}{{\partial {W_{A3}}}},\frac{{\partial E}}{{\partial {W_{A4}}}}} \right)^{\rm{T}}} = 2R{W_A} - 2P。$ | (20) |
令
| $ {W_A}(t + 1) = {W_A}(t) + \Delta {W_A}(t) 。$ |
寻优误差平方值为:
| $ {E_k}(t) = e_k^2(t) = {\left[ {{y_k} - W_A^{\rm{T}}(T){b_k}} \right]^2} 。$ |
结合鲁棒神经网络算法,设计非线性船舶的转向控制器,其原理如图6所示。
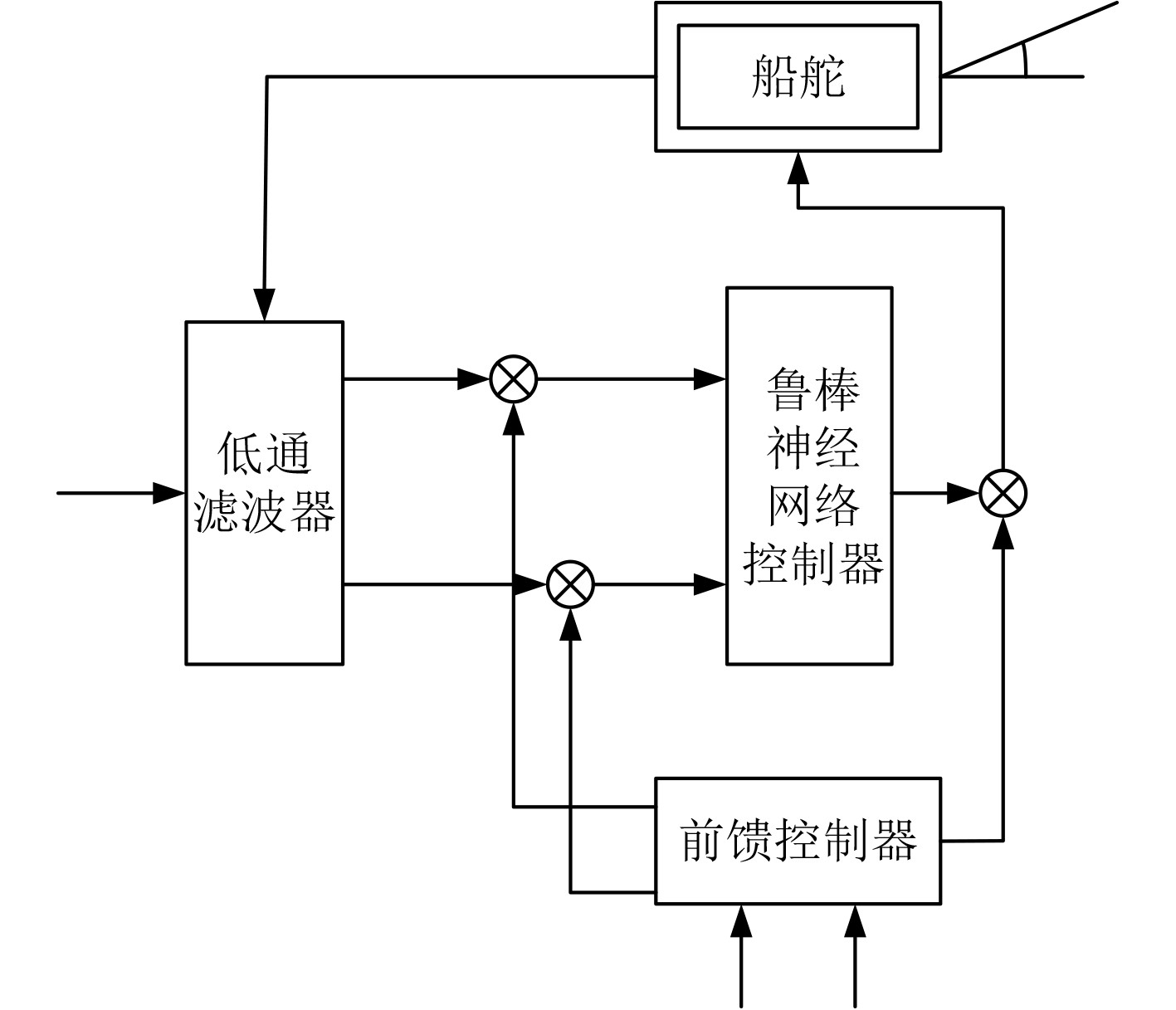
|
图 6 非线性船舶的转向控制器原理图 Fig. 6 Schematic diagram of nonlinear ship steering controller |
定义非线性船舶的航向控制指标为:
| $ J = \frac{1}{T}\int_0^{{T}} {\left\{ {{{\left[ {{\psi _r} - \psi } \right]}^2} + \lambda {\delta ^2}} \right\}} {\rm{d}}t。$ | (21) |
根据鲁棒神经网络推导控制器的输出为:
| $ \left\{ {\begin{aligned} &{\delta _r^B = {k_\psi }\left( {{\psi _r} - \hat \psi } \right) + {k_r}\left( {{r_r} - \hat r} \right)} ,\\ &{{\delta _r} = \delta _r^B + \delta _r^F} ,\\ &{{k_\psi } = 1/\sqrt \lambda } ,\\ &{{k_r} = \frac{1}{K}\left[ {\sqrt {\left. {1 + \frac{{2K}}{{\sqrt \lambda }} - 1} \right]} } \right.} 。\end{aligned}} \right. $ | (22) |
式中:
图7为无控制器策略/PID控制/鲁棒神经网络3种控制模式下的船舶航向角变化曲线。
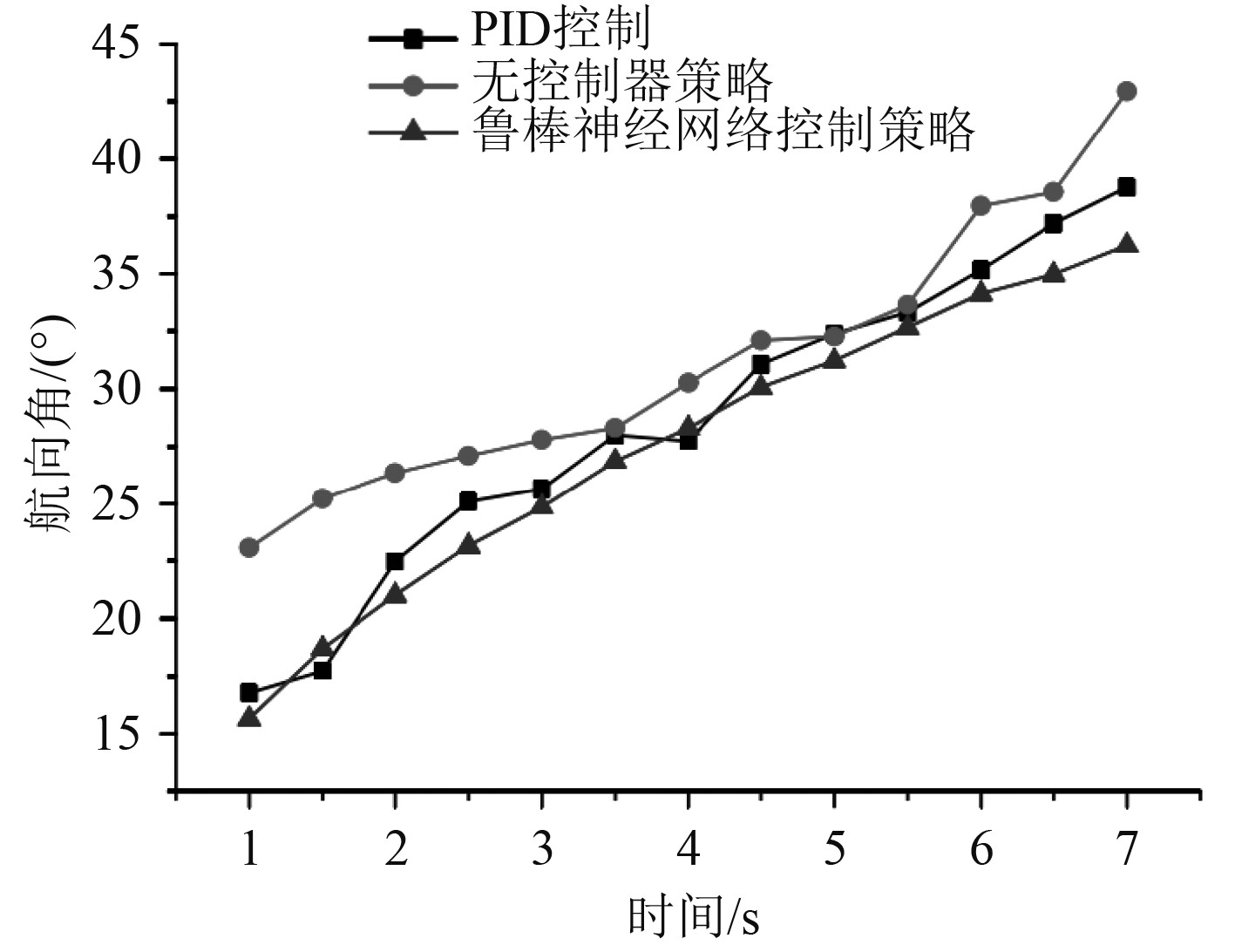
|
图 7 3种控制模式下的船舶航向角变化曲线 Fig. 7 Variation curve of ship heading angle under three control modes |
本文针对船舶非线性运动的控制技术进行研究,研究内容包括船舶非线性运动和边界条件的建模、鲁棒神经网络控制技术的原理分析、船舶航向控制器的设计与试验等,有助于提高非线性船舶的运动控制效果。
| [1] |
杜刚, 战兴群, 钟山, 等. 基于神经网络的非线性船舶航向自适应逆控制[J]. 测控技术, 2005(4): 23-26. |
| [2] |
杜佳璐, 郭晨, 张显库. 船舶运动航向自适应非线性控制的仿真研究[J]. 系统仿真学报, 2005(6): 1445-1448. DOI:10.3969/j.issn.1004-731X.2005.06.045 |
| [3] |
于萍, 刘胜. 船舶减摇非线性系统神经网络控制研究[J]. 信息与控制, 2003(3): 264-267. DOI:10.3969/j.issn.1002-0411.2003.03.015 |
| [4] |
郑则炯, 梁文祯. 基于变结构鲁棒性控制的船舶减摇鳍非线性系统研究[J]. 舰船科学技术, 2017, 39(22): 46-48. |
| [5] |
程启明, 李滋刚. 船舶航迹自动舵的神经网络控制方法研究[J]. 导航, 1999, 20(1): 36-44. |
| [6] |
曹媛. 船舶航向非线性控制的数学模型与分析[J]. 舰船科学技术, 2019, 41(4): 55−57.
|
 2022, Vol. 44
2022, Vol. 44
