2. 大连海事大学 信息科学技术学院, 辽宁 大连 116026
2. Information Science Technology College, Dalian Maritime University, Dalian 116026, China
近年来,随着深度学习在图像处理、语音识别、自然语言处理等领域的成功应用[1],在无线通信领域,引入深度学习进行系统设计的思想理念则成为学者们广泛关注的热点。特别是文献[2]开创性地提出了一种基于端到端学习优化自编码器概念的通信系统设计方案,将深度学习的“热浪”带入到了无线通信物理层关键技术研究领域。由此构建的基于深度学习的无线收发机已经显示出良好的系统性能,例如正交频分复用(orthogonal frequency division multiplexing, OFDM)无线通信系统[3],多输入多输出(multiple input multiple output, MIMO)无线通信系统[4]和单载波无线通信系统[5],均为通信系统设计提供了新的理念。
海上通信受到海洋复杂多变环境影响,信道衰落较为严重,误码率也较高。对于无线通信多载波调制系统,由于OFDM技术可以将频率选择性衰落信道划分成多个平坦衰落子信道,因此经常用来对抗频率选择性衰落的影响。然而,OFDM系统需要高精度的信道估计来恢复发送信号。通常使用基于导频的频域信道估计算法,如最小二乘(least squares, LS)算法和线性最小均方误差(linear minimum mean square error, LMMSE)算法。除去经典信道估计算法之外,文献[6]设计了一种简单全连接(full connection,FC)神经网络构成的OFDM信道估计器。文献[3]和文献[7]结合图像处理领域,信道估计问题被表述为超分辨率重建问题[8],将导频数据视为低分辨率图像,需要估计的信道频域响应(channel frequency response,CFR)被视为相应的高分辨率图像,并用神经网络实现此过程。此外,文献[3]还使用密度卷积神经网络(dense convolutional neural networks, Dense-Net)进一步降低了计算复杂度并提高了模型的表达能力,但是使用的激活函数和损失函数缺乏一定的合理性。可以看到,以上研究方案多是基于简单直接的监督深度学习来实现的。这需要在实际中获取大量的无偏差实时信道状态信息,其实现困难且成本高。无监督深度学习将神经网络从标签数据中解放出来,有效地解决目标信息不足或获取困难的问题[9]。此外,无监督深度学习方法可以与现有监督深度学习方法结合,使用容易获取的标签数据对神经网络进行预训练,帮助网络构建合理的初始化映射方案,并通过无监督学习查找标签数据中未包含的潜在特征。
在文献[3]的基础上,本文提出一种改进的无监督深度学习海上OFDM系统信道估计算法。无监督深度学习在没有真值信息约束的情况下进行训练,即训练过程中不用额外提供CFR作为标签。而且,在该算法中提出了使用双极性激活函数的思想,引入最小化曼哈顿距离作为目标函数,用以降低算法复杂度、加快模型收敛和提高信道估计精度。
针对常用非线性激活函数的软饱和问题,提出传统Elu和负极性Elu的混合使用方案,提高了神经网络隐藏层的特征表达能力,使模型更轻量化。
针对实数构成的神经网络,提出最小化曼哈顿距离的目标函数,提高了模型的迭代收敛速度和信道估计精度。
1 系统模型信道估计问题被描述为一个图像超分辨率过程[10],导频数据视为低分辨率图像,并由Dense-Net重建高分辨率的全部CFR图像[3]。本文提出的模型借助无监督深度学习摆脱了对输出真值(CFR)的束缚,同时提出的双极性激活函数使用方案和最小化曼哈顿距离的目标函数使模型更轻量化、高效化及更精确估计CFR。
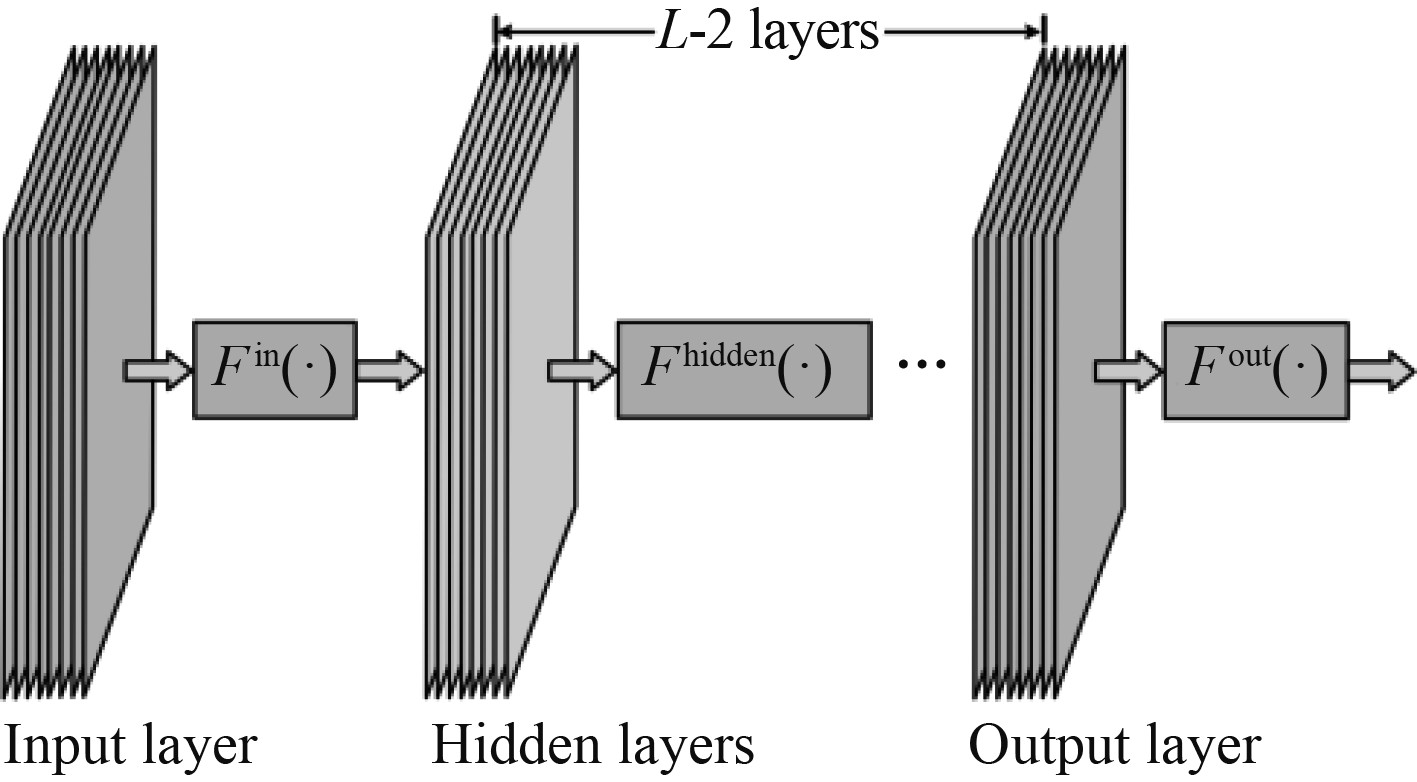
1.1 迭代过程图1展示了一个典型神经网络模型,由1个输入层,L-2个隐藏层和1个输出层构成。每一层由全连接层、卷积层或循环层等任何具有可更新参数的结构层
|
图 1 典型神经网络模型 Fig. 1 Typical neural network architecture |
|
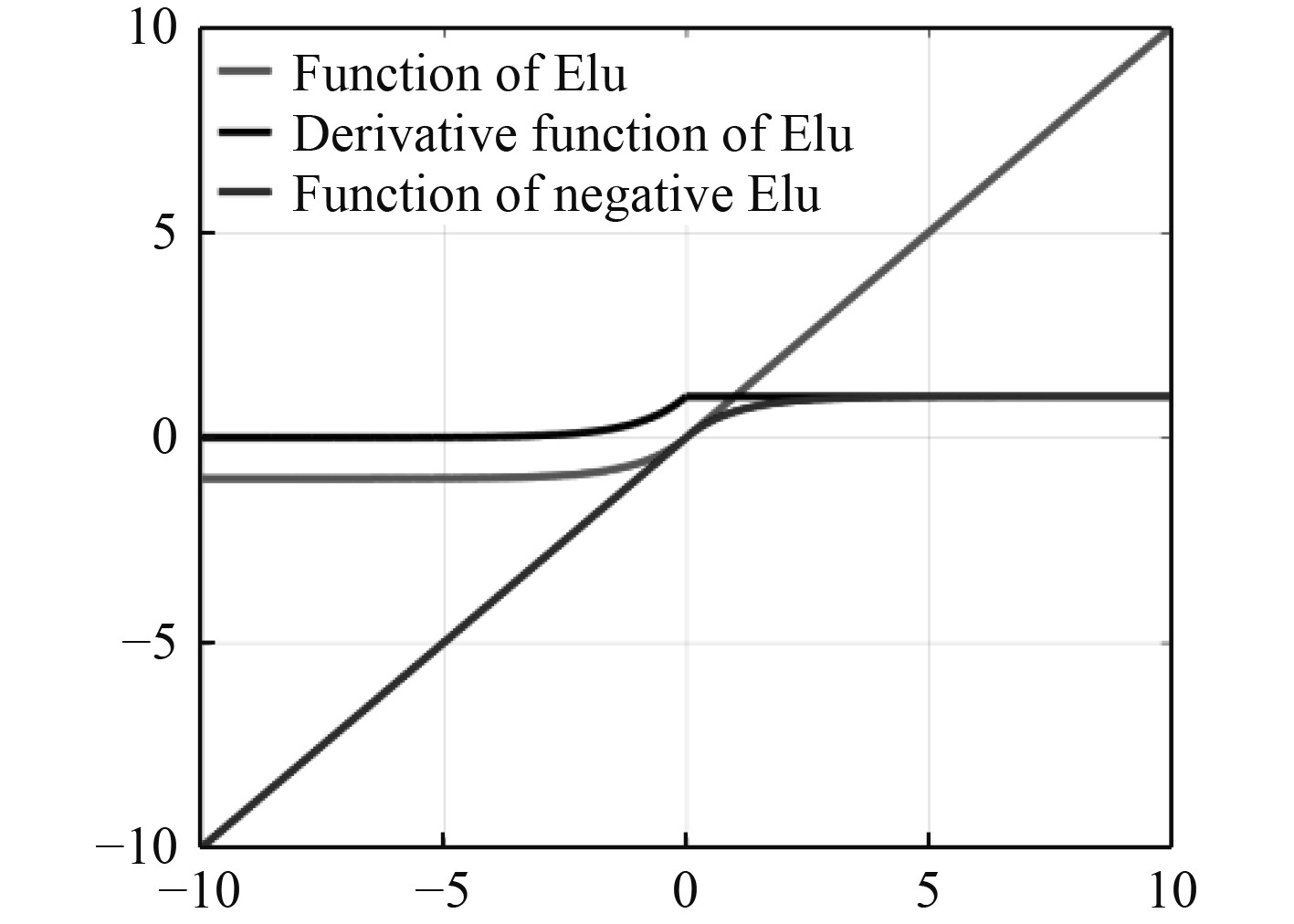
图 2 Elu激活函数和导数函数 Fig. 2 The function and derivative function of Elu |
使用梯度下降法反向传播以迭代更新参数,从而获得最小化的总估计误差。计算第l层前向传播结果Ol相对前一层前向传播结果Ol−1的偏导:
| $ {D_l} = \frac{{\partial {O_l}}}{{\partial {S_l}({O_{l - 1}})}} \times \frac{{\partial {S_l}({O_{l - 1}})}}{{\partial {O_{l - 1}}}}\text{,} $ | (1) |
因此,损失函数相对第l层的第i个(i={1,2…,nl})可更新参数的偏导可以表示为:
| $ \frac{{\partial J\left( {{O_L},y} \right)}}{{\partial {w_{{i_l}}}}} = \frac{{\partial J\left( {{O_L},y} \right)}}{{\partial {O_L}}} \times {D_L} \cdots \times \frac{{\partial {O_l}}}{{\partial {S_l}({w_{{i_l}}})}}\times \frac{{\partial {S_l}({w_{{i_l}}})}}{{\partial {w_{{i_l}}}}} \text{,}$ | (2) |
由此,得出参数
| $ w_{_{{i_l}}}^{{\text{new}}} = w_{_{{i_l}}}^{} - \alpha \frac{{\partial J\left( {{O_L},y} \right)}}{{\partial w_{_{{i_l}}}^{}}}\text{。} $ | (3) |
可知,参数
Elu激活函数在深度学习领域得到广泛应用。相对于其他主流激活函数,Elu具备非线性映射能力和输出均值接近于0,即收敛快速等优点。然而,Elu存在左侧软饱和现象,负值输入时输出逐渐趋近于固定值并且导数逐渐趋近于0,即参数值更新极小或停止更新。这些问题对于处理分类问题或计算机视觉等非负数据任务可能没有显著影响,然而对于信道估计任务来说,估计数据并非单一极性且幅度随机,这就需要使用更多的特征和更深的网络层弥补Elu左侧软饱和的缺点。因此,提出传统Elu(
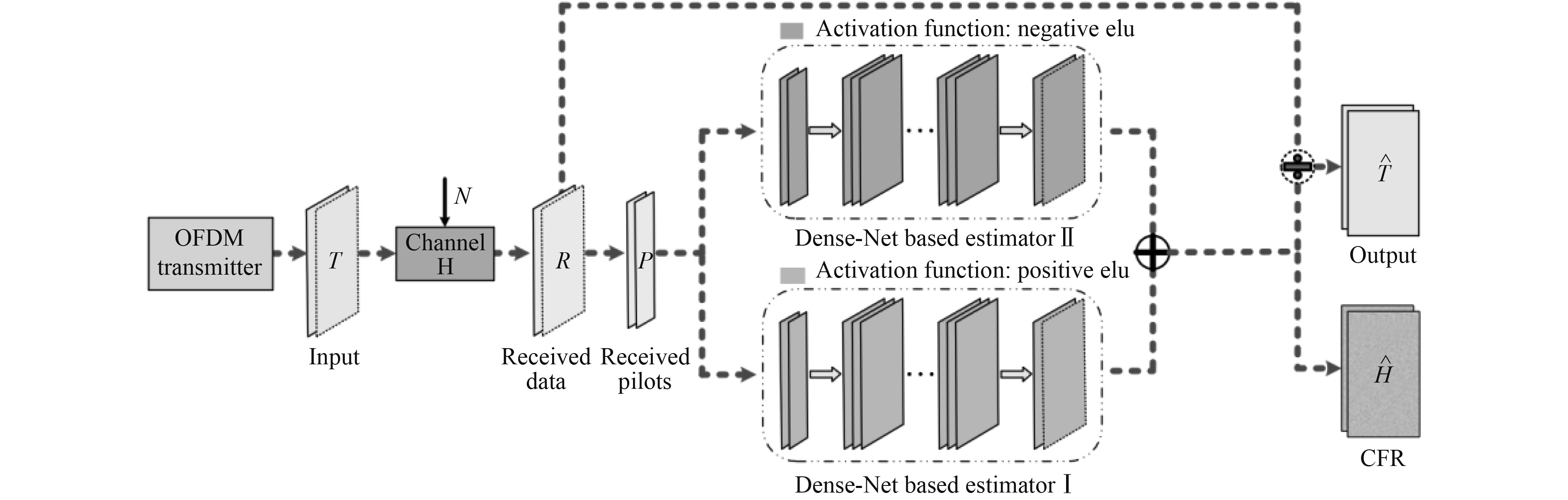
基于无监督学习的信道估计模型框图如图3所示,具体结构参数由表1给出。比特信息通过OFDM发射机生成无监督深度学习模型的输入数据T,T被映射到频域以提高神经网络学习效率,其包含e个OFDM信号,每个OFDM信号有m个子载波,每个子载波携带的复数信息由2个实数表达。发送信号T经过无线信道,信道频域响应为H、加性高斯白噪声(AWGN)为N。接收端得到频域接收信号
|
|
表 1 信道估计器结构参数 Tab.1 The parameter of the proposed channel estimator |
|
图 3 基于无监督学习的信道估计器结构 Fig. 3 The structure of the proposed channel estimator based on unsupervised learning |
整个模型,利用估计输入数据
相比于使用单一极性激活函数的网络,传统Elu和负极性Elu的混合使用方案在一定程度上解决了整体模型的软饱和问题。意味着以更少的参数和更浅的网络层深度能够完成原有信道估计任务。更重要的是,相比于监督的深度学习,无监督学习不需要数据标签(CFR)。
1.3 模型训练本文提出的无监督学习信道估计模型以OFDM发射机的频域发送信号T作为训练数据(由Python编写的OFDM系统仿真生成),并用绝对误差(mean absolute error)作为训练损失函数,其表达式为:
| $ {J_{{\text{MAE}}}} = \frac{{\text{1}}}{U}\sum\nolimits_{i = 1}^U {\left| {{t_i}^{{\text{real}}} - {{\hat t}_i}^{{\text{real}}}} \right| + \left| {{t_i}^{{\text{imag}}} - {{\hat t}_i}^{{\text{imag}}}} \right|}\text{。} $ | (4) |
其中:
MAE体现了真实值和估计值在二维空间上的曼哈顿距离[14],表述了2个值在标准二维坐标系上的各自绝对轴距之和。MAE可以描述出2个实数特征的误差并使其收敛至最优解,同时最小化了实、虚部的真实值与估计值之间的误差,保证了模型的合理收敛。
在激活函数上,选取传统Elu、负极性Elu和Linear激活函数帮助神经网络实现非线性和线性映射及快速收敛。为了防止数据过拟合,设定神经元随机失活(Dropout)的概率为0.1。更重要的是,使用ADAM算法优化反向传播过程,在训练过程中控制梯度下降的步长与方向,使神经网络更容易向最优解收敛。
此外,无监督学习无由于缺少真值信息的约束,在精度方面还无法超越有监督方案。因此需要更多的训练数据来驱动模型训练,即数据量远大于文献[3]。训练基于的比特能量信噪比Eb/N0也是收敛到最优解和影响模型泛化能力的一个重要因素。低Eb/N0下训练时,由于噪声功率大,神经网络难以学习到复杂的数据结构。另一方面,如果训练Eb/N0过高,神经网络失去了处理受噪声污染数据的能力。本文提出基于无监督学习的信道估计器在40 dB下进行训练。
2 性能分析对提出的无监督深度学习信道估计器(channel estimator,CE)设计方案进行仿真分析,系统参数如表2所示。为验证本文提出的信道估计器设计方案能够比现有基于深度学习的信道估计方案[3]有更好的性能表现,根据图3和表1给出的网络结构及参数,针对多径效应引起的频率选择性衰落,给出了慢衰落和快衰落信道条件下系统误符号率(symbol error rate,SER)及估计性能MSE的仿真结果,其中,以规定多普勒频率为5 Hz的扩展行人信道模型(extended pedestrian a model,EPA)作为慢衰落通信信道的仿真环境[15],以多普勒频率为2MHz的EPA模型作为更复杂的快衰落通信信道的仿真环境。
|
|
表 2 OFDM系统仿真参数 Tab.2 The parameters of OFDM system simulation |
实验1 快衰落信道不同训练数据规模条件下无监督深度学习信道估计器MSE性能
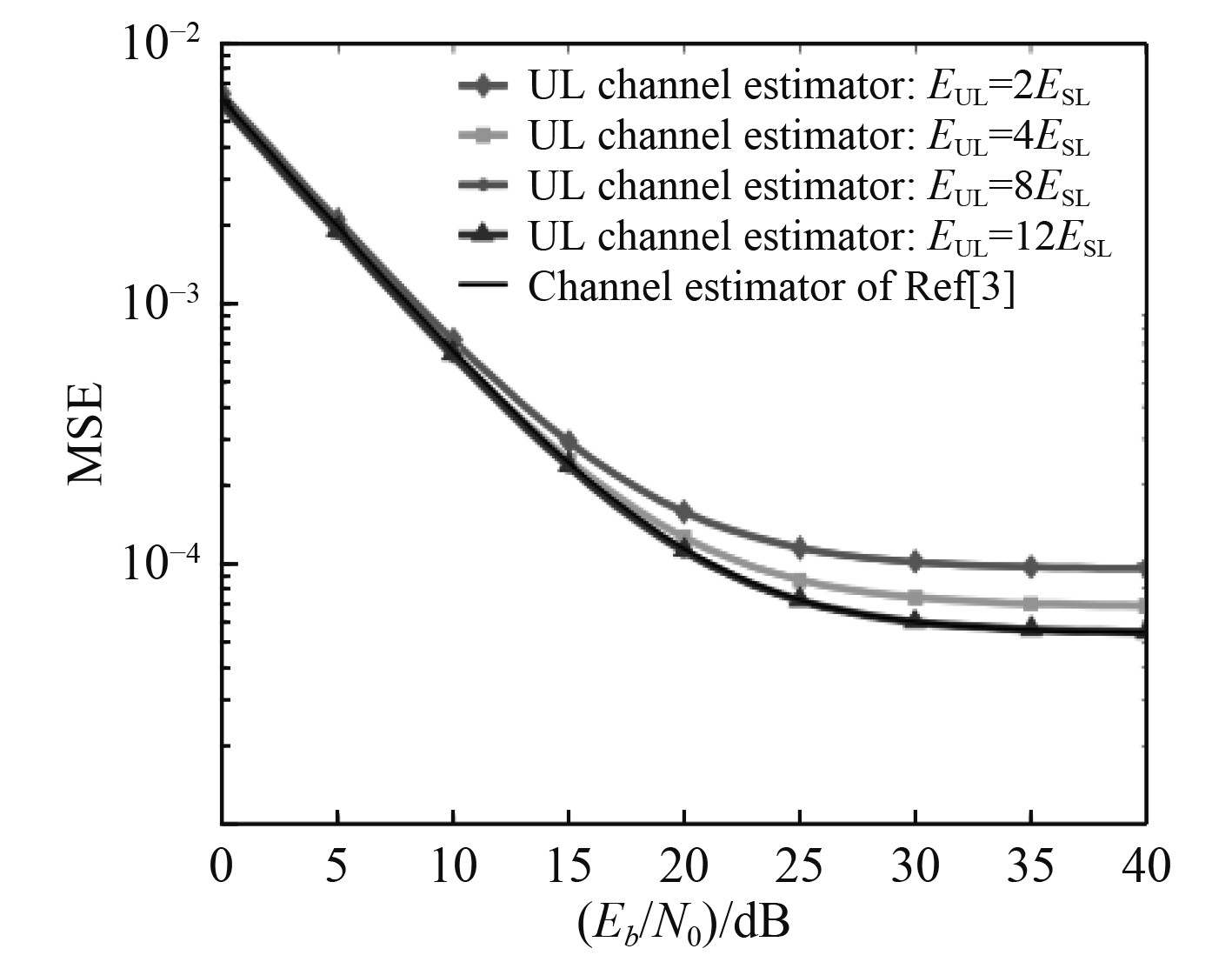
考虑多普勒频移为2 MHz时的快衰落信道,以文献[3]提出的信道估计器作为比较基准,获得的MSE性能如图4所示。图中UL表示无监督学习,SL表示监督学习。当无监督信道估计器训练集规模EUL为监督信道估计器[3]训练集规模ESL的2倍和4倍时,观察到基于无监督深度学习信道估计器的MSE性能随着训练集规模增加而提升,但仍差于文献[3]。在EUL为ESL的8倍和12倍时,基于无监督深度学习信道估计器均与文献[3]的MSE性能相当。其原因在于,无监督学习相对于监督学习缺乏真值信息CFR的直接约束,需要更大规模的训练集驱动模型训练,并且目前在精度上也无法超越基于监督学习的神经网络。但是,无监督学习信道估计器的训练过程更加简单,简化了对模型标签CFR的获取。因此,以8倍于文献[3]的训练集规模进行无监督学习。
|
图 4 快衰落信道不同训练数据规模条件下无监督学习CE的MSE性能对比 Fig. 4 The MSE performance comparison of unsupervised learning based channels estimator with different data set sizes under fast multipath fading channels using EPA model with Doppler frequency 2 MHz |
实验2 快衰落信道不同激活函数及神经网络深度下信道估计器MSE性能
考虑多普勒频移为2MHz时的快衰落信道,以文献[3]提出的信道估计器作为比较基准,获得的MSE性能如图5所示。可以看出,在Dense-Net模块的深度为3层和12层时,混合使用传统Elu和负极性Elu的信道估计器在中高信噪比下差于文献[3]的MSE性能。然而在Dense-Net模块的深度为6层和9层时,本文提出的混合Elu使用方案在全信噪比下和文献[3]的MSE性能相当。这是因为过少的神经网络层数或参数导致模型的表达能力不足,过多的神经网络层数或参数使得模型收敛困难且过拟合现象严重。而且,混合Elu使用方案相比于文献[3]解决了Elu单侧软饱和的问题,同时保证了非线性映射的能力,使得该方案可以用更浅的神经网络准确估计出CFR。因此,使用深度为6层的Dense-Net模块。

|
图 5 快衰落信道不同Dense-Net深度条件下CE的MSE性能对比 Fig. 5 The MSE performance comparison of channels estimator with depth of Dense-Net under fast multipath fading channels using EPA model with Doppler frequency 2 MHz |
相比于使用文献[3]的信道估计模型(总卷积层数为12、参数量为19192),本文提出的信道估计模型(总卷积层数为12、参数量为9082)更为轻量化。因为Dense-Net结构随着深度的增加,参数成指数增加,而混合Elu方案增加了Dense-Net模块的数量,即神经网络的宽度,减少了单个Dense-Net模块的深度,从而显著降低了模型的参数量。
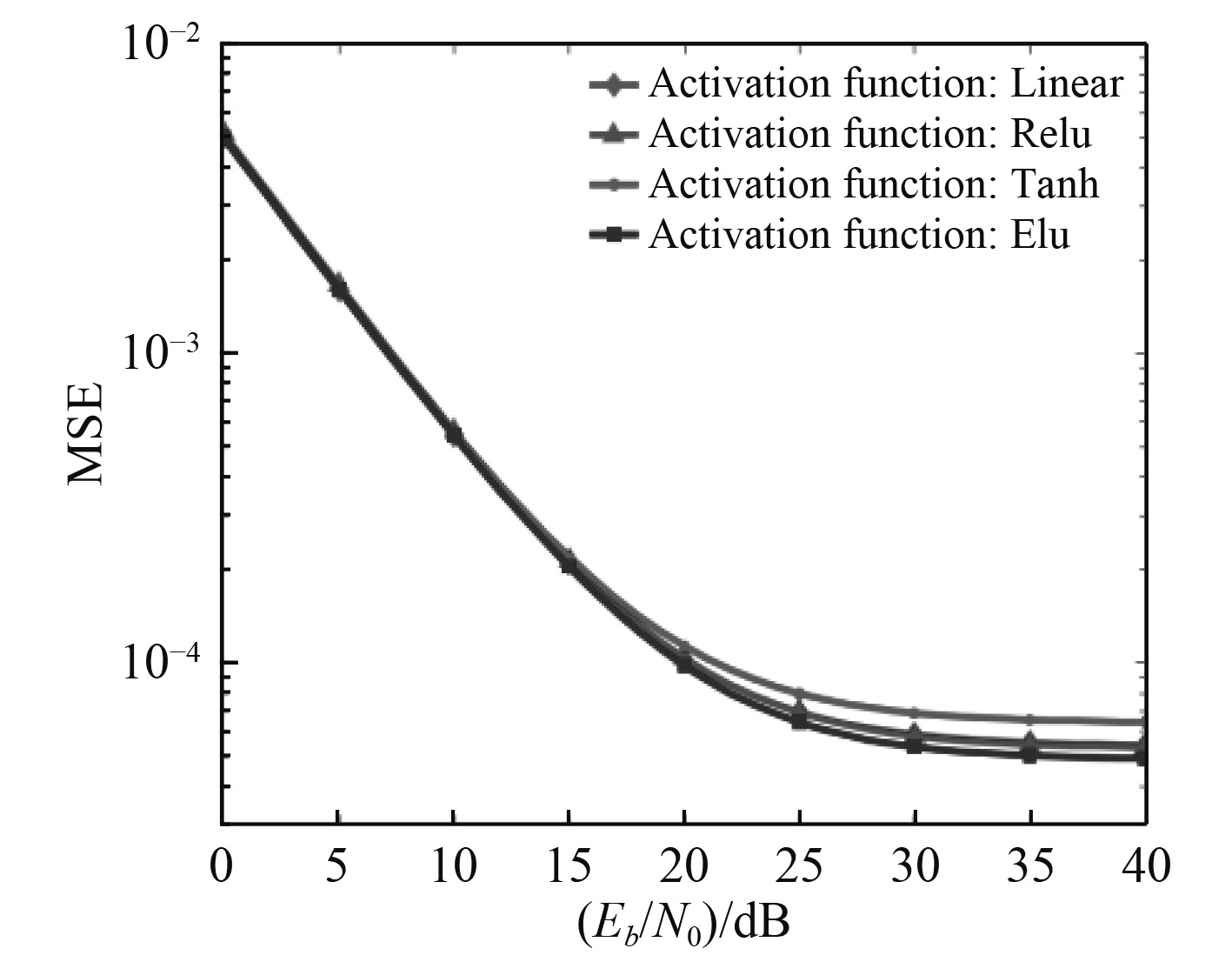
此外,验证了Elu激活函数的合理性。在多普勒频移为2MHz时的快衰落信道下,以混合使用传统Elu和负极性Elu的信道估计器(Dense-Net模块深度为6)作为比较基准,不同激活函数的MSE性能如图6所示。可以看出,使用Tanh激活函数的信道估计器性能最差,这是因为Tanh函数左右侧均饱和且幅度被压缩。使用线性函数和Relu激活函数的信道估计器略差于基准,因为线性函数缺少非线性映射的能力,而Relu激活函数的梯度存在死区现象。因此,使用Elu作为激活函数。
|
图 6 快衰落信道不同激活函数条件下CE的MSE性能对比 Fig. 6 The MSE performance comparison of channels estimator with different activation functions under fast multipath fading channels using EPA model with Doppler frequency 2 MHz |
实验3 快衰落信道不同损失函数下信道估计器性能
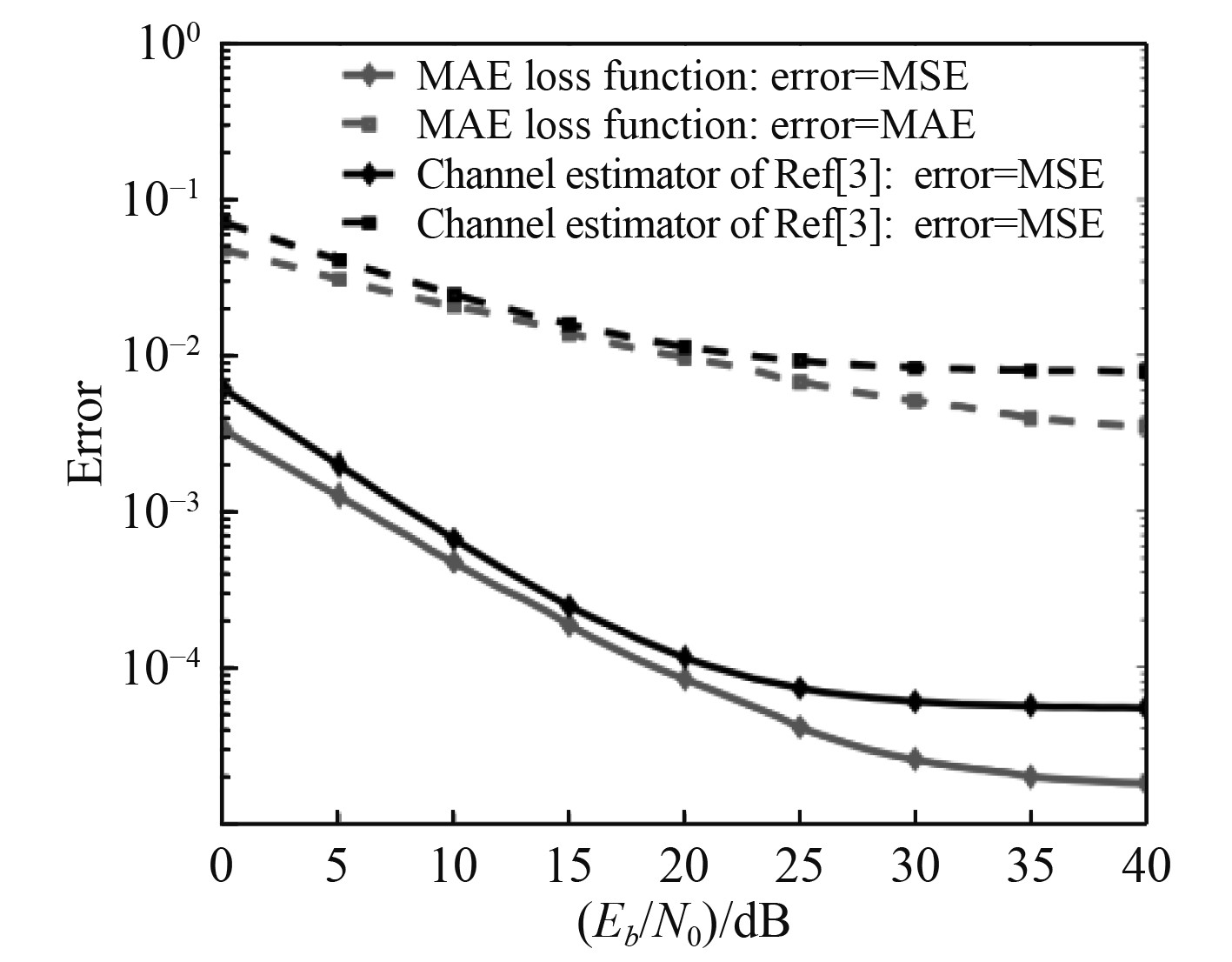
考虑多普勒频移为2 MHz时的快衰落信道,以文献[3]提出的信道估计器作为比较基准,获得的性能如图7所示。可以看出,同时以MAE和MSE作为评价标准的情况下,本文提出的以MAE为损失函数训练的信道估计器均优于文献[3]。显然,欧氏距离无法明确表达出每个实数特征的估计值与真实值误差,以最小化曼哈顿距离为目标函数可以更好地帮助实数搭建的网络模型收敛并取得更好的性能。
|
图 7 快衰落信道使用不同损失函数条件下CE的MSE性能对比 Fig. 7 The MSE performance comparison of channels estimator with different loss function under fast multipath fading channels using EPA model with Doppler frequency 2 MHz |
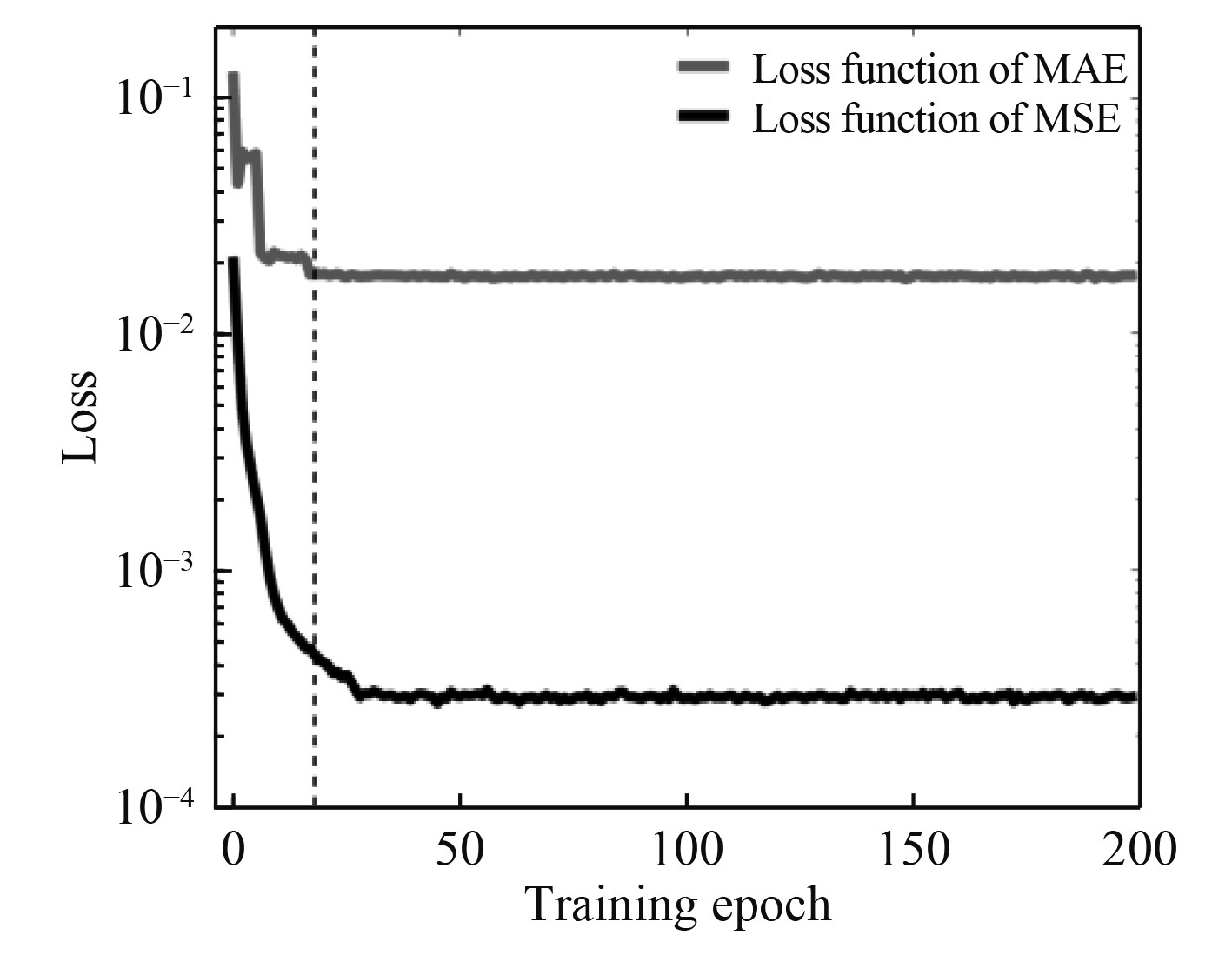
此外,验证了模型的快速收敛性。在多普勒频移为2MHz时的快衰落信道下,图8展示了信道估计模型分别使用MAE和MSE的损失函数曲线。可以看出,以MAE为损失函数的信道估计模型提前于以MSE为损失函数的信道估计模型收敛,即本文提出的信道估计模型可以用更少的迭代次数的训练并收敛。
|
图 8 使用不同损失函数的信道估计器的收敛情况 Fig. 8 Convergence of channel estimators using different loss functions |
实验4 不同衰落信下信道估计器SER性能
为了进一步证明所提出的信道估计算法的学习能力,以OFDM系统接收端具有完美CFR和文献[3]提出的基于深度学习的信道估计算法作为比较基准。
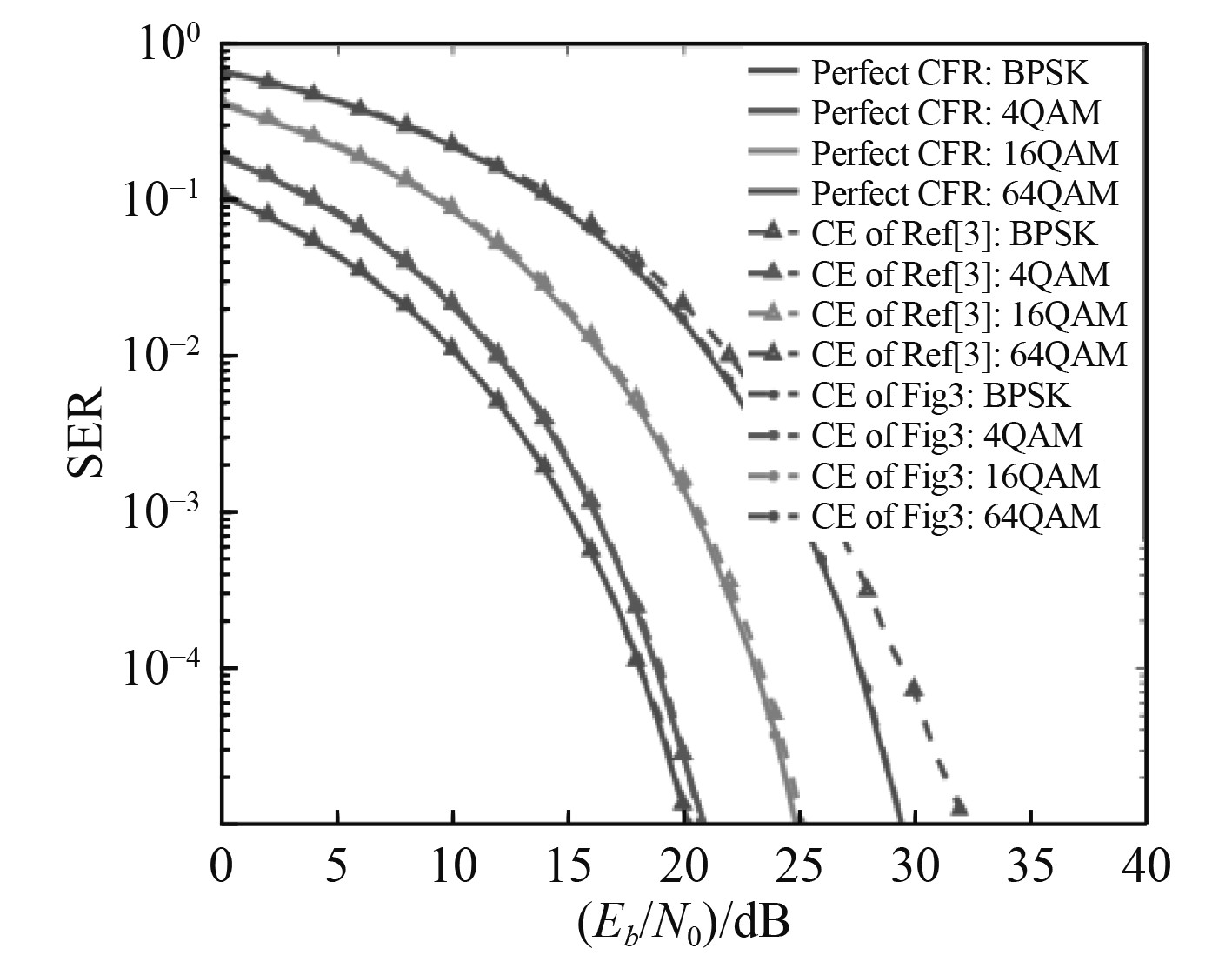
在多普勒频移为5 Hz的慢衰落信道下,图9给出了OFDM系统的SER对比曲线,图中CE表示信道估计器。当系统使用BPSK,4-QAM和16-QAM时,观察到文献[3]和本文所提出的信道估计器都可以达到与使用完美CIRs时相同的性能,但在64-QAM的情况下,文献[3]在高信噪比下存在较大误差,而本文提出的信道估计器仍然能够准确地重构CIRs,其性能和接收端已知完美CFR的OFDM系统更加接近。
|
图 9 慢衰落信道下使用不同CE的OFDM系统SER性能对比 Fig. 9 The SER performance comparison of OFDM systems with different channels estimator under slow multipath fading channels using EPA model with Doppler frequency 5 Hz |
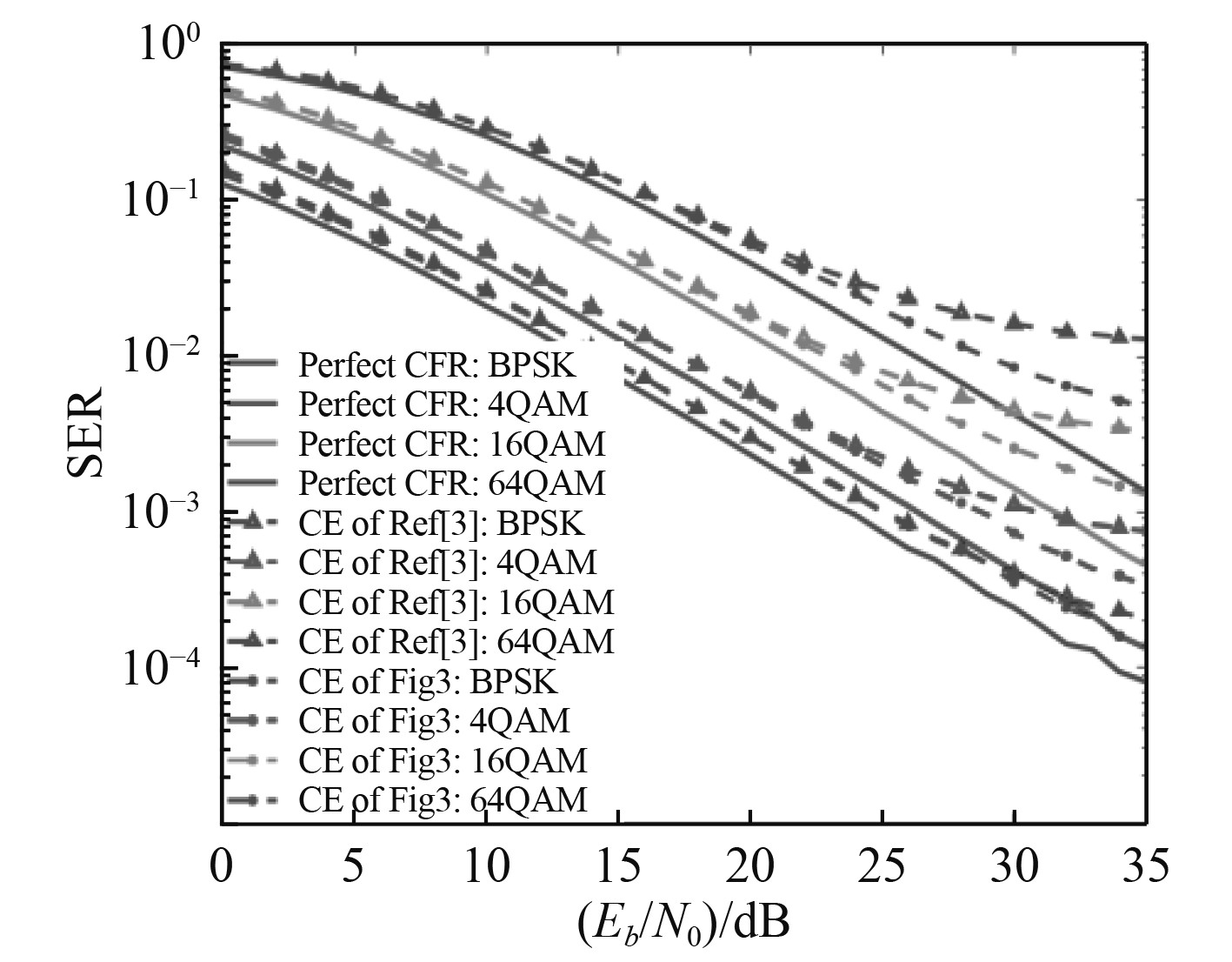
在多普勒频率为2 MHz的快衰落信道下,图10给出了OFDM系统的SER对比曲线。可以看出,当多普勒频率为2MHz时,由于信道快速变化导致所有基于信道估计器的SER性能都差于完美CFR的系统。进一步观察,图10中所有信道估计算法在高信噪比区域都表现出了地板效应,当m较大时,地板效应变得更加明显。但是,提出的信道估计算法仍然能够取得比文献[3]更好的SER性能。总之,本文信道估计模型均可获得更好的MSE、MAE和SER性能以及更少的训练迭代次数。
|
图 10 快衰落信道下使用不同CE的OFDM系统SER性能对比 Fig. 10 The SER performance comparison of OFDM systems with different channels estimator under fast multipath fading channels using EPA model with Doppler frequency 2 MHz |
表3为本文提出的信道估计算法和文献[3]提出的信道估计算法对比。
|
|
表 3 两种信道估计算法对比 Tab.3 The comparison of two channel estimation algorithms |
本文针对进一步提高OFDM信道估计精度进行研究,提出一种改进的无监督深度学习海上OFDM系统信道估计算法。采用双极性Elu混合方案,提高了神经网络隐藏层的特征表达能力,降低了模型的复杂度。此外,提出最小化曼哈顿距离的目标函数,保证了实数神经网络的合理收敛,使其可以学习复杂的信号特征以获得更高精度的信道估计结果。在多径衰落信道下,本文提出的信道估计器性能优于现有基于深度学习的信道估计算法,且算法计算复杂度更低和迭代收敛速度更快。
| [1] |
王志明, 刘志辉, 黄洋科, 等. 基于深度学习的高效火车号识别[J]. 工程科学学报, 2020, 42(11): 1525. WANG Z M, LIU Z H, HUANG Y K, et al. Efficient wagon number recognition based on deep learning[J]. Chinese Journal of Engineering, 2020, 42(11): 1525. |
| [2] |
O’SHEA T, HOYDIS J. An introduction to deep learning for the physical layer[J]. IEEE Transactions on Cognitive Communications and Networking, 2017, 3(4): 563. DOI:10.1109/TCCN.2017.2758370 |
| [3] |
LIN B, WANG X D, YUAN W H, et al. A novel OFDM autoencoder featuring CNN-based channel estimation for internet of vessels[J]. IEEE Internet of Things Journal, 2020, 7(8): 7601. DOI:10.1109/JIOT.2020.2986442 |
| [4] |
王旭东, 吴楠, 王旭. 基于卷积神经网络自编码器结构的空时分组传输方案[J]. 电讯技术, 2020, 60(7): 746. WANG X D, WU N, WANG X. A transmission scheme of CNN-based autoencoder for STBC systems[J]. Telecommunication Engineering, 2020, 60(7): 746. DOI:10.3969/j.issn.1001-893x.2020.07.002 |
| [5] |
WU N, WANG X D, LIN B, et al. A CNN-based end-to-end learning framework toward intelligent communication systems[J]. IEEE Access, 2019, 7: 110197. DOI:10.1109/ACCESS.2019.2926843 |
| [6] |
廖勇, 花远肖, 姚海梅. 基于深度学习的OFDM信道估计[J]. 重庆邮电大学学报(自然科学版), 2019, 031(003): 348. LIAO Y, HUA Y X, YAO H M. Channel estimation based on deep learning for OFDM systems[J]. Journal of Chongqing University of Posts and Telecommunications( Natural Science Edition), 2019, 031(003): 348. |
| [7] |
SOLTANI M, POURAHMADI V, MIRZAEI A, et al. Deep learning-based channel estimation[J]. IEEE Communications Letters, 2019, 23(4): 652. DOI:10.1109/LCOMM.2019.2898944 |
| [8] |
BRIFMAN A, ROMANO Y, ELAD M. Unified single-image and video super-resolution via denoising algorithms[J]. IEEE Transactions on Image Processing, 2019, 28(12): 6063. DOI:10.1109/TIP.2019.2924173 |
| [9] |
USAMA M, QADIR J, RAZA A, et al. Unsupervised machine learning for networking: Techniques, applications and research challenges[J]. IEEE Access, 2019, 7: 65579. DOI:10.1109/ACCESS.2019.2916648 |
| [10] |
YU J, GAO X, TAO D, et al. A unified learning framework for single image super-resolution[J]. IEEE Transactions on Neural networks and Learning systems, 2013, 25(4): 780. |
| [11] |
YANG L, CHEN W, LIU W, et al. Random noise attenuation based on residual convolutional neural network in seismic datasets[J]. IEEE Access, 2020, 8: 30271. DOI:10.1109/ACCESS.2020.2972464 |
| [12] |
PHUNG S L, BOUZERDOUM A. A pyramidal neural network for visual pattern recognition[J]. IEEE transactions on neural networks, 2007, 18(2): 329. DOI:10.1109/TNN.2006.884677 |
| [13] |
ZHANG Z, LI F, ZHAO M, et al. Robust neighborhood preserving projection by nuclear/l2, 1-norm regularization for image feature extraction[J]. IEEE Transactions on Image Processing, 2017, 26(4): 1607. DOI:10.1109/TIP.2017.2654163 |
| [14] |
PONNMOLI K M, SELVAMUTHUKUMARAN D S. Analysis of face recognition using manhattan distance algorithm with image segmentation[J]. International Journal of Computer Science and Mobile Computing, 2014, 3(7): 18. |
| [15] |
ARIB STD-T. Evolved universal terrestrial radio access (E-UTRA); user equipment (UE) radio transmission and reception (Release 8)[J]. 3GPP TS, 2010, 36: 8. |
 2022, Vol. 44
2022, Vol. 44

