电机是船舶航行的关键设备之一,其运行的可靠性能直接影响船舶航行的安全性。可知在船舶故障中,由电机轴承故障导致的事故占整体事故的1/3左右[1]。因此船舶电机轴承故障的诊断,对于提升船舶航行的安全性具有至关重要的意义。
肖雄等[2]采用二维卷积神经网络诊断轴承故障,通过对故障数据进行降噪处理提升诊断精度,但该方法中的网络参数预定对于故障诊断产生消极影响。张习习等[3]采用集成学习概率神经网络诊断轴承故障,但该方法中特征提取精度较差,由此导致最终的诊断精度也受到显著影响。李兵等[4]在故障诊断过程中引入随机森林算法,但该类方法有较大的概率出现过度拟合问题,由此导致最终诊断结果容易出现误差。针对以上问题,研究对抗神经网络算法在船舶电机轴承故障诊断中的应用,以此确保船舶航行的安全性。
1 船舶电机轴承故障诊断方法 1.1 船舶电机轴承故障特征提取 1.1.1 集合经验模态分解方法为提升轴承振动信号分解效果在轴承故障特征信号内添加白噪声,并依照高斯噪声的零均值特征[7],分若干次引入噪声,并从中提取分解结果均值,以此抵消引入噪声带来的消极影响,次数越多噪声带来的消极影响抵消程度越高。该方法实现流程如下:
1)以
2)以
| $ {x_i}\left( t \right) = x\left( t \right) + {b_i}\left( t \right) + \beta \left( t \right)。$ | (1) |
式中:
3)分解
| $ {x_i}\left( t \right) = \left( {\sum\limits_{s = 1}^s {{a_{i,s}}\left( t \right)} + {q_{i,s}}\left( t \right)} \right) \times \phi 。$ | (2) |
式中:
4)循环
5)确定本征模态函数的集合的均值,并以此为最终结果,由此可将
| $ {a_s}\left( t \right) = \frac{{\displaystyle\sum\limits_{i = 1}^R {{a_{i,s}}\left( t \right)} }}{R}。$ | (3) |
船舶电机轴承故障有所差异的条件下,轴承振动信号的能量同样不同,因此可通过能量熵描述船舶电机轴承故障特征。能量熵的描述为:
| $ {N_E} = - \sum\limits_{i = 1}^n {\lg {t_i}}。$ | (4) |
式中,
基于式(4)获取船舶电机轴承样本振动信号不同状态下的本征模态函数分量能量熵均值。分析船舶电机轴承正常条件与故障条件下的能量熵维数,为了符合全部故障状态的本征模态函数分量能量熵样本输入符合要求,利用相关系数法,清除同船舶电机轴承故障特征不存在关联性的虚假本征模态函数分量。
相关系数法描述为:
| $ {g_j} = \frac{{\displaystyle\sum\limits_{i = 1}^n {\left( {{X_i} - \bar X} \right)\left( {{Y_i} - \bar Y} \right)} }}{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {{{\left( {{X_i} - \bar X} \right)}^2}{{\left( {{Y_i} - \bar Y} \right)}^2}} } }}。$ | (5) |
式中:
利用式(5)确定船舶电机轴承初始振动信号同故障信号本征模态函数间的相关系数。根据不同本征模态函数分量的标准差确定阈值:
| $ \partial = \sqrt {\frac{{\displaystyle\sum\limits_{j = 1}^k {{{\left( {{r_j} - \mu } \right)}^2}} }}{k}} 。$ | (6) |
依照式(6)能够确定标准差阈值
对抗神经网络由生成器网络
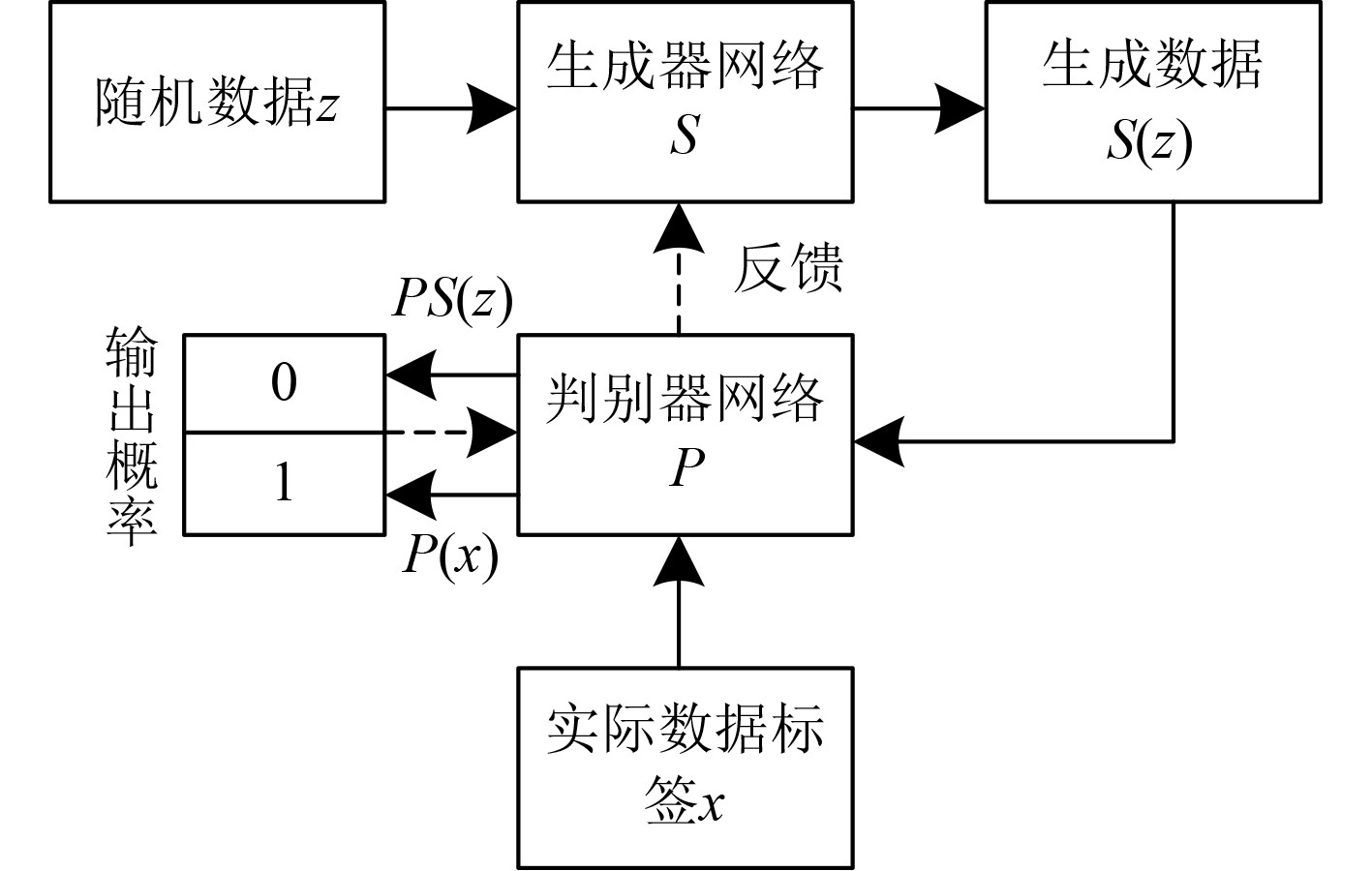
|
图 1 对抗神经网络结构图 Fig. 1 Structure diagram of countermeasure neural network |
生成器网络
| $ \mathop {\max }\limits_P {V_1}\left( P \right) = {E_{x\sim{P_g}}}\left[ {\log \left( {P\left( {\text{x}} \right)} \right)} \right],$ | (7) |
| $ \mathop {\min }\limits_S {V_1}\left( S \right) = {E_{\textit{z}\sim{P_r}}}\left[ {\log \left( {1 - P\left( {S\left( \textit{z} \right)} \right)} \right)} \right]。$ | (8) |
式中:
依照
| $ \begin{split} \mathop {\min }\limits_S \mathop {\max }\limits_P V\left( {P,S} \right) =& {E_{x,y\sim{P_g},{P_r}}}\left( {\left[ {\log \left( {S\left( {x,y} \right)} \right)} \right]}+ \right. \hfill \\ &\left. { \left[ {\log \left( {1 - S\left( {P\left( y \right),y} \right)} \right)} \right]} \right) 。\end{split} $ | (9) |
式中:
利用二人零和博弈问题能够描述对抗神经网络的训练过程,利用式(10)描述博弈过程的目标函数:
| $ \mathop {\min }\limits_S \mathop {\max }\limits_P V\left( {P,S} \right) = {E_{x\sim{P_r}\left( x \right)}}\left[ {P\left( {\text{x}} \right)} \right] - \left[ {P\left( {S\left( {\text{z}} \right)} \right)} \right]。$ | (10) |
可知,
可通过Wasserstrin距离判断方法表示式(10)内的优化目标,该方法可缓解抗神经网络训练过程中梯度消失的问题,提升训练过程的稳定性。利用式(11)能够描述Wasserstrin距离判断:
| $ L\left( {{p_r},{p_g}} \right) = \left( {\mathop {\inf }\limits_{r\sim\prod {\left( {{p_r},{p_g}} \right)} } {E_{\left( {x,y} \right)\sim r}}\left\| {x - y} \right\|} \right) \times \theta 。$ | (11) |
式中:
| $ L\left( {{p_r},{p_g}} \right) = \frac{{\mathop {\sup }\limits_{\left\| f \right\|L \leqslant K} {E_{x\sim{P_r}}}\left[ {f\left( x \right)} \right] - {E_{x\sim{P_g}}}\left[ {f\left( x \right)} \right]}}{V}。$ | (12) |
式中:
利用对抗神经网络算法构建船舶电机轴承故障诊断模型,模型结构如图2所示。
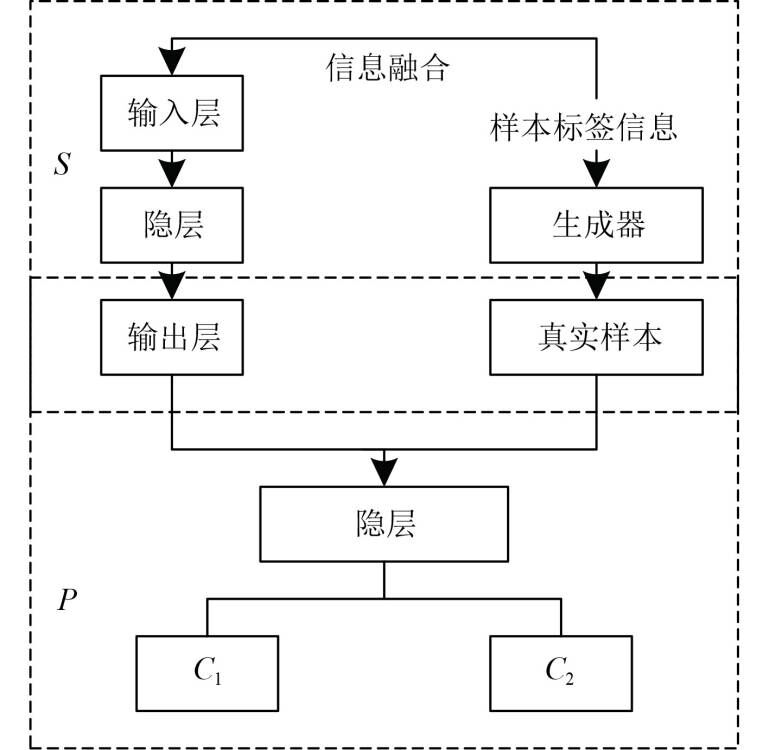
|
图 2 船舶电机轴承故障诊断模型结构 Fig. 2 Structure of fault diagnosis model of marine motor bearing |
模型内,
为验证本文方法在实际船舶电机轴承故障诊断中的应用中的应用效果,以舰船上普遍使用的某型号电机为实验对象,采用本文方法诊断实验对象内轴承故障。
设定实验对象内轴承振动信号采样频率为12 kHz,采集实验对象内各轴承振动信号并构建数据集。将预处理后的样本数据数值至对抗神经网络内实施训练,设定迭代次数为2000次,迭代过程中
以实验对象内某一滚动轴承为例,采用本文方法提取其故障特征振动信号。图3为本文方法提取结果与实际故障特征振动信号的对比结果。
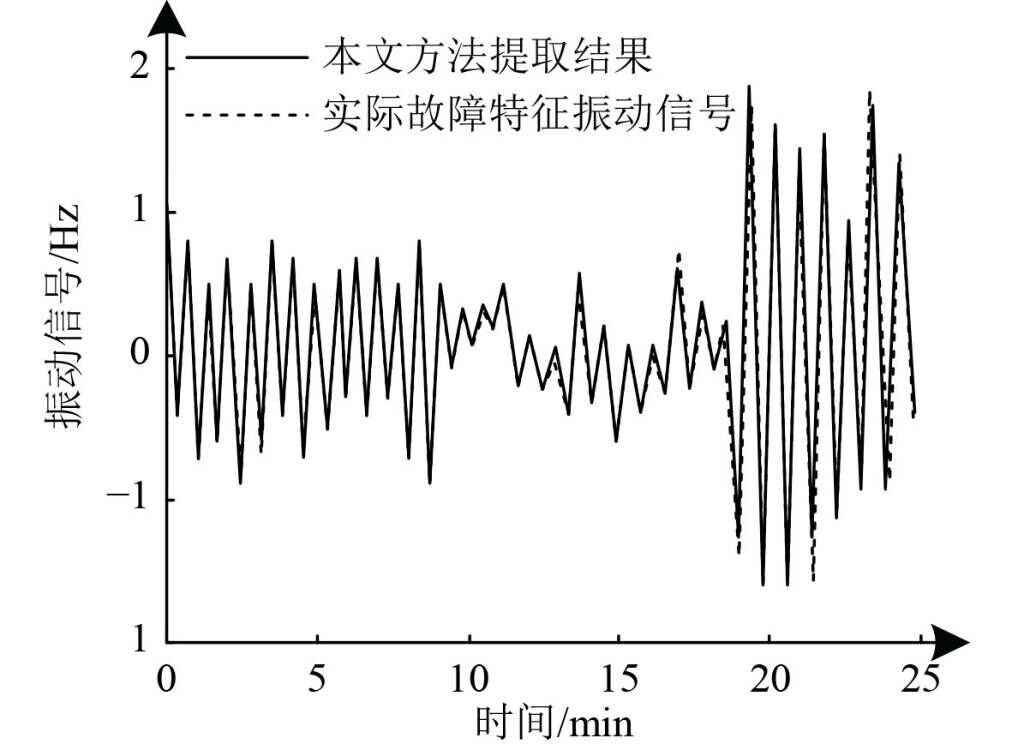
|
图 3 故障特征信号提取结果 Fig. 3 Fault characteristic signal extraction results |
分析可知,采用本文方法所提取的轴承故障振动信号与实际故障特征振动信号基本一致,由此说明本文方法能够准确提取轴承故障振动信号,有助于提升轴承故障诊断结果。
2.2 模型参数对诊断结果的影响本文方法通过对抗神经网络算法诊断实验对象内轴承故障,对抗神经网络的参数确定对于最终轴承故障诊断结果产生显著影响。图4为学习率有所差异条件下诊断模型输出的均方误差统计结果。
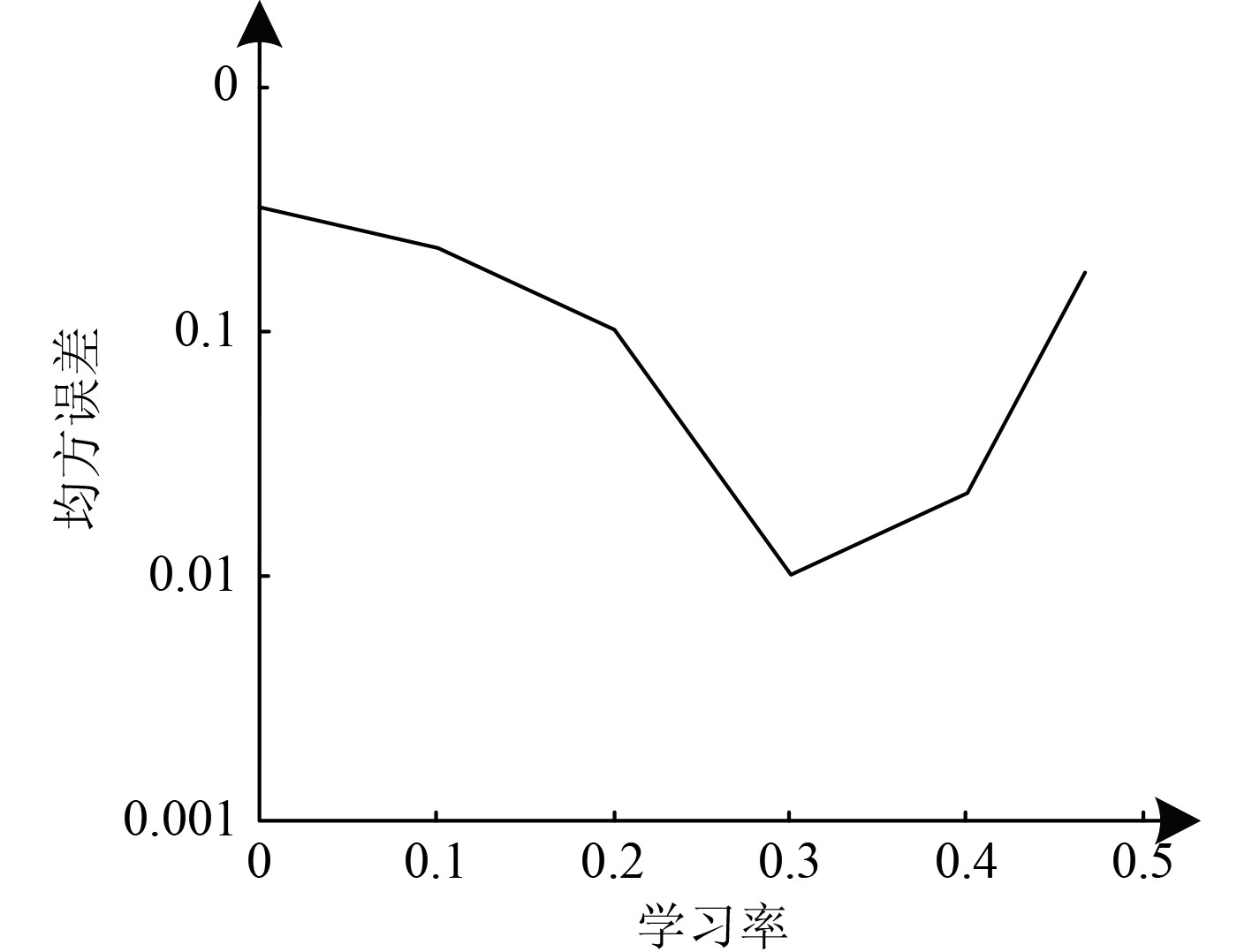
|
图 4 学习率对诊断模型输出的均方误差的影响 Fig. 4 Effect of learning rate on mean square error of diagnostic model output |
分析可知,在诊断模型学习率为0.3的条件下,本文方法中诊断模型输出的故障诊断结果均方误差为最低,在此条件下故障诊断模型的故障诊断性能达到最优状态。为确保本文方法中故障诊断模型所得故障诊断结果的准确性与实时性,在本文方法实际应用过程中设定故障诊断模型的学习率为0.3。
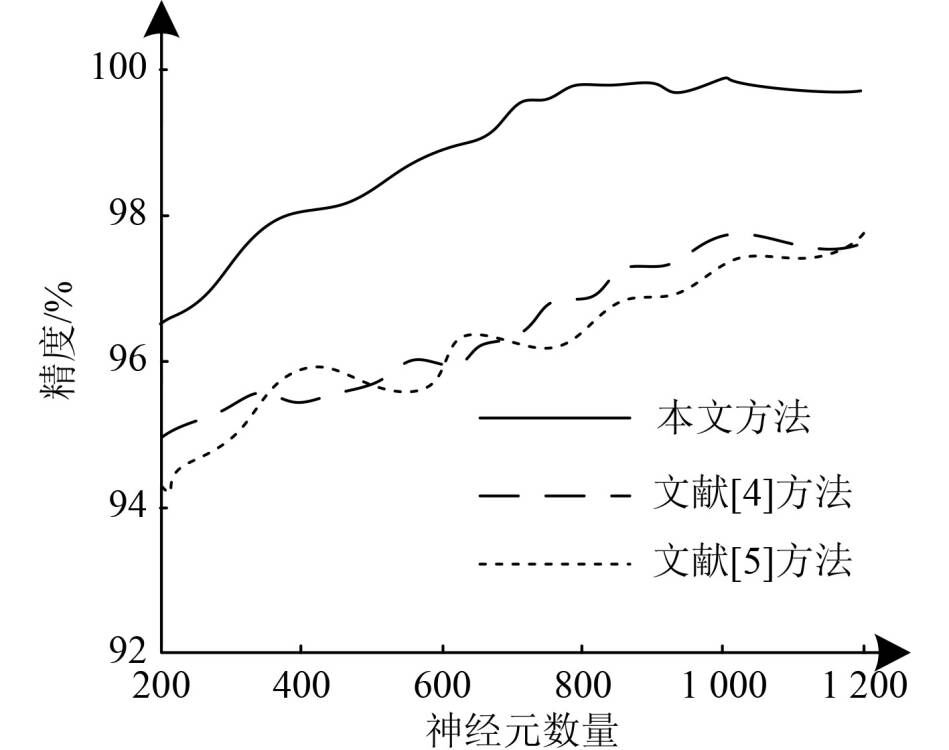
2.3 不同方法的对比结果为进一步验证本文方法的应用性能,以文献[2]直接拍卖行基于二维卷积神经网络的诊断方法、文献[3]中基于集成学习概率神经网络的诊断方法为对比方法。不同神经元数量条件下,本文方法与2种对比方法的诊断精度如图5所示。
|
图 5 不同方法诊断精度对比结果 Fig. 5 Comparison results of diagnostic accuracy of different methods |
分析可知,在神经元数量有所差异的条件下,本文方法的诊断精度均高于96%,其中神经元数量为800的条件下,本文方法的诊断精度最高,约为99.7%。2种对比方法的诊断精度上限均在97.5%左右。在神经元数量一致的条件下,本文方法诊断精度均高于2种对比方法,由此说明本文方法的诊断性能优于2种对比方法。
3 结 语本文研究基于对抗神经网络算法在船舶电机轴承故障诊断中的应用,利用对抗神经网络算法分类轴承故障类型,实验结果显示本文方法具有较高的诊断精度。
| [1] |
李远军, 孙继炫. 基于特征提取与识别两阶段的汽车电机轴承故障诊断[J]. 电子测量与仪器学报, 2019, 33(2): 56-63. |
| [2] |
肖雄, 王健翔, 张勇军, 等. 一种用于轴承故障诊断的二维卷积神经网络优化方法[J]. 中国电机工程学报, 2019, 39(15): 4558-4568. |
| [3] |
张习习, 顾幸生. 基于集成学习概率神经网络的电机轴承故障诊断[J]. 华东理工大学学报:自然科学版, 2020, 46(1): 68-76. |
| [4] |
李兵, 韩睿, 何怡刚, 等. 改进随机森林算法在电机轴承故障诊断中的应用[J]. 中国电机工程学报, 2020, 40(4): 1310-1319+1422. |
 2022, Vol. 44
2022, Vol. 44
