随着海洋油气向深水领域开发,具有相对投资少、工作水深范围大、甲板可变载荷大以及多种工作功能等优点的半潜式海洋平台得到更加广泛的运用。半潜式平台水动力性能对平台结构强度和人员安全及工作环境起到决定性作用。由于海洋平台的工作环境和地域特殊,平台承受的主要载荷包括风、浪、流、冰雪和地震等,其中波浪载荷是环境载荷的重要部分。
国外对于半潜式平台的水动力性能进行了大量的研究,Emami等[1]在GVA4000型平台底部加上多孔弹性层,有效减小了平台的垂荡响应。Lwanowski等[2]采用Com FLOW 软件进行研究,分析海洋平台气隙变化,并将理论研究与试验结果比较。Pham等[3]通过数值模拟和模型验证,研究了二阶波浪载荷对半潜式平台漂移运动的影响。Rohit等[4]对半潜式钻井平台中的模型进行变换,分为有柱和无柱2种情况比较,绘制了速度分布、压力分布和流线,将时域的实验结果转换到频域,以实验和数值模拟得到的浪荡、纵荡和垂荡功率谱密度偏差为目标函数,获得最佳拟合阻力系数。这种新的数值优化方法可以找到不同载荷情况下的一组阻力系数。Ren等[5]提出了一种模块化浮动结构,研究了在操作和极端海况条件下,微流场连接方式和功率输出参数对MTLPW系统水动力性能的影响。结果表明,连接件弯矩的极限响应取决于连续固定模块的数量。通过正确使用铰链式连接器优化MTLPW系统的连接方式。
国内对平台水动力性能也进行了大量的研究。邓小康等[6]采用频域和时域分析方法,验证了DTP平台具有优越的垂荡性能。张曼等[7]运用三维势流理论比较分析,得到相较于波浪单独作用于半潜式平台,风/浪/流联合作用时,平台气隙值更小,出现负气隙概率更大的结论。罗幼安等[8]通过研究发现,二阶运动响应会增加平台的负气隙,其中在平台的立柱周围最为严重。李男等[9]基于一阶势的二阶力计算方法,给出并验证了定常力、二阶力传递函数的相关计算公式推导。
目前工程界对半潜平台的水动力计算方法主要是对浮箱和立柱等大结构部分采用三维势流理论计算,主要是附加质量效应和绕射效应,粘滞效应微不足道,对实际工程可以省略。而对斜撑和横撑等细长结构部分采用半经验Morison方程的方法。根据CCS规范的规定[10],Morison方程和绕射理论的适用范围可参考图1。其中H为波高,D为结构特征尺度(直径和界面长宽等),L表示波长,h表示水深,k表示波数。

|
图 1 Morison方程与绕射理论适用范围 Fig. 1 Application scope of Morison equation and diffraction theory |
由于半潜式平台所承受的自然界中随机波浪波长在几米到几百米之间都会存在。浮箱是承受波浪载荷的主要部分,半潜式海洋平台浮箱的长度一般在100 m左右,而截面宽度和高度主要在10~20 m之间。对于不同的波浪,浮箱会处在不同的区间内,是否需要对半潜式平台的粘性效应是否考虑不能确定。
针对此现象,本文依据有限条件的建模方法(CMA)建立海浪波高与周期的联合模型,并由一次逆可靠度方法(IFORM)确定百年一遇波高-周期的等概率曲线,计算出波浪的极限波陡值,对北大西洋海域生成百年一遇由JONSWAP谱描述的海况。运用忽略浮箱粘性阻尼、采用Morison方程考虑浮箱粘性阻尼和直接增加临界阻尼(Critical damping)修正的3种方法,分别对半潜式平台设计中特别关注的运动响应、气隙和波浪二阶平均漂移力分别进行短期预报,根据设计波方法,预报半潜式平台所承受的纵向剪切力等6个由波浪引起的载荷,由此确定平台的设计波,并对这3种不同方法计算出的结果进行了对比分析。
1 海洋平台运动方程和波浪载荷 1.1 海洋平台在外界环境载荷作用下的运动方程运动方程可表示如下:
| $ {\boldsymbol{M}}\;\ddot x + {\boldsymbol{C}}\dot x + {\boldsymbol{K}}x = {f_{wind}} + {f_{wave}} + {f_{current}} + {f_{other}} 。$ | (1) |
式中:M为质量矩阵,包括平台质量和动态附加质量;C为阻尼矩阵;K为刚度矩阵,包括静水回复刚度矩阵和锚泊系统的刚度矩阵;fwind为平台所受风载矩阵;fwave为波浪载荷矩阵,包括一阶和二阶波浪载荷;fcurrent为平台所受流载矩阵;fother为平台所受其他载荷,如冰载、地震等。
1.2 海浪有义波高与周期的CMA联系模型根据Bitner-Gregersen 和 Haver 提出的三参数(位置、形状和尺度参数)威布尔分布描述波浪有义波高的分布密度函数[11]:
| $ {f_{Hs}}(h) = \frac{{{\beta _{Hs}}}}{{{\alpha _{Hs}}}}{\left(\frac{{h - {\gamma _{Hs}}}}{{{\alpha _{Hs}}}}\right)^{{\beta _{Hs}} - 1}}\times \exp \left[ { - {{\left( {\frac{{h - {\gamma _{Hs}}}}{{{\alpha _{Hs}}}}} \right)}^{{\beta _{Hs}}}}} \right], $ | (2) |
用对数分布函数描述波浪跨零周期与有义波高的联合分布密度函数:
| $ {f_{Tz/Hs}}(t/h) = \frac{1}{{\sigma \times t \times \sqrt {2\text{π}} }}\times \exp \left[ { - {{\frac{{(\ln t - \mu )}}{{2\sigma }}}^2}} \right], $ | (3) |
Bitner-Gregersen提出的北大西洋相关波浪平均值和标准差参数表达式:
| $ \mu = E[\ln {T_z}] = {a_0} + {a_1}\cdot{h^{{a_2}}} \sigma = std[\ln {T_z}] = {b_0} + {b_1}\cdot{e^{{b_2}\cdot h}}。$ | (4) |
其中相应的参数如表1所示。
|
|
表 1 北大西洋波浪分布参数 Tab.1 Wave distribution parameters of North Atlantic |
根据DNV-RP-C205 推荐,采用IFROM方法求解有义波高与跨零周期的百年等一遇等概率曲线[12-13]。
有义波高与周期的联合概率密度函数如下:
| $ {f_{Tz/Hs}}(t/h) = {f_{Hs}}(h)\cdot{f_{Tz/Hs}}(t/h),$ | (5) |
将其转化成标准正态分布:
| $ \varPhi (u1) = {F_{Hs}}({h_s}) \Phi ({u_2}) = {F_{Tz/Hs}}({t_z}),$ | (6) |
观察3 h为一海况的百年一遇海况概率应满足:
| $ \sqrt {{u_1}^2 + {u_2}^2} = - {\Phi ^{ - 1}}\left[ {\frac{1}{{100\times365\times8}}} \right] = 4.5 ,$ | (7) |
转化成有义波高和跨零周期的百年一遇等概率曲线:
| $ {h_s} = {F_{Hs}}^{ - 1}(\varPhi ({u_1})) {t_z} = {F_{Tz/Hs}}^{ - 1}(\varPhi ({u_2})) 。$ | (8) |
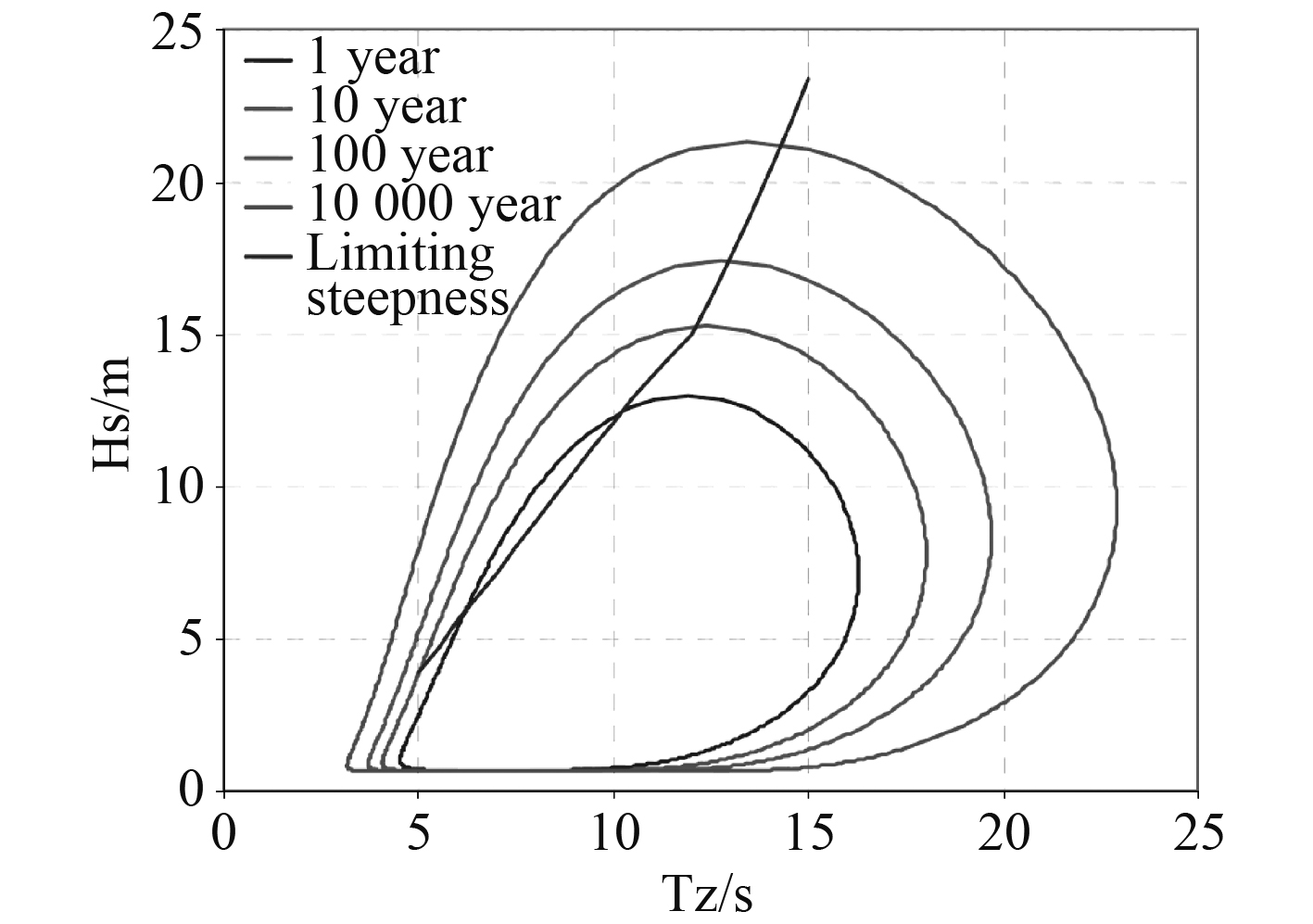
根据此方法可以得到北大西洋的1年、10年、100年和10000年的有义波高和跨零周期的等概率曲线,如图2所示。
|
图 2 北大西洋波浪有义波高与跨零周期的等概率曲线 Fig. 2 Equal probability curve of significant wave height and zero-crossing period in North Atlantic |
对某半潜式钻井平台进行运动响应、气隙、二阶波浪漂移力和结构极限强度分析设计波短期预报和分析,分析是否考虑浮箱粘性对分析和短期预报的影响,并对不考虑浮箱粘性阻尼、通过Morison方程考虑浮箱粘性阻尼和通过增加Critical damping方法修正的预报结果进行对比分析。
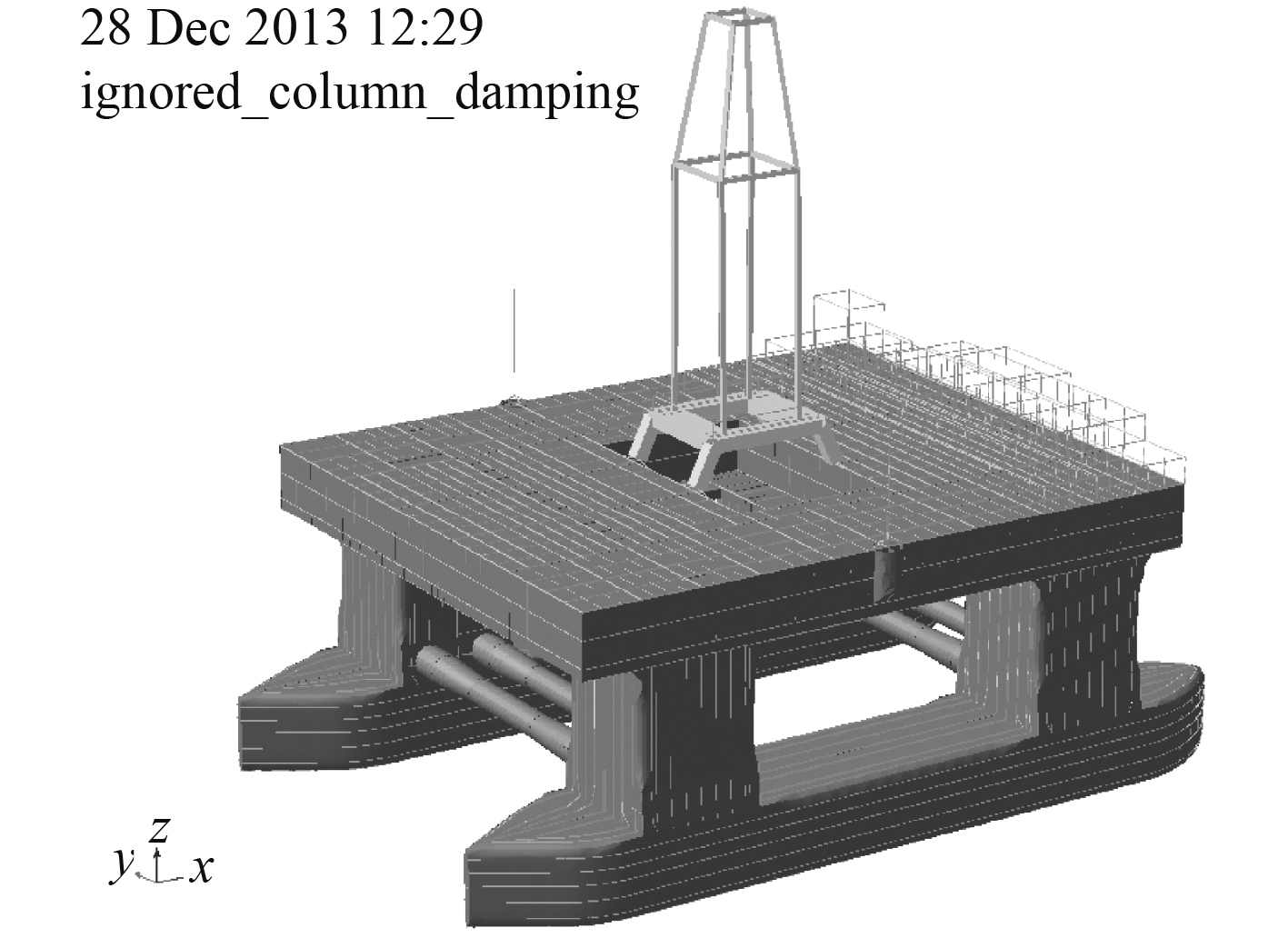
2.1 平台基本参数和模型平台的主要尺寸参数和静水力参数如表2和表3所示。水动力模型包括Morison model 和Panel Model。其中Panel model运用绕射理论求解,Morison model运用Morison方程求解。设计波分析中使用的结构和质量模型如图3所示。
|
|
表 2 平台主要尺寸 Tab.2 Main dimensions of the platform |
|
|
表 3 平台的静水力参数 Tab.3 Hydrostatic parameters of the platform |
|
图 3 平台结构和质量计算模型 Fig. 3 Structure and quality calculation model of the platform |
采用北大西洋海况进行计算分析,运用CMA和IFORM方法计算设计了北大西洋百年一遇的22个海况,如表4所示。
|
|
表 4 北大西洋100年一遇海况 Tab.4 Centennial sea conditions in the North Atlantic |
根据DNV-RP-C205规定,波峰周期Tp 与跨零周期Tz关系如下:
| $\begin{split} {T_z}/{T_P} = &0.667\;3 + 0.053\;037\cdot\gamma -\\ &0.006\;230\cdot{\gamma ^2} + 0.000\;334\;1\cdot{\gamma ^3}\end{split} $ | (9) |
其中γ定义如下:
| $ \begin{split} & \gamma = 5{\text{ for}}\frac{{{{{T}}_{{p}}}}}{{\sqrt {{{{H}}_{{s}}}} }} \leqslant 3.6 ,\\[-3pt] &\gamma = {e^{5.75 - 1.15{T_P}/\sqrt {{H_S}} }}{\text{ for 3}}{\text{.6}} \leqslant \frac{{{{{T}}_{{p}}}}}{{\sqrt {{{{H}}_{{s}}}} }} \leqslant 5 ,\\[-3pt] & \gamma = 1{\text{ for 5}} \leqslant \frac{{{{{T}}_{{p}}}}}{{\sqrt {{{{H}}_{{s}}}} }} ,\\[-3pt] &\gamma = 5{\text{ for}}\frac{{{{{T}}_{{p}}}}}{{\sqrt {{{{H}}_{{s}}}} }} \leqslant 3.6 ,\\[-3pt] & \gamma = {e^{5.75 - 1.15{T_P}/\sqrt {{H_S}} }}{\text{ for 3}}{\text{.6}} \leqslant \frac{{{{{T}}_{{p}}}}}{{\sqrt {{{{H}}_{{s}}}} }} \leqslant 5 ,\\[-3pt] & \gamma = 1{\text{ for 5}} \leqslant \frac{{{{{T}}_{{p}}}}}{{\sqrt {{{{H}}_{{s}}}} }} 。\end{split} $ |
计算中波浪方向包括0~360°,间隔为15°一个,周期为4~30 s,间隔为0.5 s。平台的运动响应在忽略浮箱粘性阻尼、Morison方程考虑浮箱粘性阻尼和直接在垂荡上增加4.3%的Critical damping 3种情况进行计算分析,结果如图4~图9所示,图中只给出了具有代表的45o入射波结果。

|
图 4 垂荡运动响应比较 Fig. 4 Comparison of heave motion response |
|
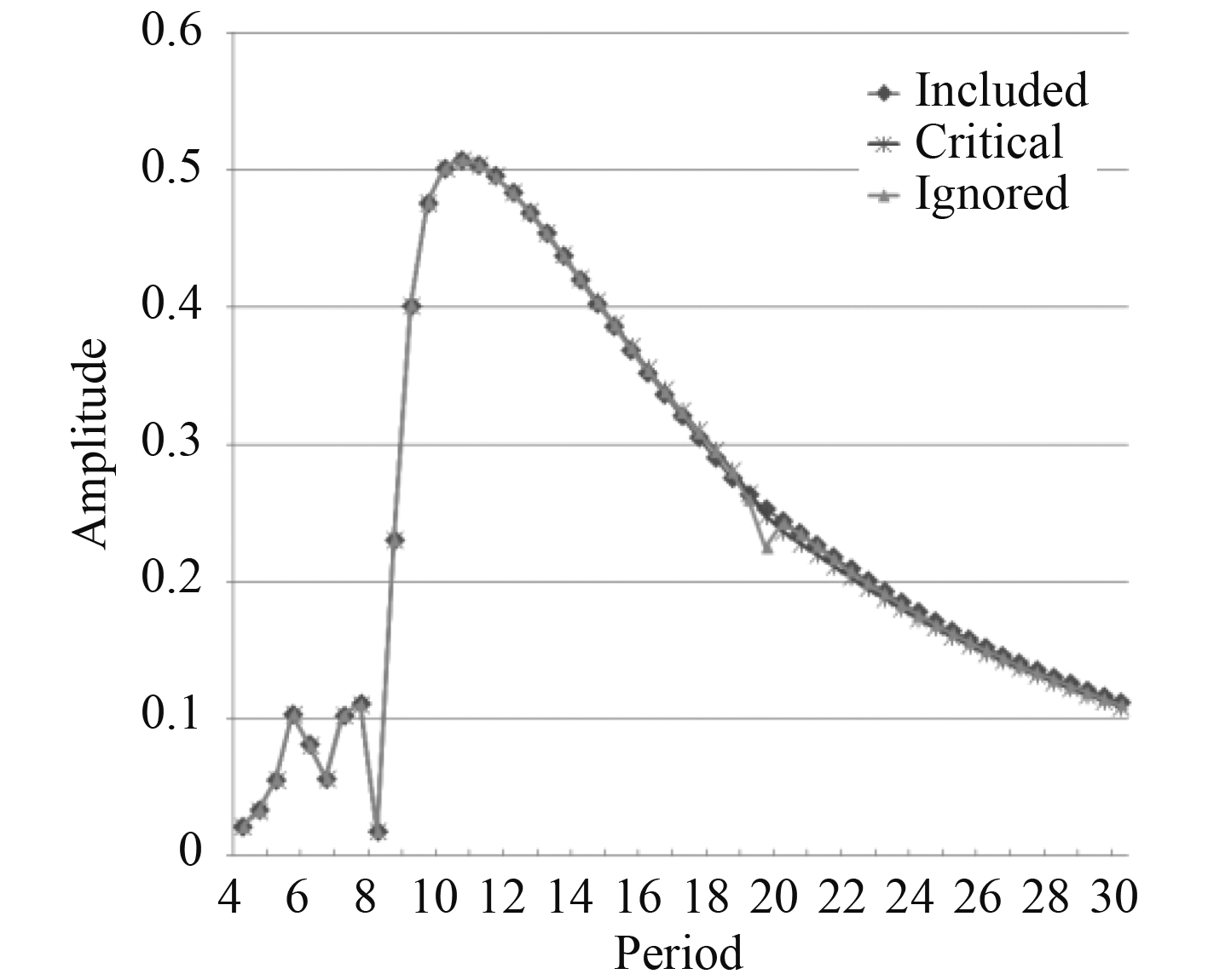
图 5 纵摇运动响应比较 Fig. 5 Comparison of pitch motion response |

|
图 6 横摇运动响应比较 Fig. 6 Comparison of rolling motion response |

|
图 7 纵荡运动响应比较 Fig. 7 Comparison of surge motion response |
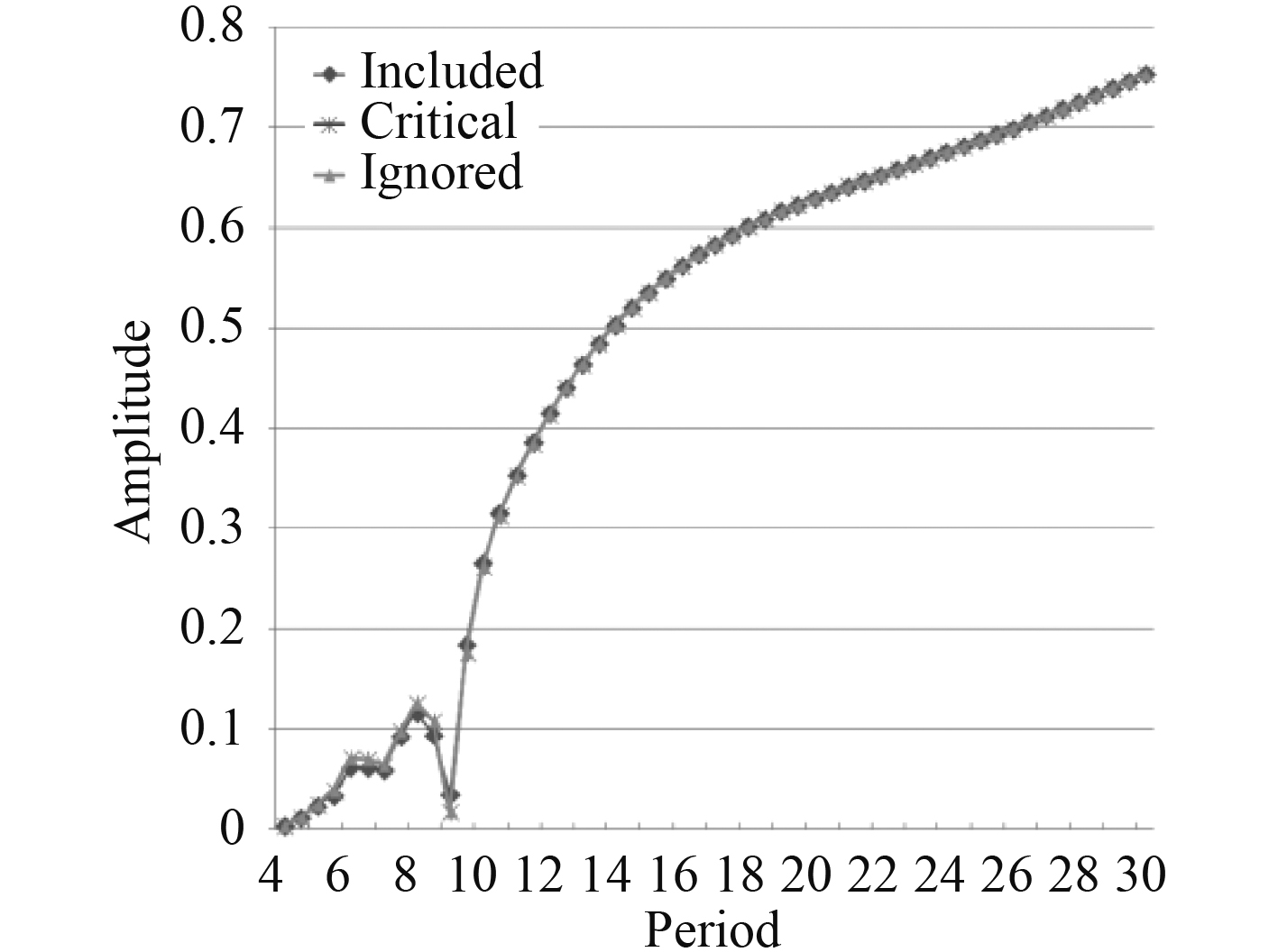
|
图 8 横荡运动响应比较 Fig. 8 Comparison of sway motion response |
|
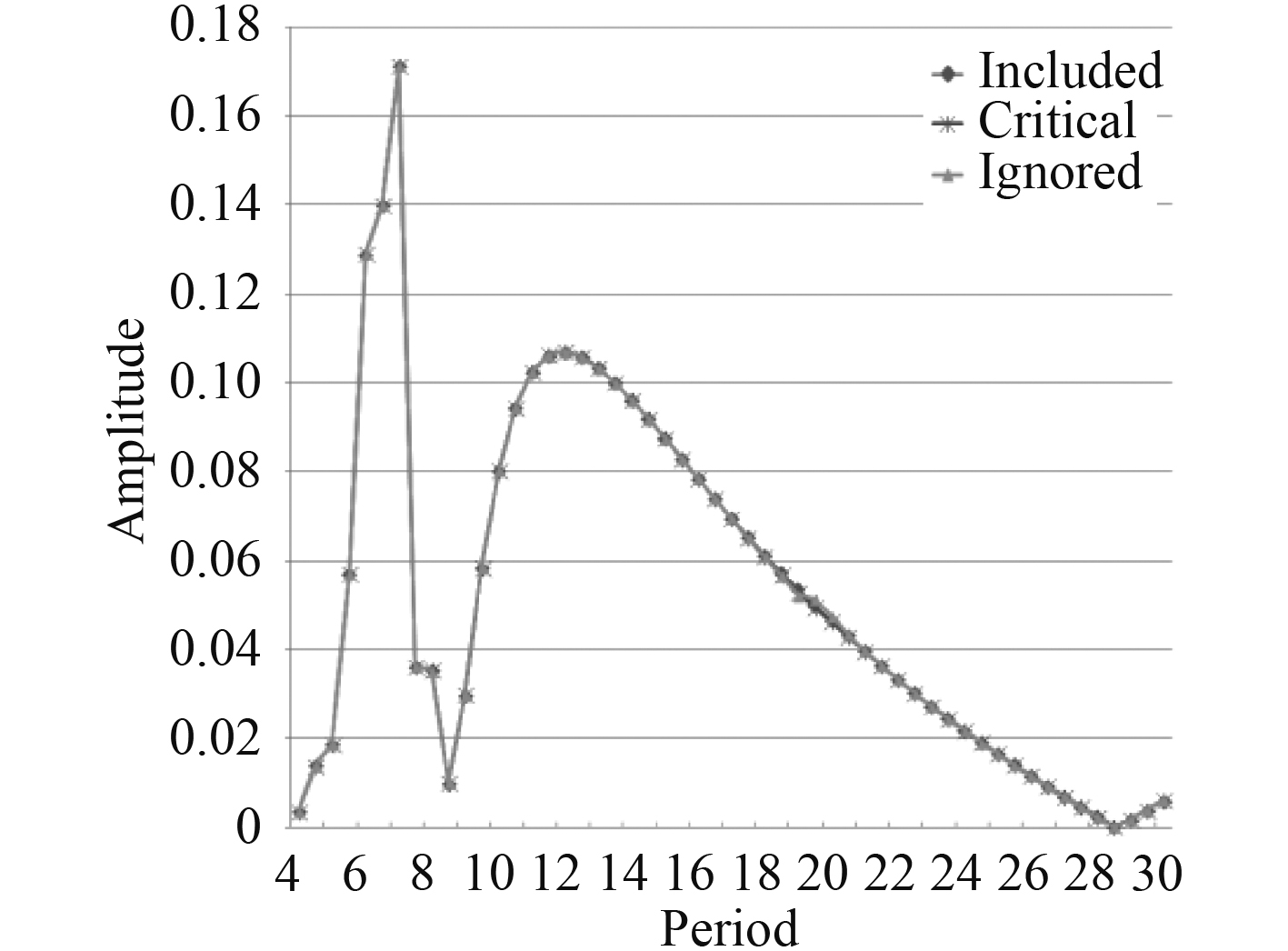
图 9 首摇运动响应比较 Fig. 9 Comparison of yaw motion response |
由计算结果可以看出浮箱的粘性阻尼对平台的运动的影响中,垂荡的运动影响比较大,其他的运动响应几乎没有影响。波浪周期在15~23 s之间是,浮箱粘性阻尼对平台垂荡方向的运动影响较大,如果不考虑浮箱粘性阻尼,垂荡的运动传递函数峰值可以达到3.66,而通过Morison考虑粘性阻尼其峰值是1.23,增加Critical damping 修正后其峰值也为1.23。在其他的周期内,浮箱的粘性阻尼对平台垂荡运动响应影响很小,可以忽略。
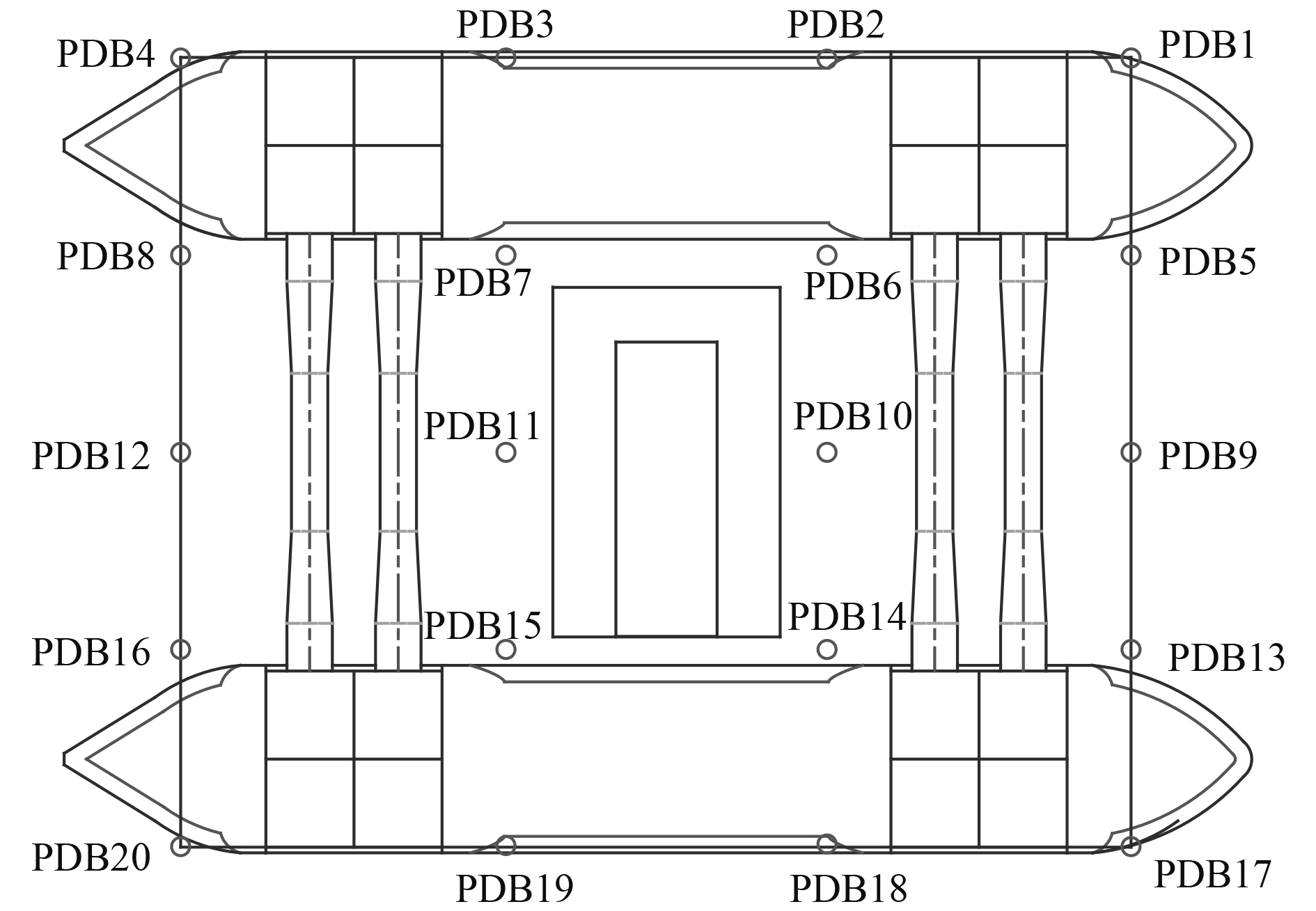
2.3.2 平台气隙计算结果本文主要以船体底部的气隙分析对象,在船体底部取20个点进行分析比较,取点坐标和示意图如表5和图10所示。图11给出了避免立柱爬浪影响的关注点9处水质点运动,图12给出了关注点9处浪向为45°时的短期预报气隙结果。
|
|
表 5 甲板关注点处的气隙 Tab.5 Air gap at deck measuring point |
|
图 10 甲板关注点位置示意图 Fig. 10 The diagram of deck measuring point position |
|
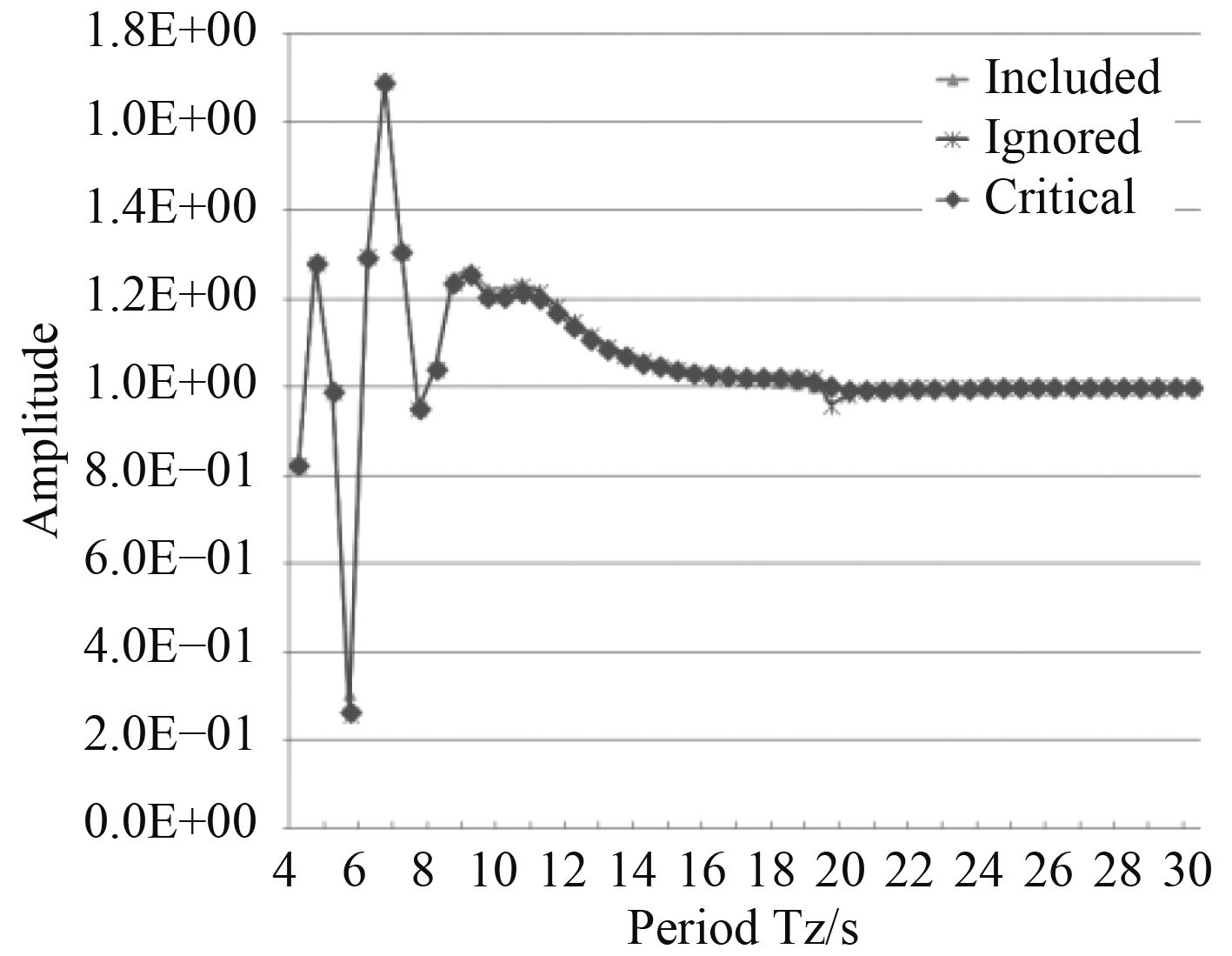
图 11 关注点9处的水质点运动比较 Fig. 11 Comparison of water quality point movement at measuring point 9 |
|
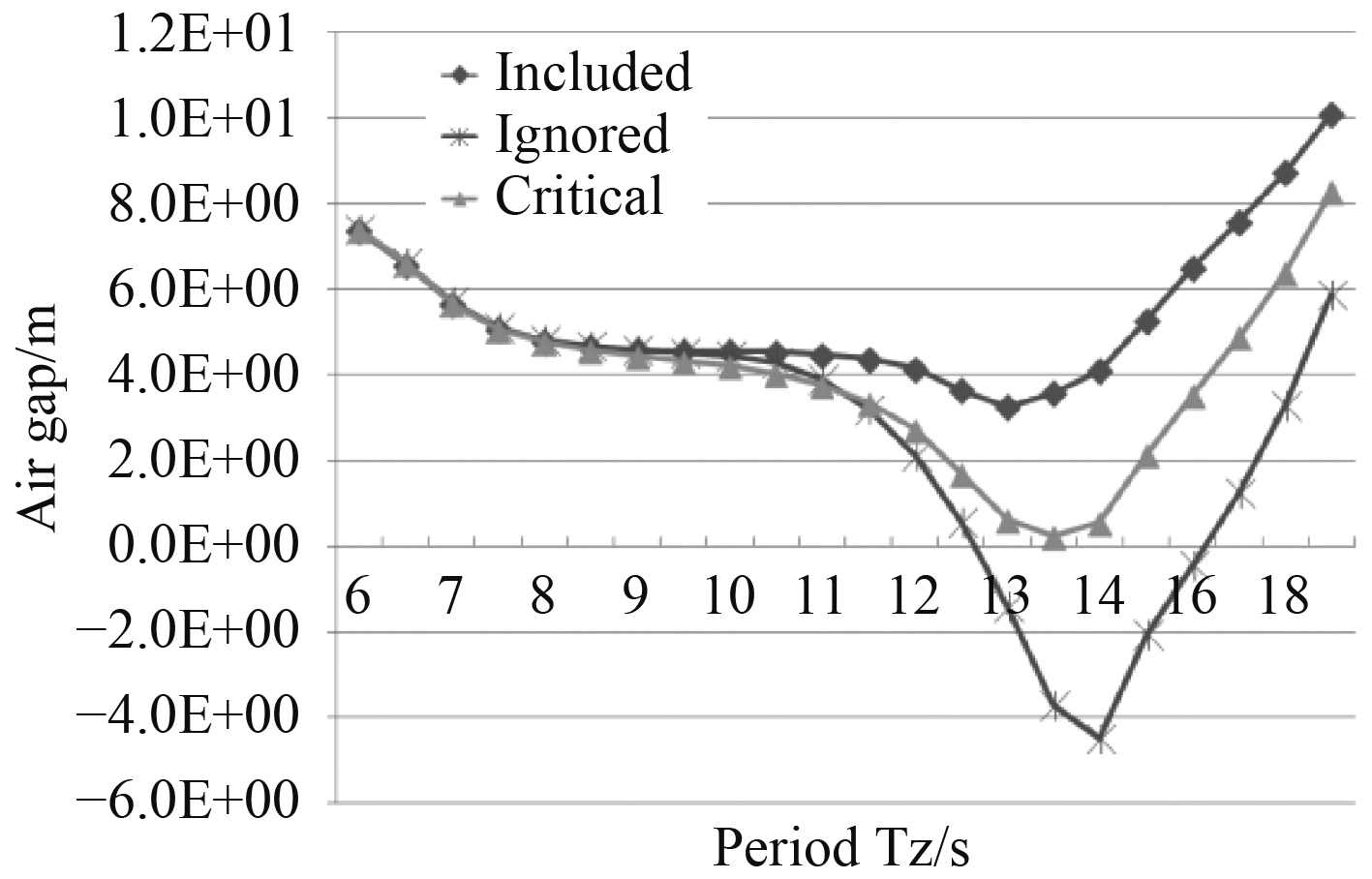
图 12 关注点9处预报气隙比较 Fig. 12 Comparison of predicted air gaps at measuring point 9 |
可以看出,水质点计算结果相同,但由于考虑平台的运动响应,气隙的短期预报在波浪周期小于10 s时,3种情况气隙结果非常接近,即浮箱的粘性阻尼对其影响很少,但在波浪周期大于12 s,平台的气隙的计算结果就差别很大。通过Morison方程考虑粘性阻尼的方法预报出来的气隙值最小为3.3 m,发生在周期13 s时,而增加Critical damping修正的方法,最小气隙值为0.3 m,发生在周期13.5 s时。如果忽略浮箱粘性阻尼的方法,最小气隙值为−4.2 m,发生在波浪周期为14 s时。浮箱的粘性阻尼对周期较长,波长较大的波浪载荷起到明显的作用,在这种情况下浮箱的粘性阻尼不能忽略。
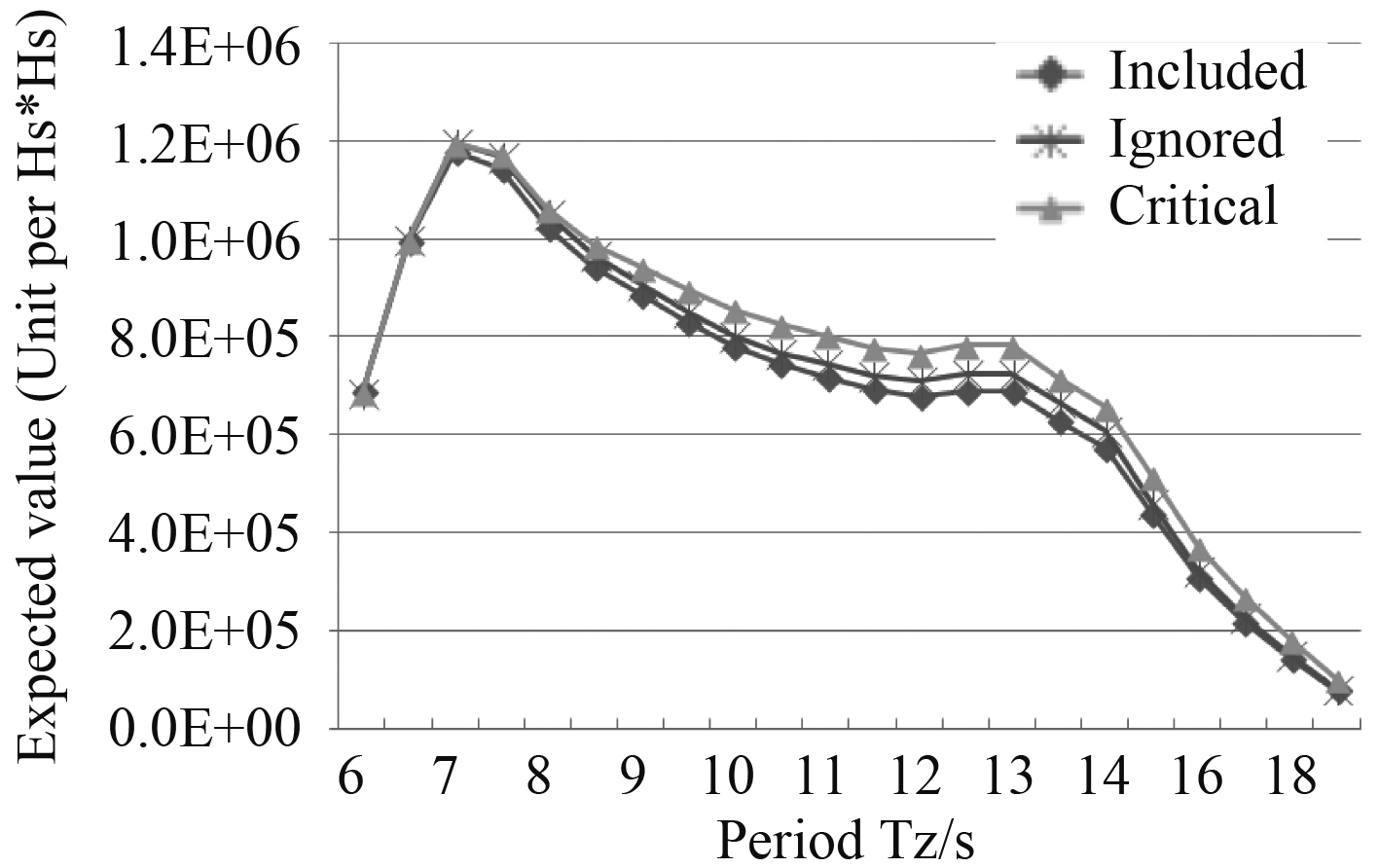
2.3.3 波浪二阶漂移力计算结果在DP/锚泊定位中,需要考虑海洋平台纵荡、横荡和首摇方向上的波浪二阶漂移力。图13~图15给出了平台具有代表性的在45o入射波情况下的波浪二阶平均漂移力短期预报值。结果表明浮箱的粘性阻尼对二阶漂移力影响很小,这就说明在进行DP或锚泊定位计算时,可以不考虑粘性阻尼的影响,在工程上可以满足响应的精度。
|
图 13 平台在Surge方向上的二阶平均漂移力在45o入射波的预报值 Fig. 13 The predicted value of the second-order average drift force of the platform in the Surge direction at 45°incident wave |
|
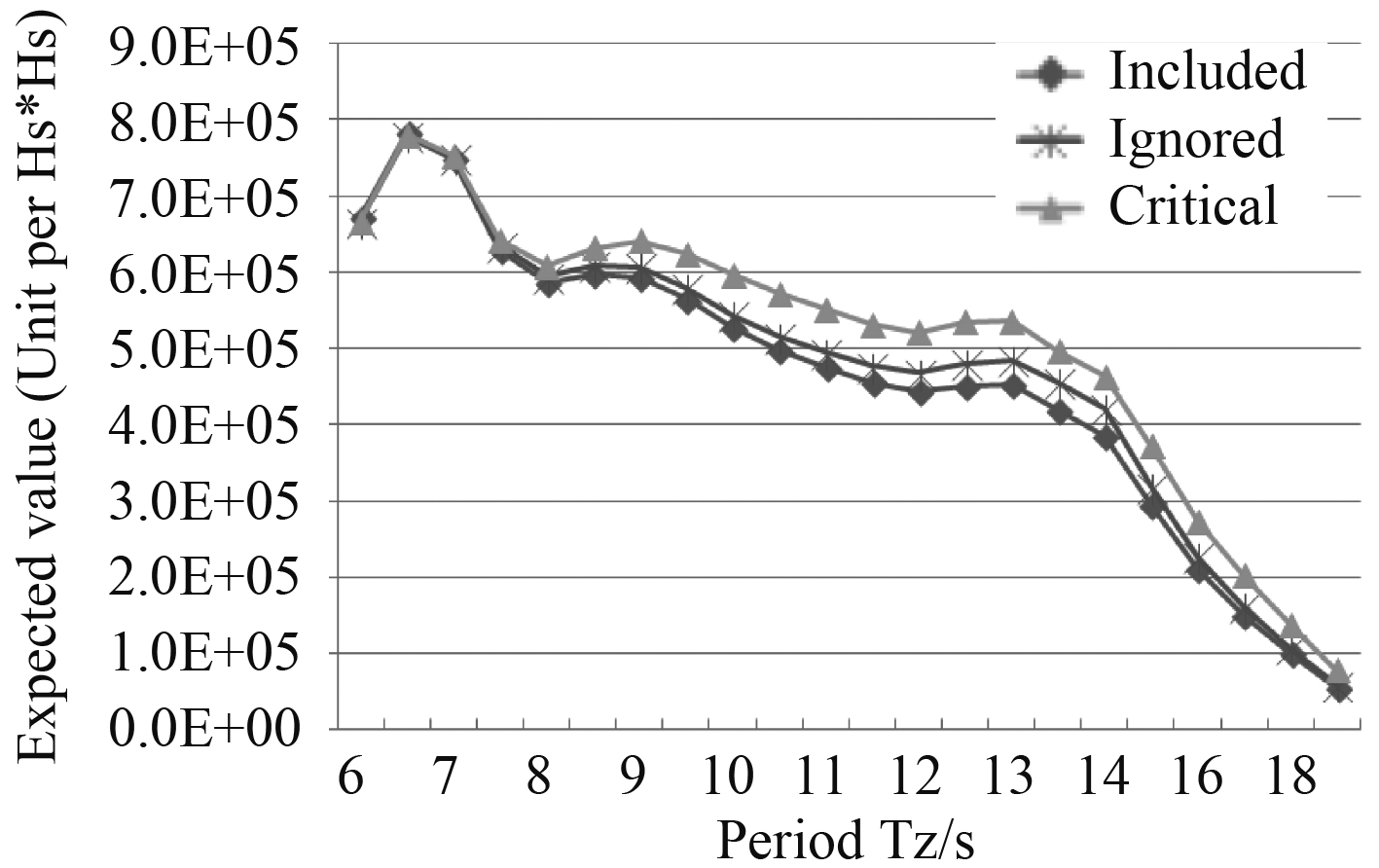
图 14 平台在Sway方向上的二阶平均漂移力在45°入射波的预报值 Fig. 14 The predicted value of the second-order average drift force of the platform in the Sway direction at 45° incident wave |
|
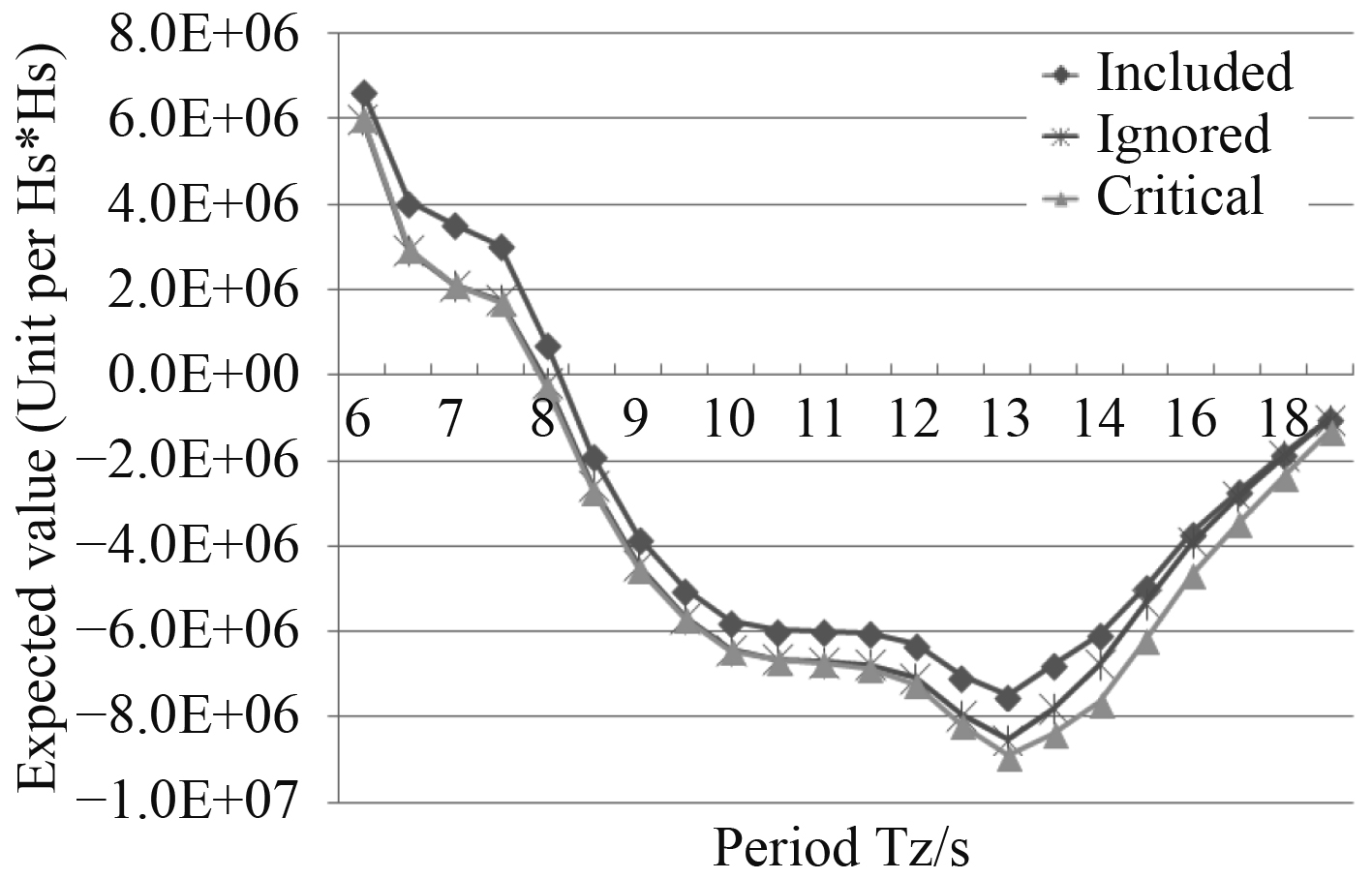
图 15 平台在Yaw方向上的二阶平均漂移力在45°入射波的预报值 Fig. 15 The predicted value of the second-order average drift force of the platform in the Yaw direction at 45° incident wave |
图16~图21给出了具有代表性的45o入射波情况下平台载荷计算结果比较。表6给出了平台在考虑Morison方程和直接增加Critical damping的最终设计波。
|
|
表 6 平台设计波计算结果比较 Tab.6 Comparison of calculation results of design wave for platform |

|
图 16 平台在45o入射波的撕裂力比较 Fig. 16 Comparison of tearing force of platform at 45° incident wave |

|
图 17 平台在45°入射波的剪切力比较 Fig. 17 Comparison of shearing forces of platform at 45° incident wave |
|
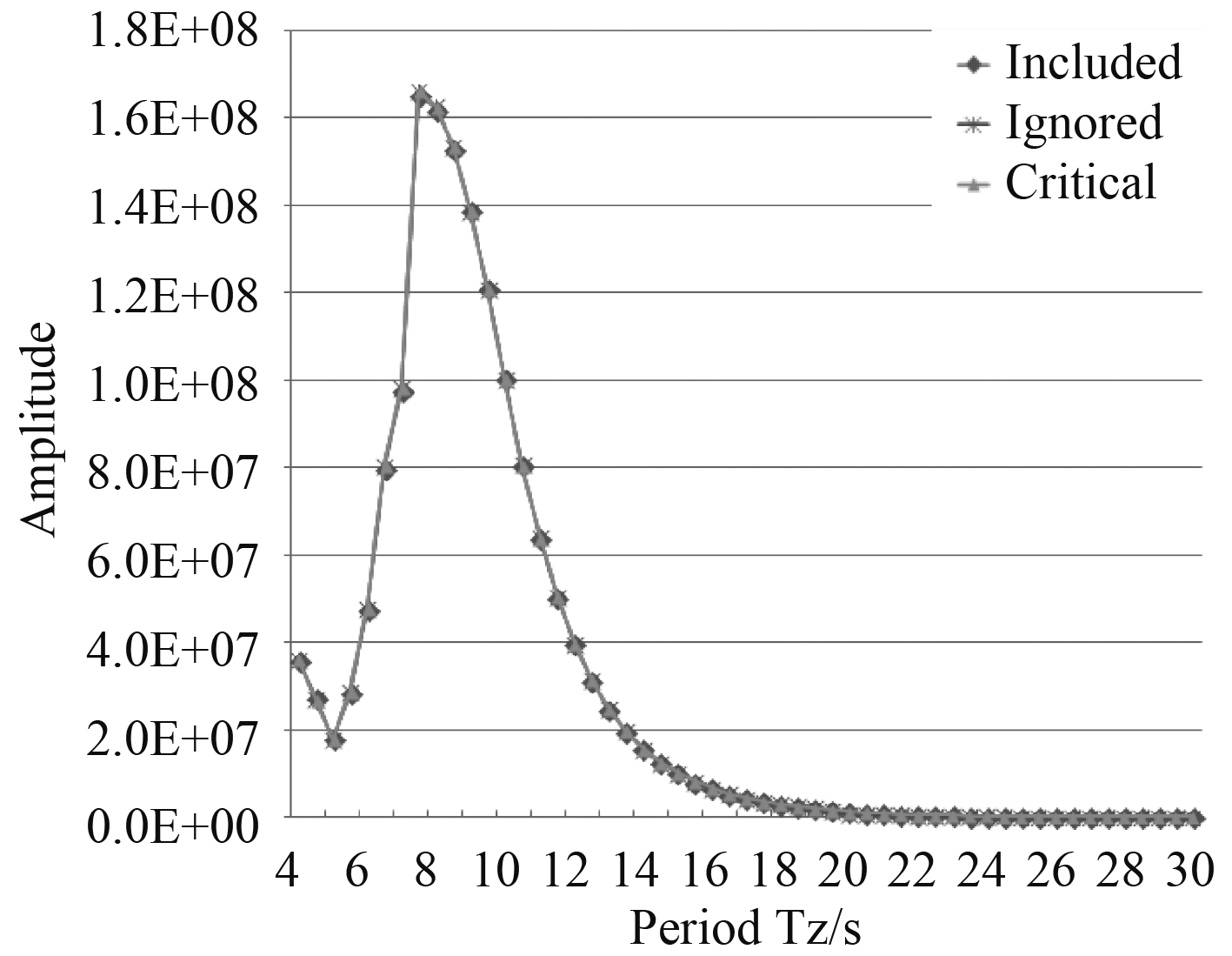
图 18 平台在45°入射波的横向扭矩比较 Fig. 18 Comparison of transverse torque of platform at 45° incident wave |
|
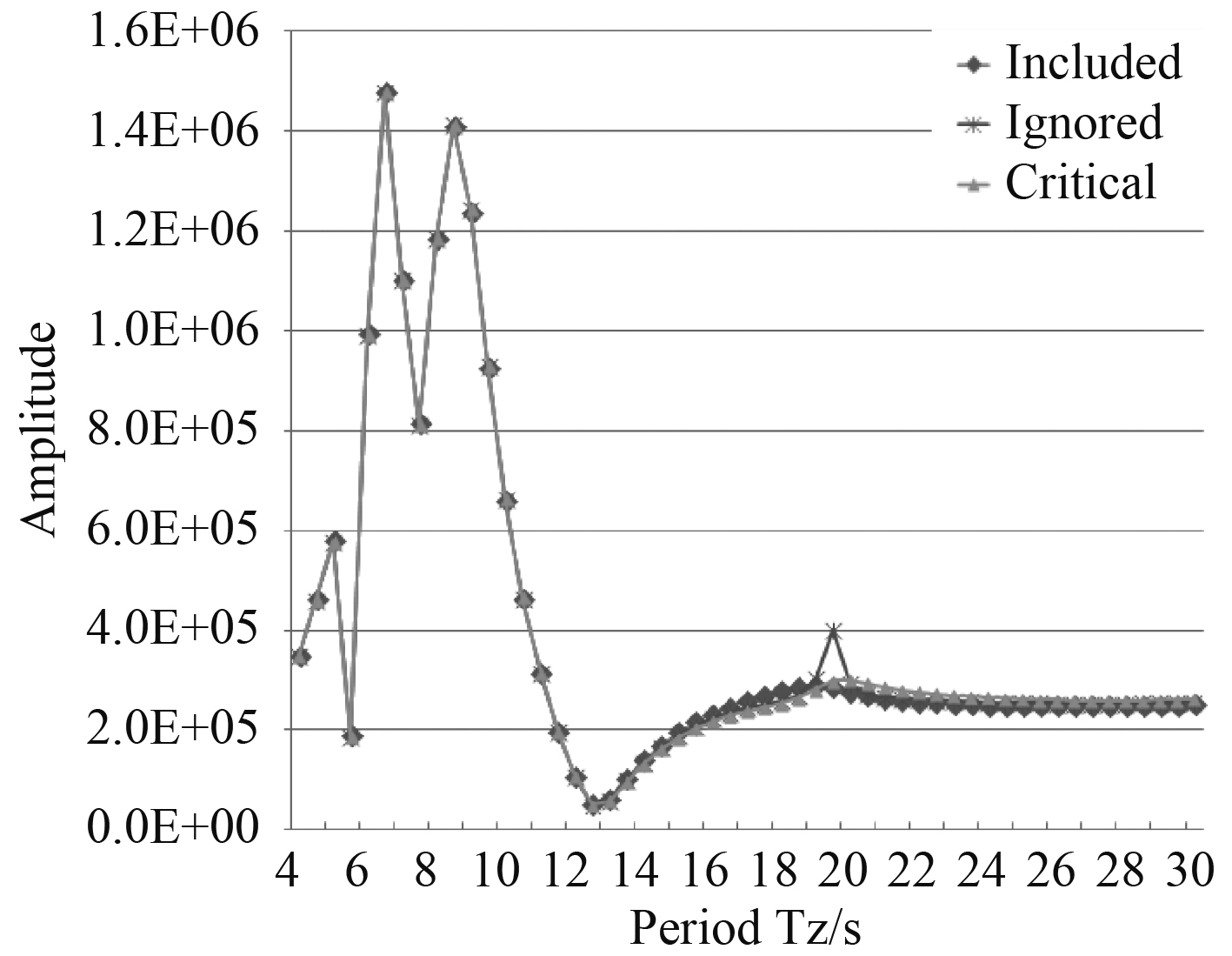
图 19 平台在45°入射波纵向惯性力比较 Fig. 19 Comparison of longitudinal inertial force of platform at 45° incident wave |

|
图 20 平台在45°入射波横向惯性力比较 Fig. 20 Comparison of transverse inertial force of platform at 45° incident wave |
|
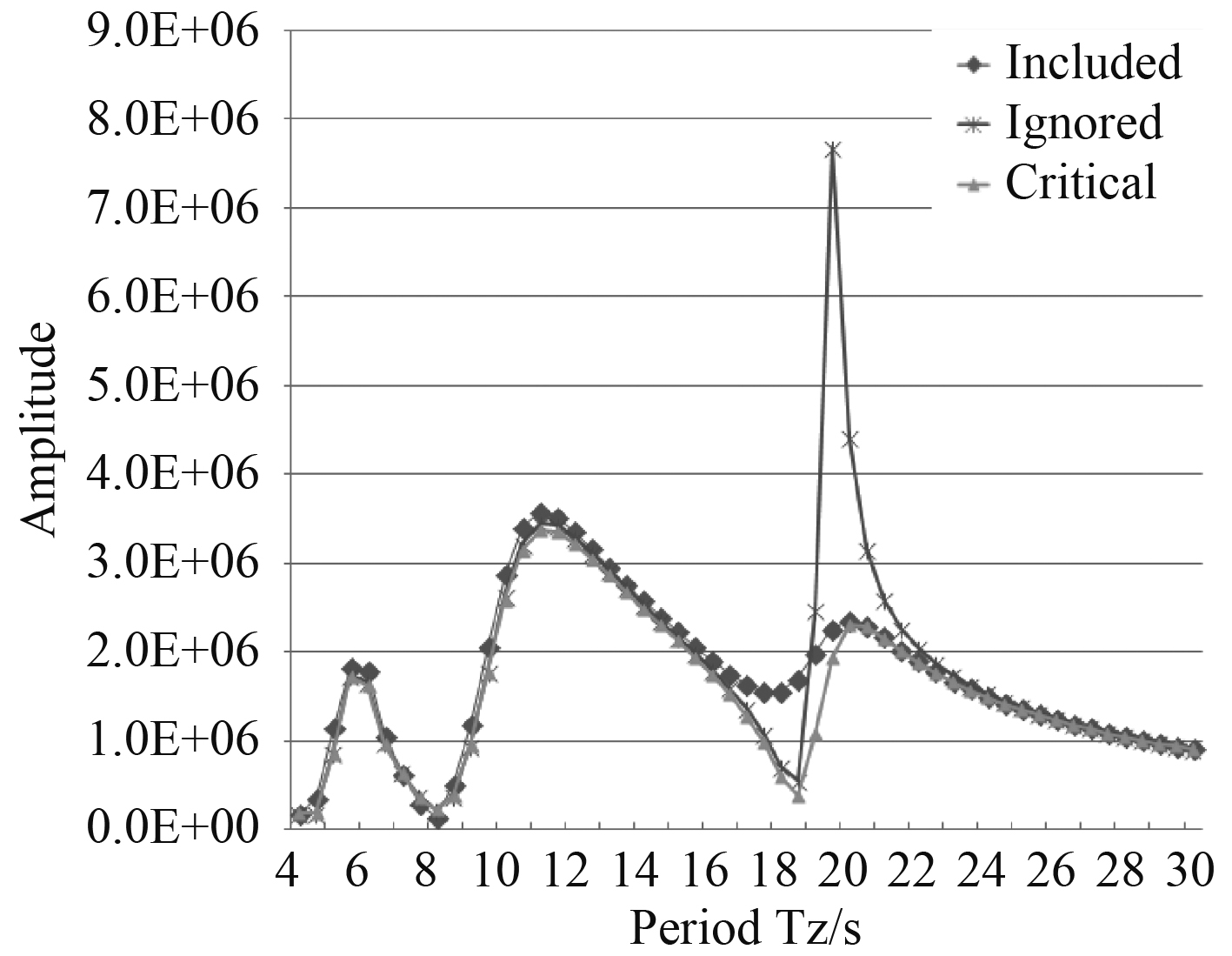
图 21 平台在45°入射波垂向惯性力比较 Fig. 21 Comparison of vertical inertial force of platform at 45° incident wave |
由平台波浪载荷计算结果可以看出,平台的撕裂力、横向扭矩和横向加速度由浮箱的粘性阻尼的影响很小,完全可以忽略。而在平台剪切力、纵向惯性力和垂向惯性力方面,浮箱的粘性阻尼对其有一定的影响,特别是垂向惯性力,但是通过Morison方程和增加Critical damping修正的方法结果比较接近,这说明浮箱的粘性阻尼对其的影响不能忽略。
本文对Morison方程和直接增加Critical damping考虑浮箱的粘性阻尼进行了设计波计算。由表5的计算结果可以看出,2种方法的设计波周期和浪向完全一样,设计波幅值非常接近,除了根据垂向加速度计算出的设计波幅值在4%,其他的都在0.5%以内。
3 结 语本文通过CAM和IFORM方法计算了北大西洋百年一遇22个海况,并通过这22个海况对以双浮箱式半潜平台的运动响应、气隙、二阶波浪漂移力和波浪引起的纵向剪切力等波浪载荷进行短期预报,设计算出平台结构极限强度分析的设计波。本文运用忽略浮箱粘性阻尼、通过Morison方程考虑浮箱粘性阻尼和增加Critical damping修正的方法对平台运动响应、气隙、二阶波浪平均漂移力和平台结构极限强度分析的设计波进行分析,结论如下:
1)浮箱粘性阻尼对平台运动只在垂荡运动中有较大影响,不能忽略浮箱的粘性阻尼,但可以通过增加Critical damping的方法进行修正。
2)浮箱的粘性阻尼对平台气隙影响很大,特别是在周期较长的海况下,应该考虑浮箱粘性阻尼的影响,而且通过增加Critical damping修正的方法也存在差别。
3)在计算平台的DP/锚泊分析时,二阶波浪漂移力主要考虑纵荡、横荡和首摇方向上的影响,而浮箱粘性阻尼对其影响比较小,在计算二阶波浪平均漂移力时可以忽略浮箱的粘性阻尼的影响。
4)平台设计波的计算中,浮箱的粘性阻尼对平台垂向加速度设计波的影响比较大,应进行考虑。通过增加Critical damping修正的方法与Morison方程考虑浮箱的粘性阻尼方法计算结果非常相似,可以通过增加Critical damping修正的方法考虑浮箱的粘性阻尼。
| [1] |
EMAMI A, MOSTAFA G, A R. Application of poroelastic layers in a semi-submersible platform: Devising an efficient heave motion response reduction method[J]. Ocean Engineering, 2020, 201: 107−148.
|
| [2] |
LWANOWSKI B, MARC L, WEMMENHOVE R. CFD Simulation of Wave run-up on a Semi-submersible and Comparison with Experiment[C]//. ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering. 2009.
|
| [3] |
PHAM T D, SHIN H. The effect of the second-order wave loads on drift motion of a semi-submersible floating offshore wind turbine[J]. Journal of Marine Science and Engineering, 2020, 8(11): 859. DOI:10.3390/jmse8110859 |
| [4] |
Rohit K, et al. Multi-phase simulation of semi-submersible platform with pencil column using CFD[J]. Journal of Physics:Conference Series, 2020, 1716(1): 012-024. |
| [5] |
REN Nianxin, et al. Hydrodynamic analysis of a modular floating structure with tension-leg platforms and wave energy converters[J]. Journal of Marine Science and Engineering, 2021, 9(4): 424. DOI:10.3390/jmse9040424 |
| [6] |
邓小康, 谢文会, 李阳, 等. 一种新型深水浮式平台及其系泊系统动力响应分析[J]. 舰船科学技术, 2021, 43(5): 95-101. |
| [7] |
张曼, 杜君峰, 常安腾, 等. 风浪流环境要素对半潜式平台气隙响应特性的影响研究[J]. 中国海洋大学学报(自然科学版), 2019, 49(S2): 107-116. |
| [8] |
罗幼安, 王飞, 位巍. 二阶运动响应对半潜平台气隙的影响研究[J]. 海洋工程装备与技术, 2018, 5(S1): 15-18. |
| [9] |
李男, 张君彦, 李文华等. 三维浮体的二阶波浪力计算研究[J]. 船舶, 2020, 31(06): 24-34. |
| [10] |
中国船级社, 海上移动平台入级与建造规范2012[M]. 北京: 人民交通出版社, 2012.
|
| [11] |
BITNER-GREGERSEN E M. Joint probabilistic description for combined seas [C]//. Proceedings of 24th International Conference on Offshore Mechanics and Arctic Engineering. Halkidiki , Greece , OMAE, 2005, June 12-17.
|
| [12] |
WINTERSTEIN S, UDE T C , CORNELL C A, et al. Environmental parameters for extreme response. inverse FORM with omission sensitivity [C]//. Proceedings of International Conference on Structural Safety and Reliability. Innsbruck, ICOSSAR-93, 1993.
|
| [13] |
DET. Norske Verital AS. DNV-RP-C205 Environmental Conditions and Environmental Loads[M]. October 2010.
|
 2022, Vol. 44
2022, Vol. 44
