2. 中国人民解放军第92767部队,山东 青岛 266000
2. No. 92767 Unit of PLA, Qingdao 266000, China
因UUV的自主性和智能化,其成为当前世界各国海洋和军事装备中的发展热点[1]。水下导航是UUV关键技术之一,常见的导航方式有船位推算、惯性导航以及惯性导航组合长短基线定位系统/地磁/重力匹配等组合导航方式,可根据UUV的用途、航程、体积以及成本需求等问题选择合适的导航方式。然而,在实际应用中,地磁导航、地形匹配导航以及重力导航等方法,因地磁、地形和重力测量数据的获取难度和数据库样本的不足,目前尚未达到可在UUV上成熟应用的水平[2]。因此,UUV较为成熟可靠的水下导航方式是惯性导航组合多普勒、GPS/北斗等其他外测信息系统即SINS/ADCP/GPS(北斗)组合导航系统[3-4]。
采用SINS/ADCP/GPS组合导航时,无论ADCP测速还是UUV浮出水面接收GPS(北斗)信息提供位置校准,在敏感海域或抵近侦察侦测时均存在UUV暴露问题,将会制约UUV在敏感区域的军事运用。美国海军于2015年1月制定计划,明确任何需要主动向外发送信号的方案一律不予通过,以防暴露水下潜器的位置,并建议采用磁场、天文或光学作为导航源[2]。
针对UUV的水下隐蔽导航问题,本文提出一种依据航程可切换的隐蔽导航方法−SINS+ADCP/电磁计程仪+石英深度计的组合导航方法,为解决UUV远程水下导航隐蔽性问题提供一种方案。
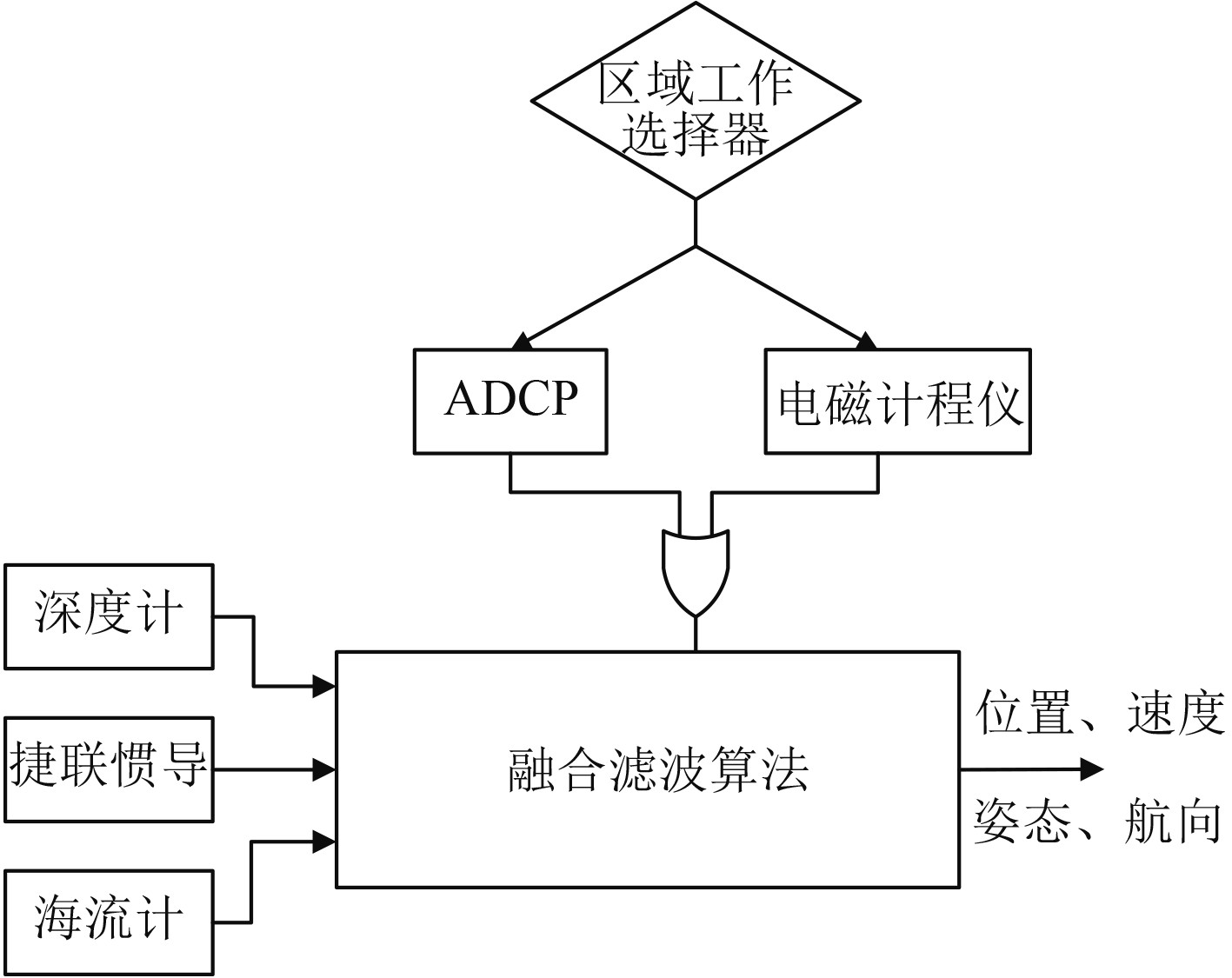
1 UUV水下隐蔽组合导航系统模型 1.1 水下隐蔽导航方案设计UUV往往需要在水下远距离航行后到达指定海域执行作业任务,其航行距离可划分为航渡阶段和执行作业任务阶段。在航渡阶段,航行隐蔽性性问题一般认为是安全的,因此可采用惯性导航+ADCP+北斗(GPS)的组合导航方法;在敏感或抵近作业危险区域,由于ADCP为声呐主动工作模式,北斗须浮出水面校准,称为暴露隐患,因此宜选用惯性导航、电磁计程仪、石英深度计组合的导航方法。航渡阶段和敏感海域可按照实际航程划分,在UUV布防前的人工航路规划时,提前人工设定于UUV航行控制系统。根据需要,还可设定作业海区海流数据信息等用于导航系统的误差补偿。根据以上分析,UUV水下隐蔽导航方案示意图如图1所示。
|
图 1 UUV水下隐蔽导航方案 Fig. 1 UUV concealed navigation project underwater |
可知,本文提出的UUV水下隐蔽导航方法,分为安全海域水下导航模式和危险作业海域水下隐蔽导航模式2种情况,在UUV布放前根据任务海域由人工设定组合导航方式和任务时长。
1)安全海域水下导航模式
安全海域水下导航系统设计为SINS/ADCP/深度计组合导航,为UUV布放后航渡阶段采用的水下导航方法。UUV可根据航程采用水面GPS或北斗校准,校准方法本文不作讨论。
2)危险和作业海域水下导航模式
危险海域水下导航方法设计为SINS/ EML /深度计组合导航模式。该种模式下可补充海流信息,海流信息的获取可根据区域海流统计数据库或进入危险区域前海流计/ADCP提前输入UUV导航系统[5]。
EML的工作原理是根据电磁感应原理实现航行器瞬时航速和累计航程测量的相对计程仪。EML虽然易受到外界磁场的干扰,但优点是不需要向外发射信号,这对军用UUV来说是重要的,经电磁防干扰处理后可满足导航隐蔽性的需求。EML测量航速为载体相对水的航速,测速误差可达1%,测速下限为0.1 kn。因此,实际使用中需考虑海流流速、流向的影响和补偿问题,以提高导航精度。同时,利用EML的导航或组合导航系统也无需全程采用,仅在军事敏感海域使用,其他区域采用导航精度更高SINS/ADCP/深度计组合导航方法。
深度计采用石英深度计,提供水下载体的绝对深度信息,以弥补ADCP、EML和惯性导航系统在垂直方向测量精度不高的缺陷,为垂直方向提供基准信息。
1.2 SINS/ADCP误差模型受UUV平台体积的限制,安装的惯导系统精度仅为战术级水平。首先建立地理坐标系下的加性四元数误差表示的非线性捷联惯导系统(SINS)姿态误差方程和速度误差方程[6-7]。ADCP优先选用底跟踪模式,其测速数据作为外部观测输入数据,其观测误差主要由速度偏移误差
| $ {\dot X_1}(t) = {F_1}(X(t)) + {W_1}(t) 。$ | (1) |
式中:
| $ \begin{split} {X_1} = & [\delta L,\delta \lambda ,\delta h,\delta {V_x},\delta {V_y},\delta {V_z},\delta {q_0},\delta {q_1},\delta {q_2}, \\ & \delta {q_3},{\varepsilon _x},{\varepsilon _y},{\varepsilon _z},\delta {V_d},\delta \Delta ,\delta K]^{\rm{T}} 。\end{split} $ |
将SINS计算出的速度误差与ADCP测速误差之差作为系统的量测值,系统测量方程表示如下:
| $ \begin{split} {Z_1} = & {V_{SINS}} - \hat C_b^n{V_{ADCP}} = \delta {V^n} + 2\left[ {\hat C_b^n{V_{ADCP}}} \right] \times \\ & {Y^{\rm{T}}}\delta Q - 2\hat C_b^n{V_{ADCP}}{{\hat Q}^{\rm{T}}} - \hat C_b^n{V_{ADCP}} 。\end{split} $ | (2) |
该导航模式下,系统无需向外发射信号,可在军事敏感海区选用。设EML测速误差为
SINS/EML组合导航的状态向量为:
| $ \begin{split} {X_2} = & [\delta L,\delta \lambda ,\delta h,\delta {V_x},\delta {V_y},\delta {V_z},\delta {q_0},\delta {q_1},\delta {q_2},\delta {q_3}, \\ & {\varepsilon _x},{\varepsilon _y},{\varepsilon _z},\delta {V_{Dx}},\delta {V_{Dy}},\delta {\alpha _D}]^{\rm{T}}。\end{split} $ |
状态方程为:
| $ {\dot X_2}(t) = {F_2}({X_2}(t)) + {W_2} ,$ | (3) |
系统量测方程为:
| $ \begin{split} {Z_2} = & {V_{SINS}} - \hat C_b^n{V_{EM}} = \delta {V^n} + 2\left[ {\hat C_b^n{V_{EM}}} \right] \times \\ & {Y^{\rm{T}}}\delta Q - 2\hat C_b^n{V_{EM}}{{\hat Q}^{\rm{T}}} - \hat C_b^n{V_{EM}}。\end{split} $ | (4) |
测速装置选用EML为SINS提供外部测量数据,量测方程中均只需考虑水平航速信息,石英深度计测量深度信息(海区深度已估)。
在港口、航道以及近海领域甚至海底不规则处的海流一般会根据季节、时间和地理位置不同而变化,但一般假设海流定常且均匀,可将海流速度合成到水下航行器测速装置上。海流数据也可采用ADCP停用前测得的流速数据修正[9]。
2 隐蔽组合导航容积卡尔曼滤波算法(CKF)对于SINS/ADCP/ EML组合导航系统,对SINS提供的位置、速度、姿态信息和ADCP、EML提供的速度信息的融合需要应用滤波算法。对于UUV战术级SINS初始对准欠精确,UUV长时间航行受到陀螺漂移影响,姿态角误差变大,导致线性误差模型不再适用,此时应用非线性滤波算法解算导航误差是必要的。UKF算法在进行UT变换时,其概率密度高斯分布下可达3阶估计精度,但存在参数选择自主性较高,导航高维滤波时易出现状态协方差阵负定以及计算量增大问题;粒子滤波(PF)算法虽不受模型限制,但会出现粒子退化问题,且粒子数目增加会大大增加算法计算量。
CKF算法是一种性能优越的非线性滤波算法,相比UKF、PF算法具有估计精度高、稳定性好、适用于高维非线性导航系统的优点[10~12]。本文将CKF算法用于分区切换的SINS/ADCP/EML组合导航系统。
本文的创新之处是提出一种UUV隐蔽导航方法,而非研究非线性滤波算法。因此,直接给出CKF滤波算法。
对于如下的非线性系统:
| $ \left\{ {\begin{array}{*{20}{c}} {{x_{k + 1}} = f({x_k}) + {v_k}},\\ {{z_k} = h({x_k}) + {w_k}} 。\end{array}} \right. $ | (5) |
式中:
| $ \left\{ {\begin{array}{*{20}{c}} {E[{v_k}v_j^{\rm{T}}] = {\delta _{kj}}Q} ,\\ {E[{w_k}w_j^{\rm{T}}] = {\delta _{kj}}R} 。\end{array}} \right. $ | (6) |
式中:
CKF滤波算法的计算步骤如下:
1)初始化
初始状态向量
| $ \left\{ {\begin{array}{*{20}{l}} {{{\hat x}_0} = E[{x_0}]},\\ {{P_0} = E[({x_0} - {{\hat x}_0}){{({x_0} - {{\hat x}_0})}^{\rm{T}}}]} 。\end{array}} \right. $ | (7) |
2)时间更新
| $ \left\{ {\begin{array}{*{20}{l}} {{P_{k - 1|k - 1}} = {S_{k - 1|k - 1}}S_{k - 1|k - 1}^{\rm{T}}}, \\ {{X_{i,k - 1|k - 1}} = {S_{k - 1|k - 1}}{\xi _i} + \hat x_{k - 1|k - 1}^{}} ,\\ {X_{i,k - 1|k - 1}^ * = f(X_{i,k - 1|k - 1}^{})} ,\\ {\hat x_{k|k - 1}^{} = \dfrac{1}{{2n}}\displaystyle\sum\limits_{i = 1}^{2n} {X_{i,k|k - 1}^ * } },\\ {P_{k|k - 1}} = \dfrac{1}{{2n}}\displaystyle\sum\limits_{i = 1}^{2n} {X_{i,k|k - 1}^ * X_{i,k|k - 1}^{ * {\rm{T}}}} - \\ \qquad \quad \,\,\,\, \hat x_{k|k - 1}^{}\hat x_{k|k - 1}^{\rm{T}} + {Q_{k - 1}} 。\end{array}} \right. $ | (8) |
式中:
| $ {\xi _i} = \sqrt n \left[ {\begin{array}{*{20}{c}} 1&{}&{}&{}&{ - 1}&{}&{}&{} \\ {}&1&{}&{}&{}&{ - 1}&{}&{} \\ {}&{}& \ddots &{}&{}&{}& \ddots &{} \\ {}&{}&{}&1&{}&{}&{}&{ - 1} \end{array}} \right] 。$ |
3)量测更新方程组
| $ \left\{ {\begin{array}{*{20}{l}} {{P_{k|k - 1}} = {S_{k|k - 1}}S_{k|k - 1}^{\rm{T}}},\\ {{X_{i,k|k - 1}} = {S_{k|k - 1}}{\xi _i} + \hat x_{k|k - 1}^{}},\\ {{Z_{i,k|k - 1}} = h({X_{i,k|k - 1}})},\\ {\hat z_{k|k - 1}^{} = \dfrac{1}{{2n}}\displaystyle\sum\limits_{i = 1}^{2n} {Z_{i,k|k - 1}^{}} },\\ {P_{zz,k|k - 1}} = \dfrac{1}{{2n}}\displaystyle\sum\limits_{i = 1}^{2n} {Z_{i,k|k - 1}^{}Z_{i,k|k - 1}^{\rm{T}}} - \\ \qquad \qquad \,\, \hat z_{k|k - 1}^{}\hat z_{k|k - 1}^{\rm{T}} + {R_k},\\ {{P_{xz,k|k - 1}} = \dfrac{1}{{2n}}\displaystyle\sum\limits_{i = 1}^{2n} {X_{i,k|k - 1}^{}Z_{i,k|k - 1}^{\rm{T}}} - \hat x_{k|k - 1}^{}\hat z_{k|k - 1}^{\rm{T}}} 。\end{array}} \right. $ | (9) |
4) 状态更新方程组
| $ \left\{ {\begin{array}{*{20}{l}} {{K_k} = {P_{xz,k|k - 1}}P_{zz,k|k - 1}^{ - 1}} ,\\ {{{\hat x}_{k|k}} = {{\hat x}_{k|k - 1}} + {K_k}({z_k} - \hat z_{k|k - 1}^{})} ,\\ {{P_{k|k}} = {P_{k|k - 1}} - {K_k}{P_{zz,k|k - 1}}K_k^{\rm{T}}} 。\end{array}} \right. $ | (10) |
考虑实际海流、水阻力等的影响,水下无人航行器运动姿态的规律设定如下:
| $ \left\{ {\begin{array}{*{20}{l}} {\theta = {A_\theta }\sin ({\omega _\theta }t + {\phi _\theta })},\\ {\gamma = {A_\gamma }\sin ({\omega _\gamma }t + {\phi _\gamma })} ,\\ {\psi = {A_\psi }\sin ({\omega _\psi }t + {\phi _\psi }) + {\psi _0}} 。\end{array}} \right.$ | (11) |
式中,各个参数含义及初值设置如表1所示。
|
|
表 1 UUV运动规律及初值 Tab.1 Motion pattern and initial value of UUV |
设UUV水下航行的初始位置设为东经120°、北纬30°,航速3 m/s,航行总时间10 h,仿真航路轨迹如图2所示。

|
图 2 UUV模拟航路轨迹 Fig. 2 Simulated track of UUV |
选用EML流速测量精度为测量值的2%±1 cm/s,流向测量精度±2°。陀螺常值漂移为0.01° /h,随机漂移为0.005° /h,加速度计零偏为10−4 g;ADCP测速误差中水平速度误差为0.2%,垂直测速误差为0.6%。
图3为解算的北向位置和东向位置误差图。图中,以实线表示的误差曲线为全航路采用SINS+ADCP组合导航的解算误差结果;点划线和点线分别为本文提出的分区域隐蔽导航方法SINS+ADCP组合导航分别为5 h(占全航路50%)和7 h(占全航路70%)、剩余时间采用SINS+EML组合导航的误差曲线。由仿真结果可知,按区域划分的SINS+ADCP/EML组合导航相比全航程SINS+ADCP组合导航误差较大,且使用SINS+ADCP组合导航占全航程的比例越大,全航程导航精度越高。SINS+ADCP/EML组合导航中,采用SINS+ADCP航程组合占比全航程70%的导航误差精度控制在全航程的6.6‰ cep以内;SINS+ADCP航程占比为50%时,导航误差精度为全航程的1% cep以内;SINS+ADCP全程导航时,导航误差精度控制在4‰ cep以内,如表2所示。

|
图 3 UUV北向位置误差和东向位置误差 Fig. 3 North and east error estimation of UUV |
|
|
表 2 UUV隐蔽导航精度解算结果 Tab.2 Resolution error of UUV with secret navigation |
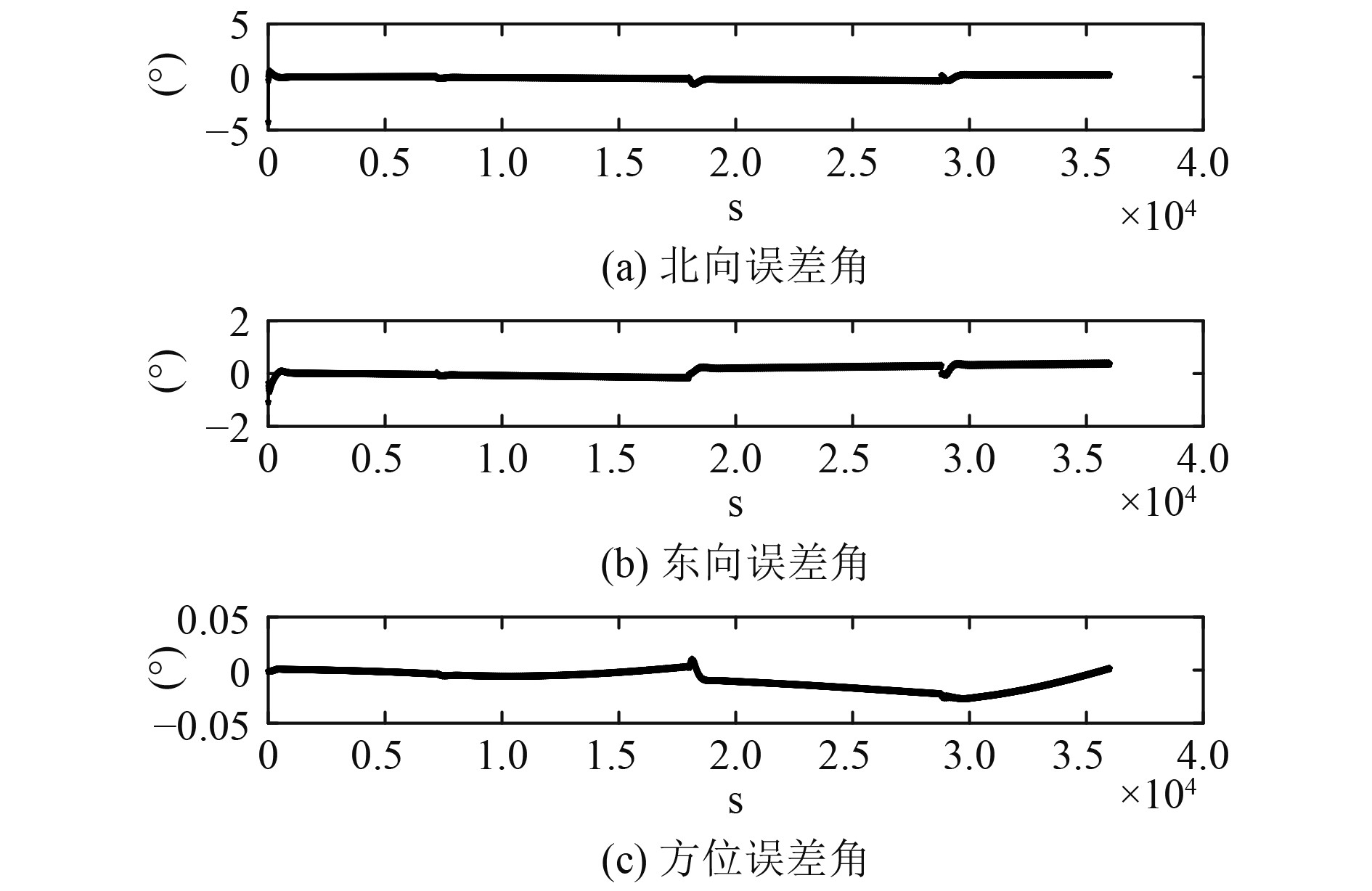
图4和图5为航路解算的SINS北向、东向和方位误差角以及陀螺漂移误差估计结果。可知,在UUV机动转向时,会造成SINS北向、东向和方位角的解算误差和陀螺漂移误差的变大,但通过CKF滤波解算后,北向和东向误差角导航误差精度在10−3度量级,方位角误差解算精度在0.03°以内,满足导航精度的要求(标准要求0.1°)。
|
图 4 UUV的SINS北向东向及方位误差角 Fig. 4 North,east and bear angle error estimation of UUV |

|
图 5 UUV的SINS陀螺漂移东北天向漂移误差估计 Fig. 5 Gyroscope drift error of SINS in UUV |
采用SINS+ADCP/EML隐蔽组合导航方法时,应尽量缩短SINS+EML组合导航模式下的航程,尽可能多的使用SINS+ADCP导航模式,在危险海域禁止使用ADCP的区域采用SINS+EML导航模式。
4 结 语针对UUV水下隐蔽导航问题,以UUV中低精度SINS设备,提出一种以按区域划分的SINS/ADCP/EML/深度计组合导航方案,仿真计算了10 h航程3种不同导航方案的导航误差精度分别为:航程50%的SINS+ADCP导航时,全航程导航精度为1%CEP以内;航程70%的SINS+ADCP导航时,导航精度为6.6‰CEP以内;全航程SINS+ADCP组合导航时为4‰CEP以内。隐蔽导航与安全区域的划分,以UUV任务前可由人工选择隐蔽导航的航程,因此,根据任务需求采用全航程分区域的SINS/ADCP/EML/深度计隐蔽导航方法,可为UUV提供一种远程隐蔽导航方法。为进一步提高导航精度,应尽量缩短SINS+EML组合导航模式下的航程,可在安全区域内,借助UUV上浮进行GPS或北斗导航校准,而采用更高精度的SINS,可进一步提高导航精度,更好地满足UUV远航程导航的要求。
| [1] |
United States Navy. Autonomous Undersea Vehicle Requirement for 2025[R]. U. S. : United States Department of Defense, 2016.
|
| [2] |
魏博文, 吕文红, 范晓静, 等. AUV 导航技术发展现状与展望[J]. 水下无人系统学报, 2019, 27(1): 1−9. WEI Bo-wen, LV Wen-hong, FAN Xiao-jing, et al. Present situation and prospect of autonomous undersea vehicle Navigation Technologies, 2019, 27(1): 1−9. |
| [3] |
李志炜, 岳崴, 高胜峰, 等. 基于可观测度反馈的SINS/ADCP组合导航算法[J]. 水下无人系统学报, 2020, 2(28): 155−161. LI Zhi-wei, YUE wei, GAO sheng-feng, et al. The SINS/ADCP integrated navigation algorithm based on observable degree feedback[M]. Journal of Unmanned Undersea Syatems, 2020, 2(28): 155−161. |
| [4] |
LEONARD J J, BAHR A. Autonomous underwater vehicle navigation[M]. Springer: Handbook of Ocean Engineering, 2016.
|
| [5] |
TAL A, KLEIN I, KATZ R. Inertial navigation system/doppler velocity log(INS/ADCP)fusion with partial ADCP measurements[J]. Sensors, 2017, 17(2): 415. DOI:10.3390/s17020415 |
| [6] |
黄莺. 基于 CKF 的 SINS/ADCP 组合导航系统设计与仿真[D]. 哈尔滨: 哈尔滨工程大学, 2013.
|
| [7] |
李厚全, 苑秉成, 唐劲松. 基于SUKF算法的组合导航方法[J] 鱼雷技术, 2010, 18(3): 209−213. LI Hou-quan, YUAN Bing-cheng, TANG Jin-song. Integra ted navigation method based on SUKF algorithm[J]. Torpedo Technology, 2010, 18(3): 209−213. |
| [8] |
黄凤荣, 朱雨晨, 杨泽清. 基于高斯混合模型的惯导/计程仪组合导航方法中国惯性技术学报, 2019, 27(1): 32−35. HUANG Feng-rong, ZHU Yu-chen, YANG Ze-qing. SINS/EML navigation method based on Gaussian mixtures unscented Kalman filter[J]. Journal of Chinese Inertial Technology, 2019, 27(1): 32−35. |
| [9] |
严浙平, 宋金雪. 模型辅助和洋流估计下的UUV 导航定位方法[J]. 水下无人系统学报2017, 4(25): 319−325. YAN Zhe-ping, SONG Jin-xue. UUV Navigation and positioning method based on model-aided and ocean current estimation[J]. Journal of Unmanned Undersea Systems, 2017, 4(25): 319−325. |
| [10] |
杨峻巍. 水下航行器导航及数据融合技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [11] |
张旭, 崔乃刚, 王小刚, 等. 一种鲁棒自适应容积卡尔曼滤波方法及其在相对导航中的应用[J]. 兵工学报, 2018, 1(39): 94-100. ZHANG Xu, CUI Nai-gang, WANG Xiao-gang, et al. Robust adaptive cubature Kalman filter and its apphcation in relative navigation[J]. Acta ArmamentarII, 2018, 1(39): 94-100. |
| [12] |
寇立伟, 何诗鸣, 项基. 基于平方根容积卡尔曼滤波的水面无人艇导航定位算法[J] 中国造船, 2020, 8(1): 60−69. KOU Li-wei, HE Shi-ming, XIANG Ji. Square root cubature kalman filter-based algorithm for positioning surface ships[J]. Shipbuilding of China, 2020, 8(1): 60−69. |
 2022, Vol. 44
2022, Vol. 44
