无人艇的工作环境一般是在水面至深层水域,由于海流对无人艇的运动具有很大影响,保证无人艇在水下更加稳定地完成作业的需要,由此对无人艇工作姿态下的水动力学进行分析[1],探究无人艇在水中航行以及浮沉运动中航行时所受到的水流造成阻力和阻力矩。无人艇在水下各类工况姿态下会受到诸多流体阻力,获得水动力学参数尤为必要[2],并以此为参数构建无人艇的分析模型。通过资料获悉一般的所采用的方法有:拖曳水池试验、基于理论或经验公式的数据计算以及计算流体力学(CFD)数值模拟[3]。伍兹霍尔海洋研究所的Prestero研究并建立REMUS水下机器人的水动力运动学方程基于拖曳水池试验,所获得的测量值可靠性不足,与真实航行运动情况具有明显的差异性;上海大学的刘和平估算船体水动力学参数的方式是分析研究船体模型试验中所积累的充足数据并修正经验公式进而估算出可供参考的船体水动力学数据,通过对比可知此类手段具有便于分析的优点,然而其中数值的精确度受船体模型试验数据积累的数量影响;哈尔滨工程大学的黄昆仑借助流体仿真软件Fluent,依据壁面函数并选用合适的湍流模型,使用网格模拟技术分析了潜水器包括升沉、俯仰与横摇运动在内的水动力仿真数值,关于模型的水动力系数理论值与仿真数值偏差较小。
CFD软件数据仿真分析对比此前的两类研究方法,其仿真计算的计算值可达到实验模型中包括水阻力与力矩、尾流场等数值相近的精确程度[4-10]。因此,借助CFD数值模拟法以无人艇为对象进行模型流场计算域的仿真分析,并利用软件后处理获取的水动力系数,在数据分析处理之后得出运动过程中最大水阻力,为无人艇后续动力性能研究打下基础。
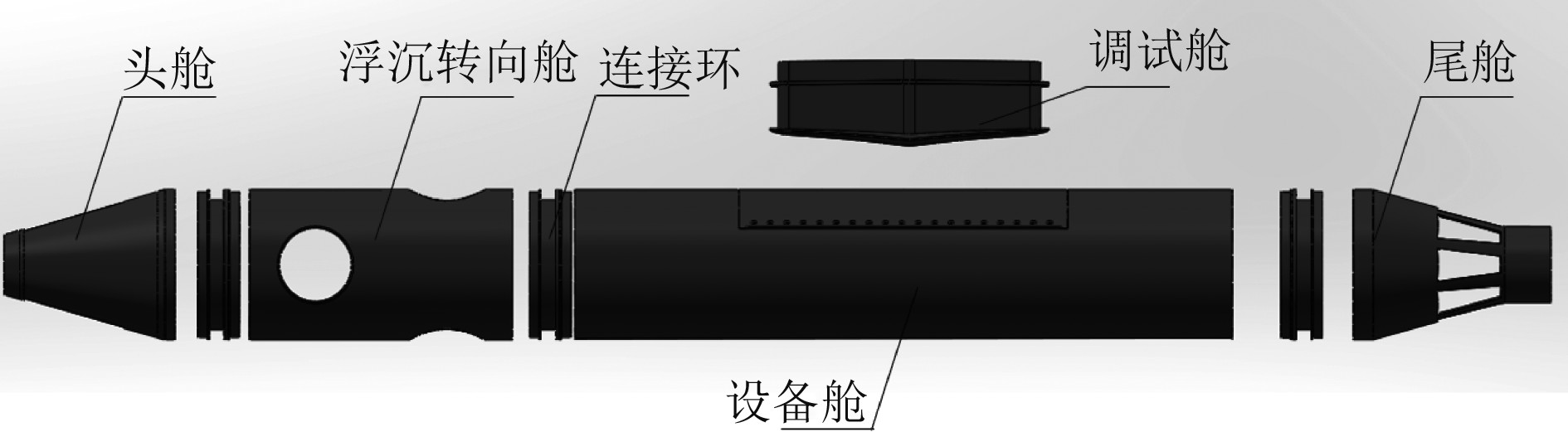
1 水动力计算模型建立 1.1 无人艇总体结构图1为无人艇的结构设计示意图。无人艇采用圆柱体外观结构,其尺寸艇体外径500 mm,长度为4 000 mm,其总体采用框架式的结构形式,总体结构布局由以下部分组成:主体由铝合金板焊接制造而成,在船体内部对称布置有头舱,浮沉转向舱,设备调试舱,尾部动力舱,由连接环将各个模块组合连接为完整艇体。
|
图 1 无人艇结构示意图 Fig. 1 Structure diagram of AUV |
质量守恒和动量守恒定律普遍适用于流体流场的运动中,并且无人艇的水动力学分析中不考虑能量交换问题,在水动力学分析计算时其方程可直接套用质量守恒与动量守恒方程[11]。
根据所选用的守恒定律,基于该方程建立不可压缩的粘性流体的连续性方程与运动方程。
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 ,$ | (1) |
| $ \frac{\partial }{{\partial {x_j}}}({u_i}{u_j}) + \frac{{\partial {u_i}}}{{\partial t}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + \upsilon \frac{\partial }{{\partial {x_j}}}\left[ {\frac{{\partial {u_i}}}{{\partial {u_j}}} + \frac{{\partial {u_j}}}{{\partial {u_i}}}} \right]。$ | (2) |
式中:
三维瞬态不可压缩流体的质量守恒方程为:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}} \right)}}{{\partial {x_j}}} = {S_m}。$ | (3) |
式中:
动量守恒方程(Navier-Stokes方程)在惯性坐标系中公式为:
| $ \frac{{\partial \left( {\rho {u_j}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i} \cdot {u_j}} \right)}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial t}} + \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}} + \rho \cdot {g_i} + {F_i}。$ | (4) |
式中:
所选取的湍流模型方程是对雷诺平均和滤波处理后的方N-S方程,也是被广泛使用的“雷诺时均方程”(RANS):
| $ \left\{ \begin{aligned} & \frac{{\partial \left( {\rho {{\bar u}_i}} \right)}}{{\partial {x_i}}} = 0 ,\\ & \frac{{\partial \left( {\rho {{\bar u}_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {{\bar u}_i} \cdot {{\bar u}_j}} \right)}}{{\partial {{\bar x}_j}}} = - \frac{{\partial p}}{{\partial {x_i}}}+\\ & \quad \frac{\partial }{{\partial {x_j}}}\Bigg( {\mu \frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}}} - \rho \cdot \overline {{u_i}^\prime {u_j}^\prime } \Bigg) + \rho \cdot \overline {{g_i}} + \overline {{F_i}} 。\end{aligned} \right. $ | (5) |
式中:
| $ - \rho \cdot \overline {{u_i}^\prime {u_j}^\prime } = {\mu _t}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}\left( {\rho k + {\mu _t}\frac{{\partial {u_i}}}{{\partial {x_j}}}} \right){\delta _{ij}} 。$ | (6) |
式中,
| $ {\mu _t} = \rho {C_\mu }\frac{{{k^2}}}{\varepsilon }。$ | (7) |
式中:
由式(6)可知,湍流粘度由
| $ \left\{ \begin{split} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k \cdot {u_i}} \right)}}{{\partial {x_i}}} =& \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{\mu }{{{\sigma _k}}}} \right) \cdot \frac{{\partial k}}{{\partial {x_j}}}} \right]\\ &+ {G_k} - \rho \cdot \varepsilon ,\\ \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i} \cdot \varepsilon } \right)}}{{\partial {x_i}}} =& \frac{\partial }{{\partial {x_i}}}\left[ {\left( {\mu + \frac{\mu }{{{\sigma _\varepsilon }}}} \right) \cdot \frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right] \\ & + {C_{1\varepsilon }} \cdot \frac{\varepsilon }{k} \cdot {G_k} - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} 。\end{split} \right. $ | (8) |
在快速张紧流体或是旋涡的情况下,标准
Reallzable
| $ \left\{ \begin{split} &\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} +\frac{{\partial \left( {\rho k \cdot {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {{\alpha _k} \cdot {\mu _{eff}} \cdot \frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} +\\ & \qquad\quad{G_b} - \rho \cdot \varepsilon - {Y_m} + {S_k} \\ & \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i} \cdot \varepsilon } \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left[ {{\alpha _k} \cdot {\mu _{eff}} \cdot \frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right] +\\ &\qquad\quad{C_{1\varepsilon }} \cdot \frac{\varepsilon }{k} \cdot \left( {{G_k} +{G_{3\varepsilon }} \cdot {G_b}} \right) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} - {R_\varepsilon } + {S_\varepsilon }。\end{split} \right. $ | (9) |
式中:
Reallzable
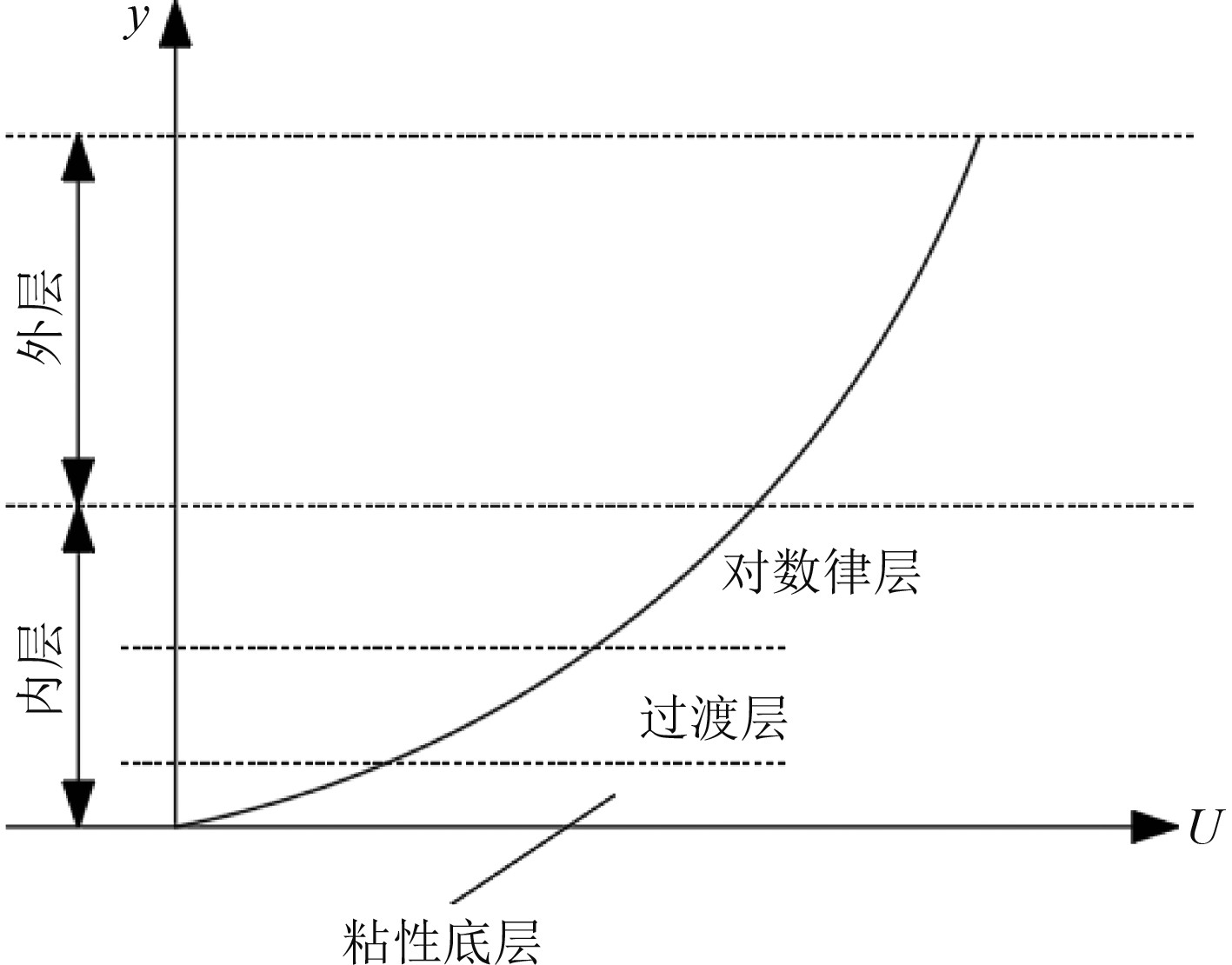
通过查阅文献,模型中湍流边界的内层会沿着外壁面法线方向形成复杂的多层次区域。根据流体流动的差异,可以将近壁区域划分为3层区域[12],由内到外分别是粘度底层(sublayer,
|
图 2 湍流近壁面边界层分部图 Fig. 2 Partition diagram of turbulent near wall boundary layer |
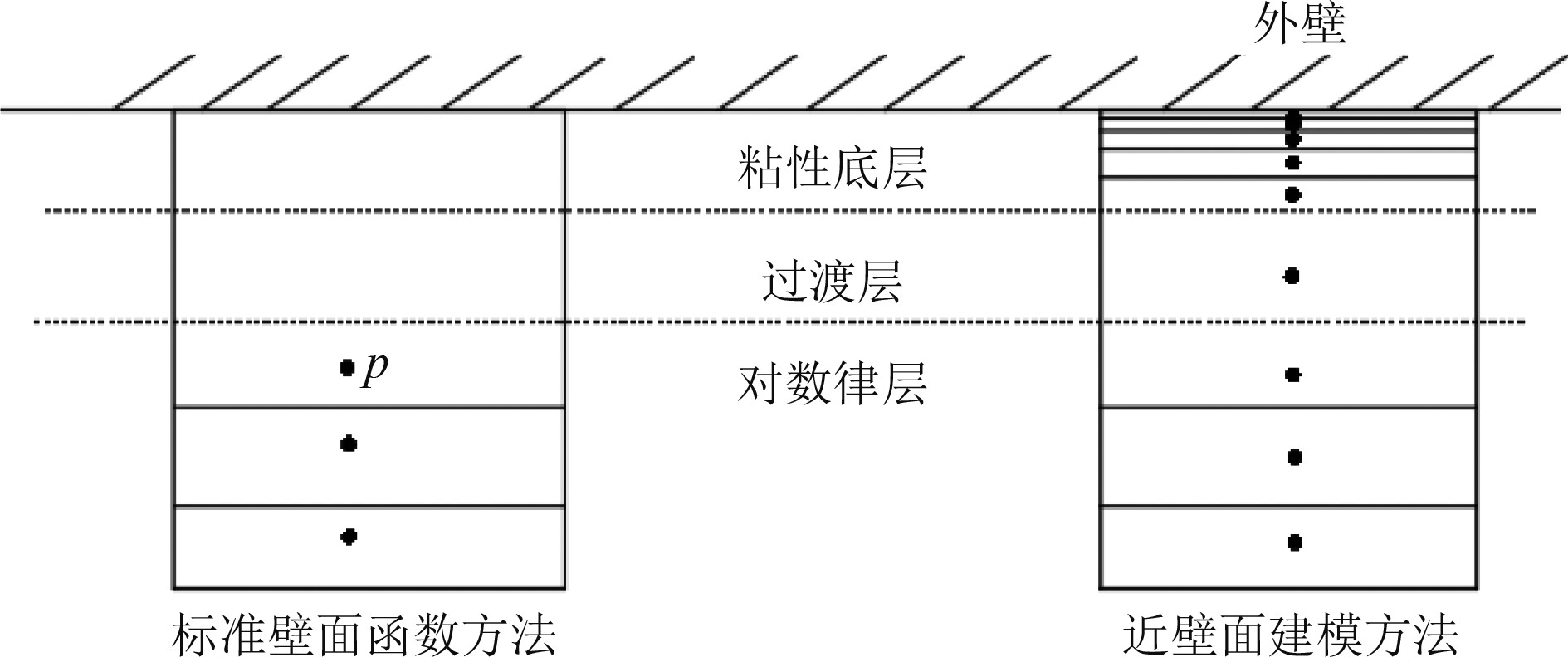
|
图 3 标准壁面函数方法与近壁面模型函数方法的对照 Fig. 3 Comparison between standard wall function method and near wall model function method |
标准壁面函数方程:
| $ {U^*} = \frac{1}{k}\ln \left( {E{y^*}} \right)。$ | (10) |
式中:
| $ {U^*} \equiv \frac{{{U_p}C_\mu ^{{1 \mathord{\left/ {\vphantom {1 4}} \right. } 4}}k_p^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}}{{{{{\tau _\omega }} \mathord{\left/ {\vphantom {{{\tau _\omega }} \rho }} \right. } \rho }}} ,$ | (11) |
| $ {y^*}{\text{ = }}\frac{{\rho C_\mu ^{{1 \mathord{\left/ {\vphantom {1 4}} \right. } 4}}k_p^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}{y_p}}}{\mu }。$ | (12) |
式中:
同时求解分析近壁区域中的湍流动能和耗散率,其变量方程为:
| $ \left\{ \begin{split} &k \approx {\tau _\omega }\frac{{\partial U}}{{\partial y}} = {\tau _\omega }\frac{{{\tau _\omega }}}{{k\rho C_\mu ^{{1 \mathord{\left/ {\vphantom {1 4}} \right. } 4}}k_p^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}{y_p}}} ,\\ & \varepsilon = \frac{{C_\mu ^{{3 \mathord{\left/ {\vphantom {3 4}} \right. } 4}}k_p^{{3 \mathord{\left/ {\vphantom {3 2}} \right. } 2}}}}{{k{y_p}}}。\\ \end{split} \right. $ | (13) |
因而在Reallzable
本文研究无人艇采用模块化组合结构,在确保水动力仿真分析的较高的准确性的基础上,将航行器整体模型做必要的简化[13],经过简化处理的模型如图4所示。

|
图 4 无人艇简化模型 Fig. 4 Simplified model of AUV |
设置流场计算域时,根据分析要求,将计算域构建成长方体,便于根据工况,灵活设置计算域流体入口与出口[14]。同时为降低流场边界条件对仿真分析中的不良影响,计算域设置成无人艇总长的10倍,无人艇与上下左右壁面距离均为其艇体直径4倍[15]。流场初入口与两侧壁面设为远场环境,上下壁面设为静压环境,经简化处理的无人艇模型置入流场中,整体模型如图5所示。

|
图 5 计算域流场 Fig. 5 Flow field in computational domain |
将计算域与模型网格划分之后,再对艇体网格细化处理。图6为流场计算域网格,图7为艇体模型细化网格。

|
图 6 流场计算域网格 Fig. 6 Flow field in computational domain |
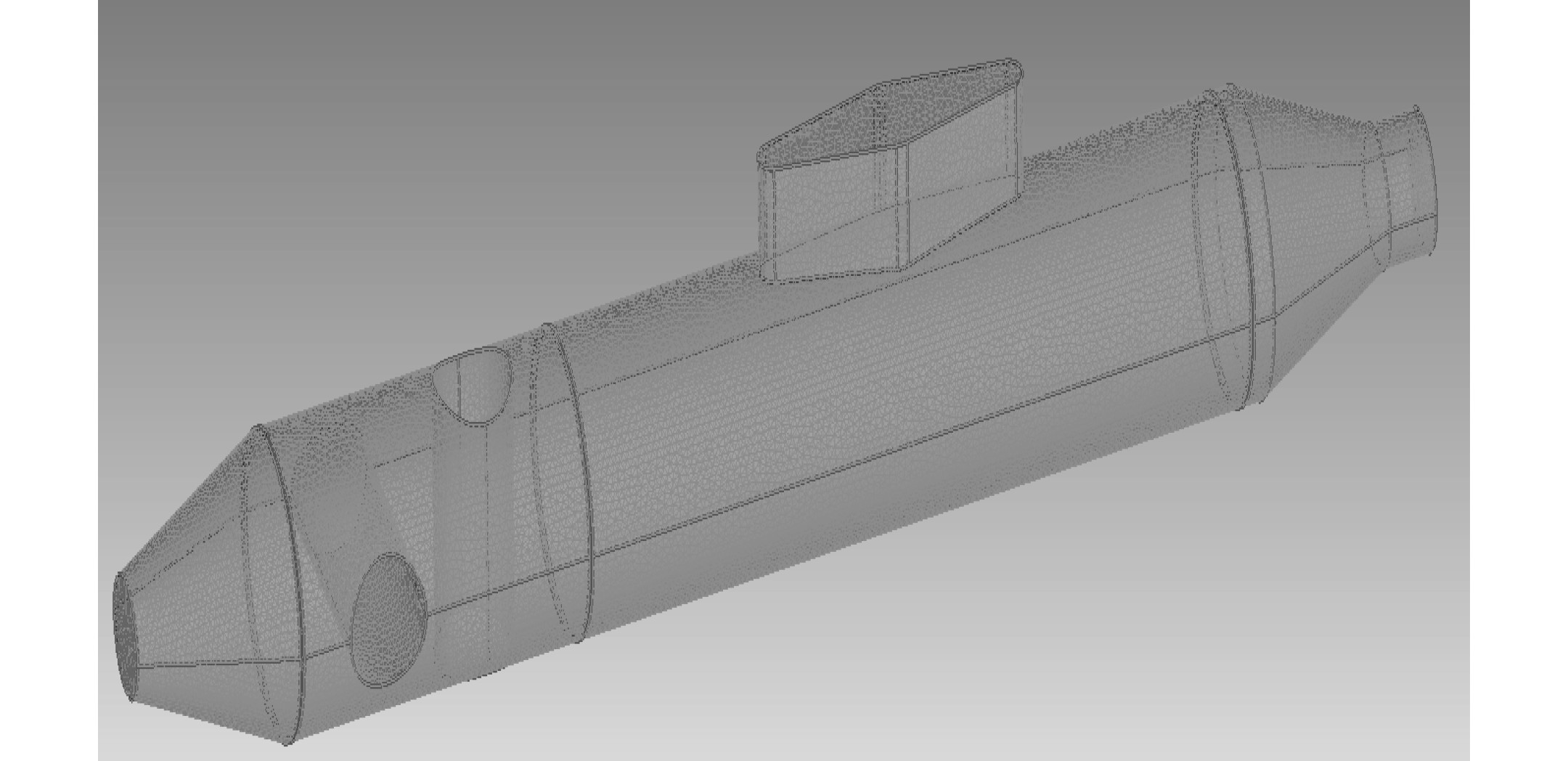
|
图 7 艇体模型细化网格 Fig. 7 Hull model refinement mesh |
流体仿真分析具体设置参数:无人艇在流场中运动中选用单向流动模型,选取改良调整的Reallzable
无人艇在水下作业时主要处于水平直航(巡航)、水平斜航(转向)和垂直俯仰(升沉)3种工况。
|
|
表 1 无人艇水动力工况表 Tab.1 Hydrodynamic condition table of AUV |
通过对各个工况求解,针对各航行运动下无人艇的阻力加以分析,将无人艇的阻力性能统计对比,得出无人艇在不同自由度下的水动力性能。另外Fluent求解器无法直接求解导出流场内阻力与阻力矩,需经过下列经验公式作转换处理:
| $ F = \frac{1}{2}\rho {v^2}A{C_d} ,$ | (14) |
| $ T = \frac{1}{2}\rho {v^2}AL{C_m} 。$ | (15) |
式中:
分析无人艇在水平直航时的水动力,在计算域的速度入口依次设置流场速度。使用Fluent求解器对无人艇4种速度下的阻力特性展开求解,分析结果如图8~图10所示。
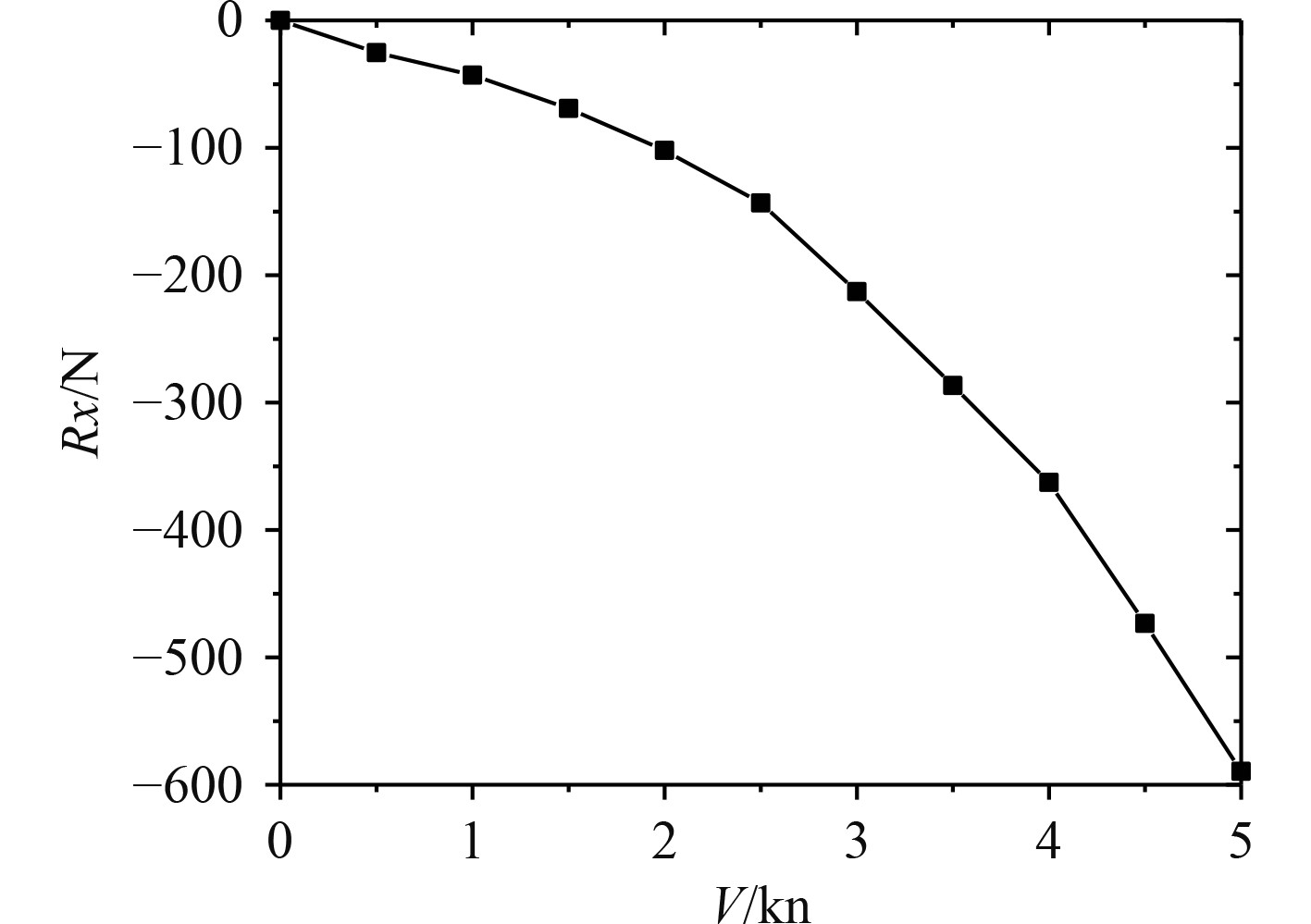
|
图 8
阻力
|
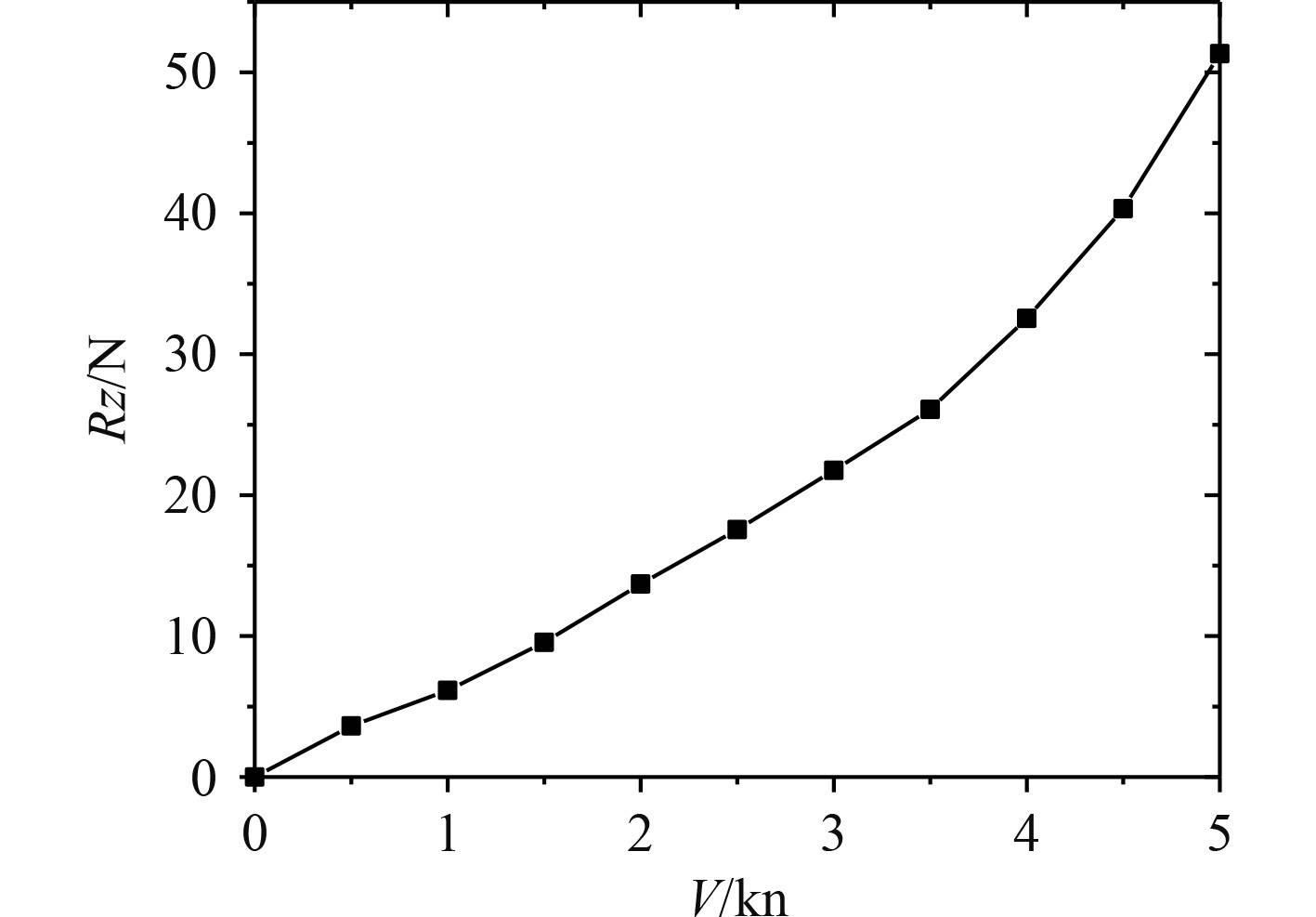
|
图 9
直航垂向阻力
|

|
图 10 阻力系数与航速关系变化曲线 Fig. 10 Curve of resistance coefficient versus speed |
可知,当计算域流速达到最高时,无人艇所受最大阻力约为580 N。无人艇本身前段推进舱设计以及各舱段内部器件的不对称,使艇体在水平直航受到作用方向向上的作用力,其数值会根据速度的增加呈上升趋势。通过分析验证阻力系数与速度的变化关系曲线,在迭代求解后与计算域仿真模型参数相近,相较传统查表法获得的参数更加准确。
2.3 俯仰斜航水动力性能分析无人艇在工作时中会进行水下诸如勘测作业或避障,借助转向舱段的副推进器进行俯仰动作,完成艇体上浮或下沉的驱动。无人艇为近圆柱体外形结构,具有对称性,对其俯仰正负攻角可取任一类进行仿真分析。
在流场计算域中设置速度参数为0.5~2 kn,速度间隔为0.5 kn,航行漂角:0°~16°,角度间隔为4°。修正设置长方体流场域边界条件,对不同攻角下随流速变化的水下阻力特性进行分析计算。图11与图12分别为无人艇正攻角垂直斜航时受到的垂向力以及俯仰力矩随攻角变化的曲线。
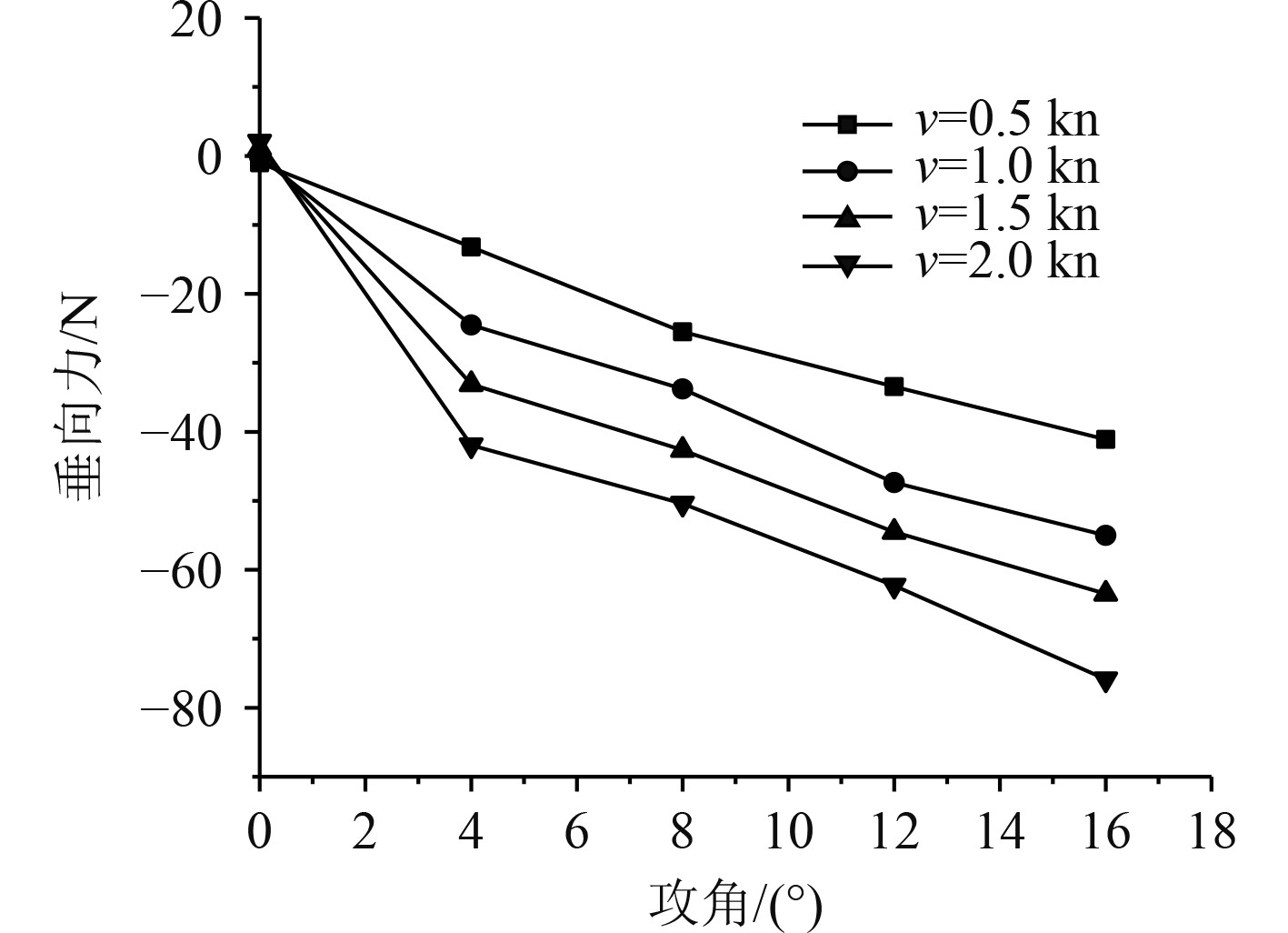
|
图 11 垂向力变化曲线 Fig. 11 Vertical force variation curve |
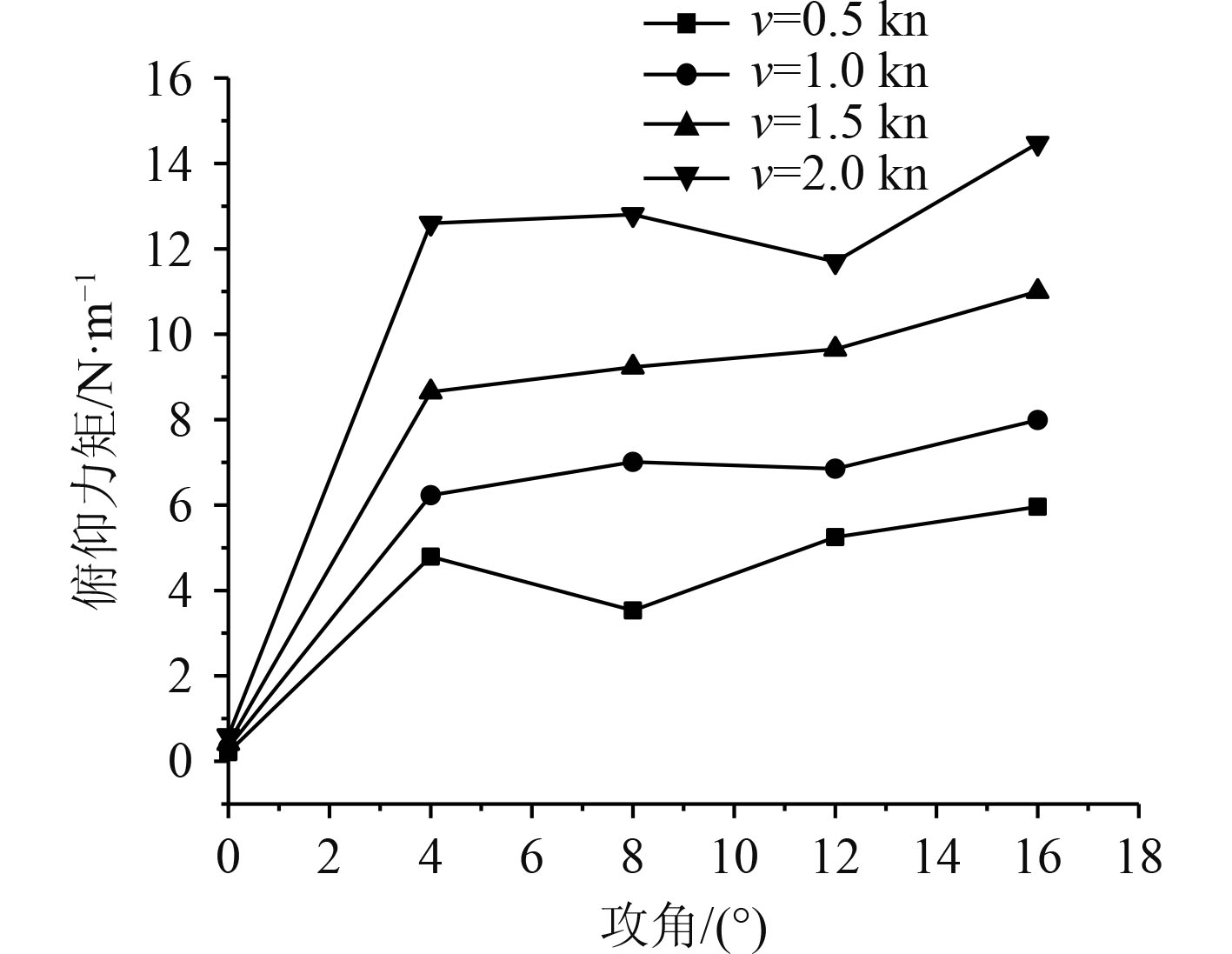
|
图 12 俯仰力矩变化曲线 Fig. 12 Pitch moment variation curve |
可知,无人艇上下结构相对对称,在正负攻角分析时可择一求解,此处取正攻角。作俯仰姿态时,在同一攻角下,无人艇所受垂向力随计算域内的航速提高而逐步增加,在相同流速下,攻角的数值增加会较为明显的使得无人艇所受垂向力增加。在俯仰位姿下,所选择的攻角数值增加,无人艇的迎流面积会随之增加,进而导致水阻力变大,峰值可到达80 N。俯仰力矩遵从同样的变化趋势,与航速与攻角的变化量呈正相关的变化关系。
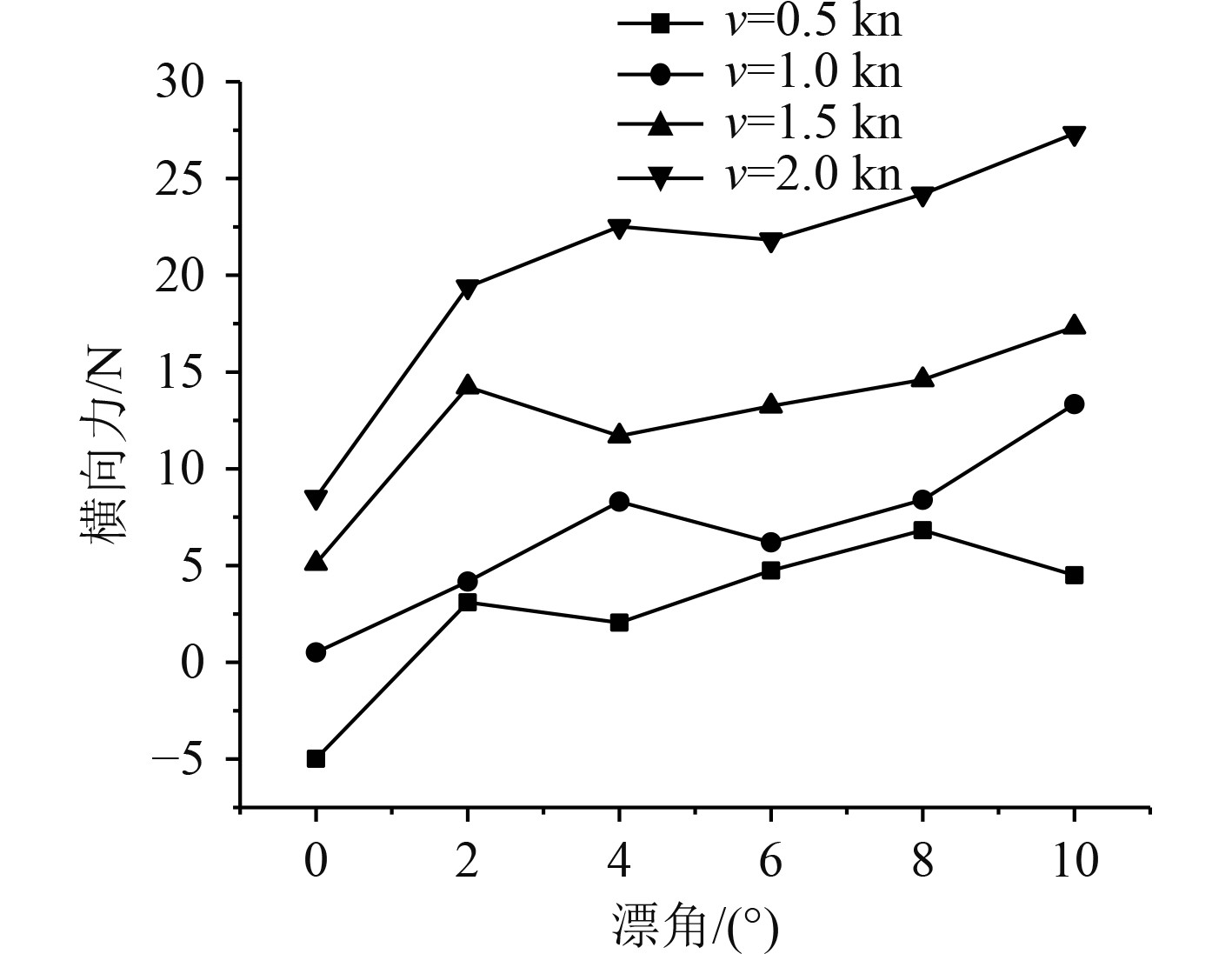
2.4 水平航行变向水动力性能分析无人艇在水下工作环境时常需要按任务要求进行变向航行的工况,因此有必要对无人艇转向航行状态下进行水动力仿真分析。无人艇航行弯转时,航速相较直航较小,在流场计算域中设置速度参数为0.5~2 kn,速度间隔为0.5 kn,航行漂角:0°~10°,角度间隔为2°。设置不同漂角,在流场计算域中对各航行速度下的无人艇的的水动力阻力性能分析求解。图13与图14分别为不同漂角下,无人艇水平变向时流场内的横向力、纵向力等阻力变化曲线。
|
图 13 航行转向横向力变化曲线 Fig. 13 Variation curve of lateral force in turning |
|
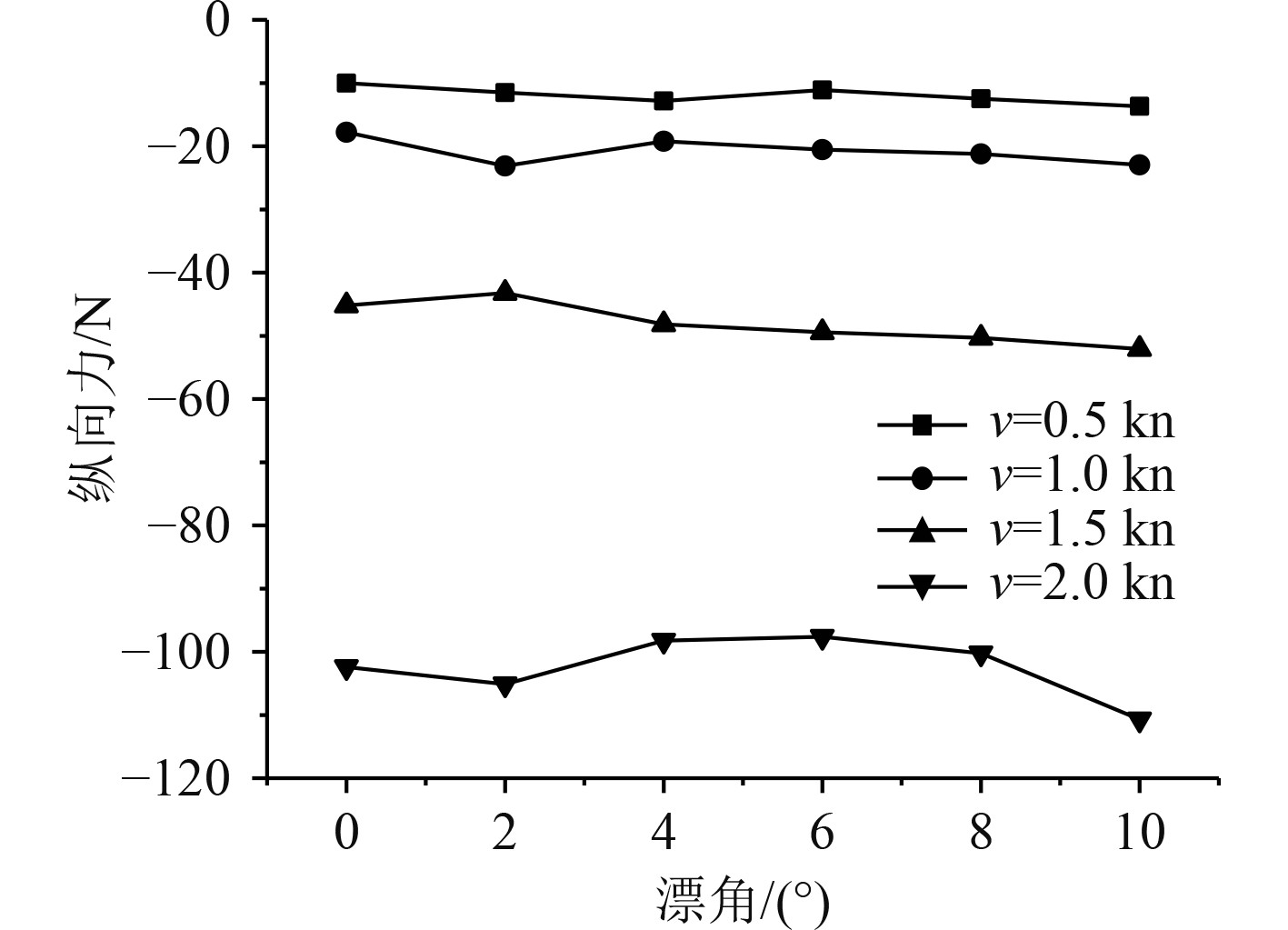
图 14 航行转向纵向力变化曲线 Fig. 14 Variation curve of longitudinal force in turning |
可知,无人艇航行变向时,流场施加在艇体的横向力受航速影响,速度越高,所受横向力越大。相同速度下,漂角的增加会导致横向力的显著增加,当无人艇处于最高航速下以最大漂角运动时,流场中施加的横向力约为28 N;变向航行运动中,无人艇所受的纵向力与漂角变化呈正相关的关系,其峰值高达112 N。此外无人艇结构在变向过程中迎流面积变化量较小,故在保持一定航速时,无人艇在运动过程中纵向力受漂角变化的影响较不明显。
3 无人艇水动力试验分析在完成对无人艇水动力性能仿真分析后,对无人艇进行下水试验,进一步评价仿真数值结果。根据仿真结果设计推进系统,尾部推进舱的推进器选型功率1.5 kW,转向舱选型0.3 kW,从效率的角度出发试验深度取水下5 m。无人艇内安装传感器测量单元,采集航速,航行位姿,水流方向与水下压力等参数,传递给岸端上位机获取试验数据。通过误差分析比对仿真值与测试值来验证仿真求解数值的准确性。
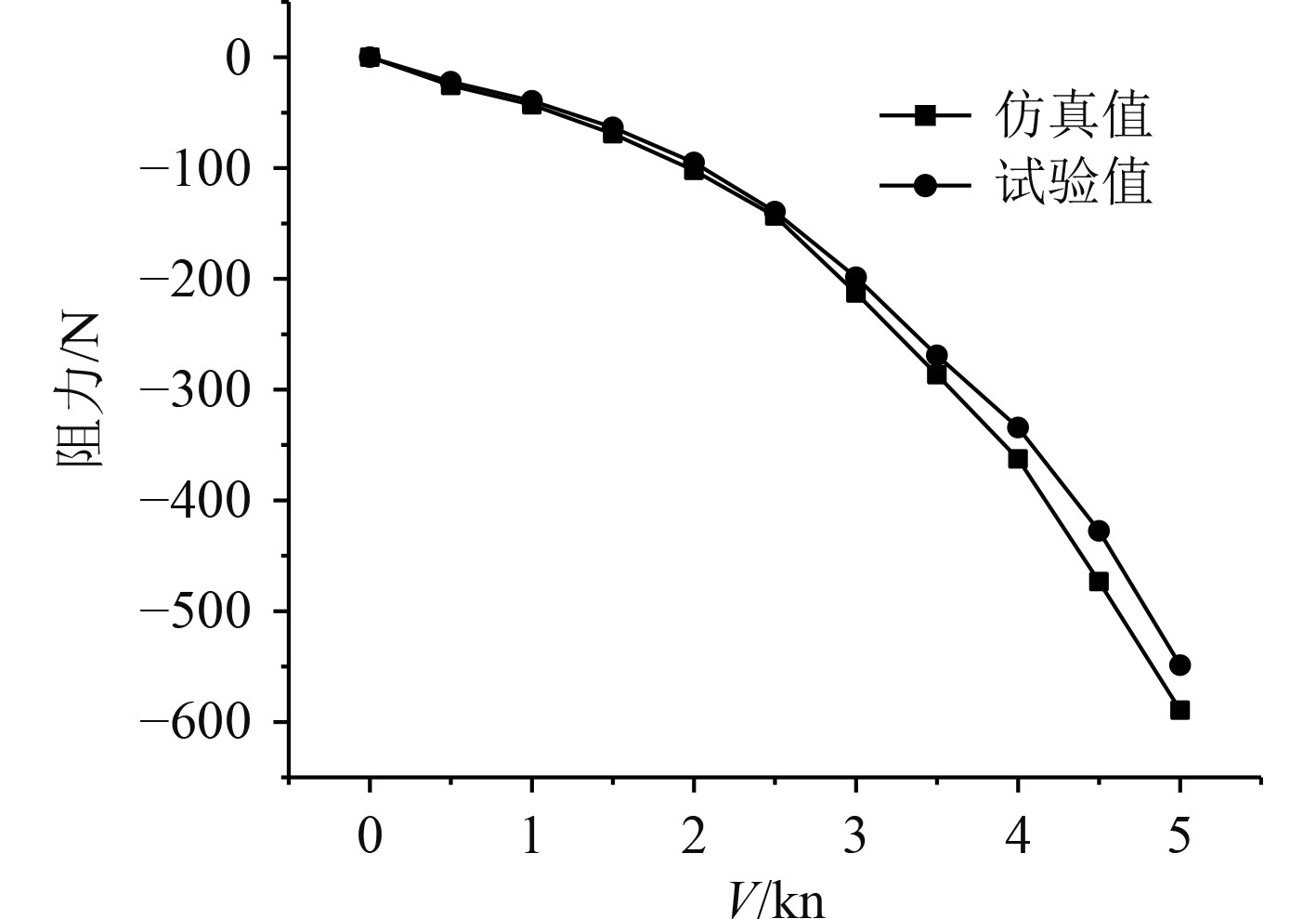
在通过试验获取测试数据后,将数据与仿真数据做比对处理可以发现,考虑到江水的物理性质不同于海水,结果必然存在一定差异性,如海水密度较大,理论上试验测得阻力应小于仿真阻力。由图15可知,在直线航行工况下,随着航速的增加,二者偏差波动范围在8%内,最大阻力为548 N。无人艇作俯仰运动时,取其中最大航速2 kn的工况作为分析,当攻角达到16°,所受最大垂向力为70 N,误差范围在9%内,如图16所示。艇体在偏转航行时,同样最大航速2 kn的工况下,所受最大横向力26 N,如图17所示。在试验过程中由于水况存在一定横流,转向时受力受到一定影响,某些漂角最大偏差接近12%。
|
图 15 直航阻力对比图 Fig. 15 Comparison of direct flight resistance |
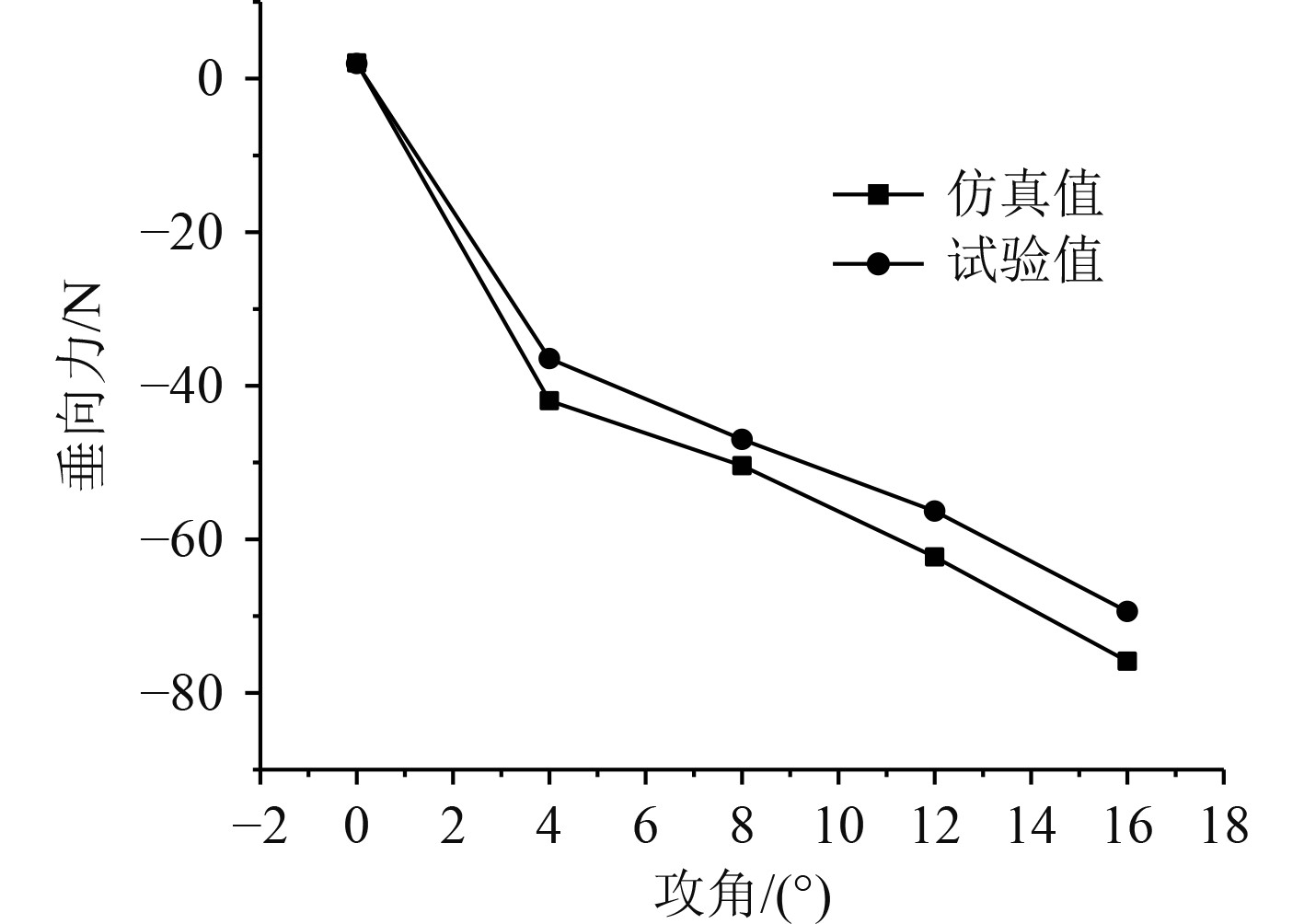
|
图 16 俯仰垂向力对比图 Fig. 16 Comparison of pitching and vertical forces |

|
图 17 偏转横向力对比图 Fig. 17 Comparison chart of deflection lateral force |
试验数据与仿真数据进行对比,并考虑设计方案中作业环境与试验环境的差异,证明仿真数据具有理想的准确性。在航行测试过程中,推进系统工作状态平稳,能够提供足够的动力进行位姿调整,并留有一定裕量,表明由仿真数据选型的推进系统具有较高的可行性。
4 结 语1)在对无人艇航行进行仿真模拟时,采用的Realizable
2)通过CFD仿真软件,将无人艇在航行过程中直航、变向与俯仰3种工况做出仿真分析并求解出水阻力,依照参数结果拟合出曲线,根据无人艇的简化结构模型加以综合考量,航速对无人艇各种运动中所受阻力施加的影响最为明显。在直航时,无人艇航速达5 kn时,流场中最大水阻力为580 N;在俯仰升沉运动过程中,无人艇运动受到垂向力影响较大,最大垂向力达到80 N;无人艇在水平变向过程中,横向力与纵向力对航行运动有较为明显的影响,流场施加的最大横向力为28 N,最大纵向力为110 N。根据仿真分析数据,在选型时保留一定裕量,主推进器选型功率为1.5 kW,转向舱推进器选择功率为0.5 kW。
3)通过样机试验,比对仿真数据,在直航,俯仰与偏转时,可知计算值仿真分析的求解结果与试验结果偏差较小,证明本文改良湍流模型仿真的可信度,并验证了推进器系统选型方案的可行性,对后续设计方案优化提供参考。
| [1] |
孙梦瑶, 刘玉红, 黄明龙, 等. 测量型深水AUV垂直面等运动稳定性设计[J]. 机械科学与技术, 2016, 35(9): 1402-1407. |
| [2] |
G YA DYNNIKOVA, P R ANDRONOV. Expressions of force and moment exerted on a body in a viscous flow via the flux of vorticity generated on its surface[J]. European Journal of Mechanics / B Fluids, 2018, 72: 293-300. DOI:10.1016/j.euromechflu.2018.06.002 |
| [3] |
漆小舟, 缪爱琴, 万德成. 水下潜器航行水动力导数CFD计算[J]. 水动力学研究与进展: A辑, 2018, 33(3): 297-304. |
| [4] |
黄东, 王成华, 徐宏水. 船体清刷机器人水动力阻力计算及其结构优化[J]. 声学与电子工程, 2016(4): 42-46. HUANG Dong, WANG Cheng-huang, XU Hong-shui. Hydrodynamic resistance calculation and structure optimization of ship cleaning robot[J]. Acoustics and Electronics Engineering, 2016(4): 42-46. |
| [5] |
姜钧喆. 水下滑翔机总体设计与水动力性能分析[D]. 上海, 上海交通大学, 2018.
|
| [6] |
高婷, 庞永杰, 王亚兴, 等. 水下航行器水动力系数计算方法[J]. 哈尔滨工程大学学报, 2019, 40(1): 178-184. GAO Ting, PANG Yong-xin, WANG Ya-xing, et al. Calculation method of hydrodynamic coefficients for underwater vehicles[J]. Journal of Harbin Engineering University, 2019, 40(1): 178-184. |
| [7] |
王太友, 胡以怀, 张宝吉, 等. 考虑螺旋桨体积力的水下机器人水动力特性仿真[J]. 船舶工程, 2018, 40(1): 12-16+60. |
| [8] |
刘芳华, 李鑫. 水下捕捞机器人水动力学性能分析[J]. 机械与电子, 2020(6): 55-61. |
| [9] |
于庚. 1200米级深水作业型机器人水动力及运动响应性能研究[D]. 镇江, 江苏科技大学, 2019.
|
| [10] |
邵杰, 李晓花, 郭振江, 等. 不同湍流模型在管道流动数值模拟中的适用性研究[J]. 化工设备与管道, 2016, 53(4): 66-71. |
| [11] |
郑海斌. 水下机器人水动力性能分析及其运动控制方法的研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
|
| [12] |
黄乐萍. 壁湍流的展向运动减阻机理研究[D]. 南京: 南京理工大学, 2012.
|
| [13] |
TANG S, URA T, NAKATANI T, et al. Estimation of the hydrodynamic coefficients of the complex-shaped autonomous underwater vehicle TUNA-SAND[J]. Journal of marine science and technology, 2009, 14(3): 373-386. DOI:10.1007/s00773-009-0055-4 |
| [14] |
PRESTERO T T J. Verification of a six-degree of freedom simulation model for the REMUS autonomous underwater vehicle[D]. Massachusetts institute of technology, 2001.
|
| [15] |
陈英龙, 宋男, 张增猛等. 低速域水下遥控机器人水动力试验系统设计[J]. 液压与气动, 2019(2): 13-17. DOI:10.11832/j.issn.1000-4858.2019.02.003 |
 2022, Vol. 44
2022, Vol. 44
