在开发海洋资源时,经常会遇见一些危险性较大的工作,为保护海上工作人员的生命安全,可以使用无人船代替人工的方式,在海面作业上进行一些风险较大的工作。作为一种可以自主作业的海面智能运动平台,无人船需要在复杂的海浪环境下持续稳定航行,并通过水中传感器进行样本数据的采集工作,因此需要时刻保证船体的稳定。在实际的海洋环境中,海洋气象、洋流活动均会导致海浪的活动变得更加复杂,而海面风力与波浪又会造成船体晃动,导致一些精度需求较高的项目无法实现,或者直接导致无人船上的精密仪器短暂失效,降低航行与工作的效率,甚至造成巨大的财产损失。想要解决船体的稳定性问题,就要从泊船姿态控制方面出发,在智能化的控制机构下,设计适应性更强的船体控制机构。在这样的环境背景下,对无人船泊船姿态的控制就成为了无人船船体稳定性研究的重要分支。本文结合混合海浪作用,设计无人船泊船姿态的自动控制方法。
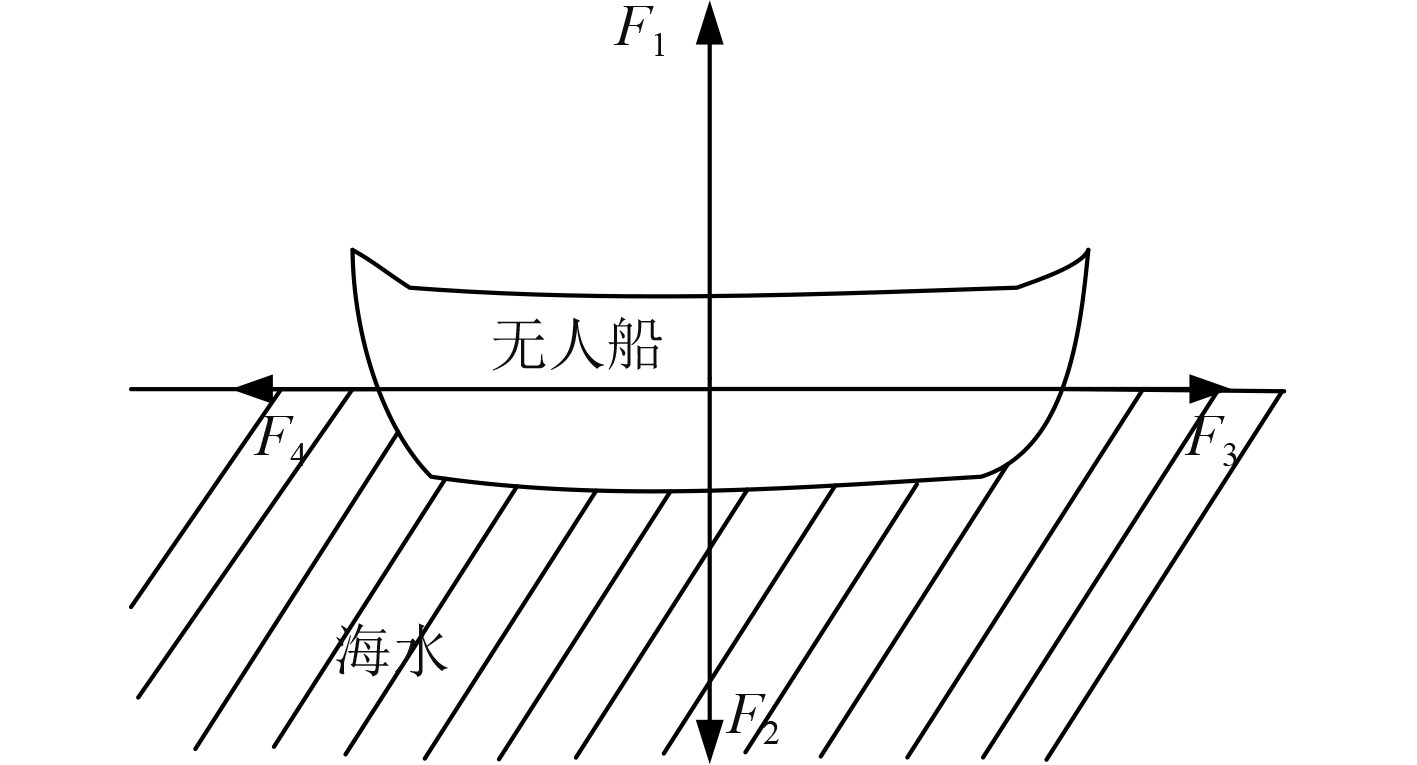
1 设计混合海浪作用下的无人船泊船姿态自动控制方法 1.1 建立无人船运动模型无人船在海洋中的航行受到惯性的影响很大,当船舶向某一方向以恒定的速度行进时,其受力结果如图1所示。
|
图 1 无人船匀速直线航行受力分析 Fig. 1 Force analysis of unmanned ship in uniform linear navigation |
如图1所示,在无人船航行的受力分析模型中,F1表示船体排水过程中受到的水面浮力;F2表示无人船自身的重力;F3表示无人船受到推进装置的航行动力,受力方向为船体的航行方向;F4则表示无人船航行过程中的水面阻力,与航行方向相反。这4种力在船体匀速直线运动时处于一种理想的平衡状态,但是由于海面上的风浪作用,船体的受力情况相较于图1中的受力分析会更加复杂,在4种力之外,还存在附加惯性力和摩擦阻尼力等[1]。为更好地定义地理参考坐标系,可以将无人船的受力分析放置于一个两两垂直的坐标系中,并将船体的前进方向定位正方向,并将理想状态的x-y轴坐标系更改为x-y-z轴坐标系。为方便公式推导,使用合外力作为船舶运动的力学方程。结合零频率与自然频率的模型假设条件,可以得到无人船运动耦合方程组:
| $ \begin{split} & \left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}} \\ {{x_{21}}}&{{x_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{a_1}} \\ {{a_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{y_{11}}}&{{y_{12}}} \\ {{y_{21}}}&{{y_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{b_1}} \\ {{b_2}} \end{array}} \right] + \\ &\qquad \left[ {\begin{array}{*{20}{c}} {{z_{11}}}&{{z_{12}}} \\ {{z_{21}}}&{{z_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{c_1}} \\ {{c_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{H_e}\left( {{\delta _p}{T_1}{k_i}} \right)} \\ {{H_e}\left( {{\delta _p}{T_2}{k_i}} \right)} \end{array}} \right]。\end{split} $ | (1) |
式中:等号前面的部分分别为海浪在x轴、y轴、z轴3个方向对船体的干扰阻力,等号后面的部分则为船体自身的前进动力。
1.2 计算混合海浪干扰力海浪形成的原因多种多样,最常见的因素是洋流与海风。因此在研究复杂海浪作用时,分开讨论,分别建立由海风导致的海浪模型以及由洋流导致的海浪模型。首先需要将海浪作为一种较为平稳,且频率、传播方向、波高、初始相位均不相同的余弦波,分别计算海浪谱与随即海浪的生成,此时理想的海浪模型为:
| $ f\left( t \right) = \sum\limits_{i = 1}^n {{{\left( {2G\left( {{S_t}} \right) + H\left( {{S_t}} \right)} \right)}^{\frac{1}{2}}}}。$ | (2) |
式中:
| $ T\left( w \right) = \frac{{8.11 \times {{10}^{ - 3}} \times {g^2}}}{{{w_t}}}\exp {\left( { - \frac{{3.11}}{{{K_i}{w_t}}}} \right)^2}。$ | (3) |
式中:
| $ \xi \left( t \right) = \sum\limits_{i = 1}^n {{\xi _i}\cos \left( {{F_d}{u_i} + {p_i}} \right)}。$ | (4) |
式中:
| $ {F_k}\left( t \right) = \sum\limits_{i = 1}^n {\sqrt {2{H_s}\left( w \right) \times {F_i}} \times \sin \left( {{w_i}t} \right)}。$ | (5) |
式中:
在设计泊船姿态自动控制算法时,需要保证无人船线性被控系统的线性方程与输出方程可以实现,其关系式为:
| $ \left\{\begin{array}{l} f(x)={{M}}(x)+b_t·N(x),\\ g(x)=b_t·H(x)。\end{array}\right. $ | (6) |
式中:
| $ \hat{f}(x)=-P(x)-\hat{d}(x)。$ | (7) |
式中:
|
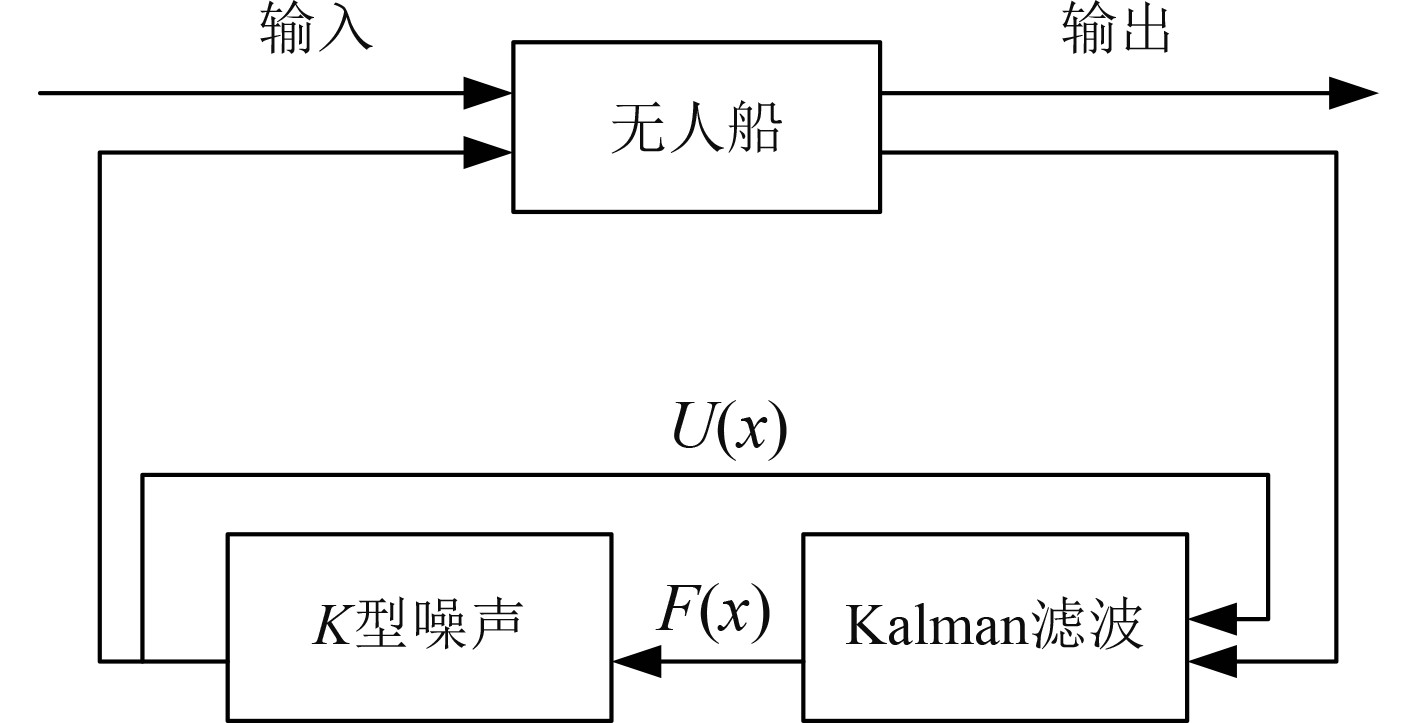
图 2 无人船姿态控制控制器原理 Fig. 2 The controller principle of the automatic attitude control |
可知,无人船为姿态控制的被控对象,噪声以及滤波控制机构为本文设计的控制器。以整体而言,控制器具备更好的反馈形式与输出标准,尤其是经过滤波过滤装置的输出量与输入量需要实时保存。在得到较为完整的控制器后,需要将其添加进控制器模块中。模块的输入参数分别为无人船的垂荡速度、纵摇角速度、垂荡位移、纵摇角度等,将其转换为向量的模式,就可以进入控制器。在输出窗口,以尾板倾角信号作为输出信号,在示波器内,无尾板与带尾板可以综合对比减摇效果,并规定减摇的攻击范围。在模型的预测控制中,需要使用更好的控制技术,用于对模型的安全约束与设备处理,在整体的无人船泊船姿态自动控制中,占据重要地位。线性控制器一般都具备相同的结构与足够完整的自由度,利用显示模型预测时间点的输出与使用,并在系统代价函数中,完成代价函数的极小值计算。最后通过后退策略,计算任意时刻内标记点的移动方向与移动速度,其中每一个控制序列的信号特征都可以作为控制信号来使用。在模型噪声的代价函数中,需要尽量保证滤波最小化处理,此时模型状态参量可以表示为:
| $ \left\{\begin{array}{l} d(b+1)=f(d(b)+u(b)),\\ y(a+1)=g(y(b)+u(b))。\end{array}\right. $ | (8) |
式中:
为验证设计的混合海浪作用下无人船泊船姿态自动控制方法的有效性,对该模型进行仿真分析,并与现有的2种姿态自动控制方法对比,比较其优越性。在仿真实验中,设定无人船的船体参数值如表1所示。
|
|
表 1 船体参数 Tab.1 Hull Parameters |
结合表1的船体参数,设定系统仿真的干扰项,将舵角的减摇作用限制在20°,令舵角角速度为10°/ s,鳍角的减摇作用限制在25°,角速度为15°/ s。排除波浪力矩的干扰,以不同的海况等级分别仿真。
2.2 不同浪向下船舶姿态控制仿真分别测试当遭遇角为45°,90°,135°时,船舶首摇角、横摇角、舵角的联合控制仿真曲线,得到如图3~图5所示的图像。
|
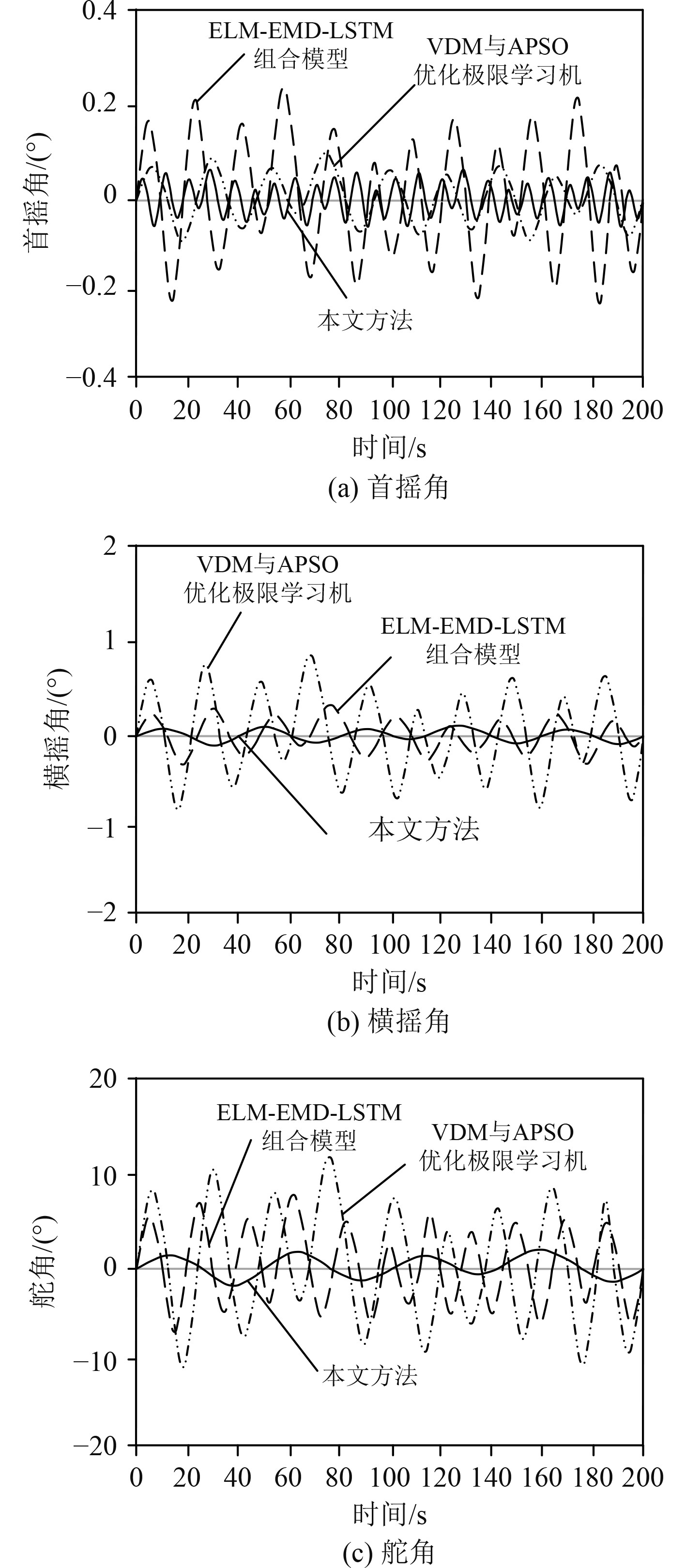
图 3 遭遇角45° Fig. 3 Encounter angle 45° |
|
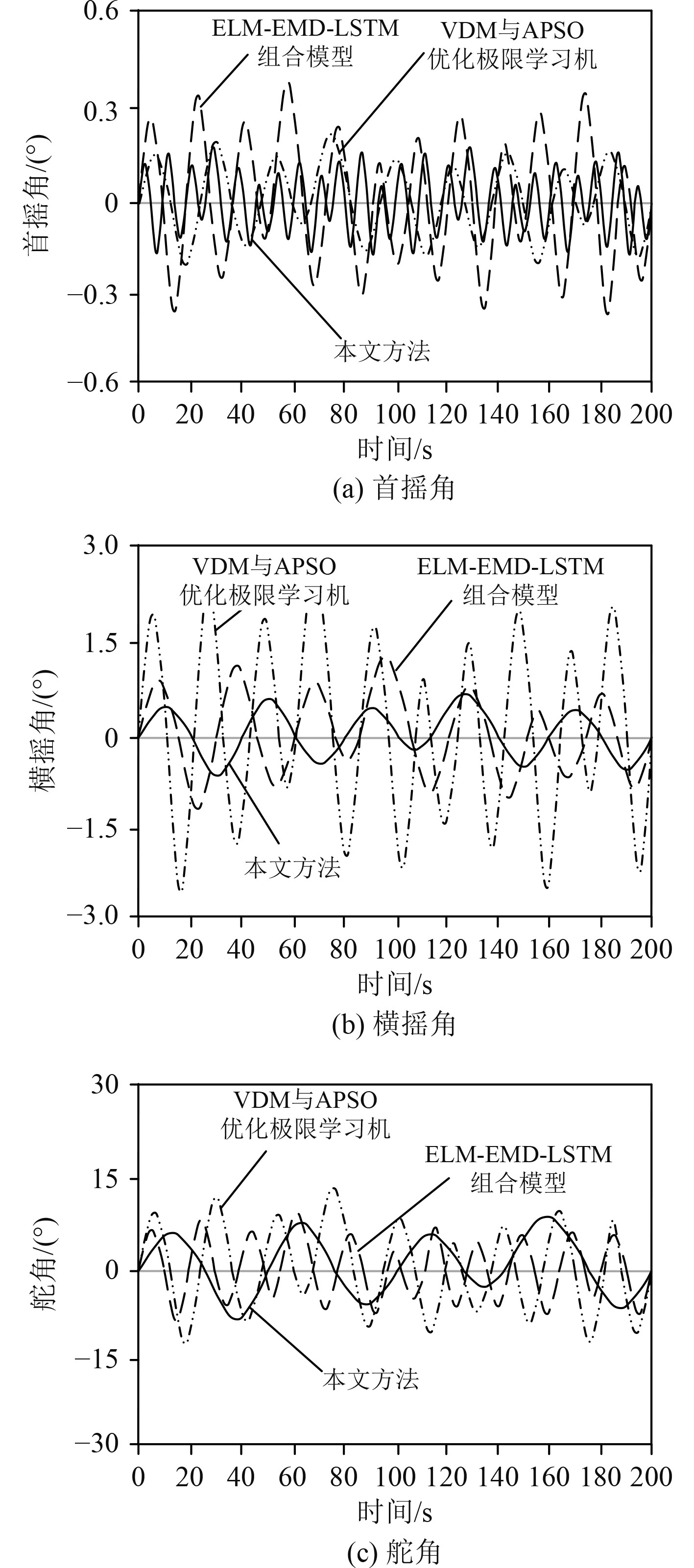
图 5 遭遇角135° Fig. 5 Encounter angle 135° |
如图3所示,当遭遇角为45°时,3种不同的船舶姿态控制方法在首摇角、横摇角、舵角的联合控制下响应角度均不相同。其中本文设计的控制方法明显较ELM-EMD-LSTM组合模型与VDM与APSO优化极限学习机方法的响应角度更小。
如图4所示,无人船泊船姿态自动控制方法在遭遇角为90°时,首摇角、横摇角、舵角等3种响应角度较45°明显增大,且本文方法所得响应角度在条件相同时明显更小。
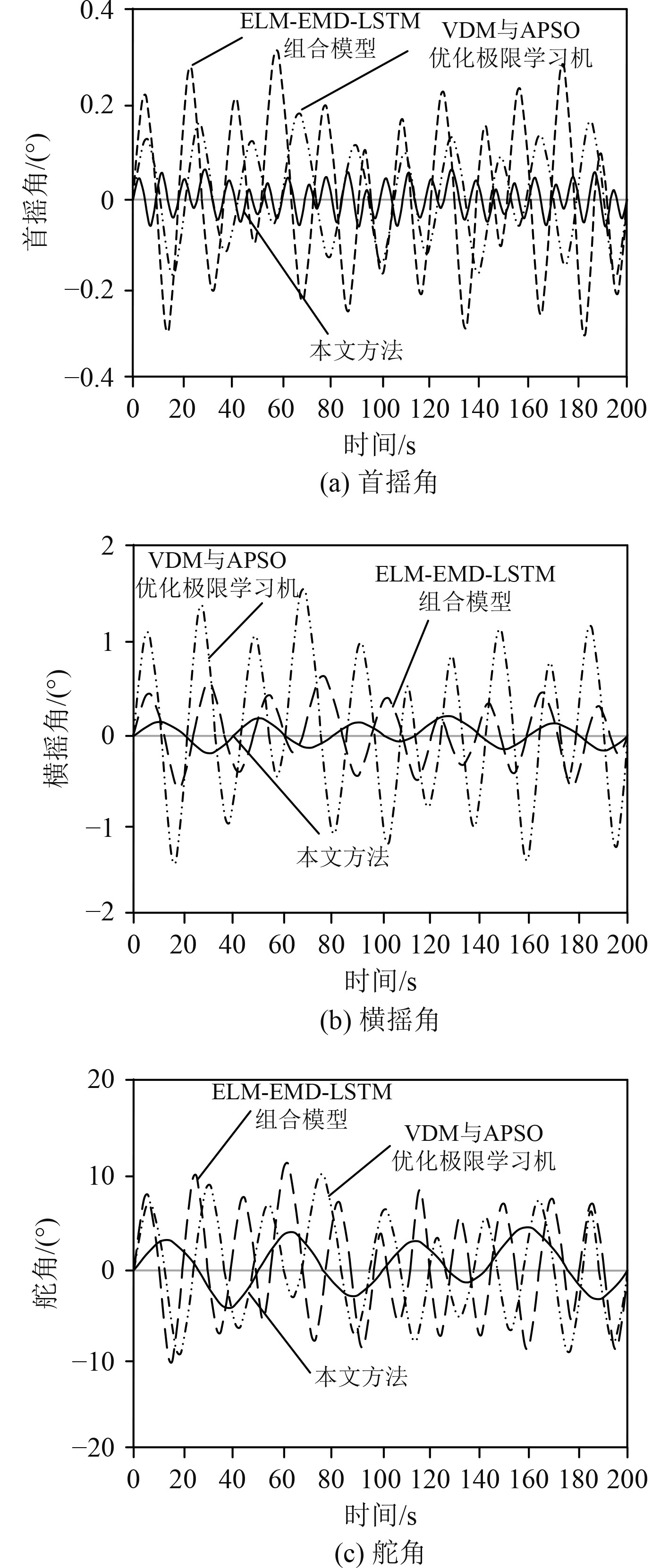
|
图 4 遭遇角90° Fig. 4 Encounter angle 90° |
遭遇角为135°时的响应角度如图5所示。对比45°,90°,135°等3种遭遇角可以得知,当遭遇角逐渐增加时,响应角度也会明显增大。在3种遭遇角中,本文设计的姿态控制方法均为相同条件下的最小值,可见本文方法较传统的2种方法控制效果更好。
3 结 语本文设计一种混合海浪作用下的无人船泊船姿态自动控制方法,建立舰船航行模型,计算混合海浪对无人船的影响,并对其力矩结果进行分析。最后对泊船姿态的控制措施设计相应算法,建立控制器。通过对比实验,验证了本文泊船姿态自动控制方法的有效性与优越性,当遭遇角为45°,90°,135°时,本文设计的方法均可以在首摇角、横摇角以及舵角的响应角度计算中获取更好的数值。基于本文设计的自动控制方法,在很多需要精密测量或者船上保存有精密仪器的无人船上,可以降低船体的晃动频率,保证船体的稳定性,具备较高的使用价值。
| [1] |
张彪, 彭秀艳, 高杰. 基于ELM-EMD-LSTM组合模型的船舶运动姿态预测[J]. 船舶力学, 2020, 24(11): 1413-1421. ZHANG B, GAO J, PENG X Y. Ship motion attitude prediction based on ELM- EMD-LSTM integrated model[J]. Journal of Ship Mechanics, 2020, 24(11): 1413-1421. DOI:10.3969/j.issn.1007-7294.2020.11.005 |
| [2] |
孙珽, 徐东星, 尹勇, 等. 基于VDM与APSO优化极限学习机的船舶运动姿态预报[J]. 船舶工程, 2019, 41(11): 89-97. SUN T, XU D X, YIN Y, et al. Ship motion attitude prediction based on VDM and APSO optimized extreme learning machine[J]. Ship Engineering, 2019, 41(11): 89-97. |
| [3] |
徐得志, 任晋宇. 水下航行器垂向操纵运动数学仿真研究[J]. 中国水运(下半月), 2015, 15(12): 87-89. XU D Z, REN J Y. Mathematical simulation of vertical maneuvering motion of underwater vehicle[J]. China Water Transport, 2015, 15(12): 87-89. |
| [4] |
任晋宇. 潜艇操纵运动粘性绕流数值模拟[D]. 武汉: 华中科技大学, 2009.
|
| [5] |
高国章, 李修宇. 基于预测控制的水下自航器抗海浪变深控制分析[J]. 船舶工程, 2020, 42(6): 91-97. GAO G Z, LI X Y. Anti-wave depth control analysis of underwater self-propelled vehicle based on predictive control[J]. Ship Engineering, 2020, 42(6): 91-97. |
| [6] |
宋义超, 王五桂, 金颀. 一种穿浪双体船纵向运动姿态控制方案设计[J]. 船电技术, 2019, 39(S1): 32-37. SONG Y C, WANG W G, JIN Q. A scheme design for WPC longitudinal motion attitude control[J]. Marine Electric & Electronic Engineering, 2019, 39(S1): 32-37. |
 2022, Vol. 44
2022, Vol. 44
