2. 海军装备部,北京 100071;
3. 哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001
2. Navy Equipment Department, Beijing 100071, China;
3. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
随着海洋资源开发的不断深入,舰载机已不再局限于军事领域的应用。在民用领域,海洋平台、科考船等也配备了直升机、无人机等装备,但由此引发的飞机着舰瞬态冲击噪声问题也日益显著,突出表现为飞机着舰冲击载荷对船舶结构及舱室噪声的影响越来越大,并呈现出瞬时性、强线谱等特征。强烈的冲击噪声威胁到结构安全性、设备稳定性及人员舒适性等[1],因此,研究飞机着舰瞬态冲击噪声特性对提升舰船振动噪声治理水平具有重要意义。
在飞机着舰动力学研究方面[2-4],聂宏等[5]基于拦阻钩、拦阻装置等结构论述了舰载机着舰拦阻涉及到的关键动力学问题。刘湘一等[6]建立了直升机/舰船动态适配仿真模型,进行了直升机舰面降落的动响应分析,得出合理的操纵速率可减小对甲板冲击的结论。熊文强等[7]采用地面试验及刚柔耦合仿真模拟2种方法,全面分析了无人机着舰过程中拦阻力冲击下中机身结构的动态响应特性,为舰载机着舰分析以及机身结构响应预测提供依据。针对舰船瞬态噪声问题[8-9],众多学者基于理论分析和试验验证的方式开展了一系列研究。庞福振等[10]围绕破冰船舶破冰时的冲击噪声问题开展了实船试验,探究了实船冲击噪声分布规律,表明破冰冲击噪声呈现沿船长方向差异较大,沿吃水方向差异较小的特点。Annie和Germain[11]基于解析模型开展了冲击板的近场初始瞬态噪声研究,得出冲击板的瞬态噪声会受结构影响的结论。杨博[12]基于虚拟模态综合法研究了冲击载荷作用时间和冲击载荷的类型对结构振动速度和结构振动幅值的影响。以上研究主要针对着舰过程中机身结构相关的动力学问题,对于着舰冲击载荷对船舶瞬态冲击噪声问题研究较少。
飞机着舰过程中将与甲板发生碰撞,极短时间内产生巨大冲量,导致甲板剧烈振动,进而引发船舶的冲击噪声。飞机质量和着舰速度是影响瞬态冲击噪声的关键因素,飞机质量直接影响着舰瞬态作用力,着舰速度是载荷作用时长的决定性因素。因此,研究飞机着舰强冲击现象,探索瞬态冲击噪声特性规律,对于保障船舶舒适性及人员安全性具有重要意义。
本文基于显式动力学和瞬态边界元方法,以某船甲板截断模型为研究对象,在飞机着舰位置处施加三角脉冲波,模拟飞机着舰时的冲击载荷,开展载荷幅值、脉宽等特性参数对甲板瞬态冲击噪声的影响研究,为甲板瞬态冲击噪声的预报评估提供支撑。
1 瞬态冲击振动声辐射计算方法 1.1 瞬态冲击振动声辐射分析方法 1.1.1 显式动力学理论显式方法是将时间维度划分为许多微小的时间增量,采用中心差分法及对角化质量矩阵的方法进行结构动力学方程的求解[13],从而得到高精度的结果,对于解决瞬态动力学问题具有明显的优势,求解思路如下:
一般结构方程可写为
| $ {{M}} u+{{C}} u+{{K}} u=F(t)。$ | (1) |
式中:M为质量矩阵,C为阻尼矩阵,K为刚度矩阵,
| $ {\boldsymbol{M}} \ddot{u}=P-I。$ | (2) |
其中:P表示外力,I表示内力,P−I为作用在节点上的合力。加速度可以表达成与初始步长到t时刻相关的方程:
| $ \ddot{u}|_{(t)}=({\boldsymbol{M}})^{-1} (p-I)|_{(t)} 。$ | (3) |
在时域范围内,采用中心差分法对加速度进行积分,初始速度为上一步的速度与增量步中速度改变量之和,即
| $ \ddot{u}|_{\left(t+\frac{\Delta{t}}{2}\right)}=\ddot{u}|_{\left(t-\frac{\Delta{t}}{2}\right)}+\frac{\left(\left.\Delta t\right |_{(t+\Delta{t})}+\left.\Delta t \right|_{(t)}\right)}{2} \ddot{u}|_{(t)}。$ | (4) |
最终位移量即为初始位移与速度对时间积分之和:
| $ \left.u\right|_{(t+\Delta t)}=\left.u\right|_{(t)}+\left.\Delta t\right|_{(t+\Delta t)} \dot{u}|_{\left(t+\frac{\Delta t}{2}\right)}。$ | (5) |
至此得到结构响应方程,同时可以发现,上式仅与时间增量步Δt有关。
1.1.2 瞬态声学边界元方法本文研究中甲板瞬态辐射噪声是基于波动方程的边界元方法进行求解的。在小振幅条件下,声波声压p的控制方程为三维波动方程:
| $ \nabla^{2} p(Y, t)-\frac{1}{c^{2}} \ddot{P}\left(Y, t\right)=0 。$ | (6) |
式中:
| $ \begin{split} & C(Y) p(Y, t)+\int_{\varGamma} \int_{0}^{t} q^{*}(Y, t, X, \tau) p(X, \tau) {\rm{d}} \tau {\rm{d}} \varGamma= \hfill\\ &\iint_{\varGamma} \int_{0}^{t} p^{*}\left(Y, t_{2} X, \tau\right) q(X, \tau) {\rm{d}} k {\rm{d}} \varGamma 。\end{split} $ | (7) |
对场点Y的声压基本解在法向n求导,得到场点Y的声通量基本解:
| $ \begin{split}p^*_0(Y,t;X,\tau)=&\frac{\partial p^*(Y,t;X,\tau)}{\partial n}= \hfill\\ &\frac{1}{4\text{π} r}\left[\delta \left\{t-\frac{r}{c}-\tau\right\}+\frac{r}{c}\dot{\delta}\left\{t-\frac{r}{c}-\tau\right\} \right]\frac{\partial r }{\partial n} 。\end{split} $ | (8) |
对方程在时间和空间中进行离散,基于边界的声压和声通量解得求解域上的各点声压,结合结构的振动响应,可以得到边界上所有节点的声压:
| $ \begin{split} & C^n_p+\sum^{\bar n}_{m=1}\sum^{n_{\alpha}}_{\alpha=1}[\alpha (m)]H^{(n-m+1)} p^{(\alpha_g)}= \hfill\\ & \sum^{\bar n}_{m=1}\sum^{n_{\alpha}}_{\alpha=1}[\alpha(m)]G^{(n-m+1)}q^{(\alpha_g)} 。\end{split} $ | (9) |
式中:
| $ \begin{split} \hat {p}^n=& -\sum^{\bar n}_{m=n_i}\sum^{n_{\alpha}}_{\alpha=1}[\alpha (m)]H^{(n-m+1)} p^{(\alpha_g)}= \hfill\\ & \sum^{\bar n}_{m=1}\sum^{n_{\alpha}}_{\alpha=n_i}[\alpha(m)]_G^{(n-m+1)}q^{(\alpha_g)}。\end{split} $ | (10) |
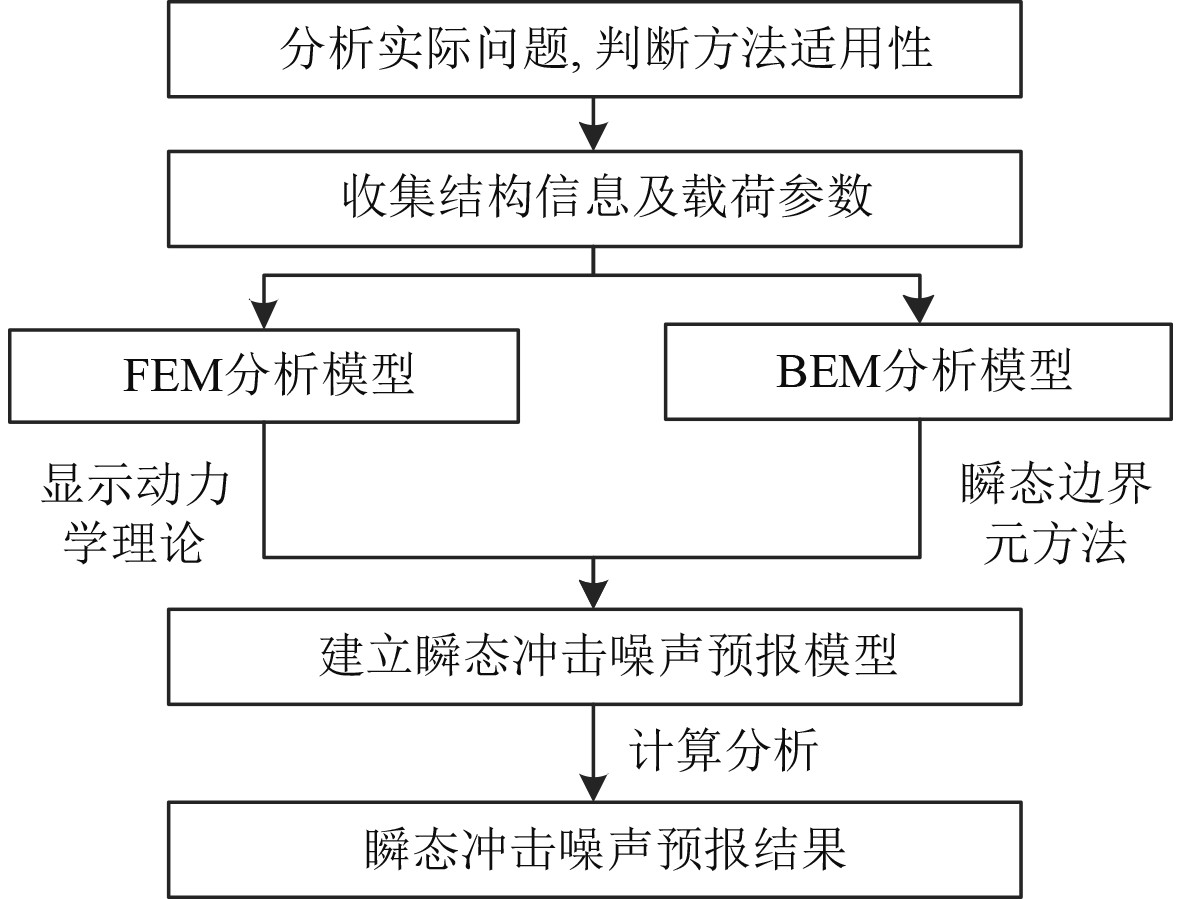
针对瞬态冲击噪声的预报评估需求,基于显式动力学理论和瞬态边界元方法,建立甲板瞬态冲击噪声预报方法及流程,如图1所示。
|
图 1 瞬态冲击噪声预报方法流程图 Fig. 1 The process diagram of transient impact noise prediction method |
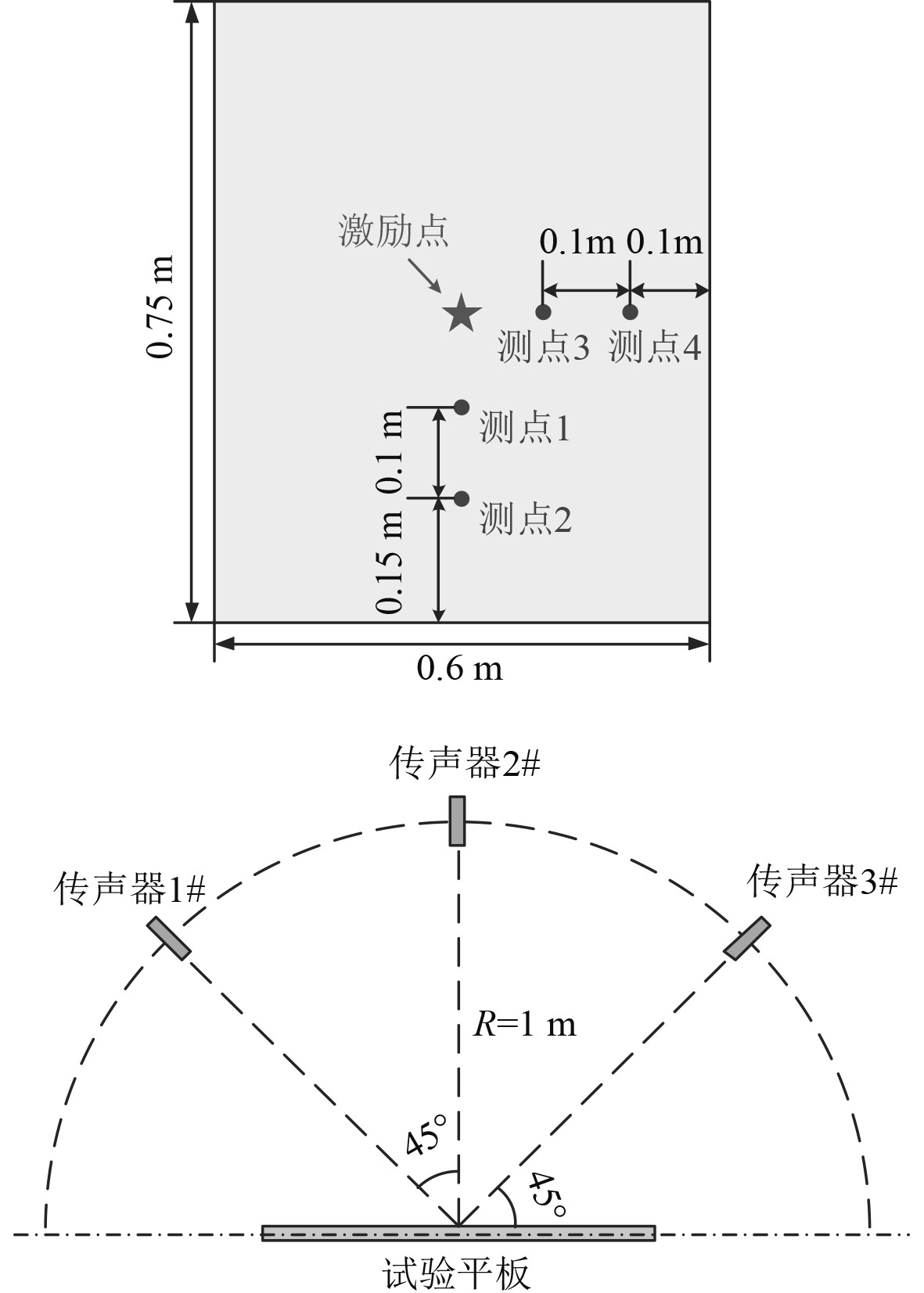
为验证瞬态冲击噪声预报方法的有效性,针对平板瞬态噪声开展试验和仿真研究。平板瞬态噪声试验模型长L=0.75 m,宽B=0.6 m,厚度D=3 mm,模型垂直于地面固定于模型架上,在模型表面布置4个加速度传感器。设置3个传声器高度与平板中心一致,传声器与模型中心距离均为1 m,保证相邻传声器之间以及传声器与平板所在平面之间夹角呈45°放置。试验主要采集在瞬态激励下板结构的振动加速度响应及瞬态噪声水平,采样频率20 kHz。
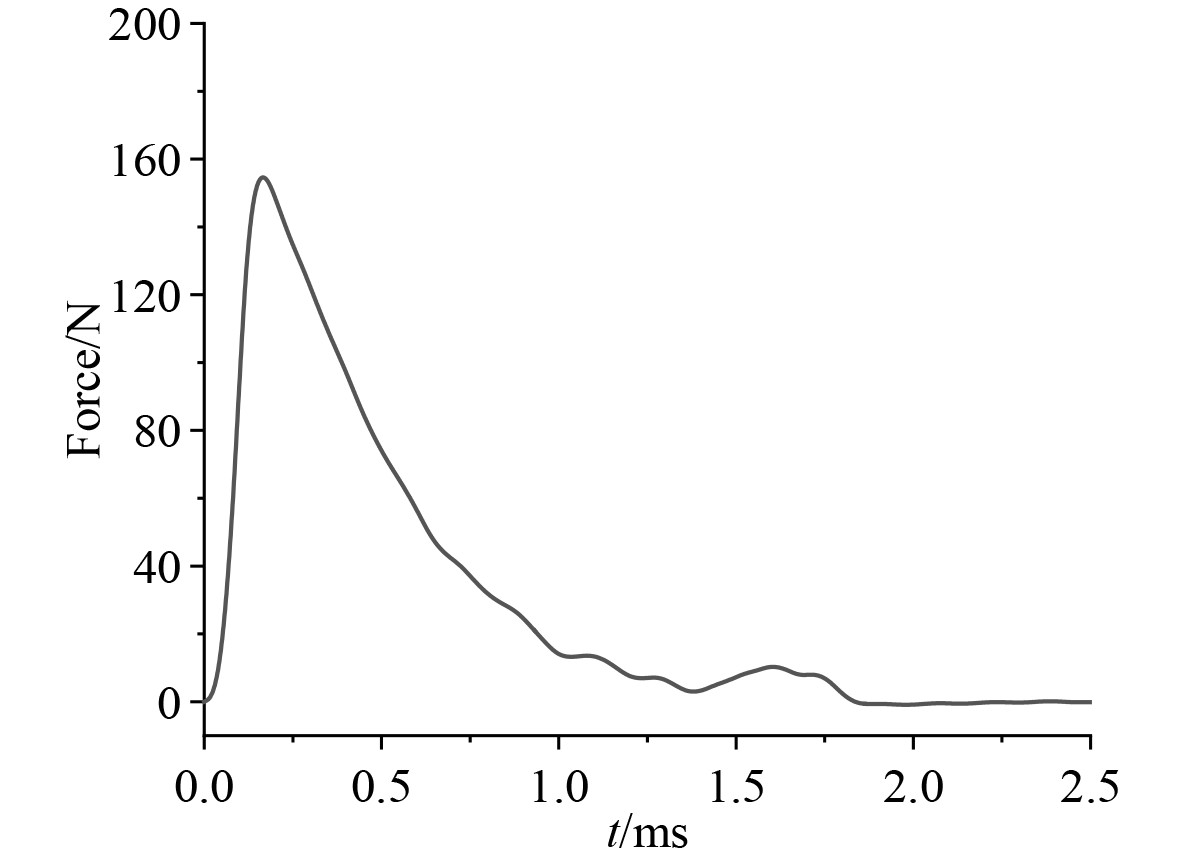
在Abaqus/Explicit和Virtual.Lab Acoustics环境中开展平板结构振动响应及瞬态冲击噪声仿真计算研究,建立与试验对应的仿真计算模型,定义材料密度ρ=7800 kg/m3,弹性模量E=210 GPa,泊松比μ=0.3,采用四角简支边界条件,施加试验过程中力传感器记录图2所示冲击载荷,设置与试验相同位置的激励点及考核点如图3所示,计算时长为1 s,分析步长
|
图 2 试验冲击时域载荷 Fig. 2 Time history curve of impact load |
|
图 3 激励点及考核点布置 Fig. 3 Layout of incentive point and observation points |
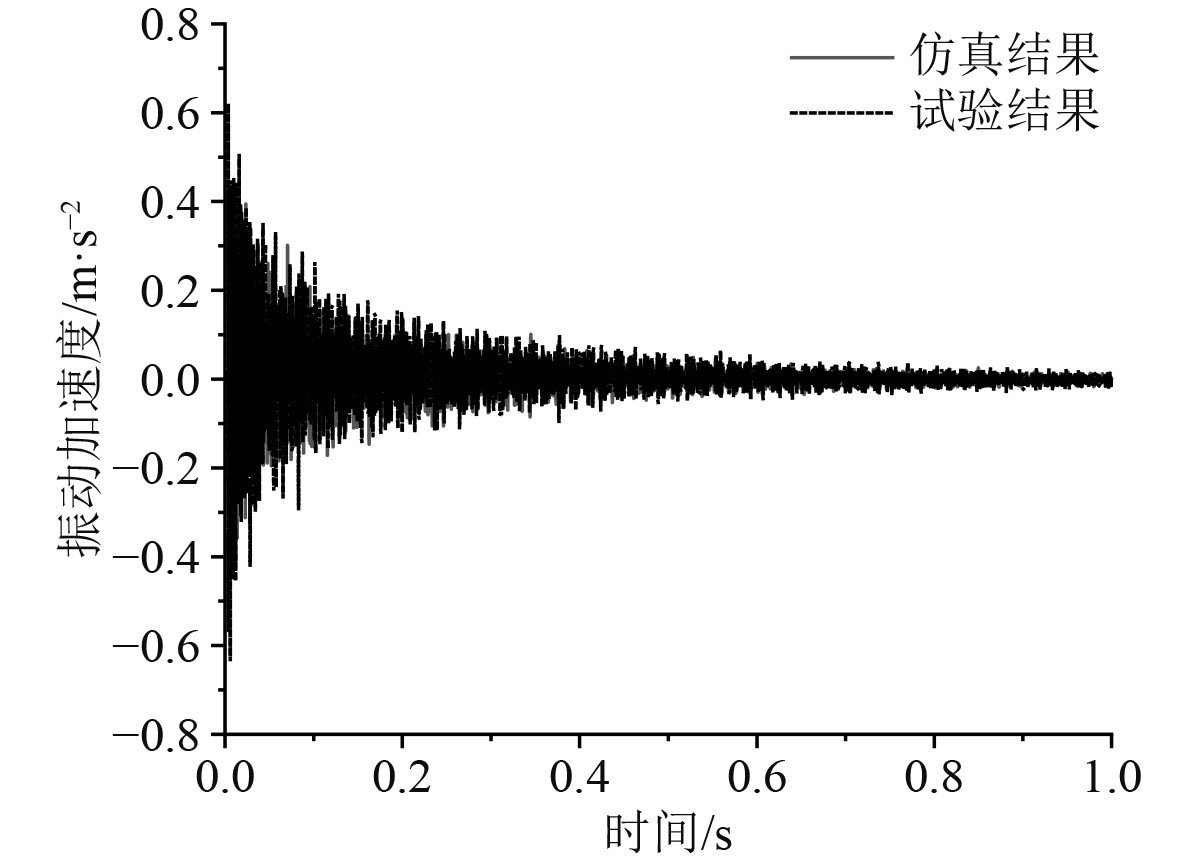
分析平板瞬态冲击试验和仿真计算结果,考核点数据所呈现规律相同,其中测点1和传声器2的时域数据如图4和图5所示。利用快速傅里叶变换(FFT)将时域结果处理为振动加速度级和辐射声压级的频谱曲线,振动加速度级、声压级参考值分别取为1×10−6 m/s2与2×10−5 Pa,对比如图6和图7所示。
|
图 4 振动加速度对比时域曲线 Fig. 4 Comparison of vibration in time domain |
|
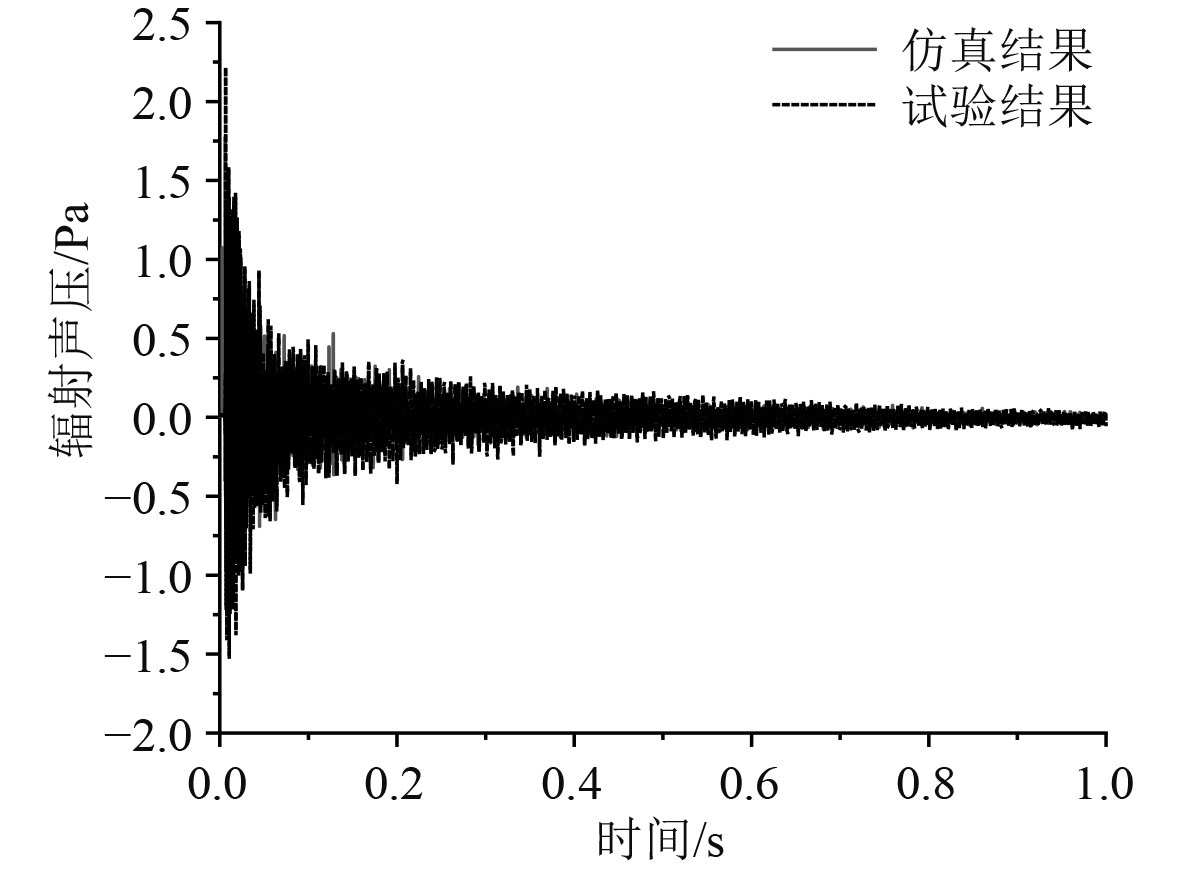
图 5 辐射噪声对比时域曲线 Fig. 5 Comparison of noise in time domain |
|
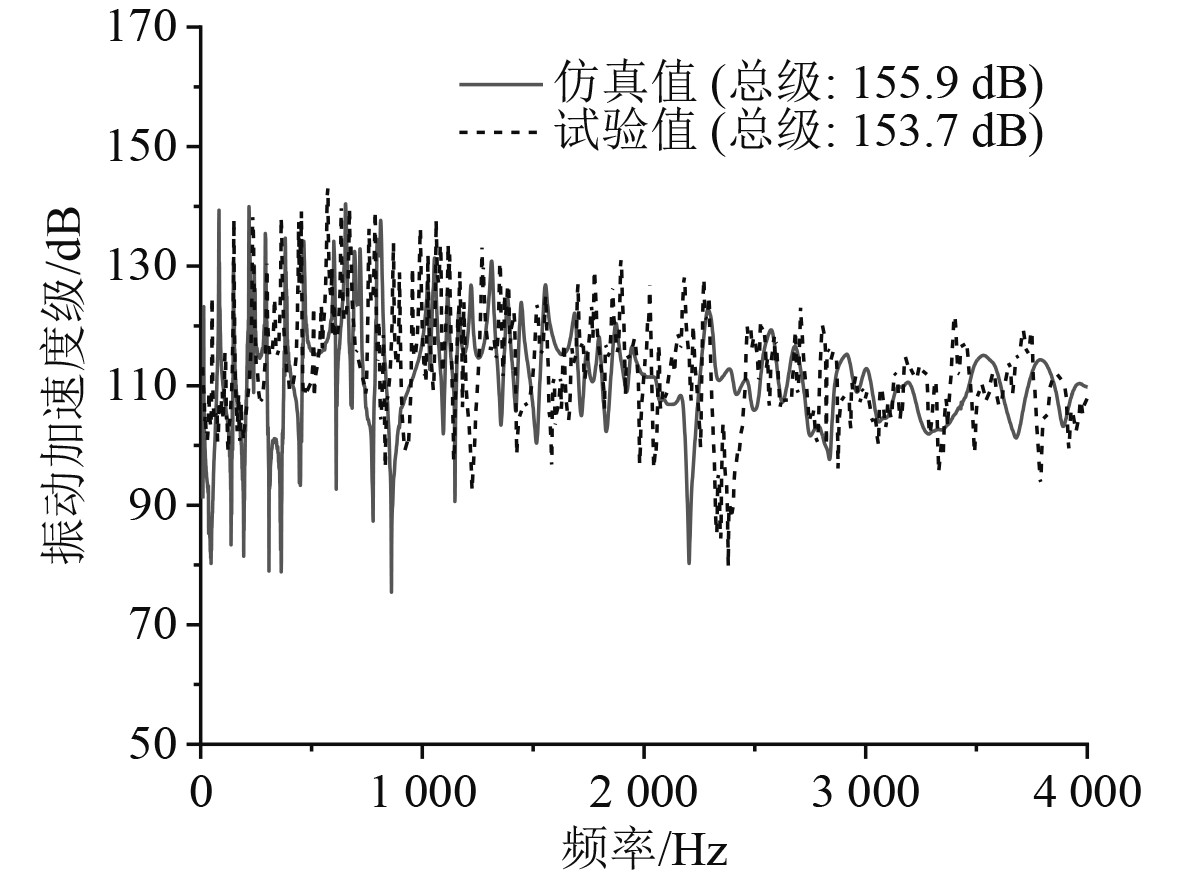
图 6 振动加速度对比频域曲线 Fig. 6 Comparison of vibration in frequency domain |
|
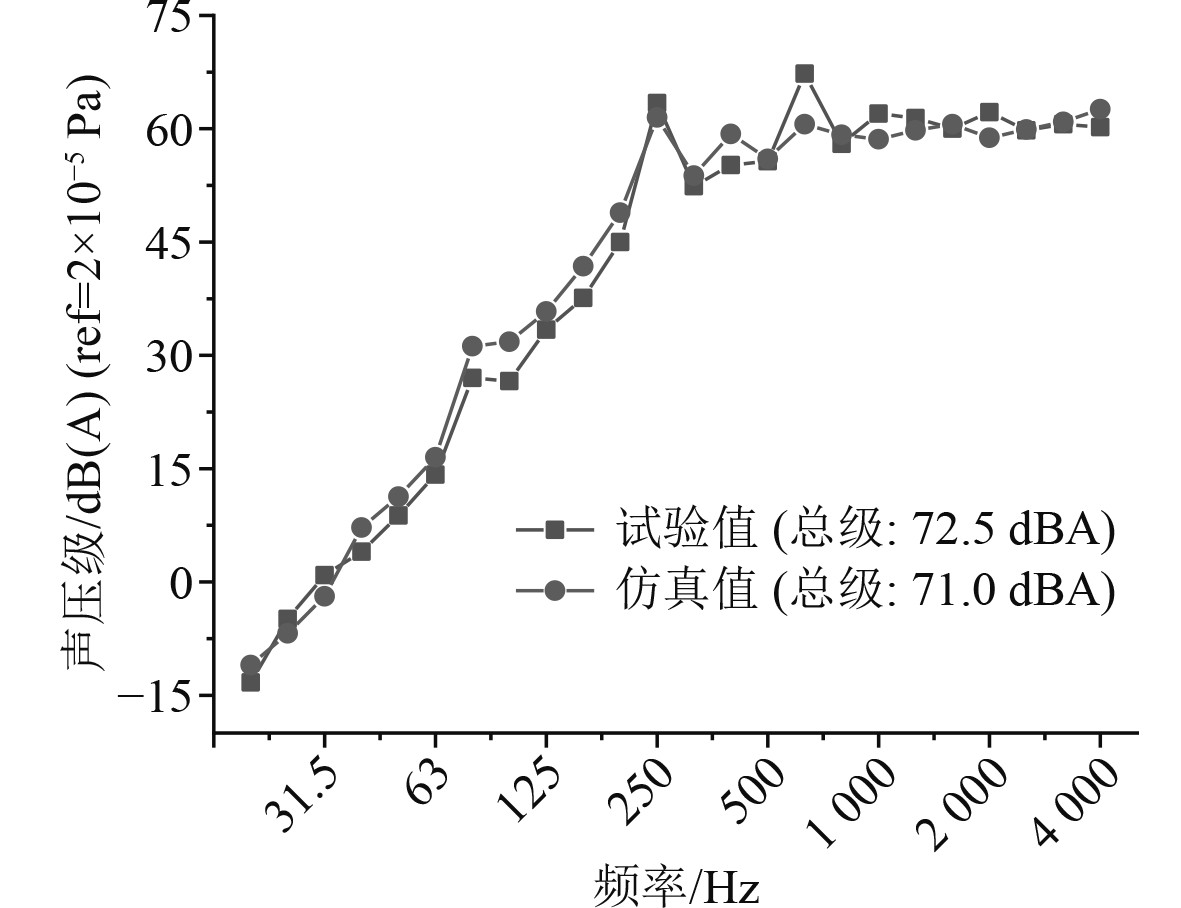
图 7 辐射噪声对比1/3oct曲线 Fig. 7 Comparison of noise in frequency domain |
分析对比结果可以发现,随着载荷的施加平板表面振动响应迅速增加,最高峰出现在0.2 s附近,随时间推移逐渐衰减,振动响应曲线在0.8s后趋于平稳。平板结构数值仿真结果与试验测试结果时频曲线趋势均保持一致,低频范围内线谱主要峰值频率、峰值大小吻合良好,振动加速度总级误差为2.2 dB、辐射噪声总级误差1.5 dBA,均满足工程精度要求。因此本文基于显示动力学和瞬态边界元方法进行的瞬态激励下结构振动响应和冲击辐射噪声的计算方法在充足数据支撑下可靠有效。
同时还可以发现,结构振动和辐射噪声结果峰值主要聚集在前2 kHz范围内,此后线谱逐渐稳定。因此后续分析与讨论将着重围绕中低频段振动噪声数据展开,振动加速度级、声压级参考值分别取为1×10−6 m/s2与2×10−5 Pa。
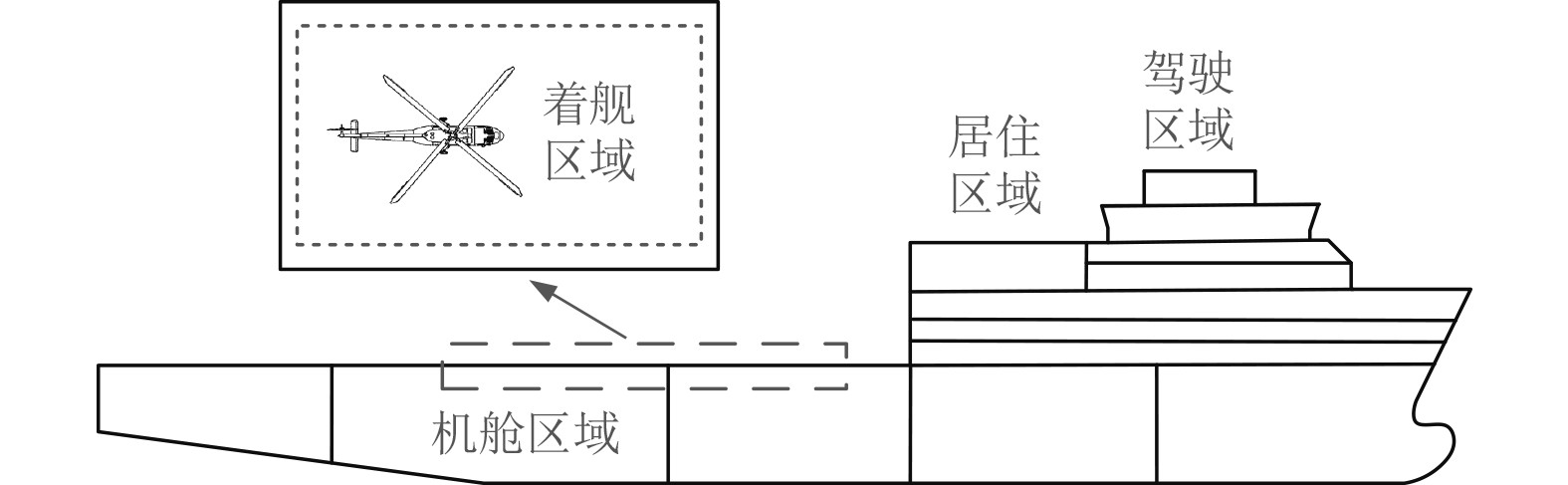
2 飞机着舰瞬态冲击噪声计算模型 2.1 飞机着舰简介飞机在船舶甲板上着陆是一个短暂而具有强冲击特性的过程。飞机会在如停机坪、降落跑道等指定位置降落,着舰时飞机对于甲板的作用力仅局限在某一范围区域内并不会涉及全船甲板结构,但由冲击引起的振动声辐射会影响甲板附属垂直空间区域及上层建筑的噪声水平,因此需对着舰特定区域甲板结构的振动噪声特性进行分析评估。
|
图 8 飞机着舰示意图 Fig. 8 Aircraft landing schematic |
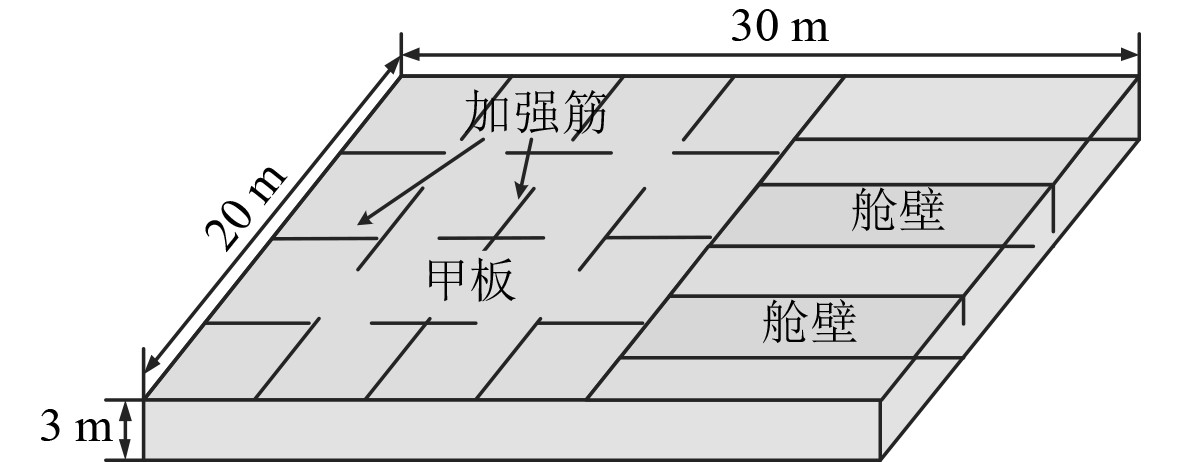
为探究飞机降落时产生的瞬态冲击对降落甲板辐射噪声的影响,参考某船飞机降落区域甲板参数,基于模型截断原理[14]建立如图9和图10所示的简化甲板截断数值模型。甲板长L=30 m,宽B=20 m,高H=3 m,横向纵向均匀布置加强筋,材料均为船用钢,密度ρ=7800 kg/m3,杨氏模量E=210 GPa,泊松比μ=0.3,为保证分析精度,结构网格尺寸满足单元长度
|
图 9 甲板截断模型示意图 Fig. 9 Truncation model of the deck |

|
图 10 甲板计算分析模型 Fig. 10 Analysis model of the deck |
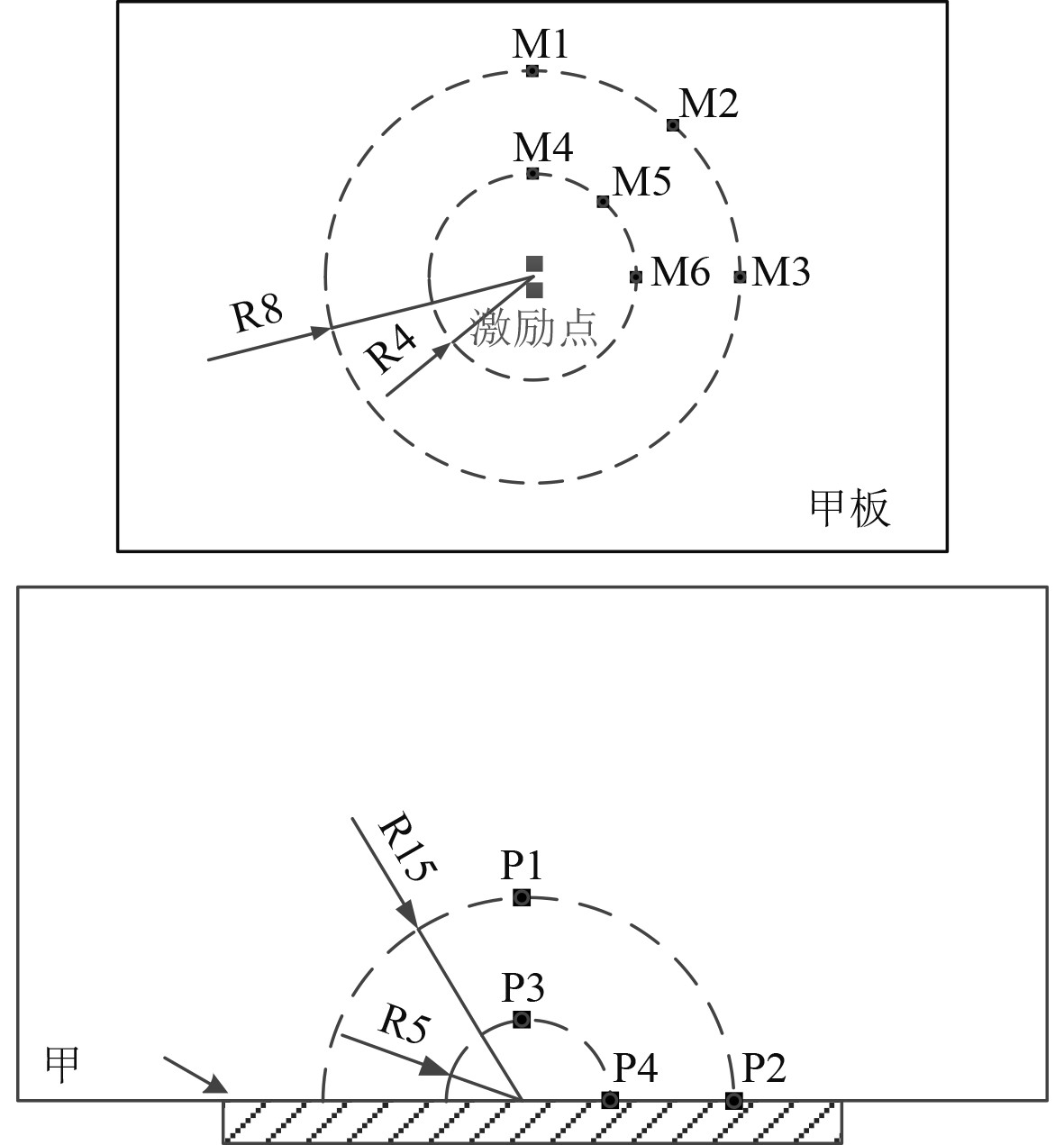
根据甲板尺寸、材料等参数,对数值模型进行离散。采用S4R、B31线性单元对有限元模型进行网格划分,并设置简支边界条件。考虑到瞬态边界元分析方法的特殊性,采用S3R单元对边界元模型离散。考虑到无人机主轮的对称性,故加载2个大小相同的垂向载荷作用于甲板中心两侧。根据甲板结构对称,在甲板表面设置振动加速度考核点M1-M6,在垂向法面距离甲板中心5 m,10 m处分别设辐射声压考核点P1~P4,振动及声压考核点布置如图11所示。
|
图 11 振动噪声考核点 Fig. 11 Observation points of vibration and sound pressure |
鉴于飞机着舰特点,结合飞机质量和着舰速度等因素,开展载荷特性分析工作。由于飞机种类、携带装备不同,导致飞机质量有所差异,从而影响着舰载荷幅值大小。同时在飞机降落时,起落架作为与甲板直接接触的唯一结构,而起落架材质、结构阻尼特性以及甲板防护措施均会影响飞机的着舰速度,因此建立起落架结构特性与着舰速度之间的联系,开展着舰速度对甲板结构声辐射影响具有一定工程意义。
为此选取具有典型工程意义的三角脉冲波作为瞬态载荷输入,三角波幅值与飞机自身质量直接相关,脉宽与降落速度存在联系。根据文献[15]计算公式,结合工程经验,估算出不同质量飞机降落时产生的冲击载荷,根据能量关系估算着舰时长,并以此作为载荷输入。开展三角波的脉宽和幅值大小对结构振动响应以及辐射噪声的影响研究,其中T为脉宽,载荷幅值出现在T/2时刻。三角波载荷在甲板瞬态冲击噪声计算分析内容如表1所示。
|
|
表 1 三角波载荷下甲板振动响应及冲击噪声计算工况 Tab.1 Calculation of deck vibration response and impact noise under triangular wave loading |
通过开展仿真计算工作,初步掌握了飞机着舰瞬态冲击噪声特性规律。在模型激励点处施加典型三角脉冲波,甲板结构振动响应随之产生并迅速达到峰值,此后随时间的推移响应逐渐衰减。由冲击引起的结构声辐射同样呈现上述时域规律,且在频谱曲线中随频率的升高辐射声压级逐渐降低,能量主要集中在低频范围内,同时冲击导致的空气噪声会在空间范围内传播。以图12所示甲板垂直空间截面为例,冲击噪声以结构激励点为中心向周围扩散,随距离的增加而降低,因此需对甲板垂直低空区域采取噪声防护措施。

|
图 12 甲板瞬态冲击噪声分布云图 Fig. 12 Transient impact noise distribution of the deck |
脉宽表征了脉冲载荷持续时间的长短,反映了飞机降落着舰时的速度大小。根据飞机起落架与降落甲板之间接触形式的不同,分别以脉宽为10 ms,20 ms,30 ms三种情况讨论甲板冲击噪声特性及规律,此时设定飞机质量M=700 kg。
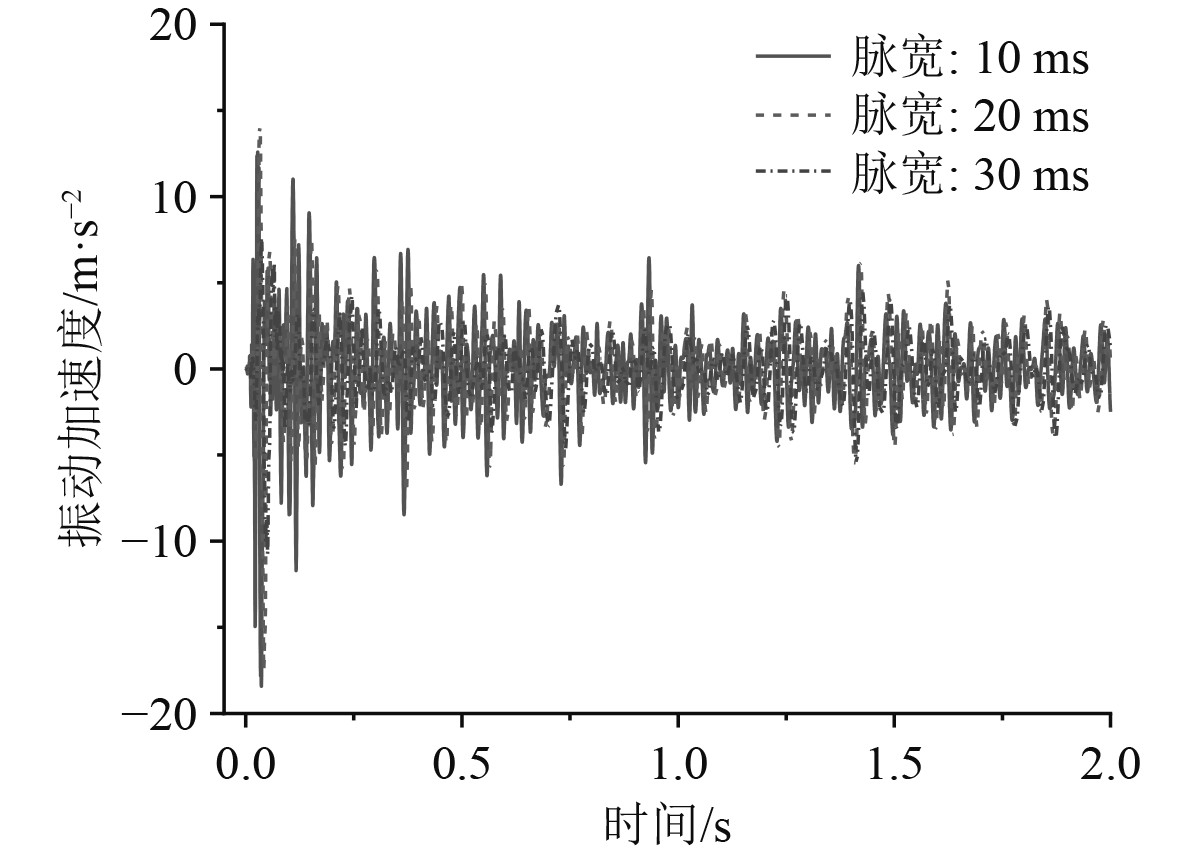
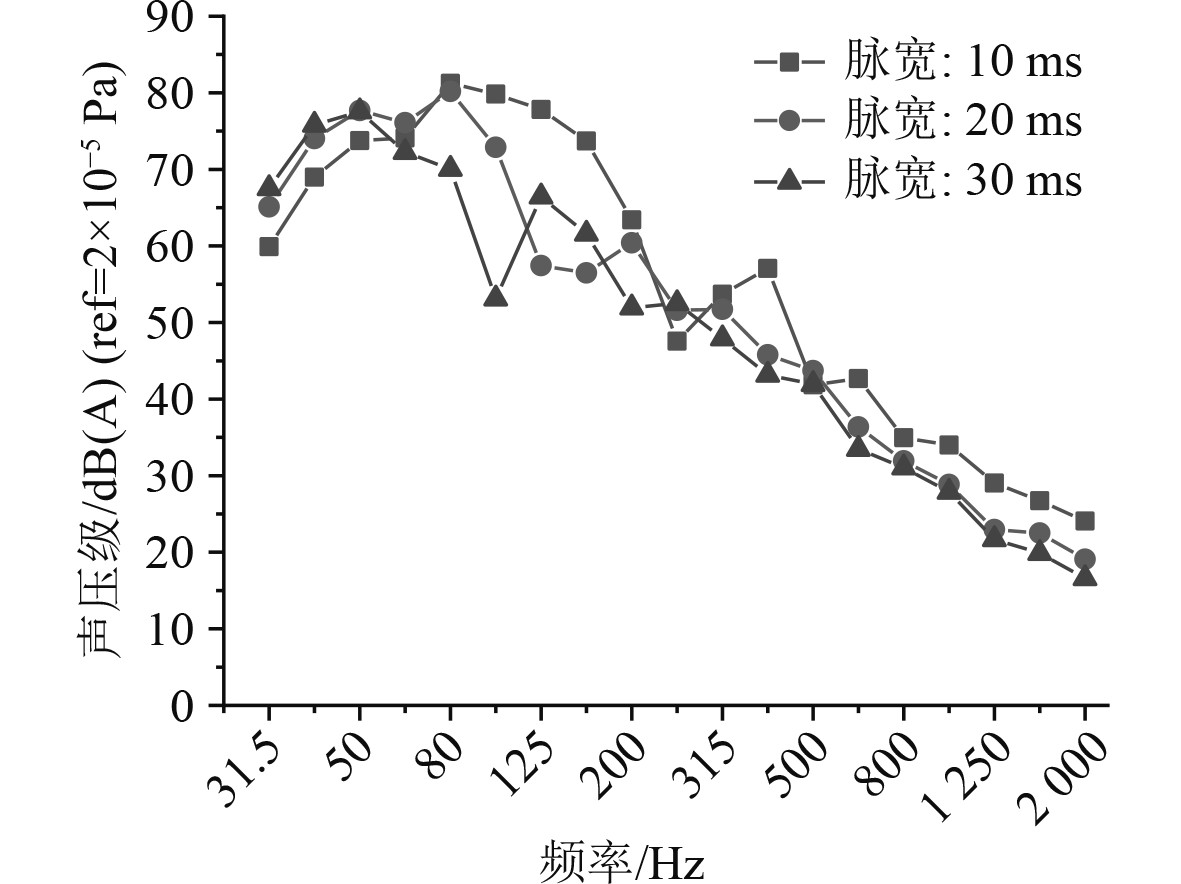
3.1.1 冲击载荷下结构振动响应分析首先开展甲板在瞬态激励下的振动响应分析。在激励点位置先后加载三角波脉冲载荷,得到典型考核点M2处响应曲线如图13所示,对该时域结果进行快速傅里叶变换(FFT),可得到M2考核点20 Hz~2 kHz频段内振动加速度频谱曲线。为了便于分析讨论,将计算结果转化为如图14所示的1/3倍频程曲线。
|
图 13 考核点振动加速度时域曲线 Fig. 13 Time-domain curve of vibration acceleration at observation points |
|
图 14 考核点振动加速度1/3oct曲线 Fig. 14 1 / 3oct curve of vibration acceleration at observation points |
可知,随着冲击载荷的施加,甲板表面考核点处的振动加速度迅速增加,在短时间内达到加速度峰值,随着载荷的衰减,考核点处的振动响应也逐渐减小。在载荷幅值相同的情况下,载荷脉宽的改变对甲板振动响应存在一定影响。随着脉宽的增加,振动加速度总级逐渐降低,脉宽T=10 ms时振动加速总级最高为128.2 dB,脉宽T=30 ms时振动加速总级最低为124.1 dB。
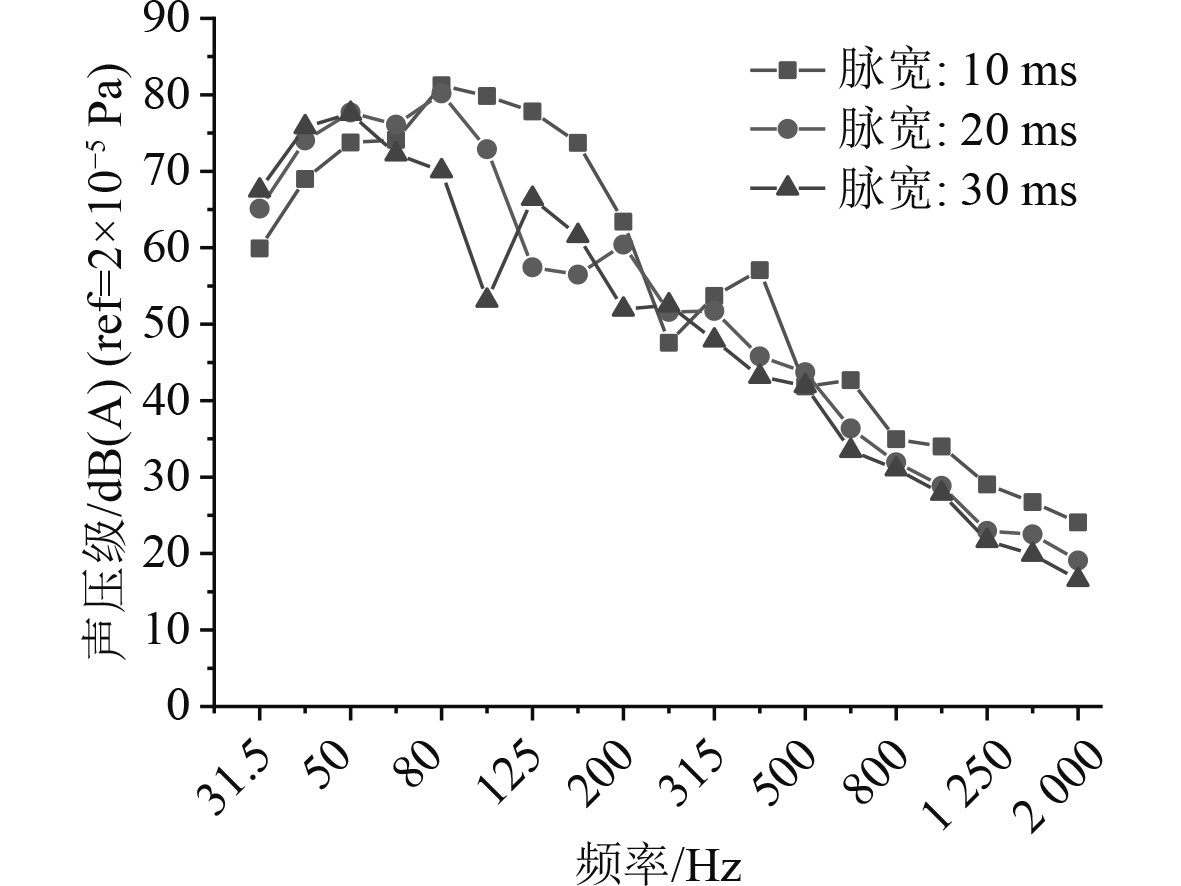
3.1.2 甲板瞬态冲击噪声分析将瞬态冲击下甲板振动响应计算结果作为瞬态边界元分析的数据输入,开展载荷脉宽对甲板瞬态冲击噪声的影响研究。提取P3考核点处的声压值,对时域结果作快速傅里叶变换,处理成1/3倍频程结果。考核点在31.5 Hz~2 kHz频段内声压级曲线如图15所示。
|
图 15 辐射声压级频谱曲线 Fig. 15 The spectrum curve of SPL |
对计算结果A计权处理,3种工况曲线均呈现处低频大高频小的特点,表明在载荷作用下的冲击噪声能量主要分布在低频范围内。随着飞机着舰速度降低,冲击载荷脉宽增加,甲板瞬态辐射噪声逐渐减小,脉宽T=10 ms时,噪声总级最大为85.7 dBA,脉宽T=30 ms时,噪声总级最小为81.3 dBA。
3.2 载荷幅值对甲板冲击噪声的影响飞机自身质量是直接影响冲击载荷大小的重要因素,将质量为300 kg,700 kg,1 000 kg飞机着舰产生的冲击载荷简化为幅值为10 kN,20 kN,30 kN的三角波载荷加载在考核点上[15],并设定载荷脉宽T=20 ms,开展瞬态冲击噪声研究。
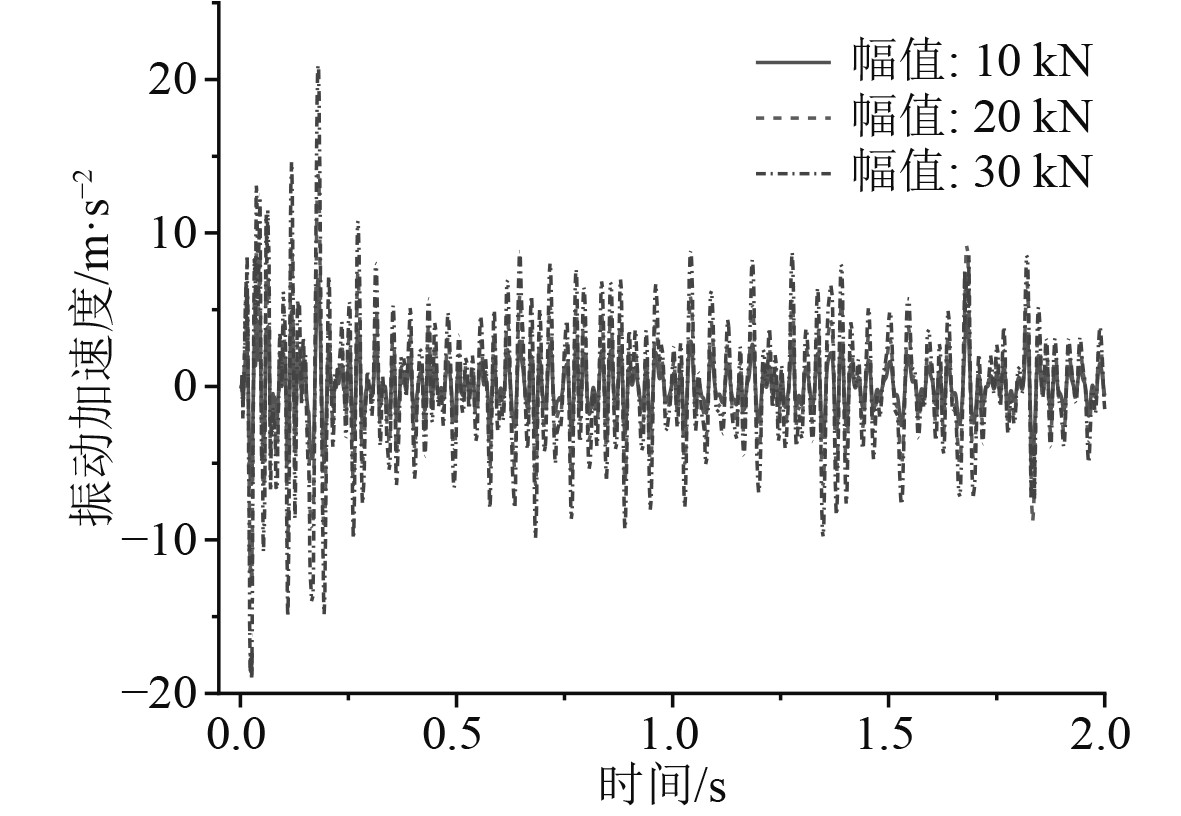
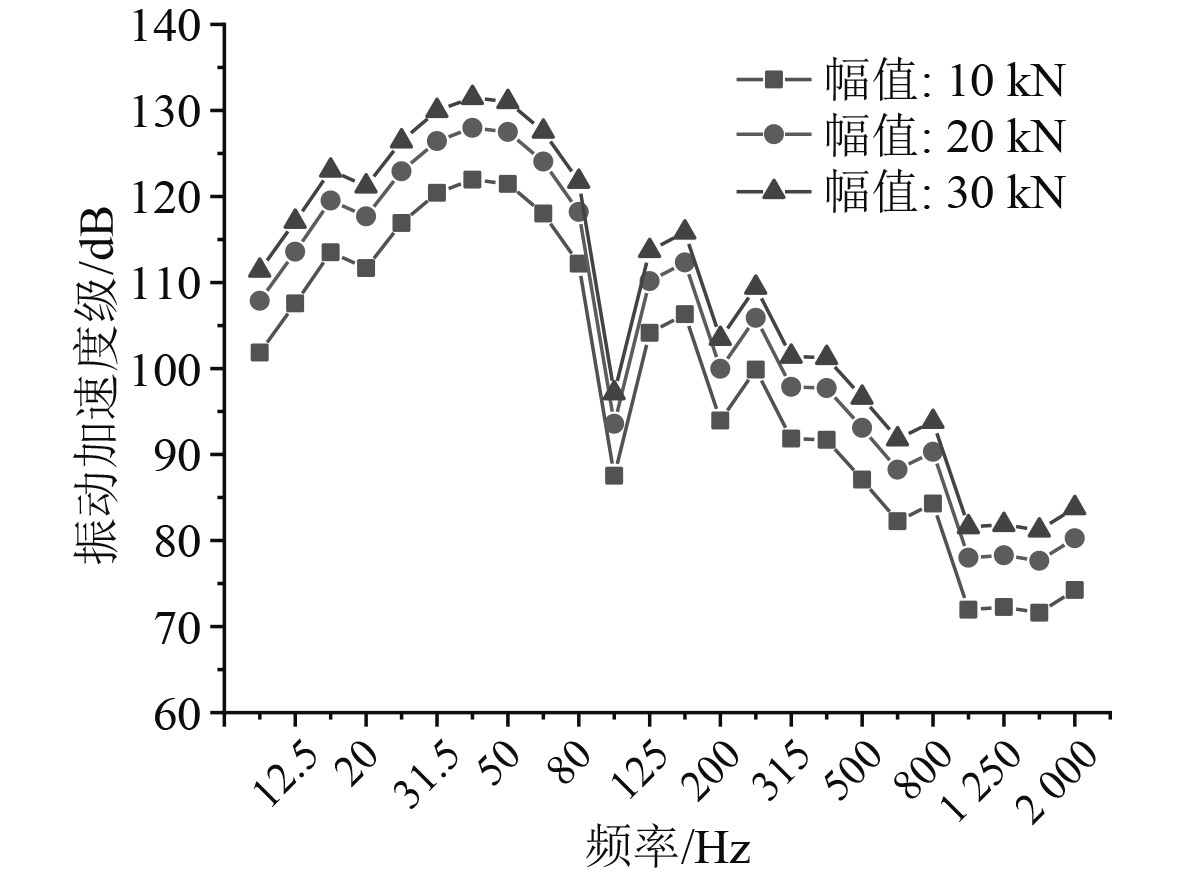
3.2.1 冲击载荷下结构振动响应分析针对甲板结构进行动力学响应分析。对时域振动加速度结果进行快速傅里叶变换,得到M4考核点20 Hz~2 kHz频率范围内的计算结果,并绘制1/3倍频程曲线,如图17所示。
|
图 16 考核点振动加速度时域曲线 Fig. 16 Time-domain curve of vibration at observation points |
|
图 17 考核点振动加速度级1/3oct曲线 Fig. 17 1/3 oct curve of vibration at observation points |
可知,在施加不同幅值载荷后,考核点振动加速度曲线趋势一致,呈现低频大高频小的规律。随着施加载荷的幅值逐渐变大,考核点振动响应也随之变大,因此飞机自身质量与降落时甲板的振动响应水平呈正相关,飞机质量M=100 kg时甲板的振动加速度总级最高,为137.3 dB。
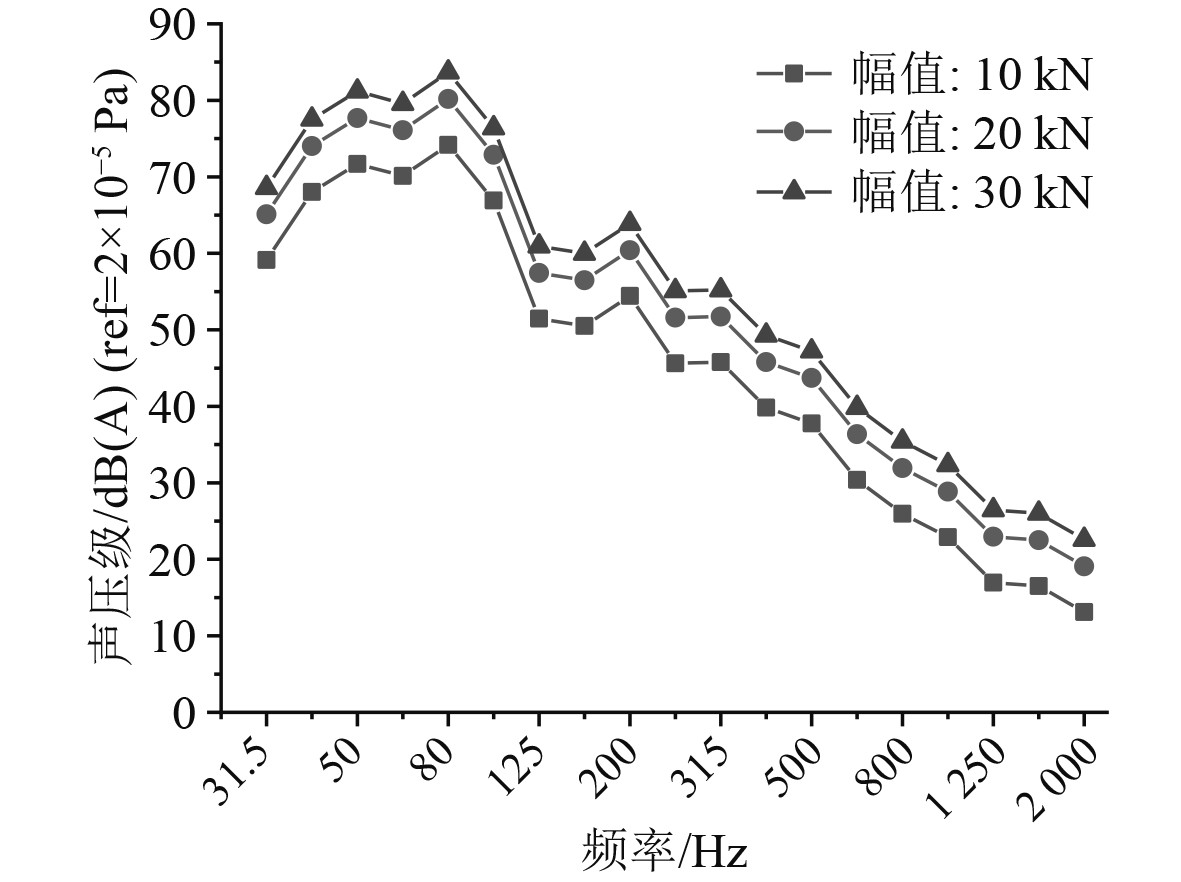
3.2.2 甲板瞬态冲击噪声分析基于甲板振动加速度响应结果,在Virtual.Lab Acoustics中开展幅值大小对甲板瞬态冲击噪声的影响分析,图18为P3考核点31.5 Hz~2 kHz频段内辐射声压级1/3倍频程曲线。
|
图 18 辐射声压级频域曲线 Fig. 18 The spectrum curve of SPL |
分析考核点1/3倍频程数据发现,飞机质量改变所引起的载荷幅值变化,对曲线趋势影响不大,在中高频范围内甲板辐射声压级均随频率增加而不断减小,整体呈现低频大高频小的趋势。载荷幅值的增加对甲板辐射噪声声压级影响明显,当飞机质量M=1 000 kg时,声压总级达到最高为87.5 dBA,飞机质量M=300 kg时最低是78.1 dBA。
4 结 语为实现飞机着舰过程中甲板瞬态冲击噪声预报评估,提出基于显示动力学理论和瞬态边界元分析的预报分析方法,建立了甲板在冲击载荷下瞬态辐射噪声预报流程,以工程典型三角脉冲波作为输入载荷,开展载荷脉宽、幅值对甲板冲击噪声的影响分析,从而探究飞机着舰时着舰速度和飞机质量对甲板冲击噪声的影响程度,结论如下:
1)基于显示动力学和瞬态边界元分析方法进行冲击噪声预报分析是有效可行的,计算结果与试验误差均小于3 dBA,计算精度满足工程要求;
2)飞机着舰速度和飞机自身质量是影响着舰瞬态冲击噪声水平的重要因素,甲板瞬态冲击噪声随着舰速度的增加而增大,随飞机质量的减小而逐渐降低;
3)甲板冲击噪声整体呈现低频大高频小的趋势,声振能量主要分布在低频范围内,因此在实际工程应用中,需结合规范要求对甲板开展低频噪声防护工作。
| [1] |
丁猛, 杨阳, 黄建松. 美军航母飞行甲板噪声水平及防护措施分析[J]. 舰船科学技术, 2021, 43(17): 182-185. |
| [2] |
齐龙舟, 冯和英, 彭叶辉, 等. 舰载机发动机冲击射流温度场及噪声特性分析[J]. 中国舰船研究, 2021, 16(3): 17-23. |
| [3] |
贾玉红. 起落架着陆冲击载荷及减震性能分析[C]//北京力学会第11届学术年会论文摘要集. 2005: 131−133.
|
| [4] |
梁宵. 舰载直升机助降着舰动力学特性研究 [D].南京: 南京航空航天大学, 2019.
|
| [5] |
聂宏, 彭一明, 魏小辉, 等. 舰载飞机着舰拦阻动力学研究综述[J]. 航空学报, 2014, 35(1): 1-12. |
| [6] |
刘湘一, 徐广, 吴靖, 等. 直升机着舰降落操纵与动态响应研究[J]. 飞行力学, 2021, 1-6. |
| [7] |
熊文强, 张闰, 张晓晴, 等. 舰载无人机拦阻着舰中机身冲击响应分析[J]. 航空学报, 2019, 40(12): 97-108. |
| [8] |
李应刚, 陈天宁, 王小鹏, 等. 圆柱碰撞冲击噪声理论分析与数值仿真[J]. 振动与冲击, 2014, 33(15): 162-166+173. |
| [9] |
余桐奎, 刘文帅, 于树华, 等. 舰船瞬态噪声测试分析方法[J]. 哈尔滨工程大学学报, 2017, 38(9): 1365-1372. |
| [10] |
庞福振, 马建强, 李海超, 等. 船舶破冰冲击噪声试验研究[J]. 华中科技大学学报:自然科学版, 2017, 45(12): 107-111+117. |
| [11] |
OSTIGUY R G. Propagation of the initial transient noise from an impacted plate [J]. Journal of Sound and Vibration, 2007.
|
| [12] |
杨博. 冲击载荷作用下舱室噪声预报方法研究 [D].哈尔滨: 哈尔滨工程大学, 2011.
|
| [13] |
庞福振, 李海超, 王雪仁, 等. 船舶结构振动噪声时域预报方法研究[J]. 船舶力学, 2021, 25(05): 659-669. DOI:10.3969/j.issn.1007-7294.2021.05.015 |
| [14] |
庞福振. 船舶结构噪声截断模型数值预报方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [15] |
彭兴宁, 吴有生. 飞机轮载作用下的甲板动响应[J]. 中国造船, 1996(2): 7. |
 2022, Vol. 44
2022, Vol. 44
