0 引　言

近年来，随着复合材料研制技术的快速发展，复合加筋板以其强度高、重量轻以及良好的声学性能等优势日益广泛应用于航空航天、船舶工程等领域。加筋板作为飞机、舰船以及潜艇上的一种典型形式结构，是重要的振动和噪声辐射源。因此，研究复合材料加筋板结构的振动和声辐射机理，可为结构的低噪声设计奠定理论基础。

针对匀质周期加筋板壳结构的声辐射问题已有不少研究。Mace^[1]修正了Greenspon^[2]采用的方法，给出了点力作用下流体负载的双周期平行加筋板水下声辐射预报方法，然后又进一步将该方法拓展，研究了正交加筋板的声辐射^[3]，但仅考虑了加强筋的等效拉力作用。Burroughs^[4-5]将 Mace工作拓展到2组环肋加强无限长圆柱壳的声辐射，指出相似物理特性的有限长和无限长圆柱壳的声辐射具有很好的一致性。吴文伟^[6]应用傅里叶变换技术给出了等间距相同加强筋平板辐射声压解析表达式，该表达式对平板结构适用于所有频段，对壳体结构则适用于高于环频率的频段。Mead^[7]研究了在流体载荷作用下正交加筋板的自由波传播，指出在周期结构中亚声速谐波能辐射声，在环频率以上，柱壳和平板有相似的声辐射特性^[8-9]。Maxit^[10]充分考虑了加强筋的弯曲和扭转运动，利用离散Fourier变换方法建立了平行加筋各向同性薄板振动和声辐射模型。Yin^[11-12]在加筋复合板壳方面的工作具有开创性，基于经典层合板理论（CLPT），分别针对2组平行筋加强层合板结构以及2组环肋加强复合圆柱壳结构，建立了远场声辐射模型，并采用位移螺旋波谱亮点的形式阐述了波数转换效应，但忽略了复合材料横向剪切变形和转动惯量。在此基础上，Cao^[13-14]采用一阶剪切变形理论（FSDT），分析了加筋层合板壳结构的水下声辐射特性，研究表明在中高频段范围必须考虑剪切变形影响。

目前围绕周期加筋复合板壳结构的相关研究主要基于CLPT和FSDT展开，本文基于分层理论进一步讨论剪切变形加筋层合板的远场声辐射特性。首先基于分层理论以及对流波动方程，建立双周期加筋层合板流固耦合运动方程，利用傅里叶变换方法和泊松比公式，求解波数域位移解析解，并结合稳相法，给出远场声压解析表达式。通过各向同性周期加筋板算例验证理论模型有效性，并系统研究不同参数对加筋复合板的远场声辐射特性影响。

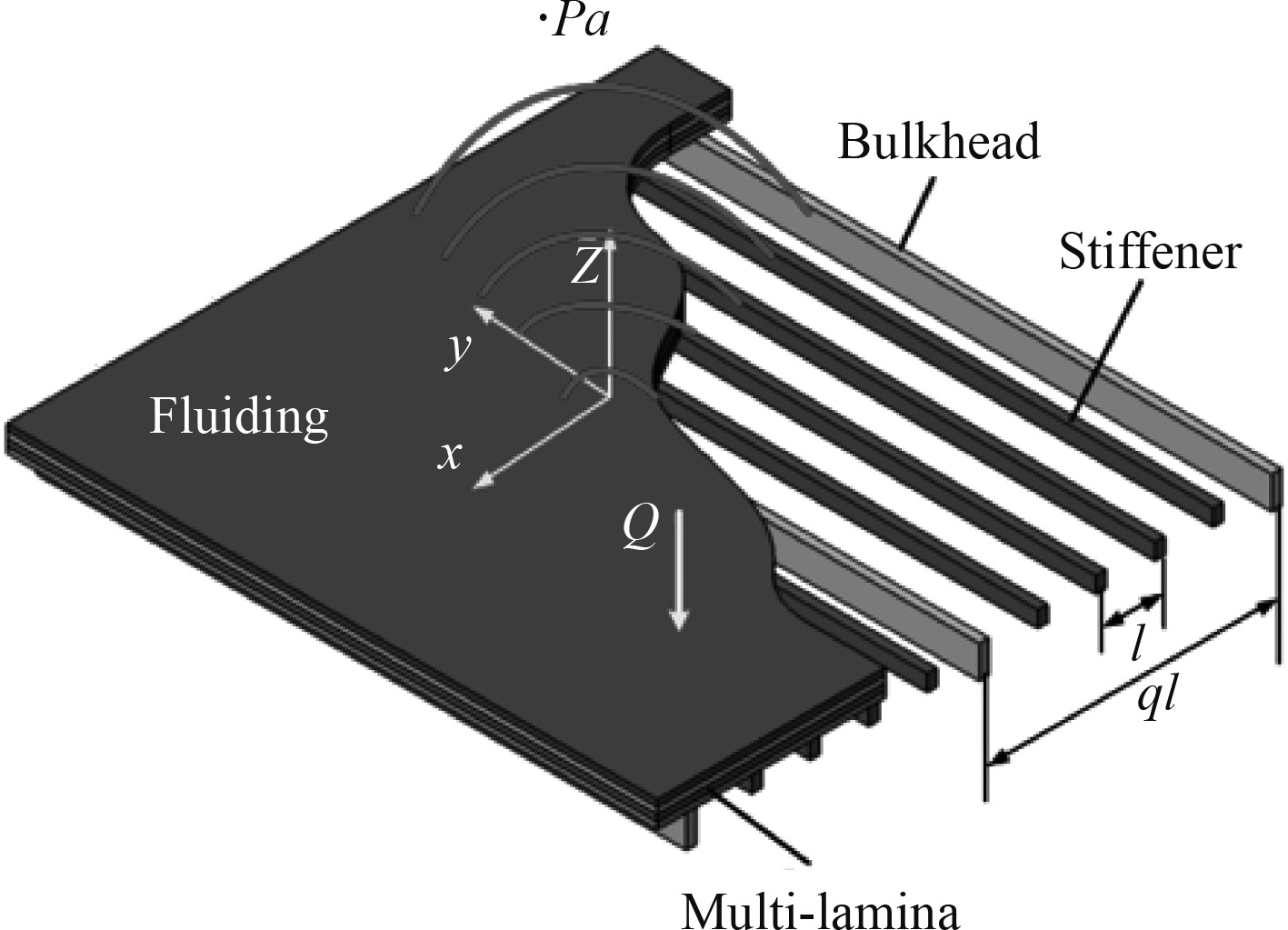
1 理论分析

2组平行于y轴的周期加强复合材料层合板结构如图1所示。l和ql分别为相邻小筋和相邻大筋的间距；x-y平面位于层合板中面位置，假设下半空间(z<0)为真空，上半空间z>0为水域，P_o为流体密度，C_o流体声速；Pa为远场声压点，Q为简谐激振力幅值，简谐时间项e^–jωt将被省略。

1.1 流体载荷

加筋复合板上半空间内声场声压 $ {P_a}\left( {x,{\text{ }}y,{\text{ }}z} \right) $ 满足Helmholtz方程：

$ c_0^2\nabla {p_a} + \omega _1^2{p_a} = 0 。$

(1)

声压在流固交界面上满足如下边界条件：

$ {\left. {\frac{{\partial {p_a}}}{{\partial z}}} \right|_{z = 0}} = \omega _1^2{\rho _0}w 。$

(2)

式中： $ {\nabla ^2} $ 为拉普拉斯算子；w为结构横向位移。

函数 $ f\left( {x,y} \right) $ 关于空间位置的Fourier变换及其逆变换定义为：

$ \tilde f\left( {\alpha ,\beta } \right) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {\int {f\left( {x,y} \right)} } } {e^{i(\alpha x + \beta y)}}{\rm{d}}x{\rm{d}}y，$

$ f\left( {x,y} \right) = \frac{1}{{4{\pi ^2}}}\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {\int {\tilde f\left( {\alpha ,\beta } \right)} } } {e^{ - i(\alpha x + \beta y)}}{\rm{d}}\alpha {\rm{d}}\beta。$

(3)

利用波数变换法，可由方程（1）和方程（2）得到均匀流中流固耦合面的波数域声压

$ {\tilde P_a}(\alpha ,\beta ,0) = - {\rho _0}\omega _1^2\tilde w(\alpha ,\beta )/{\lambda _1}(\alpha ,\beta )，$

(4)

$ {\lambda _1}(\alpha ,\beta ) = \left\{ \begin{gathered} \sqrt {{\alpha ^2} + {\beta ^2} - k_1^2} ,{\alpha ^2} + {\beta ^2} > k_1^2，\hfill \\ i\sqrt {k_1^2 - {\alpha ^2} - {\beta ^2}} ,{\alpha ^2} + {\beta ^2} < k_1^2。\hfill \\ \end{gathered} \right. $

(5)

式中：w₁为计算频率；k₁=w₁/c_o为流体波数； $ \alpha $ 和 $ \beta $ 分别为声波在x及y方向上的波数。

1.2 两类加筋作用力

采用欧拉-伯努利梁运动方程进行傅里叶变换，并利用周期特征以及泊松公式，最终得到2组平行加强肋的作用力。

第一类小筋作用力表达式为：

$ {\tilde P_f}\left( {\alpha ,\beta } \right) = \left( {\frac{{{K_f}}}{l}} \right)\sum\limits_{n = - \infty }^{n = + \infty } {\tilde w\left( {\alpha - 2n\text{π} /l,\beta } \right)}，$

(6)

第二类强筋作用力表达式为：

$ {\tilde P_b}\left( {\alpha ,\beta } \right) = \left( {\frac{{{K_b} - {K_f}}}{{ql}}} \right)\sum\limits_{n = - \infty }^{n = + \infty } {\tilde w\left( {\alpha - 2n\text{π} /l,\beta } \right)} ，$

(7)

$ {K_f} = {E_f}{I_f}{\beta ^4} - {\rho _f}{A_f}{\omega ^2},{K_b} = {E_b}{I_b}{\beta ^4} - \rho {}_b{A_b}{\omega ^2}。$

(8)

式中： $ {E_f}{I_f} $ 和 $ {\rho _f}{A_f} $ 分别为第一类小筋的弯曲刚度及单位线质量； $ {E_b}{I_b} $ 和 $ {\rho _b}{A_b} $ 分别为第二类强筋的弯曲刚度及单位线质量。

1.3 简谐点力作用下加筋复合板的波数域位移

由线性分层位移模型，建立简谐点力 $ {\tilde P_e} = Q{e^{ - i\left( {\alpha {x_0} + \beta {y_0}} \right)}} $ 作用下加筋复合结构的平衡运动方程；并对方程进行傅里叶变换，得到波数域内的表达式如下：

$ \begin{split} &\left[ {\begin{array}{*{20}{c}} {\tilde L_{11}^{N \times N}}&{\tilde L_{12}^{N \times N}}&{\tilde L_{13}^{N \times 1}} \\ {\tilde L_{21}^{N \times N}}&{\tilde L_{22}^{N \times N}}&{\tilde L_{23}^{N \times 1}} \\ {\tilde L_{31}^{1 \times N}}&{\tilde L_{32}^{M \times N}}&{\tilde L_{33}^{1 \times 1}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\tilde u}^{N \times 1}}} \\ {{{\tilde v}^{N \times 1}}} \\ {\tilde w} \end{array}} \right\} = \hfill\\ &\left\{ {\begin{array}{*{20}{c}} {{{[0]}^{N \times 1}}} \\ {{{[0]}^{N \times 1}}} \\ {[{{\tilde P}_e} - {{\tilde P}_a} - {{\tilde P}_b} - {{\tilde P}_f}]} \end{array}} \right\}。\end{split}$

(9)

式中各表达式具体参见文献[15]。

复合板横向波数域位移 $ \tilde w(\alpha ,\beta ) $ 可进一步化简得到

$ \tilde w(\alpha ,\beta ) = ({\tilde P_e} - {\tilde P_a} - {\tilde P_b} - {\tilde P_f})/\tilde Ks(\alpha ,\beta ) 。$

(10)

其中：

$ \tilde Ks(\alpha ,\beta ) = {\left( {{\rm{det}}\left(\left[ \begin{gathered} \tilde L_{11}^{N \times N}\;\tilde L_{12}^{N \times N} \hfill \\ \tilde L_{21}^{N \times N}\;\tilde L_{22}^{N \times N} \hfill \\ \end{gathered} \right]\right)/{\rm{det}}(\tilde L)} \right)^{ - 1}} ，$

(11)

$ \tilde Ks(\alpha ,\beta ) $ 为板的动刚度。

将式（4）、式（6）和式（7）代入方程（10），联立求解并化简可得波数域位移解，得

$ \begin{split} \tilde w\left( \alpha \right) =& F\left( \alpha \right) - \left\{ {G{P_0}(\alpha ) + \frac{{H\displaystyle\sum\limits_{r = 0}^{q - 1} {\frac{{{P_r}(\alpha )}}{{G \times Y{b_r}(\alpha )}}} }}{{\left\{ {1 + H\displaystyle\sum\limits_{r = 0}^{q - 1} {\frac{{{Y_r}(\alpha )}}{{1 + G \times {Y_r}(\alpha )}}} } \right\}}}} \right\} \hfill \\ & {\raise0.7ex\hbox{${}$} \mathord{\left/ {\vphantom {{} {\left\{ {S\left( \alpha \right) \times (1 + G \times {Y_0}\left( \alpha \right))} \right\}}}}\right.} \hbox{${\left\{ {S\left( \alpha \right) \times (1 + G \times {Y_0}\left( \alpha \right))} \right\}}$}} \hfill。\\[-10pt] \end{split} $

(12)

式中： $ F\left( \alpha \right) = {\tilde p_e}/S\left( \alpha \right) $ , $ S\left( \alpha \right) = \tilde Ks(\alpha ,\beta ) $ $ - \omega _1^2{\rho _0}/{\lambda _1} $ , $ G = {K_f}/l $ , $ H = ({K_b} - {K_f})/ql $ , $e = 2\text{π} /l$ , ${P_r}(\alpha ) = \displaystyle\sum\limits_{m = - \infty }^\infty F \Biggr(\alpha - \dfrac{{er}}{q} - em\Biggr)$ , ${Y_r}(\alpha ) = \displaystyle\sum\limits_{m = - \infty }^\infty {1/S\left(\alpha - \frac{{er}}{q} - em\right)}。$

1.4 远场辐射声压

利用稳相法，远场声压能够在球坐标系(R, θ, φ)中确定下来 $ \theta $ 和 $ \varphi $ 分别为球坐标系下的极角和圆周角。

$ {P_a}\left( {R,\theta ,\varphi } \right) = - {\rho _0}\omega _1^2\tilde w\left( {{\alpha _0},{\beta _0}} \right){e^{ - i{k_1}R}}/2\text{π} R，$

(13)

其中稳相点定义为：

$ {\alpha _0} = \left( {\omega /{c_0}} \right)\sin \theta \cos \varphi \;\;\;{\beta _0} = \left( {\omega /{c_0}} \right)\sin \theta \sin \varphi，$

(14)

声压级(SPL)定义为：

$ SPL = 20\lg (\left| {{P_a}/{P_0}} \right|) 。$

(15)

式中： $ {P_0} $ 为1×10⁻⁶ Pa。

2 数值结果与讨论

2组加强筋几何和材料参数如表1所示。结构阻尼通过复弹性模量E(1+iη)起作用，其中η是损失因子。η_f和η_b分别为第1组筋、第2组筋的损失因子。平板可以为各项同性材料，也可以为各向异性复合材料。平板上半空间流体为水，其密度ρ₀=1 000 kg/m³，水中声速c₀=1 500 m/s，点激励力的幅值Q=1 N，作用点的位置为（x₀，0），球坐标系中声压考察点P_a的坐标为（R，θ，φ）=（60 m，53°，37°）。如果没有特别说明上述所选定的参数在接下来的分析中将保持不变。

2.1 各向同性加筋板声辐射

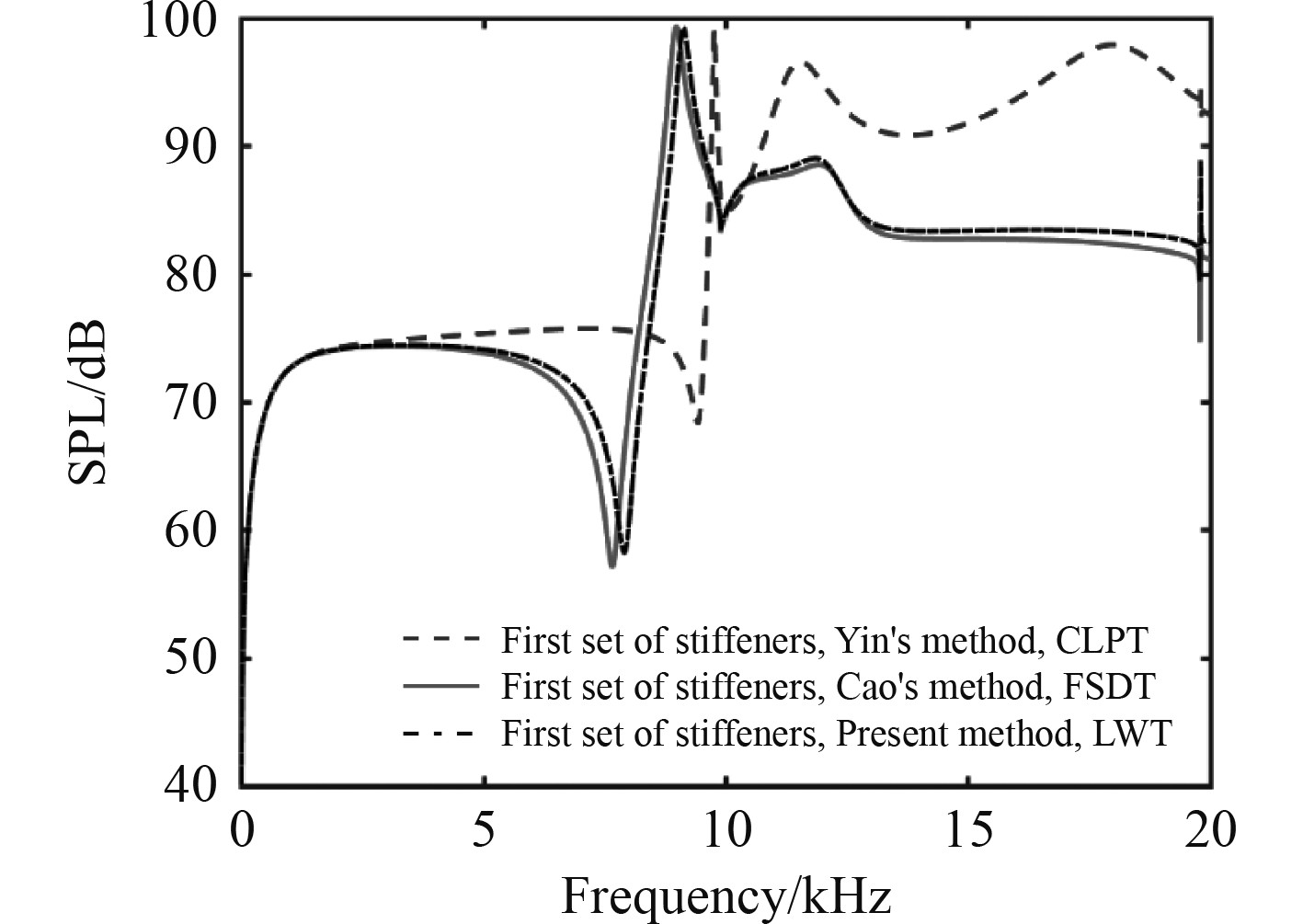
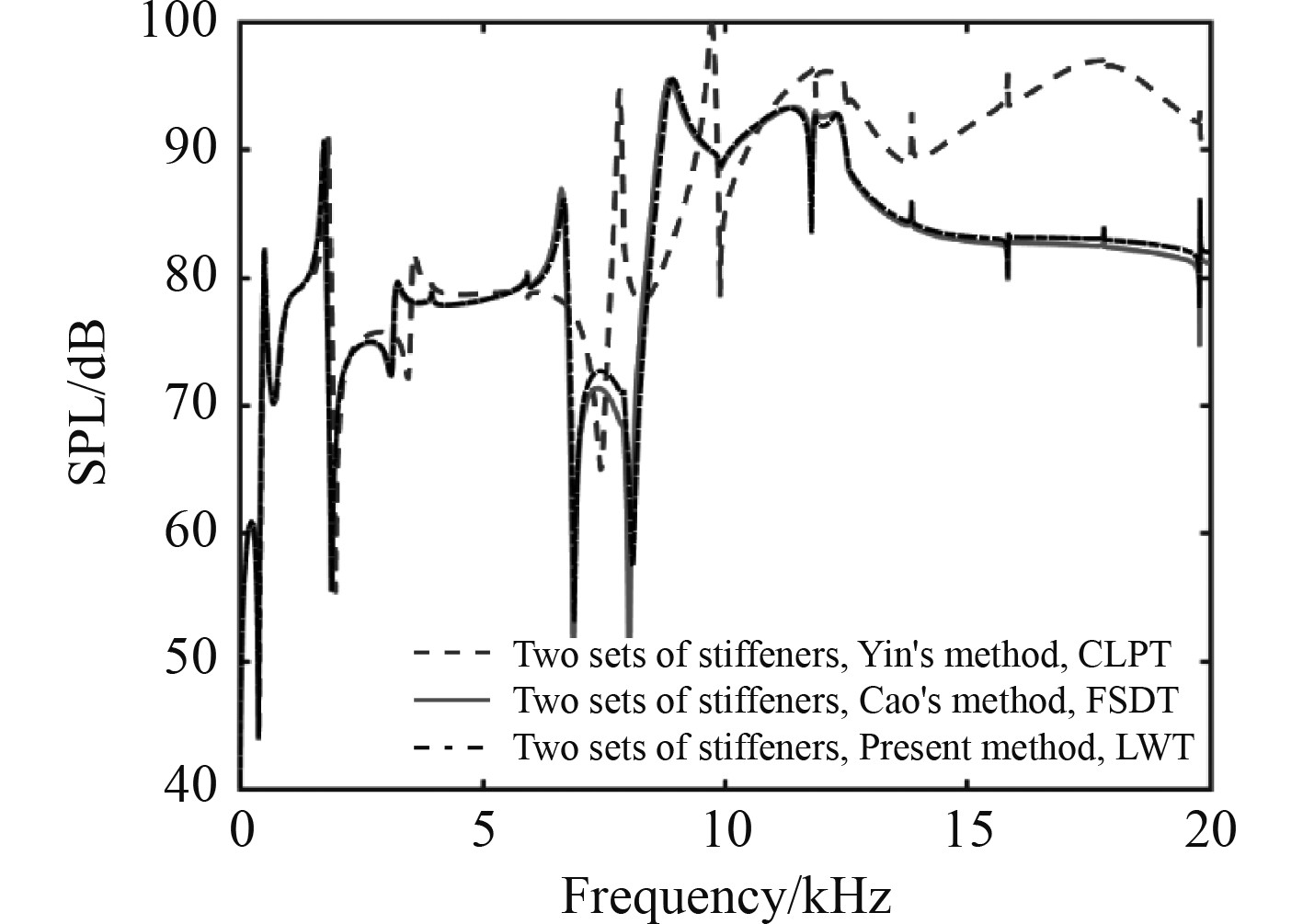
为验证本文基于LWT模型的准确性，以静止流体中的各向同性板为例，首先通过本文方法分别计算得到第1组加强筋板、2组加强筋板的远场辐射声压级；然后采用Yin^[11]的方法和Cao^[12]的方法分别得到基于CLPT以及FSDT的结果。最后将3种理论的计算结果进行对比，如图2和图3所示。各向同性板厚度为3 mm，材料参数与加强筋一致，激振位置为（0.25 m，0）。图中显示在中低频范围，3种方法的计算结果具有很好的一致性。随着频率升高，基于CLPT的计算结果与另外2种方法的计算结果差异逐渐增大，表明在中高频必须考虑剪切变形影响，CLPT具有局限性，但即使在高频，LWT与FSDT的计算结果差异不大，因此本文建立的理论模型准确有效。

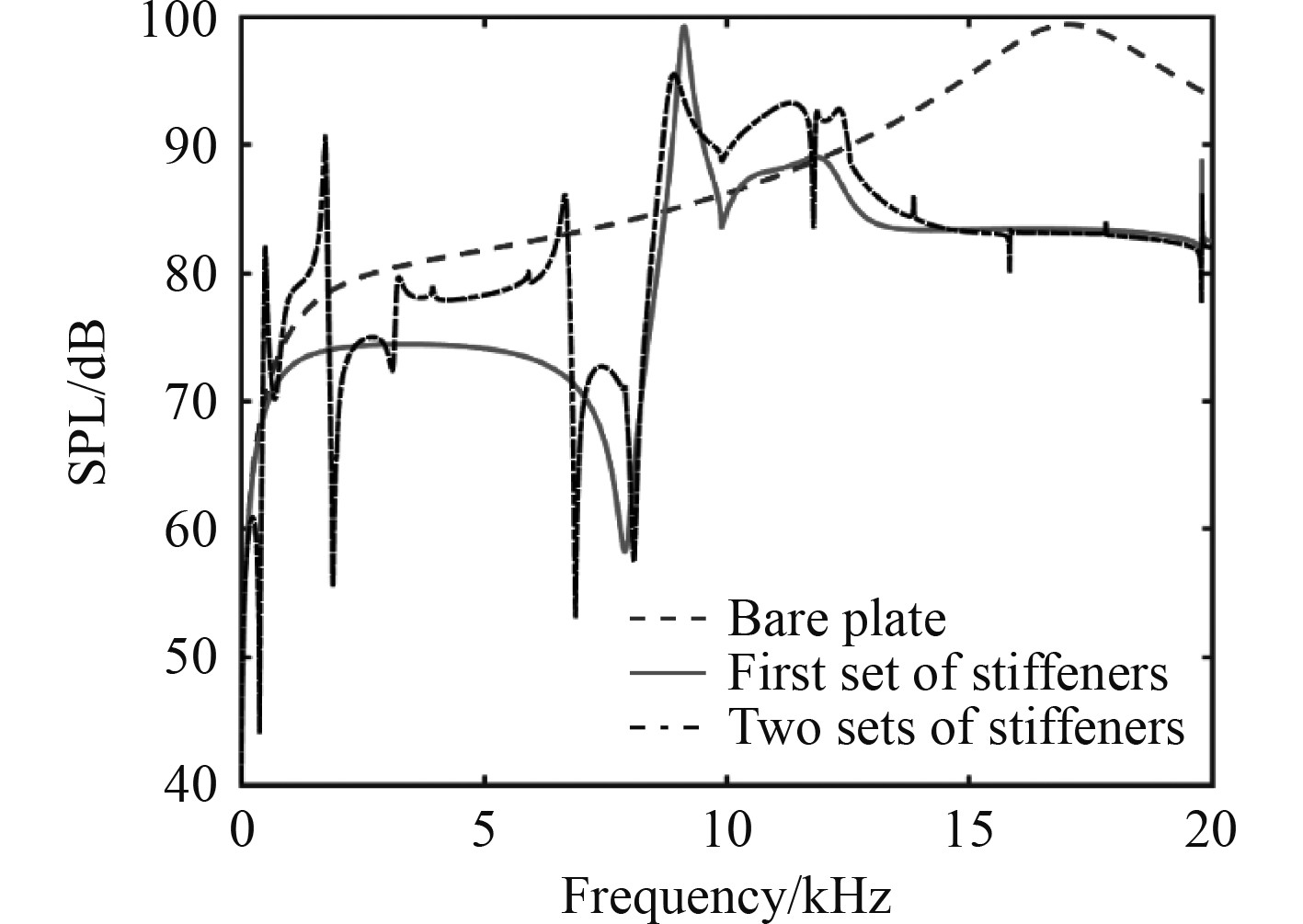
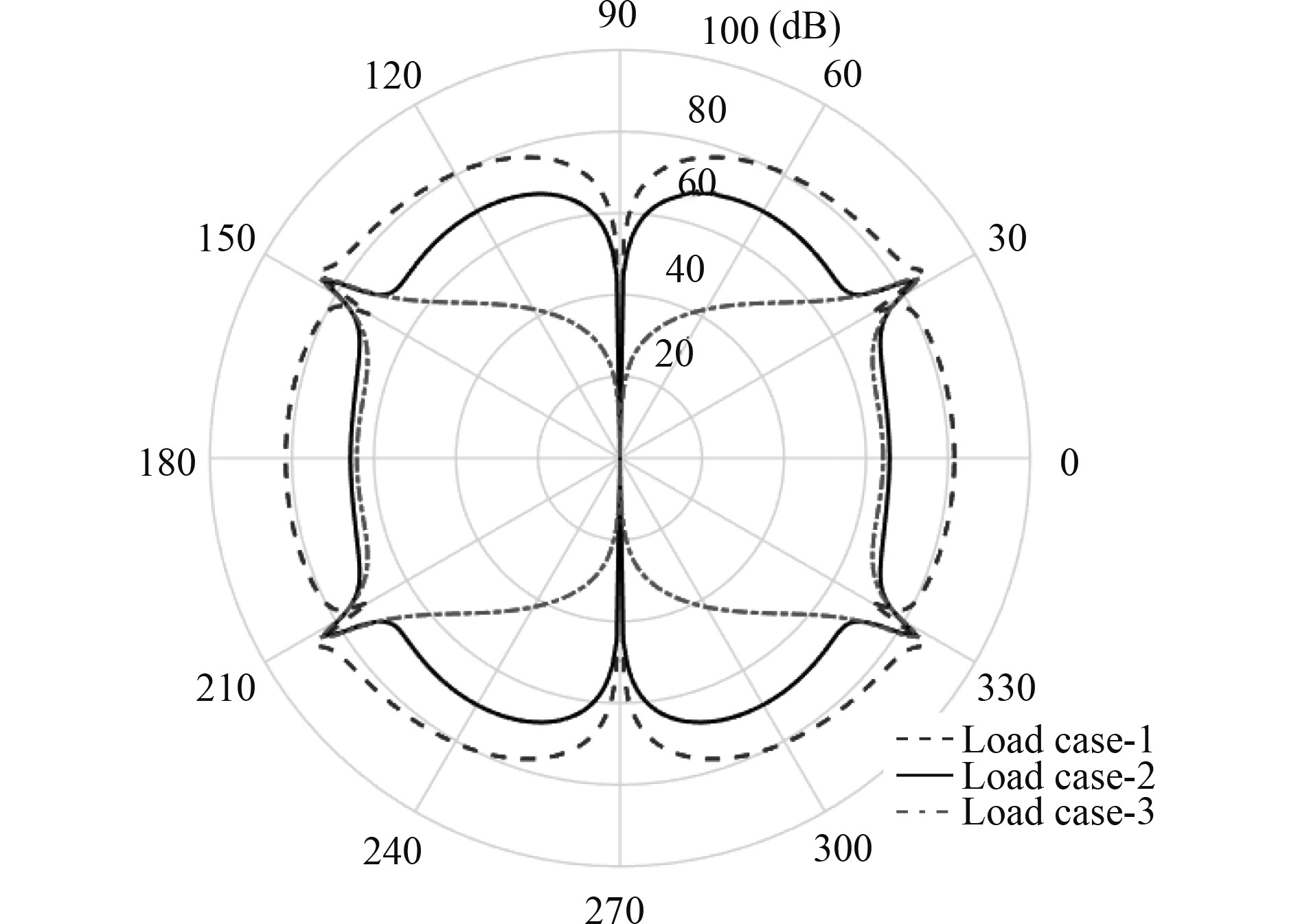
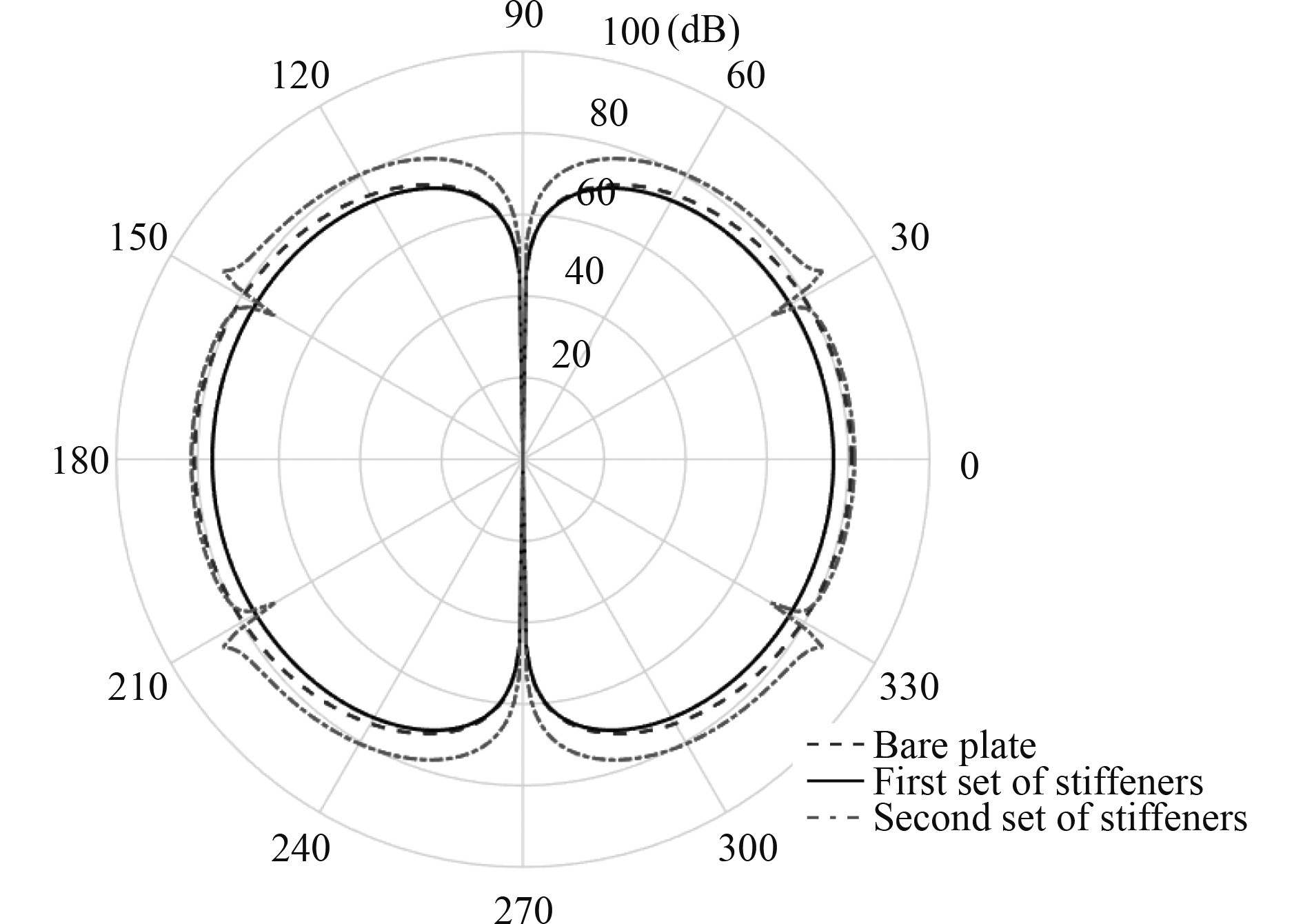
图4为光板、第1组加筋加强板和第2组筋加强板这3种模型的远场辐射声压级对比。可以看到，不同方式的周期加强筋通过波数转换效应导致了不同的声场特征以及SPL的强烈起伏，具体体现在由于加强筋的存在，在某些频段内能显著降低声压级，而在有些频段内增加了声压级；2种加筋板在高频声压级趋于一致，这是由于弯曲波在行进一个相邻强筋周期间距之前能量已全部被耗散掉，因此第2组强筋在高频对结构振动和声特性几乎没有影响。图5为3种不同激振位置下双周期加筋薄板的声压级曲线。Load case-1，Load case-2和Load case-3分别对应于点力作用在（0.25 m，0）的板上、（0.2 m，0）的第1组筋上以及（0，0）的第2组强筋上。比较发现，辐射声压级曲线与激振位置相关，尤其当激振力作用在强筋上时，在整个计算频率范围内辐射声压级显著降低，并且随着频段升高，该特征越来越明显。这是由于强筋阻抗随着频率升高而增加，进而有效抑制了结构声辐射。因此实际船舶结构设计时可考虑将激励尽可能设计在强构件处。

2.2 复合材料加筋层合板声辐射

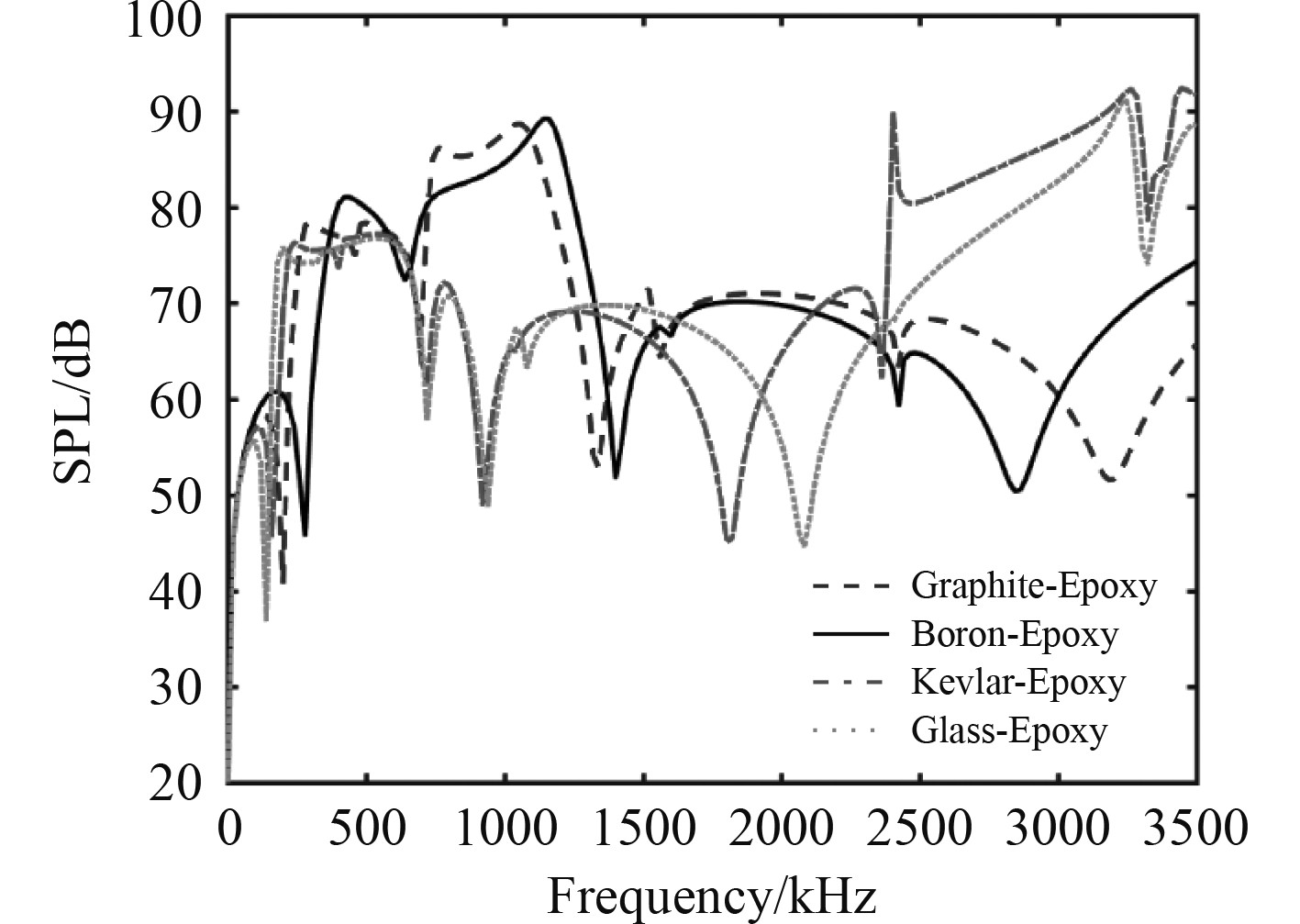
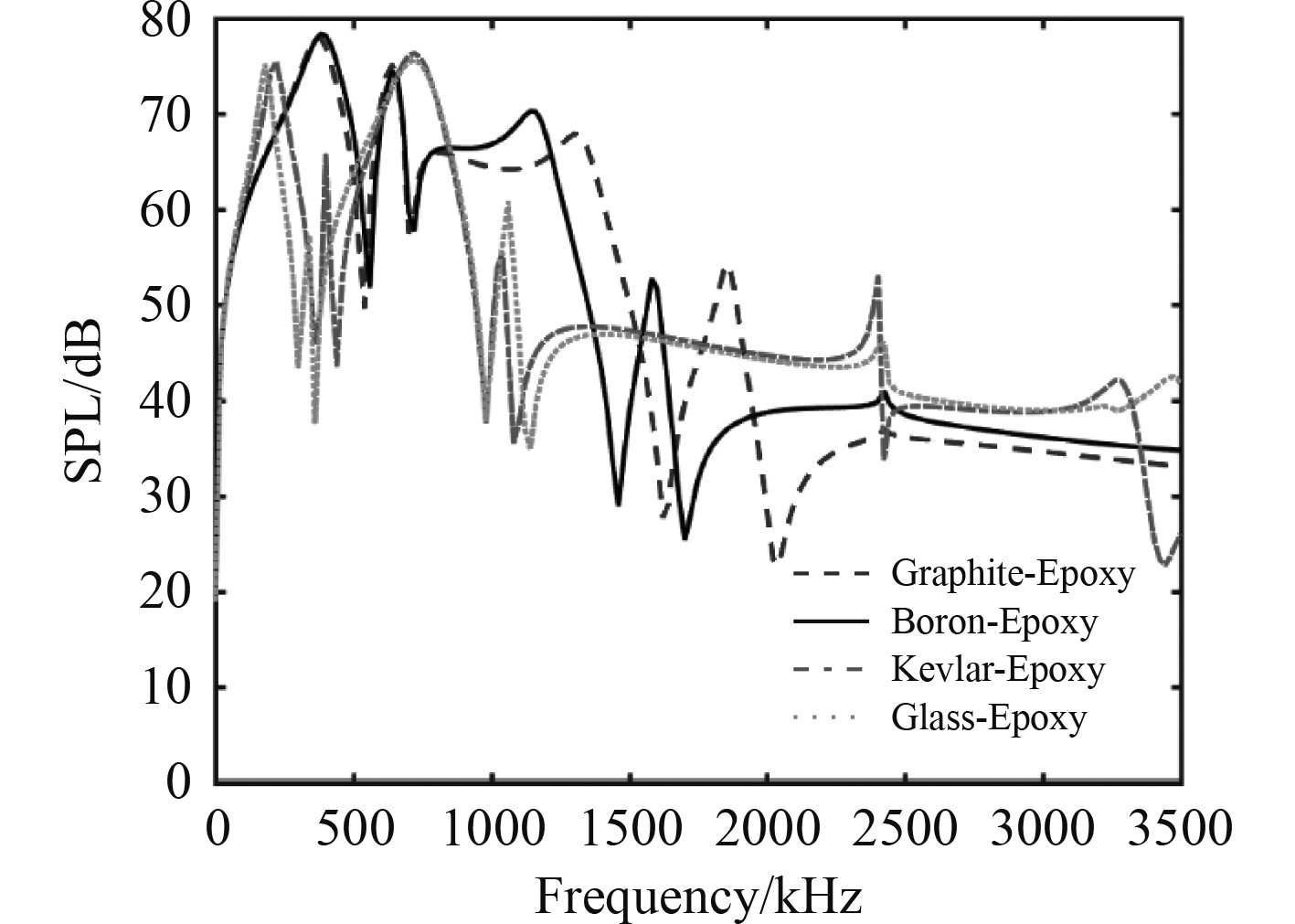
利用分层理论模型，首先比较4种不同材料的加筋层合板分远场声辐射特性。加强筋几何以及材料参数见表1，复合材料参数见表2。铺设方式为(0°/90°/90°/0°)，单层板厚度均为7.5 mm。图6和图7分别为点力作用在板（0.25 m, 0）位置和作用在强筋(0, 0)处时4种不同复合材料双周期加筋层合板结构的辐射声压级曲线。铺设方式和单层板厚度保持不变，4种复合材料参数差异主要体现在主方向弹性模量上。可以看到，当主方向弹性模量量级相同时，2种材料的SPL曲线变化趋势一致。Graphite-Epoxy与Boron-Epoxy材料主方向弹性模量量级高于Kevlar-Epoxy与Glass-Epoxy，此时结构总体刚度较大，有利于抑制结构振动。但在中低频范围，由于声辐射效率较高，最终体现为辐射声压级升高。而在高频范围，声辐射效率下降，表现为SPL曲线也随之降低。此外，当点力作用在强筋上时，Kevlar-Epoxy与Glass-Epoxy两种材料在降低结构中低频声辐射优势变小，主要体现为相对另外2种材料，声压级较低时对应的频带变窄。该现象表明点力作用在强筋上时，尽管整体上抑制了结构的振动声辐射，但同时有利于激发结构在更宽范围内的振动，进一步提高了中高频的声辐射效率，导致优势频带变窄。

图8和图9分别为不同激振频率、不同激振位置下Graphite-Epoxy材料的双周期加筋复合板的远场指向性曲线（ $ \varphi $ =37°）。可以发现，当激振力作用在板上，靠近板平面处的场点声压级较低，在垂直板面上方处场点声压级相对较高。激振频率越高，远场指向性特征越明显，在多个角度位置声压级呈现出锯齿型变化，这是由于在高频结构的模态特征较为丰富，导致声场指向性变化显著。观察图9可以看到，在1 000 Hz处，当点力分别作用在强筋上、小筋上以及板上时，任意角度的场点位置远场辐射声压级依次降低，再次表明当外力作用在阻抗较高的加强结构上时，可以有效降低结构振动声辐射。进一步观察发现：当点力作用在强筋上时结构声辐射表现出强指向性，在与极轴呈（−30°，30°）夹角范围内的场点声压幅值以及指向性特征与点力作用在小筋上几乎一致。随着角度增大，场点声压快速减小。这说明点力作用在强筋上时主要有效抑制了与板面呈小角度空间内的声传播。此外，从图8和图9中观察到f=1 000 Hz时双周期加筋模型的远场指向性在30°，150°，210°，330°附近均出现了一个波动。图10给出了光板、第1组加筋板、第2组加筋板的远场指向性对比曲线。观察发现，这个波动是由于第2组强筋导致的，因此波数转换效应不仅对SPL曲线有影响，还会影响到声场指向性特征。这些远场指向性图均关于θ=90°这条轴线对称。

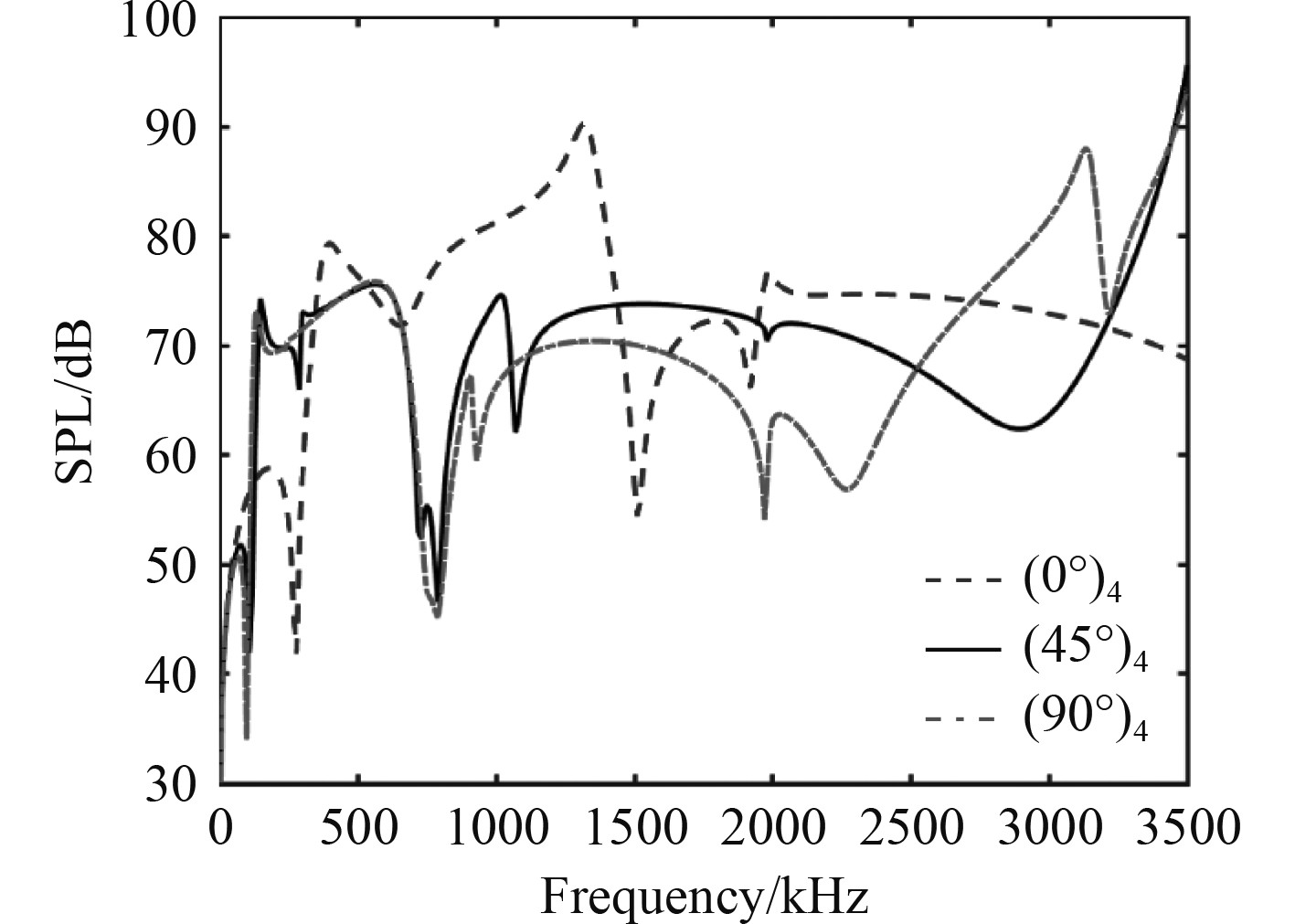
图11为Graphite-Epoxy材料的3种不同单向铺设方式下SPL曲线。3种铺设方案分别为：(0°)₄，(45°)₄和(90°)₄，其他参数不变。由于材料的各向异性以及单方向加筋的作用，铺层角度对SPL曲线有显著影响。其中，(45°)₄和(90°)₄铺设方式下SPL变化趋势相近，在中低频范围对降低声辐射有优势。由于(0°)₄铺设方式与沿y方向加强筋形成互补，提高了结构整体刚度，共振峰向高频偏移，但同时提高了中低频的声辐射效率，因此总体辐射声压级相对升高，在高频具有隐身优势，这与前面结论一致。

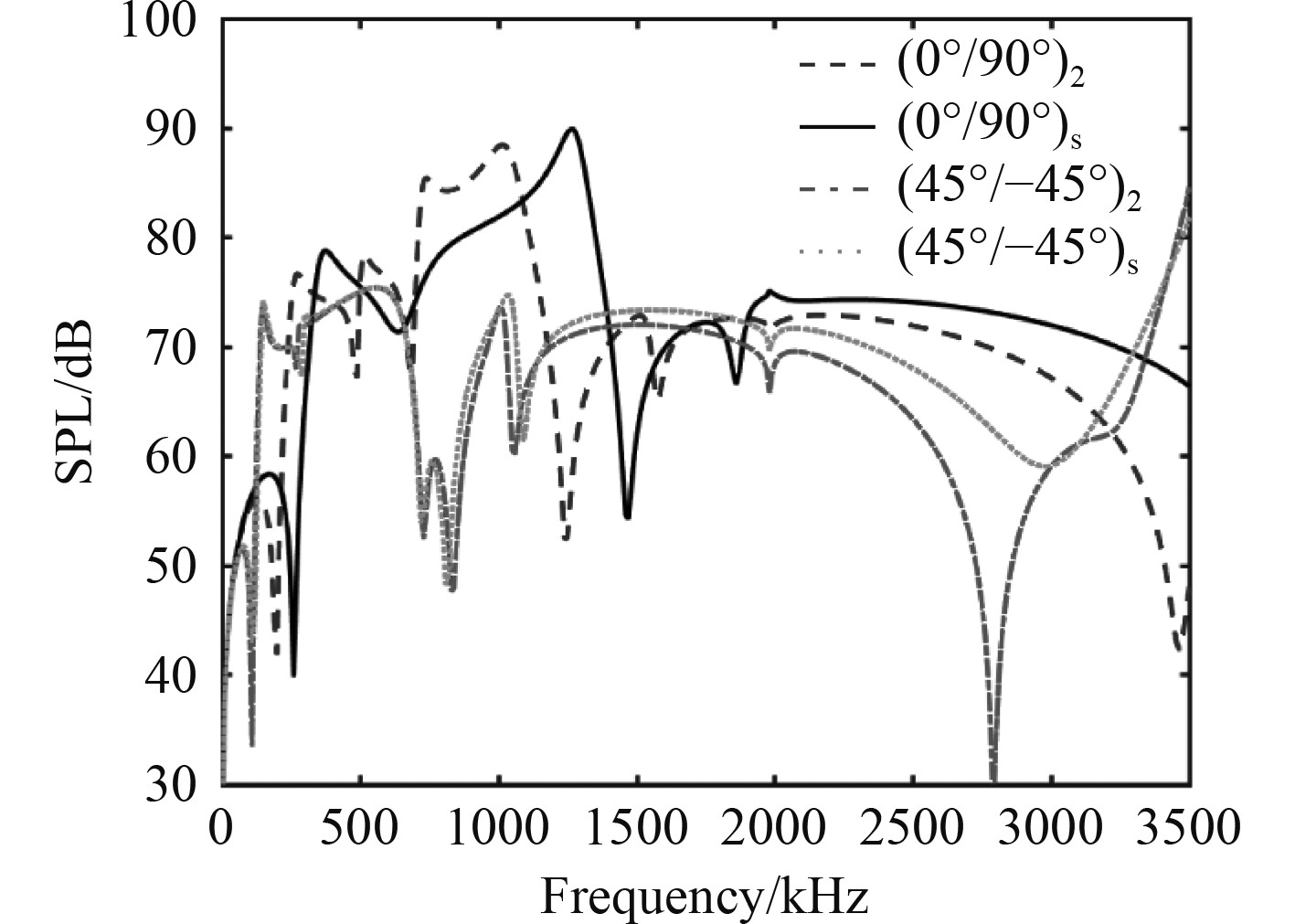
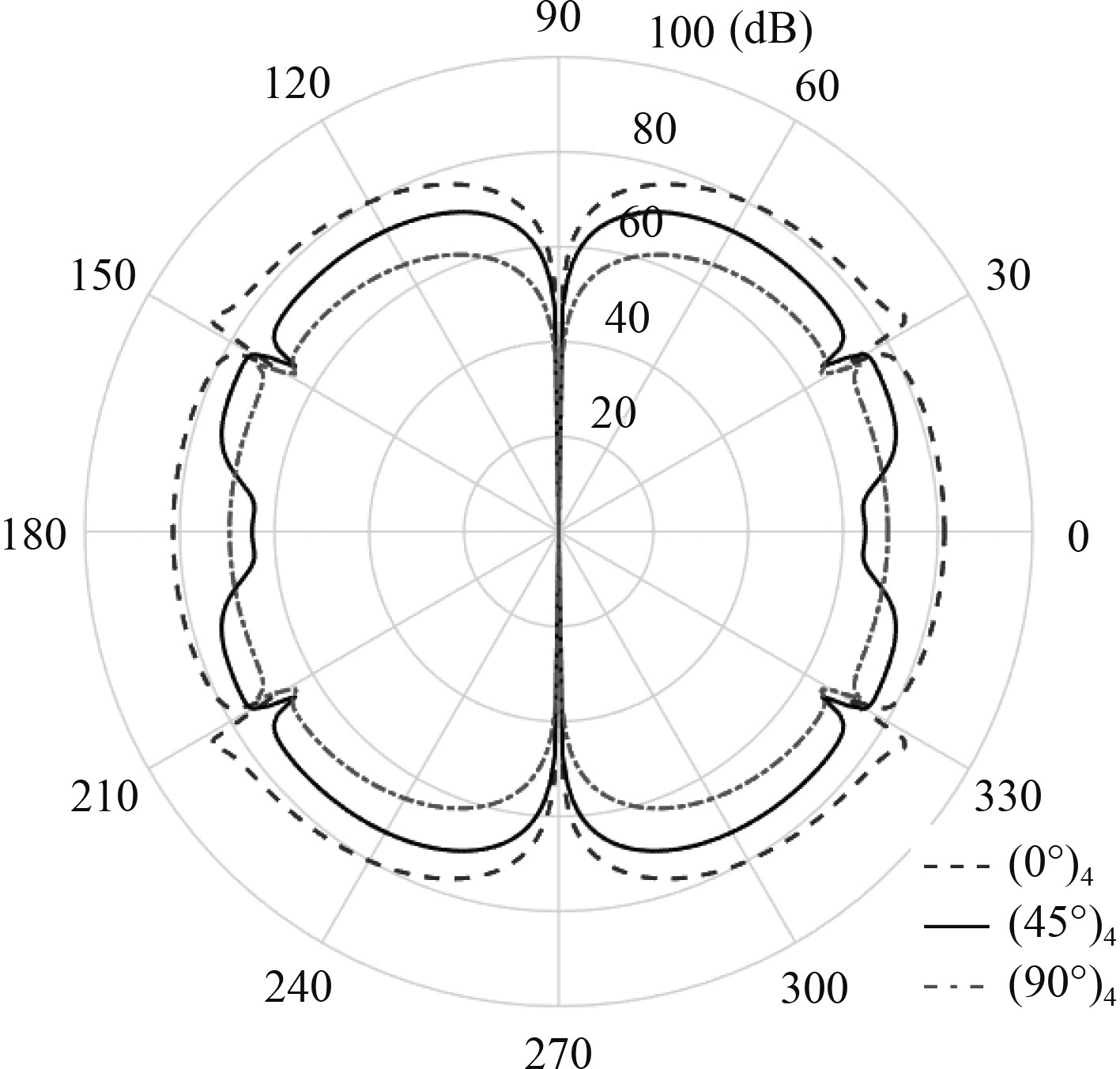
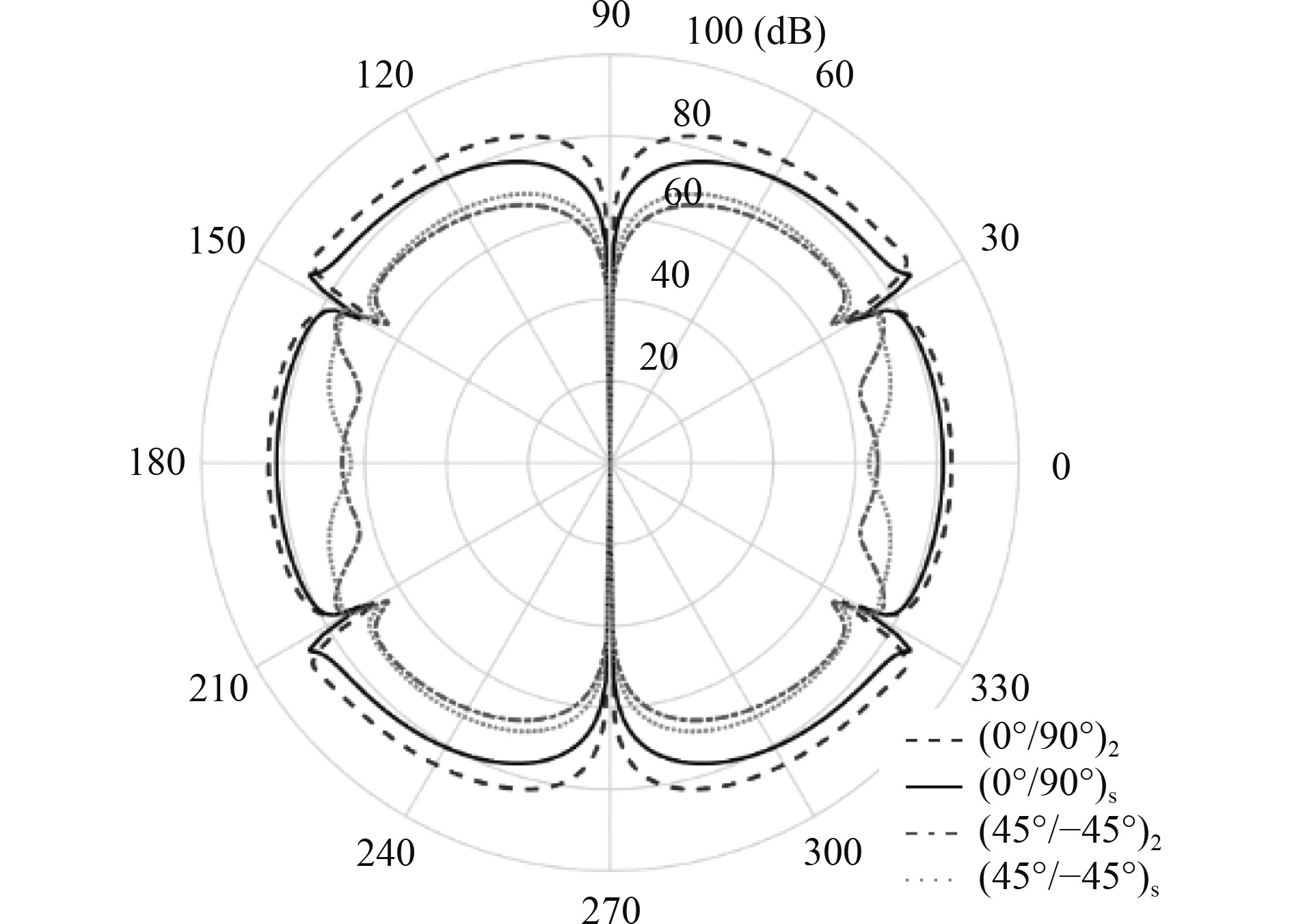
进一步比较4种铺设方式的SPL特征，对称正交铺设方式(0°/90°)_s、反对称正交铺设方式(0°/90°)₂、对称角铺设方式(45°/−45°)_s、反对称角铺设方式(45°/−45°)₂，如图12所示。观察发现，在中低频，与角铺设方式相比，对称性对正交铺设方式下的SPL影响显著，且对称铺设方式提高了结构整体刚度，有利于抑制结构振动，但远场声压级反而有所提高。而角铺设方式下，对称与反对称下两周SPL曲线差异不大，相对于正交铺设方式，结构刚度较低，但远场声压级反而较低。因此可通过进一步优化铺层角度来降低结构的声辐射特性。激振频率为1 000 Hz时，上述3种单向铺设方式的远场指向性曲线如图13所示。(45°)₄角铺设方式下，结构的各向异性特征更加明显，从而使得结构声场指向性特征丰富。4种对称与反对称铺设方式下的远场指向性曲线如图14所示。可以发现，正交铺设时，反对称性主要降低了贴近结构表面空间内的场点声压级。而角铺设时，二者指向性差异主要体现在远离结构表面夹角空间范围内。

3 结　语

1）激振力作用在强筋上时，强筋阻抗随着频率升高而增加，能有效降低结构振动和声辐射；远场声压指向性发生显著变化，与板面呈小夹角的空间内的声传播得到了有效抑制。

2）Kevlar-Epoxy与Glass-Epoxy两种材料在中低频对降低加筋复合结构辐射噪声具有优势；当外力作用在强筋上时，这种优势会减小。

3）对称性对正交铺设方式下的SPL曲线影响较大；角铺设方式有利于降低结构声辐射，可通过优化铺层角度进一步提高复合材料隐身优势。