水下非接触爆炸一般针对的攻击模式为水雷的远场爆炸,该模式一般不会直接击穿船体结构,却会导致舰船上各类设备的冲击破坏。众多海上战例及实船水下爆炸冲击试验结果表明舰船在水下非接触爆炸中的薄弱环节为舰船设备,因此设备的抗冲击是舰船抗冲击设计的主要内容。
冲击环境预报是设备抗冲击设计的输入和依据,目前主要通过数值仿真方法进行计算[1-4]。设备冲击环境预报的准确性会受到动力学建模方法[5-6]以及水下非接触爆炸载荷计算的影响[7-8]。现有的冲击环境预报模型一般将设备以质量单元的型式赋予到相应位置的甲板或舱壁有限元网格节点上,鲜有研究设备本身尺度、安装方式以及基座建模方式对冲击环境预报结果的影响。
本文根据舰船的板架结构和设备安装布置特点设计动力学分析模型并针对典型设备进行水下非接触爆炸载荷下的冲击环境预报,研究船体结构-设备的动力学建模方法,分析了船体板架结构、设备基座以及设备本身的建模方式对冲击环境预报结果的影响。
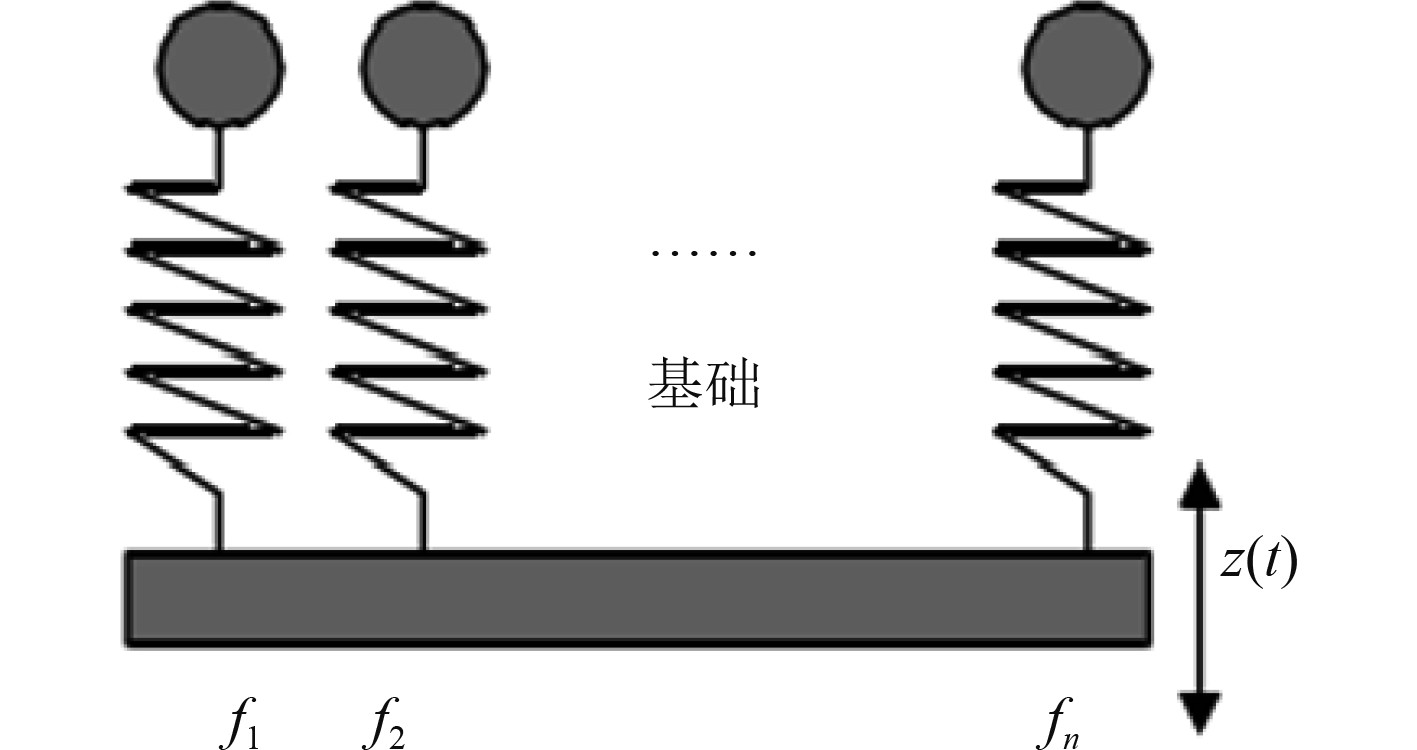
1 冲击环境谱分析方法在水下非接触爆炸载荷作用下,设备冲击动响应包含复杂的频域信息,工程中通常采用冲击响应谱对冲击环境进行描述。冲击响应谱为安装在同一基础上,经受同样冲击激励的一系列不同固有频率的线性振子响应的最大幅值与其固有频率的关系曲线,如图1所示。
|
图 1 冲击响应谱计算模型 Fig. 1 Calculation model of shock response spectrum |
设圆频率为
| $ {\ddot y_i}(t) + \omega _i^2[y(t) - z(t)] = 0。$ | (1) |
相对运动方程为:
| $ {\ddot x_i}(t) + \omega _i^2{x_i}(t) = - \ddot z(t) 。$ | (2) |
假设冲击初始速度和位移为0,则可得:
| $ {x_i}\left( t \right) = - \frac{1}{{{\omega _i}}}\int\nolimits_0^t {\ddot z\left( \tau \right)} \sin {\omega _i}\left( {t - \tau } \right){\rm{d}}\tau。$ | (3) |
取
| $ D\left( {{\omega _i}} \right) = {\left[ {\frac{1}{{{\omega _i}}}\int\nolimits_0^t {\ddot z\left( \tau \right)} \sin {\omega _i}\left( {t - \tau } \right){\rm{d}}\tau } \right]_{\max }}。$ | (4) |
得到位移谱后,速度谱和加速度谱也就可以确定,三者之间的关系为:
| $ {V_i} = {\omega _i}{D_i},\;\;\;\;\;\;\;{A_i} = {\omega _i}^2{D_i} 。$ | (5) |
其中,
水下爆炸载荷与水中船体结构的相互作用采用二阶双重渐近方法解耦[9],将动响应时程曲线转化成冲击谱进行分析。最后基于冲击响应谱确定抗冲击设计谱,设计谱一般为包含等位移、等速度和等加速度3部分的三折线谱。
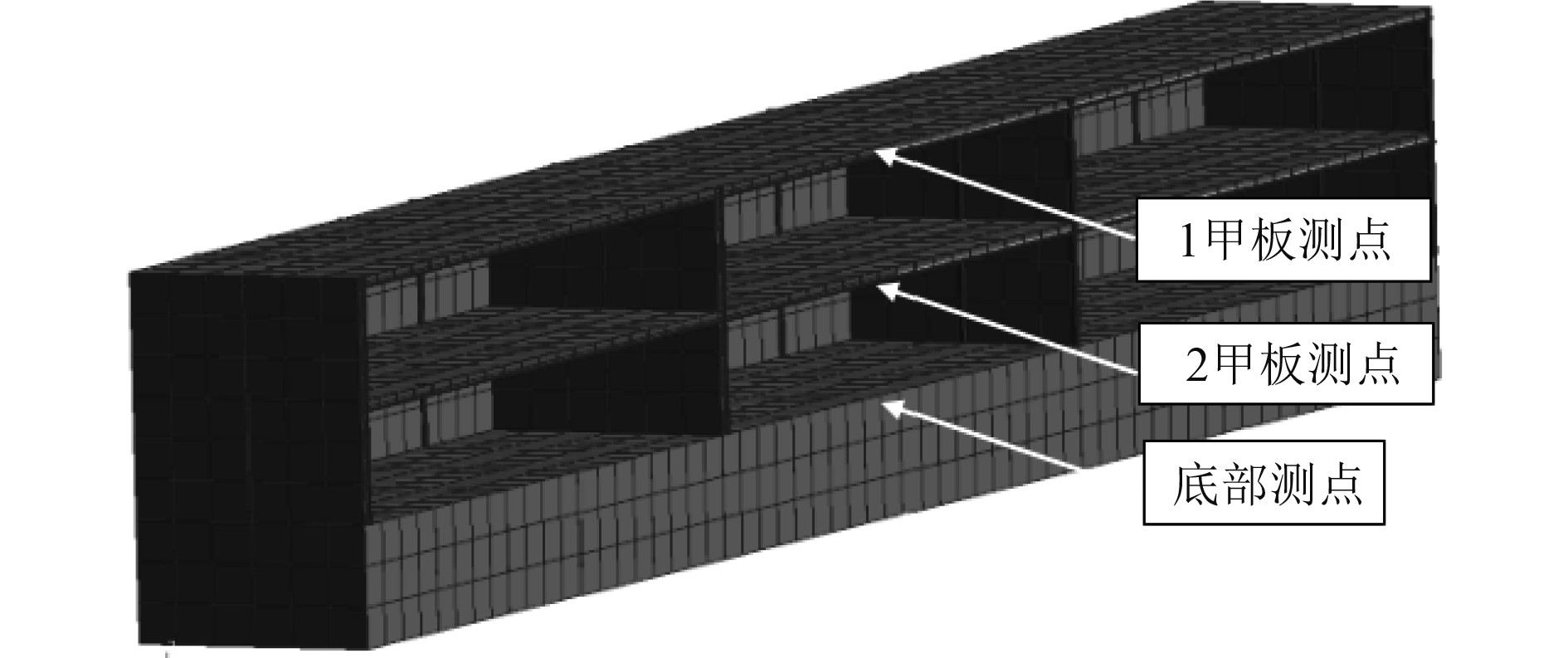
2 船体板架结构模型冲击环境预报动力学模型长8.1 m,宽1.8 m,高1.35 m,设有双层底、2层甲板和2道道横舱壁结构。甲板厚度为4 mm,强横梁为T(4×40/4×20),间距900 mm。纵桁为T(4×40/4×20),间距450 mm。纵骨为T(3×20/3×12),间距150 mm。模型吃水0.45 m,炸药选取10 kg TNT当量,龙骨冲击因子0.105,爆距30 m,攻角90°,爆炸位置位于船中。冲击环境输出点选取内底板、2甲板和1甲板的典型设备位置,如图2所示。
|
图 2 冲击环境预报动力学有限元模型 Fig. 2 Dynamic finite element model of hock environment prediction |
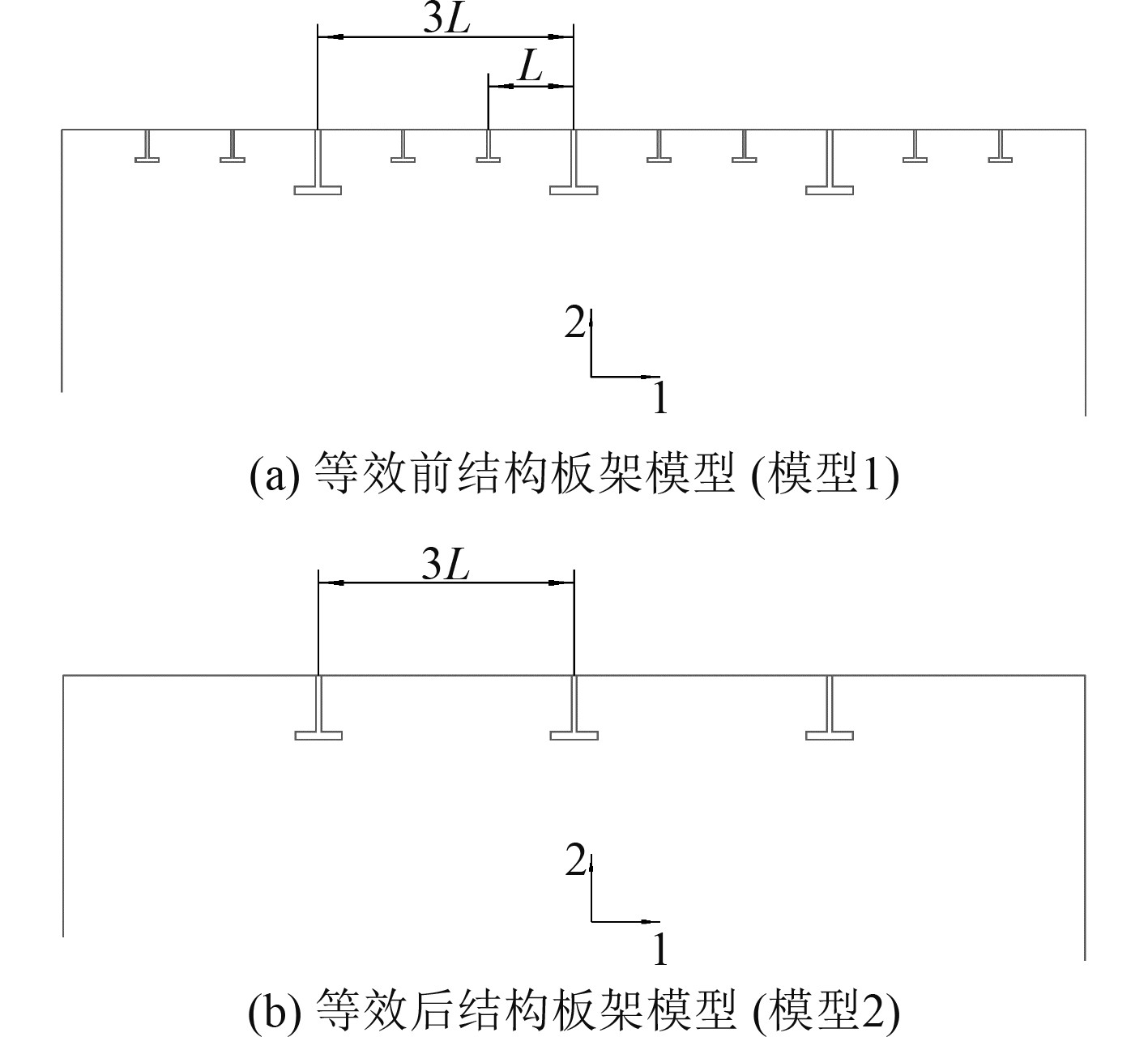
结构板架的动力学建模根据刚度和质量等效原则,对纵骨等弱构件进行等效处理,保留纵桁和强横梁结构,等效前后的模型如图3所示。
|
图 3 船体结构板架等效模型 Fig. 3 Equivalent model of plate-girder structure |
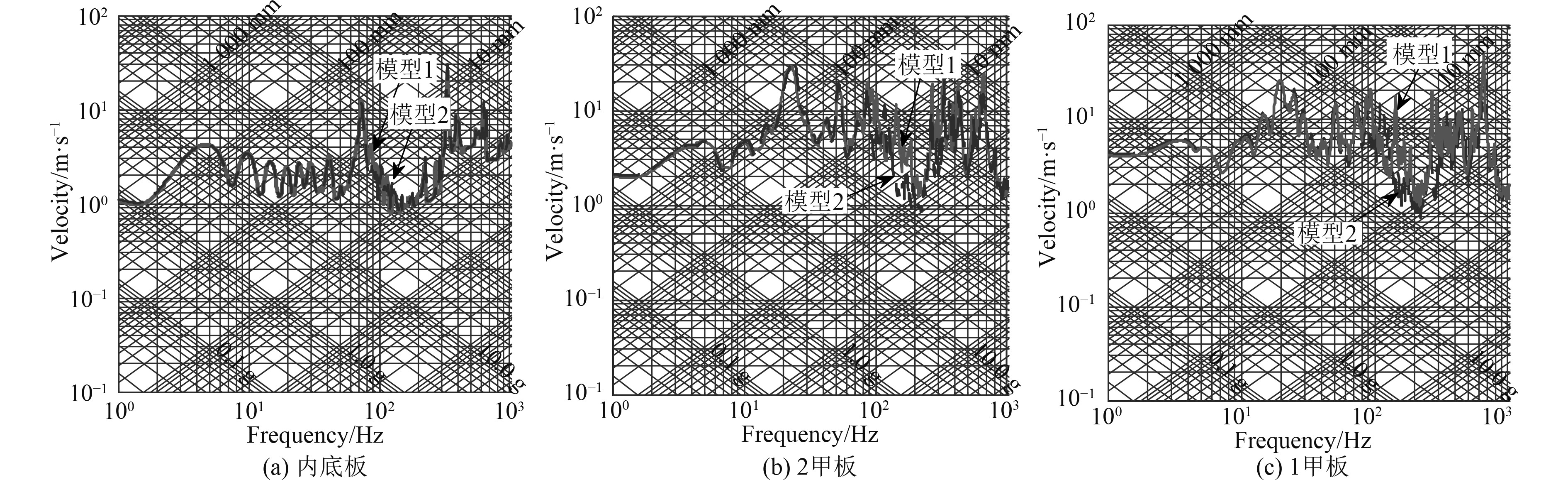
如图4所示,板架结构等效前后内底板测点冲击环境一致性较好,1甲板和2甲板测点的冲击环境主要在100~200 Hz间存在差异,究其原因为等效前模型建有纵骨结构,其引起的局部频率特征比等效后的模型更为准确。舰船设备的安装频率一般不会超过100 Hz,因此对纵骨进行等效处理后获得的冲击环境结果能够满足工程设计的精度。
|
图 4 板架模型等效前后冲击环境对比 Fig. 4 Comparison of shock environment before and after model equivalence |
单元网格尺度也是影响预报结果的重要因素,采用不同的网格尺度进行船体结构建模,网格尺度分别为150 mm(模型1)、300 mm(模型2)和450 mm(模型3)。
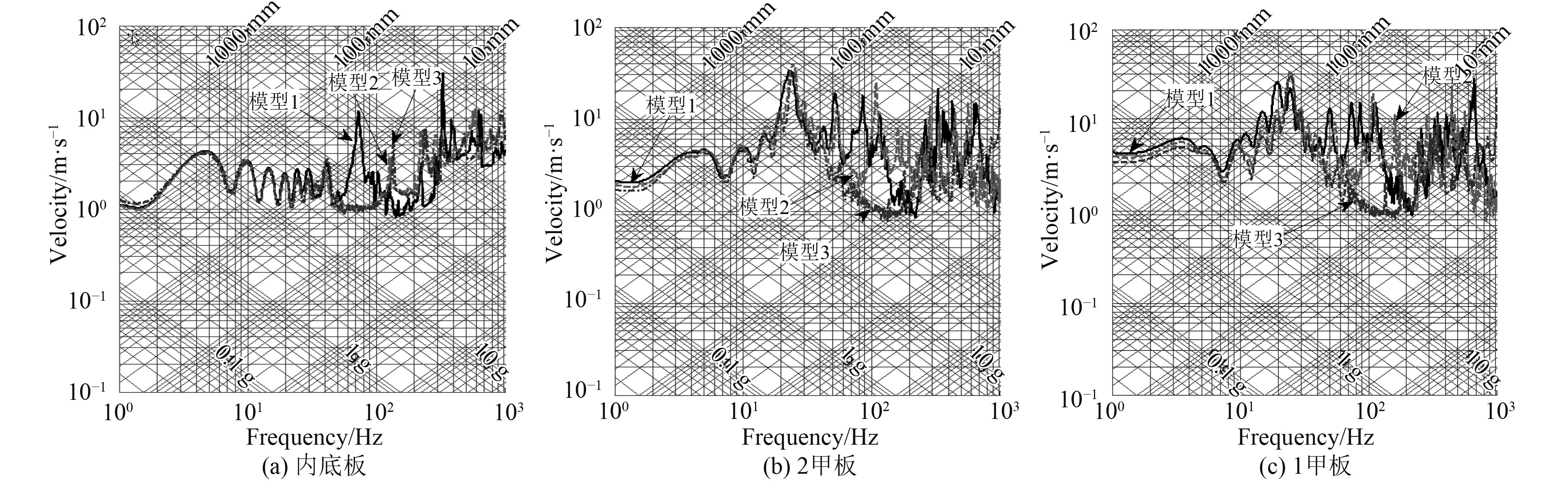
如图5所示,内底板、2甲板和1甲板的测点在50 Hz以下频段几乎不受网格尺度的影响。但在50~200 Hz间,模型1的预报结果虽与模型2吻合度较高,但部分响应主频存在差异,而模型3在此区间内的响应主频基本消失。基于上述分析,模型1和模型2的网格尺度能够反映冲击环境的整体频率特征,但高频区域存在局部差异。模型3的网格尺度在50 Hz以下能够合理地反映冲击环境特征,但在中高频区域无法合理表达冲击环境的特征。网格尺寸过大会影响到板架结构自身高频特性计算结果的准确性,进而影响到其上设备冲击环境高频区域的预报结果。因此对于较高安装频率的设备应采用小尺度的网格,以准确表达板架结构自身的高频响应特征。而对于安装频率较低的设备,如弹性安装的设备,可适当放大结构网格的尺度以提高预报效率。
|
图 5 不同网格尺度冲击环境预报结果对比 Fig. 5 Comparison of shock environment of different grid scales |
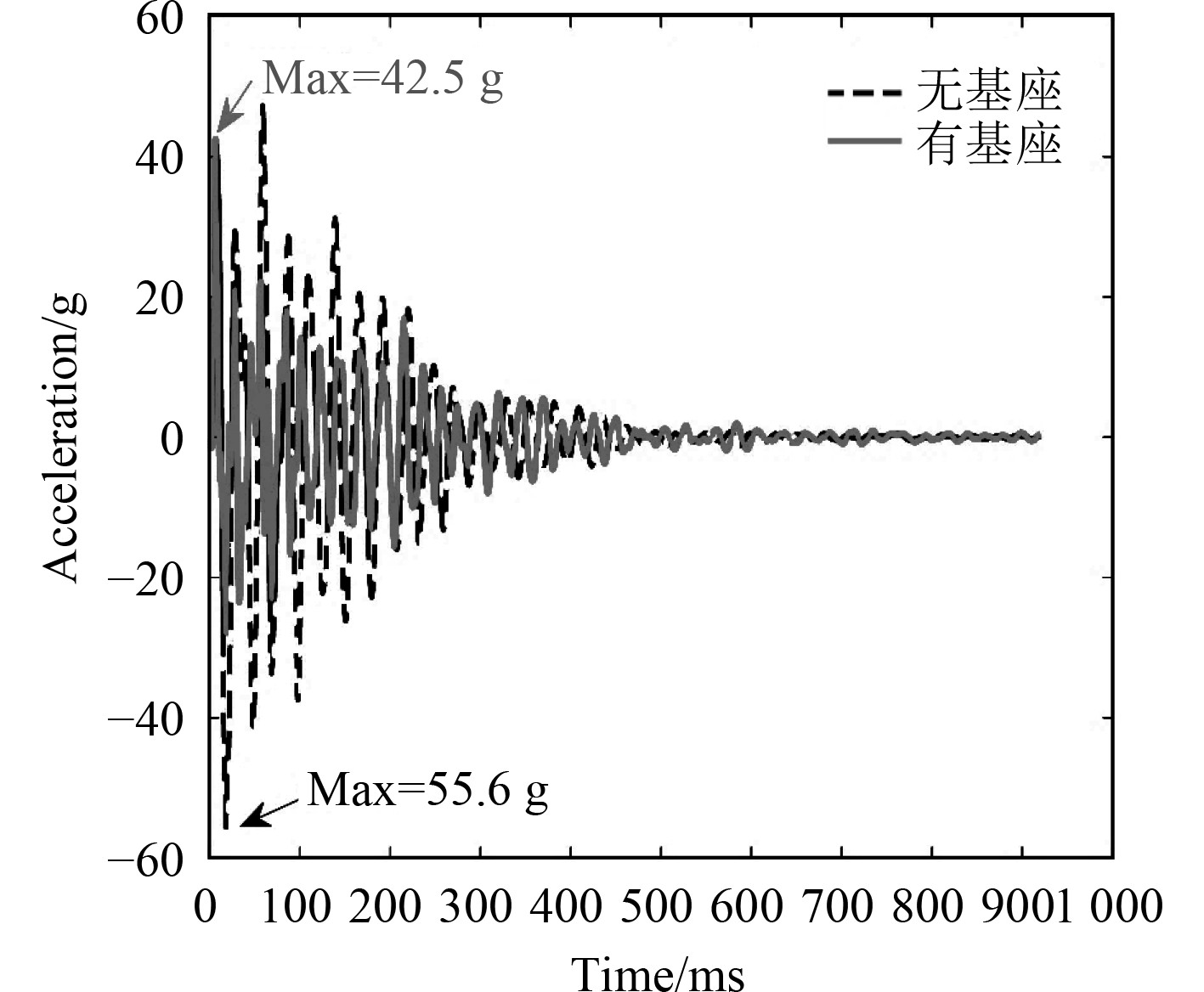
大型设备上舰安装时需要设置基座结构,基座本身也具有一定的刚度,因此会影响上方设备的冲击环境预报结果。船体结构基座建模时基于质量和刚度等效的原则,采用板、梁单元进行模拟。建立内底上一大型设备的基座结构,分析有无基座模型对设备冲击环境的影响,如图6所示。在建立设备基座模型后,设备质心处的加速度响应峰值降低了约20%。说明在对设备进行冲击环境预报时不能忽略基座结构的影响。
|
图 6 有无基座模型时设备的加速度响应 Fig. 6 Acceleration response of ship equipment with and without foundation models |
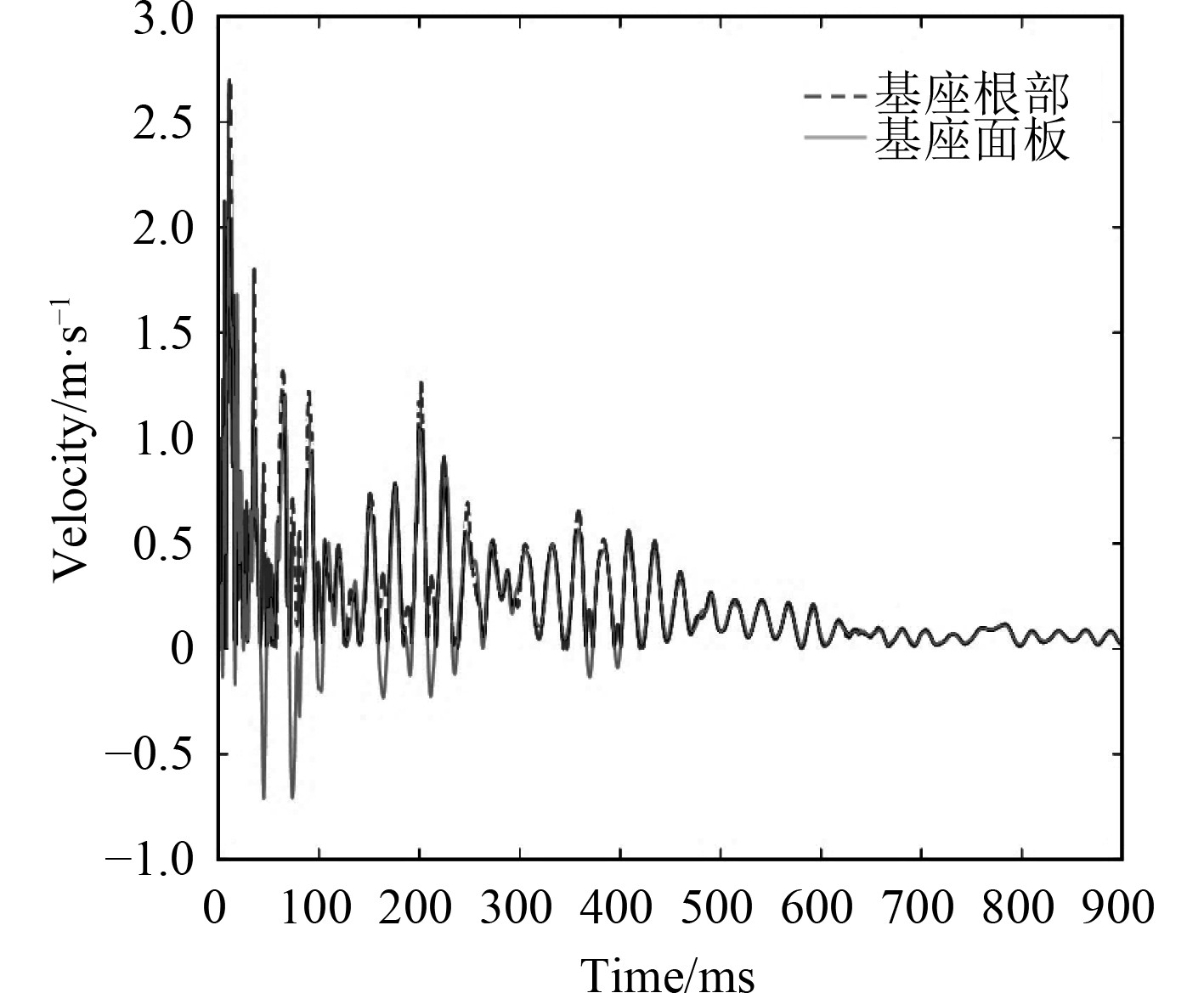
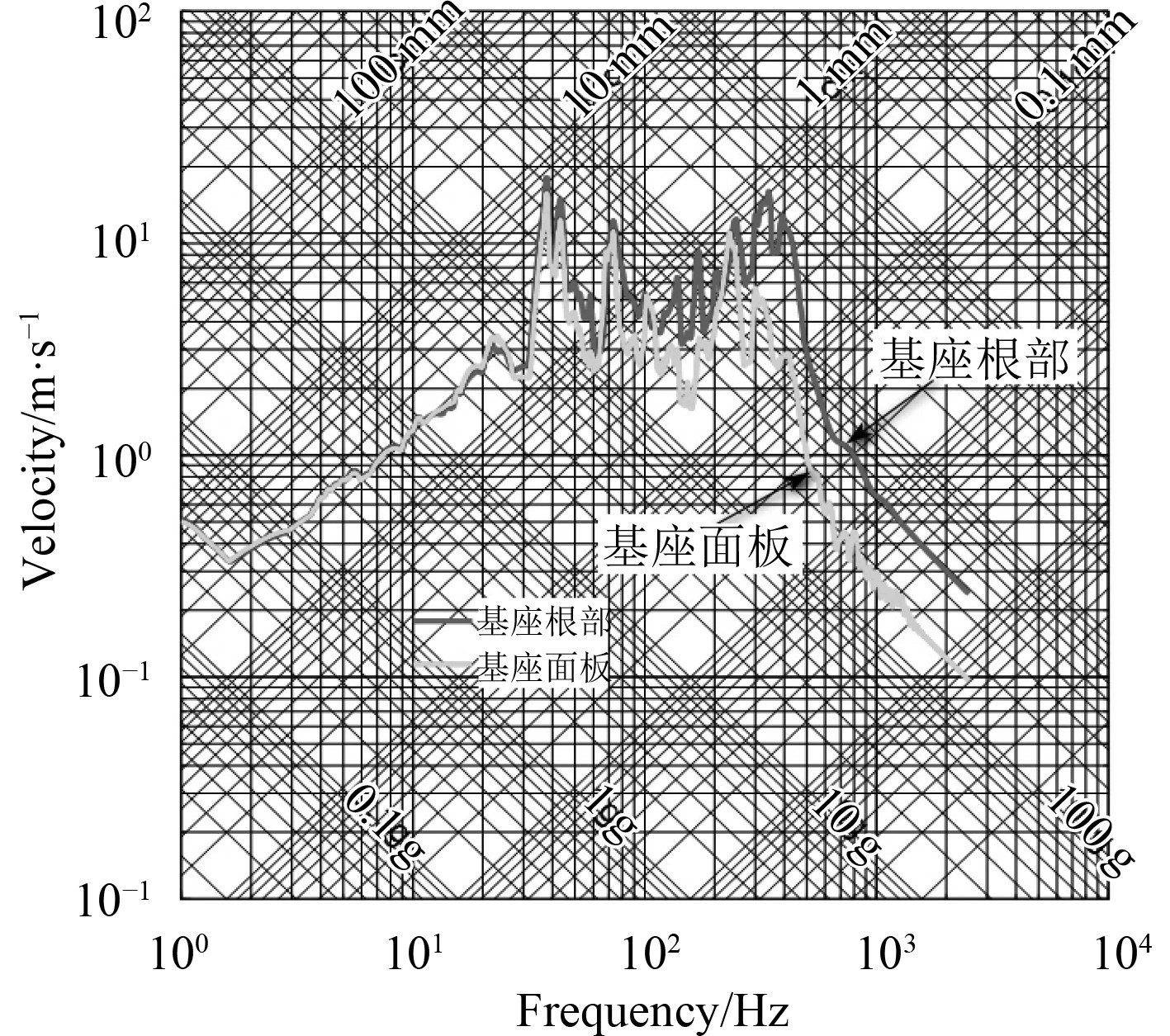
在建立基座模型后,基座根部和面板测点的响应及冲击环境也会有所不同。图7为基座根部和基座面板测点处加速度响应的对比,两者的冲击响应谱如图8所示。基座根部与面板处的中频段谱速度和高频段谱加速度存在差异,低频段谱位移值基本吻合。因此在对设备进行冲击环境预报时,需要考虑结构基座建模对设备冲击环境预报结果的影响,根据设备抗冲击设计及考核的需要选择设备基座根部或基座面板处的冲击环境。对于舰上的大型设备,结构基座本身也要进行抗冲击设计以满足强度和刚度的抗冲击设计要求。
|
图 7 基座根部和面板的加速度响应 Fig. 7 Acceleration response of the web and panel of the foundation models |
|
图 8 基座根部和基座面板冲击谱 Fig. 8 Shock response spectrum of the web and panel of the foundation models |
舰上众多设备相对舰船主尺度较小,可采用弹簧振子的型式进行动力学分析建模,即采用质量点模拟设备,弹簧单元模拟设备的安装频率。分别采用质量点和质量块对设备进行建模,其中质量块模型根据设备空间尺度采用体单元网格进行划分。
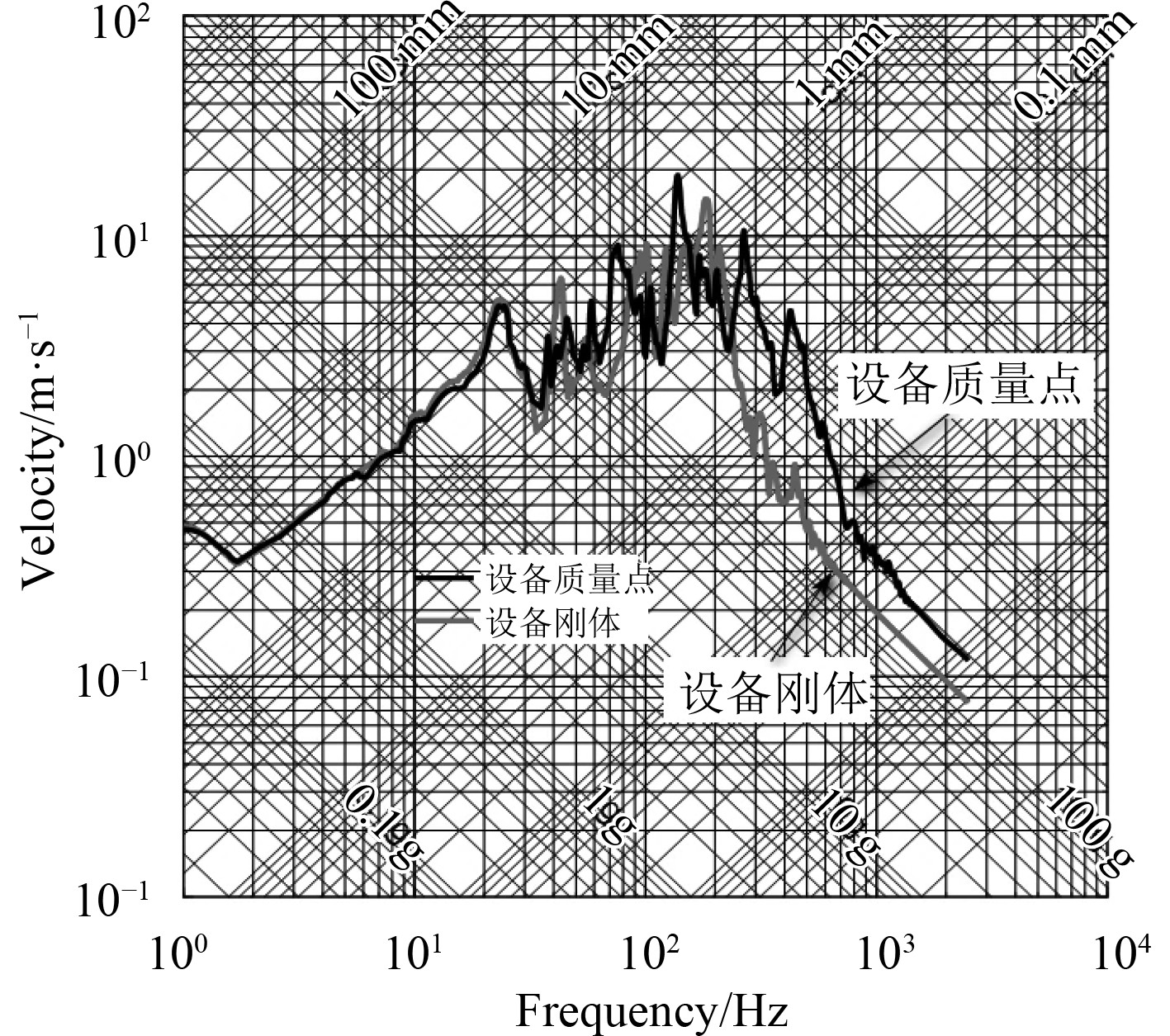
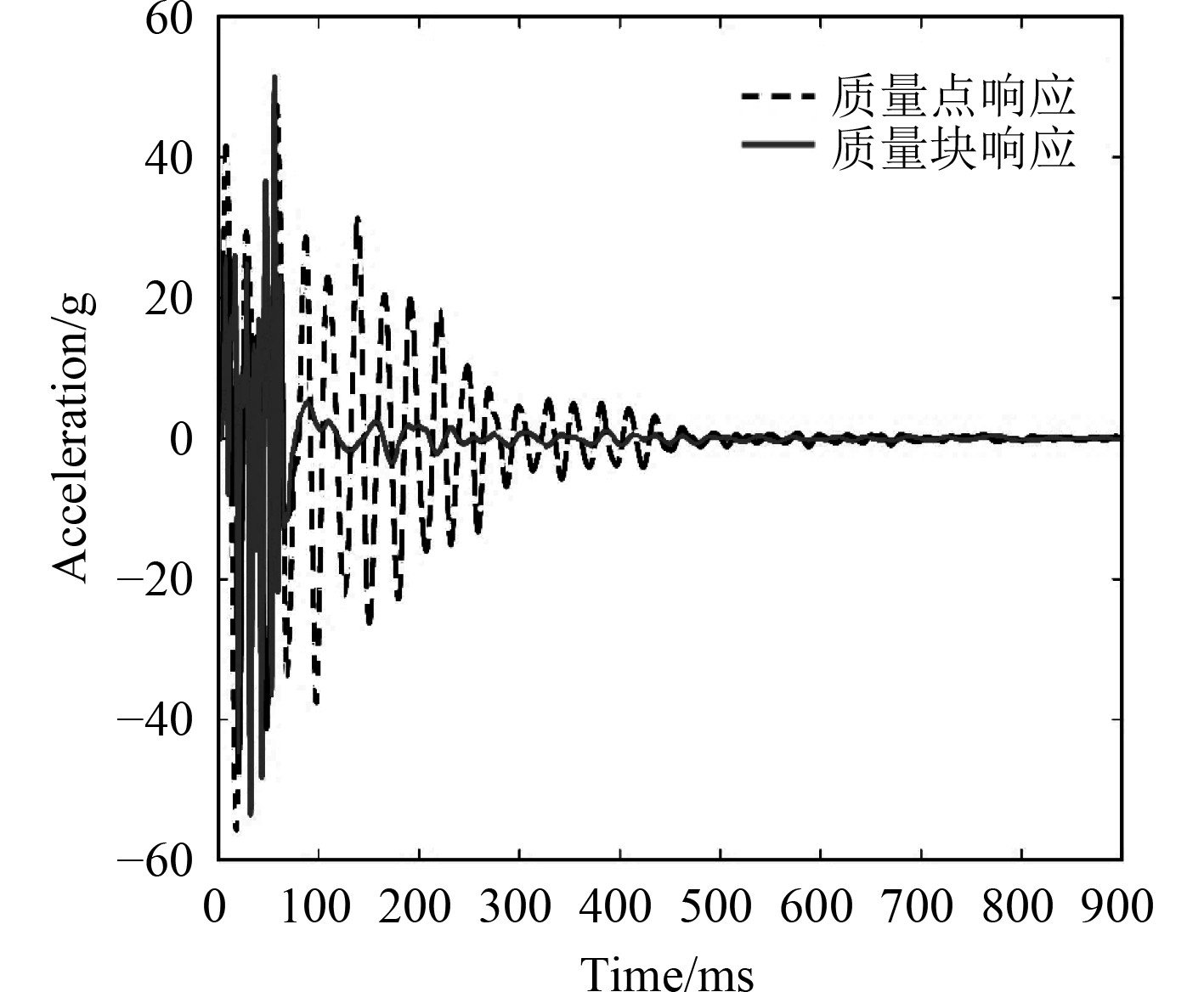
图9对比了分别采用质量点和质量块建模时冲击环境的预报结果,可以发现不同的建模方式对低频段响应谱基本没有影响,由于引入了质量块自身的刚度,相比质量点模型,其响应谱速度有所降低,高频段谱加速度也有所下降,2种建模方式在中低频区域吻合度较高,高频段则差异较大。图10为2种建模方式下设备的加速度响应时历曲线,两者响应峰值相差约5%。考虑到设备的安装频率一般在中低频区域,此区间内2种建模方式得到的设备冲击环境的预报结果差异很小,因此使用弹簧振子质量模型可以满足工程精度的需要同时可以显著提高建模的效率。
|
图 9 质量点及质量块模型冲击响应谱对比 Fig. 9 Comparison of shock environment spectrum of mass point model and mass body model |
|
图 10 质量点及质量块模型加速度响应对比 Fig. 10 Comparison of acceleration response of mass point model and mass body model |
对于舰上大型分布式设备,其覆盖范围内不同位置处的冲击环境必然存在差异。设备抗冲击设计主要关注安装频率处的响应,而在冲击环境的定义中,冲击响应谱在设备安装频率处的谱值即为此频率上的最大响应。因此只需要确定设备的响应即可获得设备安装频率处的冲击环境值。选取设计谱时,应以设备安装频率处的响应为主,同时结合各安装点的冲击环境综合评估设备的冲击环境。
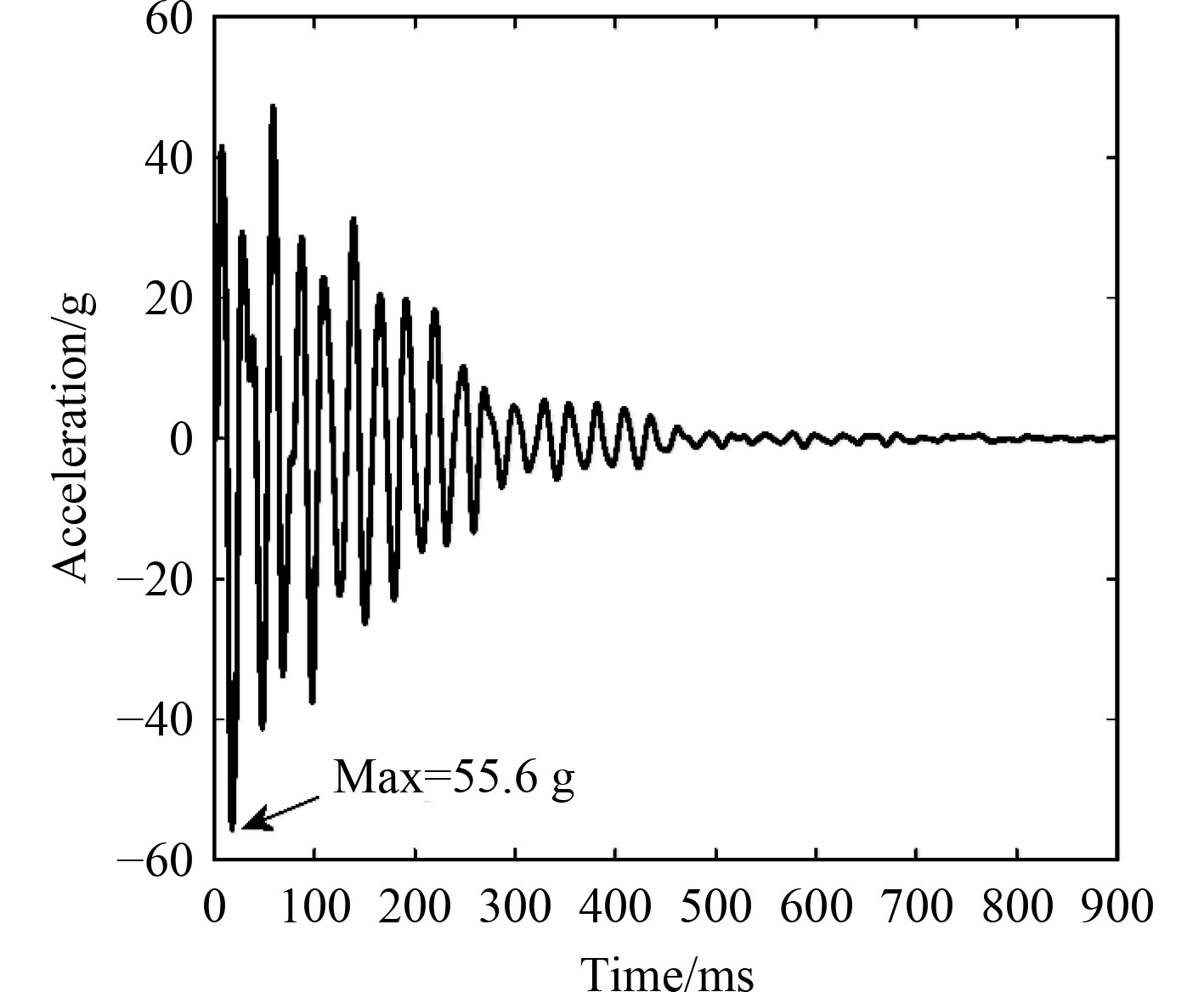
以设置在2甲板上的设备为例,其安装频率设定为50 Hz,设备冲击环境设计谱的等速度段以设备质心处响应的最大值来确定,该设备质心处的加速度时程响应如图11所示,最大加速度为55.6 g,对应的谱速度为V=A/2πf=1.73 m/s,故设备冲击环境的设计谱速度可以取为1.73 m/s,以此确定设计谱的等速度段,而等位移段和等加速度段并不在设备的安装频率处,则可以根据设备各安装点的冲击响应谱来确定。以6个安装点为例,各安装点的位移和加速度设计谱值如表1所示。
|
|
表 1 设备各安装点冲击环境 Tab.1 Shock environment of equipment installation points |
|
图 11 分布式设备安装频率处加速度响应 Fig. 11 Acceleration response on equipment installation frequency |
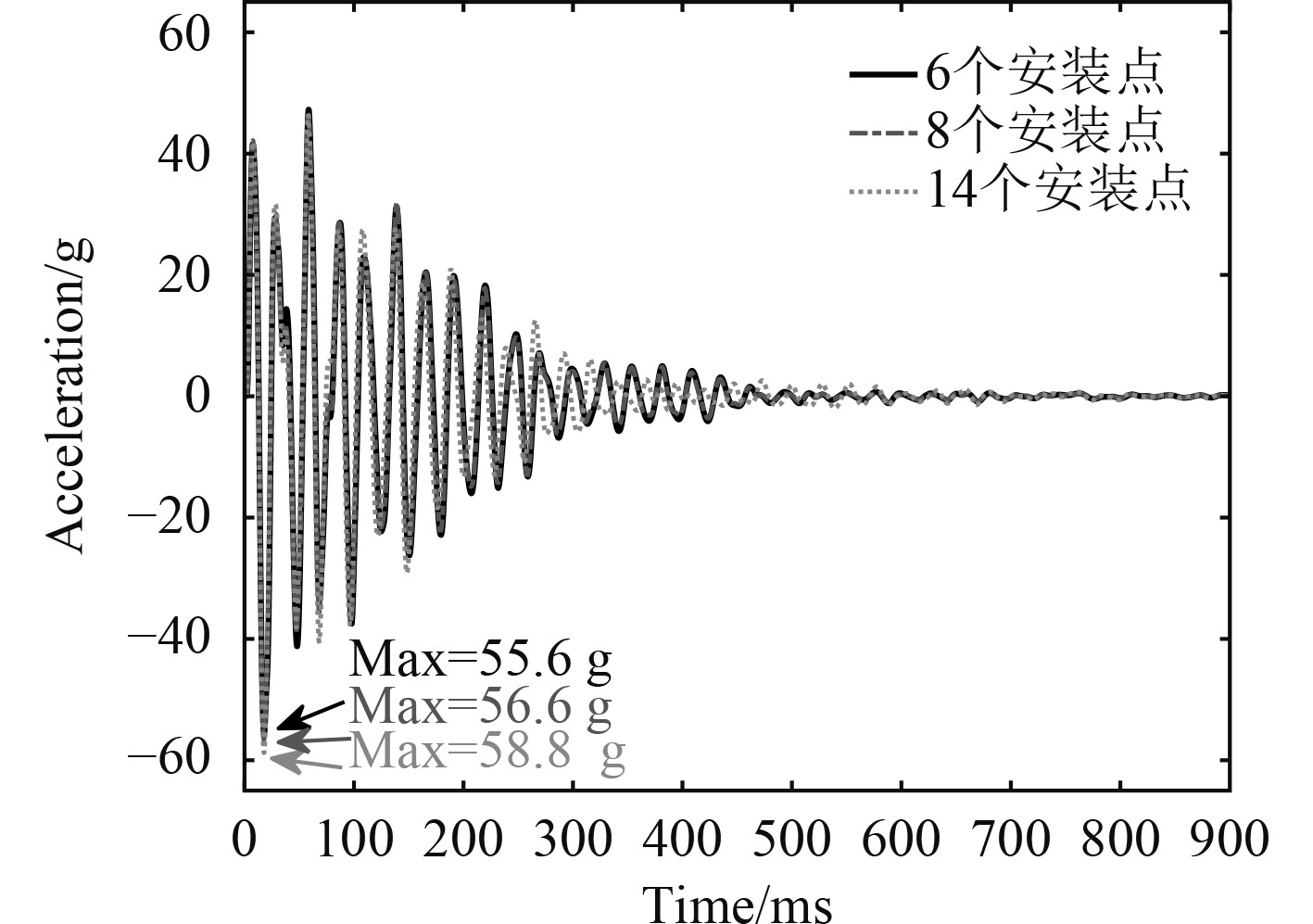
舰上大型设备与结构基座需要通过螺栓进行连接,而在设备冲击环境预报的阶段,设备的详细安装方式往往无法确定,尤其是安装螺栓的数量。考虑到安装点数量的不确定性对设备的冲击环境预报产生的影响,仍以该设备为研究对象,分别建立8个安装点和14个安装点的动力学预报模型,得到不同安装点数量对设备冲击响应的影响,如图12所示。可以看出,设备安装点数量变化时,设备质心处的加速度峰值及时历曲线差异较小,因此可以忽略设备安装点数量的不确定性对冲击环境预报结果的影响。
|
图 12 不同数量安装点设备加速度响应 Fig. 12 Acceleration response of different equipment installation points |
本文针对典型设备进行了水下非接触爆炸载荷下的冲击环境计算,研究船体结构-设备的冲击环境预报动力学建模方法,得到以下结论:
1)船体结构板架的动力学建模可以根据板架刚度和质量等效的原则进行简化。结构网格尺度对低频段区域的冲击环境预报结果影响较小,在中高频段区域会引起较大的差异,在进行全舰冲击环境预报之前,应综合考虑船体板架的骨材布置和设备的安装情况,选取合适的网格尺寸。
2)设备的基座结构会影响设备的冲击环境,在对基座结构进行建模时可遵循刚度和质量等效的原则,同时需要关注设备基座根部及面板处冲击环境的差异,根据设备的安装情况选择合适的冲击环境输出位置。
3)小尺度设备可采用弹簧振子型式进行模拟。大型分布式设备应以设备安装频率处的响应为主,同时结合各安装点处的冲击环境预报值来确定,安装点数量的不同对大型设备的冲击环境预报结果影响较小。
| [1] |
崔杰, 李烨, 陈莹玉, 等. 舰船全船冲击环境数值预报方法研究[J]. 振动与冲击, 2015, 34(17): 88-93.
|
| [2] |
董九亭, 刘建湖, 汪俊, 等. 水下爆炸下舰艇不同部位冲击环境数值分析[J]. 中国舰船研究, 2018, 13(5): 32-38. |
| [3] |
吴子奇, 王耀辉, 吕帅, 等. 水下爆炸作用下箱型梁舰船冲击环境数值研究[J]. 舰船科学技术, 2013, 35(3): 19-26. DOI:10.3404/j.issn.1672-7649.2013.03.005 |
| [4] |
谷鸿平, 黄河, 孟献策, 等. 舰载导弹在水下爆炸作用下的冲击环境数值仿真[J]. 舰船科学技术, 2020, 42(11): 35-39. DOI:10.3404/j.issn.1672-7649.2020.11.007 |
| [5] |
孙丰, 吴彬, 王喆, 等. 舰船水下爆炸冲击环境实用建模方法[J]. 舰船科学技术, 2014, 36(4): 22-26. DOI:10.3404/j.issn.1672-7649.2014.04.004 |
| [6] |
周璞, 许庆新, 华宏星. 舰船设备冲击动力响应在不同边界条件下的比较[J]. 噪声与振动控制, 2003(4): 19-21. DOI:10.3969/j.issn.1006-1355.2003.04.006 |
| [7] |
贾则, 陈高杰, 高浩鹏, 等. 水下爆炸冲击波和气泡脉动载荷联合作用下舰船冲击响应研究[J]. 中国测试, 2018, 44(12): 28-32. DOI:10.11857/j.issn.1674-5124.2018.12.005 |
| [8] |
仇栋熠, 尹群. 浅层水中爆炸载荷作用下舰船动态响应及设备冲击环境研究[J]. 江苏科技大学学报, 2007, 21(4): 12-17. |
| [9] |
刘云龙, 汪玉, 张阿漫. 基于二阶双渐近法的双层圆柱壳在水下爆炸作用下的鞭状运动[J]. 爆炸与冲击, 2014, 34(6): 691-700. DOI:10.11883/1001-1455(2014)06-0691-10 |
 2022, Vol. 44
2022, Vol. 44
