2. 武汉长江船舶设计院有限公司,湖北 武汉 430062
2. Wuhan Changjiang Ship Design Institute Co., Ltd., Wuhan 430062, China
船舶在航行过程中难免会遇到较大的风浪,对船舶安全航行造成了较大的威胁[1]。强大的风压和波浪流冲击船体,使其发生摇摆,轻则导致船舶偏离既定航线,重则导致船上货物发生倾覆等情况[2]。为保障船舶在海上安全航行,对其受到风浪流冲击时的阻力进行研究成为航海领域首要研究目标之一。
文献[3]和文献[4]中对风浪流中船舶运动阻力进行仿真分析。前者通过对船舶、波浪和船受到的荷载进行时域数值计算,依据该数值建立高阶边界元,再使用二阶曲面元对船阻力进行模拟。但该方法受船舶速度势空间偏导数影响,其模拟结果不够准确。后者使用Green函数源对船舶频域求解后,实现风浪流中船舶阻力模拟。但该方法仅从漂移力角度展开研究,其研究范围较狭窄。
面对上述风浪流中船舶阻力仿真分析中存在的缺陷,本文提出风浪流变化对船舶航行阻力的影响仿真分析方法,并在其中应用到了三维模拟技术。
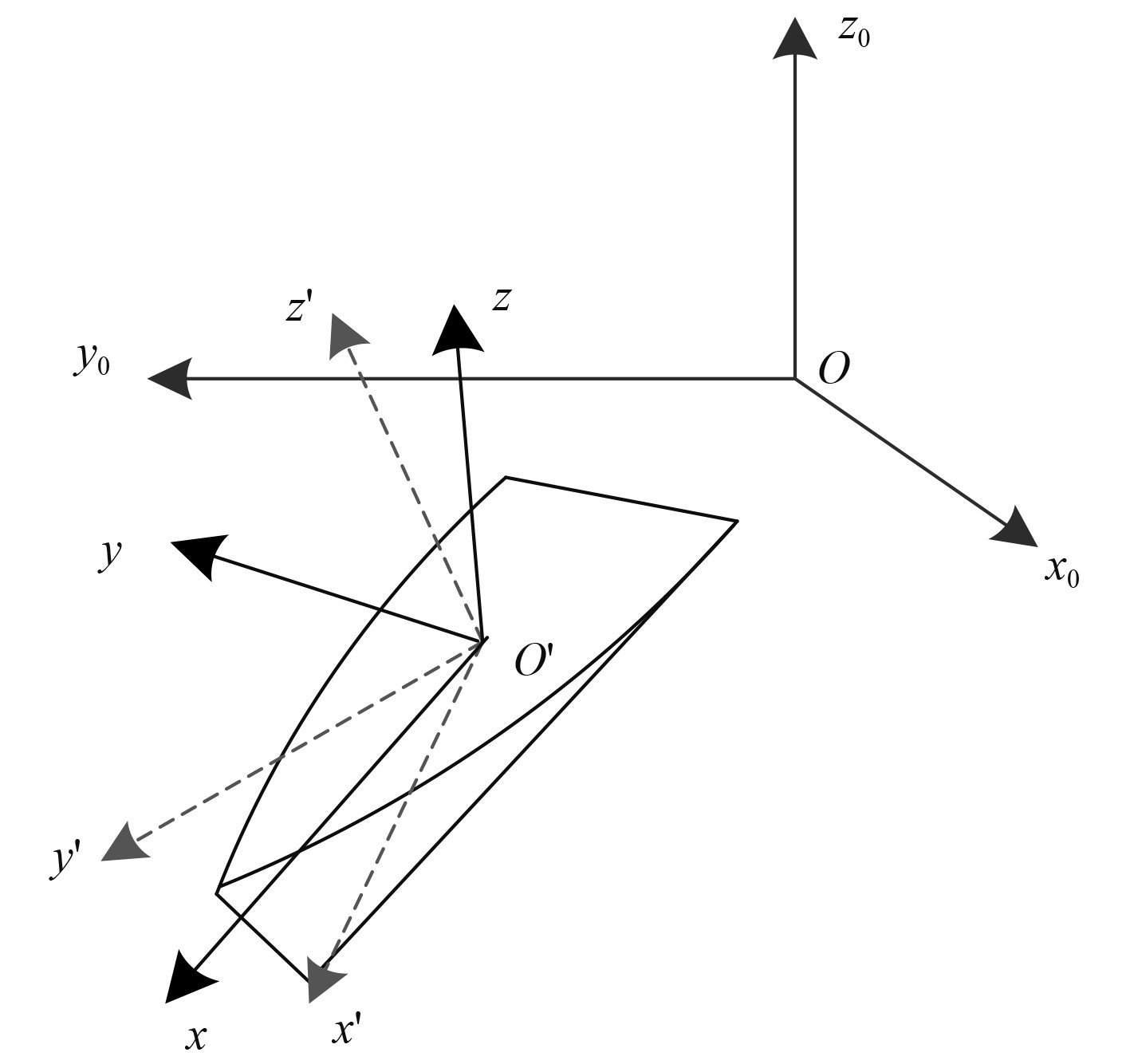
1 风浪流变化对船舶航行阻力的影响 1.1 运动坐标系当船舶在风浪流中航行时,通常使用空间固定坐标系、船体上的运动坐标系和参考坐标系对其进行标定。空间固定坐标系也称为大地坐标系,是负责对风浪流场进行标记的坐标系,不受船体和风浪流运动影响。船体上运动坐标系的圆心是船体重心,该坐标系随着船体运动而转动。参考坐标系是当船舶为静止状态时域船上运动坐标系重合的坐标系,其横纵坐标分别描述船舶的运动姿态。当船舶为0时速时,建立船舶运动坐标系如图1所示。
|
图 1 船舶航行运动坐标系示意图 Fig. 1 Schematic diagram of ship navigation motion coordinate system |
依据船舶运动坐标系关联关系,使用数学方法计算风作用到船体上的作用力。令
| $ \left\{ \begin{aligned} & {X_{wind}} = 0.5 \times \zeta {B_f}U_R^2{Q_{wx}}({\alpha _R}) \text{,} \\ & {Y_{wind}} = 0.5 \times \zeta {B_s}U_R^2{Q_{wy}}({\alpha _R}) \text{,} \\ & {N_{wind}} = 0.5 \times \zeta {B_s}{L_{OA}}U_R^2{Q_{wn}}({\alpha _R}) \text{。} \end{aligned} \right. $ | (1) |
式中:
波浪流作用到船体上时,会产生一阶波浪干扰力和二阶波浪干扰力。其中二阶波浪干扰力具备非线性特征,可改变船舶航行的轨迹和航向。因此,在此仅考虑二阶波浪干扰力对船舶的作用力。令
| $ \left\{ \begin{gathered} {X_{wave}} = 0.5 \times \zeta 'LI_D^2{Q_{XD}}(\lambda )\cos \theta\text{,} \hfill \\ {Y_{wave}} = 0.5 \times \zeta 'LI_D^2{Q_{YD}}(\lambda )\sin \theta \text{,} \hfill \\ {N_{wave}} = 0.5 \times \zeta '{L^2}I_D^2{Q_{ND}}(\lambda )\sin \theta \text{。} \end{gathered} \right. $ | (2) |
式中:
以作用到船舶上的风压和波浪作用力为基础,建立船舶横摇阻力运动数学模型。先构建纵向风浪流的船舶横摇运动方程。当船舶的横摇和纵摇角度较为微小时,其排水量保持不变,此时船舶横摇阻力力矩和恢复阻力力矩之间为非线性关系,其可描述为:
| $ {E_{\phi \phi }} \times \ddot \phi + \delta {E_{\phi \phi }} \times \ddot \phi + F(\dot \phi ,t) + K(\phi ,t) = 0 \text{。} $ | (3) |
式中:
以1次加3次立方项阻力描述船舶横摇阻力,其表达式如下:
| $ F(\dot \phi ,t) = {F_1}\dot \phi + {F_3}{\dot \phi ^3} \text{。} $ | (4) |
式中:
对公式(4)展开处理并代入公式(3),得到船舶横摇阻力运动数学模型,其表达式如下:
| $ \begin{gathered} {E_{\phi \phi }} \times \ddot \phi + \delta {E_{\phi \phi }} \times \ddot \phi + {F_1}\phi + {F_3}\ddot \phi + \hfill \\ \Delta \cdot \left\{ {\vartheta \phi + gm(t)\phi + {K_3}{\phi ^3} + {K_5}{\phi ^5}} \right\} = 0 \text{。} \end{gathered} $ | (5) |
式中:
使用虚拟现实技术建立船舶航行阻力三维仿真模型,在此利用Creator三维软件构建船舶航行阻力三维模型。Creator三维软件构建船舶航行阻力三维模型详细过程如下:
步骤1 确定船舶三维模型位置。利用专业相机拍摄船舶图像后,将其转换成.dwg格式,然后使用AutoCAD绘图软件将其分成若干个单元,然后导入到Creator三维软件内生成初始船舶三维模型。
步骤2 制作模型纹理。依据船舶实际纹理,使用Vega Prime视景仿真软件对船体以及海面进行纹理贴图。
步骤3 将船舶航行阻力运动数学模型计算的数据导入到三维仿真模型内,构建数据类型结构并完成数据预处理。
步骤4 整理完船舶航行阻力运动数学模型数据后,依据该数据在船舶航行阻力三维模型内展开模拟仿真分析。
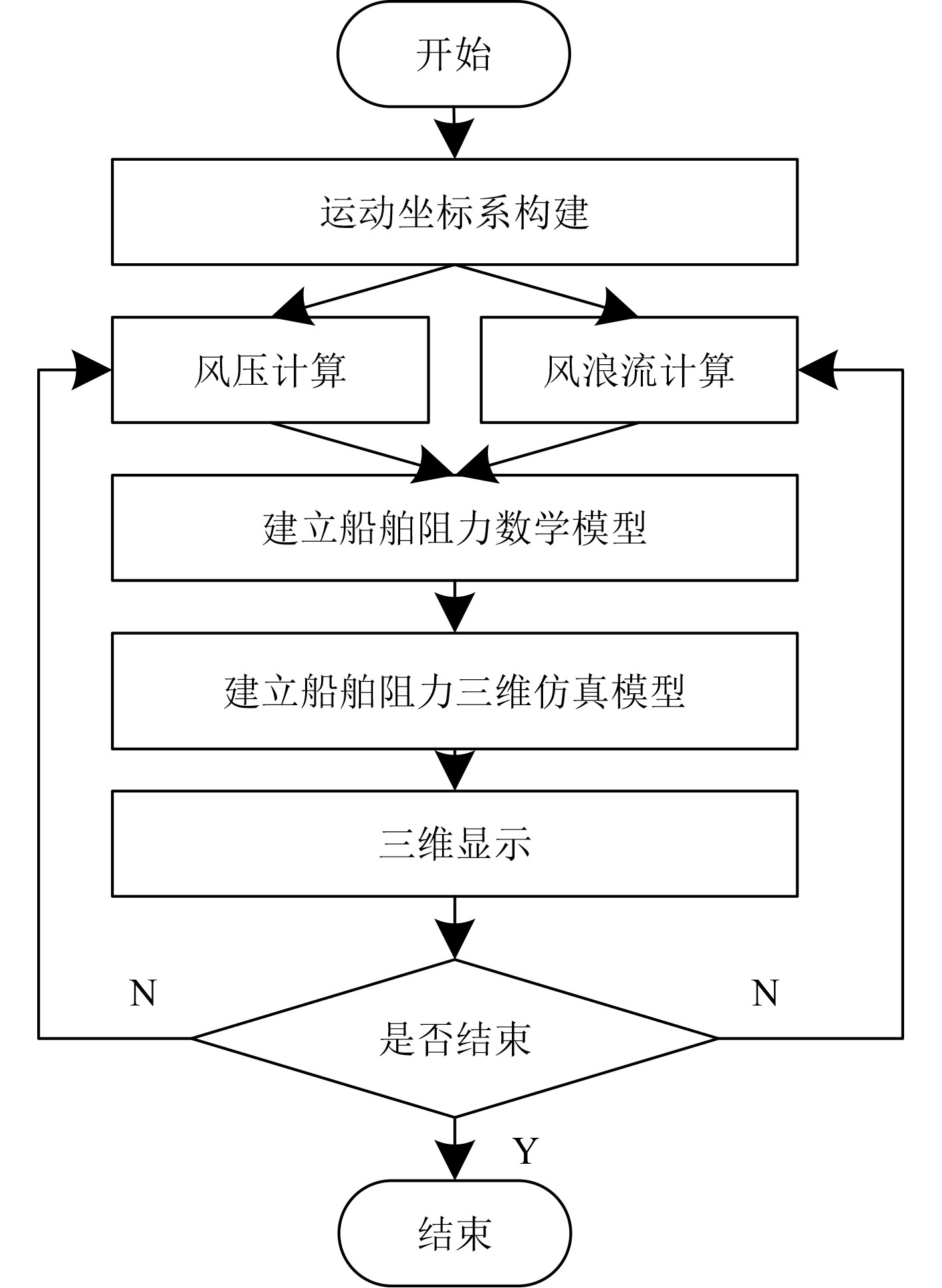
结合上述船舶航行阻力三维仿真建模过程,考虑风浪流变化对船舶航行阻力分析流程如图2所示。
|
图 2 考虑风浪流变化对船舶航行阻力分析流程示意图 Fig. 2 Flow diagram of resistance analysis considering wind, wave and current changes |
以某大型集装箱运输船作为实验对象,对本文方法的应用性能展开验证。表1为该大型集装箱运输船主要参数,表2为仿真实验模拟环境。
|
|
表 1 大型集装箱运输船主要参数 Tab.1 Main parameters of large container ships |
|
|
表 2 仿真实验条件设置 Tab.2 Setting of simulation experiment conditions |
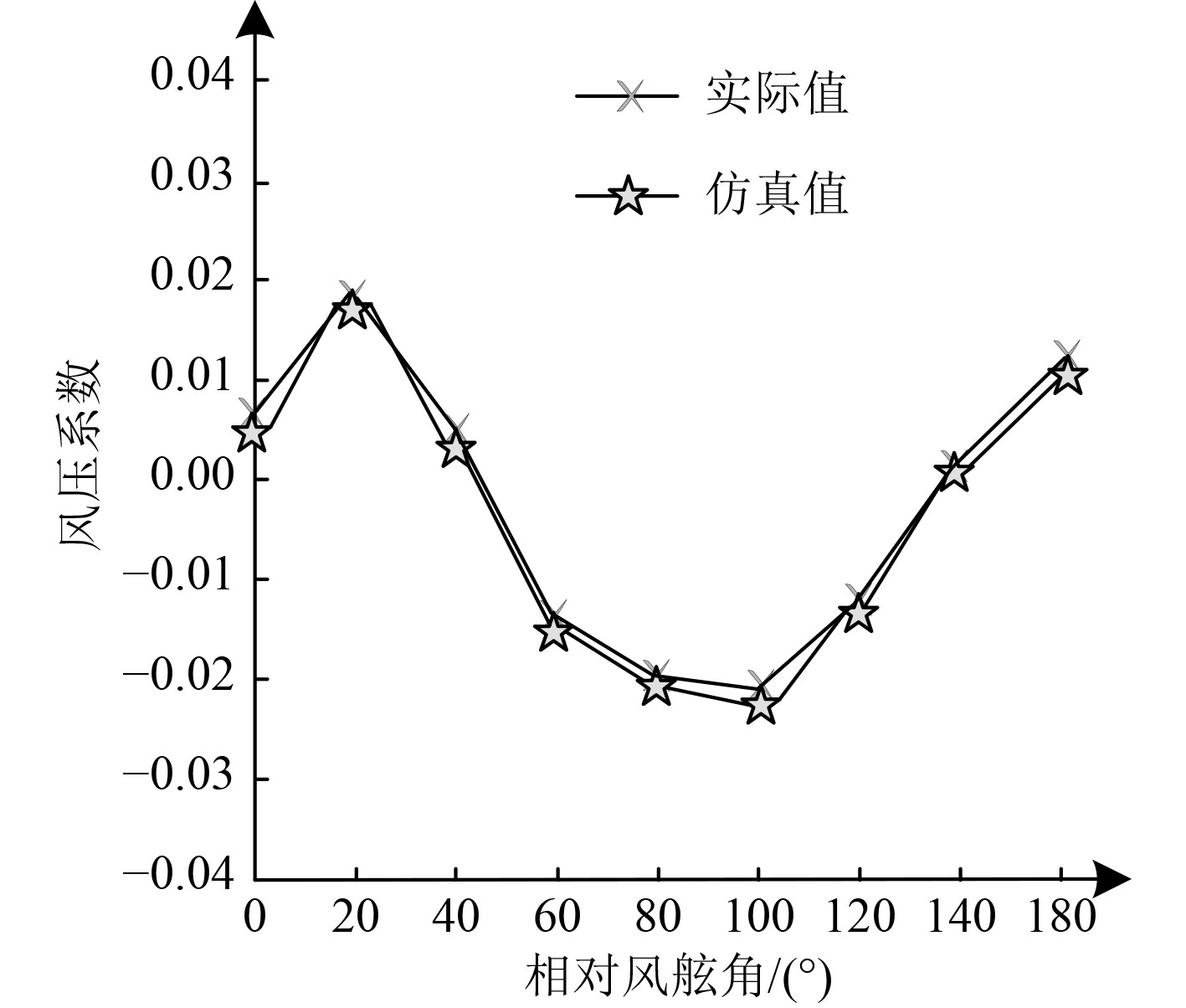
以风压系数计算结果作为衡量本文方法仿真分析船舶航行时受风浪流影响可靠性指标,测试在不同相对风舷角情况下,本文仿真风压结果和实际仿真结果,如图3所示。可知,本文方法仿真的风压系数数值与其实际数值几乎完全重合。该结果说明,本文方法计算船舶受风压力数值较为精准。
|
图 3 可靠性验证结果 Fig. 3 Results of reliability verification |
相对于船型建模来说,海面建模则较为复杂。以海面建模为衡量指标,设置海面风速为2 m/s和6 m/s情况下,测试本文方法建立海浪运动画面能力,结果如图4所示。

|
图 4 海浪运动三维建模效果 Fig. 4 Effect of 3D modeling of ocean wave motion |
分析可知,本文方法可较好地呈现船舶航行阻力仿真画面,具备良好的交互性和仿真画面呈现能力。
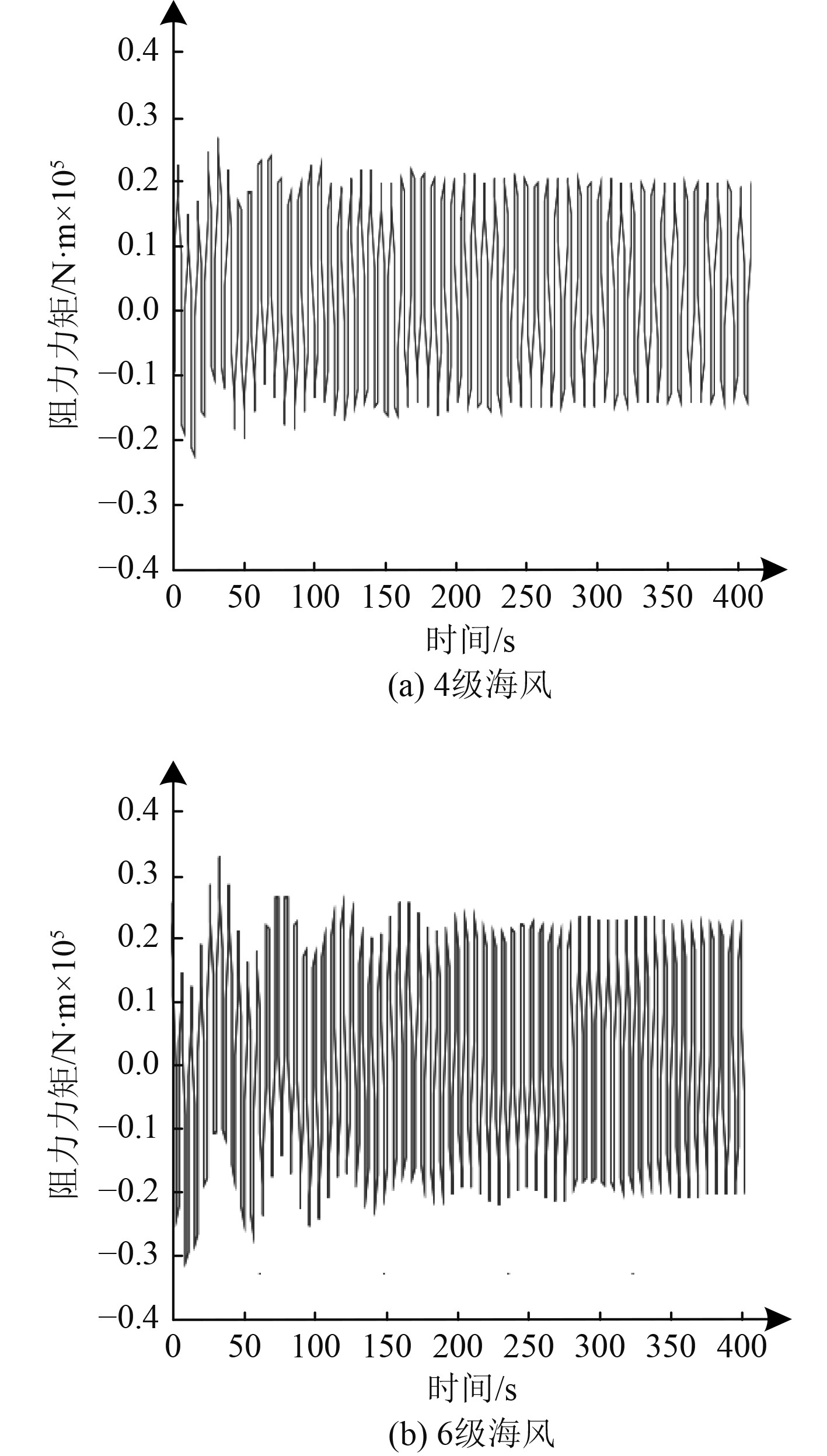
2.3 船舶航行阻力分析在三维仿真环境内设置4级海风和6级海风情况,在该情况下,对该船舶所受风浪流阻力力矩变化进行仿真,结果如图5所示。
|
图 5 不同海风情况下船舶航行阻力力矩变化情况 Fig. 5 Variation of ship navigation resistance torque under different sea winds |
分析可知,当海面风力较小时,船舶航行受风浪流冲击后的阻力力矩也较小,同理海面风力较大时船舶航行的阻力力矩也较大。当风浪流冲击到船体上时,船舶在不同海风级数时的船舶阻力力矩均会发生振荡情况,但4级海风时其振荡情况较为轻微。当风浪流冲击到船体上后,随着时间的增加,船体上的阻力力矩呈现逐渐平稳状态,其中4级海风时,船体阻力力矩恢复较为迅速。综上所述,本文方法可在不同级数海风情况下对其受风浪流冲击后的阻力力矩变化进行模拟,其具备良好的应用效果。
以船舶偏航角度作为衡量指标,设置船舶航行速度为12 km/h,风浪流强度为3级。从船舶航行阻力遭遇风浪流频率角度展开测试,结果如图6所示。
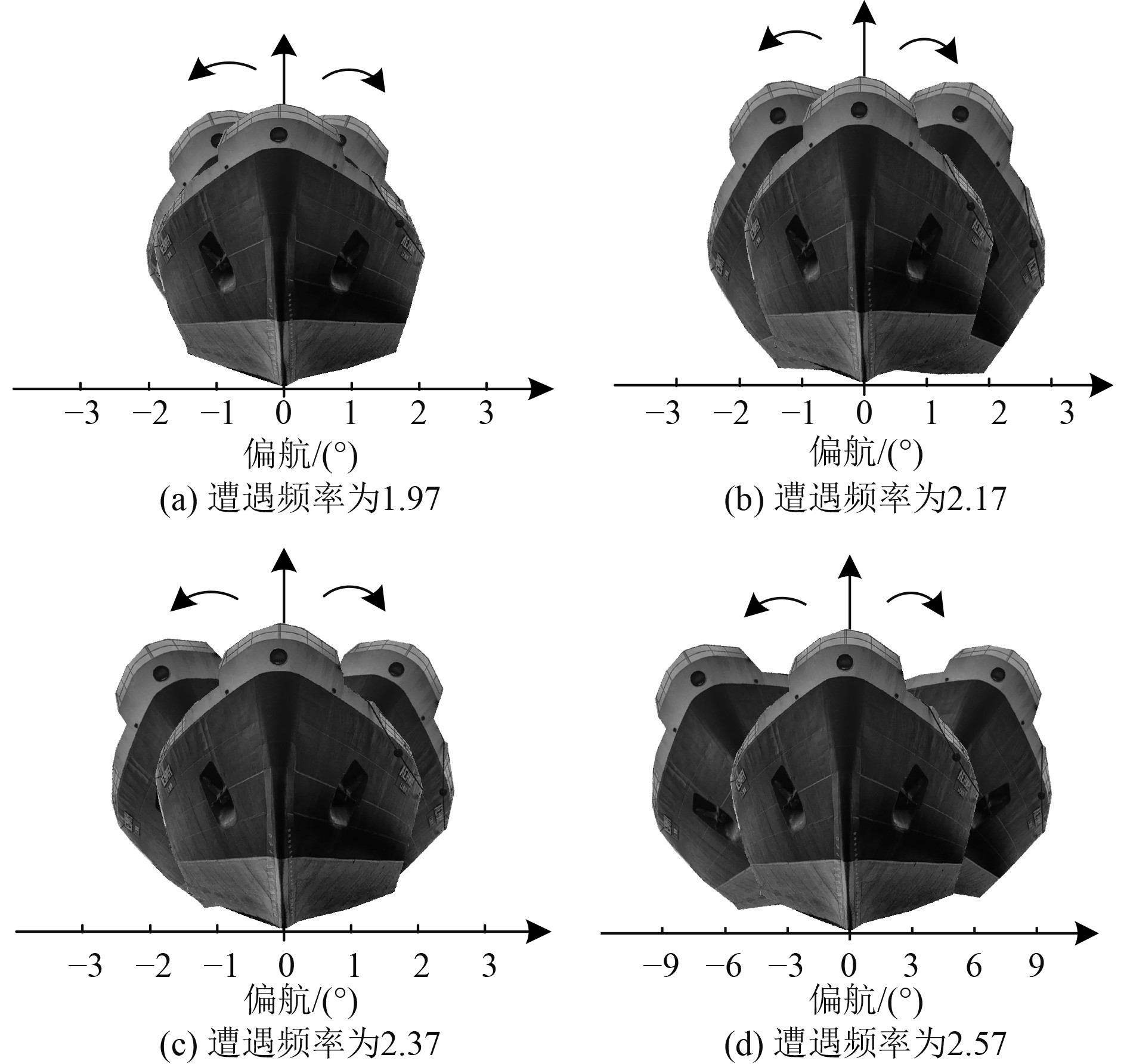
|
图 6 不同遭遇频率时船舶航行受阻力影响偏航情况 Fig. 6 Yawing of ship under the influence of resistance at different encounter frequencies |
分析可知,船舶在航行过程中,风浪流的遭遇频率越小,则其受阻力数值越小,偏航程度越低。在风浪流遭遇频率为1.97和2.17时,该船舶航行偏航度数为−2°~2°。但风浪流遭遇频率为2.17时,船舶虽然偏航程度与风浪流遭遇频率为1.97时相差不大,但船舶横摆程度略大。随着风浪流遭遇频率增加,该船舶航行偏航度数也逐渐增加,船舶的横摆程度也在增加。其原因在于风浪流遭遇频率越大,说明此时海面上风压和船受到的阻力越大,因此其偏航程度也较高。
3 结 语本文提出风浪流变化对船舶航行阻力的影响仿真分析方法,在该方法内应用到了三维仿真技术,利用三维模拟软件构建船舶航行受风浪流影响其阻力变化仿真环境,可清晰明了地呈现不同情况下船舶偏航、阻力力矩等变化情况。本文方法所构建的三维场景较为逼真,其在应用过程中具备良好的交互能力和画面呈现效果。
| [1] |
曹洪建. 某内河船型线变化对阻力和自航性能的影响分析[J]. 船海工程, 2020, 49(1): 40-44. DOI:10.3963/j.issn.1671-7953.2020.01.010 |
| [2] |
李亮, 刘登成, 洪方文, 等. 风浪作用下船体纵摇运动对螺旋桨激振力特性影响分析[J]. 中国造船, 2020, 61(2): 1-13. DOI:10.3969/j.issn.1000-4882.2020.02.001 |
| [3] |
李志富, 任慧龙, 石玉云. 基于加速度势和高阶边界元的船舶在波浪中运动数值模拟[J]. 船舶力学, 2019, 23(9): 1034-1044. DOI:10.3969/j.issn.1007-7294.2019.09.002 |
| [4] |
张晓磊, 熊伟, 王祖温. 波浪漂移力作用下的救助船操纵运动计算与仿真[J]. 大连海事大学学报, 2019, 45(3): 75-84. |
 2022, Vol. 44
2022, Vol. 44
