2. 广东海洋大学 海洋工程学院,广东 湛江 524088
2. Guangdong Ocean University, College of Ocean Engineering, Zhanjiang 524088, China
沿海小型风电运维船是一种专业化作业船舶,主要任务是运维保障海上风力发电机组正常运行。双体船由于拥有宽敞的甲板和良好的稳性,是沿海小型风电运维船船型的优先选择。随着国内风电产业的发展,粤西海域也已开始投建海上风电场。此海域风能丰富,但地处潮间带,岛礁暗礁多,涌浪大,水流急,风浪大。目前工作于该海域风电场的风电运维船主要是其他海域相近船舶改造而来,作业和环境适应性等方面存在各种不足。因此,有必要结合船舶快速性需求和双体船性能优点,针对该海域设计建造专用的风电运维船。
对国内外现有同类船舶的总体技术参数进行对比分析后,进一步优化方案。优化思路是在保持主机方案不变和满足甲板载荷要求的前提下,适当牺牲续航力和舒适性等,尽量提高航速和减小吃水等。本文基于Maxsurf软件,开展快速性多方案对比分析,能够在较短时间内得到一个定性的结论,为方案设计提供参考。
1 设计目标设定原设计方案水线长19.80 m,型宽8.30 m,片体宽度2.60 m,型深2.70 m,设计吃水1.59 m(含基线以下首部部分则为1.80 m),排水量75 t(设计吃水)、甲板载荷5 t,航速19 kn。
根据风电场的布局,认为原设计航速过低,需要从19 kn提高到22 kn以上,并具有最大26 kn以上的应急航速。通过分析粤西海域环境及风电作业特点,并统计其他尺寸和载荷相近的双体风电运维船的总体技术参数[1-2],初步认为原设计方案的75 t排水量对于甲板载荷5 t而言过大,存在25 t以上的优化空间。这就为通过减小片体宽度和吃水、缩短船长等措施以取得阻力性能较好的方案提供了可能。
2 Maxsurf进行船舶快速性预报的基本理论Maxsurf适用于各种船舶设计、分析和建造,具有船体建模、稳性分析、运动和阻力预测、结构建模、结构分析等功能。
假定船体总阻力由与雷诺数有关的粘性阻力和傅汝德数有关的兴波阻力组成,Maxsurf选用ITTC-57摩擦阻力计算公式来求解粘性阻力,并按19th ITTC所的规定设置粗糙度补贴系数[3]。Maxsurf计算双体船兴波阻力使用基于Michell[5]“薄船”理论的细长体方法,参见Tuck等[6-7]和Couser等[8]的研究。
2.1 粘性阻力计算粘性阻力计算公式,即
| $ R_{\upsilon }={{C}}_{f}(1+k)\frac{1}{2}\rho {V}^{2}S \text{。} $ | (1) |
式中:V为航速,kn;S为湿面积,m2;
ITTC-57推荐的计算摩擦阻力系数
应用细长体法计算双体船阻力时,Maxsurf应用Molland方法自动计算船体形状修正因子[4]:
| $ (1+\beta k)=3.03(L/{▽}^{1/3}{)}^{0.40} \text{,}$ | (2) |
亦可手工指定船体形状修正因子。
2.2 兴波阻力计算计算兴波阻力的细长体方法要求船型关于中轴线对称、长宽比大于5.0~6.0。当长宽比大于7.0时,傅汝德数Fr高达1.0,方法亦可给出合理结果。该方法可适用于多种船型,包括多体船型。
假设流体无黏、无漩、不可压缩,且不计破波影响,基于理想流体力学的“映像”假设,把并列的等速平行运动的2条相同船,基于Michell积分,用压力积分可推导出双体船的Michell型“薄船”兴波阻力积分公式[6-11]:
| $ \begin{split}{l}{R}_{w}= & 8\text{π} \rho {k}_{\text{0}}{\displaystyle {\int }_{ \frac{\text{π} }{\text{2}}}^{\frac{\text{π} }{\text{2}}}{\mathrm{sec}}^{3}\theta }(I^{\text{2}}+J^{\text{2}})\times \\ & 2[1+\mathrm{cos}({k}_{0}{\mathrm{sec}}^{2}\theta \mathrm{sin}\theta \cdot S)]{\rm{d}} \theta \text{。} \end{split} $ | (3) |
其中:
| $ \begin{split} I= & \displaystyle {\int }_{-T}^{0}{\displaystyle {\int }_{-\frac{{L}}{{2}}}^{\frac{{L}}{{2}}}{fx}({x}\text{,}{z}){\rm exp}[{k}_{0}{{\rm sec}}^{2}\theta \cdot z]} \times \\ &\mathrm{cos}({k}_{0}\mathrm{sec}\theta \cdot x){\rm{d}}x\cdot {\rm{d}}z \text{,}\\ {J}= &\displaystyle {\int }_{-{T}}^{0}{\displaystyle {\int }_{-\frac{{L}}{{2}}}^{\frac{{L}}{{2}}}{fx}({x}\text{,}{z}){\rm exp}[{k}_{0}{\mathrm{sec}}^{2}\theta \cdot z] }\times \\ &\mathrm{sin}({k}_{0}\mathrm{sec}\theta \cdot {x}){\rm{d}}x \cdot {\rm{d}}z \text{。} \end{split} $ |
双体船的兴波阻力由2部分组成,可认为
为验证方法的可行性,首先利用原设计方案开展快速性计算,并与船模阻力实验结果进行对比。
建立船体模型并划分网格,如图1所示。需要指出的是,Maxsurf默认在船尾生成虚拟附体的网格,若移除将会影响自由表面的波型和波阻计算,故应保留。

|
图 1 网格划分 Fig. 1 Meshing |
求解得到航行速度8~32 kn时,双体风电运维船的阻力和船模实验预报阻力数据见表1,两者对比如图2所示。
|
|
表 1 双体风电运维船阻力计算结果与船模实验预报结果对比表 Tab.1 Resistance calculation results and ship model experiment prediction results |
|
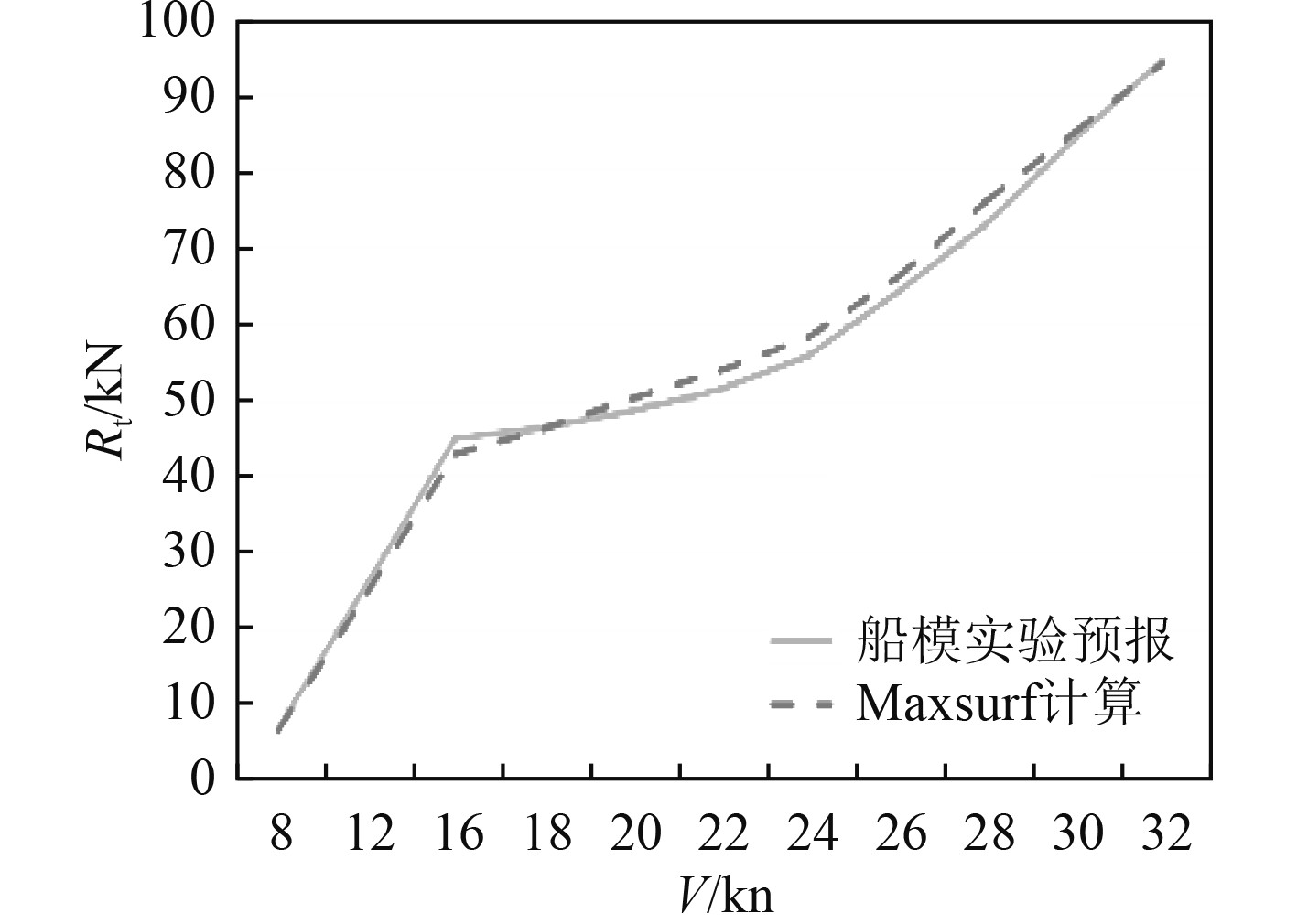
图 2 Maxsurf软件计算阻力与船模实验预报结果对比 Fig. 2 Comparison between resistance calculation results and ship model experiment prediction results |
结果显示,Maxsurf软件计算结果与船模实验预报阻力结果趋势一致,量值接近,误差均小于5%。说明Maxsurf软件计算结果较准确,可信性较高,满足本次评估的计算精度要求。
3.2 快速性改进评估 3.2.1 主尺度调整取值分析双体船阻力可简化为片体阻力和片体间干扰阻力2部分。双体船主尺度系数和线型对片体阻力的影响,具有单体船性质,只是片体长宽比L/b(或长度排水量系数
因此阻力分析应同时关注片体的主尺度系数和线型与片体间关联参数。由于是快速评估,为避免线型优化的难度,仅在Maxsurf软件中利用建模功能对线型进行拉伸。参考文献[14-15],确定评估流程为:初步确定船长L、吃水d、片体宽度b的取值,以K/b,L/b先后作为设计变量在Maxsurf软件中进行快速性计算。
1)船长和吃水
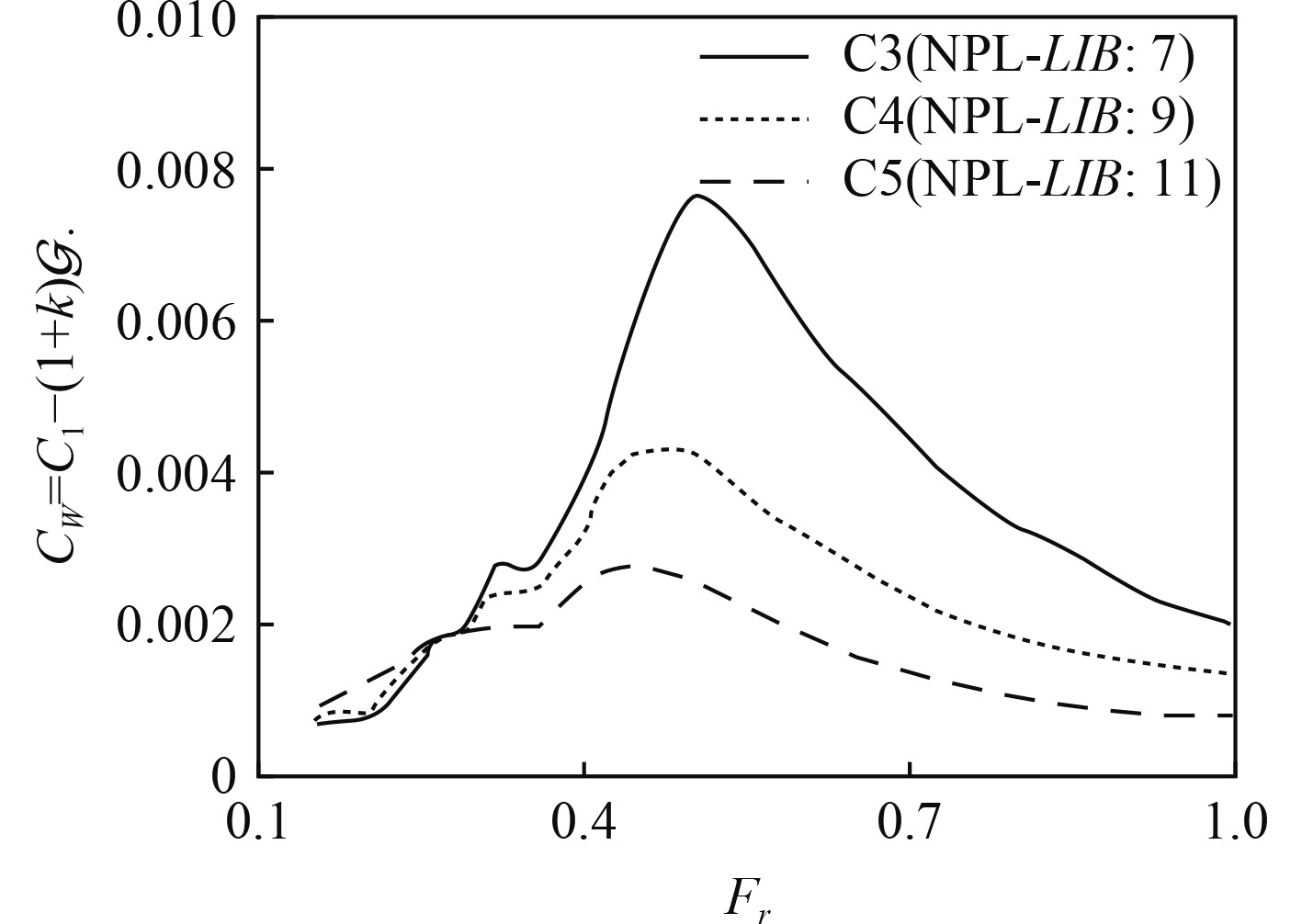
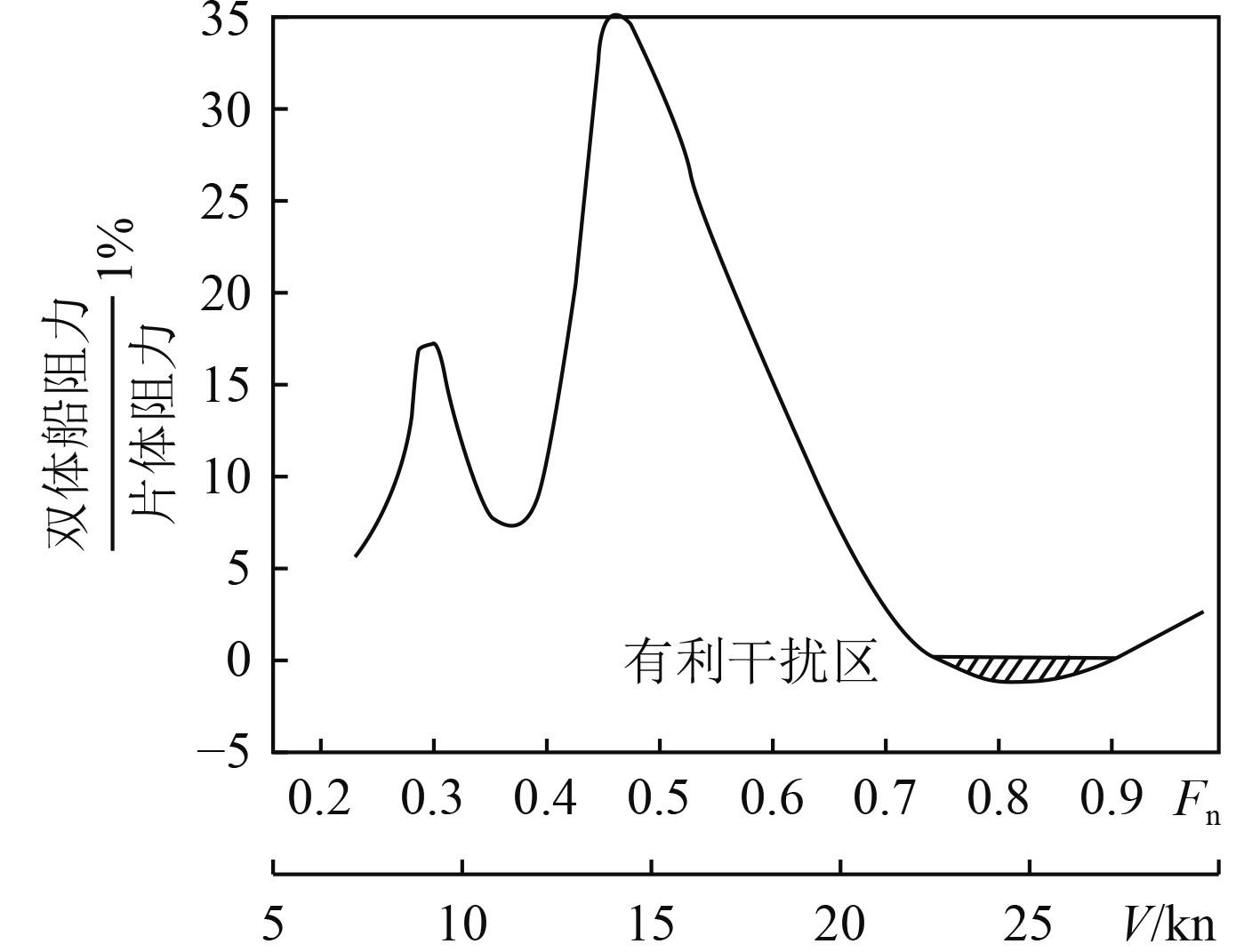
傅汝德数Fr与兴波阻力系数Cw之间的关系曲线如图3所示[11]。可见当傅汝德数Fr>0.6时,兴波阻力呈下降趋势且趋于平缓。根据任务分析,航速22~26 kn,船长不大于20 m,则傅汝德数Fr>0.8,属于高速区,在此基础上分析片体间干扰阻力的有利因素。根据上海船舶设计研究院的双体船试验结果,傅汝德数Fr=0.74~0.9,干扰阻力会出现一个有利干扰区[13],如图4所示。据此,初步选取船长18.5 m,航速22 kn,Fr=0.840。
|
图 3 兴波阻力系数曲线 Fig. 3 Wave resistance coefficient curve |
|
图 4 双体船干扰阻力曲线 Fig. 4 Interference resistance curve of catamaran |
对于吃水d,采取去除首部基线以下部位并光顺首部型线的简单方法,调整为1.47 m。
2)片体宽度b
片体宽度b减小有利于提高L/b比值,也有利于减小排水量,但考虑船舶主机等设备的布置要求,片体宽度不宜过小,初步取2.1 m。
3)片体间距比K/b取值范围
实验研究表明,双体船的兴波附加干扰阻力与片体间距有关,见图5[12]。当片体的间距比K/b取值1.7~2.0时,片体间波系相互干扰剧烈,引起的兴波干扰阻力很大。同时顾及阻力和连接桥重量下,以往设计一般可取K/b=2.0左右,目前为获取更大的甲板面积和进一步减少首波,高速双体船趋于K/b>2.0[13]。

|
图 5 圆舭高速双体船片体间距对兴波阻力的影响 Fig. 5 Effect of hull spacing on wave resistance of catamaran |
分别取片体间距比K/b=1.8,2.2,2.4,2.5,2.6,2.8,2.7,2.8,3.2,3.6,共10组数值,使用Maxsurf计算V=22 kn时的航行阻力。阻力随K/b的变化情况见图6。可知,阻力随着片体间距比K/b增大而减小,并在K/b约大于2.5后趋于平缓。

|
图 6 阻力随K/b不同取值变化情况 Fig. 6 Variation of resistance with different values of K/b |
利用Maxsurf进行兴波模拟计算,可观察到随着K/b增大兴波干扰减缓,部分兴波模拟结果(K/b分别取值为1.8,2.7,2.8)如图7所示。可知,K/b取2.8时2片体间的兴波干扰最为缓和,于是初步确定K/b取值2.8。

|
图 7 兴波情况 Fig. 7 Wave making |
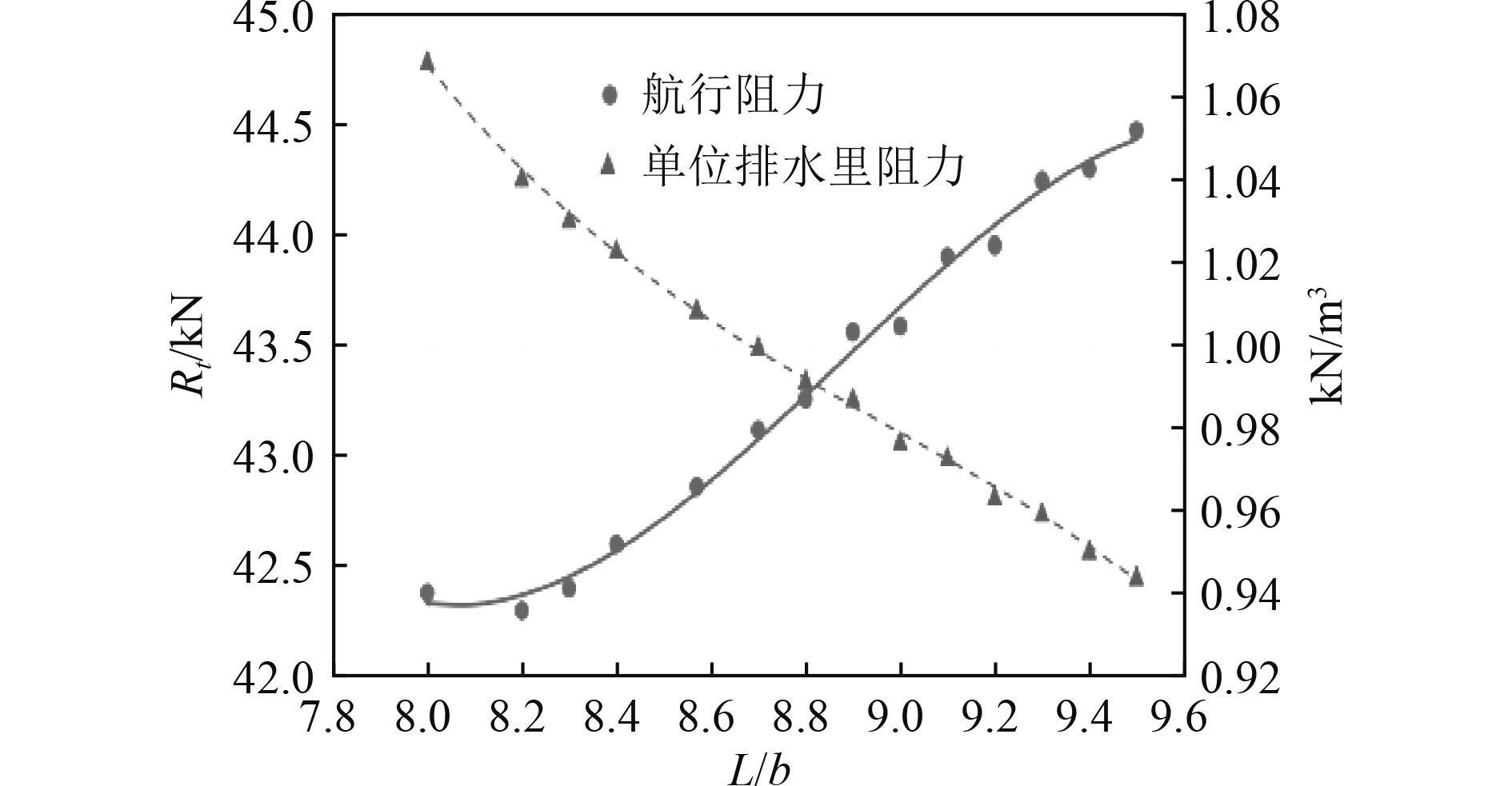
确定片体宽b=2.1 m,K/b=2.8后,长宽比L/b分别取值8,8.2,8.3,8.4,8.57,8.7,8.8,8.9,9,9.1,9.2,9.3,9.4,9.5,共14个数值,利用Maxsurf计算得到阻力及单位排水量阻力,如图8所示。可知在片体宽b取值(受控制排水量和设备维修空间要求影响)确定后,阻力随着L/b增大而持续增大,但单位排水量阻力随着L/b增大而减小。为方便航速预报,折中考虑选取两者交点处即L/b=8.8。
|
图 8 不同K/b船舶阻力与单位排水量阻力对比图 Fig. 8 Comparison of resistance with different K/b and resistance per unit displacement |
修改后的主尺度参数为水线长18.50 m,型宽7.98 m,片体宽度2.10 m,型深2.40 m,设计吃水1.47 m,排水量45.7 t。
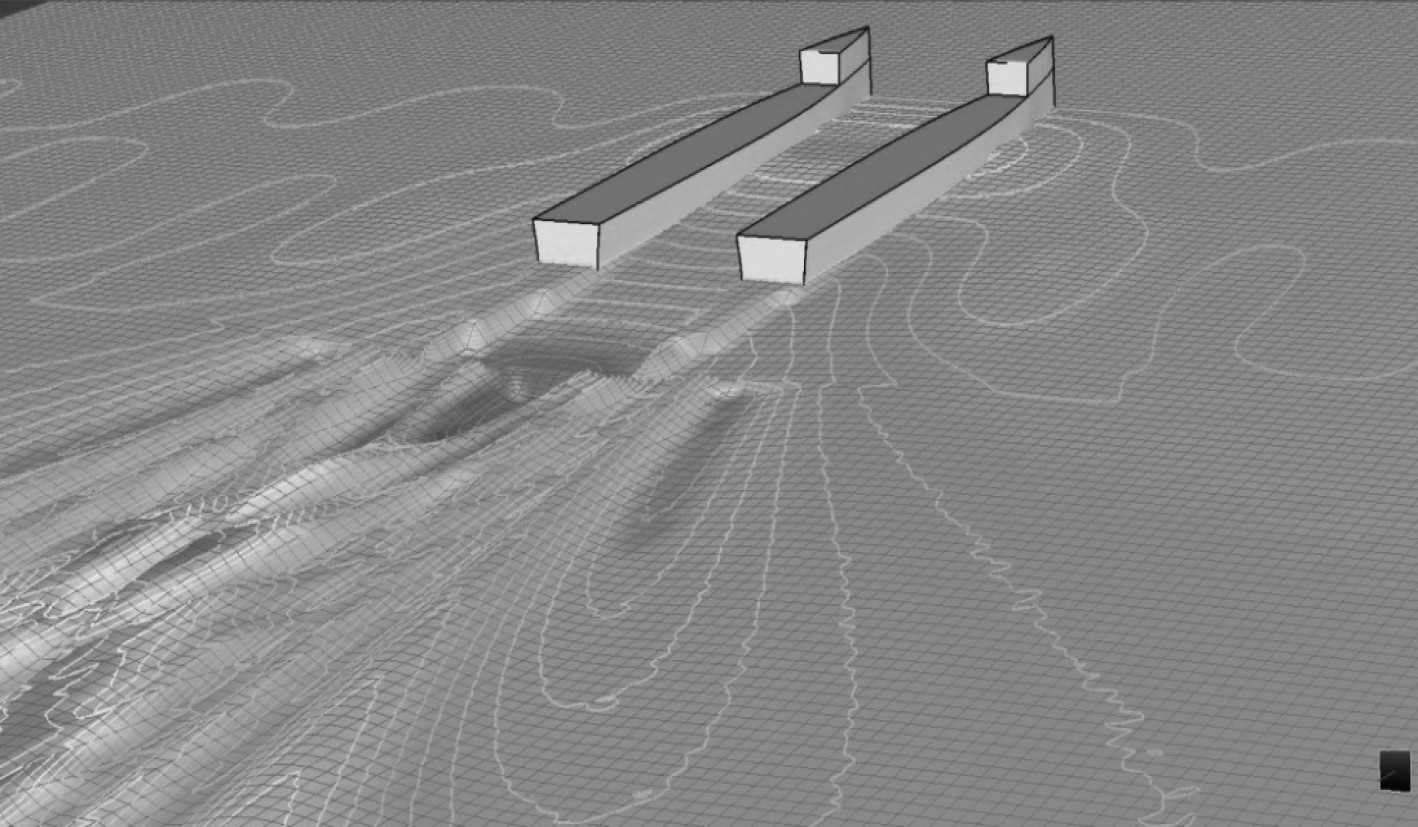
|
图 9 兴波情况(修改后) Fig. 9 Wave making (modified) |
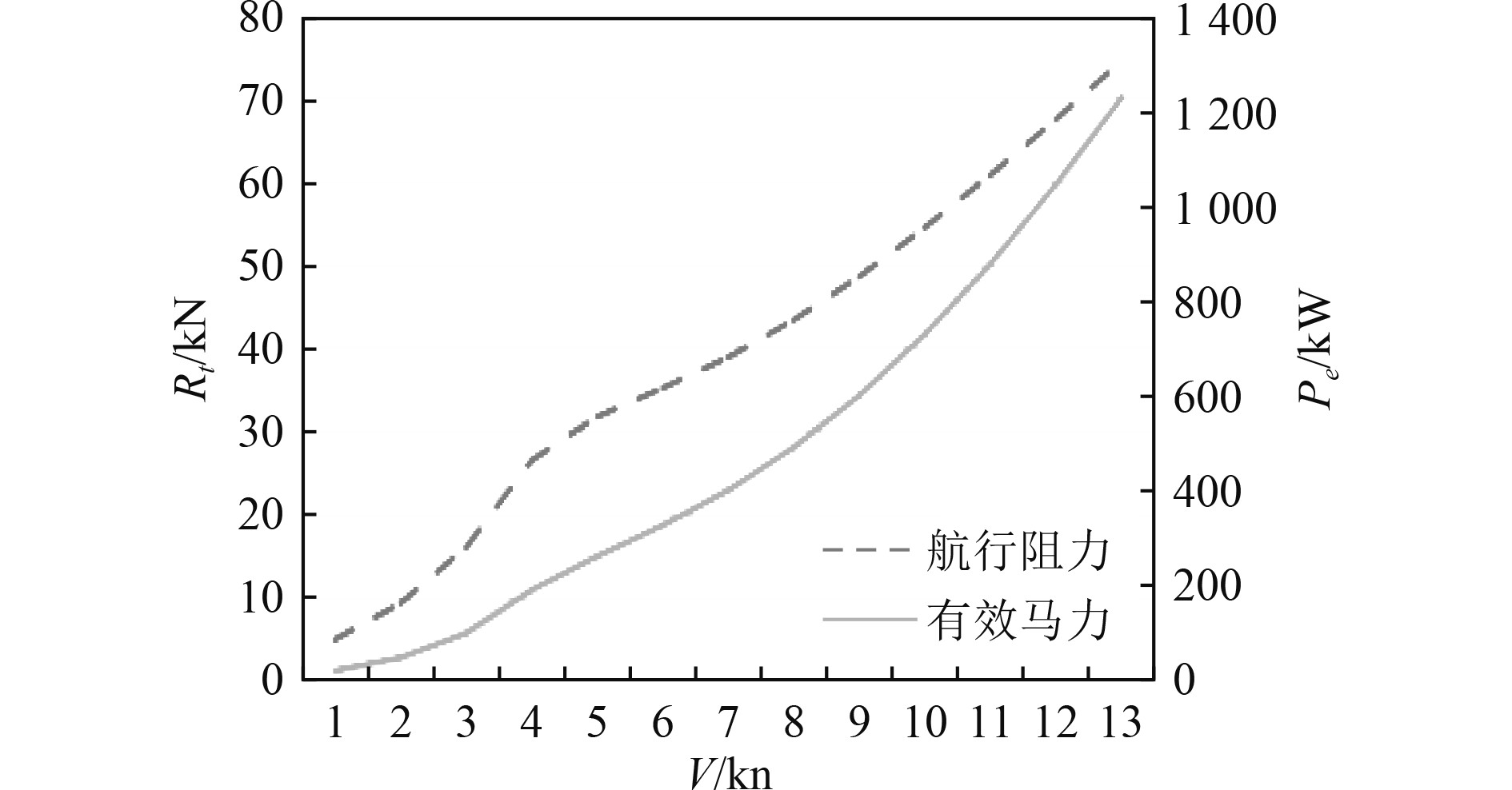
|
图 10 航行阻力与有效马力曲线 Fig. 10 Curve of resistance and effective horsepower |
根据给定的主机功率参数,参考航速预报的经验,利用Maxsurf计算的航速结果见表2。在双主机100%负荷状态下,最大航速Vmax=26.5 kn,较期望的最大应急航速V=26 kn有一定裕度,可在满足总体布置的情况下,适当减小K/b的取值,以减小双体船连接桥的重量,或减小L/b比值(即减小船长),以减小船体结构重量,从而进一步降低全船排水量。
|
|
表 2 Maxsurf预报航速结果 Tab.2 Speed results predicted by Maxsurf |
通过利用Maxsurf对沿海小型双体风电运维船进行快速性分析,可以得到以下结论:
1)经与船模阻力实验预报结果对比,Maxsurf的计算结果精度较高(误差小于5%),可供概念设计、方案设计及评估等船舶设计工作参考。
2)保持主机方案不变的前提下,迅速评估了双体风电运维船的调整方案,该方案能满足最大应急航速不低于26 kn的要求。
3)双体船阻力受片体间距比K/b影响较大。阻力随着K/b增大而减小,并在K/b>2.5后趋于平缓。
4)双体船阻力同样受长宽比L/b影响。对于小型船舶,由排水量控制和设备维修空间要求确定片体宽b取值后,阻力随着L/b增大而持续增大,但单位排水量阻力随着L/b增大而减小,这意味着设计工作应结合总体方案不断优化排水量。
| [1] |
金晨露. 风电双体维护船船型设计研究与水动力性能优化[D]. 镇江: 江苏科技大学, 2018.
|
| [2] |
陈钇西, 柯逸思, 张忠中, 等. 国内海上风电运维船发展现状及分析[J]. 风能, 2017(12): 40-44. DOI:10.3969/j.issn.1674-9219.2017.12.010 |
| [3] |
Maxsurf Resistance User Manual. Bentley Systems, Incorporated. 2014.
|
| [4] |
MOLLAND A F, WELLICOME J F, COUSER P R. Resistance experiments on a systematic series of high speed displacement catamaran forms: variation of length-displacement ratio and breadth-draught ratio[R]. University of Southampton, 1994.
|
| [5] |
MICHELL J H. The wave resistance of a ship[J]. Philosophical Magazine, 1898, 45(5): 106-123. |
| [6] |
TUCK E O, LUZAUSKAS L, SCULLEN D C, Sea wave pattern evaluation. part 1 report: primary code and test results (surface vessels)[R]. Applied Mathematics Department, The University of Adelaide. 1999, 4. 30.
|
| [7] |
TUCK E O, SCULLEN D C, LUZAUSKAS L, Sea wave pattern evaluation. part 4 report: extension to multihulls and finite depth[R]. Applied Mathematics Department, The University of Adelaide, 2000, 6. 19.
|
| [8] |
COUSER P. An investigation into the performance of high-speed catamarans in calm water and waves[D]. Department of Ship Science, University of Southampton, 1996, 5.
|
| [9] |
杨伟. 双体船考虑方艉影响的兴波阻力计算[D]. 武汉: 武汉理工大学, 2001.
|
| [10] |
迟百宏, 杨卫民, 丁飞, 等. Maxsurf软件在双体帆船阻力计算中的应用[J]. 船舶工程, 2015, 37(S1): 39-41+75. |
| [11] |
赵连恩, 韩端锋. 高性能船舶水动力原理与设计[M]. 哈尔滨工程大学出版社, 2007.
|
| [12] |
吴晓光, 吴启锐. 高速船快速性[M]. 国防工业出版社, 2015.
|
| [13] |
宋国华. 双体船的总体性能设计[J]. 船舶, 1998(01): 3-5. |
| [14] |
杜友威, 李彪, 周新院. 基于阻力分析的穿浪双体船船型设计及优化[J]. 舰船科学技术, 2019, 41(13): 31-34+44. |
| [15] |
邓芳, 邓魏彬. 双体船阻力性能计算及船型设计优化[J]. 青岛科技大学学报(自然科学版), 2015, 36(01): 72-76. |
 2022, Vol. 44
2022, Vol. 44
