水翼船作为高性能船,具有阻力低、经济航速高、波浪中失速小、耐波性好等特点。早期水翼船仅在船首加装水翼,高速航行时仅仅船首抬出水面,尾部未离开水面,仍为滑行状态,因此尾部抨击较为严重,受波浪扰动较大。随着时代的发展,双水翼船逐渐取代单水翼船成为了水翼船的主流,其耐波性、快速性等水动力性能较单水翼船而言,有了大幅度的提高。分析水翼参数对水翼船水动力性能的影响,从而设计水翼的剖面形状。浸深、攻角、水翼支柱高度等参数是水翼船设计的关键。本文利用水翼升力预估理论,结合经验公式对某观光船水翼参数进行设计,并采用流体力学的方法,探究水翼参数变化时,水翼船阻力、升阻比、湍流动能特性等水动力性能的影响,为水翼船的设计提供一定的支持。
在水翼运动机理以及理论方面,针对波浪能滑翔器以及水下滑翔机带有水翼的机械装置或机构开展了大量研究,并取得了一系列研究成果[1-3]。近年来,随着水翼船的发展,国内外学者越来越多地开展针对水翼船水翼的设计研究[4-10],通常以双体船、高速艇、滑行艇等船型为研究对象,针对水翼支柱、水翼翼型、水翼展弦比以及水翼安装位置等水翼要素,利用流体力学、经验公式等方法探究水翼是否存在对水翼船阻力、升力、深沉纵倾等水动力性能的影响,为水翼船水翼的设计提供依据。
本文选取一艘高速观光游船,针对该船开展水翼的设计。首先开展水翼的翼型剖面对升力、阻力以及升阻比的研究,确定选用的翼型。然后估算水翼面积,根据翼型展弦比对升阻比的影响确定翼型主尺度,再根据安装位置对水动力性能的影响确定水翼的安装部位,最终确定水翼的安装形式。
1 数值方法 1.1 水翼升力计算水翼艇的升力和阻力计算公式为:
| $ {F_L} = \frac{1}{2}\rho {V^2}S{C_L}。$ | (1) |
式中:ρ代表液体密度,V代表船速,CL代表翼形升力系数,S代表水翼面积。A=λb2,λ为展弦比。升力系数CL根据攻角的变化而发生变化,在有限的长宽比下,自由液面下的升力系数CL可表示为:
| $ {C_L} = \dfrac{{{k_\varphi }{{\left(\dfrac{{\partial {C_L}}}{{\partial \alpha }}\right)}_0}(\alpha + {\alpha _0} - \Delta {\alpha _0})}}{{1 + {{\left(\dfrac{{\partial {C_L}}}{{\partial \alpha }}\right)}_0}\dfrac{{{k_\varphi }}}{{\pi \lambda }}\dfrac{{1 + \tau }}{{\varsigma + \theta }}}} 。$ | (2) |
式中:(∂CL/∂α)0为升力导数,适用于无限浸没水深与有限展弦比的的水翼;攻角α为水翼后缘前缘连线和水平线的夹角;α0为零攻角,即水翼升力为零时的攻角。这个角度对于水翼而言为翼型曲面,雷诺数以及翼型尾部闭合角的函数。Δα0和kφ是零攻角和升力导数自由液面处的修正值。τ为Glauert修正。ς为水翼尾涡影响修正,θ为水翼位置影响修正。
1.2 数学模型对N-S方程采用时均雷诺法以及Realizable k-ε湍流模型,并结合带VOF的有限体积分数法,解决非定常的不可压缩粘流问题。
不可压缩流体连续性方程:
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0。$ | (3) |
动量守恒方程:
| $ \frac{{\partial \rho \varepsilon }}{{\partial t}} + \frac{{\partial \rho \varepsilon {u_{_i}}}}{{\partial x}} = \frac{\partial }{{{\partial _j}}}\left[ {\left(\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}\right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {C_1}E\varepsilon - \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }} 。$ | (4) |
Realizable k-ε湍流模型中,k和ε的运输方程分别为:
| $ \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_{_i}})}}{{\partial {x_{_i}}}} = \frac{\partial }{{\partial {x_i}}}\left[ {\left(\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}\right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon,$ | (5) |
| $ \frac{{\partial \rho \varepsilon }}{{\partial t}} + \frac{{\partial \rho \varepsilon {u_{_i}}}}{{\partial x}} = \frac{\partial }{{{\partial _j}}}\left[ {\left(\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}\right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {C_1}E\varepsilon - \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }} 。$ | (6) |
带自由液面的VOF方程如下:
| $ \frac{{\partial F}}{{\partial t}} + u\frac{{\partial F}}{{\partial x}} + v\frac{{\partial F}}{{\partial y}} + w\frac{{\partial F}}{{\partial z}} = 0。$ | (7) |
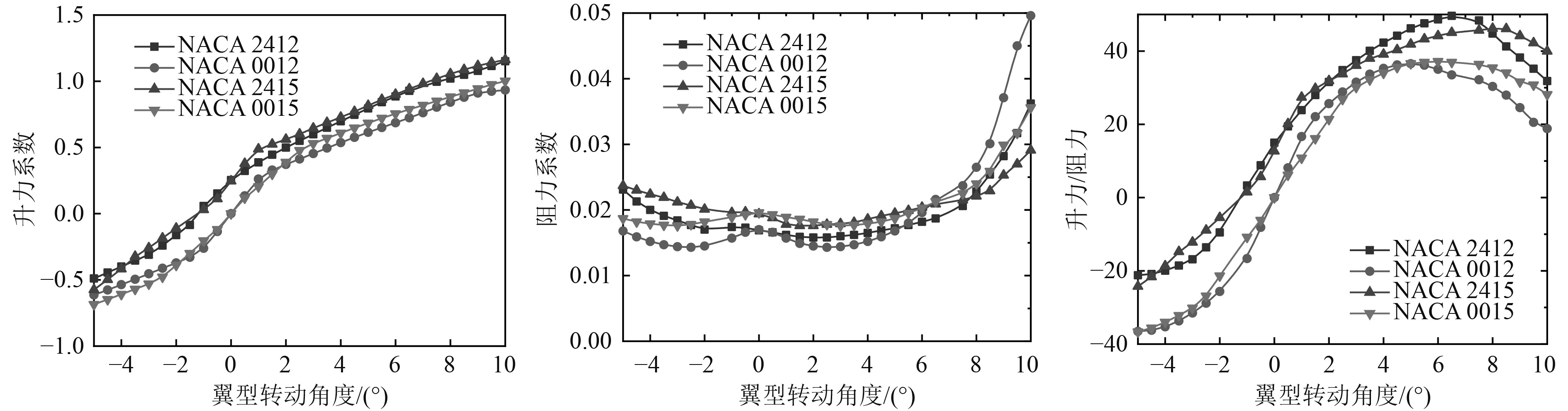
水翼的翼型设计中,设计具有较小阻力以及较大升力的水翼,是翼型设计中的重要要素。NACA翼型是水翼设计中最常用的翼型系列,常用的翼型有无弯度翼型NACA0012,NACA0015以及有弯度翼型NACA2412,NACA2412等。对于无弯度的翼型而言,由于翼型对称,翼处于水平状态时,升力系数为0,阻力最大,翼型的阻力会随着厚度的增加而增加。
图1给出了上述4种翼型升力系数,可以看出攻角为正时,厚度比较小的翼型,具有较小的阻力以及较大的升阻比;攻角为负数时,厚度比较小的翼型,同样具有绝对值较小的阻力以及较大的升阻比。另一方面,相对于没有弯度的翼型NACA0012,有弯度的翼型具有更大的升阻比。综上,选取NACA2412作为设计的进一步依据。
|
图 1 不同NACA翼型的升力系数、阻力系数以及升阻比 Fig. 1 Lift coefficient, drag coefficient and lift drag ratio of different NACA airfoils |
水翼决定着翼航状态的性能,是水翼船的关键部分。在尽可能设计出满足快速性以及适航性的水翼同时,还需保证其具有足够的强度和钢度,满足稳性和操纵性要求,不发生空泡和通气等。因此除了考虑水翼系统的形式和翼剖面形状外,还必须合理地选择水翼系统的主尺度。
通常而言,较小的水翼升力系数对应着较高的水翼阻力。然而由于无空泡,无通气以及强度的要求,不能过分加大升力系数。根据分析,以设计航速Vd为变量,对浸深范围不同的实艇数据进行大量统计分析,获得估算水翼设计升力系数的经验公式。对不同浸深水翼计算如下:
| $ {C}_{Y}=\left\{ {\begin{array}{*{20}{l}} 1.93{V}_{d}^{-0.66}(h=0.2-0.3\;{\rm{m}})浅浸水翼,\\ 线性插值(h=0.3-0.9\;{\rm{m}}),\\ 12.7{V}_{d}^{-1.06}(h=0.9-1.5\;{\rm{m}})浅浸水翼。\end{array}} \right. $ | (8) |
根据水翼升力系数定义,可推出水翼浸水部分的投影面积为:
| $ S = {Y \mathord{\left/ {\vphantom {Y {\frac{1}{2}\rho V_d^2{C_Y}}}} \right. } {\frac{1}{2}\rho V_d^2{C_Y}}}。$ | (9) |
根据Vd和所选的h代入公式(8)求取CY,由公式(9)计算S,然后选择合适的展弦比λ并计算水翼浸水部分的投影长l和平均弦长b,或者选定投影长而计算平均弦长。
| $ l = \sqrt {\lambda S} ,b = {S \mathord{\left/ {\vphantom {S l}} \right. } l} 。$ | (10) |
本船主要尺度参数如表1所示。根据水翼的浸深参数,属于浅浸水翼,结合设计航速,根据式(8)计算得到本船的升力系数为:
|
|
表 1 实船主要参数 Tab.1 Principal dimensions of the ship |
| $ {C_Y} = 1.93V_d^{ - 0.66} = 1.93 \times {40^{ - 0.66}} = 0.169 。$ |
另一方面,要将水翼抬出水面,预估水翼产生的升力等于本船的排水量,则初步估算水翼面积为:
| $\begin{split} S =& {Y \mathord{\left/ {\vphantom {Y {\frac{1}{2}\rho V_d^2{C_Y}}}} \right. } {\frac{1}{2}\rho V_d^2{C_Y}}} = {{10 \times 4.52 \times {{10}^3}} \mathord{\left/ {\vphantom {{10 \times 4.52 \times {{10}^3}} {(0.5}}} \right. } {(0.5}} \times 998.1 \times \hfill\\ & {(40 \times 0.514\;4)^2} \times 0.185) = 1.35\;{{\rm{m}}^2}。\end{split}$ |
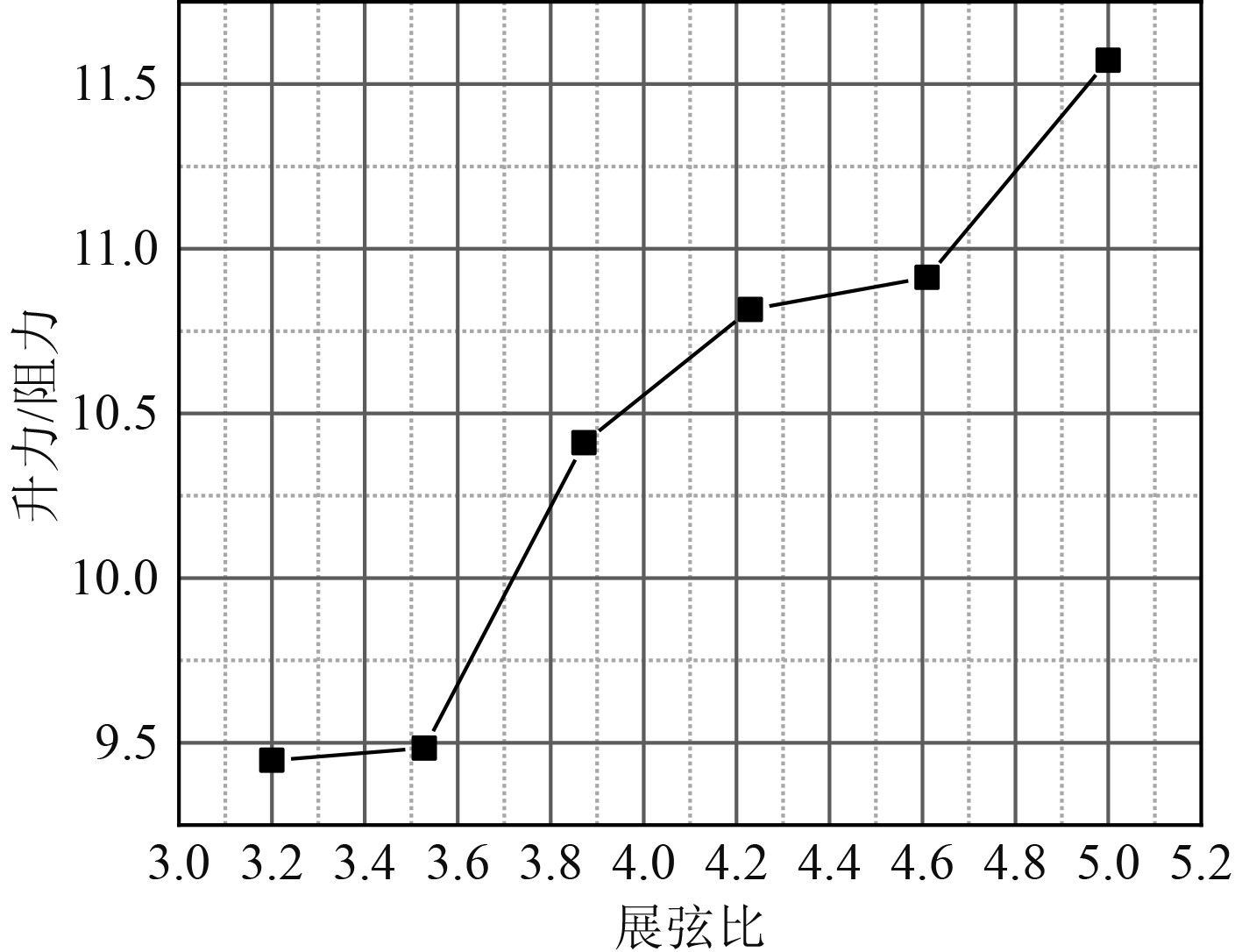
根据水翼初步尺度的估算可知,在确定水翼投影部分的面积S后,只需确定水翼展弦比λ,即可得到水翼的主尺度。展弦比较小的水翼,其转动产生升力的效率低;展弦比较大时,则会受到结构的限制。开展展弦比对水动力性能影响的研究,根据预估结果合理选择展弦比。研究表明,展弦比为3~5时,水翼升阻比较高。为了确定水翼的最佳升阻比,选择在确定水翼投影面积情况下,选取若干展弦比进行数值计算。
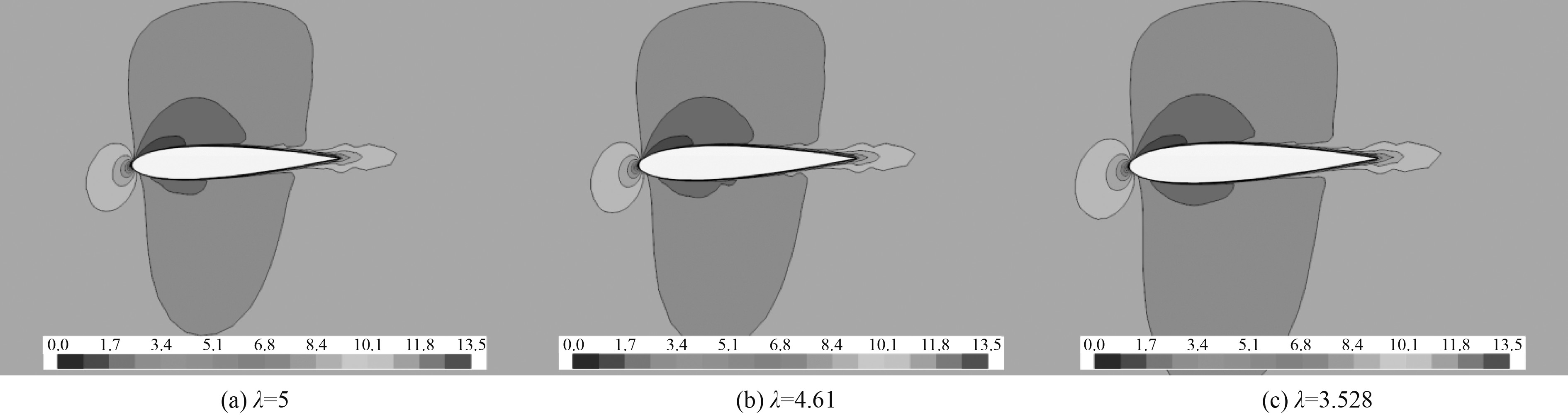
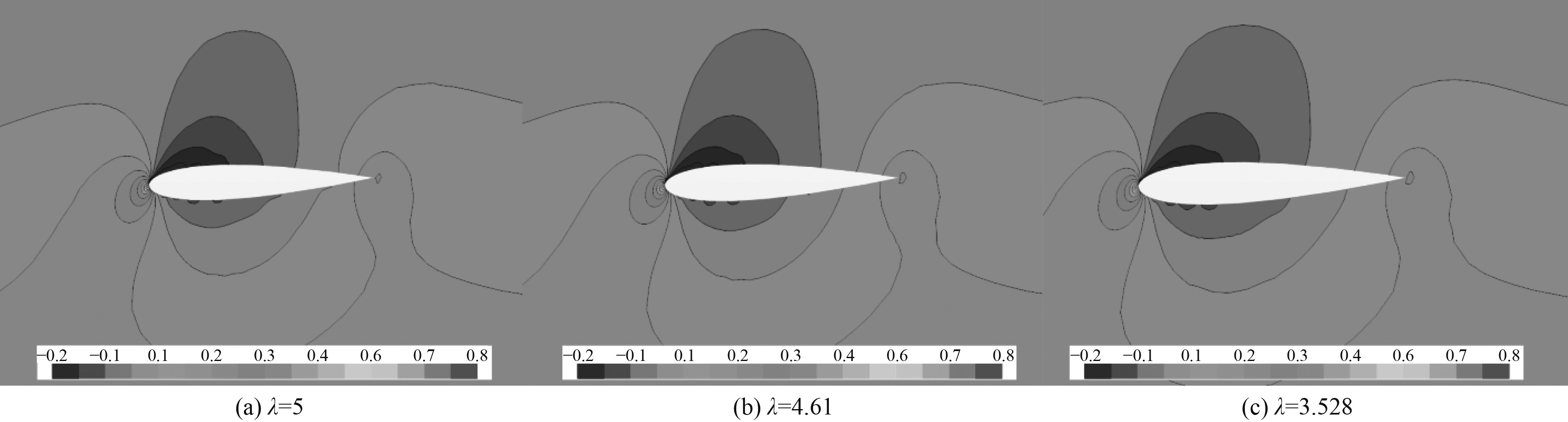
图2和图3为相同水翼投影面积,不同展弦比下的速度以及压力截面云图。在相同的投影面积下,展弦比越大,则展长越大,弦长则越小。从不同展弦比的速度以及压力截面云图来看,随着展弦比的变大,水翼上缘高速负压区变化范围不大,而在下缘速度较低区域则变小,由伯努利原理,低速区变小使得压强增大,从而使得展弦比越大的水翼具有单位长度下更大的升力。另一方面展弦比更大的水翼较较小的水翼长度更长,因而具有更大的升力。从数值计算的结果看也应证了这一点。综上所述,选取展弦比为5的翼型作为水翼翼型设计输入。
|
图 2 不同展弦比下的速度云图(迎流角2°) Fig. 2 Velocity scalar graphs at different aspect ratios (attack angle of 2 degrees) |
|
图 3 不同展弦比下的压力云图(迎流角2°) Fig. 3 Pressure scalar graphs at different aspect ratios (attack angle of 2 degrees) |
|
图 4 展弦比与升阻比的变化关系 Fig. 4 Relationship between aspect ratio and lift drag ratio |
水翼船首尾水翼纵向位置与艇体总纵强度、航行性能以及首尾水翼的载荷分配以及艇的重心位置有密切关系。在海浪中,若首尾水翼间距接近设计海况的波长,船体会产生较大的深沉以及摇摆运动,因此非自控水翼船的水翼间距应当小于或大于设计波长,并有足够的裕度。对于设计航速不太高的浅浸水翼,合理地选取水翼间距可使尾水翼的上洗处于首水翼的上洗尾流之中,从而减小阻力。
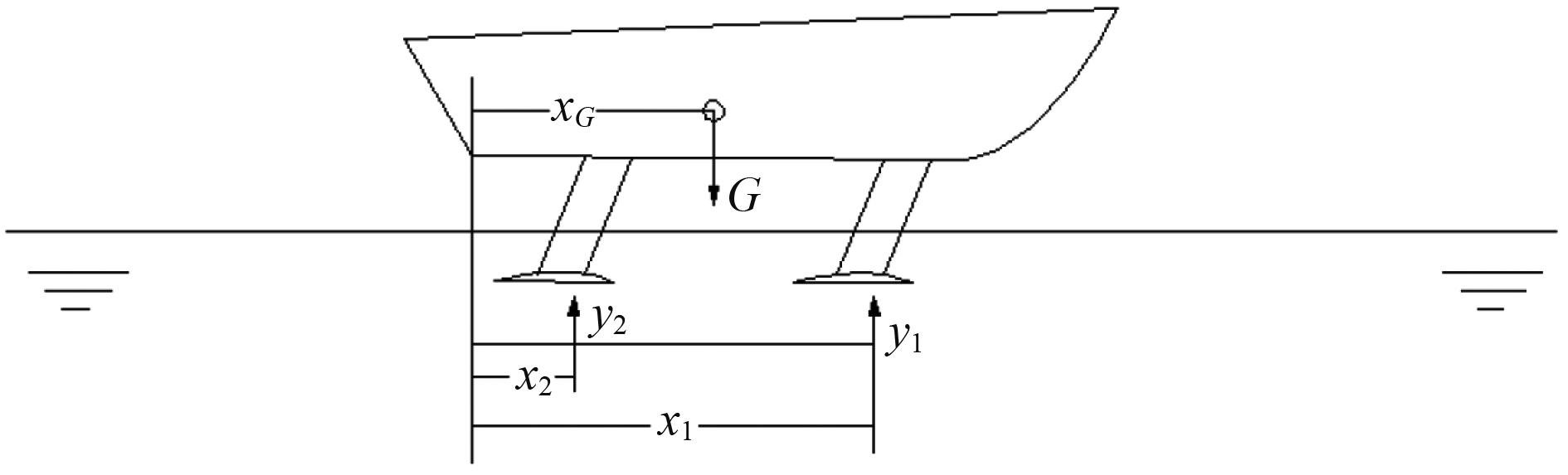
水翼的载荷分配和艇的重心位置关系如图5所示。根据首尾水翼的载荷分配和艇的重心位置,它们与首尾水翼的纵向位置有确定的数值关系。
|
图 5 水翼受力分布示意图 Fig. 5 Force distribution diagram of ship hydrofoils |
| $ \theta {{{x_1}} \mathord{\left/ {\vphantom {{{x_1}} {{L_{WL}}}}} \right. } {{L_{WL}}}} + (1 - \theta ){{{x_1}} \mathord{\left/ {\vphantom {{{x_1}} {{L_{WL}}}}} \right. } {{L_{WL}}}} = {{{x_G}} \mathord{\left/ {\vphantom {{{x_G}} {{L_{WL}}}}} \right. } {{L_{WL}}}}。$ | (11) |
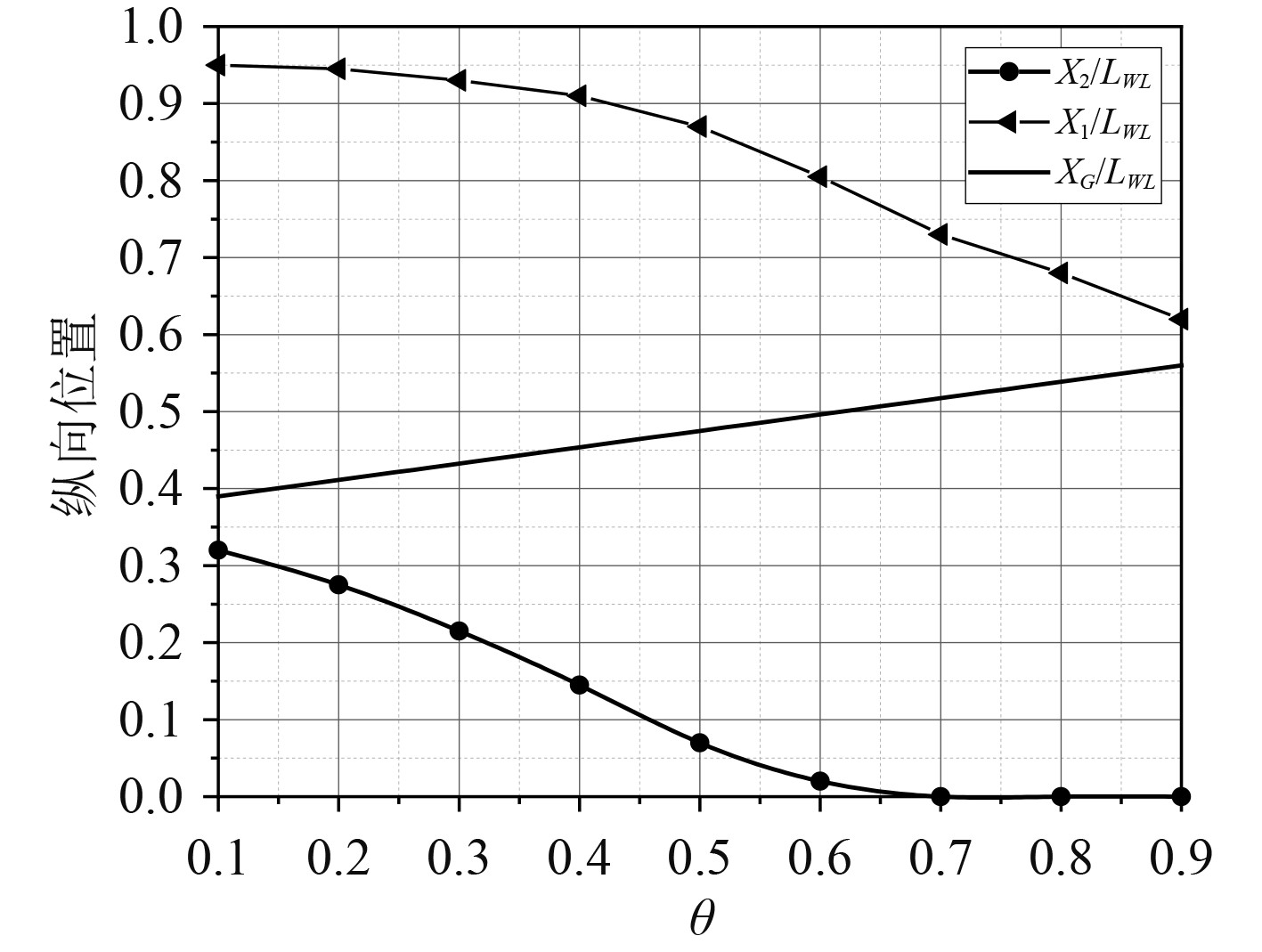
式中:θ=Y1/G为首翼载荷比,LWL为水线长。由实艇数据分析,首尾水翼纵向位置x1/LWL和x2/LWL与首翼载荷比θ有一定的相关关系,由公式(11)可推出重心位置xG/LWL与首翼载荷比θ的关系,图6为实艇数据点首翼载荷比θ与首尾水翼纵向位置形成的统计关系曲线,据此对水翼船重量重心进行初步估算后,即可以由重心纵向位置,初步推算水翼的位置。
|
图 6 水翼纵向位置以及重心纵向位置与首翼载荷比关系曲线 Fig. 6 Relation curves between wing longitudinal position, center of gravity longitudinal position and bow wing load ratio |
根据重心初步位置,确定了首尾水翼的纵向初步位置,同时为了研究首水翼位置对本船水动力性能的影响,根据主尺度,设计3种首水翼,并分别研究3种水翼在相同航速下的阻力、升力、深沉等特性,选取最优水翼。
3种方案首尾水翼的距离分别为4.43 m,5.23 m,6.03 m,在流体力学仿真软件中进行了仿真计算(缩尺比为2),计算工况如表2所示。图7和图8给出了3种工况下自由液面的波形图。可知:随着首尾水翼距离的加大,船尾产生的兴波显著减小,船首抬升更大;在尾水翼位置不变的情况下,首水翼越靠近船首,越能产生更大的深沉和纵倾。这主要是由于首水翼与尾水翼距离越大时,由杠杆原理,能产生更大的纵倾力矩,从而使船体产生更大的深沉和纵倾。比较可知,抬升更大的船舶,也能使得船体与水面接触面积更小从而减小船舶的总阻力。另一方面,首尾水翼的距离增大,从而产生更大的深沉纵倾时,水翼与水面的接触面积同样也减小,升力增大,从而产生了更大的升阻比。
|
|
表 2 不同水翼方案的主要参数以及数值计算值 Tab.2 Parameters and numerical values of different hydrofoil schemes |

|
图 7 不同方案下的自由液面兴波云图(俯视图) Fig. 7 Free surface wave making scalar diagrams under different schemes (top view) |

|
图 8 不同方案下的自由液面兴波云图(侧视图) Fig. 8 Free surface wave making scalar diagrams under different schemes (side view) |
根据对不同方案的水动力性能分析的基础上,可以看出方案C在阻力、水翼升力以及水翼升阻比方面更优,可以作为最优方案输出。然而,在水翼的设计中,除需考虑需要设计一定的首尾水翼距离,从而使水翼船产生足够的俯仰力矩,使水翼船发生抬升,减小阻力和功耗之外,还需考虑船舶在高速航行中的适航性以及耐波性,避免因纵倾角过大从而使船舶在高速航行中处于危险之中。
5 水翼形式细化优化根据确定水翼的最优形式方案C,高速时首水翼行进过程中仍然会产生较大的兴波,这主要是由于方案C的船首水翼部分出水,从而产生兴波。另一方面,船尾的兴波仍然较大,船尾抨击较为严重。可适当增大尾水翼的面积,使其获得足够升力将船尾完全抬离水面。
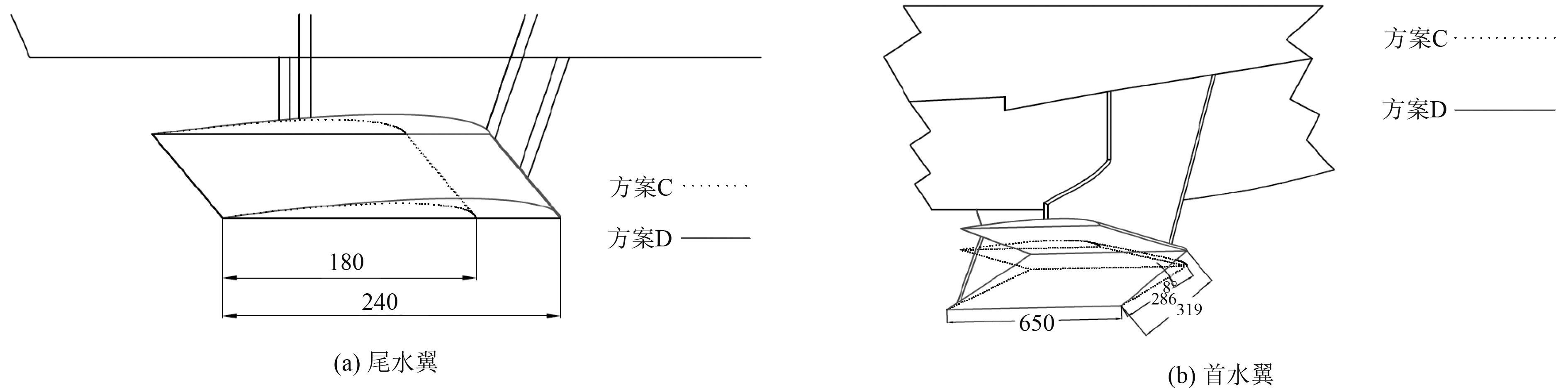
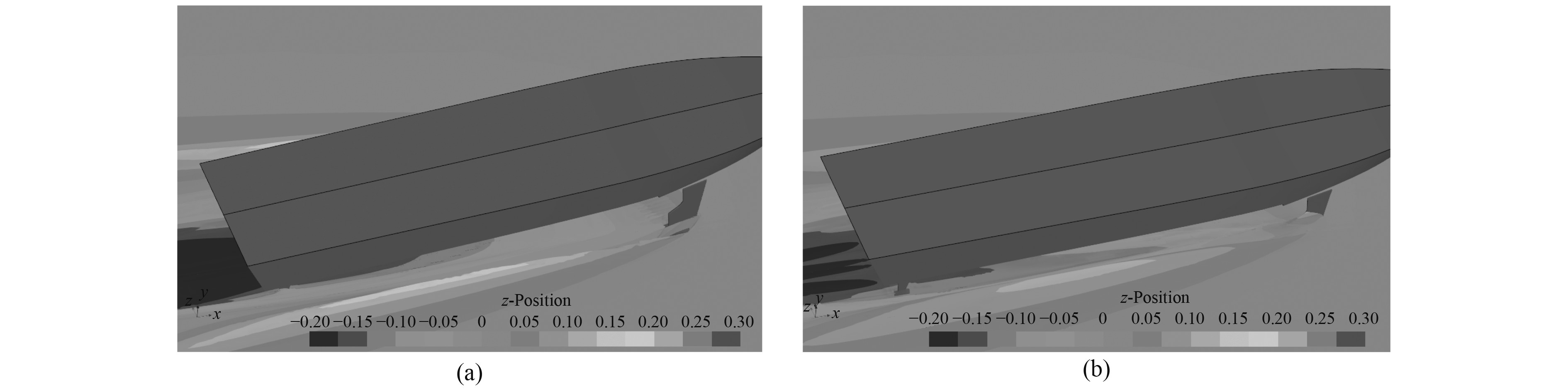
根据此设计思路,将船尾船首水翼进行优化,得到优化方案D,如图9所示。将尾水翼加宽,并将首水翼自由端的角度作出修改。由计算结果可知,相对于方案C,方案D在模型以及水翼总阻力方面均有减小。另一方面由于加大了尾水翼的受力面积,使得首尾水翼载荷分配更加均匀,从而减小了纵倾,水翼提供了更大的升力从而提高了深沉,也使得升阻比加大。观察方案C和方案D的自由面兴波云图(见图10),方案D在船尾行波方面更加平缓,舷侧兴波峰值也较方案C更小。
|
图 9 方案C和方案D尺寸对比图 Fig. 9 Dimension comparison of scheme C and D |
|
图 10 方案C与方案D下的自由液面兴波云图(侧视图) Fig. 10 Free surface wave making scalar diagram under scheme C and D (side view) |
针对某水翼船开展翼型剖面研究,确定选用的翼型。进一步对水翼面积进行估算,根据翼型展弦比对升阻比的影响确定翼型主尺度,根据安装位置对水动力性能的影响确定水翼的安装部位。根据确定的水翼位置对水翼进行细化优化设计,在设计以及优化预报的过程中,得到如下结论:
1)在水翼翼型剖面选取中,在满足强度的要求下,可选取厚度比较小的翼型,因其具有较大的升阻比以及较小的阻力。
2)在水翼面积相同时,在满足布置要求的前提下,选取展弦比大的水翼,可获得较大的升阻比,使水翼具有更加优良的水动力性能。
3)在固定尾水翼时,首水翼距尾水翼距船首越近,距离越大,纵倾力矩越大,则水翼的升阻比越大,在满足耐波性以及适航性的设计前提下,可适当使首水翼远离尾水翼。
| [1] |
常宗瑜, 波浪驱动推进机构的最优水翼倾角的确定[J]. 中国海洋大学学报, 2021, 51(1): 111−116.
|
| [2] |
张喆, 赵文川. 基于流体机械的水翼压力分布计算[J]. 现代制造, 工艺装备, 2019(3): 31-34. |
| [3] |
李靖璐, 王鹏, 牛宏磊, 等. 自由变形在水翼外形优化设计中的应用[J]. 哈尔滨工程大学学报, 2020, 41(9): 1249-1254. |
| [4] |
孟毅. 水翼参数对双体小水线面水翼复合船耐[D]. 上海: 上海交通大学, 2018.
|
| [5] |
LI Hao-jie, PUTRA Arfis Maydino Firmansyah1, SUN Ke, LENG Jian-xing, ZHAO Han-xing, CHEN Jia-Hong. Boat Trial Validation and Resistance Prediction of a 36-Foot Hydrofoil Catamarans Using CFD[J]. 船舶力学, 2020, 24(6): 740-753. DOI:10.3969/j.issn.1007-7294.2020.06.005 |
| [6] |
唐建飞, 杨帅. 高速艇水翼减阻方案及翼滑艇阻力估算方法[J]. 船舶力学, 2015, 19(1-2): 69-77. |
| [7] |
许慧洋, 崔耀菲. 截流板/尾楔对加装T型水翼的双体船阻力影响的数值计算[J]. 广东造船, 2019(2): 21-24. |
| [8] |
魏子凡, 井升平, 杨松林. 新型高速艇的CFD模拟和对比分析[J]. 中国舰船研究, 2016, 11(4): 22-28. |
| [9] |
李双林. 穿浪艇控制水翼优化及系统设计[D]. 哈尔滨工程大学, 2015.
|
| [10] |
周进. 带固定水翼滑行艇阻力与耐波性能研究[D]. 哈尔滨工程大学, 2017.
|
 2022, Vol. 44
2022, Vol. 44
