2. 天津瀚海蓝帆海洋科技有限公司,天津 300457;
3. 天津科技大学 机械工程学院,天津 300222
2. Tianjin Hanhai Lanfan Marine Technology Co., Ltd., Tianjin 300457, China;
3. Tianjin University of Science and Technology, School of Mechanical Engineering, Tianjin 300222, China
泵喷推进器以其高效率和低横滚扭矩,在水下推进领域具有较高的发展潜力。目前国外大部分核潜艇选用的推进器都是泵喷推进器。泵喷推进器由定子系统、转子系统和导管系统组成[1]。泵喷推进器按定子安装的位置,可以分为前置定子泵喷推进器和后置定子泵喷推进器[2]。自主水下机器人(autonomous underwater vehicle,AUV)为提高其续航力,减小横滚力矩,通常采用后置定子泵喷推进器作为其动力来源。后置定子具有将周向流动改变成轴向流动的作用,回收了尾流的能量,提高了推进器的效率。同时后置定子还具有平衡转子扭矩的作用,使泵喷推进器的整体扭矩接近于0[3]。
不同的后置定子及安装位置的差别对泵喷推进器的水动力性能也具有影响。饶志强[4]采用CFD仿真方法,对不同前置定子及其安装角度的导管推进器进行了水动力性能分析,得出了前置定子的不同几何参数对水动力性能的影响规律。彭云龙[5]分别对前置与后置定子泵喷推进器分别进行仿真计算,得出了2种泵喷推进器在敞水性能、空化性能、脉动特征三方面的差别。蔡昊鹏[6]采用面元法预报方法对其设计的后置定子泵喷推进器的定子弦长与定转子间距进行了分析,得出其对水动力性能的影响规律及合适的取值范围。毛卫[7]通过试验验证了CFD仿真技术应用于前置定子导管桨的可行性。文献[8-9]验证了CFD方法在泵喷推进器水动力性能预报方面的可行性及准确性。泵喷推进器的横滚扭矩往往是被忽略的参数,对其开展系统性的研究是有必要的。
本文采用正交模拟试验方法结合CFD技术,在泵喷推进器主体尺寸不变的情况下,改变后置定子的不同参数,研究后置定子对泵喷推进器的横滚扭矩及效率的影响,并进行参数优化。
1 几何模型以某AUV设计的Whela10030泵喷推进器(见图1)为基础,为其添加不同类型的后置定子,平衡扭矩提高效率。为方便网格划分,对泵喷推进器的模型进行适当几何处理,并对迎流端进行圆滑处理,处理后的几何模型如图2所示。
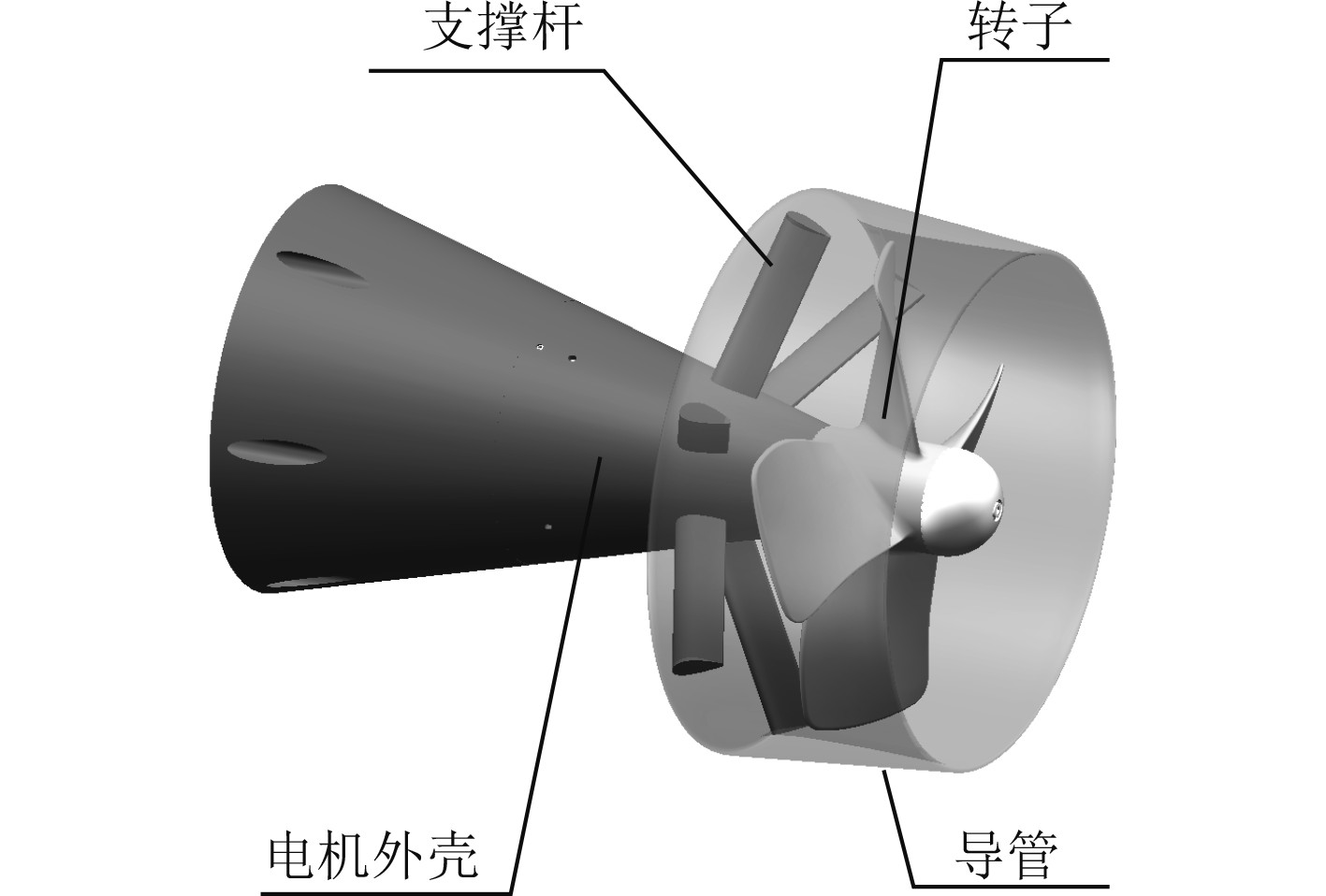
|
图 1 Whale 10030推进器结构图 Fig. 1 Whale 10030 propeller structure graphing |
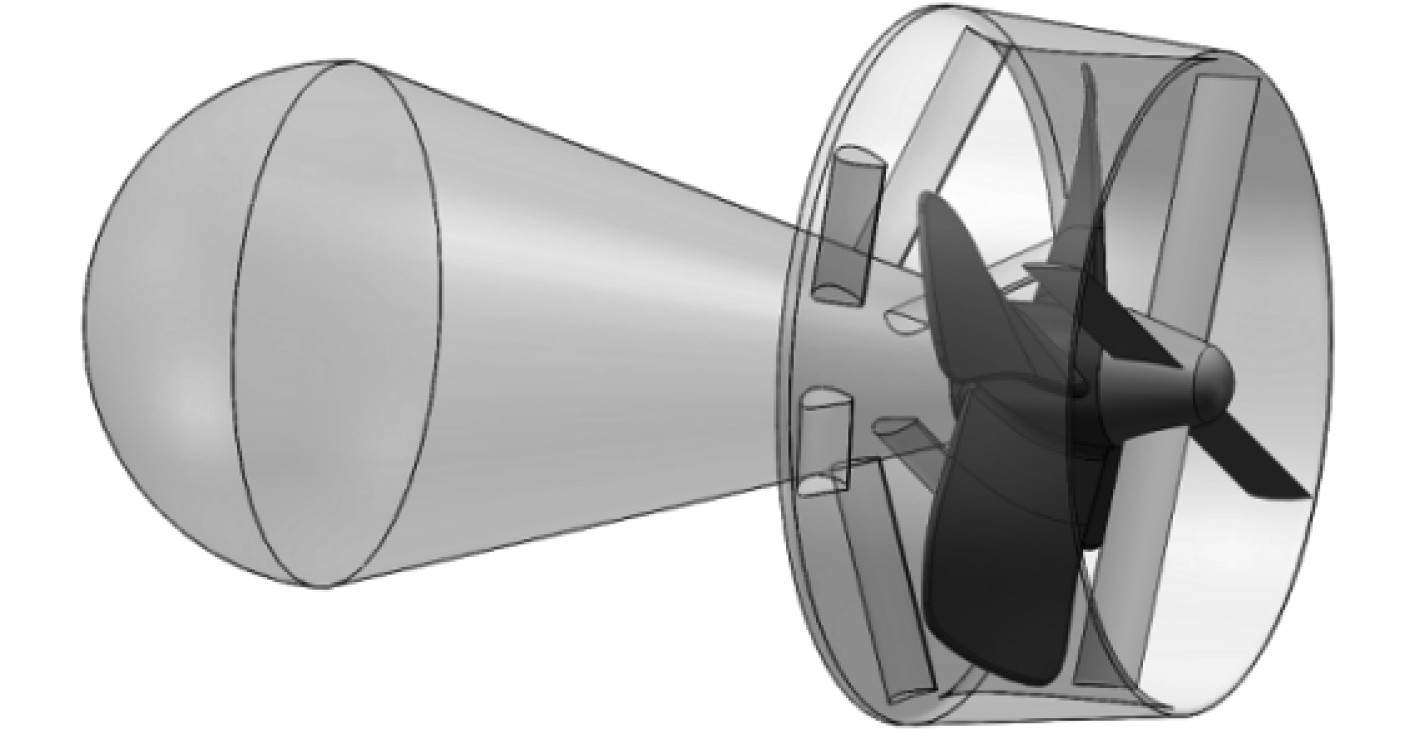
|
图 2 推进器仿真模型 Fig. 2 Propeller simulation model |
对于不可压缩流体流动问题的数值模拟计算,通常通过求解其连续性方程和RANS方程来实现,其张量形式为:
| $ \frac{{\partial {{\bar u}_i}}}{{\partial {x_i}}} = 0 ,$ | (1) |
| $ \begin{split} \rho \frac{{\partial {{\bar u}_i}}}{{\partial t}} + \rho {{\bar u}_j}\frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}} = \rho {{\bar F}_i} - \frac{{\partial \bar P}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left(\mu \frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}} - \rho \overline {{{\dot u}_i}{{\dot u}_f}} \right) \hfill \end{split} 。$ | (2) |
式中:
为更好利用计算机计算资源,保证结算结果的准确,采用RNG
| $ \begin{split} \frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {x_i}}} \left(\rho k{u_i}\right) = &\frac{\partial }{{\partial {x_j}}}({\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial {x_j}}})+ \hfill \\ &{G_k} + {G_b} - p\varepsilon - {Y_M} + {S_k} ,\hfill \end{split} $ | (3) |
| $ \begin{split} \frac{\partial }{{\partial t}}(\rho \varepsilon ) + \frac{\partial }{{\partial {x_i}}}(\rho \varepsilon {u_i}) = \frac{\partial }{{\partial {x_j}}}\left({\alpha _\varepsilon }{\mu _{eff}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}\right) +\hfill \\ {C_{1\varepsilon }}\frac{\varepsilon }{k}({G_k} + {C_{3\varepsilon }}{G_b}) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} - {R_\varepsilon } + {S_\varepsilon } 。\hfill \end{split} $ | (4) |
其中:
| $ {C_{1\varepsilon }} = 1.42 ,{C_{2\varepsilon }} = 1.68 。$ |
式中:
为模拟真实的试验环境,仿真计算域为长5 m、宽3 m、高2 m的长方体区域,与真实的试验水箱尺寸相同,保证了仿真环境与试验环境的一致性。计算域分为转子旋转域、加密域和外部流场域。为建立均匀的流场环境,采用均匀流的速度进口作为进口边界条件,为提高计算收敛速度,节约计算成本,出口边界条件选择压力出口。转子、定子与推进器表面均采用无滑移壁面,外部流场域的其余4个表面均采用无滑移壁面。
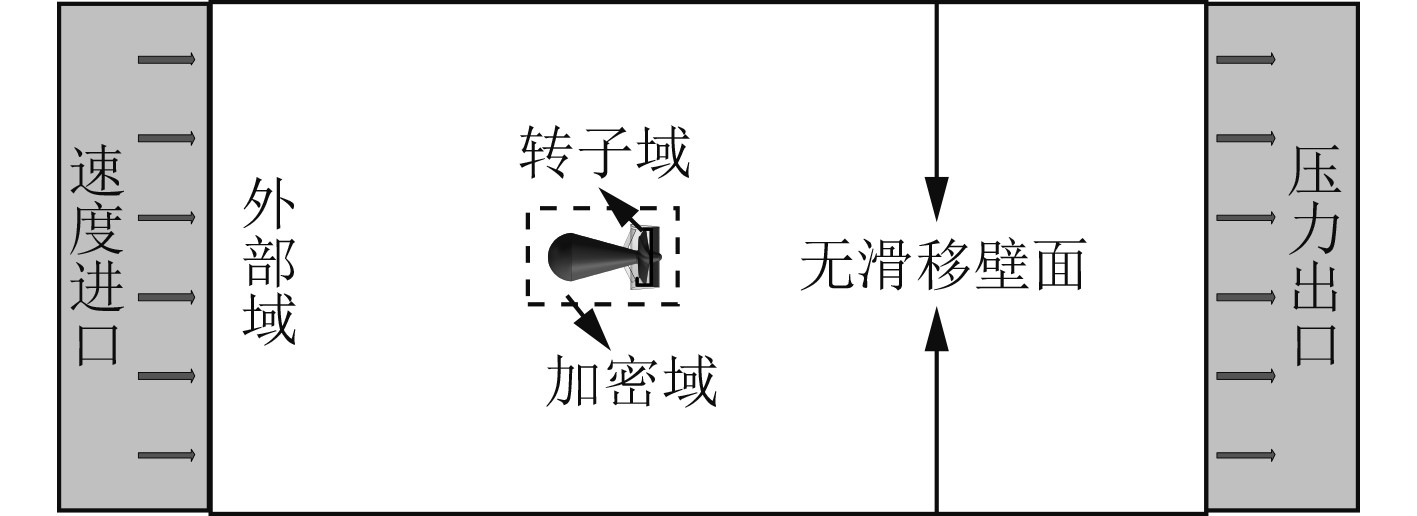
|
图 3 计算域与边界条件 Fig. 3 Computational domain and boundary conditions |
采用非结构化四面体网格进行离散,并对泵喷推进器附近流动比较剧烈的部分进行网格加密,以提高计算结果的准确性。为消除网格数量对计算结果的影响,分别对转子域、加密域和外域进行网格对立性分析。通过对面网格尺寸的加密,来控制各个计算域网格的数量。对各个计算域分别准备1套粗网格系统和1套细网格系统。经计算外域与加密域的的网格密度对计算结果无影响,转子域网格数量对计算结果影响较大。对转子域网格进一步加密,整体网格数量分别为152万、203万、260万、310万,其结算结果如表1所示。由结果可知转子域网格数量越大,计算结果越接近,网格数量在260万与310万时,扭矩变动率为1.2%,证明计算结果基本保持不变。综合考虑计算精度与计算速度,采用260万的网格系统进行网格划分。
|
|
表 1 各网格系统泵喷推进器水动力性能计算结果 Tab.1 Calculation results of hydrodynamic performance of pump jet thrusters in each grid system |
为验证仿真数据的真实性,对原始模型(见图4)进行系泊推力试验,验证CFD仿真结果的准确性。推进器仿真值与试验测试值之间对比如图5所示。可知仿真值与试验值的误差在5%以内,考虑到水箱壁面的回流影响,仿真值与试验值的误差在工程应用允许范围内,因此以上仿真结果数据可靠。

|
图 4 试验模型图 Fig. 4 Experimental model diagram |
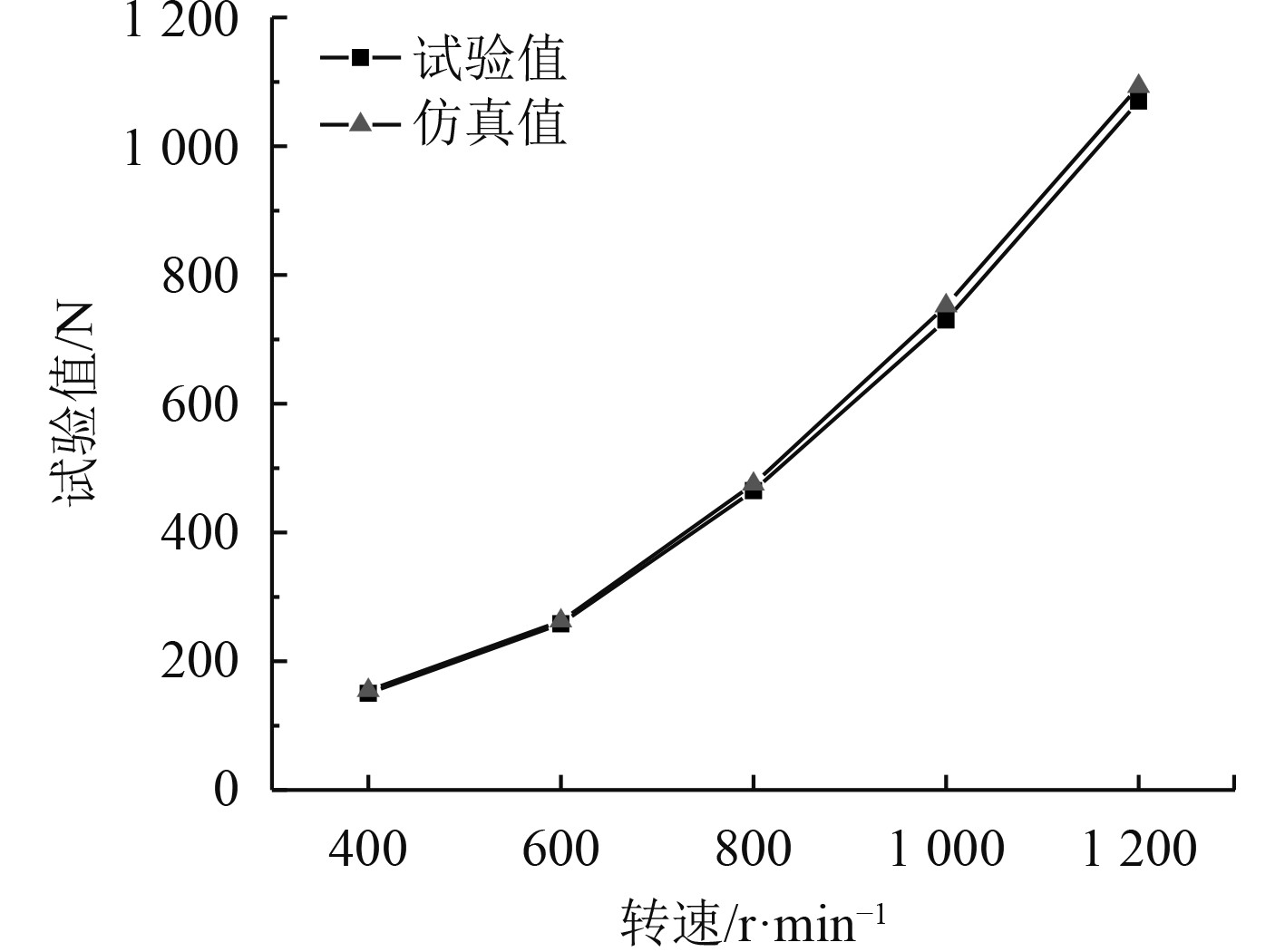
|
图 5 试验值与仿真值对比图 Fig. 5 Comparison diagram of experimental value and simulation value |
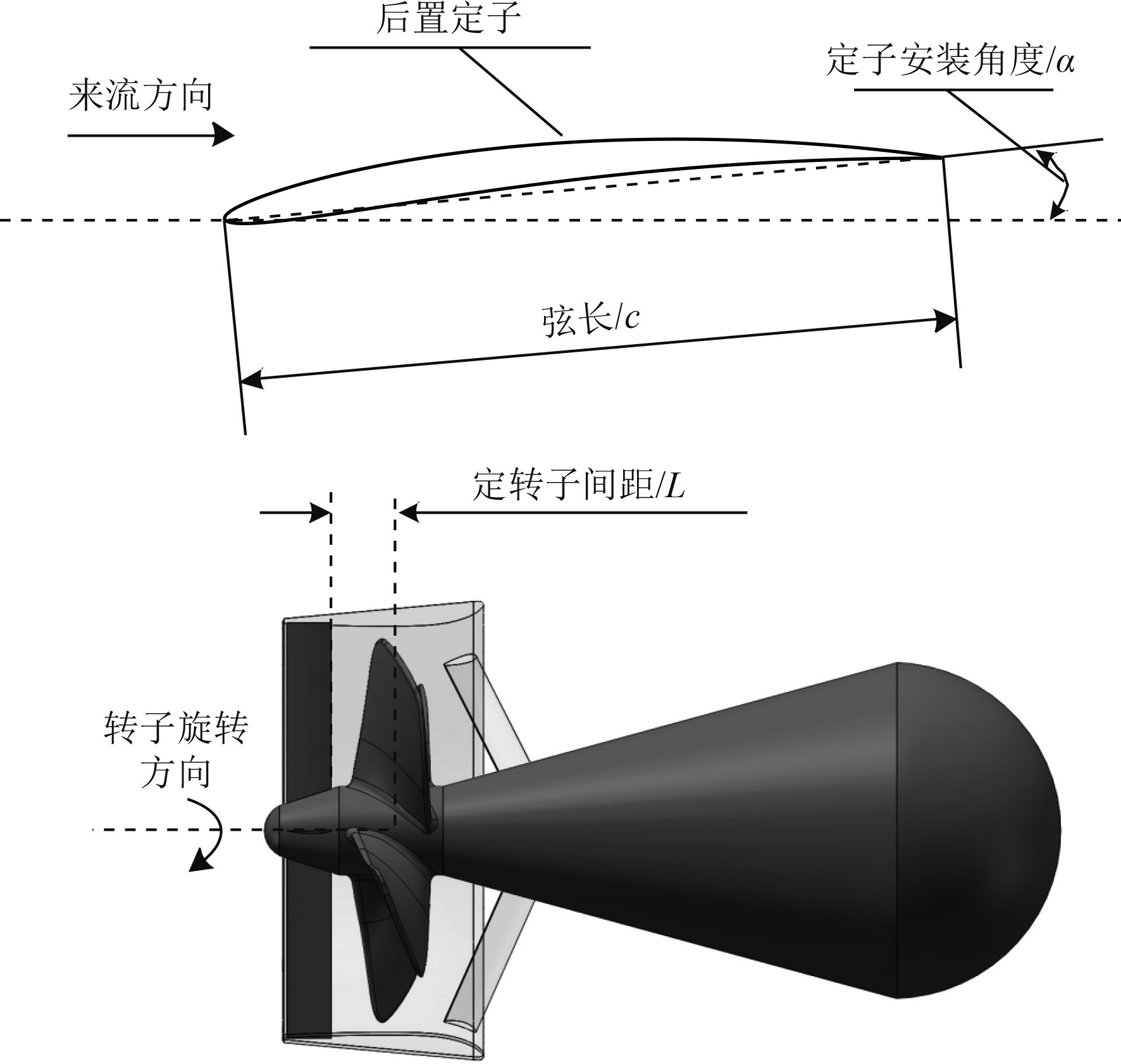
研究4种因素对泵喷推进器水动力性能的影响,4种因素分别为定子安装角度、定子数量、定转子安装距离和定子弦长。采用正交试验的方法,该方法具有试验均衡分散,数据计算简单,水平整齐可比的优点。在保证螺旋桨和导流罩的主体尺寸及相对位置不变的情况下,通过改变后置定子安装角度、定子数量、定转子距离和定子弦长,在流速为3 m/s,螺旋桨转速为1 200 r/min的工况下进行4种因素4个水平的正交模拟试验。正交试验表如表2所示,各试验因素示意图如图6所示。
|
|
表 2 正交试验表 Tab.2 Orthogonal experiment table |
|
图 6 试验因素示意图 Fig. 6 Schematic diagram of test factors |
推进器的几个重要的水动力性能系数及其计算公式分别为:
| $ J = V/(nD) ,$ | (5) |
| $ 10{K_{Qr}} = 10{Q_r}/(\rho {n^2}{D^5}) ,$ | (6) |
| $ 10{K_Q} = 10Q/(\rho {n^2}{D^5}),$ | (7) |
| $ {K_{Tr}} = {T_r}/(\rho {n^2}{D^4}),$ | (8) |
| $ {K_T} = T/(\rho {n^2}{D^4}),$ | (9) |
| $ \eta = \frac{{{K_T}}}{{{K_{Qr}}}} \cdot \frac{J}{{2\text{π} }}。$ | (10) |
式中:
推进器的横滚扭矩对航行器的运动控制具有重大影响,推进器的横滚扭矩越小,航行器的运动控制难度越高。同时推进器的效率对航行器的续航时间有重大影响,为增加航行器的续航时间,必须要提高泵喷推进器的推进效率,提高能源利用率。因此选择泵喷推进器的的效率
通过计算极差,分析不同因素对整体扭矩和效率的影响程度。4个因素对效率的影响程度为
|
|
表 3 正交表L16(44)及试验结果 Tab.3 Orthogonal table and experimental results |
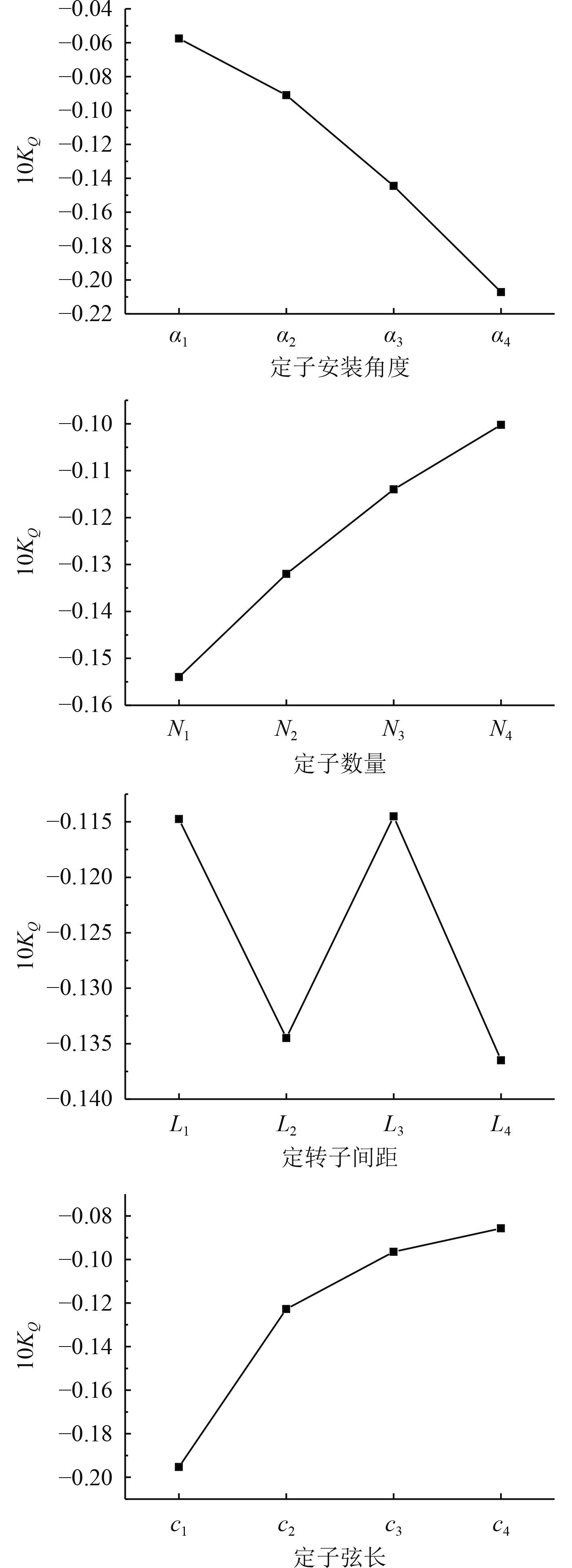
由图7可以看出,定子安装角度对泵喷推进器扭矩的影响趋势是呈下降趋势,最优水平为α1。定子弦长与定子数量对泵喷推进器的影响趋势为增长趋势,因此最优水平为c4与N4。定转子间距的最优水平为L1和L3,因此使泵喷推进器的横滚扭矩最小的组合为α1c4N4L1或α1c4N4L3。
|
图 7 10KQ变化趋势 Fig. 7 10KQ trend of change |
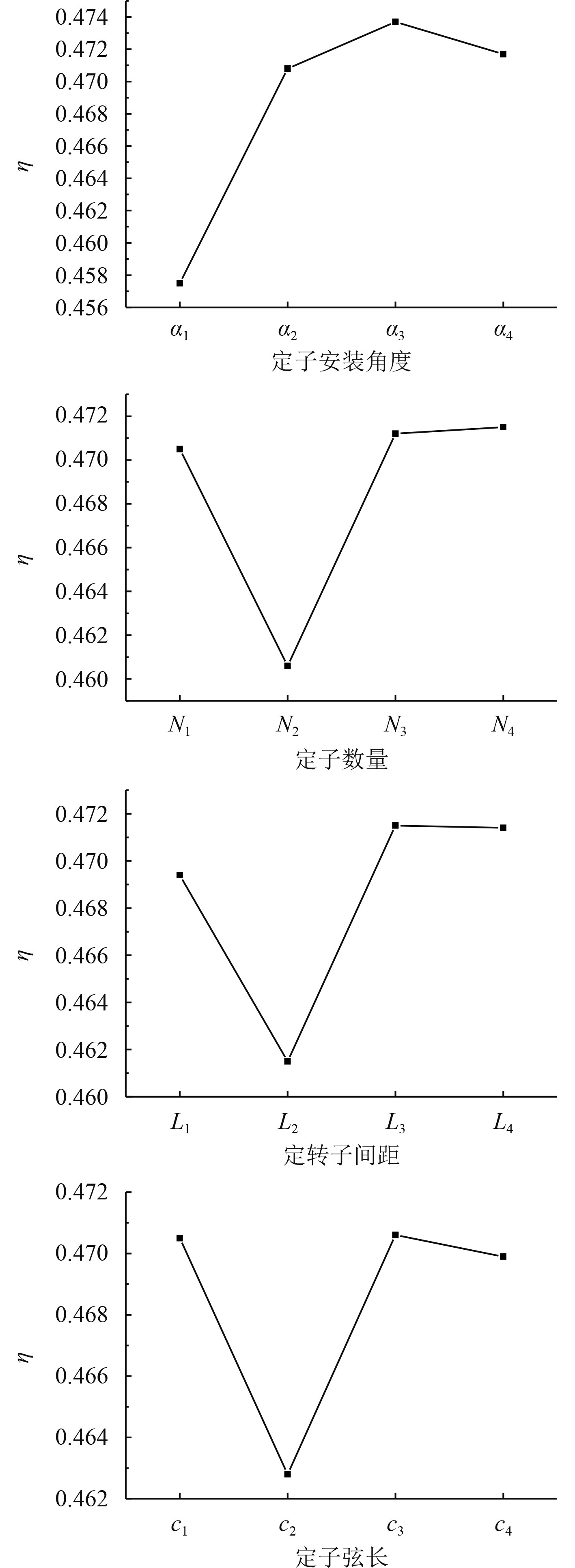
由图8可以看出,定子安装角度对效率的影响趋势是先上升后下降的趋势,在α3处效率取得最高值,定子数量、定转子安装距离、定子弦长对效率的影响趋势是一种先下降后平缓的趋势,定子数量在N4处取得效率最高值,定转子安装距离和定子弦长在L3处和c3取得最高值,因此最优方案为α3N4L3c3,最优方案在正交试验中未有出现,因此可信度较高。各个因素对泵喷推进器的整体扭矩系数的影响按,影响程度的大小顺序排列。泵喷推进器的整体扭矩系数越接近0,表示后置定子对泵喷推进器的扭矩平衡效果越好。
|
图 8 η变化趋势 Fig. 8 η trend of change |
为进一步研究优化模型相对于原始模型的水动力性能,分别对初始模型和3种优化模型进行CFD仿真计算,根据计算结果得出最优模型,并对比最优模型与原始模型的流场特性。4种模型的后置定子的参数及计算结果如表4所示。
|
|
表 4 具体模型参数及仿真结果 Tab.4 Parameters of specific models and simulation result |
可知,模型2的效率相对原始模型的效率提升了4%,整体扭矩系数降低了76%。模型3与模型4相对原始模型的效率提升了1.7%左右,模型3相对原始模型整体扭矩系数降低了74%,模型4相对原始模型整体扭矩系数降低了84%。3种优化模型对转子扭矩的平衡效果最为显著,模型2对效率的提升较为明显,因此模型2为本次优化的最优模型。
原始模型与最优模型的尾部流场湍流动能图分别如图9和图10所示。流场的稳定性随着湍流动能的增大而降低。由计算可以看出,原始模型的最高湍流动能大于最优模型的湍流动能。由此可得最优模型的尾部流场的稳定性要优于原始模型,后置定子还具有改善尾部流场稳定性的优点。

|
图 9 原始模型湍流动能图 Fig. 9 Turbulent kinetic energy diagram of original model |

|
图 10 最优模型湍流动能图 Fig. 10 Turbulent kinetic energy diagram of optimal model |
1)后置定子的参数对泵喷推进器的效率的影响程度排序是:定子安装角度>定子数量>定转子距离>定子弦长;后置定子的参数对泵喷推进器的整体扭矩的影响程度排序是:定子安装角度>定子弦长>定子数量>定转子距离。
2)优化模型相对原始模型效率提高了4%,整体扭矩降低了76%。
3)最优模型的后置定子对提高尾部流场的稳定性具有促进作用。
| [1] |
QIU Cheng-cheng, HUANG Qiao-gao, PAN Guang, et al. Numerical simulation of hydrodynamic and cavitation performance of pump jet propulsor with different tip clearances in oblique flow[J]. Ocean Engineering, 2020, 209. |
| [2] |
刘业宝. 水下航行器泵喷推进器设计方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
|
| [3] |
BRUCE E P, GEARHART W , ROSS J. The design of pumpjets for hydrodynamic propulsion[J] Fluid Mechanics, Acoustics and Design of Turbomachinery, Part 1, NASA SP-1974, 304: 795–839.
|
| [4] |
饶志强, 李巍, 杨晨俊. 定子参数变化对前置定子导管桨性能的影响[J]. 上海交通大学学报, 2013, 47(2): 269-273 RAO Z Q, LI W, YANG C J. The effect of stator parameters on performance of ducted propeller with pre-swirl stators[J]. Joural of Shanghaijiaotong University, 2013, 47(2): 269-273 |
| [5] |
彭云龙, 王永生, 刘承江, 等. 前置与后置定子泵喷推进器的水动力性能对比[J]. 哈尔滨工程大学学报, 2019, 40(1): 132-140. PENG Y L, WANG Y S, LIU C J, et al. Comparative analysis of the hydrodynamic performance of front-stator and rear-stator pump-jets[J]. Journal of Harbin Engineering University, 2019, 40(1): 132-140. |
| [6] |
蔡昊鹏, 苏玉民. 扭矩平衡式水下机器人推进器研究[J]. 船舶力学, 2009, 13(2): 210-216. CAI H P, SU Y M. A study on torque balanced propulsors for autonomous underwater vehicles[J]. Journal of Ship Mechanics, 2009, 13(2): 210-216. DOI:10.3969/j.issn.1007-7294.2009.02.008 |
| [7] |
毛卫. 带前置定子导管桨流场数值分析及验证[J]. 舰船科学技术, 2014, 36(6): 92-96+101. MAO W. The flow field numerical analysis and validation for ducted propeller with pre-stator[J]. Ship Science And Technology, 2014, 36(6): 92-96+101. DOI:10.3404/j.issn.1672-7649.2014.06.018 |
| [8] |
谷浪. 鱼雷泵喷推进器设计及水动力性能预报方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [9] |
段相杰, 董永香, 冯顺山, 等. 泵喷推进航行体有动力流场数值仿真[J]. 弹箭与制导学报, 2012, 32(3): 161-163+170. DUAN X J, DONG Y X, FENG S S, et al. The numerical simulation of flow field for underwater vehicle with pump jet propulsion[J]. Journal of Projectiles Rockets Missiles and Guidance, 2012, 32(3): 161-163+170. DOI:10.3969/j.issn.1673-9728.2012.03.044 |
| [10] |
王福军. 计算流体动力学分析-CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004.
|
 2022, Vol. 44
2022, Vol. 44
