转子是燃气轮机核心部件之一,在高温、高压、高转速的恶劣工作条件下,长时间承受离心力、气动力、热应力等作用,转子性能直接影响到整个燃气轮机运行的安全可靠性。燃气轮机在启动、停机及变载荷时,转子上形状突变部位将产生较大的热应力集中,这些部位的热应力有可能会超过材料对应温度下的屈服极限,产生较大的塑性变形,经过一定周次的交变应力循环作用,在某些应力集中区域会产生疲劳初始裂纹,而转子上的裂纹不易修复,在此后的循环载荷下,裂纹将进一步扩展直至发生断裂[1]。因此,对燃气轮机转子的强度研究具有十分重要的意义。而对转子温度场、应力场的准确计算是强度研究的重要前提。
针对燃气轮机转子温度分布与热应力的研究,众多国内外学者已经做了许多研究。Gong[2]对某核电汽轮机的低压转子瞬态应力场进行了分析,针对转子寿命两大影响因素热应力和离心接触应力,分别构建了二维气热耦合有限元分析模型及三维接触应力分析模型,在启动和停机工况下分析获得了转子瞬态热应力及三维接触应力,指出了产生疲劳损伤的两大因素。Mohaideen[3]对某涡轮发动机转子进行了分析,指出涡轮转子承受了惯性力、压力、热载荷等多重载荷,结构安全性极为重要,构建了转子的三维模型,采用了Ansys软件分析了边界载荷作用下的应力状态。卓明等[4]对燃气轮机转子分别进行了结构分析和热-结构偶合分析,得到了冷态、稳态、启停、盘车工况下各盘间接触应力分布的变化规律,指出冷态启动过程的盘间接触应力均值最大降幅远大于稳态温度场引起的降幅。Zhu等[5]针对某300 MW的重型燃气轮机系统,构建了转子部分的三维有限元模型,采用有限元方法获得了燃气轮机在启动、停机状态时的热应力场,该结果为重型燃气轮机转子系统的应力分析提供了可靠参考。张清雷[6]对某燃气轮机周向拉杆转子进行了二维轴对称有限元计算,并据此预测了转子在不同启停工况下的低周疲劳寿命。黄金娥[7]对处于离心载荷和温度梯度影响下的燃气轮机涡轮盘寿命进行了预估,指出涡轮盘在设计转速下运行时,其中心孔部位出现了应力屈服,因此应当被视为疲劳断裂的危险关键部位进行寿命预估。Barella等[8]研究了某60 MW机组的转子寿命,该机组运行10年后出现了明显的材料疲劳破坏现象,采用不同的分析方法对该现象进行复原,发现转子表面应力集中区域出现了热应力极大的部位,启动及停机时巨大的交变热应力是产生低周疲劳寿命破坏的主要原因。刘昕等[9]采用三维接触非线性有限元方法对燃气轮机组合转子进行了分析,指出拉杆凸肩与拉杆孔的静态安装间隙里不影响拉杆在正常工作状态下的应力,但是影响转子升速时拉杆最大应力;增加拉杆凸肩数、减小凸肩跨距能够有效减小拉杆最大应力,且与不等跨距增加拉杆凸肩数的改进方案相比,等跨距方案降低应力效果更显著。宋文超等[10]采用有限元方法分析了热载荷、机械载荷及螺栓预紧力对动力涡轮盘的影响,结果表明,动力涡轮盘最大等效应力主要由机械在和产生,温度场不均匀引起的热载荷在集中在榫槽处,对该处应力影响较大。刘庆亚等[11]基于有限元方法对拉杆蠕变松弛状态下,材料参数、转速、结构尺寸参数等不确定性因素对转子系统可靠度及其灵敏度的影响进行了分析,结论指出适当降低轮盘径向尺寸D1,采取高屈服强度材料,可以显著提高组合转子的结构可靠性。史进渊等[12]提出了构件存在初始裂纹情况下的高周疲劳安全性分析方法,并成功应用于焊接转子的安全性评估中,为汽轮机转子的优化运行提供了依据。
涉及燃气轮机转子应力场的研究集中在对某级轮盘、简单转子模型整体的应力分布研究,而考虑拉杆凸台与拉杆孔非线性接触,观察轮盘内部温度梯度,对比轮盘在热载荷、机械载荷下应力分布的研究则较少。以某周向拉杆转子为研究对象,依据周向拉杆转子、拉杆的实际结构及运行特点,建立了周向拉杆转子的三维接触有限元模型,考虑温度场、离心力、拉杆预紧力,对转子的瞬态温度场、应力场进行了分析。根据瞬态应力场的计算结果,确定了较为容易发生断裂的危险位置,并据此对转子启动曲线进行优化,从而使转子的应力水平降低,寿命得以延长。
1 计算方法 1.1 转子基本情况本文研究对象是周向拉杆转子部分。该转子由17级叶轮盘、前轴后轴头组成,由24只周向长拉杆预紧。各级轮盘材料为30Cr2Ni4Mov,拉杆材料为Inconel718材料。为更准确得模拟转子运行过程的应力分布情况,必须考虑拉杆凸台与相应拉杆孔之间的接触,因此建立了转子的三维有限元接触模型,如图1所示。

|
图 1 转子三维模型 Fig. 1 3D model of rotor |
如图2所示,在启动过程中,转子转速和轮缘处温度在启动初期急速升高,转子在启动后300 s时达到满转速(12000 r/min),600 s时达到满负荷(轮缘处温度达到最大值),此后转子以满转速、满负荷状态稳定运行。根据温度场、应力场计算结果,人为地将转子的整个启动过程划分为3个时期:启动初期(0~300 s)、启动中期(300~2000 s)和启动后期(2000~6000 s)。

|
图 2 转子冷态启动曲线 Fig. 2 Cold start-up curve |
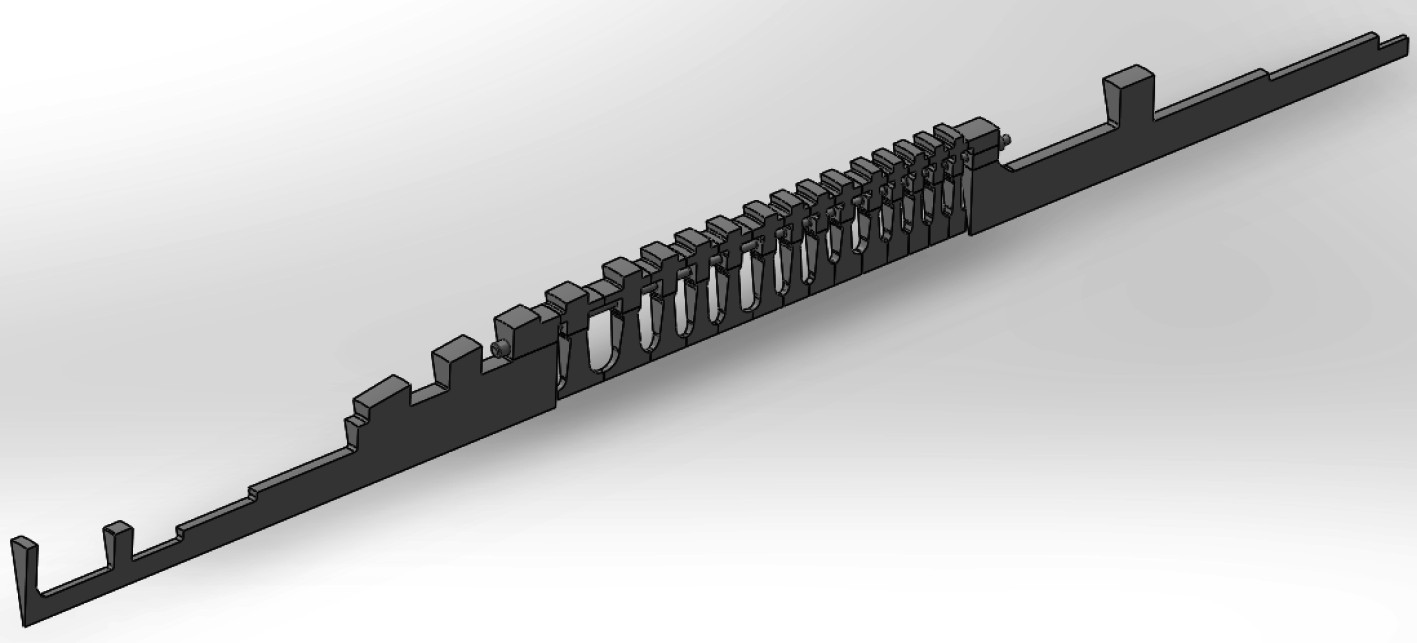
考虑到转子的周期对称结构特点以及24只长拉杆结构,建立包含一只长拉杆的1/24循环对称模型如图3所示。
|
图 3 转子1/24循环对称模型 Fig. 3 1/24 model of rotor |
该模型考虑了各轮盘间的环面、拉杆与拉杆孔之间、螺母头与轮盘之间的摩擦接触,摩擦接触算法均为罚函数法。通过前期试算,综合考虑计算结果准确性、计算效率及接触面网格的精细处理,最终确定模型单元总数为202319,节点数为745387。拉杆、拉杆孔、各级轮盘圆角处等结构处网格做细化处理,有限元模型如图4所示。

|
图 4 转子有限元模型 Fig. 4 FEA model of rotor |
采用顺序偶合[13]的方法对转子进行热固耦合分析,先对转子的瞬态温度场进行计算,计算结果将作为转子瞬态应力场计算时的热载荷。对转子瞬态温度场进行分析时,与工质直接接触的转子外表面给定已知温度和对流换热系数的第三类边界条件,转子的前后轴头、转子内部空腔均设置为绝热。
对转子瞬态应力场进行分析时,转子的载荷包括瞬态温度场、离心力与拉杆预紧力。其中,叶片的离心力将等效为作用在各级轮盘外缘处随转速变化的径向压力,拉杆预紧力通过PRES174单元加载,转子的转速则按照图2设置。转子前轴头处给定轴向位移约束,转子循环对称面上给定循环对称约束。
需要说明的是综合应力为同时考虑热载荷(瞬态温度场)与机械载荷(离心力与拉杆预紧力)情况下转子的等效应力,热应力为考虑热载荷、拉杆预紧力情况下转子的等效应力,机械应力为考虑机械载荷情况下转子的等效应力,以上等效应力均为Von Mises应力。若无特殊说明,本文提到的应力均指综合应力。
为了详细展示转子温度的变化规律以及温度变化引起的热应力、综合应力变化规律,取处于最高工作温度的第17级轮盘和拉杆跨度最大的第5级轮盘作为监测对象,分别对轮盘内径、外经和拉杆孔壁面的温度及应力变化状态进行跟踪。
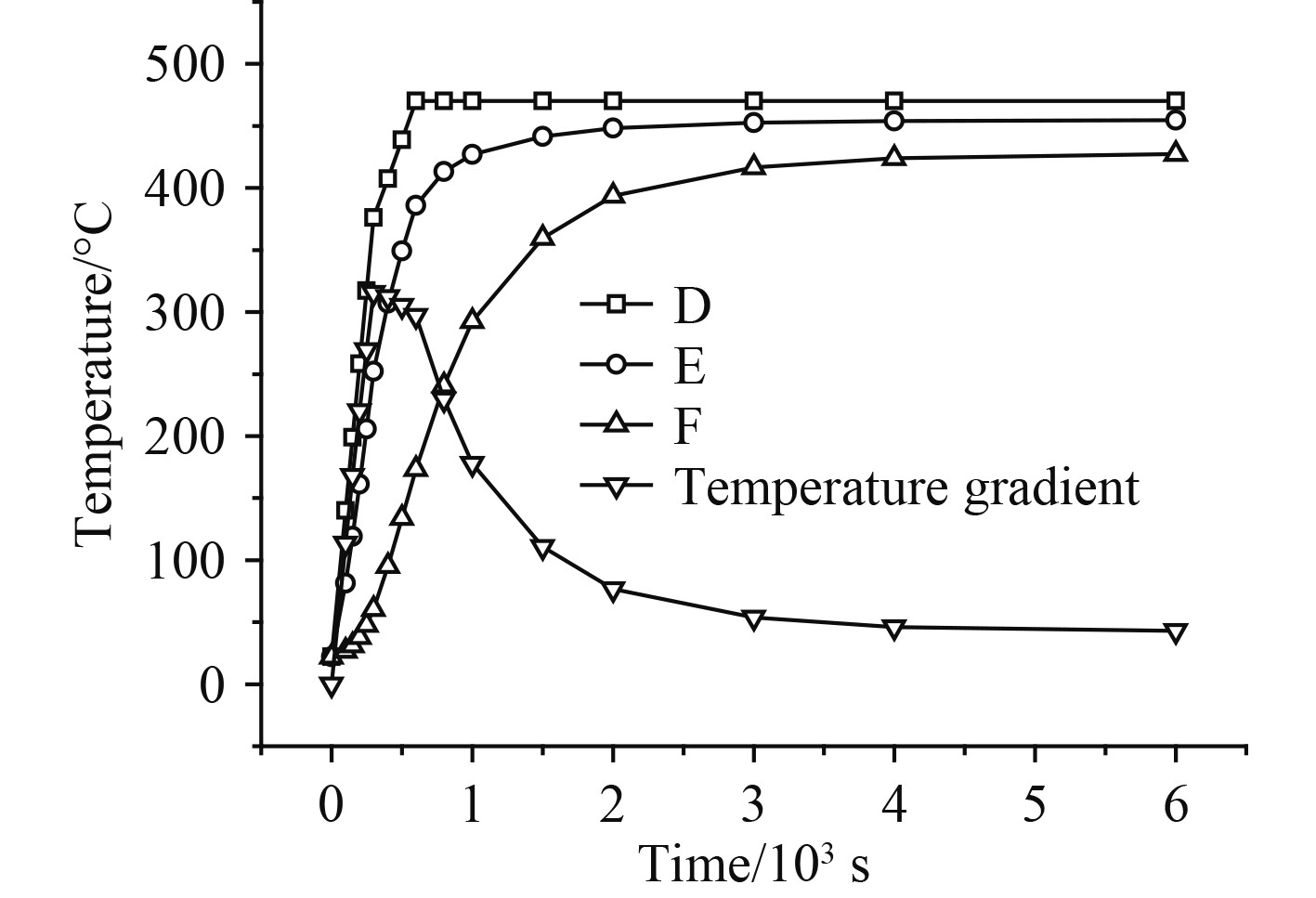
2 转子温度场计算结果 2.1 轮盘温度变化规律图5和图6分别为启动过程中第5级、第17级轮盘监测位置处的最高温度变化规律,两图中的温差为启动过程中轮盘内外径的温度差值随时间的变化规律,该曲线可为轮盘内部温度梯度变化的提供参考。两轮盘内外径温差最大值均出现在启动后300 s,第5级轮盘最大温差为97.63℃,而第17级轮盘最大温差为315.55℃。

|
图 5 第5级轮盘监测位置温度时变曲线 Fig. 5 Temperature variation curve of monitoring position on 5th disc |
|
图 6 第17级轮盘监测位置温度时变曲线 Fig. 6 Temperature variation curve of monitoring position on 17th disc |
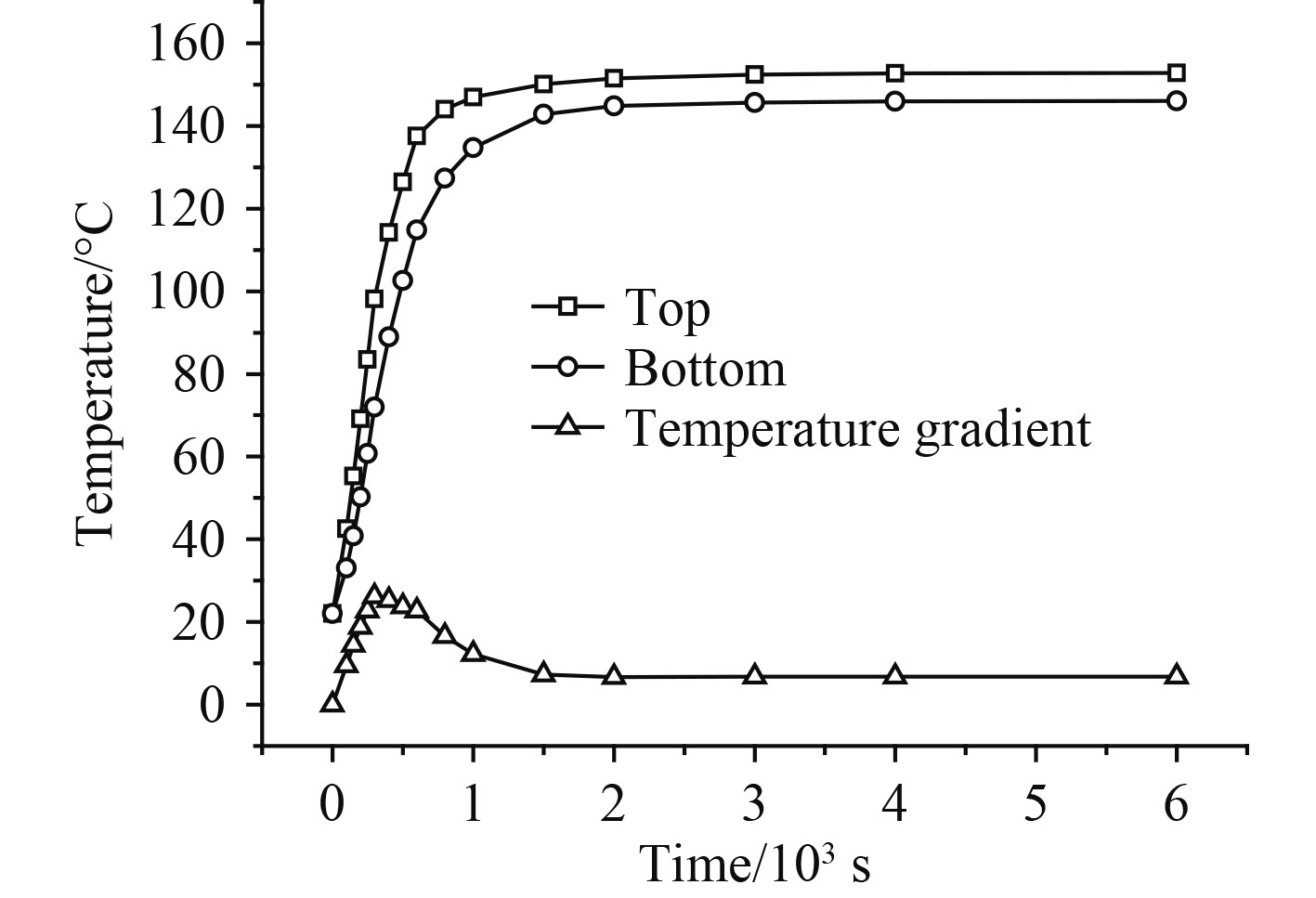
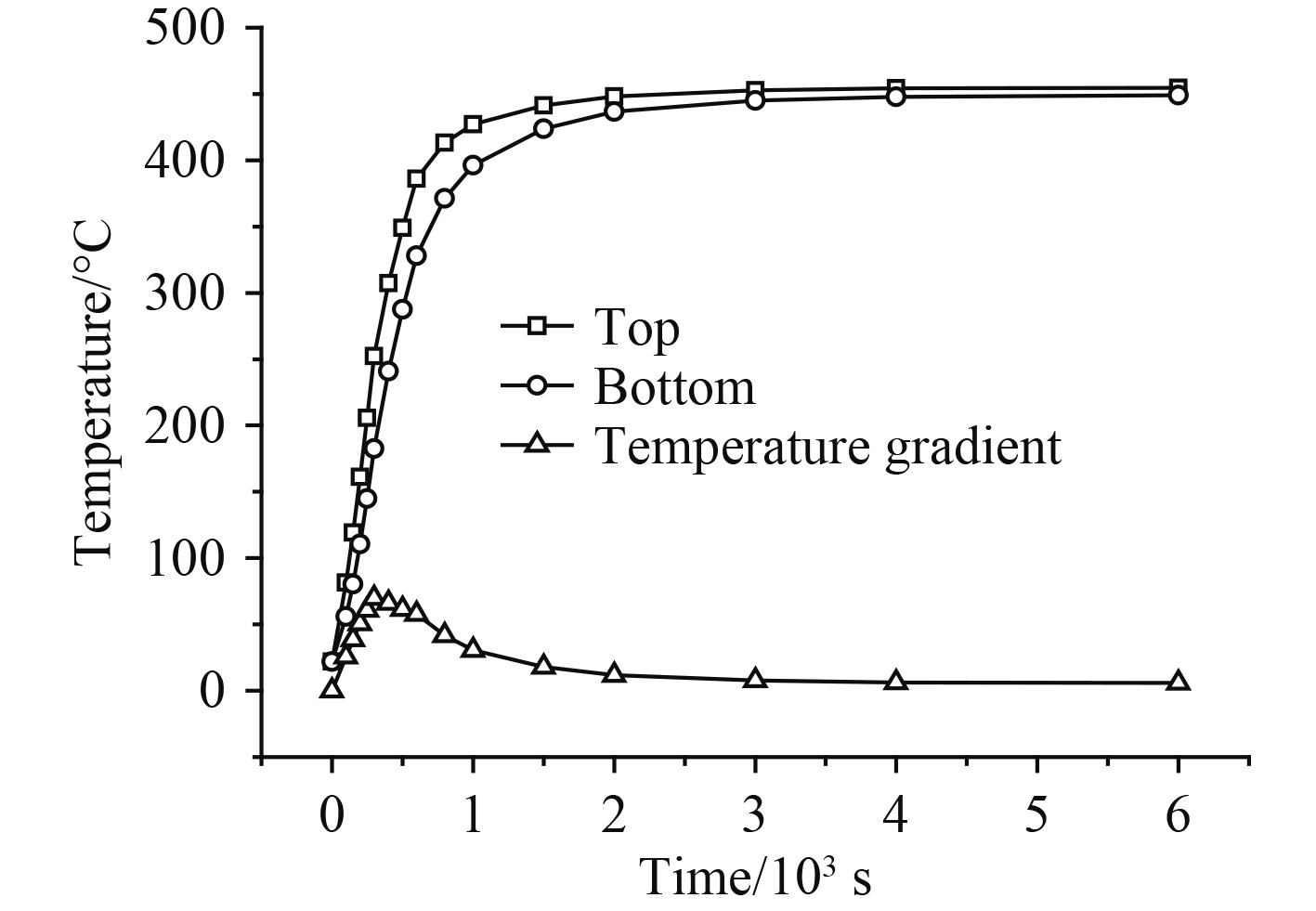
对拉杆孔上、下壁面的温度进行监测,以便观察冷态启动过程中拉杆孔温度、温度梯度随时间的变化规律。图7 与图8为第5级、第17级轮盘拉杆孔温度随时间的变化规律,两级轮盘拉杆孔温度均呈现启动初期迅速升高,之后逐渐趋于稳定的趋势。温差曲线为启动过程中拉杆上下壁面的温度差值,可为拉杆孔温度梯度变化、热应力变化提供参考。两轮盘拉杆孔的温差最大值均出现在启动后300 s,第5级轮盘拉杆孔最大温差为26.2℃,第17级轮盘拉杆孔最大温差为69.8℃。
|
图 7 第5级轮盘拉杆孔温度时变曲线 Fig. 7 Temperature variation curve of rod hole on 5th disc |
|
图 8 第17级轮盘拉杆孔温度时变曲线 Fig. 8 Temperature variation curve of rod hole on 17th disc |
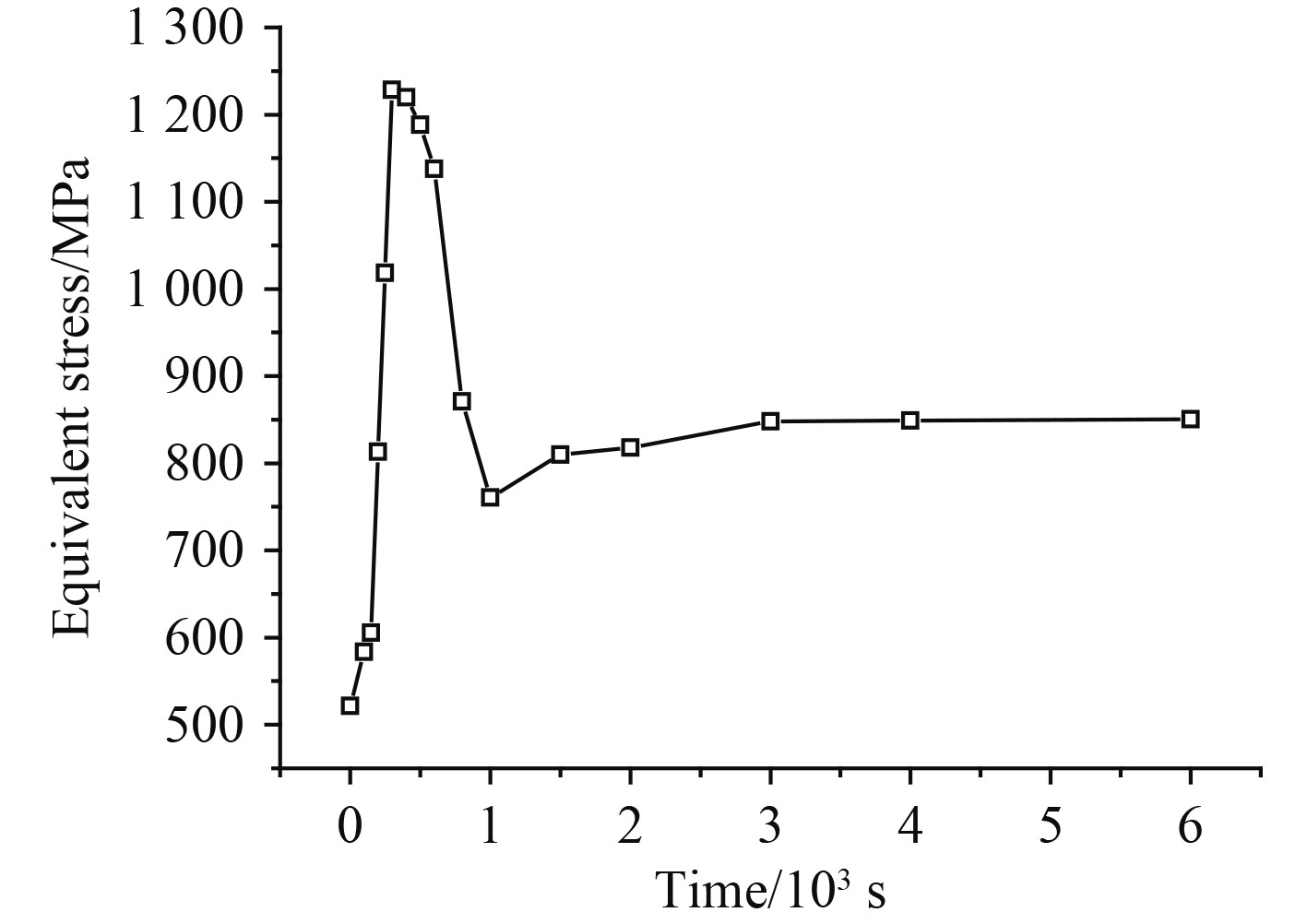
图9为冷态启动过程中转子最大应力的变化规律。在启动初期,转子最大应力迅速增大,并在启动后300 s时达到最大值1 228.5 MPa,位于第17级轮盘出气侧内圆角处;启动中期最大应力迅速降低至818.1 MPa,位于后轴头拉杆孔上壁面处;在启动后期稳定在850.5 MPa,位于第5级轮盘拉杆孔上壁面处。
|
图 9 转子最大应力时变曲线 Fig. 9 Maximum stress variation curve |
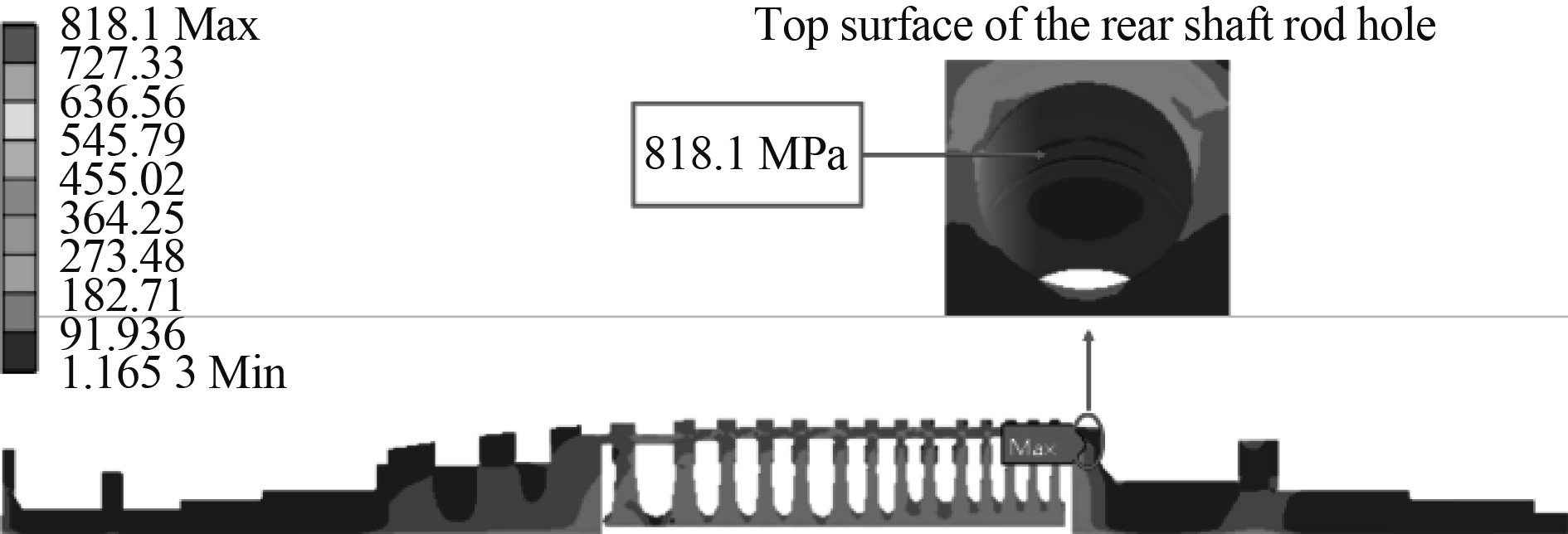
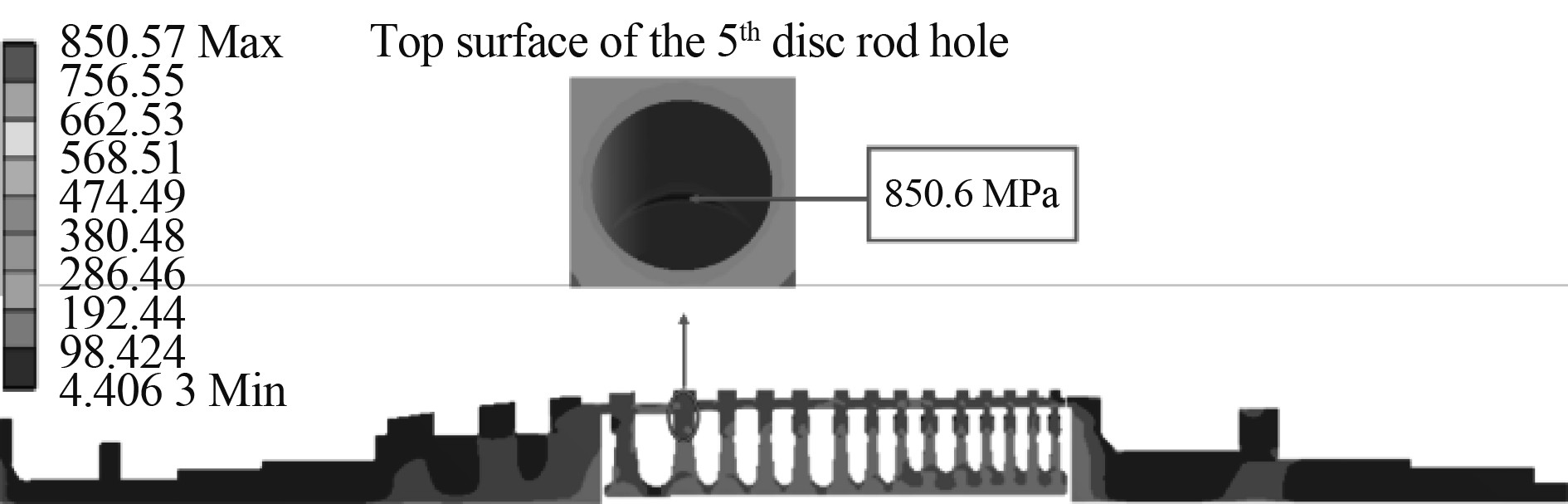
图10~图12分别为转子冷态启动后300 s、2 000 s和6000 s时的应力分布图,转子整体呈现应力由内径向外径逐渐减小的规律,各级轮盘内径处应力约为300~500 MPa,轮缘处应力均低于150 MPa;转子前、后轴头应力水平较低;各级轮盘进出气侧圆角处、拉杆孔处均有不同程度的应力集中。启动初期转子最大应力位于第17级轮盘拉杆孔侧壁面处,应力值为1228.5 MPa;启动中期转子最大应力位于后轴头拉杆孔上壁面处,应力值为818.1 MPa;启动后期转子最大应力位于第5级轮盘拉杆孔上壁面处,应力值为850.6 MPa。

|
图 10 启动300 s后转子应力分布/MPa Fig. 10 Rotor stress distribution at 300 s |
|
图 11 启动2000 s后转子应力分布/MPa Fig. 11 Rotor stress distribution at 2000 s |
|
图 12 启动6000 s后转子应力分布/MPa Fig. 12 Rotor stress distribution at 6000 s |
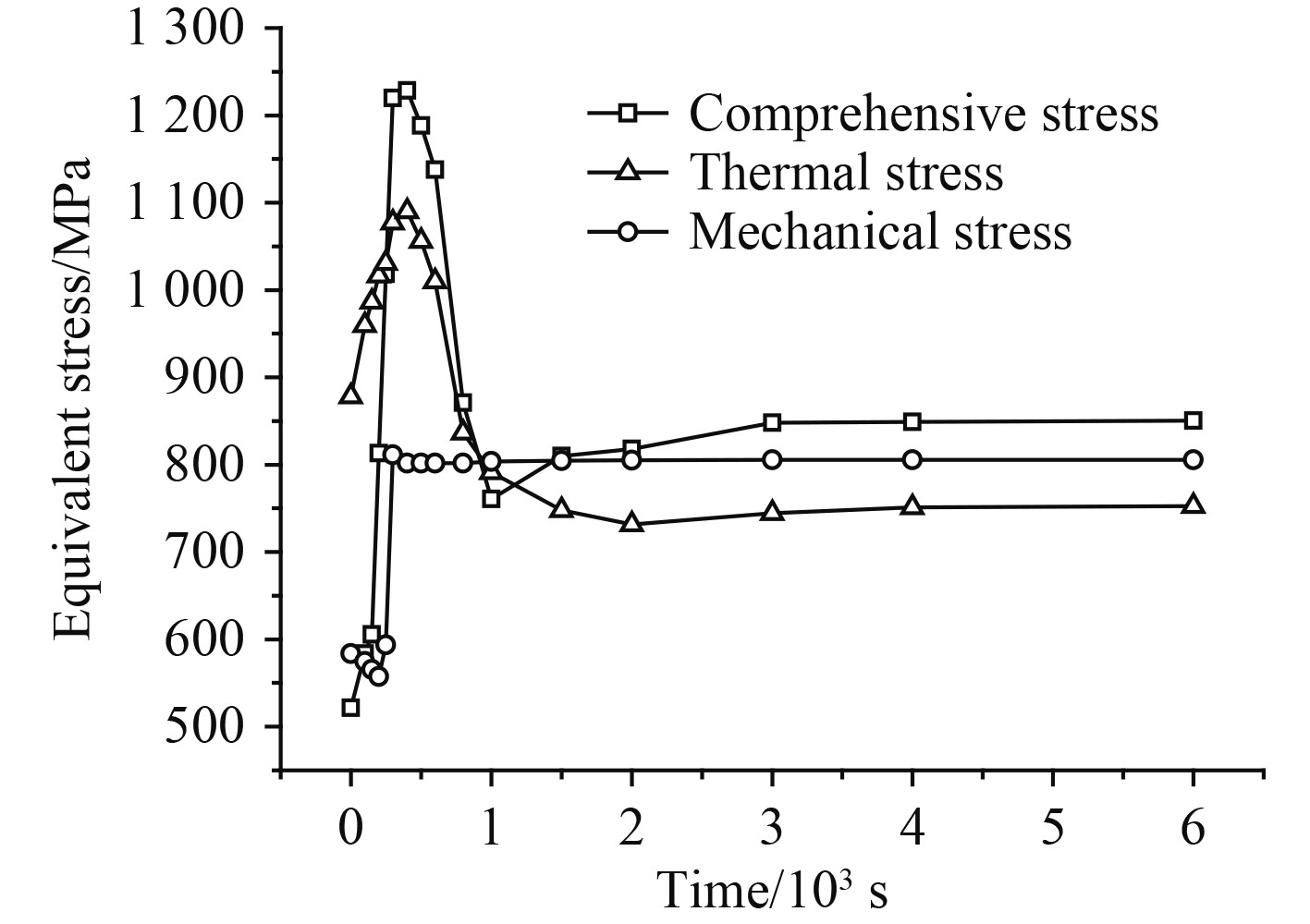
图13为启动过程中转子3种应力(综合应力、热应力和机械应力)最大值随时间的变化规律,通过该图可直观地观察到三者之间的关系。启动初期3种应力迅速升高,热应力相比机械应力较高,综合应力随着二者同步升高;启动中期机械应力保持稳定,热应力、综合应力迅速下降;启动后期3种应力均进入稳定状态。可见在启动的初期,转子综合应力主要受热应力影响,随着启动逐渐进入中后期,热应力对综合应力的影响逐渐减小。
|
图 13 转子3种应力最大值时变曲线 Fig. 13 All stress variation curve of rotor |
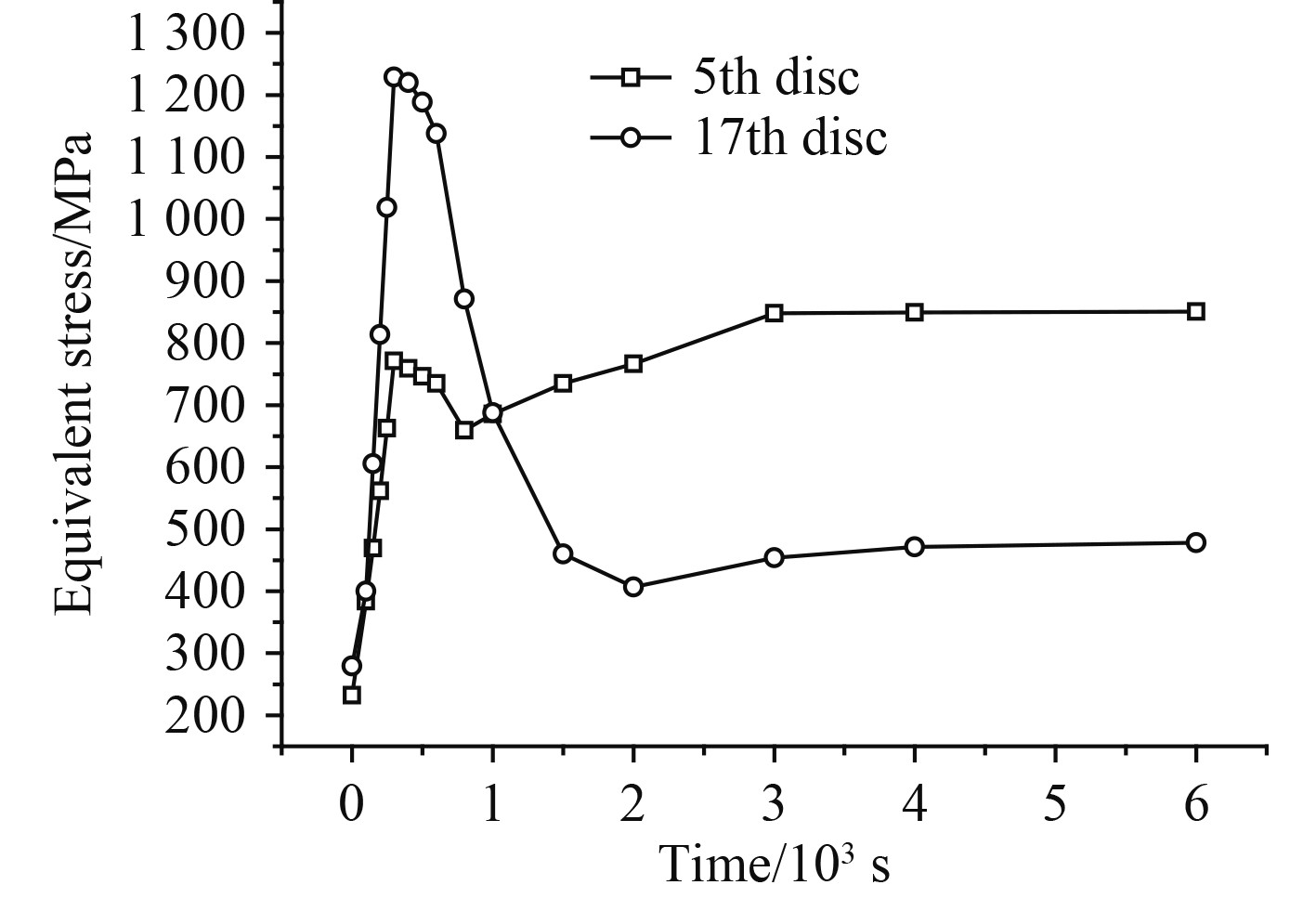
图14 为冷态启动过程中第5级和第17级轮盘最大应力随时间变化规律,二者变化趋势不同。对第5级轮盘:启动初期,轮盘应力水平迅速上升并于300 s时达到771.5 MPa;在启动中期先降低后上升至766.2 MPa;启动后期应力值再次小幅上升并稳定在850.6 MPa。对于第17级轮盘:启动初期轮盘应力水平迅速上升并于300 s时达到最大值1228.5 MPa;启动中期轮盘的应力水平迅速降低至406.8 MPa;启动后期轮盘最大应力值稳定在在478.4 MPa。
|
图 14 第5、第17级轮盘最大应力时变曲线 Fig. 14 Maximum stress variation curve of 5th and 17th disc |
第5级和第17级轮盘于冷态启动后300 s时,整体应力水平呈现由内径向外经逐渐减小的趋势,圆角、拉杆孔处均出现应力集中现象。第5级轮盘最大应力出现在轮缘进气侧外圆角处,大小为771.5MPa;拉杆孔上壁面应力水平较高,应力值为612.4MPa。第17级轮盘最大应力出现在轮盘出气侧内圆角处,大小为1228.5MPa;拉杆孔侧壁面应力水平较高,应力值为1027.7MPa。
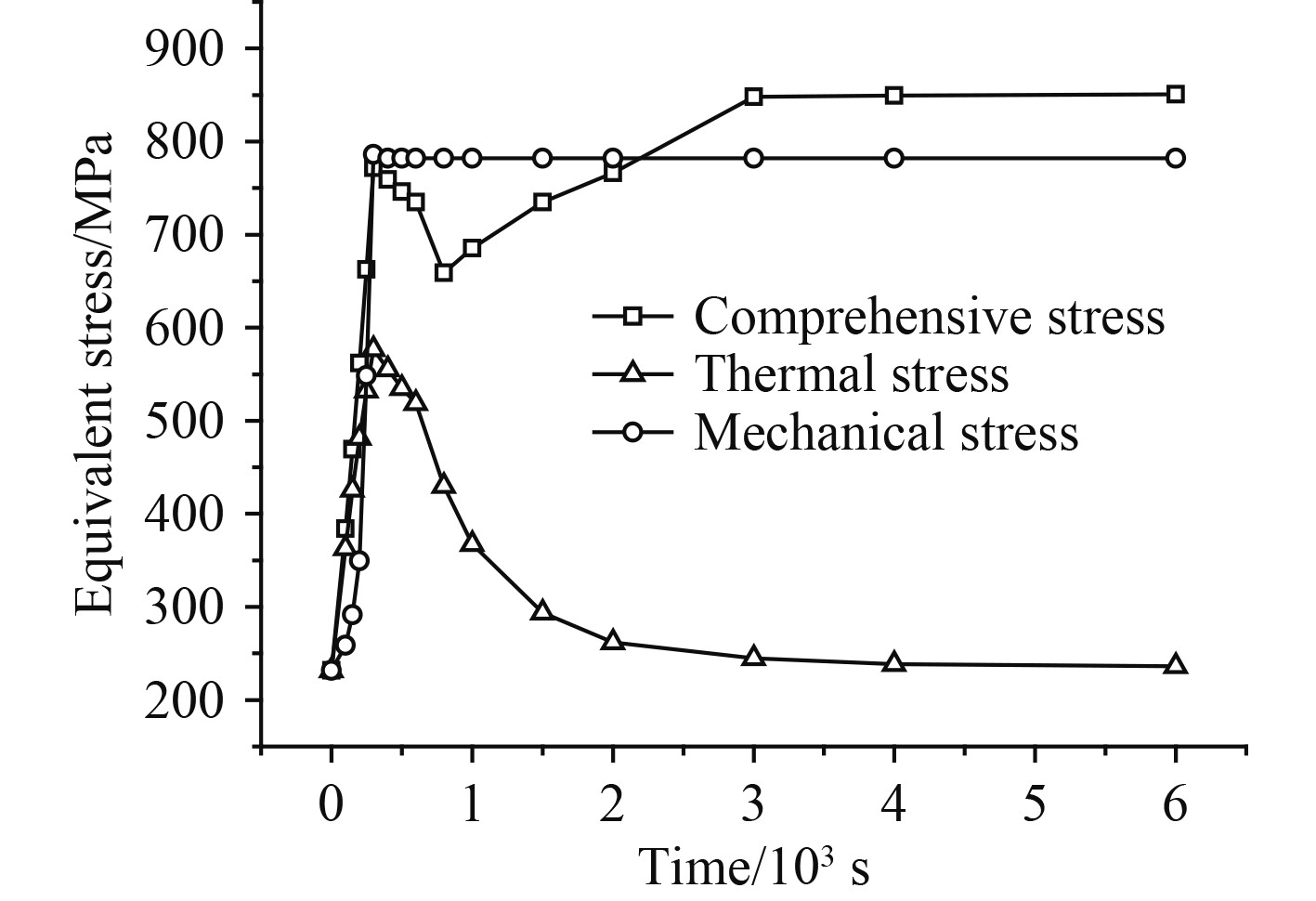
图15和图16为启动过程中第5级和17级轮盘3种应力最大值随时间的变化规律。由图可见,在启动初期第5级轮盘的机械应力高于热应力,而第17级轮盘的热应力则远高于机械应力。因此可认为,在该启动初期,对于所处环境温度较低的第5级轮盘而言,机械应力占主导地位;对于所处环境温度较高的第17级轮盘而言,热应力占主导地位,而热应力的大小则受温度梯度的影响。
|
图 15 第5级轮盘3种应力最大值时变曲线 Fig. 15 All stress variation curve of 5th disc |

|
图 16 第17级轮盘3种应力最大值时变曲线 Fig. 16 All stress variation curve of 5th disc |
在启动初期,各级轮盘外缘处的温度由于与高温工质密切接触而迅速升高,而内径处温度则在热传导作用下逐渐上升,上升速度较外缘处缓慢,温度水平较外缘处低,很容易在轮盘内部产生较大的温度梯度,引起较高的热应力。对比图5和图6的温差变化曲线和图15和图16热应力时变曲线可知,随着启动初期温度、温度梯度的迅速上升,转子的热应力也随之迅速提高。转子温度梯度和热应力的最大值均出现在启动后300 s,由于第17级轮盘此时的温差大于第5级轮盘,因此第17级轮缘附近的圆角处热应力高于第5级轮盘。
与此同时,随着转子转速的迅速上升,拉杆凸台与拉杆孔上壁面之间的接触压力随之增大,继而拉杆孔上壁面的机械应力水平也迅速提高,且拉杆孔上壁面为各级轮盘最大机械应力位置。因此在启动初期,第5级和第17级轮盘的机械应力(拉杆孔上壁面应力)呈现在启动初期迅速上升的变化规律。
对比图7和图8发现,在启动初期第17级轮盘拉杆孔温度梯度较大,在热应力主导下,拉杆孔最大应力出现在侧壁面处;而第5级轮盘拉杆孔温度梯度较小,机械应力主导下,拉杆孔最大应力出现在上壁面处。
3.2.2 启动中期轮盘应力分布第5级、17级轮盘冷态启动后2000 s时的整体应力分布规律与启动后300 s时类似。第5级轮盘轮缘进气侧上圆角处应力降低至527.6 MPa,而拉杆孔上壁面处应力上升至766.2 MPa。第17级轮盘整体应力水平大幅降低,轮盘出气侧内圆角处应力降低至206.6 MPa,拉杆孔处应力降低至406.8 MPa,拉杆孔处最大应力位置由300 s时的侧壁面处转移至上壁面处,侧壁面处仍有一定程度的应力集中。
在启动中期,各级轮盘内径处的温度已经达到最大值,转子整体的温度分布已经稳定,转子内部的温度梯度开始降低,转子内部热应力也随之降低。随着热应力的衰退,机械应力(主要是拉杆凸台与拉杆孔之间的接触应力)在综合应力中逐渐占据主导地位。
此时,由于转子的转速已经稳定,拉杆凸台与拉杆孔的接触压力保持稳定,机械应力不再变化。
3.2.3 启动后期轮盘应力分布启动6000 s时第5级轮盘轮缘进气侧外圆角处应力进一步降低至480.4 MPa,拉杆孔上壁面处应力上升至840.6 MPa,且该位置为第5级轮盘冷态启动过程中最大应力所处位置。第17级轮盘轮缘进气侧内圆角处应力降低至140.8 MPa,而拉杆孔上壁面处应力则上升至478.4 MPa,拉杆孔侧壁面处的应力集中现象已消失。
在启动后期,转子已经被充分加热,全局温度保持稳定,转子内部的温度梯度、热应力相较启动中期进一步下降,并稳定在较低水平。在该阶段,机械应力占主导地位,各级轮盘最大应力位置不再变化,应力值逐渐稳定。
综上,导致第5级和第17级轮盘启动过程中应力分布规律不同的原因有2个:轮盘内部温度梯度不同;拉杆凸台与拉杆孔上壁面接触压力不同。
4 启动曲线优化 4.1 优化方案通过以上分析可知,启动过程中转子内部的温度梯度会引起高额的热应力,拉杆凸台与拉杆孔接触会引起较高的接触应力。就该转子而言,启动初期产生的巨大热应力是转子整个启动过程中最大应力值较高的原因,因此通过降低转子启动初期转子内部温度梯度的方法降低转子的最大应力值。
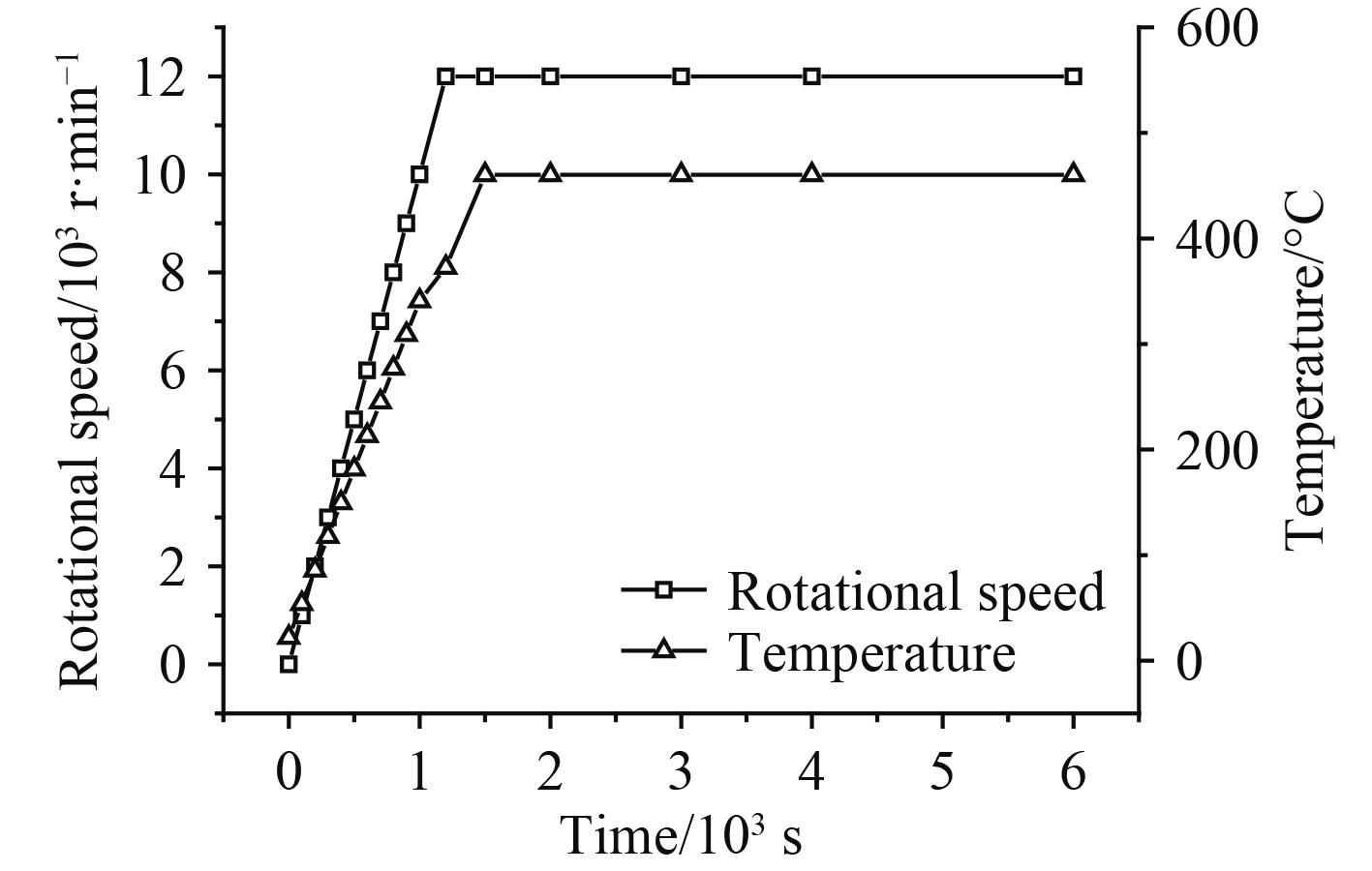
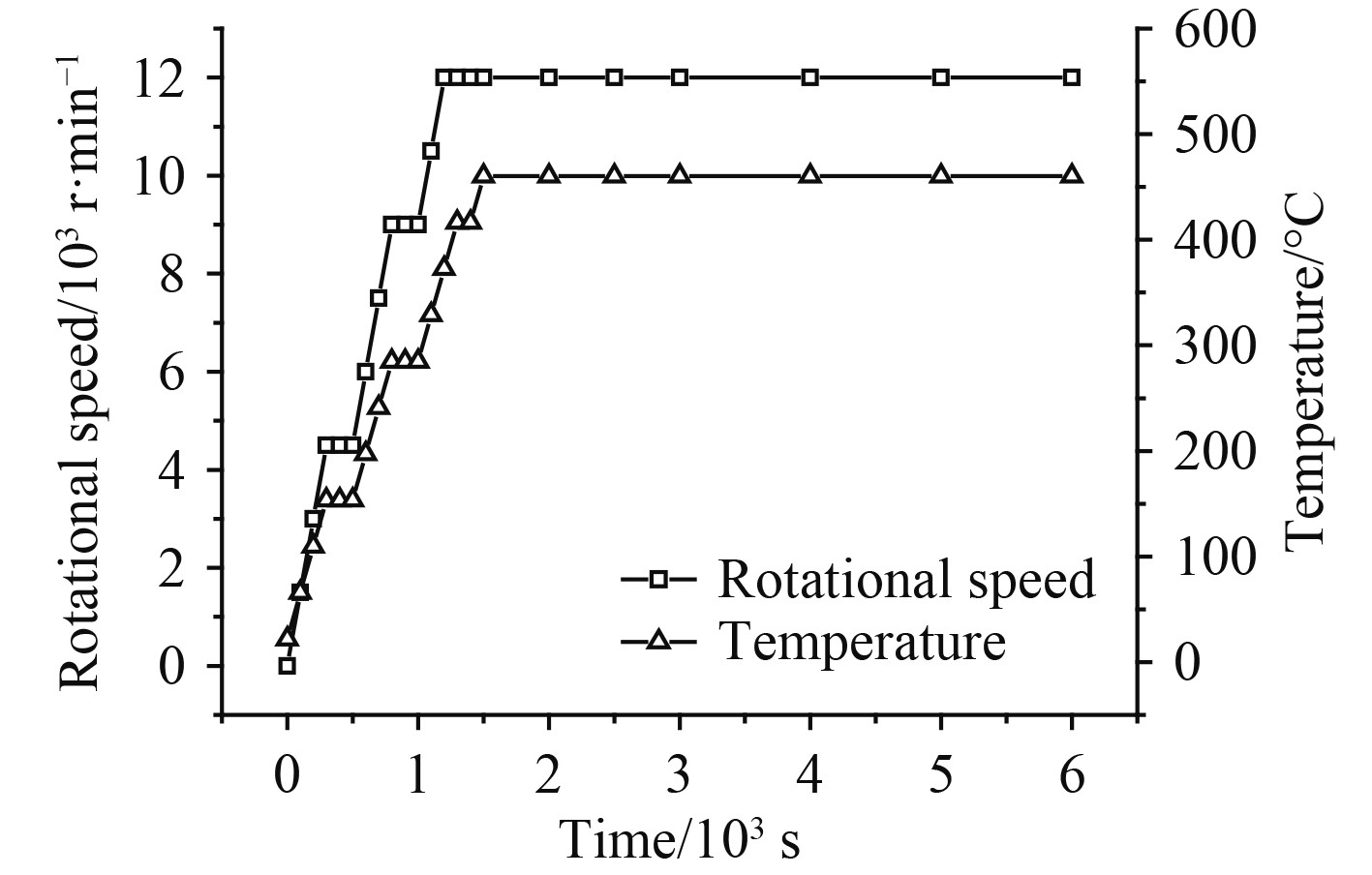
降低转子热应力最典型的方法之一就是优化转子的启动曲线。图17和图18为新启动曲线,按照优化后的启动曲线重新对转子进行瞬态热固耦合分析。在启动曲线A中,转子在启动后1200 s到达满转速,1500 s时达到满负荷;在启动曲线B中,转子的转速、温度负荷按阶梯式上升,转子在启动后1200 s达到满转速,1500 s达到满负荷。
|
图 17 启动曲线A Fig. 17 New start-up curve A |
|
图 18 启动曲线B Fig. 18 New start-up curve B |
图19 为转子采用3种不同启动曲线时最大应力随时间的变化规律。在进入稳定运行阶段前,转子最大应力均位于第17级轮盘出气侧内圆角处,3种启动曲线下应力值差别较大;进入稳定运行阶段后,转子最大应力均位于在第5级轮盘拉杆孔上壁面处,3种启动曲线下应力值差别较小,如表1所示。通过对比,采用新的启动曲线均使转子启动初期的最大应力显著降低,不同启动方式对转子稳态应力水平影响较小。
|
|
表 1 不同启动曲线下转子最大应力比较/MPa Tab.1 Rotor maximum stress under different start-up strategies |

|
图 19 不同启动曲线下转子最大应力时变曲线 Fig. 19 Rotor Maximum stress variation curve under different start-up strategies |
本文以周向拉杆转子为研究对象,考虑拉杆凸台与拉杆孔间接触,建立了三维循环对称有限元模型。通过顺序耦合方法对转子冷态启动过程的温度场、应力场进行了计算,并对计算结果进行了详细展示与分析。最后对冷态启动方案进行了优化,达到了降低转子应力最大值,延长转子运行寿命的目的。具体结论如下:
1)以第5级和第17级轮盘为监测对象,得到了轮盘内径、外缘、拉杆孔在冷态启动过程中的温度变化规律,得到了两轮盘内部、拉杆孔上下壁面温差。温度梯度均呈现在启动初期迅速增大,随后逐渐降低并稳定在较低水平的变化规律,且第17级轮内部、拉杆孔处的最高温差均大于第5级轮盘。
2)启动过程中各级轮盘整体呈现应力水平由内径向外径逐渐降低的分布规律,圆角处、拉杆孔处均呈现应力集中现象。在启动初期,在较高的温度梯度和转速的共同作用下,第17级轮盘出气侧内圆角处应力最高,其值为1 228.5 MPa;转子进入稳定运行状态后,在拉杆凸台与拉杆孔极大的接触压力下,第5级轮盘拉杆孔上壁面处应力最高,其值为850.6 MPa。
3)启动过快是导致热应力、综合应力较大的原因,为此本文采用了2种新的启动方案。计算对比发现,阶梯式升转速、负荷(启动曲线B)能使转子启动过程中的最大应力值大幅降低(由1 228.5 MPa降至836.7 MPa),优化效果显著。
| [1] |
SURESH S. 材料的疲劳[M]. 北京: 国防工业出版社, 1999.
|
| [2] |
GONG M X, GUO D, WANG Z X, et al. Transient anslysis of LP rotor from NPP 900MW turbine[J]. Procedia Engineering. 2012, 27: 1575−1581.
|
| [3] |
MOHAIDEEN M M. Optimization and analysis on turbine rotor of a turbo shaft engine[J]. Procedia Engineering, 2012, 38: 867−871.
|
| [4] |
卓明, 杨利花, 夏凯等. 考虑热场的重型燃气轮机组合转子盘间接触应力分析[J]. 西安交通大学学报, 2018, 52(11): 58-64. |
| [5] |
ZHU R, MENG G, LI H G, et al. Transient characteristics analysis of thermal stress in start-stop condition for rotot system in gas turbine[J]. Advances in vibration engineering. 2013, 12(6): 571−586.
|
| [6] |
张清雷, 黄魏平, 陈堰芳. 周向均布拉杆转子低周疲劳寿命研究[J]. 机械设计与制造. 2016, 1: 238-242.
|
| [7] |
黄金娥. 多场偶合下燃气轮机涡轮盘的寿命预估[J]. 舰船科学技术, 2018, 40(7): 86-88. |
| [8] |
BARELLA S, BELLOGINI M, BONIARDI M, et al. Failure analysis of a steam turbine rotor[J]. Engineering Failure Analysis. 2011, 18(6): 1511−1519.
|
| [9] |
刘昕, 袁奇, 欧文豪. 燃气轮机周向拉杆转子拉杆应力分析和改进设计[J]. 西安交通大学学报2016, 50(10): 105-110
|
| [10] |
宋文超, 陈英涛, 徐让书, 等. QD128燃气轮机动力涡轮盘组件温度场计算及静强度分析[J]. 燃气涡轮试验与研究2015, 28(6): 45−48
|
| [11] |
刘庆亚, 申僑林, 何竟飞, 等. 重型燃气轮机组合转子透平端可靠性仿真分析[J]. 计算机仿真, 2019, 36(2): 183-200. |
| [12] |
史进渊, 杨宇, 邓志成, 等. 大功率电站汽轮机寿命预测与可靠性设计[M]. 北京: 中国电力出版社, 2011: 126−202.
|
| [13] |
徐宁, 王庆超, 王震林, 等. 考虑接触热阻的非连续转子快速启动热分析[J]. 航空动力学报, 2017(12): 86−92
|
 2022, Vol. 44
2022, Vol. 44

