船舶航向控制作为船舶运动控制领域中最为基础且重要的研究方向,事关船舶航行时的安全问题。20世纪20年代最初的机械自动舵出现,标志着船舶航向控制由人工控制逐渐转向自动控制。对于线性控制器,PID控制器具有形式简洁、设定参数较少、易于调节等优点。Banazadeh等[1]提出一种基于卡尔曼滤波辨识系统参数的PID自动航向控制器。孙武臣等[2]针对船舶转向时的横倾特性,在PID控制器中引入了微分项进行补偿,同时根据横倾角度变化设计模糊控制规则,调节PID控制器中的参数。然而,线性控制器所要求的线性状态和参数条件的假设往往难以满足。因此,近些年一些非线性控制器被提出用来克服这类问题。张显库等[3]提出一种在不改变控制器结构情况下利用正弦函数来调整控制误差的控制方法,提高了控制器性能。Liu[4]提出一种基于非线性观测器的船舶航向自适应滑模控制器。Zhang等[5]在Backstepping框架下引入通过航向误差信号传递的反正切非线性函数,简化了设计步骤,提高了控制器性能。王永涛[6]提出一种融合粒子群优化算法的改进Backstepping方法,设计船舶航向控制器。
由于船舶系统中具有非线性和不确定性,给系统控制器设计带来严峻挑战,引入一种确定的补偿机制应对不确定参数非常困难。对于船舶航向系统,其控制系数的符号是未知的,意味着其控制方向是未知的,传统的反馈控制方法在面对这类问题时具有一定的困难。直到引入Nussbaum函数[7],形成一种基于Nussbaum增益的自适应策略才实现对未知控制方向的补偿。针对具有未知控制增益方向和系统参数不确定的船舶航向系统,利用Nussbaum函数应对控制方向未知的问题[8-9]。相比于上述自适应策略,逻辑切换自适应方法能够处理更加严重的不确定性及干扰[10-12]。利用基于Lyapunov的逻辑切换机制应对系统中未知的控制方向,实现了对设定航向跟踪误差的广义指数收敛和有限时间收敛[13-14]。
现有研究大多采用基于时间触发的控制策略,即以固定的时间间隔进行控制信号的更新。这种控制策略会产生冗余的控制行为并且造成执行器的多余损耗,浪费能源。而基于事件触发的控制器仅当预先设定的触发条件触发时才进行控制信号的更新,因此采用基于事件触发的控制策略可以有效降低执行机构的损耗,达到节约能源、提高经济效益的目的。
本文针对船舶航向系统中强非线性和控制方向未知的特性,利用Backstepping方法,融合了逻辑切换机制和事件触发机制,设计了基于事件触发的船舶航向逻辑切换自适应控制算法。此外,引入一种由跟踪误差决定的动态增益应对采样误差对系统性能的影响。该控制算法实现了对设定航向的跟踪误差指数收敛到可调的原点邻域内,降低了控制信号更新频率,同时避免了事件触发控制中违背其意义的奇诺现象(即有限时间内发生无限次更新)。最后,通过仿真结果验证了该控制算法的有效性。
1 系统描述与控制目标 1.1 系统描述本文的船舶航向控制系统为Norrbin非线性模型:
| $ T\ddot \varphi + \dot \varphi + \alpha {\dot \varphi ^3} = K\eta。$ | (1) |
其中:
选择状态变量
| $\left\{ \begin{gathered} {{\dot x}_1} = {x_2},\hfill \\ {{\dot x}_2} = {\theta _0}u + {\theta ^\text{T}}\phi ({x_2})。\hfill \\ \end{gathered} \right. $ | (2) |
其中:
本文的主要结果建立在如下假设基础之上:
假设1 存在正常数
假设2 存在正常数
针对船舶航向系统(2),在满足假设1和假设2的前提下,设计一个事件触发自适应控制器
定义一种新的坐标变换
| $ \left\{ \begin{gathered} {z_1} = {x_1} - {\varphi _d},\hfill \\ {z_2} = {x_2} - {\alpha _1},\hfill \\ \end{gathered} \right. $ | (3) |
设计如下事件触发自适应控制器:
| $ \begin{split} u(t) =&S\left( {L\left( {{t'_{m,k}}} \right)} \right) \cdot {\alpha _2}\left( {x\left( {{t_k}} \right),d({t_k})} \right) = \\ &- S\left( {L\left( {{{t'}_{m,k}}} \right)} \right){z_2}{\beta _2}\left( {x\left( {{t_k}} \right),d({t_k})} \right),\;t \in \left[ {{t_k},{t_{k + 1}}} \right),\end{split} $ | (4) |
| $ S\left( {L\left( {{t'_{m,k}}} \right)} \right) = b\left( {L\left( {{t'_{m,k}}} \right) + 1} \right){\left( { - 1} \right)^{L\left( {{t'_{m,k}}} \right)}},$ | (5) |
| $ \dot d = \max \left\{ {\left| {{x_1} - {\varphi _d}} \right| - \varepsilon ,0} \right\},{\text{ }}d\left( 0 \right) = 1。$ | (6) |
其中:
| $ \left\{ \begin{gathered} {t'_{m,k}} = {t'_m},\hfill \\ m = \arg \mathop {\max }\limits_j {t'_j} \leqslant {t_k}。\hfill \\ \end{gathered} \right. $ | (7) |
根据式(4)的定义可以看出,在事件触发控制中,控制信号仅在事件触发时刻
由动态增益的定义式(6)可知,
定义如下事件触发机制,记
| $\begin{split} &{t}_{k+1}=\mathrm{inf}\left\{t\right|t > {t}_{k},事件1和事件2中至少一个成立,\\ &其中{{t}^{\prime }}_{j}={{t}^{\prime }}_{m,k}\}。\end{split} $ | (8) |
定义如下事件:
| $ \left\{\begin{array}{l}{\bf{事件1}}\;\;\left|u\left(t\right)-S\left(L\left({{t}^{\prime }}_{j}\right)\right){\alpha }_{2}\left(x\left(t\right),d\left(t\right)\right)\right| \geqslant {\delta }_{1},\\ {\bf{事件2}}\;\;\dfrac{1}{2}{\Vert z(t)\Vert }^{2} > \left(\dfrac{1}{2}{\Vert z({{t}^{\prime }}_{j})\Vert }^{2}-\dfrac{\Theta }{\rho d}+{\delta }_{2}\right){e}^{-\rho \left(t-{{t}^{\prime }}_{j}\right)}+\dfrac{\Theta }{\rho d}。\end{array} \right.$ | (9) |
其中:
定义如下逻辑切换机制,记
| $ \left\{\begin{array}{l} t'_{j+1}=\mathrm{inf}\left\{t|t > t'_{j},在时刻t\text{,}事件2成立\right\},\\ L(t'_{j})={L}_{j}。\end{array}\right. $ | (10) |
其中:
由上述机制可知
注1:由式(7)可知,
考虑如下Lyapunov函数:
| $ V(t) = \dfrac{1}{2}z_1^2 + \dfrac{1}{2}z_2^2,$ | (11) |
对Lyapunov函数求导得到:
| $ \begin{gathered} \frac{{{\text{d}}V}}{{{\text{d}}t}} = {z_1}{z_2} - z_1^2{\beta _1} + {\theta _0}{z_2}u + {\theta _1}{z_2}\left( {{z_2} - {z_1}{\beta _1}} \right)+ \\ {\theta _2}{z_2}{\left( {{z_2} - {z_1}{\beta _1}} \right)^3} - \frac{{{\text{d}}{\alpha _1}}}{{{\text{d}}{x_1}}}{z_2}\left( {{z_2} - {z_1}{\beta _1}} \right) - \frac{{\partial {\alpha _1}}}{{\partial d}}{z_2}\dot d。\hfill \\ \end{gathered} $ | (12) |
利用假设1和假设2及事件触发机制并结合式(6)有:
| $ {z_1}{z_2} \leqslant \frac{1}{2}z_1^2 + \frac{1}{2}z_2^2,$ | (13) |
| $ {z_2}u \leqslant {z_2}{\delta _1} - z_2^2S\left( {L\left( {{{t'}_j}} \right)} \right){\beta _2}\left( {x\left( t \right),d\left( t \right)} \right),$ | (14) |
| $ {\theta _0}{z_2}u \leqslant \frac{{{{\theta ''}^2}\delta _1^2}}{{2d}} + \frac{d}{2}z_2^2 - \left( {S\left( {L\left( {{{t'}_j}} \right)} \right){\theta _0} - 1} \right)z_2^2{\beta _2} - z_2^2{\beta _2},$ | (15) |
| $ - \frac{{\partial {\alpha _1}}}{{\partial {x_1}}}{z_2}\left( {{z_2} - {z_1}{\beta _1}} \right) \leqslant \frac{1}{2}z_1^2 + \frac{1}{2}z_2^2 + \frac{1}{2}z_2^2{\left( {\frac{{\partial {\alpha _1}}}{{\partial {x_1}}}} \right)^2}{\left( {1 + {\beta _1}} \right)^2},$ | (16) |
| $ - \frac{{\partial {\alpha _1}}}{{\partial d}}{z_2}\dot d \leqslant \left| {\frac{{\partial {\alpha _1}}}{{\partial d}}} \right|\left| {{z_2}} \right|\left| {{z_1}} \right| \leqslant \frac{1}{2}z_1^2 + \frac{1}{2}z_2^2{\left( {\frac{{\partial {\alpha _1}}}{{\partial d}}} \right)^2},$ | (17) |
| $ \begin{gathered} {\theta _1}{z_2}\left( {{z_2} - {z_1}{\beta _1}} \right) + {\theta _2}{z_2}{\left( {{z_2} - {z_1}{\beta _1}} \right)^3} \leqslant \hfill \frac{1}{2}z_2^2 - \\ \frac{1}{2}z_1^2 + \frac{1}{2}z_2^2{{\hat \theta }^2}{\left( {1 + {{\left( {{z_2} - {z_1}{\beta _1}} \right)}^2}} \right)^2}{\left( {1 + {\beta _1}} \right)^2}。\hfill \\ \end{gathered} $ | (18) |
为便于分析,将
将式(13)~式(18)代入式(12)右侧,得到:
| $\begin{split}& \frac{\text{d}V}{\text{d}t}\leqslant \left(1-{\beta }_{1}\right){z}_{1}^{2}-\left({\theta }_{0}S-1\right){z}_{2}^{2}{\beta }_{2}+\bigg(\frac{3+d}{2}-{\beta }_{2}+\\ &\frac{1}{2}\left({\overline{\varphi }}^{2}+{\left(\frac{\partial {\alpha }_{1}}{\partial {x}_{1}}\right)}^{2}\right)\times{\left(1+{\beta }_{1}\right)}^{2}+\frac{1}{2}{\left(\frac{\partial {\alpha }_{1}}{\partial d}\right)}^{2}\bigg){z}_{2}^{2}+\frac{\Theta }{d}。\end{split}$ | (19) |
选择:
| $ \begin{gathered} {\beta _1} = 1 + \frac{\rho }{2},\hfill \\ {\beta _2} = \frac{{3 + d + \rho }}{2} + \frac{1}{2}\left( {{{\bar \phi }^2} + {{\left( {\frac{{\partial {\alpha _1}}}{{\partial {x_1}}}} \right)}^2}} \right){\left( {1 + {\beta _1}} \right)^2} + \frac{1}{2}{\left( {\frac{{\partial {\alpha _1}}}{{\partial d}}} \right)^2}。\hfill \\ \end{gathered} $ | (20) |
代入式(19),得到:
| $ \frac{{{\text{d}}V}}{{{\text{d}}t}} \leqslant - \rho V - \left( {{\theta _0}S - 1} \right)z_2^2{\beta _2} + \frac{\Theta }{d}。$ | (21) |
为保证系统的跟踪误差收敛至可调的原点邻域内,需使
对于事件触发控制器的采样误差“
对系统在控制器(4)~(6)和逻辑切换事件触发机制(8)~(10)作用下的稳定性进行分析。
首先证明对于系统中的设计参数
取
| $ \frac{{{\text{d}}V}}{{{\text{d}}t}} \leqslant - \rho V + \frac{\Theta }{d},t > {t'_{\bar m}},$ | (22) |
进而得到:
| $\begin{split} V(t) \leqslant &\left( {V\left( {{t'_{\bar m}}} \right) - \frac{\Theta }{{\rho d}}} \right){e^{ - \rho \left( {t - {t'_{\bar m}}} \right)}} + \frac{\Theta }{{\rho d}} \ne\\ &\left( {V\left( {{t'_{\bar m}}} \right) - \frac{\Theta }{{\rho d}} + {\delta _2}} \right){e^{ - \rho \left( {t - {t'_{\bar m}}} \right)}} + \frac{\Theta }{{\rho d}}。\end{split} $ | (23) |
这意味着在时刻
接下来证明系统的解
为确保控制器的可执行性,证明动态增益
| $ d\left( t \right) \geqslant \frac{{2\Theta }}{{{\varepsilon ^2}\rho }},{\text{ }}\forall t > {T_1},$ | (24) |
结合式(22),得到:
| $ \frac{{\text{d}V}}{{\text{d}t}} \leqslant - \rho V + \frac{{{\varepsilon ^2}\rho }}{2},{\text{ }}\forall t > {T_1},$ | (25) |
进而得到:
| $ V\left( t \right) \leqslant V\left( {{T_1}} \right){e^{ - \rho \left( {t - {T_1}} \right)}} + \frac{{{\varepsilon ^2}}}{2}\left( {1 - {e^{ - \rho \left( {t - {T_1}} \right)}}} \right),$ | (26) |
根据
| $ \left| {{z_1}} \right| \leqslant \sqrt {2V(t)} \leqslant \varepsilon ,{\text{ }}\forall t > {T_2},$ | (27) |
根据式(6)的定义可知,
基于前文分析,有下列不等式成立:
| $ \frac{1}{2}{\left\| {z(t)} \right\|^2} \leqslant \left( {\frac{1}{2}{{\left\| {z({t_0})} \right\|}^2} + \bar m{\delta _2}} \right){e^{ - \rho \left( {t - {t_{\bar m}}} \right)}} + \frac{\Theta }{{\rho d}}\left( {1 - {e^{ - \rho \left( {t - {t_{\bar m}}} \right)}}} \right),$ | (28) |
所以,
最后证明,对任意切换区间
| $ \inf \left\{ {{t_{k + 1}} - {t_k}|[{t_k},{t_{k + 1}}) \subseteq [{{t'}_j},{{t'}_{j + 1}})} \right\} > 0,$ | (29) |
针对任意固定切换区间
如果
如果
| $ \begin{split}&\frac{{\text{d}\left( {S({L_j}){\alpha _2}\left( t \right)} \right)}}{{\text{d}t}} = S({L_j})\times \\ &\left( {\frac{{\partial {\alpha _2}}}{{\partial {x_1}}}{x_2} + \frac{{\partial {\alpha _2}}}{{\partial {x_2}}}({\theta _0}u + {\theta ^\text{T}}\phi ({x_2})) + \frac{{\partial {\alpha _2}}}{{\partial d}}\dot d} \right),\end{split} $ | (30) |
由控制器(4)~(6)得:
| $ \left\{ \begin{gathered} \mathop {\sup }\limits_{t \in [0,{T_f})} \left| {u(t)} \right| = \mathop {\sup }\limits_{\{ (m,k)\} } \left| {S\left( {L\left( {{t'_{m,k}}} \right)} \right){\alpha _2}\left( {x\left( {{t_k}} \right),d\left( {{t_k}} \right)} \right)} \right|,\hfill \\ \dot d \leqslant \left| {{x_1} - {\varphi _d}} \right| \leqslant \left| {{x_1}} \right| + \left| {{\varphi _d}} \right|。\hfill \\ \end{gathered} \right. $ | (31) |
由前文可知
| $ \left| {\frac{{\text{d}(S({L_j}){\alpha _2}(t))}}{{\text{d}t}}} \right| < \lambda ,\forall t \in [{t_k},{t_{k + 1}}),$ | (32) |
由控制器(4)~(6)和事件触发机制(8)得到:
| $ \left| {u(t) - S({L_j}){\alpha _2}(t)} \right| \leqslant {\delta _1},\forall t \in [{t_k},{t_{k + 1}}),$ | (33) |
结合(32)式得到:
| $ \begin{split}&\left| {\frac{{\text{d}{{(u(t) - S({L_j}){\alpha _2}(t))}^2}}}{{\text{d}t}}} \right| = 2\left| {u(t) - S(L){\alpha _2}(t)} \right| \times\\ &\left| {\frac{{\text{d}\left( {S({L_j}){\alpha _2}(t)} \right)}}{{\text{d}t}}} \right| \leqslant 2{\delta _1}\lambda ,\forall t \in [{t_k},{t_{k + 1}})。\end{split} $ | (34) |
此外,由于
| $ \left\{ \begin{gathered} {\left( {u({t_k}) - S({L_j}){\alpha _2}({t_k})} \right)^2} = 0,\hfill \\ {\left( {u(t_{k + 1}^ - ) - S({L_j}){\alpha _2}(t_{k + 1}^ - )} \right)^2} = {\delta _1}^2,\hfill \\ \end{gathered} \right. $ | (35) |
得到:
| $ \begin{gathered} \delta _1^2 = {\left( {u(t_{k + 1}^ - ) - S({L_j}){\alpha _2}(t_{k + 1}^ - )} \right)^2} - {\left( {u({t_k}) - S({L_j}){\alpha _2}({t_k})} \right)^2} \hfill \leqslant \\ \int_{{t_k}}^{t_{k + 1}^ - } {\left| {\frac{{\text{d}{{\left( {u(t) - S({L_j}){\alpha _2}(t)} \right)}^2}}}{{\text{d}t}}} \right|} {\text{d}}t \leqslant 2{\delta _1}\lambda \left( {{t_{k + 1}} - {t_k}} \right),\hfill \\ \end{gathered} $ | (36) |
进而得到:
| $ {t_{k + 1}} - {t_k} \geqslant \frac{{{\delta _1}}}{{2\lambda }},$ | (37) |
注意到
| $ \inf \left\{ {{t_{k + 1}} - {t_k}|[{t_k},{t_{k + 1}}) \subseteq [{{t'}_j},{{t'}_{j + 1}})} \right\} \geqslant \frac{{{\delta _1}}}{{2\lambda }} > 0。$ | (38) |
即奇诺现象不会发生。
4 仿 真在仿真中采用文献[15]中的模型参数。假设系统的初始状态为
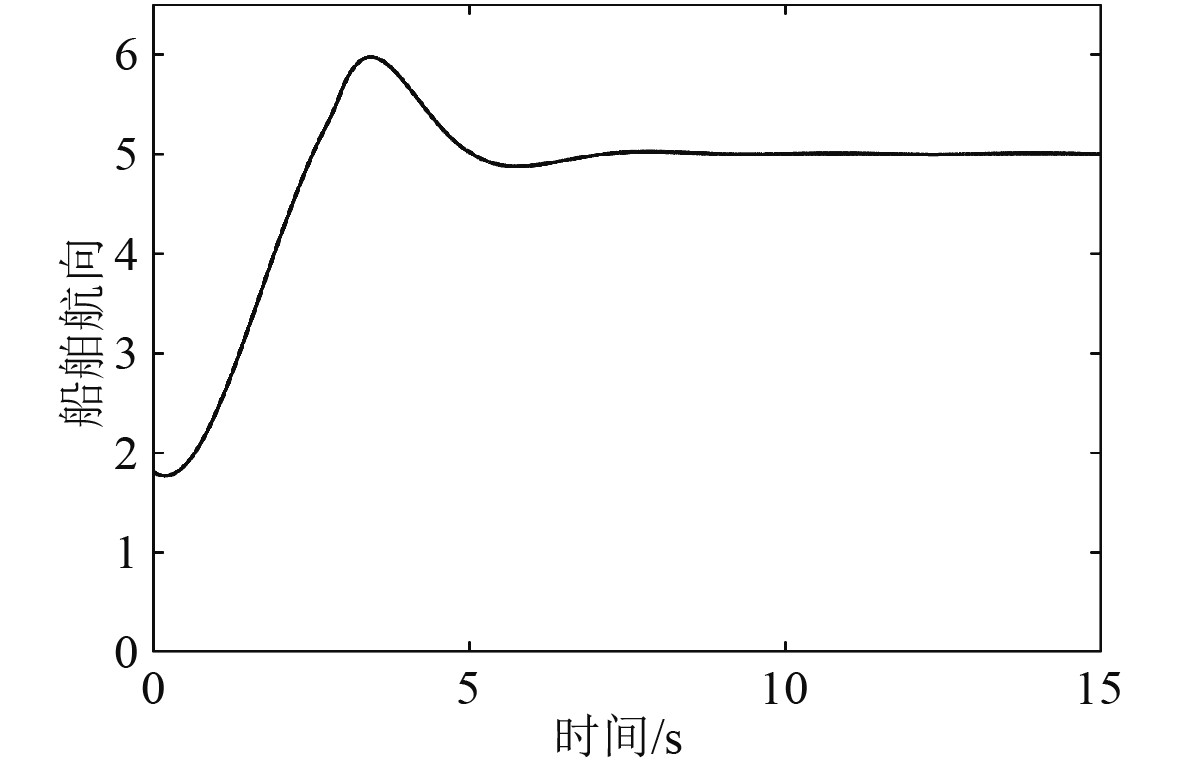
|
图 1 船舶航向 Fig. 1 Ship course |
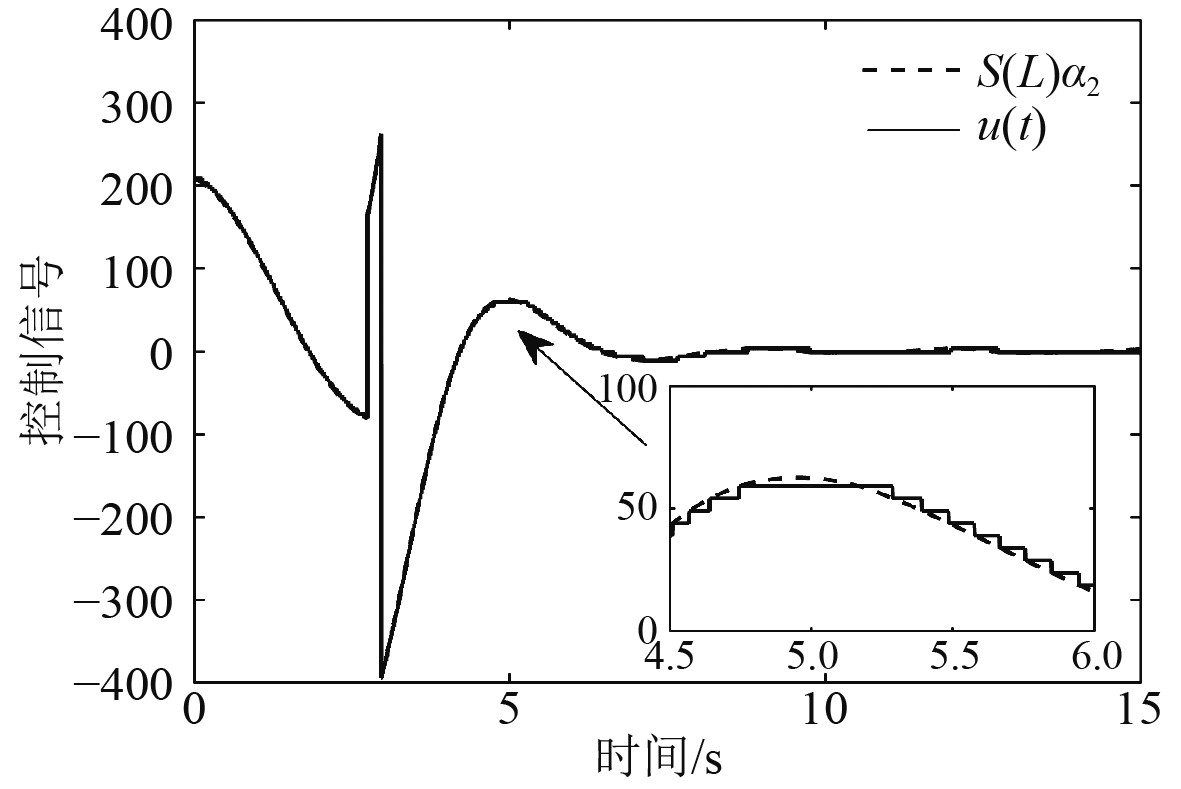
|
图 2 控制信号 Fig. 2 Control signal |
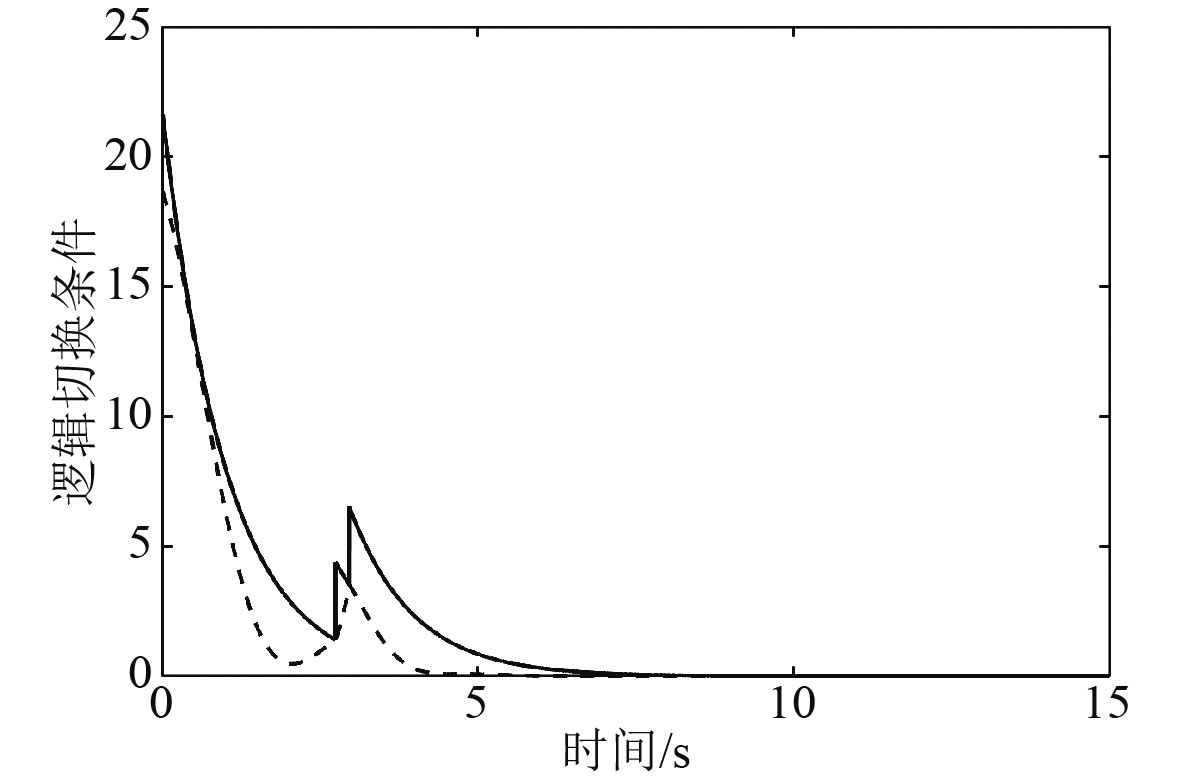
|
图 3 逻辑切换条件 Fig. 3 Logic switching condition |

|
图 4 动态增益 Fig. 4 Dynamic gain |
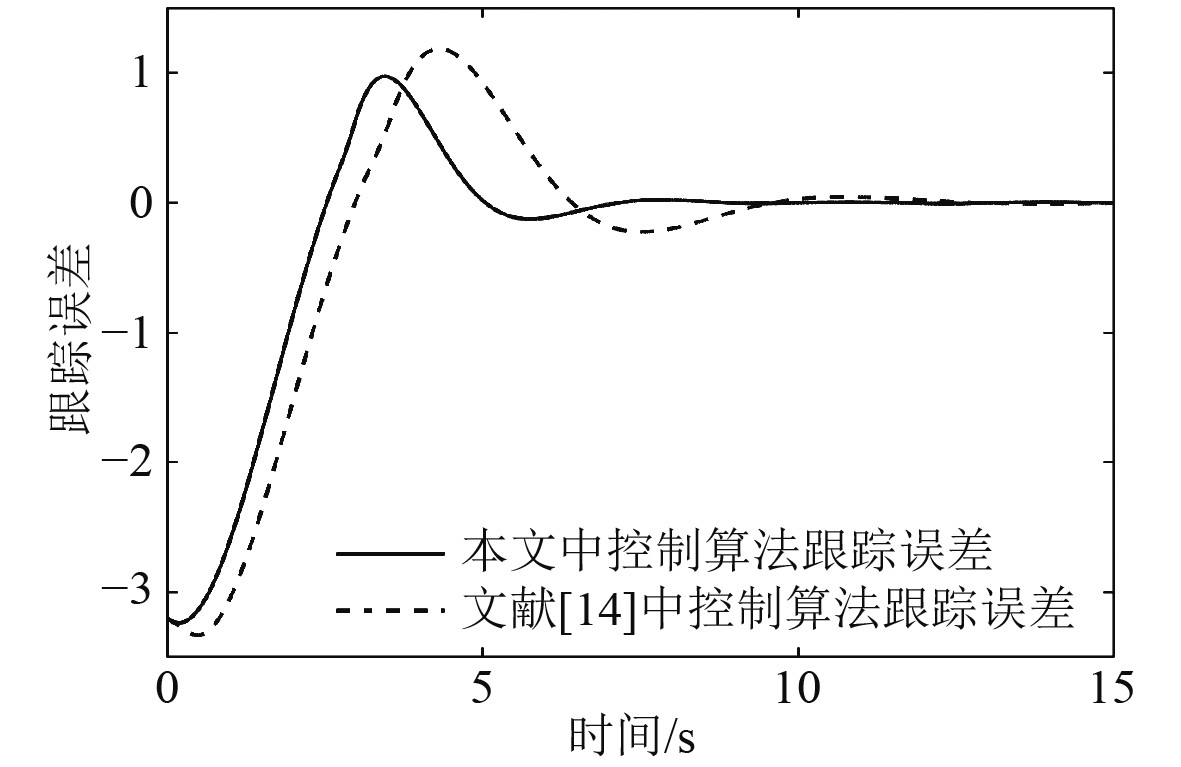
|
图 5 跟踪误差 Fig. 5 Tracking error |
|
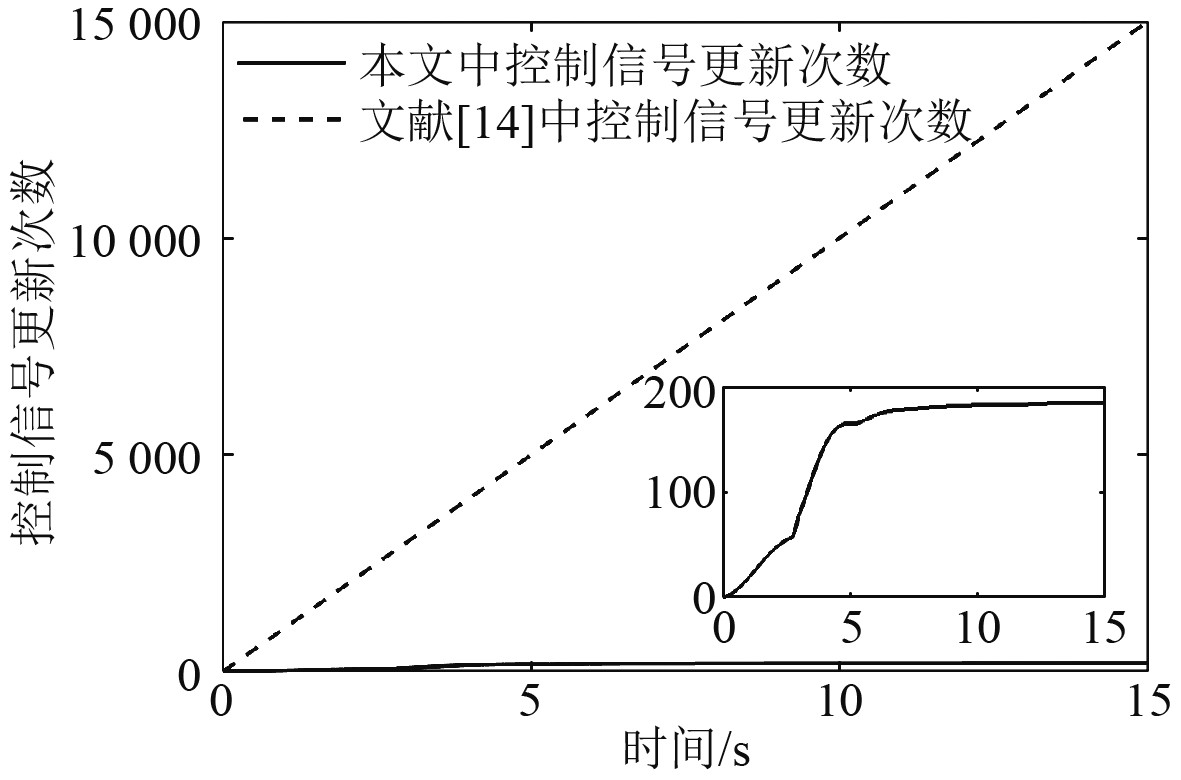
图 6 控制信号更新次数 Fig. 6 Control signal update times |
|
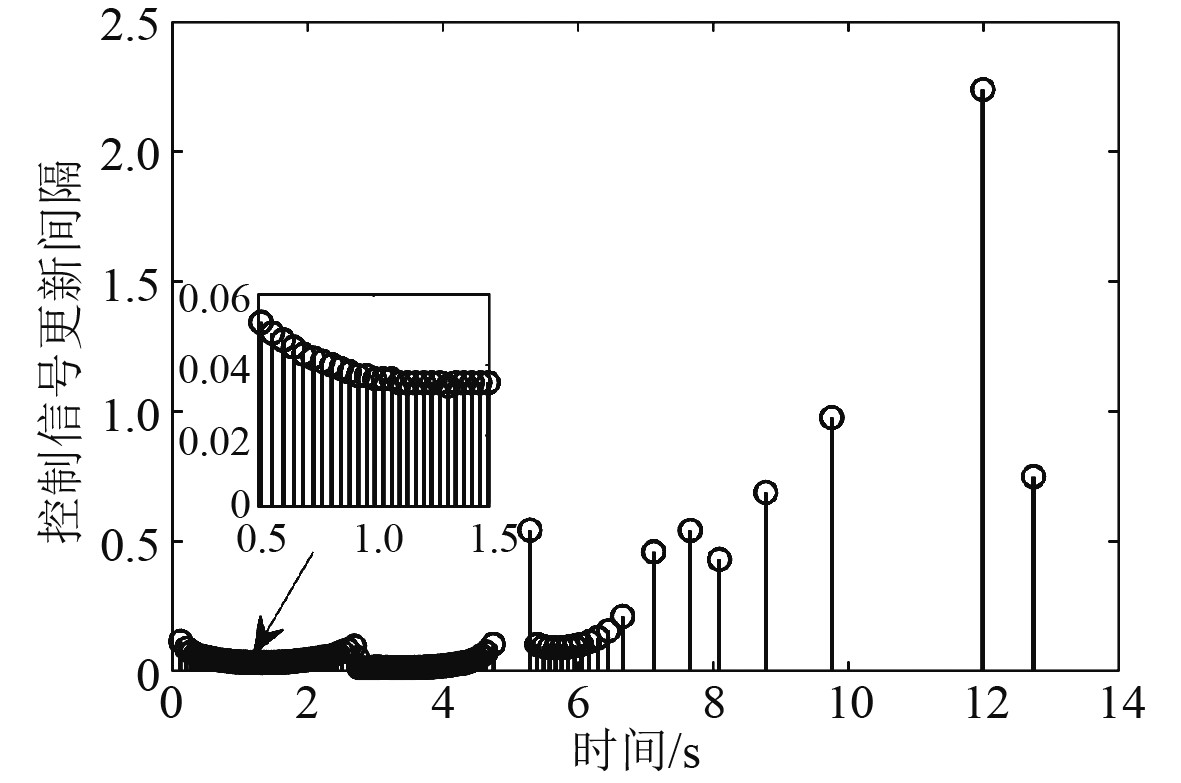
图 7 控制信号更新间隔 Fig. 7 Control signal update interval |
本文针对具有未知控制方向的船舶航向控制系统,采用基于系统当前状态所确定的逻辑切换机制来切换控制器参数以应对系统中的不确定性。同时融合事件触发机制,提出一种基于事件触发的船舶航向逻辑切换自适应控制算法,且利用动态增益减少了事件触发机制引入的测量误差的不良影响,实现了对设定航向的实际跟踪。仿真结果验证了基于事件触发的控制器在不影响系统性能的情况下可以有效降低控制信号的更新频率,提高了执行器的执行效率,降低了执行器损耗,节约了能源。
| [1] |
BANAZADEH A, GHORBANI M T. Frequency domain identification of the Nomoto model to facilitate Kalman filter estimation and PID heading control of a patrol vessel[J]. Ocean Engineering, 2013, 72(1): 344-355. |
| [2] |
孙武臣, 卜仁祥, 刘勇. 具有横倾抑制功能的船舶PID微分补偿航向控制[J]. 上海海事大学学报, 2020, 41(3): 19-24. |
| [3] |
ZHANG X, ZHANG G. Design of ship course-keeping autopilot using a sine function-based nonlinear feedback technique[J]. Journal of Navigation, 2016, 69(2): 246-256. DOI:10.1017/S0373463315000612 |
| [4] |
LIU Z. Ship adaptive course keeping control with nonlinear disturbance observer[J]. IEEE Access, 2017(5): 17567-17575. |
| [5] |
ZHANG Q, ZHANG X. Nonlinear improved concise backstepping control of course keeping for ships[J]. IEEE Access, 2019(7): 19258-19265. |
| [6] |
王永涛. 基于粒子群优化反步法的船舶航向控制器设计[J]. 中国航海, 2020, 43(1): 78-82. DOI:10.3969/j.issn.1000-4653.2020.01.015 |
| [7] |
NUSSBAUM R D. Some remarks on a conjecture in parameter adaptive control[J]. Systems & Control Letters, 1983, 3(5): 243-246. |
| [8] |
袁雷, 吴汉松. 船舶航向控制的多滑模鲁棒自适应设计[J]. 控制理论与应用, 2010, 27(12): 1618−1622.
|
| [9] |
沈智鹏, 邹天宇. 控制方向未知的无人帆船自适应动态面航向控制[J]. 哈尔滨工程大学学报, 2019, 40(1): 94−101.
|
| [10] |
YE X. Global adaptive control of nonlinearly parametrized systems[J]. IEEE Transactions on Automatic Control, 2003, 48(1): 169-173. DOI:10.1109/TAC.2002.804464 |
| [11] |
WU J, CHEN W, LI J. Global finite-time adaptive stabilization for nonlinear systems with multiple unknown control directions[J]. Automatica, 2016, 69: 298-307. DOI:10.1016/j.automatica.2016.03.005 |
| [12] |
GUO T, LIU Y, MAN Y. Adaptive controller of nonlinear systems with unknown control directions and unknown input powers[J]. International Journal of Robust and Nonlinear Control, 2020, 30: 7670-7689. DOI:10.1002/rnc.5213 |
| [13] |
SUN X, CHEN W. Global generalized exponential/finite-time control for course-keeping of ships[J]. International Journal of Control, 2016, 89(6): 1169-1179. DOI:10.1080/00207179.2015.1125020 |
| [14] |
CHEN W, WEN C, WU J. Global exponential/finite-time stability of nonlinear adaptive switching systems with applications in controlling systems with unknown control direction[J]. IEEE Transactions on Automatic Control, 2018, 63(8): 2738-2744. DOI:10.1109/TAC.2018.2791346 |
| [15] |
TZENG C Y, GOODWIN G C, CRISAFULLI S. Feedback linearization design of a ship steering autopilot with saturating and slew rate limiting actuator[J]. International Journal of Adaptive Control and Signal Processing, 1999, 13: 23-30. DOI:10.1002/(SICI)1099-1115(199902)13:1<23::AID-ACS532>3.0.CO;2-E |
 2022, Vol. 44
2022, Vol. 44
