变深机动是水下航行体常用的机动方式之一。与水平面操方向舵实现定向、变向运动控制的单控制变量—单运动控制目标不同,垂直面变深运动往往是在首尾升降舵,甚至有时结合均衡系统和纵倾平衡系统的多系统配合下协调完成,变深过程中需要关注纵倾、深度、垂向速度等多个运动参数。如何实现无超调、无振荡的最短时间变深,也是操舵人员的训练目标。
由于实际操纵机构执行速度、执行能力有限,且根据实际战术使用要求,在变深过程中往往对水下航行体的纵倾角等会加以限制,因此操舵变深问题本质上是已知初末状态、存在控制变量和状态变量约束的多输入—多输出的最短时间最优控制问题。
自从将现代控制理论引入水下航行体操纵研究后,对于水下航行体最优变深控制就开展了相应的研究。孙元泉[1]通过分段寻找最大轨迹角函数,结合中点法确定阶段转换点的方法,近似求解了最优控制函数及对应的运动轨迹;闵耀元[2]根据有状态和控制变量不等式约束时极值解的必要条件,基于理论方法求解了单操尾升降舵变换深度最短时间问题。受早期研究计算能力限制,上述研究多基于变分极值原理理论,采用的水下航行体动力学方程为线性方程,且不考虑水下航行体变深过程中的速降,难以处理多操纵手段下协同最优控制。
伪谱法也称为正交配点法,该方法利用全局或局部插值多项式的有限基来近似状态量和控制量,用配点规则保证微分方程组满足约束条件,对多项式进行求导来近似动力学方程中的状态变量对时间的导数,且在一系列的配点上满足动力学方程右函数约束,从而将微分方程约束转化为代数约束,最终将最优控制问题转换为一个非线性规划问题。作为一种高效率、高精度的数值计算方法,近年来,伪谱法被广泛应用于航天飞行器轨迹优化[3-8]、汽车智能控制[9]方面。
1 hp-RPM算法 1.1 最优控制问题的一般描述最优控制问题一般可以描述为,寻找控制变量
| $ J = \varPhi (x({t_f}),{t_f}) + \int_{{t_0}}^{{t_f}} {L(x(t),u(t),t){\rm{d}}t} ,$ | (1) |
满足:
| $ \dot x = f(x(t),u(t),t),t \in [{t_0},{t_f}] ,$ | (2) |
| $ c(x(t),u(t),t) = 0,$ | (3) |
| $ d(x(t),u(t),t) \leqslant 0,$ | (4) |
| $ x({t_0}) = {x_0},$ | (5) |
| $ \psi (x({t_f})) = 0 。$ | (6) |
式中:
式(2)为系统状态方程,式(3)为状态变量、控制变量和固定参量的等式约束,式(4)为状态变量、控制变量和固定参量的不等约束,式(5)为状态变量的初始条件,式(6)为状态变量和固定参量的端点条件。
1.2 求解最优控制问题的自适应hp-Radau伪谱法伪谱法采用正交插值多项式在配点处近似状态变量和控制变量,以差分形式将微分方程约束转换为代数约束,从而将连续空间的最优控制问题转化为非线性规划问题,最终通过数值方法求解非线性规划问题得到最优控制和最优轨迹。
根据插值基函数和配点类型的不同,可分为Legendre伪谱法、Radau伪谱法、Gauss伪谱法以及Chebyshev伪谱法。
传统的伪谱法是一类全局方法,即在求解问题的整个时间区间
近年来,为解决航天飞行器多阶段轨迹优化和轨迹曲率大、震荡强的问题,形成了hp自适应伪谱法,而在配点的选取上,由于Radau伪谱法与Gauss伪谱法或Legendre伪谱法相比,在区间切换点的状态变量连续性条件的实现上更具优势,且求解精度较高的综合特点,尤以hp自适应Radau伪谱法应用最为广泛。
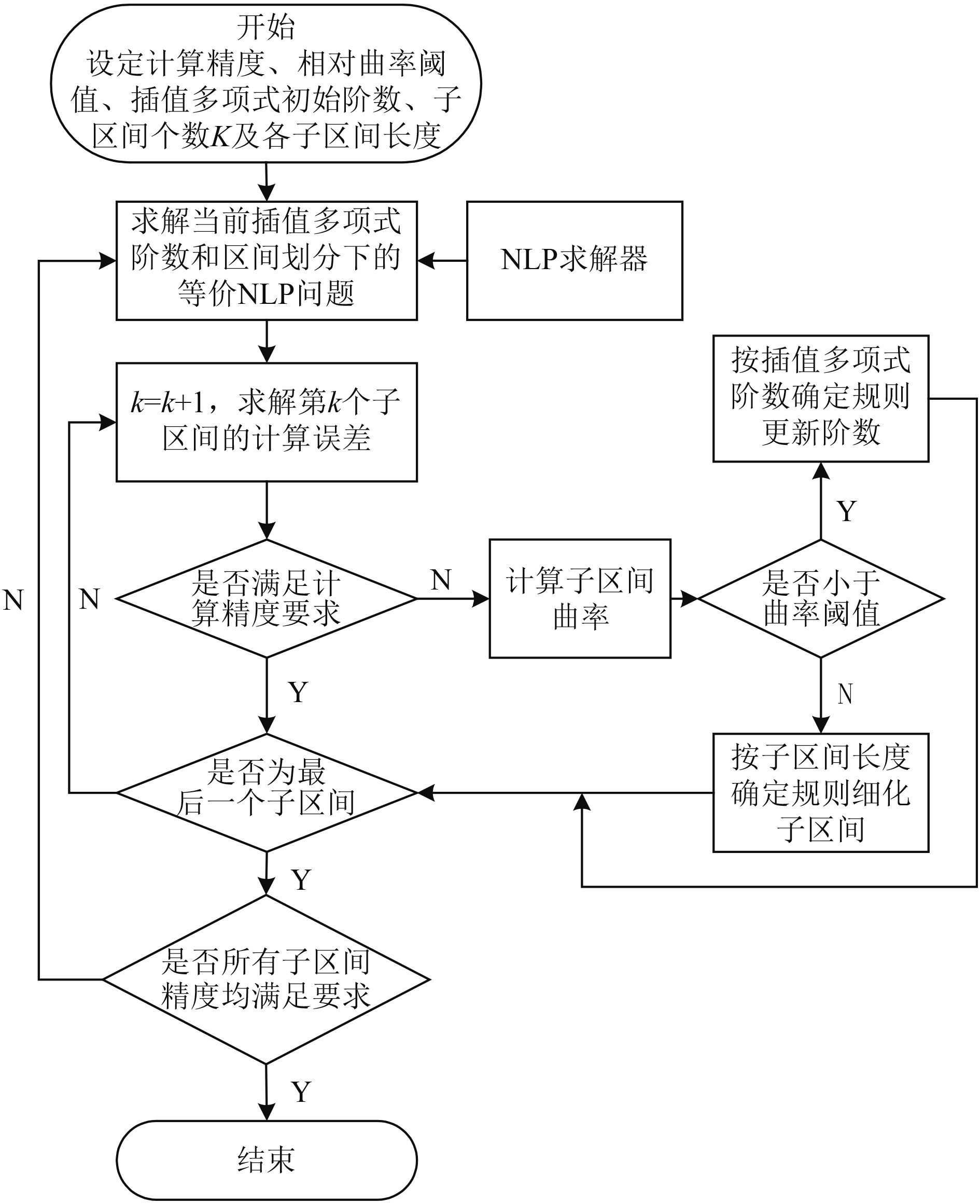
hp自适应Radau伪谱法中的h为允许区间长度,p为基函数阶次。与传统伪谱法只有一个求解时间区间
hp自适应Radau伪谱法的求解流程见图1。
|
图 1 hp自适应Radau伪谱法计算流程图 Fig. 1 Flow chart of hp adaptive Radau pseudo-spectral method |
水下航行体垂直面三自由度非线性方程如下[10]:
| $ \begin{split} &m(\dot u + wq + {z_G}\dot q - {x_G}{q^{_2}}) = \frac{1}{2}\rho {L^4}{{X'}_{qq}}{q^2} +\\ &\qquad\frac{1}{2}\rho {L^3}[{{X'}_{\dot u}}\dot u + {{X'}_{wq}}wq]+\frac{1}{2}\rho {L^2}[{{X'}_{uu}}{u^2} + \\ &\qquad{{X'}_{ww}}{w^2} + {{X'}_{\delta b\delta b}}{u^2}\delta _b^2 + {{X'}_{\delta s\delta s}}{u^2}\delta _s^2] +\\ &\qquad\frac{1}{2}\rho {L^2}[{a_T}{u^2} + {b_T}u{U_c} + {c_T}U_c^2],\end{split} $ | (7) |
| $ \begin{split} & m(\dot w - uq - {x_G}\dot q - {z_G}{q^{_2}}) = \frac{1}{2}\rho {L^4}{{Z'}_{\dot q}}\dot q +\\ &\qquad \frac{1}{2}\rho {L^3}[{{Z'}_{\dot w}}\dot w + {{Z'}_q}uq + {{Z'}_{w|q|}}w|q| + {{Z'}_{|q|{\delta _s}}}u|q|{\delta _S}] +\\ &\qquad \frac{1}{2}\rho {L^2}[{{Z'}_0}{u^2} + {{Z'}_w}uw + {{Z'}_{|w|}}u|w| +\\ &\qquad {{Z'}_{w|w|}}w|w| + {{Z'}_{ww}}ww + {{Z'}_{\delta b}}{u^2}{\delta _b} + {{Z'}_{\delta s}}{u^2}{\delta _s}] ,\end{split} $ | (8) |
| $ \begin{split} {I_y}\dot q - & m[{x_G}(\dot w - uq) - {z_G}(\dot u - wq)] =\frac{1}{2}\rho {L^5}[{{M'}_{\dot q}}\dot q +\\ & {{M'}_{q|q|}}q|q|] + \frac{1}{2}\rho {L^4}[{{M'}_{\dot w}}\dot w + {{M'}_q}uq + {{M'}_{|w|q}}|w|q+ \\ & {{M'}_{|q|{\delta _s}}}u|q|{\delta _S}] + \frac{1}{2}\rho {L^3}[{{M'}_0}{u^2} + {{M'}_w}uw +\\ &{{M'}_{|w|}}u|w| + {{M'}_{w|w|}}w|w| + {{M'}_{ww}}ww +\\ & {{M'}_{\delta b}}{u^2}{\delta _b} +{{M'}_{\delta s}}{u^2}{\delta _s}] - mgh\sin \theta 。\end{split} $ | (9) |
运动学关系如下:
| $ \begin{split} &\bar{\zeta}=-u \sin \theta+w \cos \theta ,\\ &\dot{\theta}=q。\end{split} $ | (10) |
设状态变量为
根据式(7)~式(10),可得本问题的状态空间方程为:
| $ \left[ {\begin{array}{*{20}{c}} {\dot u} \\ {\dot w} \\ {\dot q} \\ {\dot \theta } \\ {\dot \zeta } \\ {{{\dot \delta }_b}} \\ {{{\dot \delta }_s}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\dot x}_1}} \\ {{{\dot x}_2}} \\ {{{\dot x}_3}} \\ {{{\dot x}_4}} \\ {{{\dot x}_5}} \\ {{{\dot x}_6}} \\ {{{\dot x}_7}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{p_1}} \\ {{p_2}} \\ {{p_3}} \\ {{x_3}} \\ { - {x_1}\sin {x_4} + {x_2}\cos {x_4}} \\ 0 \\ 0 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{q_1}} \\ {{q_2}} \\ {{q_3}} \\ 0 \\ 0 \\ {{u_1}} \\ {{u_2}} \end{array}} \right]。$ | (11) |
式中:
在变深机动开始前,水下航行体处于平衡状态作定常运动,当变深机动结束后也必须恢复平衡状态,并在目标深度上作定常运动。在机动的过程中,从实际操作和使用安全的角度,水下航行体的纵倾往往会受到一定的限制。另外,将首舵转舵速率、尾舵转舵速率作为控制变量,将首舵舵角、尾舵舵角均视为状态变量,由于舵角执行机构行程为有限值,故在变深过程中,其值应限定在实际使用值范围内。故状态变量约束如下:
| $ \begin{split} & u \leqslant {U_0},|\theta | \leqslant {\theta _{\max }},\\ & {\zeta _{|t = {t_0}}}={\zeta_0},{\zeta _{|t = {t_f}}} = {\zeta _d},\\ & {\theta _{|t = {t_0}}} = 0,{\theta _{|t = {t_f}}} = 0,\\ & {\delta _{b\min }} \leqslant {\delta _b} \leqslant {\delta _{b\max }},\\ &{\delta _{s\min }} \leqslant {\delta _s} \leqslant {\delta _{s\max }} 。\end{split} $ | (12) |
受舵装置性能设计限制,转舵速率应限制在实际使用值范围内。本文的控制变量约束如下:
| $ \begin{split} & {{\dot \delta }_{b\min }} \leqslant {{\dot \delta }_b} \leqslant {{\dot \delta }_{b\max }} ,\\ & {{\dot \delta }_{s\min }} \leqslant {{\dot \delta }_s} \leqslant {{\dot \delta }_{s\max }} 。\end{split} $ | (13) |
本文性能指标要求在上述约束下,从初始深度
从最优控制的角度,考虑不同航速、不同变深范围、不同最大纵倾角限制等因素对最短变深时间的影响。仿真计算工况见表1。
|
|
表 1 仿真计算工况 Tab.1 Simulation cases |
共9种航速,5种变深范围,8种最大纵倾角限制,共形成360种仿真工况。
仿真过程中,水下航行体相关总体参数及水动力系数参见文献[11]。上浮和下潜研究方法一致,本文仅讨论上浮情况。相关状态参数及控制参数的限界值为:
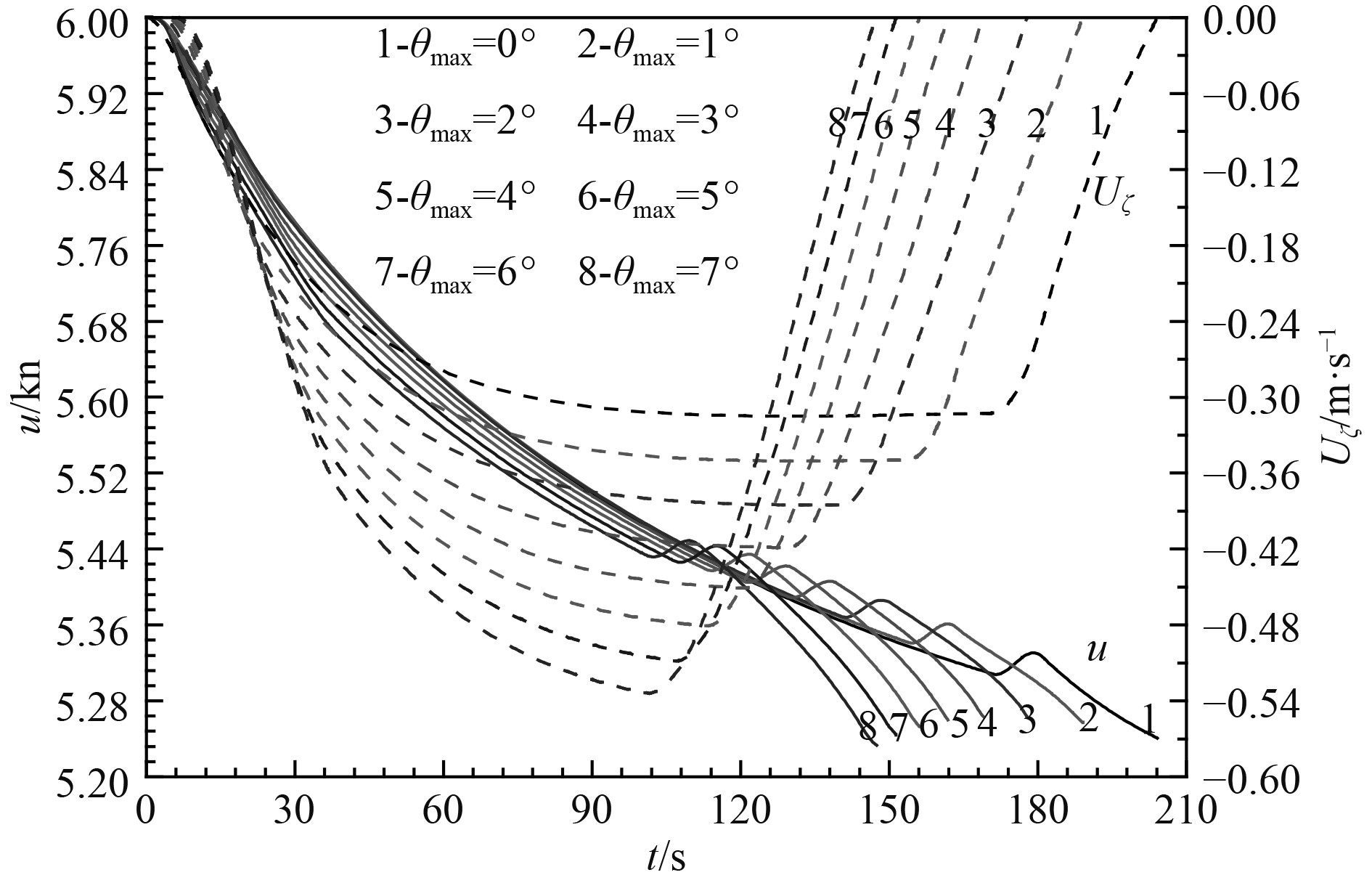
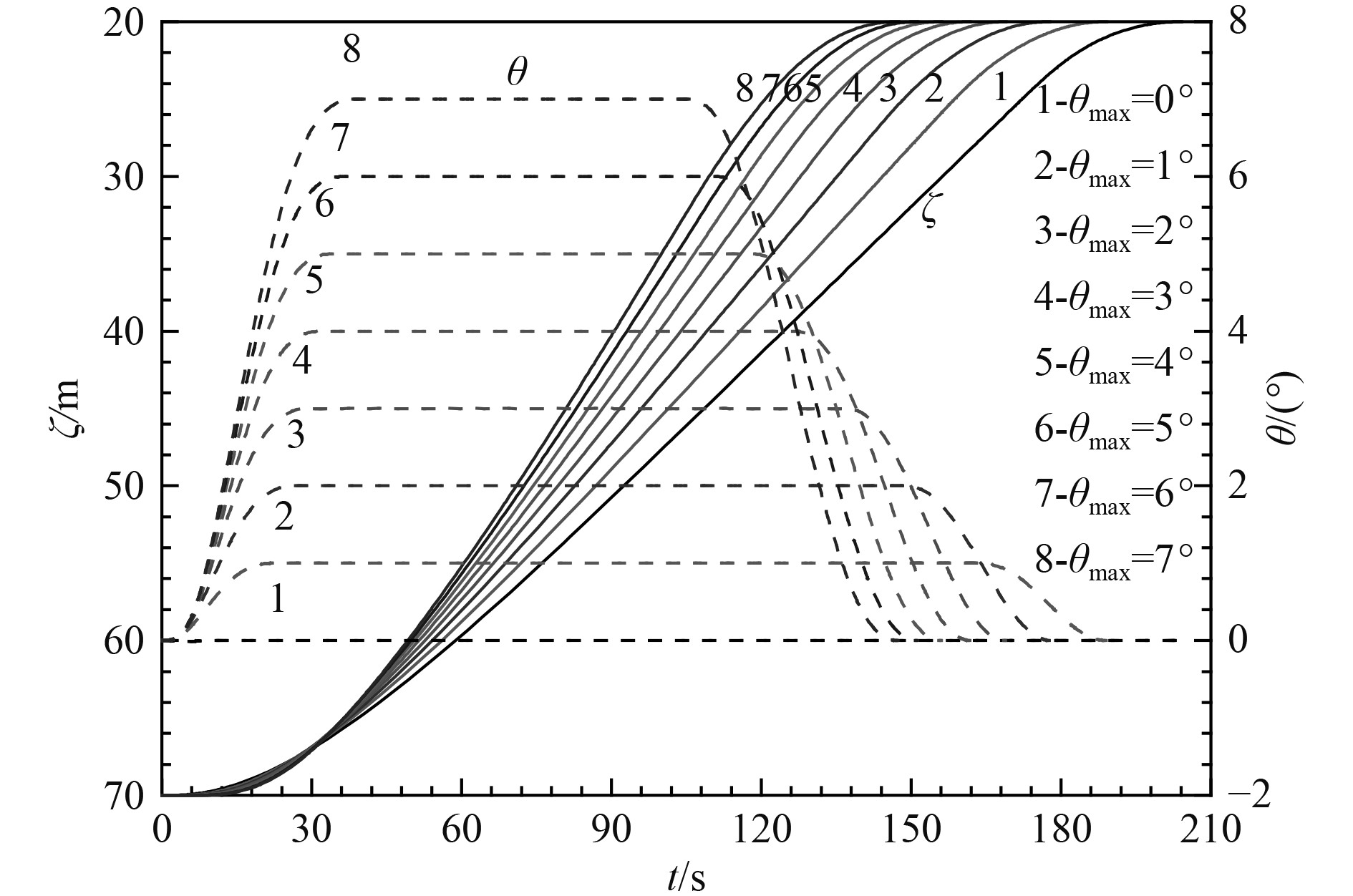
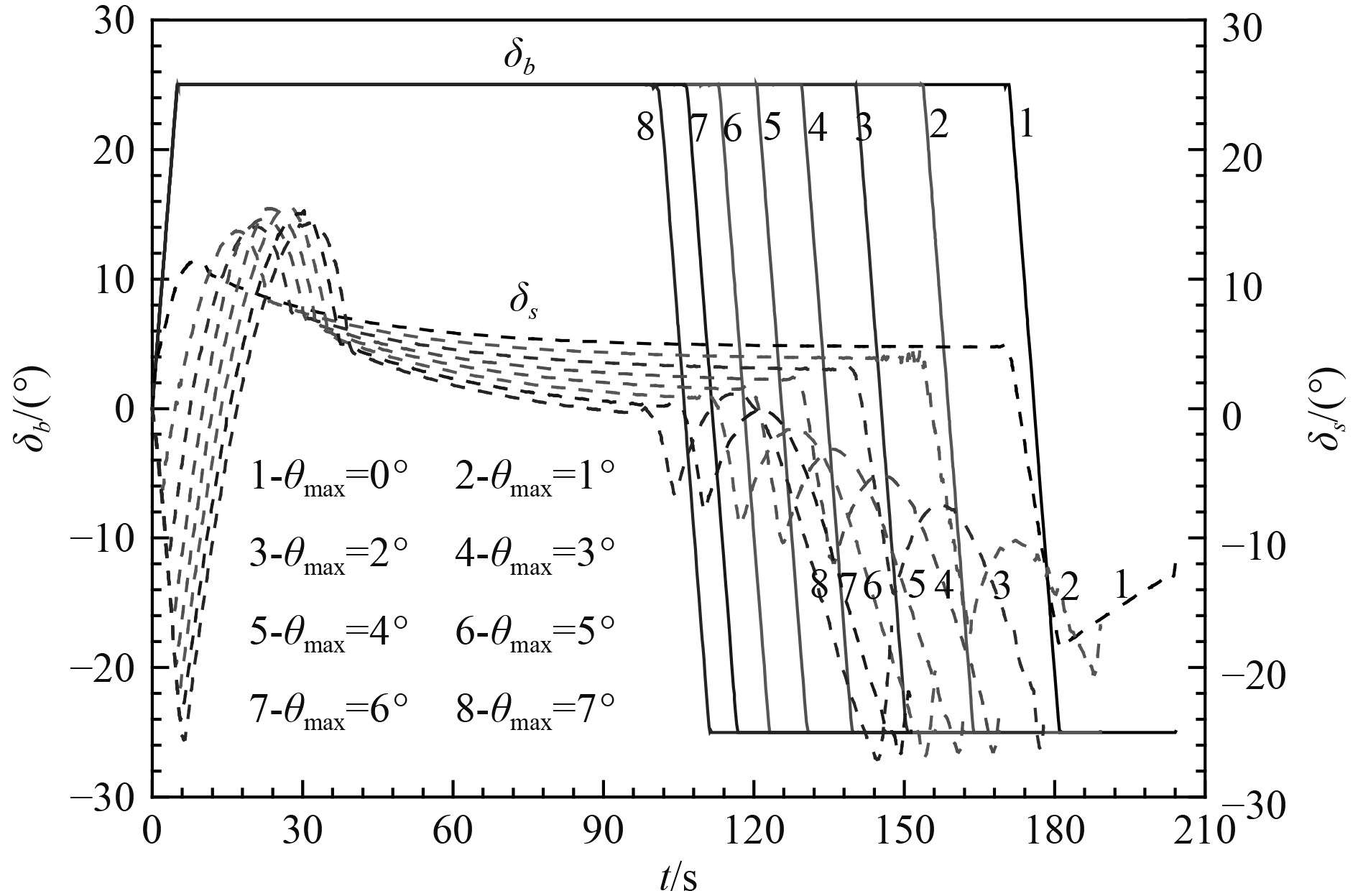
利用hp自适应Radau伪谱法对上述360个计算工况进行最优控制求解,结果如图2~图4所示,分析可知:
|
图 2 不同最大纵倾角限制下轴向速度和上浮对比(6 kn) Fig. 2 Comparison of axial speed and ascending speed under different pitch restriction(6 kn) |
|
图 3 不同最大纵倾角限制下深度和纵倾对比(6 kn) Fig. 3 Comparison of depth and pitch angle under different pitch restriction(6 kn) |
|
图 4 不同最大纵倾角限制下升降舵舵角对比(6 kn) Fig. 4 Comparison of diving plane angle under different pitch restriction(6 kn) |
1) 从运动控制的角度来看,最优控制的过程基本上是先操相对上浮舵形成最大允许纵倾,后保持最大允许纵倾,最后操相对下潜舵压纵倾,平滑地向零纵倾状态过渡;
2) 首舵控制规律相对简单,在形成最大允许纵倾过程中,以最大操舵速率、最大上浮舵角为目标舵角操舵,后一直保持最大上浮舵角直至开始反向操舵压纵倾,反向操舵过程中以最大操舵速率以最大下潜舵角为目标舵角操舵,后一直保持最大下潜舵角;
3) 所允许的最大纵倾越大,保持最大纵倾时间越短,反向操舵的时刻越需要提前;
4) 开始反向操舵压制纵倾时刻,水下航行体的垂向速度达到最大。
统计各仿真工况的变深总时间,将变深范围一定时,上浮总时间随初始航速,最大允许纵倾的变化用图5表示。
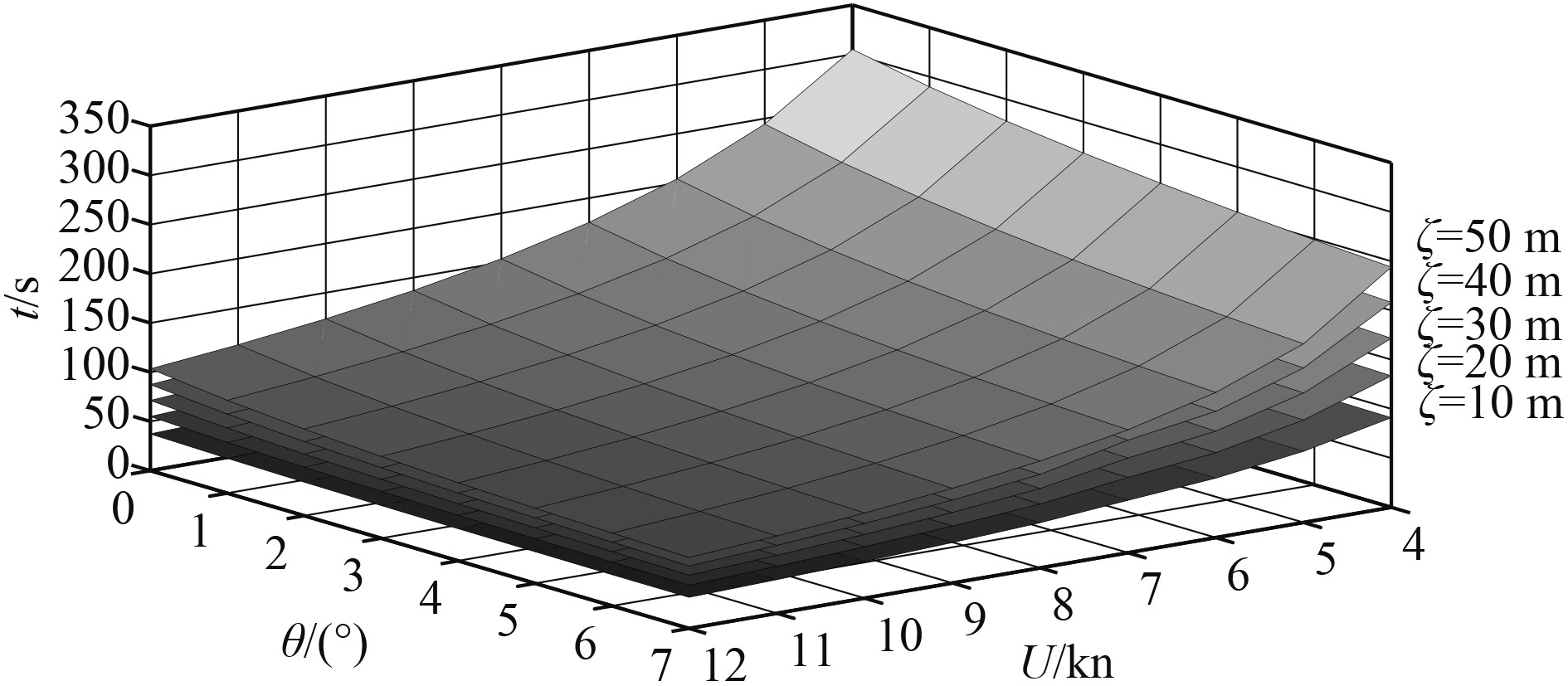
|
图 5 各变深范围下上浮总时间随初始航速、最大纵倾角限制的变化 Fig. 5 Total ascent time under different initial speed and allowable maximum pitch angle for each depth changing range |
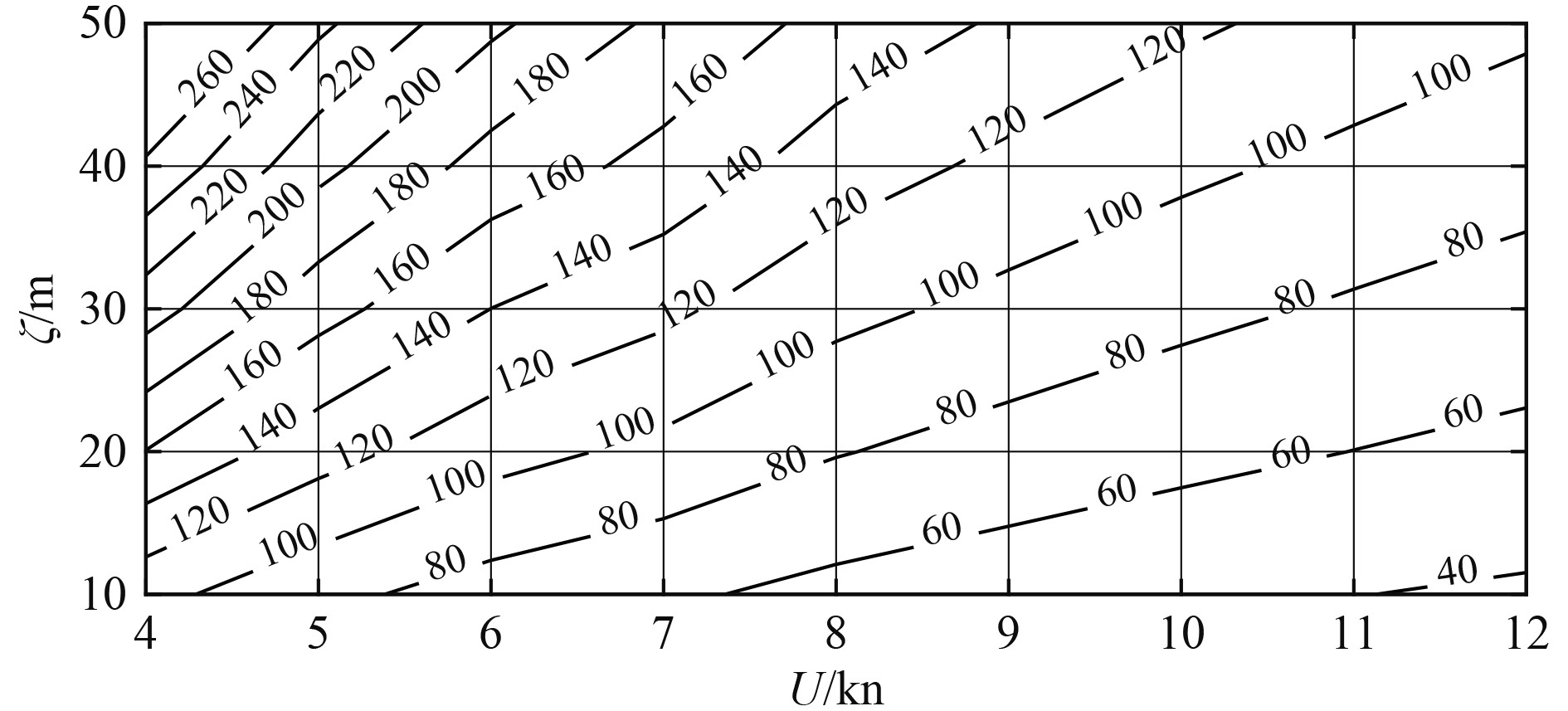
为保证仿真结果的直观性与实用性,将结果以变深总时间二维等值线图谱的形式表示(见图6~图8)。

|
图 6
上浮总时间的航速—最大允许纵倾图谱
|
|
图 7
上浮总时间的航速—变深范围图谱(
|

|
图 8
上浮总时间的最大允许纵倾—变深范围图谱
|
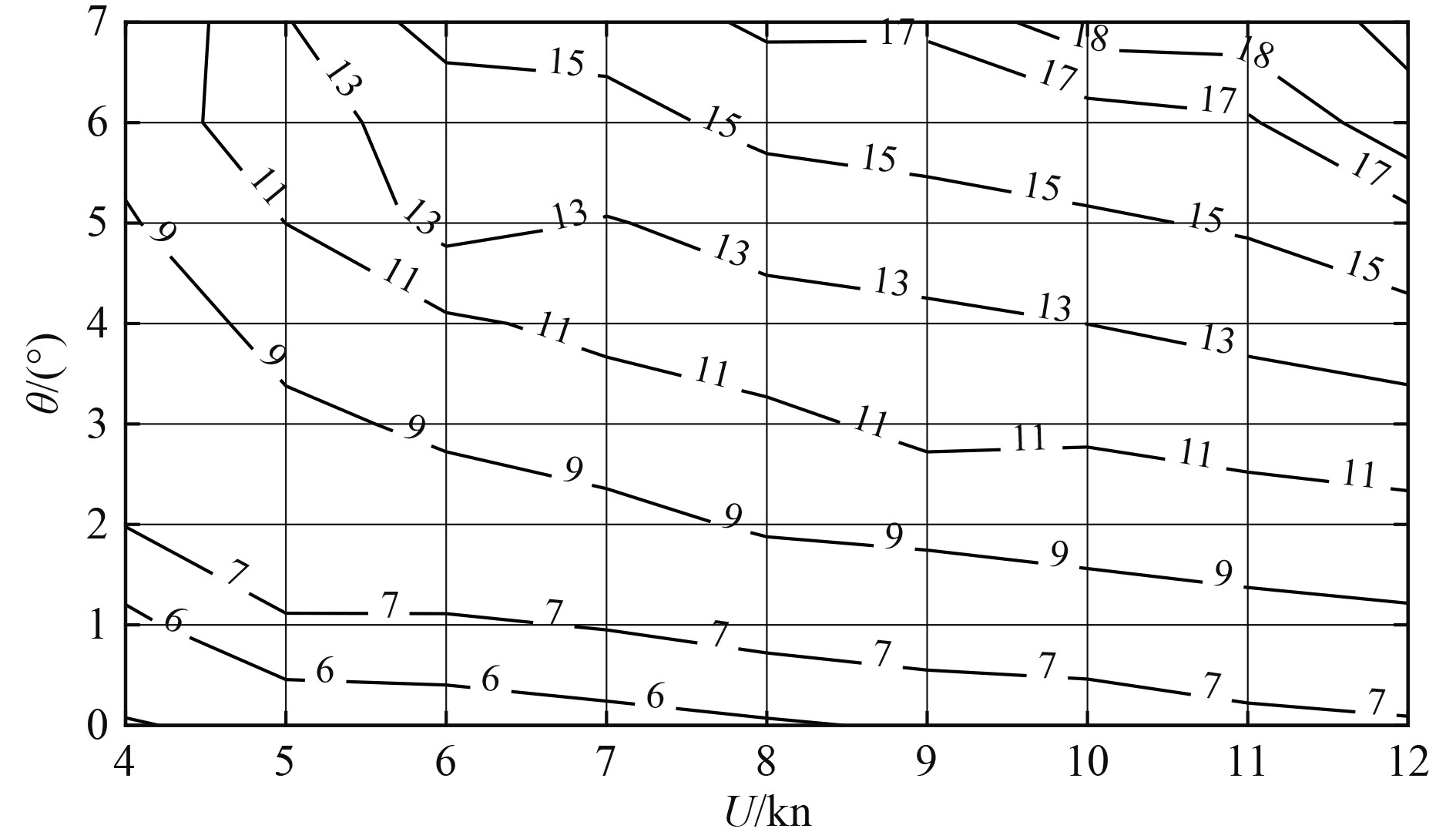
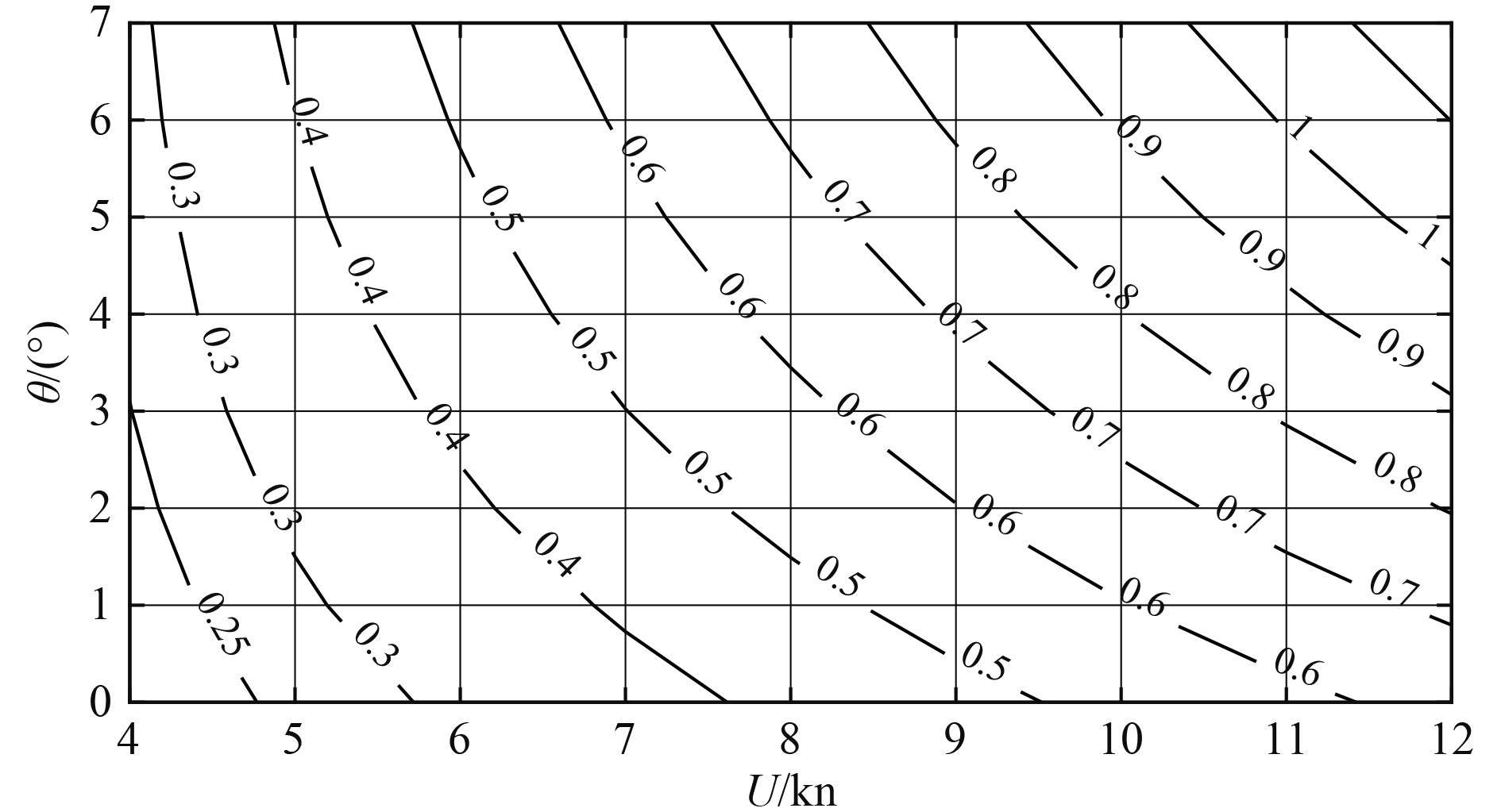
另一方面,从最优控制结果的垂速变化和升降舵舵角变化来看,开始反向操舵的时刻是一个重要的控制因素,由于变深过程中,深度和垂速是操舵人员重点观察的参数,为便于操纵训练时准确掌握该时刻,以反向操舵时与目标深度的深度差和最大垂向速度为指标,确定不同工况下的反向操舵深度提前量和最大垂向深度图谱(见图9和图10)。可知,初始航速越高、上浮过程中的最大允许纵倾越大、反向操舵时的垂向速度越大,反向操舵时的深度提前量越大。
|
图 9
反向操舵时深度提前量的初始航速—最大允许纵倾图谱(
|
|
图 10
反向操舵时最大垂向速度的初始航速—最大允许纵倾图谱(
|
实际变深过程中,初始航速和变深深度范围是一定的,因此,需考虑:1) 变深时间要求一定,确定最小的纵倾角度;2) 纵倾限制一定,确定最短的变深时间。
对于第一类问题,可根据变深总时间的航速—最大允许纵倾图谱,找出变深总时间要求对应的等值线,等值线上横坐标对应初始航速的点,该点对应的纵倾,就是可满足变深总时间要求的最小纵倾角,纵倾角大于该纵倾角的情况下,从最优控制的角度,变深时间都会小于设定的变深总时间。
对于第二类问题,可直接查找与要求的变深范围、初始航速和最大纵倾限制要求的变深总时间图谱,得到最短的变深时间。
在变深范围、初始航速、最大允许纵倾确定后,从操纵的角度,在造纵倾阶段,以尽快形成纵倾为原则操舵;然后以保持纵倾为目标操舵,最后根据对应的反向操舵时深度提前量图谱或者最大垂速图谱可确定反向操舵时刻。
由于图谱是基于最优控制的结果,因此其可以指导变深机动训练相关考核和评价标准的制定。
5 结 语基于可变子区间长度和子区间插值多项式阶数的hp自适应Radau伪谱法,结合考虑水下航行体垂直面三自由度运动方程,求解了不同航速、不同最大允许纵倾、不同变深范围的最快上浮问题。从变深最短时间的角度,建立了初始航速—最大允许纵倾图谱、初始航速—变深范围图谱、最大允许纵倾—变深范围图谱;从操纵的角度,建立了不同变深范围下的深度提前量图谱和最大垂向速度图谱,并说明了图谱的使用方法。结论如下:
1) 最优控制解随航速、最大允许纵倾、变深范围的变化规律符合水下航行体操纵特性,说明了hp自适应Radau伪谱法求解操舵变深优化控制问题的可行性和合理性;
2) 基于最优控制的变深图谱指导变深机动训练具有较强的可操作性,可作为相关考核和评价标准制定的依据;
3) 为使得图谱更贴近实际使用,可考虑在伪谱法求解快速变深的方法基础上,将实水下航行体变深相关数据与动力学模型融合的方式,采用系统辩识等方法,提高变深运动的预报精度。
| [1] |
孙元泉. 潜艇的一种速潜操纵方法(I)[J]. 舰船科学技术, 1983, 6: 1-17. SUN Y Q. A quick diving operation method for submarine(I)[J]. Ship Science and Technology, 1983, 6: 1-17. |
| [2] |
闵耀元. 潜艇深度变换最短时间问题的解法[J]. 武汉船舶力学论文集, 1991, 10: 97-106. MIN Y Y. The solution for fastest depth changing problem for submarine[J]. Wuhan Ship dynamics, 1991, 10: 97-106. |
| [3] |
任高峰, 崔平远, 崔祜涛, 等. 一种新型火星定点着陆轨迹快速优化方法[J]. 宇航学报, 2013, 34(4): 464-472. REN G F, CUI P Y, CUI H T, et al. A new method of rapid trajectory optimization for mars pin-point landing[J]. Journal of Astronautics, 2013, 34(4): 464-472. DOI:10.3873/j.issn.1000-1328.2013.04.003 |
| [4] |
杨希详, 杨慧欣, 王鹏. 伪谱法及其在飞行器轨迹优化设计领域的应用综述.[J]. 国防科技大学学报, 2015, 37(4): 1-8. YANG X X, YANG H X, WANG P. Overview of pseudo - spectral method and its application in trajectory optimum design for flight vehicles.[J]. Journal of National University of Defense Technology, 2015, 37(4): 1-8. DOI:10.11887/j.cn.201504001 |
| [5] |
陈功, 傅瑜, 郭继峰. 飞行器轨迹优化方法综述[J]. 飞行力学, 2011, 29(4): 1-5. CHEN G, FU Y, GUO J F. Survey of aircraft trajectory optimization methods.[J]. Flight Dynamics, 2011, 29(4): 1-5. |
| [6] |
袁宴波, 张科, 薛晓东. 基于Radau伪谱法的制导炸弹最优滑翔弹道研究[J]. 兵工学报, 2014, 35(4): 1179-1186. YUAN Y B, ZHANG K, XUE X D. Optimization of glide trajectory of guided bombs using a Radau pseudo-spectral method.[J]. Acta Armamentarii, 2014, 35(4): 1179-1186. |
| [7] |
于功健, 廖守亿, 闫循良, 等. 基于HP-RPM的高超声速滑翔飞行器轨迹优化[J]. 飞行力学, 2017, 35(2): 59-63. YU G J, LIAO S Y, YAN X L, et al. HP-RPM based trajectory optimization for hypersonic glide vehicle.[J]. Flight Dynamics, 2017, 35(2): 59-63. |
| [8] |
王海涛, 李军营, 梁立威, 等. 基于hp自适应Radau伪谱法的再入飞行器轨迹优化[J]. 科学技术与工程, 2015, 15(2): 165-171. WANG H T, LI J Y, LIANG L W, et al. Track optimizing for re-entry vehicle based on hp-adaptive Radau pseudo-spectral method.[J]. Science Technology and Engineering, 2015, 15(2): 165-171. DOI:10.3969/j.issn.1671-1815.2015.02.029 |
| [9] |
段建民, 房泽平, 杨晨. 基于Radau伪谱法和MPC的智能电动车辆生态驾驶[J]. 北京工业大学学报, 2016, 42(5): 774-781. DUAN J M, FANG Z P, YANG C. Eco-driving based on radau Pseudo-spectral method and model predictive control for intelligent electric vehicle[J]. Journal of Beijing University of Technology, 2016, 42(5): 774-781. |
| [10] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995.
|
| [11] |
程嘉欢. 低速潜器在连续冲击载荷下的水动力研究[D]. 上海: 上海交通大学, 2013.
|
 2022, Vol. 44
2022, Vol. 44
