夹层结构一般由2层高强度薄面板与中间承载能力相对较弱的轻质厚芯层通过焊接或胶接而成。面板提供较高的弯曲刚度,主要承受由弯矩引起的面内拉压载荷;而芯层主要承受由横向力产生的剪应力[1]。复合材料夹芯结构具有质量轻、强度高和可设计性强等优点,在船舶工程等诸多领域有着广泛的用途[2]。
针对普通的层合板结构的振动问题,一般使用经典板理论(CPT)[3]和一阶剪切变形理论(FSDT)[4-5]进行求解,但经典板理论忽略了厚度方向的剪切效应,仅适用于薄板结构,当研究对象是中厚板时计算误差较大。而FSDT在板的上下表面没有剪应力作用时,不能满足剪应力为零的条件。因此FSDT需要引入剪切修正因子来提高精确度[6],但对复合材料层合板,剪切因子和每层的铺层形式、结构参数、载荷形式和边界条件都有关,很难直接确定。为了克服引入剪切因子的难点,各种高阶剪切变形理论被提出:3阶剪切变形理论[7],5阶剪切变形理论[8],三角函数位移模式的剪切变形理论[9]等。其中Reddy[7]的HSDT比较具有代表性,其简化了一般高阶剪切变形理论的复杂程度,既能满足板上下表面剪应力为零的边界条件,又保证了良好的计算精度。上述剪切变形理论各异,在将其运用到夹芯复合材料结构时,要根据实际情况合理选择不同的剪切理论。
刘炳昌等[10]分析了正交对称铺层的各向同性阻尼层复合材料板的自由振动问题,并研究了复合材料的弹性参数对结构的固有频率的影响。Di[11]基于能同时满足分界面处位移和横向剪切应力协调条件的分段线性位移场,研究了四边简支的3层复合材料夹芯板自由无阻尼振动问题,并与经典层压理论(Kirchhoff)和剪切变形理论(Timoshenko和Mindlin)进行对比,证明了方法的正确性。李飘[12]推导了普通均质复合材料夹芯板的弯曲力学微分方程组,并结合Helmholtz-Huygens辐射积分公式,推导了该结构的水下振动方程,分析了该结构的水下固有振动特性。以上的研究对象均是复合材料夹芯结构,并未对含加筋的结构做进一步研究。
针对加筋层合板结构的振动问题,Xu等[13]用改进的傅里叶级数建立了单一材料加筋板的位移函数,解决了该结构的自由振动问题。WANG等[14]利用有限元的方法对比分析了嵌入式共固化复合材料薄板及十字加筋薄板的固有振动特性,并得到了加筋宽度和高度对结构固有频率的影响规律。结果表明:加强筋大大提高了薄板结构的固有频率,其各阶固有频率随着加强筋高度及宽度增大而增加,其中1阶固有频率增加幅度最大,且增大加筋高度对结构的影响要大于增加宽度。Bhaskar等[15]用修正的传递矩阵法详细研究了无阻尼复合材料加筋板结构的振型和固有频率。杨智雄[16]通过建立混合有限元模型,对夹芯复合材料加筋板在真空中的自由振动问题进行了分析,系统探究了不同加强筋形式、尺寸、布置方式与结构模态之间的关系。路庆贺[17]基于1阶剪切变形理论和Hamilton原理,建立了真空中阻尼夹芯复合材料加筋板的控制微分方程,探讨了不同筋条尺寸、数量、分布方式对结构动力学性能的影响,但并未对该结构水下振动性能做研究。
目前国内外的相关动力学研究中,大量的理论工作集中于普通的层合板结构;夹芯复合材料加筋板的研究主要为真空中或空气中的研究,水中的研究主要为无限大理论和试验方法。无限大理论的结构模型在实际工程中不存在;而基于实际模型的试验方法往往耗费较大的人力、物力、财力及时间成本,研究效率较低,不适合机理研究和特性分析。为此,建立一种快速、高效率的理论方法,用于研究夹芯复合材料加筋板的水中振动特性,具有较大意义。
本文首先基于FSDT理论和Hamilton原理,利用狄拉克函数描述加筋,推导了夹芯复合材料加筋板在真空中的自由振动控制方程;进一步,将浸没于水中的夹芯复合材料加筋板视为薄板,根据流固耦合面上的法向加速度连续条件,对横向振动方程进行重构,得到整体结构在水中的自由振动控制方程。在四边简支边界条件下,采用双傅里叶级数求解的夹芯复合材料加筋板的自由振动问题,并与文献及数值仿真结果进行对比,验证了本文方法的有效性。进一步研究了加筋位置和数量、面板厚度和芯层厚度对夹芯复合材料加筋板自由振动的影响,为工程实际的结构优化设计提供参考。
1 夹芯复合材料加筋板自由振动理论建模 1.1 基本假设本文基于FSDT建立夹芯复合材料加筋板自由振动的理论模型,有如下假设:1)中面法线在变形后仍保持直线,但不再垂直于中面;2)各层界面位移连续;3)复合材料夹芯板在厚度方向的变形忽略不计;4)板壳处于平面应力状态。
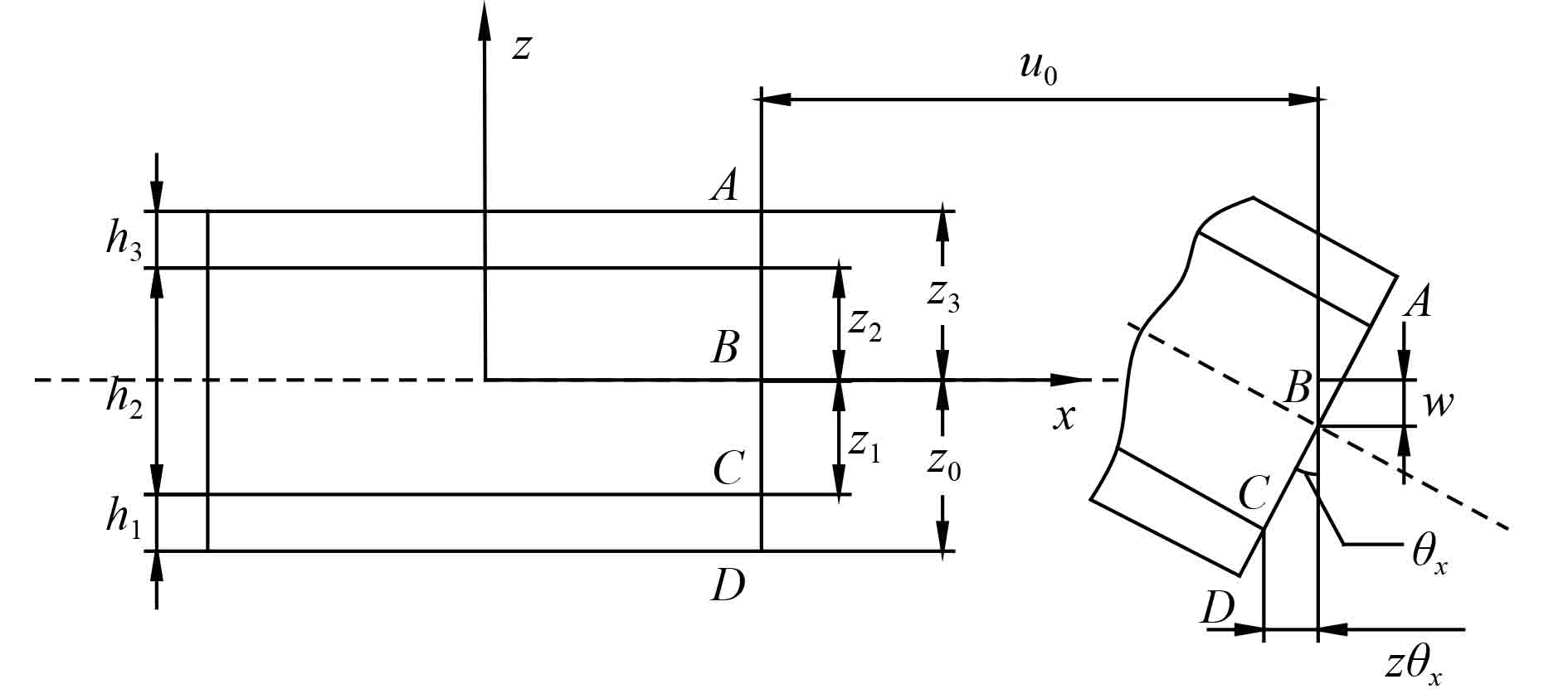
夹芯复合材料加筋板的几何模型示意图如图1所示。z向垂直于板的平面,zk为第k层分界层z向坐标,hk为第k层板的厚度(k=1,2,3)。夹芯复合材料加筋板各层间的位移坐标及变形前后示意图如图2所示。

|
图 1 夹芯复合材料加筋板几何模型 Fig. 1 Geometric model of sandwich composite stiffened plate |
|
图 2 夹芯复合材料加筋板位移坐标及变形示意图 Fig. 2 Displacement coordinates and deformation diagram of sandwich composite stiffened plate |
基于1阶剪切变形理论和上述假设,设夹芯复合材料加筋板变形前垂直于中面的法线于变形后,在x和y方向的转角分别为θx和θy,设板的中性面为xoy平面,中面上点的x,y,z方向的位移分别为u0,v0,w0,则板上任意一点的位移分量U,V,W可表示为:
| $\left\{ \begin{array}{l} U\left( {x,y,z,t} \right) = {u_0}(x,y,t) + z \cdot {\theta _x}\left( {x,y,t} \right) , \\ V\left( {x,y,z,t} \right) = {v_0}(x,y,t) + z \cdot {\theta _y}\left( {x,y,t} \right) , \\ W\left( {x,y,z,t} \right) = {w_0}\left( {x,y,t} \right) , \\ \end{array} \right.$ | (1) |
则板的位移-应变关系为:
| $\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _x}} \\ {{\varepsilon _y}} \\ {{\gamma _{xy}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\varepsilon _x^m + z \cdot \varepsilon _x^f} \\ {\varepsilon _y^m + z \cdot \varepsilon _y^f} \\ {\gamma _{xy}^m + z \cdot \gamma _{xy}^f} \end{array}} \right\} ,\;\ \;\ \left\{ {\begin{array}{*{20}{c}} {{\gamma _{yz}}} \\ {{\gamma _{xz}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{\theta _y} + \dfrac{{\partial {w_0}}}{{\partial y}}} \\ {{\theta _x} + \dfrac{{\partial {w_0}}}{{\partial x}}} \end{array}} \right\},$ | (2) |
式中:
| $\left\{ \begin{array}{l} \varepsilon _x^m = \dfrac{{\partial {u_0}}}{{\partial x}},\varepsilon _x^f = \dfrac{{\partial {\theta _x}}}{{\partial x}} , \\ \varepsilon _y^m = \dfrac{{\partial {v_0}}}{{\partial y}},\varepsilon _y^f = \dfrac{{\partial {\theta _y}}}{{\partial y}} ,\\ \gamma _{xy}^m = \dfrac{{\partial {u_0}}}{{\partial y}} + \dfrac{{\partial {v_0}}}{{\partial x}},\gamma _{xy}^f = \dfrac{{\partial {\theta _x}}}{{\partial y}} + \dfrac{{\partial {\theta _y}}}{{\partial x}} 。\end{array} \right.$ | (3) |
第k层板的应力-应变关系表示为:
| $ \begin{split}&{\left\{\begin{array}{c}{\sigma }_{x}\\ {\sigma }_{y}\\ {\tau }_{xy}\end{array}\right\}}_{(k)}=\left[\begin{array}{ccc}{Q}_{11}^{(k)}& {Q}_{12}^{(k)}& 0\\ {Q}_{12}^{(k)}& {Q}_{22}^{(k)}& 0\\ 0& 0& {Q}_{66}^{(k)}\end{array}\right]{\left\{\begin{array}{c}{\varepsilon }_{x}\\ {\varepsilon }_{y}\\ {\gamma }_{xy}\end{array}\right\}}_{(k)},\\ &{\left\{\begin{array}{l}{\tau }_{xz}\\ {\tau }_{yz}\end{array}\right\}}_{(k)}=\left[\begin{array}{cc}{Q}_{55}^{(k)}& 0\\ 0& {Q}_{44}^{(k)}\end{array}\right]{\left\{\begin{array}{c}{\gamma }_{xz}\\ {\gamma }_{yz}\end{array}\right\}}_{(k)},\end{split}$ | (4) |
式中:
| $\begin{split} & Q_{_{11}}^{\left( k \right)} = \frac{{E_{_{11}}^{\left( k \right)}}}{{1 - v_{_{12}}^{\left( k \right)}v_{_{21}}^{\left( k \right)}}},\;\;Q_{_{12}}^{\left( k \right)} = \frac{{v_{_{12}}^{\left( k \right)}E_{_{11}}^{\left( k \right)}}}{{1 - v_{_{12}}^{\left( k \right)}v_{_{21}}^{\left( k \right)}}}\;,\;\;Q_{_{22}}^{\left( k \right)} = \frac{{E_{_{22}}^{\left( k \right)}}}{{1 - v_{_{12}}^{\left( k \right)}v_{_{21}}^{\left( k \right)}}}\; , \\ & Q_{_{44}}^{\left( k \right)} = G_{_{23}}^{\left( k \right)},\;\;\;Q_{_{55}}^{\left( k \right)} = G_{_{13}}^{\left( k \right)},\;\;\;Q_{_{66}}^{\left( k \right)} = G_{_{12}}^{\left( k \right)} \text{。}\\[-10pt] \end{split} $ | (5) |
式中:
板的内力N、内力矩M和沿厚度方向的剪力Q的表达式如下:
| $\left\{ {\begin{array}{*{20}{c}} {{N_x}}&{{N_y}}&{{N_{xy}}} \\ {{M_x}}&{{M_y}}&{{M_{xy}}} \\ {{Q_x}}&{{Q_y}}&{} \end{array}} \right\} = \sum\limits_{k = 1}^3 {\int_{{z_{k - 1}}}^{{z_k}} {{{\left\{ {\begin{array}{*{20}{c}} {{\sigma _x}}&{{\sigma _y}}&{{\tau _{xy}}} \\ {z{\sigma _x}}&{z{\sigma _y}}&{z{\tau _{xy}}} \\ {{\tau _{xz}}}&{{\tau _{yz}}}&{} \end{array}} \right\}}_{(k)}}{\rm{d}}z} } \text{。}$ | (6) |
将式(2)~式(5)代入式(6)可得:
| $\left\{ {\begin{array}{*{20}{c}} {{N_x}} \\ {{N_y}} \\ {{N_{xy}}} \\ {{M_x}} \\ {{M_y}} \\ {{M_{xy}}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{12}}}&0&{{B_{11}}}&{{B_{12}}}&0 \\ {{A_{12}}}&{{A_{22}}}&0&{{B_{12}}}&{{B_{22}}}&0 \\ 0&0&{{A_{66}}}&0&0&{{B_{66}}} \\ {{B_{11}}}&{{B_{12}}}&0&{{D_{11}}}&{{D_{12}}}&0 \\ {{B_{12}}}&{{B_{22}}}&0&{{D_{12}}}&{{D_{22}}}&0 \\ 0&0&{{B_{66}}}&0&0&{{D_{66}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {\varepsilon _x^m} \\ {\varepsilon _y^m} \\ {\gamma _{xy}^m} \\ {\varepsilon _x^f} \\ {\varepsilon _y^f} \\ {\gamma _{xy}^f} \end{array}} \right\}。$ | (7) |
式中:
| $\begin{split} &{A_{ij = }}\sum\limits_{k = 1}^3 {{{({Q_{ij}})}_k}} ({z_k} - {z_{k - 1}}) , \\ & {B_{ij = }}\frac{1}{2}\sum\limits_{k = 1}^3 {{{({Q_{ij}})}_k}} (z_k^2 - z_{k - 1}^2) ,\\ & {D_{ij = }}\frac{1}{3}\sum\limits_{k = 1}^3 {{{({Q_{ij}})}_k}} (z_k^3 - z_{k - 1}^3),\;\ \;\ \;\ (i,j = 1,2,6) 。\end{split} $ | (8) |
沿厚度方向的剪力为:
| $Q = \left\{ {\begin{array}{*{20}{c}} {{Q_{xz}}} \\ {{Q_{yz}}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {{C_{55}}}&0 \\ 0&{{C_{44}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\theta _x} + \dfrac{{\partial {w_0}}}{{\partial x}}} \\ {{\theta _y} + \dfrac{{\partial w{}_0}}{{\partial y}}} \end{array}} \right\}。$ | (9) |
在1阶剪切变形理论中,假定变形前的中面法线在变形后仍为直线,但是不再垂直于中面。即横向剪切应变γxz和γyz不随板厚发生变化,于是板的上下表面也存在剪应力。然而当板的上下表面没有剪应力作用时,其剪应力应该等于零,可见就出现了矛盾。因此需要对剪切刚度系数进行修正[18]。修正后的系数为:
| $\begin{split} & {C_{44}} = \frac{{4{h^2}}}{9}{\left( {\sum\limits_{k = 1}^3 {\frac{{{Z_k}}}{{{{({Q_{44}})}_k}}}} } \right)^{ - 1}},\;\ \;{C_{55}} = \frac{{4{h^2}}}{9}{\left( {\sum\limits_{k = 1}^3 {\frac{{{Z_k}}}{{{{({Q_{55}})}_k}}}} } \right)^{ - 1}} ,\\ & {Z_k} = {z_k} - {z_{k - 1}} - \frac{8}{3}\frac{{{{\left( {{z_k}} \right)}^3} - {{\left( {{z_{k - 1}}} \right)}^3}}}{{{h^2}}} + \frac{{16}}{5}\frac{{{{\left( {{z_k}} \right)}^5} - {{\left( {{z_{k - 1}}} \right)}^5}}}{{{h^4}}}{\text{。}} \\[-15pt] \end{split} $ | (10) |
夹芯复合材料加筋板的结构如图1所示。当加强筋的宽度和高度远小于加强筋的长度时,可以将加强筋简化为梁,采用Timosimko梁理论对加强筋进行理论建模。
根据剪切变形理论,平行于x轴方向的加强筋的位移可表达为如下形式:
| $\left\{ \begin{array}{l} {U_b}(x,{y_j},z,t) = {u_b}(x,{y_j},t) + {z_b} \cdot {\theta _x}(x,{y_j},t) ,\\ {W_b}(x,{y_j},z,t) = {w_b}(x,{y_j},t) 。\end{array} \right.$ | (11) |
式中:Ub,Wb分别为加强筋在x,z方向的位移;θx为加强筋的转角;ub,wb为加强筋中性轴的位移。
定义上标(j)表示y=yj,即x方向的第j根加筋,上式可简写为:
| $\left\{ \begin{array}{l} U_b^{(j)} = u_0^{(j)} + ({z_b} - {e_x}) \cdot \theta _x^{(j)} , \\ W_b^{(j)} = w_0^{(j)}{\text{。}} \end{array} \right.$ | (12) |
其中:
加强筋的应变-位移关系为:
| $\left\{ \begin{array}{l} \varepsilon _x^{(j)} = \dfrac{{\partial U_b^{(j)}}}{{\partial x}}\;{\rm{ = }}\dfrac{{\partial u_0^{(j)}}}{{\partial x}} - {e_x}\dfrac{{\partial \theta _x^{(j)}}}{{\partial x}} + {z_b}\;\dfrac{{\partial \theta _x^{(j)}}}{{\partial x}} , \\ \gamma _{xz}^{(j)} = \dfrac{{\partial U_b^{(j)}}}{{\partial z}} + \dfrac{{\partial W_b^{(j)}}}{{\partial x}} = \theta _x^{(j)} + \dfrac{{\partial w_0^{(j)}}}{{\partial x}} , \end{array} \right.$ | (13) |
应力-应变关系为:
| $\sigma _x^{(j)} = Q_{11}^{bx}\varepsilon _x^{(j)},\;\tau _{xz}^{(j)} = {k_s}Q_{55}^{bx}\gamma _{xz}^{(j)},$ | (14) |
式中:ks为加强筋剪切模量修正系数。
x方向加强筋的内力,内力矩的表达式如下:
| $\left\{ {\begin{array}{*{20}{c}} {N_x^{(j)}} \\ {M_x^{(j)}} \end{array}} \right\}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {A_{11}^{bx}}&{B_{11}^{bx}} \\ {B_{11}^{bx}}&{D_{11}^{bx}} \end{array}} \right\}\left\{ {\begin{array}{*{20}{c}} {{{(\varepsilon _x^{(j)})}^m}} \\ {{{(\varepsilon _x^{(j)})}^f}} \end{array}} \right\},$ | (15) |
式中:hbx为x方向加强筋的高度。
| $\begin{split} & A_{11}^{bx} = Q_{11}^{bx}{h_{bx}},B_{11}^{bx} = 0,D_{11}^{bx} = {{Q_{11}^{bx}h_{bx}^3\;\ } / {12}} , \\ & {(\varepsilon _x^{(j)})^m} = \frac{{\partial u_0^{(j)}}}{{\partial x}} - {e_x}\frac{{\partial \theta _x^{(j)}}}{{\partial x}},{(\varepsilon _x^{(j)})^f} = \frac{{\partial \theta _x^{(j)}}}{{\partial x}} , \end{split} $ | (16) |
对于沿厚度方向的剪力,有以下关系:
| $Q_{xz}^{(j)} = C_{55}^{bx}\left(\theta _x^{(j)} + \frac{{\partial w_0^{(j)}}}{{\partial x}}\right),\;C_{55}^{bx} = {h_{bx}}{k_s}Q_{55}^{bx} = {h_{bx}}{k_s}G_{13}^{bx},$ | (17) |
式中:hbx为x方向加强筋的高度。
同理可得平行于y轴方向的加强筋的应变-位移关系为:
| $\left\{ \begin{array}{l} \varepsilon _y^{(i)} = \dfrac{{\partial V_b^{(i)}}}{{\partial y}}{\rm{ = }}\dfrac{{\partial v_0^{(i)}}}{{\partial y}} - {e_y} \cdot \dfrac{{\partial \theta _y^{(i)}}}{{\partial y}} + {z_b} \cdot \dfrac{{\partial \theta _y^{(i)}}}{{\partial y}}, \\ \gamma _{yz}^{(i)} = \dfrac{{\partial V_b^{(i)}}}{{\partial z}} + \dfrac{{\partial W_b^{(i)}}}{{\partial y}} = \theta _y^{(i)} + \dfrac{{\partial w_0^{(i)}}}{{\partial y}} ,\end{array} \right.$ | (18) |
定义上标(i)表示x=xi,即y方向的第i根加筋,ey=h2/2+h1+hby/2。
应力-应变关系为:
| $\sigma _y^{(i)} = Q_{22}^{by}\varepsilon _y^{(i)},\; \tau _{yz}^{(i)} = {k_s}Q_{44}^{by}\gamma _{yz}^{(i)}\text{。}$ | (19) |
式中:ks为加强筋剪切模量修正系数。
y方向加强筋的内力、内力矩的表达式如下:
| $\left\{ {\begin{array}{*{20}{c}} {N_y^{(i)}} \\ {M_y^{(i)}} \end{array}} \right\}{\rm{ = }}\left\{ {\begin{array}{*{20}{c}} {A_{22}^{by}}&{B_{22}^{by}} \\ {B_{22}^{by}}&{D_{22}^{by}} \end{array}} \right\}\left\{ {\begin{array}{*{20}{c}} {{{(\varepsilon _y^{(i)})}^m}} \\ {{{(\varepsilon _y^{(i)})}^f}} \end{array}} \right\},$ | (20) |
式中:
| $\begin{split} & A_{22}^{by} = Q_{22}^{by}{h_{by}},B_{22}^{by} = 0,D_{22}^{by} = {{Q_{22}^{by}h_{by}^3\;\ } / {12}}, \\ & {(\varepsilon _y^{(i)})^m} = \frac{{\partial v_0^{(i)}}}{{\partial y}} - {e_y}\frac{{\partial \theta _y^{(i)}}}{{\partial y}},{(\varepsilon _y^{(i)})^f} = \frac{{\partial \theta _y^{(i)}}}{{\partial y}} ,\end{split} $ | (21) |
对于沿厚度方向的剪力,有以下关系:
| $Q_{yz}^{(i)} = C_{44}^{by}\left(\theta _y^{(i)} + \frac{{\partial w_0^{(i)}}}{{\partial y}}\right),\; C_{44}^{by} = {h_{by}}{k_s}Q_{44}^{by} = {h_{by}}{k_s}G_{23}^{by}\text{。}$ | (22) |
由Hamilton原理可得,夹芯复合材料加筋板在真空中的自由振动方程为
| $\int_{{t_1}}^{{t_2}} {(\delta T - \delta U) = 0}。$ | (23) |
式中:T表示夹芯复合材料加筋板的总动能;U表示总应变能;δ为变分符号。
将复合材料板和加强筋的应变能和动能分别相加可得夹芯复合材料加筋板的总应变能δU和总动能为:
| $\begin{split} &\delta T= \delta {T_p} + \delta {T_{bx}} + \delta {T_{by}}, \\ & \delta U = \delta {U_p} + \delta {U_{bx}} + \delta {U_{by}} 。\end{split} $ | (24) |
复合材料板的应变能为:
| $\begin{split} \delta {U_p} =& \int_S {\sum\limits_{k = 1}^3 {\int_{{z_{k - 1}}}^{{z_k}} {\left( \begin{gathered} {\sigma _x}\delta {\varepsilon _x} + {\sigma _y}\delta {\varepsilon _y} + {\sigma _z}\delta {\varepsilon _z} + \\ {\tau _{xy}}\delta {\gamma _{xy}} + {\tau _{yz}}\delta {\gamma _{yz}} + {\tau _{xz}}\delta {\gamma _{xz}} \\ \end{gathered} \right){\rm d}z} } } {\rm d}x{\rm d}y 。\end{split} $ | (25) |
式中:S表示复合材料板中性面的面积。
复合材料板的动能为:
| $\begin{split} \delta {T_p} =& \int_S {\sum\limits_{k = 1}^3 {\int_{{z_{k{\rm{ - }}1}}}^{{z_k}} {{\rho ^{\left( k \right)}}\left( {\dot u\delta \dot u + \dot v\delta \dot v + \dot w\delta \dot w} \right){\rm{d}}z} } } {\rm{d}}x{\rm{d}}y = \\ &- \int_S {\left( \begin{gathered} \left( {{{\bar \rho }_0}{{\ddot u}_0} + {{\bar \rho }_1}{{\ddot \theta }_x}} \right)\delta {u_0} + \left( {{{\bar \rho }_1}{{\ddot u}_0} + {{\bar \rho }_2}{{\ddot \theta }_x}} \right)\delta {\theta _x} + \\ \left( {{{\bar \rho }_0}{{\ddot v}_0} + {{\bar \rho }_1}{{\ddot \theta }_y}} \right)\delta {v_0} + \left( {{{\bar \rho }_1}{{\ddot v}_0} + {{\bar \rho }_2}{{\ddot \theta }_y}} \right)\delta {\theta _y} + \\ {{\bar \rho }_0}{{\ddot w}_0}\delta {w_0} \\ \end{gathered} \right)} {\rm d}x {\rm d}y{\text{。}} \end{split}$ | (26) |
式中:
| $\left( {{{\bar \rho }_0},{{\bar \rho }_1},{{\bar \rho }_2}} \right) = \sum\limits_{k = 1}^3 {\int_{{z_{k - 1}}}^{{z_k}} {{\rho ^{\left( k \right)}} \cdot \left( {1,z,{z^2}} \right){\rm d}z} } ,$ | (27) |
x方向加强筋的应变能可表示为:
| $\begin{split} \delta {U_{bx}} = &\sum\limits_{j = 1}^{n1} {b_j}\int_{\varOmega} { { { {\left( {\sigma _x^{(j)}\delta \varepsilon _x^{(j)} + \tau _{xz}^{(j)}\delta \gamma _{xz}^{(j)}} \right)} } } }\delta '(y - {y_j}){\rm d}x{\rm d}y 。\end{split}$ | (28) |
式中:
同理,y方向加强筋的应变能可表示为:
| $\begin{split} \delta {U_{by}} =& \sum\limits_{i = 1}^{n2}{b_i}\int_\Omega { { { {\left( {\sigma _y^{(i)}\delta \varepsilon _y^{(i)} + \tau _{yz}^{(i)}\delta \gamma _{yz}^{(i)}} \right) \delta '(x - {x_i}){\rm d}x{\rm d}y} } } }。\end{split}$ | (29) |
式中:bj ,bi分别为平行于x,y轴方向第j,i根梁的横截面宽度;n1,n2分别为x,y方向的加筋数量。
x方向加强筋的动能为:
| $\begin{split} \delta {T_{bx}} =& \sum\limits_{j = 1}^{n1} \int_{ - {b_j}/2}^{{b_j}/2} \int_{ - a/2}^{a/2} \int_{ - {h_{bj}}/2}^{{h_{bj}}/2} {\rho ^{bx}}\Bigr( U_b^{(j)}\delta \dot U_b^{(j)} +\\ &W_b^{(j)}\delta \dot W_b^{(j)} \Bigr){\rm d}z {\rm d}x{\rm d}y =\\ & - \sum\limits_{j = 1}^{n1} {b_j}\int_{ - a/2}^{a/2} \left( \begin{array}{l} \left( {\bar \rho _{x0}^b\ddot u_0^{(j)} + \bar \rho _{x1}^b\ddot \theta _x^{(j)}} \right)\delta u_0^{(j)}+\\ \left( {\bar \rho _{x1}^b\ddot u_0^{(j)} + \bar \rho _{x2}^b\ddot \theta _x^{(j)}} \right)\delta \theta _x^{(j)}+\\ \bar \rho _{x0}^b\ddot w_0^{(j)}\delta w_0^{(j)} \end{array} \right)\times\\ &\delta '(y - {y_j}) {\rm d}x {\rm d}y, \end{split}$ | (30) |
式中:
| $\left( {\bar \rho _{x0}^b,\bar \rho _{x1}^b,\bar \rho _{x2}^b} \right) = \int_{ - {h_{bj}}/2}^{{h_{bj}}/2} {{\rho ^{bx}} \cdot \left( {1,({z_b} - {e_x}),{{({z_b} - {e_x})}^2}} \right){\rm d}{z_b}} 。$ | (31) |
y方向加强筋的动能为:
| $\begin{split} \delta {T_{by}} = &\sum\limits_{i = 1}^{n2} \int_{ - b/2}^{b/2} \int_{ - {b_i}/2}^{{b_i}/2} \int_{ - {h_{bi}}/2}^{{h_{bi}}/2} {\rho ^{by}}\Bigr( V_b^{(i)}\delta \dot V_b^{(i)} +\\ &W_b^{(i)}\delta \dot W_b^{(i)} \Bigr){\rm d}z {\rm d}x{\rm d}y =\\ & - \sum\limits_{i = 1}^{n2} {b_i}\int_\Omega {\left( \begin{array}{l} \left( {\bar \rho _{y0}^b\ddot v_0^{(i)} + \bar \rho _{y1}^b\ddot \theta _y^{(i)}} \right)\delta v_0^{(i)}+\\ \left( {\bar \rho _{y1}^b\ddot v_0^{(i)} + \bar \rho _{y2}^b\ddot \theta _y^{(i)}} \right)\delta \theta _y^{(i)} +\\ \bar \rho _{y0}^b\ddot w_0^{(i)}\delta w_0^{(i)} \end{array} \right)} \times\\ &\delta '(x - {x_i}){\rm d}x{\rm d}y{\text{。}} \end{split}$ | (32) |
式中:
| $\left( {\bar \rho _{y0}^b,\bar \rho _{y1}^b,\bar \rho _{y2}^b} \right) = \int_{ - {h_{bi}}/2}^{{h_{bi}}/2} {{\rho ^{by}} \cdot \left( {1,({z_b} - {e_y}),{{({z_b} - {e_y})}^2}} \right){\rm d}{z_{bi}}}。$ | (33) |
将式(25)和式(26)、式(28)~式(30)和式(32)代入式(24)中,联立式(23),结合夹芯复合材料加筋板的本构关系,并根据变分原理可得夹芯复合材料加筋板的自由振动微分方程为:
| $\left\{ \begin{array}{l} \delta {u_0}:\dfrac{{\partial {N_x}}}{{\partial x}} + \dfrac{{\partial {N_{xy}}}}{{\partial y}} + \displaystyle\sum\limits_{j = 1}^{n1} {{b_j}\frac{{\partial N_x^{(j)}}}{{\partial x}}} \delta '(y - {y_j})\; - \left( {{{\bar \rho }_0}{{\ddot u}_0} + {{\bar \rho }_1}{{\ddot \theta }_x}} \right) - \\ \qquad\displaystyle \sum\limits_{j = 1}^{n1} {{b_j}\left( {\bar \rho _{x0}^b\ddot u_0^{(j)} + \bar \rho _{x1}^b\ddot \theta _x^{(j)}} \right)} \delta '(y - {y_j})= 0 ,\\ \delta {v_0}:\dfrac{{\partial {N_y}}}{{\partial y}} + \dfrac{{\partial {N_{xy}}}}{{\partial x}} + \displaystyle\sum\limits_{i = 1}^{n2} {{b_i}\frac{{\partial N_y^{(i)}}}{{\partial y}}\delta '(x - {x_i})} - \left( {{{\bar \rho }_0}{{\ddot v}_0} + {{\bar \rho }_1}{{\ddot \theta }_y}} \right) -\\ \qquad \displaystyle\sum\limits_{i = 1}^{n2} {{b_i}\left( {\bar \rho _{y0}^b\ddot v_0^{(i)} + \bar \rho _{y1}^b\ddot \theta _y^{(i)}} \right)\; } \delta '(x - {x_i}) = 0 , \\ \delta {\theta _x}:\dfrac{{\partial {M_x}}}{{\partial x}} + \dfrac{{\partial {M_{xy}}}}{{\partial y}} + \displaystyle\sum\limits_{j = 1}^{n1} {b_j}\left( \frac{{\partial M_x^{(j)}}}{{\partial x}} -\right.\\ \left.\qquad {e_x}\dfrac{{\partial N_x^{(j)}}}{{\partial x}} \right)\; \delta '(y - {y_j})\; -{Q_{xz}} -\\ \qquad \displaystyle \sum\limits_{j = 1}^{n1} {{b_j}Q_{xz}^{(j)}\delta '(y - {y_j})\; } - \left( {{{\bar \rho }_1}{{\ddot u}_0} + {{\bar \rho }_2}{{\ddot \theta }_x}} \right)- \\ \qquad \displaystyle\sum\limits_{j = 1}^{n1} {{b_j}\left( {\bar \rho _{x1}^b\ddot u_0^{(j)} + \bar \rho _{x2}^b\ddot \theta _x^{(j)}} \right)\delta '(y - {y_j})\; } \; {\rm{ = }}0 , \\ \delta {\theta _y}:\dfrac{{\partial {M_y}}}{{\partial y}} + \dfrac{{\partial {M_{xy}}}}{{\partial x}} + \displaystyle\sum\limits_{i = 1}^{n2} {b_i}\left( \frac{{\partial M_y^{(i)}}}{{\partial y}} -\right.\\ \qquad\left. {e_y}\dfrac{{\partial N_y^{(i)}}}{{\partial y}} \right)\delta '(x - {x_i}) - {Q_{yz}} - \\ \qquad\displaystyle\sum\limits_{i = 1}^{n2} {{b_i}Q_{yz}^{(i)}} \delta '(x - {x_i}) - \left( {{{\bar \rho }_1}{{\ddot v}_0} + {{\bar \rho }_2}{{\ddot \theta }_y}} \right) - \\ \qquad \displaystyle\sum\limits_{i = 1}^{n2} {{b_i}\left( {\bar \rho _{y1}^b\ddot v_0^{(i)} + \bar \rho _{y2}^b\ddot \theta _y^{(i)}} \right)} \delta '(x - {x_i}){\rm{ = }}0 ,\\ \delta {w_0}:\dfrac{{\partial {Q_{xz}}}}{{\partial x}} + \dfrac{{\partial {Q_{yz}}}}{{\partial y}} + \displaystyle\sum\limits_{j = 1}^{n1} {{b_j}\frac{{\partial Q_{xz}^{(j)}}}{{\partial x}}} \delta '(y - {y_j})\; + \\ \qquad \displaystyle\sum\limits_{i = 1}^{n2} {{b_i}\frac{{\partial Q_{yz}^{(i)}}}{{\partial y}}\delta '(x - {x_i})} - {{\bar \rho }_0}{{\ddot w}_0} -\\ \qquad \displaystyle\sum\limits_{j = 1}^{n1} {{b_j}\bar \rho _{x0}^b\ddot w_0^{(j)}} \delta '(y - {y_j})\; -\\ \qquad \displaystyle\sum\limits_{i = 1}^{n2} {{b_i}\bar \rho _{y0}^b\ddot w_0^{(i)}\delta '(x - {x_i})} = 0\text{。} \end{array} \right.$ | (34) |
复合材料板浸没于水中时,可将结构视为薄板来建立振动方程,需考虑板两侧的水介质对结构运动的影响。
根据Hamilton原理,考虑水介质的影响后夹芯复合材料加筋板的自由振动方程为:
| $\int_{{t_1}}^{{t_2}} {(\delta T - \delta U{\rm{ + }}\delta W)} = 0,$ | (35) |
式中:T表示夹芯复合材料加筋板的总动能;U为总应变能;W为总外力功。
外力功由水介质作用在复合材料板两侧的压力提供,压力项可表示为:
| $\bar p(x,y) = {p^ - }(x,y) - {p^ + }(x,y)。$ | (36) |
式中:p-(x,y),p+(x,y)分别是作用在复合材料板Z向上、下表面的压力。
外力功可表示为:
| $\delta W = \int_0^a {\int_0^b {\bar p(x,y)} } \delta {w_0}{\rm d}x{\rm d}y,$ | (37) |
则夹芯复合材料加筋板在水中的自由振动微分方程同式(35)类似,不同的是考虑水介质的影响后,式(35)中的第5项表示为:
| $\begin{split} \delta {w_0}:&\frac{{\partial {Q_{xz}}}}{{\partial x}} + \frac{{\partial {Q_{yz}}}}{{\partial y}} + \sum\limits_{j = 1}^{n1} {{b_j}\frac{{\partial Q_{xz}^{(j)}}}{{\partial x}}} \delta '(y - {y_j})+\\ &\sum\limits_{i = 1}^{n2} {{b_i}\frac{{\partial Q_{yz}^{(i)}}}{{\partial y}}\delta '(x - {x_i})} - {{\bar \rho }_0}{{\ddot w}_0} - \sum\limits_{j = 1}^{n1} {{b_j}\bar \rho _{x0}^b{{\ddot w}_0}} \delta '(y - {y_j})-\\ &\sum\limits_{i = 1}^{n2} {{b_i}\bar \rho _{y0}^b{{\ddot w}_0}\delta '(x - {x_i})} + \bar p(x,y) = 0 , \\[-20pt] \end{split} $ | (38) |
| ${\nabla ^2}p({M_0}) + k_0^2p({M_0}) = 0{\text{。}}$ | (39) |
式中:
当板浸没在水中时,其声压表达式为[15]:
| $\begin{split} & p({M_0}) = \int_{{S_p}} {\left[{p^ - }(x,y) - {p^ + }(x,y)\right]} \frac{{\partial G(M,{M_0})}}{{\partial {z_M}}}{\rm d}{S_p} , \\ &\qquad\qquad\qquad\quad M(x,y,z) \in {S_p} \end{split} $ | (40) |
式中:Sp为加筋板的表面积,zM为M处的面法向,
| $G(M,{M_0}) = \frac{j}{{8{\text{π} ^2}}}\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {\frac{{{e^{j{k_x}(x - {x_0})}}{e^{j{k_y}(y - {y_0})}}{e^{j{k_z}\left| {z - {z_0}} \right|}}}}{{{k_z}}}{\rm{d}}{{\rm{k}}_x}\;\ {\rm{d}}{{\rm{k}}_y}} }, $ | (41) |
其中j为虚数单位,kx和ky为傅里叶变量。
| $ {k}_{z}=\left\{\begin{array}{l}\sqrt{{k}_{0}{}^{2}-{k}_{x}^{2}-{k}_{y}^{2}},{k}_{0}^{2}\geqslant {k}_{x}^{2}+{k}_{y}^{2},\\ j\sqrt{{k}_{x}^{2}+{k}_{y}^{2}-{k}_{0}{}^{2}},{k}_{0}^{2}\leqslant {k}_{x}^{2}+{k}_{y}^{2},\end{array}\right.$ | (42) |
在流固耦合面(
| $\begin{split} {\rho _0}{\omega ^2}{w_0}({x_0},{y_0}) =& {\left. {\frac{{\partial p({M_0})}}{{\partial {z_0}}}} \right|_{{z_0} = 0}}= \\ & \int_{{S_p}} {[\bar p(x,y)]} \frac{{\partial {G^2}(M,{M_0})}}{{\partial {z_M}\partial {z_0}}}{\rm{d}}{S_p} 。\end{split} $ | (43) |
式中:ρ0为水的密度。
将式(38)代入式(43)中有
| $\begin{split} - \int_{{S_p}}& {\left[ \begin{array}{l} \dfrac{{\partial {Q_{xz}}}}{{\partial x}} + \dfrac{{\partial {Q_{yz}}}}{{\partial y}} + \displaystyle\sum\limits_{j = 1}^{n1} {{b_j}\frac{{\partial Q_{xz}^{(j)}}}{{\partial x}}} \delta '(y - {y_j})\; + \\[-2pt] \displaystyle\sum\limits_{i = 1}^{n2} {{b_i}\frac{{\partial Q_{yz}^{(i)}}}{{\partial y}}\delta '(x - {x_i})} - {{\bar \rho }_0}{{\ddot w}_0} - \\[-2pt] \displaystyle \sum\limits_{j = 1}^{n1} {{b_j}\bar \rho _{x0}^b{{\ddot w}_0}} \delta '(y - {y_j}) - \displaystyle\sum\limits_{i = 1}^{n2} {{b_i}\bar \rho _{y0}^b{{\ddot w}_0}\delta '(x - {x_i})} \\ \end{array} \right]} \times\\[-2pt] &\frac{{\partial {G^2}(M,{M_0})}}{{\partial {z_M}\partial {z_0}}}d{S_p} ={\rho _0}{\omega ^2}{w_0}({x_0},{y_0}) \text{。}\\[-15pt] \end{split} $ | (44) |
在四边简支边界条件下,夹芯复合材料加筋板的FSDT微分方程的求解可采用双傅里叶三角级数解法,设微分方程组有如下形式的解:
| $\begin{split} & {u_0} = {e^{j\omega t}}\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{u_{0mn}}\cos \alpha x\sin \beta y} } , \\ & {v_0} = {e^{j\omega t}}\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{v_{0mn}}\sin \alpha x\cos \beta y} } , \\ & {\theta _x} = {e^{j\omega t}}\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{\theta _{xmn}}\cos \alpha x\sin \beta y} }, \\ & {\theta _y} = {e^{j\omega t}}\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{\theta _{ymn}}\sin \alpha x\cos \beta y} } , \\ & {w_{\rm{0}}} = {e^{j\omega t}}\sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{w_{\rm{0}}}_{mn}\sin \alpha x\sin \beta y} }\text{。} \end{split} $ | (45) |
式中:u0mn,v0mn,θxmn,θymn和w0mn为广义位移幅值,是待定的值,m和n分别为板在x和y方向的半波数,
将式(45)及N,M和Q代入式(34)中,并在5个方程左右两边分别同时乘以:cos(kπx/a) sin(lπy/b),sin(kπx/a) cos(lπy/b),cos(kπx/a) sin(lπy/b),sin(kπx/a) cos(lπy/b)和sin(kπx/a) sin(lπy/b),进一步将方程组写成矩阵形式,则可得到:
| $\left[ {\begin{array}{*{20}{c}} {{R_{11}}}&{{R_{12}}}&{{R_{13}}}&{{R_{14}}}&{{R_{15}}} \\ {{R_{21}}}&{{R_{22}}}&{{R_{23}}}&{{R_{24}}}&{{R_{25}}} \\ {{R_{31}}}&{{R_{32}}}&{{R_{33}}}&{{R_{34}}}&{{R_{35}}} \\ {{R_{41}}}&{{R_{42}}}&{{R_{43}}}&{{R_{44}}}&{{R_{45}}} \\ {{R_{51}}}&{{R_{52}}}&{{R_{53}}}&{{R_{54}}}&{{R_{55}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{u_{0mn}}} \\ {{v_{0mn}}} \\ {{\theta _{xmn}}} \\ {{\theta _{ymn}}} \\ {{w_{0mn}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array}} \right\},$ | (46) |
式中:Rij(i,j=1,2,3,4,5)为刚度系数。为使上述方程组有非零解,则方程组系数矩阵的行列式必须为零,由此求得相应m和n对应的固有频率值。
1.4.2 水中微分方程求解在四边简支边界条件下,仍可用双傅里叶三角级数解来求解水中振动微分方程。不同于真空中的求解,水中振动微分方程左右两边同时乘sin(kπx0/a) sin(lπy0/b),且积分域为
| $\left[ {\begin{array}{*{20}{c}} {{T_{11}}}&{{T_{12}}}&{{T_{13}}}&{{T_{14}}}&{{T_{15}}} \\ {{T_{21}}}&{{T_{22}}}&{{T_{23}}}&{{T_{24}}}&{{T_{25}}} \\ {{T_{31}}}&{{T_{32}}}&{{T_{33}}}&{{T_{34}}}&{{T_{35}}} \\ {{T_{41}}}&{{T_{42}}}&{{T_{43}}}&{{T_{44}}}&{{T_{45}}} \\ {{T_{51}}}&{{T_{52}}}&{{T_{53}}}&{{T_{54}}}&{{T_{55}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{u_{0mn}}} \\ {{v_{0mn}}} \\ {{\theta _{xmn}}} \\ {{\theta _{ymn}}} \\ {{w_{0mn}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array}} \right\} 。$ | (47) |
式中:Tij(i,j=1,2,3,4,5)为刚度系数。
2 模型验证与特性分析 2.1 理论模型验证 2.1.1 无量纲固有频率为验证上述理论推演的正确性,以无量纲形式的3层复合材料夹芯板为例。其芯层的材料参数为E22/E11=0.543,G12/E11=0.2629,G13/E11=0.1599,G23/E11=0.2668,泊松比v12=0.3。面板的材料参数为芯层的材料参数分别乘比率R所得,R的值取1,2,5,10,15,上下2层面板的材料参数一致且芯层和面板的密度相同,且h1/h=h2/h=0.1,h/a=h/b=0.1,无量纲基频由式
|
|
表 1 无量纲1阶固有频率结果对比 Tab.1 Comparison of dimensionless first order natural frequency results |
由表1可知,本文结果与文献结果之间的误差最大不超过3%,具有比较良好的一致性。此外,上述材料参数代入Ansys中采用Shell181单元进行建模计算,并将结果无量纲化同解析方法进行对比,其结果如表2所示。
|
|
表 2 无量纲1阶固有频率结果对比 Tab.2 Comparison of dimensionless first order natural frequency results |
由表2可知,2种方法计算的结果比较接近,相对误差最大不超过3%,满足工程允许实际需要,说明了理论模型和求解方法的有效性。
2.1.2 真空中理论模型验证将理论分析方法与Ansys有限元方法进行比较,使用Ansys16.0进行建模计算,其中板单元采用Shell181单元,加强筋采用Beam188单元。计算模型采用2×2纵横加筋,加筋位置分别在板架长宽的三等分线处,其有限元模型如图3所示。

|
图 3 夹芯复合材料加筋板有限元模型 Fig. 3 Finite element model of sandwich composite stiffened plate |
夹芯复合材料加筋板的材料参数见表3~表5。其中面板为正交各向异性材料,铺层角度为0°(本文的复合材料面板铺层角度均为0°),芯层材料视为各向同性材料。Ansys中输入正交各向异性材料的材料参数时,3个平面的剪切模量设为相同的值。
|
|
表 3 夹芯复合材料加筋板上下面板材料参数 Tab.3 Material parameters of upper and lower panels of sandwich composite stiffened plate |
|
|
表 4 夹芯复合材料加筋板黏弹性层材料参数 Tab.4 Material parameters of viscoelastic layer of sandwich composite stiffened plate |
|
|
表 5 加强筋材料参数 Tab.5 Material parameters of reinforcement |
使用Matlab对解析方法进行求解,并与Ansys有限元建模计算方法对比,计算结果取前5阶固有频率,结果如表6所示。
|
|
表 6 真空中前5阶固有频率计算结果 Tab.6 The first five natural frequencies in vacuum are calculated |
从表6可看出,本文所用解析法与数值仿真结果比较吻合,具有良好的一致性,相对误差在2%以内,满足工程实际需求。
2.1.3 水中理论模型验证水中模型验证采用与真空中相同的有限元模型,利用Ansys结合Virtual. Lab的方法得到浸没于水中的夹芯复合材料加筋板的前5阶模态,同时使用Matlab对解析方法进行求解,并将两者的结果进行比较,结果如表7所示。
|
|
表 7 水中前5阶固有频率计算结果 Tab.7 Calculation results of the first five natural frequencies in water |
从表7可看出,2种方法计算结果的相对误差在4%以内,满足实际工程需要。对比表6和表7的结果可知,由于流体介质的影响,夹芯复合材料加筋板在水中自由振动的1阶固有频率较真空中会有很大幅度的下降,约为真空中1阶固有频率的1/4。
2.2 特性分析上述解析方法建模简便、计算速度较快且结果准确,因此可用该解析方法对结构进行特性分析,研究影响结构自由振动的因素。
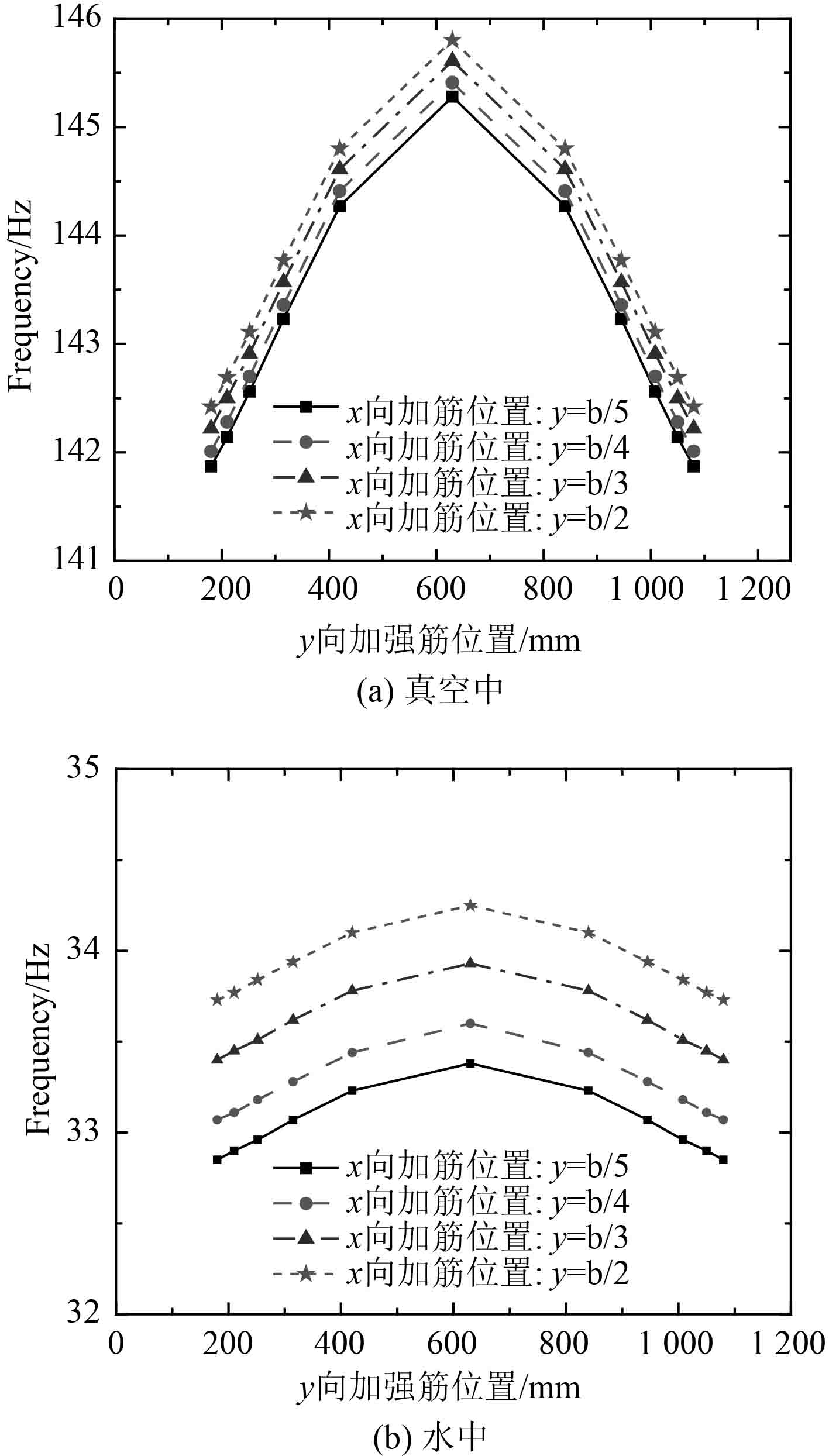
2.2.1 加强筋位置对结构基频的影响以纵横1×1加筋的夹芯复合材料加筋板为例,利用上述解析法研究加强筋位置变化对板架的1阶固有频率的影响,结果如图4所示。
|
图 4 加强筋位置变化对板架基频的影响 Fig. 4 Influence of position change of stiffener on fundamental frequency of plate fram |
从图4的结果看出,x方向加筋的位置固定,改变y方向加筋位置,当其在板架中间位置时,结构的1阶固有频率最大。当纵横加筋均在复合材料板的几何中心时,板架在真空中和在水中的固有频率同时达到最大值,说明加筋在板架中心处能使整体结构的刚度达到最大。
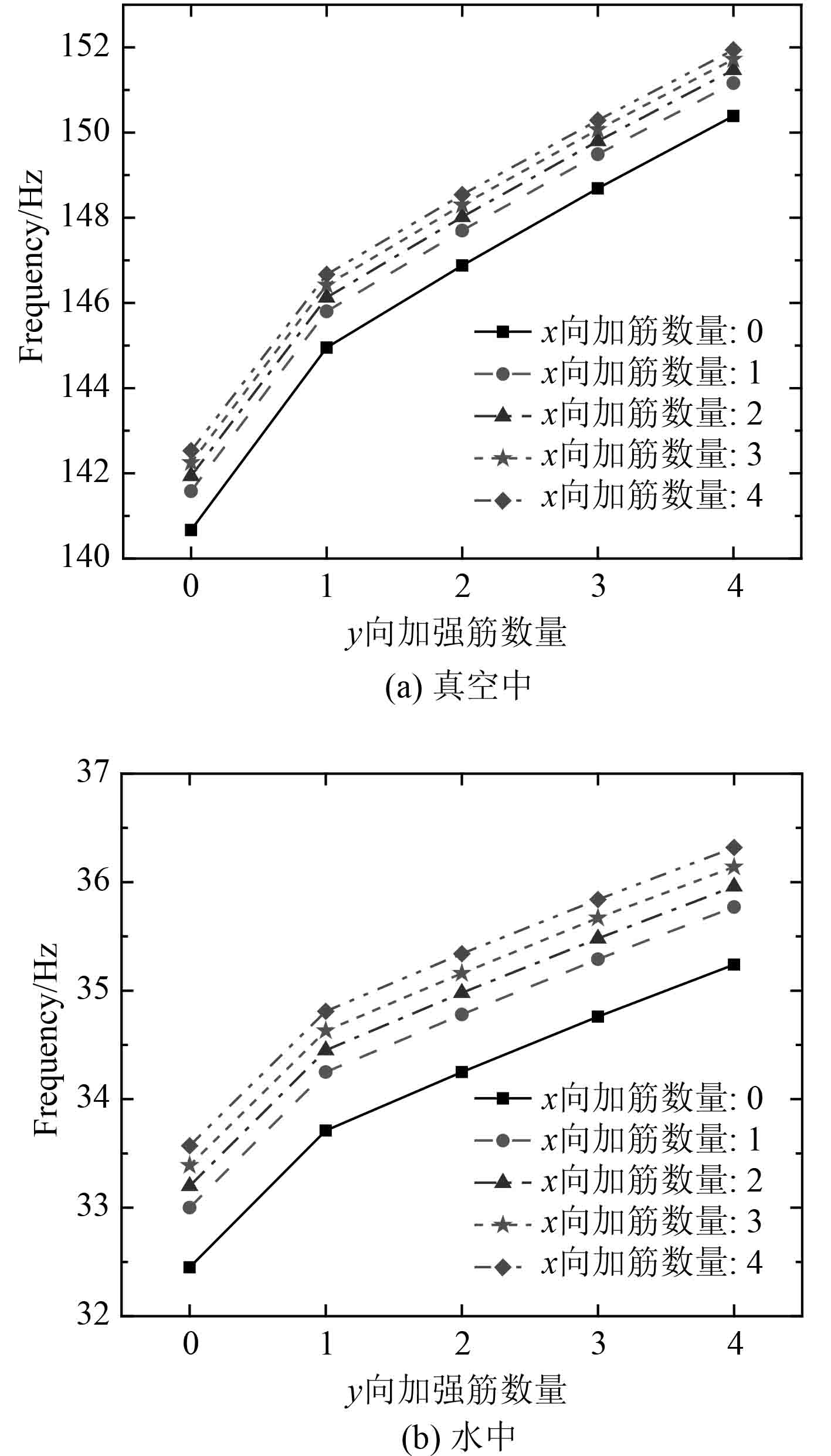
2.2.2 加强筋数量对结构基频的影响保持夹芯复合材料加筋板的尺寸参数不变,研究不同加筋数量对结构的1阶固有频率的影响,结果如图5所示。
|
图 5 加强筋数量对板架基频的影响 Fig. 5 The influence of the number of stiffeners on the fundamental frequency of the plate frame |
由图5可知,加筋板的1阶固有频率相比于无筋板有较大幅度的提升,说明加强筋能很大程度上提高结构的固有频率。随着加筋数量的增加,夹芯复合材料加筋板真空中和水中的1阶固有频率不断增大,说明增加板架的加筋数量可以有效提高结构整体的刚度。且通过对比不同方向增加加强筋的数量,可以看出增加板架短边的加筋对整体结构的影响较大。
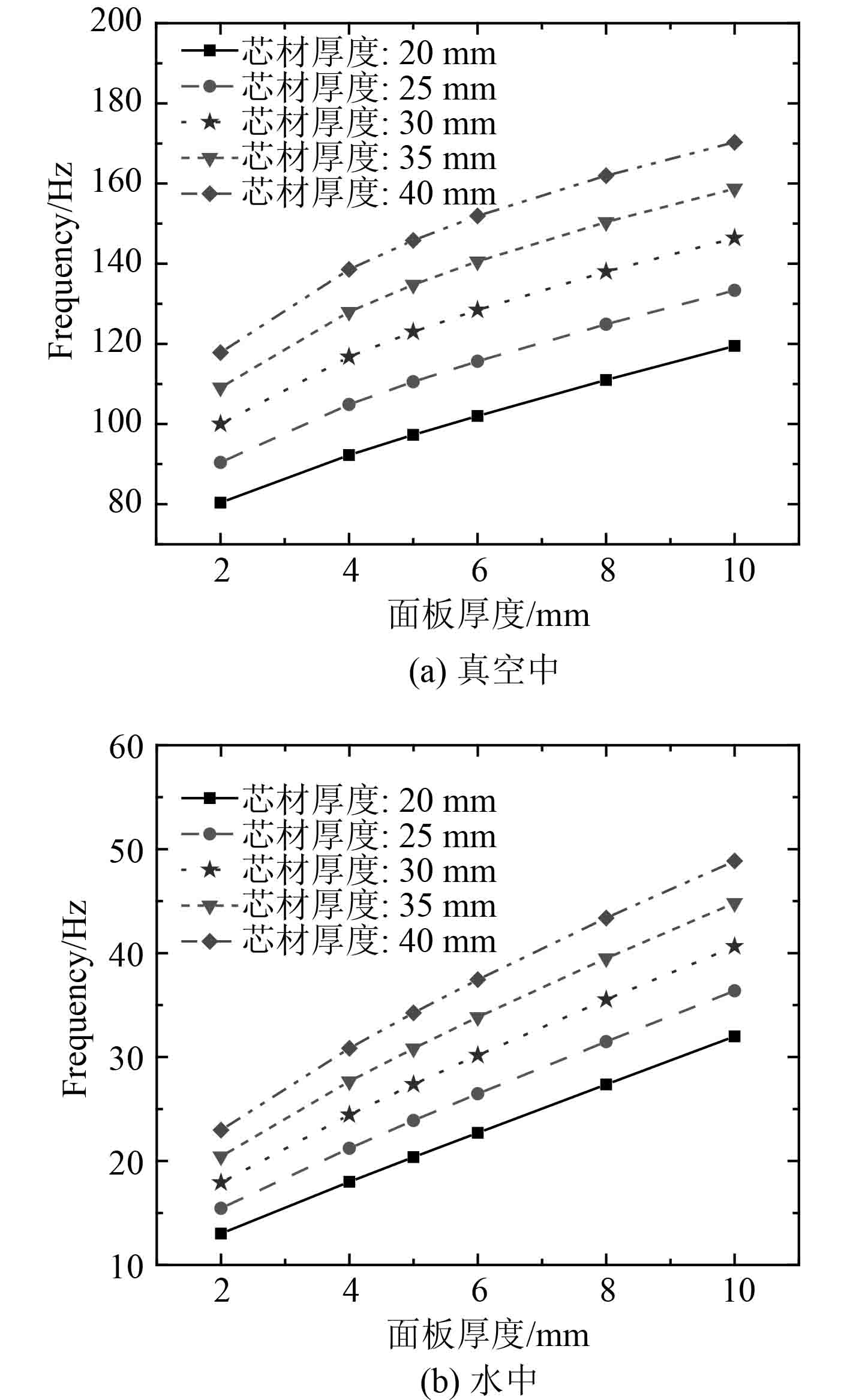
2.2.3 面板和芯层厚度对结构基频的影响以纵横1×1加筋的夹芯复合材料加筋板为例,保持加强筋尺寸不变,研究面板和芯层的厚度变化对结构基频的影响,结果如图6所示。
|
图 6 面板厚度变化对板架基频的影响 Fig. 6 The influence of panel thickness variation on the fundamental frequency of the pane |
由图6可知,当芯层厚度一定时,随着面板厚度增加夹芯复合材料加筋板在真空中和水中的1阶固有频率均增大,当面板厚度增加到一定尺寸后,结构的固有频率增长率逐渐下降,这种趋势在真空中表现得较为明显。同时,当面板厚度一定时,芯层厚度增加也会使结构的1阶固有频率增大。当实际工程对结构的固有频率有要求时,从图6可看出有不同的面板及芯层厚度组合方案,根据实际工程需求可合理选择方案。
2.2.4 加强筋和面板弹性模量比对结构基频的影响以纵横2×2加筋的夹芯复合材料加筋板为例,保持加强筋尺寸不变,仅改变加强筋的弹性模量,研究加强筋和面板的弹性模量比对结构固有频率的影响,取解析法的前5阶固有频率同数值仿真结果对比,如表8所示。
|
|
表 8 加强筋和面板弹性模量比对板架前5阶固有频率的影响 Tab.8 Influence of the ratio of elastic modulus of stiffener and panel on the first five natural frequencies of the plate |
可以看出,随着加强筋和面板之间的弹性模量比逐渐增大,解析方法和数值方法之间的误差逐渐增大,且水中的误差较真空中更大,逐渐大于5%。取加强筋和面板的弹性模量比为3时解析法和数值法在真空中的第5阶模态云图作对比,如图7所示。

|
图 7 两种方法下结构第五阶固有频率振型云图 Fig. 7 The fifth-order natural frequency mode cloud diagram of the structure under the two methods |
由图7可以看出,当加强筋和面板的弹性模量比为3时,加筋对结构整体振型造成了一定的影响,而理论方法中加筋对结构振型的影响很小,此时,用1阶剪切理论建立该结构的振动方程存在一定误差,且随着加强筋和面板的弹性模量比逐渐增大,这种误差会越来越大。
3 结 语本文基于1阶剪切理论(FSDT)和Hamilton原理,利用狄拉克函数描述加筋,借助Helmholtz方程,Euler方程及Green函数,建立了夹芯复合材料加筋板在真空中和水中的自由振动理论模型。并采用双三角级数法求解了该结构在四边简支边界条件下的自由振动特性,理论计算结果与数值仿真结果具有较好的一致性,说明了本文的解析法理论和有限元数值仿真都有较高的准确度。同时通过计算对比,也体现出了解析法建模简便、计算速度较快和结果准确的优点。
进一步使用解析法研究加筋位置、数量及面板和芯层厚度变化对结构整体振动的影响,结果表明:
1)将加强筋布置在复合材料夹芯板的几何中心时,结构的固有频率最大;
2)增加加强筋的数量能有效提高结构的固有频率,当板架长宽不一致时,增加短边的加强筋数量结构的固有频率提升得更快;
3)增加夹芯复合材料加筋板的面板和芯层厚度均能提高结构的固有频率,结合工程实际需求,可选择合适的面板和芯层厚度组合方案;
4)当加强筋和面板的弹性模量数值比较接近时,使用FSDT所得的结果较为准确,随着加强筋和面板弹性模量比的增大,使用FSDT所得结果的误差也会越大。
| [1] |
朱锡, 石勇, 梅志远. 夹芯复合材料在潜艇声隐身结构中的应用及其相关技术研究[J]. 中国舰船研究, 2007(3): 34-39. ZHU X, SHI Y, MEI Z Z. Application of sandwich composite material in submarine acoustic stealth structure and related technology research[J]. Chinese Journal of Ship Research, 2007(3): 34-39. |
| [2] |
肖锋, 谌勇, 章振华, 等. 夹层结构冲击动力学研究综述[J]. 振动与冲击, 2013, 32(18): 1-7+20. XIAO F, SHEN Y, ZHANG Z H, et al. Summary of research on impact dynamics of sandwich structure[J]. Jouranl of Vibration and Shock, 2013, 32(18): 1-7+20. |
| [3] |
KIRCHHOFF GR. Uber das gleichgewicht und die bewegung einer elastischen Scheibe[J]. Jouranl of Reine Angew Math (Crelle′s J), 1850, 40: 51-88. |
| [4] |
MINDLIN R D. Influence of rotatory inertia and shear on flexural motions of isotropic elastic plates[J]. Jouranl of Applied Mechanics, 1951, 18: 31-38. DOI:10.1115/1.4010217 |
| [5] |
REISSNER E. The effect of transverse shear deformation on the bending of elastic plates[J]. Journal of Applied Mechanics, 1945, 12(2): 69-77. DOI:10.1115/1.4009435 |
| [6] |
WHITNEY J M, PAGANO N J. Shear deformation in heterogeneous anisotropic plates[J]. Journal of Applied Mechanics, 1970, 37(4): 1031-1036. DOI:10.1115/1.3408654 |
| [7] |
REDDY JN. A simple higher-order theory for laminated composite plates[J]. Journal of Applied Mechanics, 1984, 51: 745-752. DOI:10.1115/1.3167719 |
| [8] |
KARAMA M, AFAQ KS, MISTOU S. Mechanical behavior of laminated composite beam by new multi-layered laminated composite structures model with transverse shear stress continuity[J]. International Journal of Solids and Structures, 2003, 40: 1525-1546. DOI:10.1016/S0020-7683(02)00647-9 |
| [9] |
AYDOGDU M. A new shear deformation theory for laminated composite plates[J]. Composite Structures, 2009, 89: 94-101. DOI:10.1016/j.compstruct.2008.07.008 |
| [10] |
刘炳昌, 翟彦春. 复合材料夹芯板材料参数对自由振动的影响[J]. 塑料科技, 2020, 48(6): 39-43. LIU B C, ZHAI Y C. Effect of material parameters of composite sandwich panel on free vibration[J]. Plastics Science and Technology, 2020, 48(6): 39-43. |
| [11] |
DI SCIUVA M. Bending vibration and buckling of simply supported thick multilayered orthotropic plates: an evaluation of a new displacement model[J]. Jouranl of Sound Vibration, 1986, 105: 425-442. DOI:10.1016/0022-460X(86)90169-0 |
| [12] |
李飘. Z向增强复合材料夹芯板的力学与声学特性研究[D]. 武汉: 华中科技大学, 2013. LI P. Research on mechanical and acoustic properties of z-reinforced composite sandwich Panels[D]. WuHan: Huazhong University of Science and Technology, 2013. |
| [13] |
XU H, DU J, LI W L. Vibrations of rectangular plates reinforced by any number of beams of arbitrary lengths and placement angles[J]. Jouranl of Sound Vibration, 2010, 329(18): 3759-3779. DOI:10.1016/j.jsv.2010.03.023 |
| [14] |
Shao-qing WANG, Jian-min SU, Li LUO, et al. Free vibration of embedded co-cured damping composite cruciform stiffened plates[J]. Machine Tool & Hydraulics, 2019, 47(24): 47-51. |
| [15] |
K. BHASKAR, Anup Pydah. An elasticity approach for simply-supported isotropic and orthotropic stiffened plates[J]. International Journal of Mechanical Sciences, 2014, 89. |
| [16] |
杨智雄. 夹芯复合材料结构振声特性分析及优化设计[D]. 武汉: 华中科技大学, 2019. YANG Z X. Vibro-Acoustic analysis and optimum design of composite structures with viscoelastic core. [D]. WuHan: Huazhong University of Science and Technology, 2019. |
| [17] |
路庆贺, 梁森, 周运发, 等. 阻尼夹芯复合材料加筋板的振动分析与数值模拟[J]. 振动与冲击, 2020, 39(05): 250-261. LU Q H, LIANG S, ZHOU Y F, et al. Vibration characteristics analysis and numerical simulation for stiffened plates with damping core composite[J]. Jouranl of Vibration and Shock, 2020, 39(05): 250-261. |
| [18] |
王震鸣, 刘国玺, 吕明身. 各向异性多层扁壳的大挠度方程[J]. 应用数学和力学, 1982, 3(1): 49-65. WANG Z M, LIU G X, LU M S. The finite deflection equations of anisotropic laminated shallow shells[J]. Applied Mathmatics Mechanics–English, 1982, 3(1): 49-65. DOI:10.1007/BF01897387 |
| [19] |
LAULAGNET B. Sound radiation by a simply supported unbaffled plate[J]. Journal of Acoust Society of America, 1998, 103(5): 2451-2462. DOI:10.1121/1.422765 |
 2022, Vol. 44
2022, Vol. 44
