弹药储供系统是大口径舰炮火力输出的重要决定部分,在中心伺服扬弹、推送对中及箱式补给等新技术应用下大口径舰炮的发射可靠性水平得到了一定的改善[1]。同时,战备完好性及任务成功性相比传统方案有了极大的提升[2-3]。本文从工程实际需求出发研究弹药储供系统如何进行高效的可靠性分配。将故障树(FTA)与模糊数学综合建立模型,同时从任务可靠度角度进行分析在新技术应用下对弹药储供系统的可靠性分配影响。
新技术应用下的弹药储供系统设计方案如图1所示。
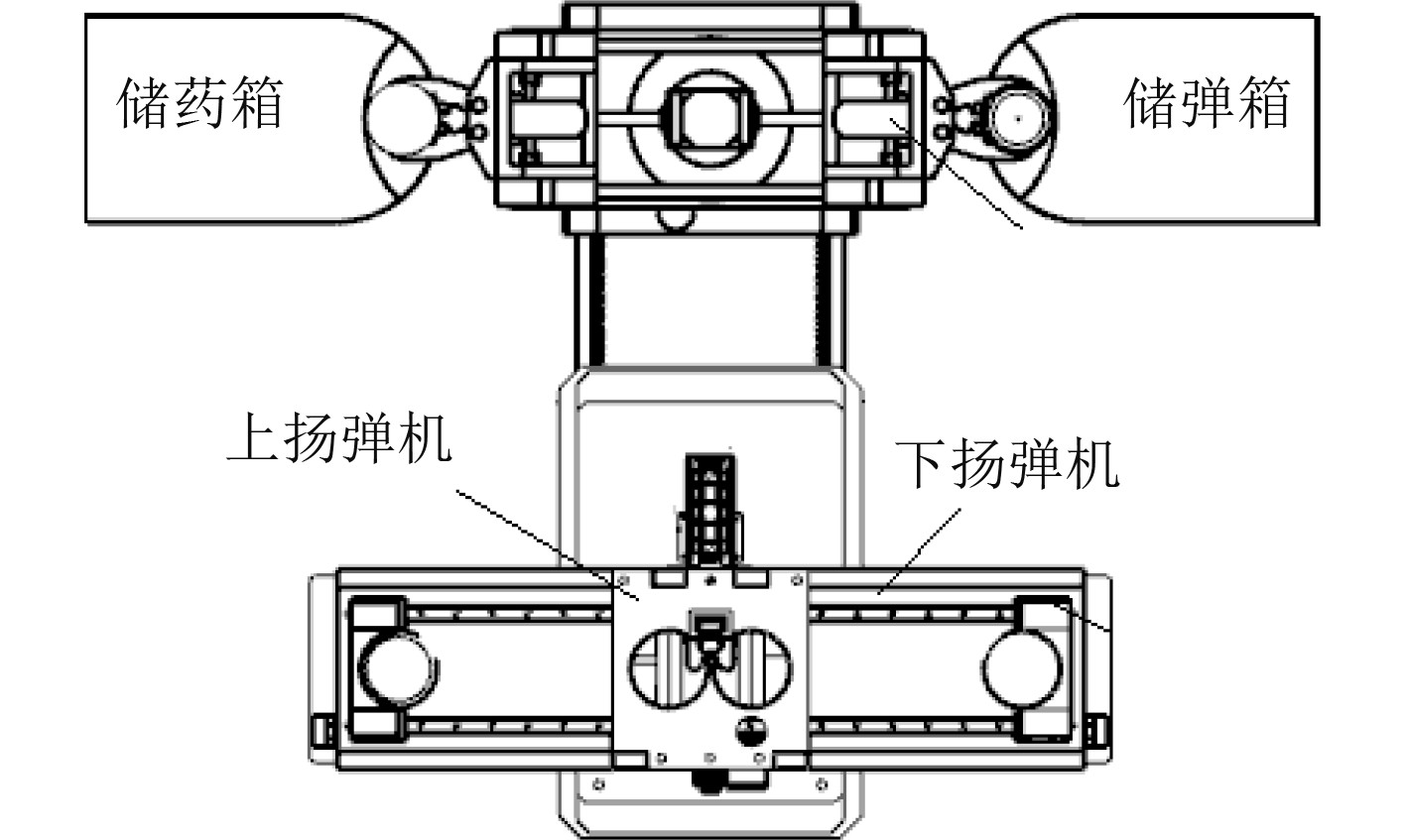
|
图 1 弹药储供系统设计方案 Fig. 1 Scheme of ammunition storage and supply system |
进行FTA过程也是一个更深入认识系统的过程,可以提高固有可靠性、安全性及为后期故障归零提供依据。以舰炮弹药储供系统的FTA是在维修记录和相似系统经验的前提下分析,将“非正常扬弹”作为故障顶事件进行分析。分别以储供系统约定层次的直接故障事件为中间事件分析,运用演绎法分析得到最基本的原因[4-5]。同时结合储供系统FMECA整理可得,构建的故障树由图2给出,主要底事件故障如表1所示。
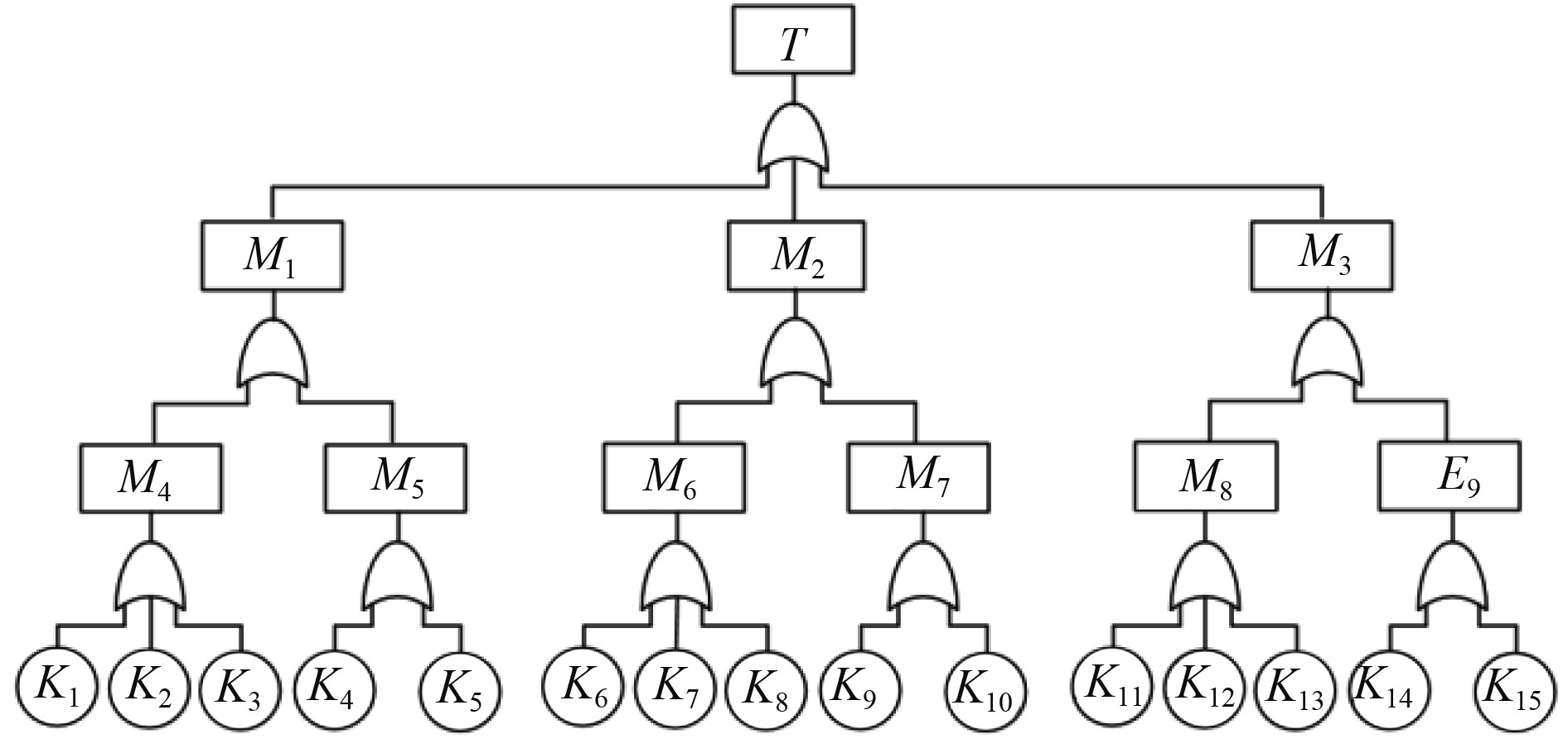
|
图 2 弹药储供系统“非正常扬弹”故障树 Fig. 2 "Abnormal raising ammunition" fault tree of ammunition storage and supply system |
|
|
表 1 弹药储供系统的相关故障模式 Tab.1 Failure modes of ammunition storage and supply system |
从工程实际需求出发,基于FTA模型及模糊数学同时结合各部件故障模式进行可靠性分配探索性研究[6]。基本技术路线为对顶事件不发生所规定的平均故障间隔发数采取概率重要度的方法进行分配,进而对中间事件分别采取再分配法及AHP法进行。
2.1 综合模糊数学与评判法分析过程1)将模糊语言转化为模糊数
将专家定性经验利用模糊数学理论有效转化为可以定量计算的模糊数参与可靠性分配决策。结合工程经验对模糊集的隶属函数进行指派,决定采用适配性较高的梯形和三角分布,如式(1)[7],根据工程中对“现代”级驱逐舰舰载双管130 mm大口径舰炮维修保障跟踪数据生成了相关参数值。
| $ \begin{split}&\underset{˜}{A}(x)=\left\{\begin{array}{*{20}{c}}0,&x < a,\\ \dfrac{x-a}{b-a},&a\leqslant x < b,\\ 1,&b\leqslant x < c,\\ \dfrac{d-x}{d-c},&c\leqslant x < d,\\ 0,&x\geqslant d,\end{array}\right.\\ &\underset{˜}{A}(x)=\left\{\begin{array}{*{20}{c}}0,&x < a,\\ \dfrac{x-a}{b-a},&a\leqslant x < b,\\ \dfrac{c-x}{c-b},&b\leqslant x < c,\\ 0,&x\geqslant c。\end{array}\right.\end{split} $ | (1) |
2)求出模糊数区间及专家权重
利用
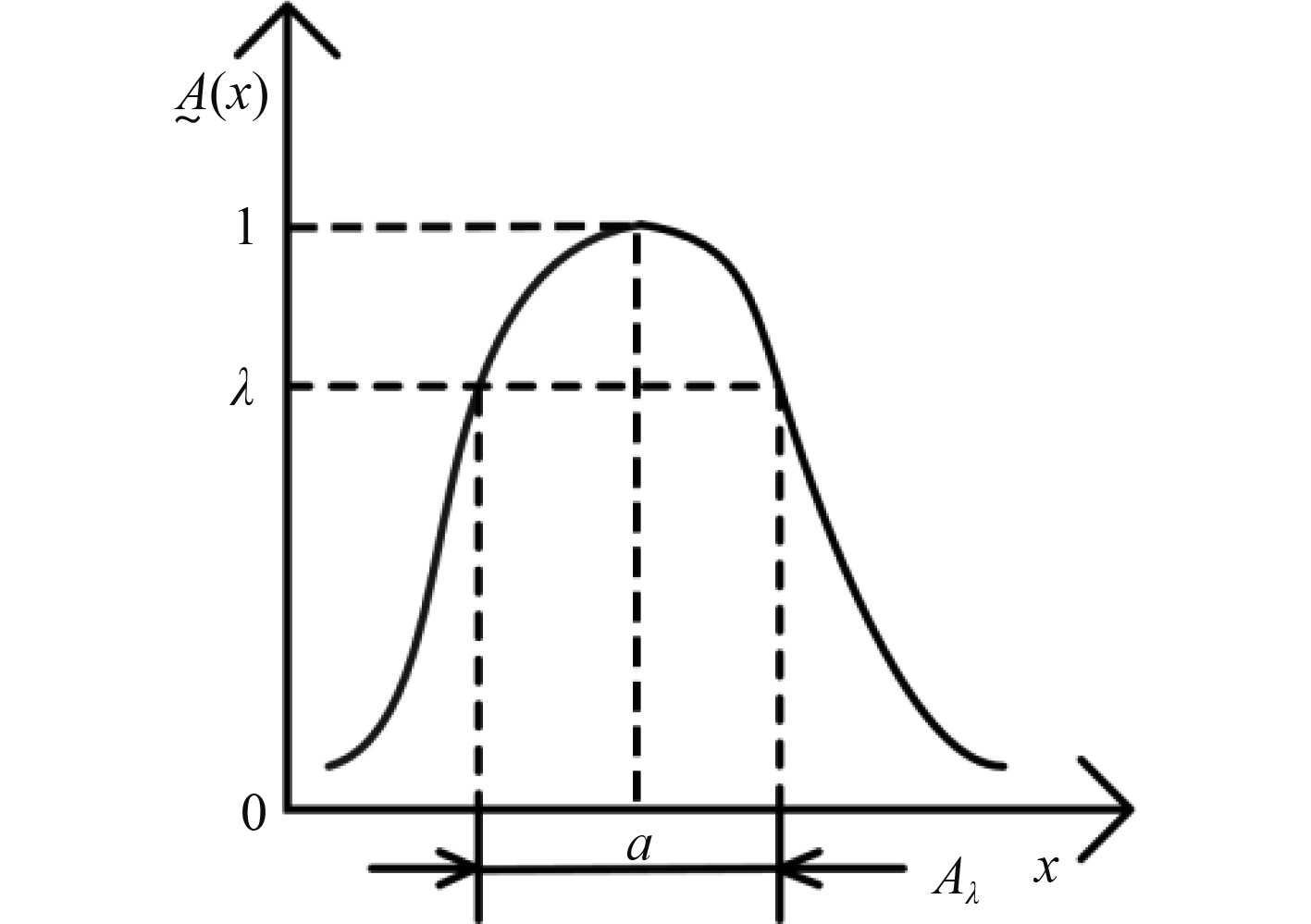
|
图 3
置信水平为
|
结合专家权重给出置信水平
| $ \underset{˜}{A} (x) = \sum\limits_{n = 1}^k {{w_n}\underset{˜}{A}_i}(x) 。$ | (2) |
其中:
3)求取模糊可能性值
实际工程中通常采用左右模糊排序法给出模糊可能性值(FPS),主要计算过程如下式:
| $\begin{split} &{f}_{\mathrm{min}}(x)=\left\{\begin{array}{*{20}{c}}1-x,&0 < x < 1,\\ 0,& {\rm{others}}。\end{array}\right.\\ &{f}_{\mathrm{max}}(x)=\left\{\begin{array}{*{20}{c}}x,&0 < x < 1\\ 0,&{\rm{others}}。\end{array}\right.\end{split} $ | (3) |
| $ \begin{split}&FP{S}_{左}(W)=\underset{x}{\mathrm{sup}}\left[\underset{˜}{A}(x)^{f}_{\mathrm{min}}(x)\right],\\ &FP{S}_{右}(W)=\underset{x}{\mathrm{sup}}\left[\underset{˜}{A}(x)^{f}_{\mathrm{max}}(x)\right],\\ &FPS(W)=\frac{FP{S}_{左}(W)-FP{S}_{右}(W)+1}{2}。\end{split} $ | (4) |
4)求出模糊平均故障间隔发数(FMRBF)
平均故障间隔发数可以直观反映舰炮试验考核的综合可靠性指标,其可以基于模糊可能性值(FPS)转化求得,具体计算过程如下式:
| $\begin{split} &FMRBF=\bigg\{\begin{array}{l} {10}^{C},(FPS\ne 0),\\ 0,(FPS=0)。\end{array}\\ &C=2.301\times \sqrt[3]{\frac{1-FPS}{FPS}} 。\bigg.\end{split} $ | (5) |
各专家采用规定模糊语言极小(Ⅰ级)、很小(Ⅱ级)、偶然(Ⅲ级)、有时(Ⅳ级)、经常(Ⅴ级)5个层级对故障树底事件发生概率进行评判。其中,具体隶属函数
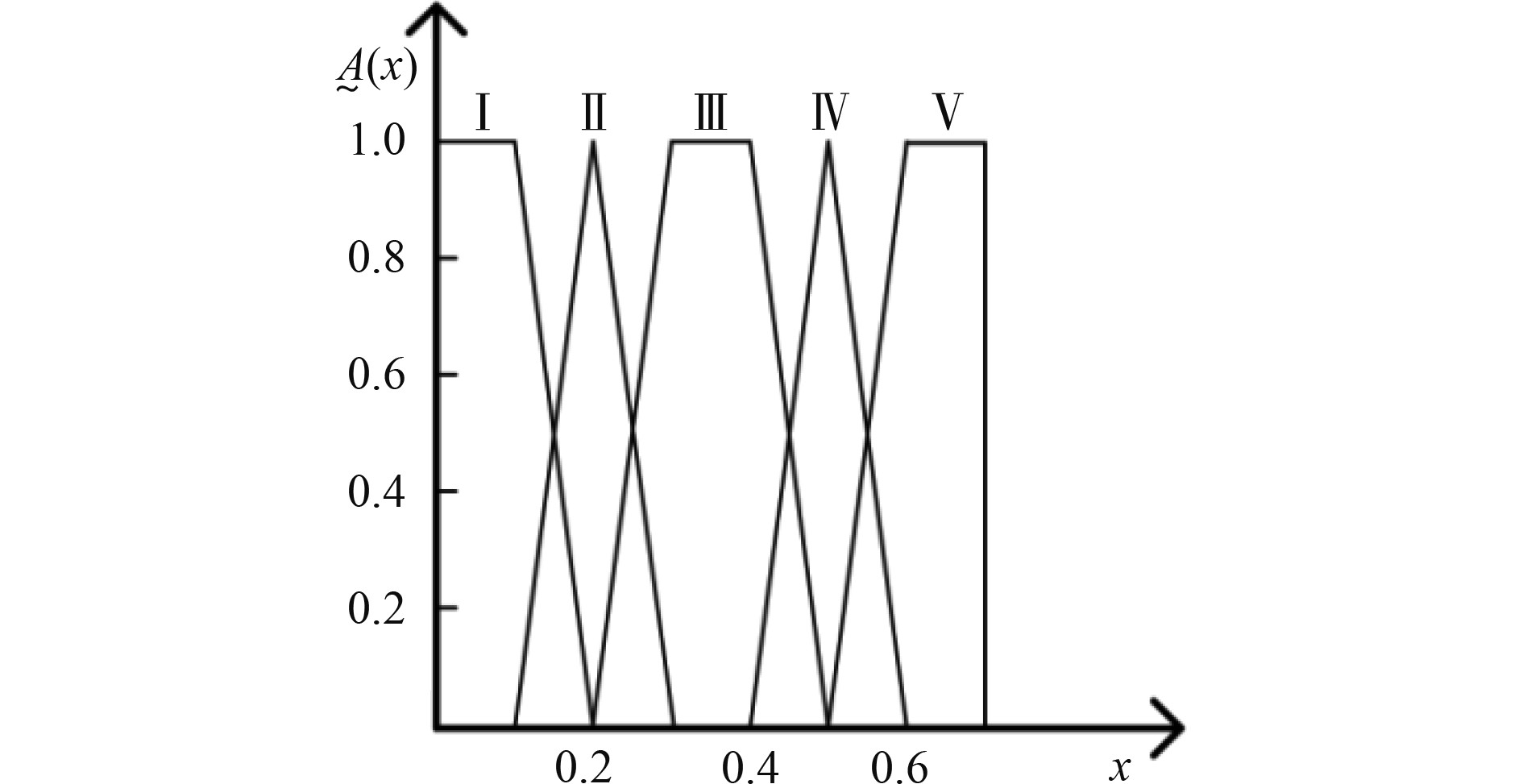
|
图 4
隶属函数
|
专家权重主要依据行业相关度、职称、工龄、学历因素采用AHP得出相应的权重,根据5名舰炮领域设计及保障经验丰富的专家对故障树底事件发生概率进行模糊评判。权重计算结果如下:
| $ \begin{gathered} {w_k} = ({w_1},{w_2},{w_3},{w_4},{w_5}) = (0.2232, \hfill \\ {\text{ }}0.2232,0.1964,0.1964,0.1607) 。\hfill \\ \end{gathered} $ |
根据指派的模糊语言隶属函数及专家对底事件的评判结果,可以通过图4的隶属函数和式(5)计算所有底事件的模糊平均故障间隔发数,具体如表2所示。
|
|
表 2 非正常扬弹故障树底事件模糊平均故障间隔发数 Tab.2 Fuzzy mean interval between failures of abnormal events at the bottom of the fault tree |
大口径舰炮在射击任务剖面中的上扬弹机、下扬弹机及转运机器人为全串联系统[8]。同时“非正常扬弹”故障树均为逻辑或运算,因此顶事件不发生的概率可由其所有底事件发生概率通过式(6)求得。
| $ \overline{{q}_{顶}}=1-{\displaystyle \prod _{i={E}_{1}}^{{E}_{3}}(1-{q}_{i})}\text=1-{\displaystyle \prod _{i={X}_{1}}^{{X}_{15}}(1-{q}_{i})}。$ | (6) |
大口径舰炮非正常扬弹故障的发生概率
|
|
表 3 各底事件对顶事件的概率重要度
|
| $ {I_g}(i) = \frac{{\partial g}}{{\partial {q_i}}} = \prod\limits_{j = 1,j \ne i}^k {(1 - {q_j})} 。$ | (7) |
基于重要度的分配具体分析计算过程如下:其中,事件
|
|
表 4 顶事件分配结果 Tab.4 Top event distribution results |
| $ {Q_x} = 1 - \prod\limits_{i = 1}^n {\left[ {1 - ({q_i} + \Delta {q_i})} \right]} 。$ | (8) |
可以得出上扬弹机的1/FMRBF值较高,可能会造成后期改进优化难度加大[9]。其指导意义为:在进行分配过程中上扬弹机需分配较低的可靠性指标。同时,经过与实际工程比较,在新技术应用下上文中各组成的FMRBF值分配较为科学。
顶事件分配完成后需对中间事件进行分配,采用再分配法对装填装置为实施例且满足式(9)进行分析计算,具体计算过程如表5所示。
|
|
表 5 中间事件分配结果 Tab.5 Intermediate event distribution results |
| $ {q_i} + \Delta {q_i} \leqslant 1 - {(1 - {q_0})^n} \times \prod\limits_{i = n + 1}^k {(1 - {q_i})} 。$ | (9) |
其中:
以M1重新分配后的
由于
当
| $ {q_0} = 1.3578 \times {10^{ - 4}} < {q_{{M_5}}} \text{;} $ |
当
| $ {q_0} = 1.4013 \times {10^{ - 4}} < {q_{{M_4}}} 。$ |
因此,需对上扬弹机M1下的2个二级事件同时调整。即将M4和M5事件
可以得出需要调整的中间事件为M4,M5,M6和M8。将以上调整后的中间事件所涉及的底事件基于AHP二次分配。底事件的分配准则层依据主要为维修可达性、重要度以及改进难度3个方面,通过构造相应的判断(成对比较)阵以及一致性检验。以中间事件M4为例,准则层对目标层的成对比较阵为:
| $ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 1&3&4 \\ {1/3}&1&3 \\ {1/4}&{1/3}&1 \end{array}} \right] 。$ |
通过计算可得其最大特征值为3.0735,准则层对目标层权重比为0.6144∶0.2684:0.1172,判断(成对比较)阵一致性比例CR=0.07067<0.1,其一致性检验通过。给出方案层对准则层的权重比以及一致性检验,底事件K1,K2,K3的权重比计算结果为:
| $ {h_{{\text{ }}11}}:{h_{{\text{ }}12}}:{h_{{\text{ }}13}} = 0.4472:0.2922:0.2606 。$ |
根据以上权重分析结果结合式(10)可以得出底事件K1,K2,K3重新分配后的1/FMRBF值为
| $ {q_{{X_i}}} + \Delta {q_{{X_i}}} = \left( {{q_8} + \Delta {q_8}} \right) \cdot \frac{{{h_i}^{ - 1}}}{{\displaystyle\sum\limits_{i = 11}^{13} {{h_i}^{ - 1}} }} 。$ | (10) |
继而对中间事件M4,M5,M6,M8涉及底事件进行FMRBF值重新分配,分配结果如表6所示。
|
|
表 6 底事件重新分配结果 Tab.6 Bottom event redistribution results |
从图5的计算结果可以得出,大口径舰炮“非正常扬弹”故障原因中链条或齿轮箱故障(K5)、活门组件失效(K6)以及回转模块故障(K11)等事件在后续可靠性设计迭代优化过程中应着重考虑其可靠性指标不能太高,以及其技术难度和费效比较大的问题。这与实际工程中的情况相同,即大负载导致的链条和齿轮箱故障和转运机器人工作状态下惯量大的问题,需对其结构刚强度进行优化。
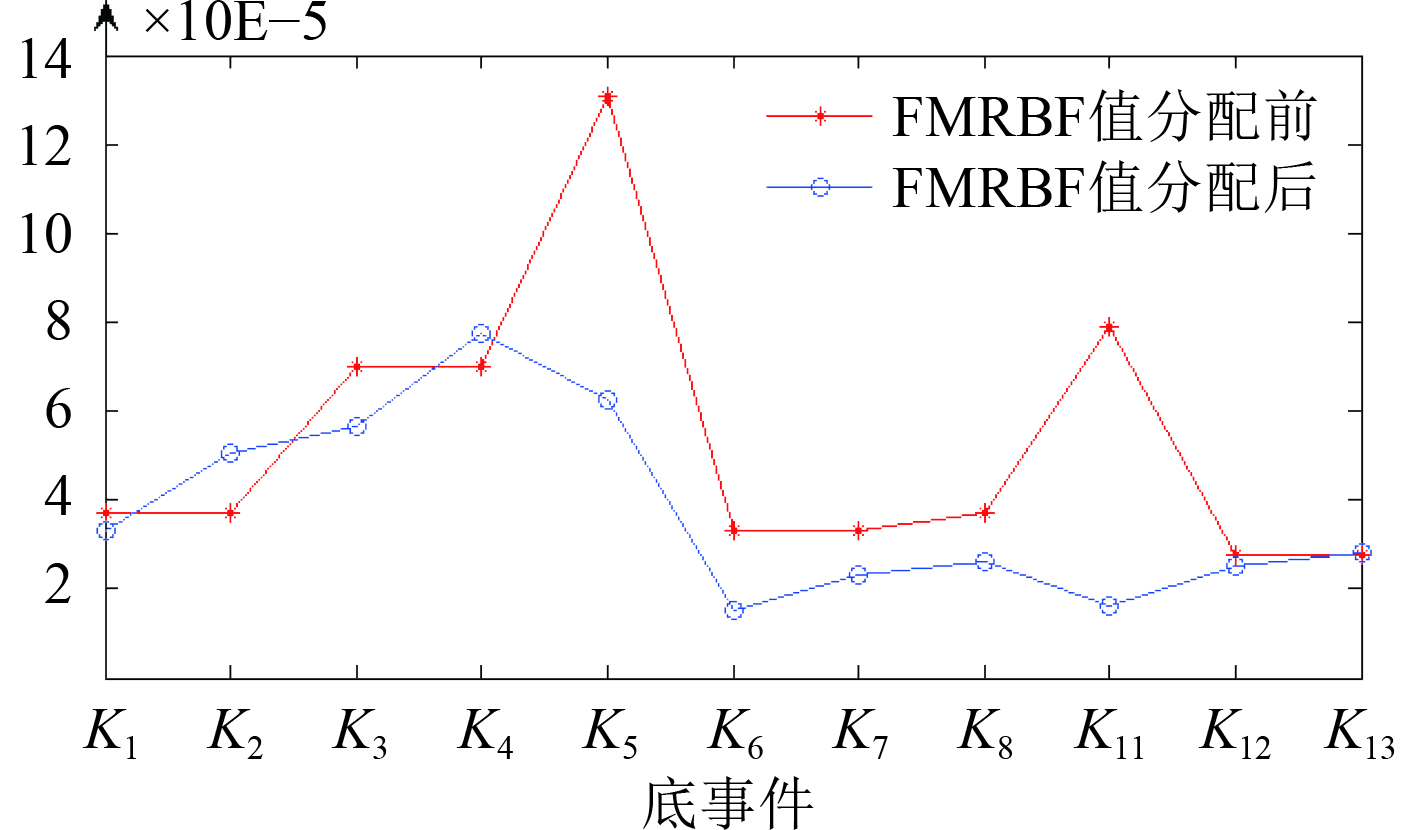
|
图 5 底事件分配前后FMRBF值变化过程 Fig. 5 FMRBF value change process before and after the bottom event allocation |
本文分析了在中心伺服扬弹、推送对中及箱式补给等新技术应用下的定量分析过程,构建了大口径舰炮在新技术融入过程中涉及的特有底事件故障模式。通过构建故障树(FTA)定性分析给出15种导致非正常扬弹的故障原因,采取模糊数学与专家评判相结合的方法对其进行基于事件的可靠性分配。最后,通过分析计算得出在后续设计迭代优化中需要注意的底事件,为后续单体改进及费效比提供依据。
| [1] |
石晨光. 舰炮武器原理[M]. 北京: 国防工业出版社, 2014.
|
| [2] |
姚忠, 张满慧. 高新技术驱动下大口径舰炮的发射可靠性改进研究[C]//2019火炮发展学术研讨会, 2019. YAO Zhong, ZHANG Man-hui. Research on the improvement of launch reliability of large-caliber naval guns driven by high-tech [C]//2019 Artillery Development Symposium, 2019. |
| [3] |
邢昌风, 李敏勇, 吴玲. 舰载武器系统效能分析[M]. 北京: 国防工业出版社, 2008.
|
| [4] |
柏广强, 吴茂林, 王华, 等. 舰载大口径弹药扬弹机的液压系统设计与仿真[J]. 机床与液压, 2018, 46(14 ) : 72−75. BAI Guang-qiang, WU Mao-lin, WANG Hua, et al. Hydraulic system design and simulation of ship-borne large-caliber ammunition lifter[J]. Machine Tool and Hydraulics, 2018, 46(14): 72−75. |
| [5] |
康锐, 石荣德, 等 型号可靠性维修性保障性技术规范[M]. 北京: 国防工业出版社, 2010.
|
| [6] |
谢群亚. 基于故障树的数控伺服刀架可靠性分配方法研究[D]. 南京: 南京理工大学, 2017.
|
| [7] |
谢季坚, 刘承平. 模糊数学方法及其应用[M]. 武汉: 华中科技大学出版社, 2006.
|
| [8] |
郑刚, 邵中年, 罗战宁. 某舰炮扬弹系统过载问题研究[J]. 火炮发射与控制学报, 2014, 35(3): 89-92. ZHENG Gang, SHAO Zhong-nian, LUO Zhan-ning. Research on the overload problem of a naval gun raising system[J]. Journal of Artillery Launching and Control, 2014, 35(3): 89-92. |
| [9] |
张云杰, 贾兰俊, 李洪果, 等. 大口径舰炮制导炮弹装填方式[J]. 舰船科学技术, 2015(5): 245-249. ZHANG Yun-jie, JIA Lan-jun, LI Hong-guo, et al. Loading method of guided projectiles for large-caliber naval guns[J]. Ship Science and Technology, 2015(5): 245-249. |
 2022, Vol. 44
2022, Vol. 44
