燃烧轻气炮是使用低分子量的可燃气体作为发射药,通过燃烧后产生的高温高压气体膨胀做功,推动弹丸运动的一种新概念发射系统[1]。传统火炮采用固体发射药,火药气体分子量较大,滞止声速较小,弹丸获得的最大速度受到限制。燃烧轻气炮一般选用氢氧混合气体作为可燃气体,氦气作为稀释气体,低分子量气体具有更高的逃逸速度,可以获得更高的弹丸速度,研究表明相比传统火炮,燃烧轻气炮的炮口动能可提高30%[2]。
燃烧轻气炮已有数十年的研究历史,美国GT公司和通用动力公司[3]最先进行16 mm口径燃烧轻气炮的研究,使用氢氧氦混合气体发射弹丸,初速可达4200 m/s。UTRON公司[4]先后对45 mm和155 mm口径的燃烧轻气炮进行了研究,建立了单步反应和8步反应简化模型,并进行了45 mm燃烧轻气炮射击试验,计算模型与试验结果误差为5.8%。目前国内已开展相关研究工作,邓飞等[5]采用数值方法建立了燃烧轻气炮氢氧燃烧单区模型,研究表明初始装填条件对内弹道性能有着显著影响。黄韬等[6]采用计算流体力学方法对燃烧轻气炮内弹道气体流场进行数值模拟分析,研究了点火具结构对内弹道性能的影响。Zhou等[7]完成了燃烧轻气炮的一维模拟仿真,研究了燃烧轻气炮的膛内爆轰现象对初速的影响,提出合理的点火方案和稀释气体能够避免爆轰现象。孙从煌等[8]开展氢氧燃烧数值模拟,研究了点火条件对密闭管道中预混氢气/空气燃爆特性的影响,结果表明点火位置、点火温度和点火面积等因素能够影响密闭管道中预混气体燃爆过程的温升速率、火焰面传播速度和气体动能等。
燃烧轻气炮的发射过程比较复杂,涉及膛内气体的高压密闭燃烧和流体运动。本文通过流体动力学软件,结合氢氧19步反应详细机理,将化学动力学机理与湍流流动基础模型相结合,建立了燃烧轻气炮发射过程的二维轴对称模型,在不同的初始条件下,模拟氢氧燃烧过程,研究氢氧燃烧特性,进而分析初始温度、初始压力和燃烧室容积对内弹道特性的影响。
1 模型描述 1.1 计算模型与网格设置利用ICEM CFD进行计算域模型的网格划分,燃烧室容积V=5 L,身管长L=4.5 m,口径D=45 mm,弹丸质量m=0.52 kg。计算采取二维轴对称结构化网格,为提高计算精度,对燃烧室内网格进行局部加密,网格数量20万。发射过程中采用动网格模拟弹丸前进,动网格更新方式采用Layering法。

|
图 1 燃烧轻气炮基本结构简化模型 Fig. 1 The simplified structure model of combustion light gas gun |
采用二维可压缩流动的Navier-Stokes方程[10],其流动及燃烧基本控制方程包含质量守恒、动量守恒、能量守恒方程和反应组分扩散方程,基本公式如下:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial \mathop \chi \nolimits_j }}\left( {\mathop {\rho \upsilon }\nolimits_j } \right) = 0, $ | (1) |
| $ \frac{\partial }{{\partial t}}\left( {\rho \mathop \upsilon \nolimits_i } \right) + \frac{\partial }{{\partial \mathop \chi \nolimits_j }}\left( {\rho \mathop \upsilon \nolimits_i \mathop \upsilon \nolimits_j + \frac{2}{3}\mathop \delta \nolimits_{ij} \rho k} \right) = - \frac{{\partial p}}{{\partial \mathop \chi \nolimits_i }} + \frac{{\partial \mathop \tau \nolimits_{ij} }}{{\partial \mathop \chi \nolimits_j }}, $ | (2) |
| $ \frac{\partial }{{\partial t}}\left( {\rho E} \right) + \frac{\partial }{{\partial \mathop \chi \nolimits_j }}\left( {\rho \mathop \upsilon \nolimits_j H} \right) = \frac{\partial }{{\partial \mathop \chi \nolimits_j }}\left( {\rho \mathop a\nolimits_{eff} \frac{{\partial H}}{{\partial \mathop \chi \nolimits_j }} + \mathop \tau \nolimits_{ij} \mathop \upsilon \nolimits_i } \right) ,$ | (3) |
| $ \frac{\partial }{{\partial t}}\left( {\rho \mathop Y\nolimits_k } \right) + \frac{\partial }{{\partial \mathop \chi \nolimits_j }}\left( {\rho \mathop Y\nolimits_k \mathop u\nolimits_j } \right) = \frac{\partial }{{\partial \mathop x\nolimits_j }}\left( {\rho \mathop D\nolimits_{eff} \frac{{\partial \mathop Y\nolimits_k }}{{\partial \mathop \chi \nolimits_j }}} \right) + \mathop {\dot \omega }\nolimits_{_k}。$ | (4) |
式中:ρ为密度;t为时间;υ为速度矢量,i,j,k为方向分量;р为静压,E和H分别为总能量和焓;τij为粘性应力张量;Yk为组分的质量浓度;ωk为组分生成速率;αeff为有效导热系数;Deff为有效扩散系数。
1.3 湍流模型燃烧室内气体流动的湍流计算模型采用标准κ-ε双方程模型,标准κ-ε模型对湍流粘度和长度比的计算通过2个独立的输运方程求解得到:
| $ \begin{split} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k\mathop u\nolimits_i } \right)}}{{\partial \mathop \chi \nolimits_i }} = &\frac{\partial }{{\partial \mathop \chi \nolimits_j }}\left[ {\left( {\mu + \frac{{\mathop \mu \nolimits_t }}{{\mathop \sigma \nolimits_k }}} \right)\frac{{\partial k}}{{\partial \mathop \chi \nolimits_j }}} \right] +\\ & \mathop G\nolimits_k + \mathop G\nolimits_b - \rho \varepsilon - \mathop Y\nolimits_M + \mathop S\nolimits_k , \end{split}$ | (5) |
| $ \begin{split} \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} +& \frac{{\partial \left( {\rho \varepsilon \mathop u\nolimits_i } \right)}}{{\partial \mathop \chi \nolimits_i }} = \frac{\partial }{{\mathop {\partial \chi }\nolimits_j }}\left[ {\left( {\mu + \frac{{\mathop \mu \nolimits_t }}{{\mathop \sigma \nolimits_\varepsilon }}} \right)\frac{{\partial \varepsilon }}{{\partial \mathop \chi \nolimits_j }}} \right] + \\ & \mathop C\nolimits_{1\varepsilon } \frac{\varepsilon }{k}\left( {\mathop G\nolimits_k +\mathop C\nolimits_{3\varepsilon } \mathop G\nolimits_b } \right) - \mathop C\nolimits_{2\varepsilon } \rho \frac{{\mathop \varepsilon \nolimits^2 }}{k} + \mathop S\nolimits_\varepsilon。\end{split} $ | (6) |
式中:C1ε,C2ε和Cμ是经验常数,取C1ε=1.44,C2ε=1.92,Cμ=0.09;σk和σε是湍动能k和耗散率ε对应的Prandtl数,分别为σk=1.0,σε=1.3。
1.4 燃烧模型氢氧燃烧反应是复杂的链分支化学反应过程,为更好地了解各个基元反应和反应组分对发射过程的影响,考虑化学动力学对燃烧化学反应速率的影响。本文燃烧反应流模型采用有限速率模型,其使用Arrhenius公式计算化学源项:
| $ w = \mathop k\nolimits_0 \mathop T\nolimits^b \mathop e\nolimits^{ - E/RT} \left[ A \right]\left[ B \right]。$ | (7) |
式中:k0为指前因子;b为温度指数;E为活化能;R为气体常数;[A]和[B]分别为反应物A和B的浓度。反应机理选取文献[8]中的氢氧9种组分19步基元反应的化学动力学机理。采用化学反应动力库ChemKin程序,将氢氧19步反应Chemkin Mechanism文件及热力学数据导入计算流体动力学软件进行计算。
|
|
表 1 H2/O2 燃烧机理 Tab.1 The combustion mechanism of H2/O2 |
为验证本文中建立模型的准确性,以文献[3]进行的45 mm燃烧轻气炮试验射击结果为例,各参数选用试验中的相应数据,建立燃烧轻气炮仿真计算模型
表2为计算结果与试验结果的对比表。计算所得结果与试验数据一致性较好,说明本文建立的仿真模型合理可行。类似地,通过改变初始参数,依次分析初始温度、初始压力和燃烧室容积对燃烧轻气炮内弹道性能的影响。
|
|
表 2 45 mm燃烧轻气炮试验与计算结果对比 Tab.2 The comparison of test and calculation results of 45 mm combustion light gas gun |
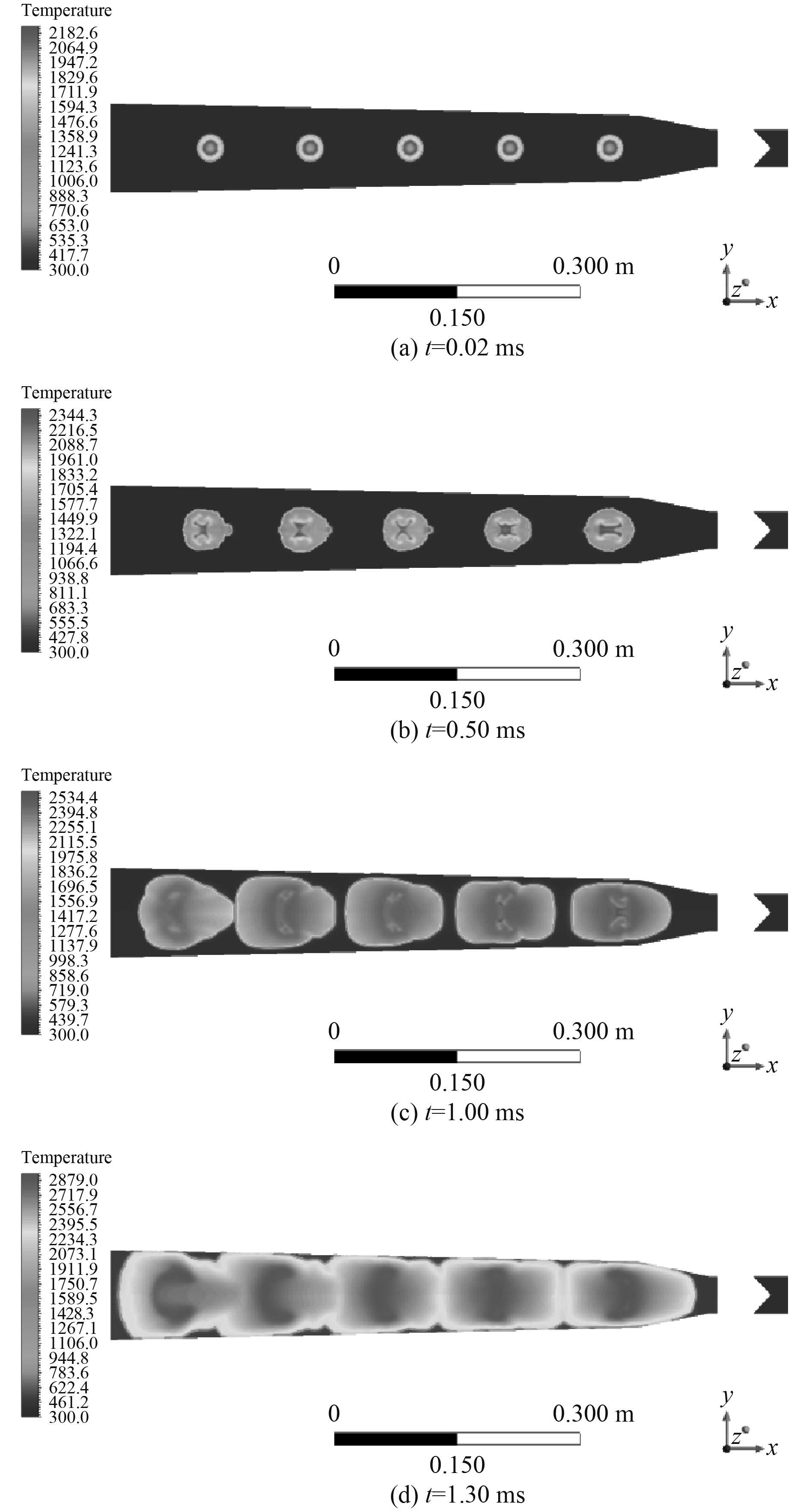
点火后,燃烧室内气体先经历高压密闭燃烧过程,随后推动弹丸运动做功。图2为点火后的初始阶段,氢氧燃烧过程的火焰传播变化情况。点火后火核向外扩展,可以将相应截面分为已反应区、燃烧区和未反应区,初始时刻由不同位置点火区域产生的火焰锋面随时间不断向外推移,边燃烧边膨胀,已燃区体积逐渐扩大并相互作用,当2个火焰锋面相碰时,已燃区会相互融合。图2(a)中,在点火初始时刻的极短时间内,燃烧火焰保持光滑的球形,火核以层流燃烧的速度发展,随后受压力波的壁面反射和湍流机制影响,燃烧火焰传播过程中所受到的约束效应不同,燃烧火焰的前锋面呈现出剧烈的凹凸与褶皱,表现为湍流火焰特征,如图2(b)和图2(c),火焰沿轴向发展的趋势更强,燃烧区呈现出近似椭圆的不规则体形状。随着燃烧区的增大,膨胀火焰的应变作用及其对未反应区气体的压缩作用逐渐明显,湍流火核的发展逐渐加速,使得火焰传播速度加快。
|
图 2 初始阶段温度变化云图 Fig. 2 The cloud image of temperature in initial stage |
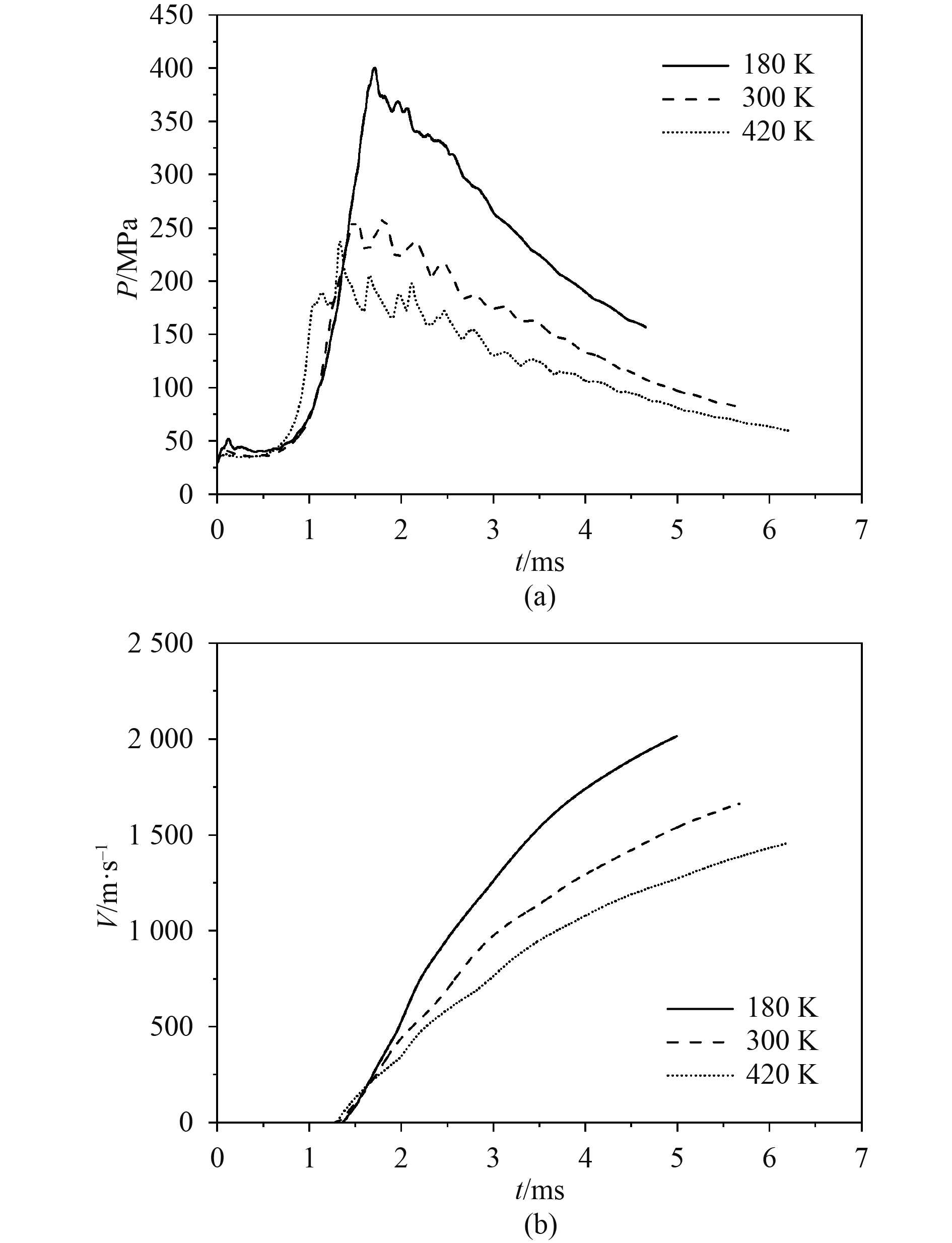
为了研究初始温度对燃烧轻气炮发射过程的影响,采用3种不同的初始温度进行仿真计算,且燃烧室内的初始压力等其余条件保持不变。图3(a)给出了不同初始温度下的膛内最大压力曲线,可以看出,随着初始温度的降低,最大燃烧压力值明显增加,燃烧室内的压力波震荡减小,压力升高速率减小,压力升高到最大值的时刻也会延迟。由理想气体状态方程PV=nRT可知,燃烧室内气体的体积和压力一定时,温度降低使充入燃烧室内的混合气体总量增加,即发射药的质量增加,故而引起燃烧反应峰值压力的增大。同时,温度又影响着氢氧燃烧反应速率,当初始温度降低时,氢氧燃烧速率减小,燃烧持续时间增加,达到最大压力所需时间有所延长,因此燃烧稳定性增加,膛内压力波动减小。从图3(b)可以看出,降低初始温度可明显提高弹丸初速,当温度降低至180 K时,弹丸速度增加至2015.6 m/s。当燃烧室内混合气体初始温度分别为180 K,300 K和420 K时,发射药总能量分别为6.37 MJ,3.82 MJ和2.73 MJ。温度降低时,燃烧生成气体的压力峰值增加,对弹丸的做功增加,弹丸获得更高的加速度,造成弹丸炮口初速增大。
|
图 3 不同初始温度对膛压和弹丸速度的影响 Fig. 3 The influence of different initial temperatures on chamber pressure and muzzle velocity |
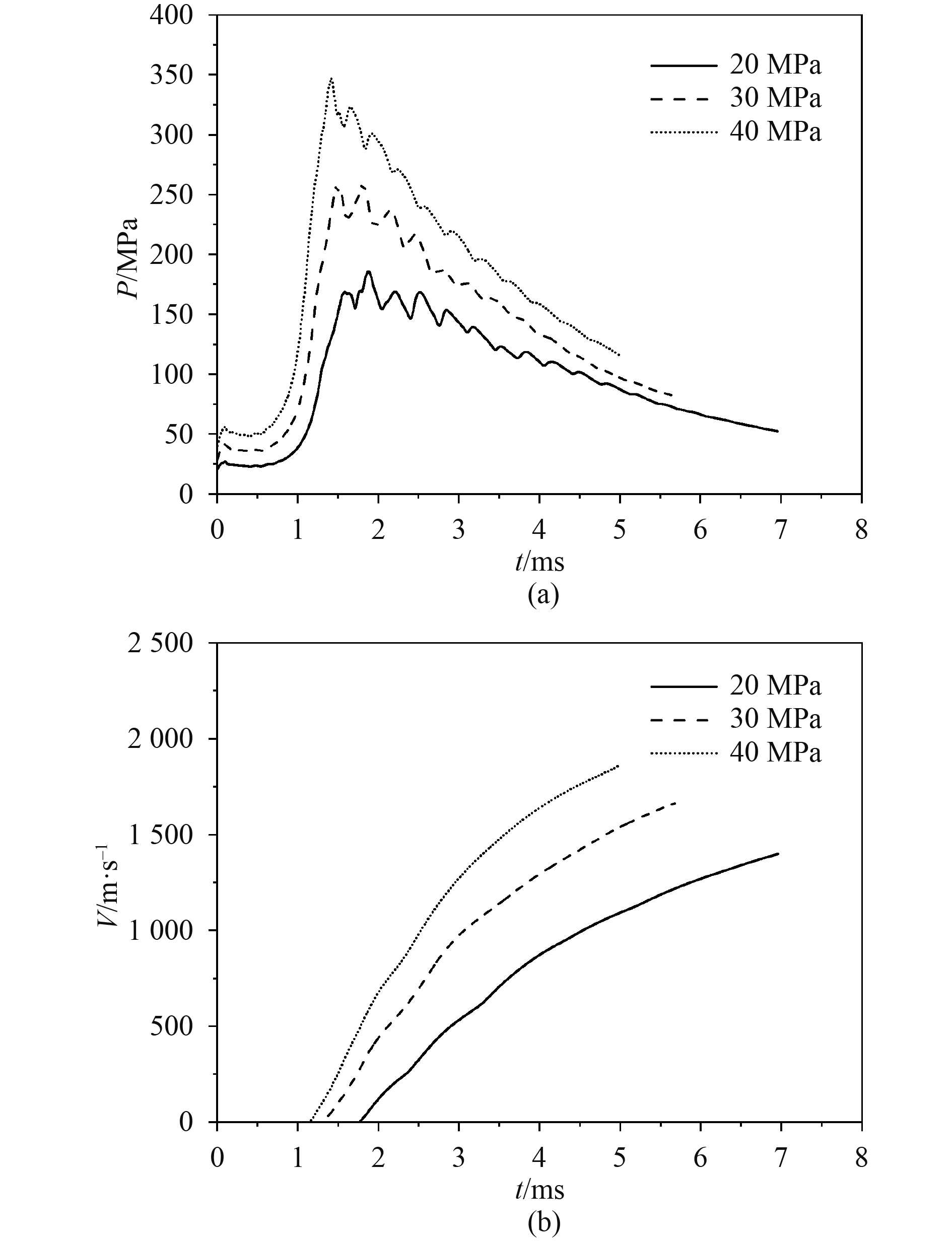
在燃烧室内温度、容积等其他条件不变的情况下,进行不同初始压力对燃烧轻气炮发射过程的影响规律的仿真分析。由图4(a)可以看出,初始压力大者,燃烧压力峰值大。且随着初始压力的增大,压力升高速率增大,到达压力峰值的时刻减小,同时压力下降速度也更快。从图4(b)可看到弹丸速度的变化趋势:弹丸在初始阶段获得很高的加速度,速度迅速增大,随后加速度逐渐减小,速度增长放缓。初始压力的增大对弹丸速度的影响效果显著,3个不同初始压力下的弹丸速度分别为1398.9 m/s,1664.3 m/s,1863.2 m/s。
|
图 4 不同初始压力对膛压和弹丸速度的影响 Fig. 4 The influence of different initial pressures on chamber pressure and muzzle velocity |
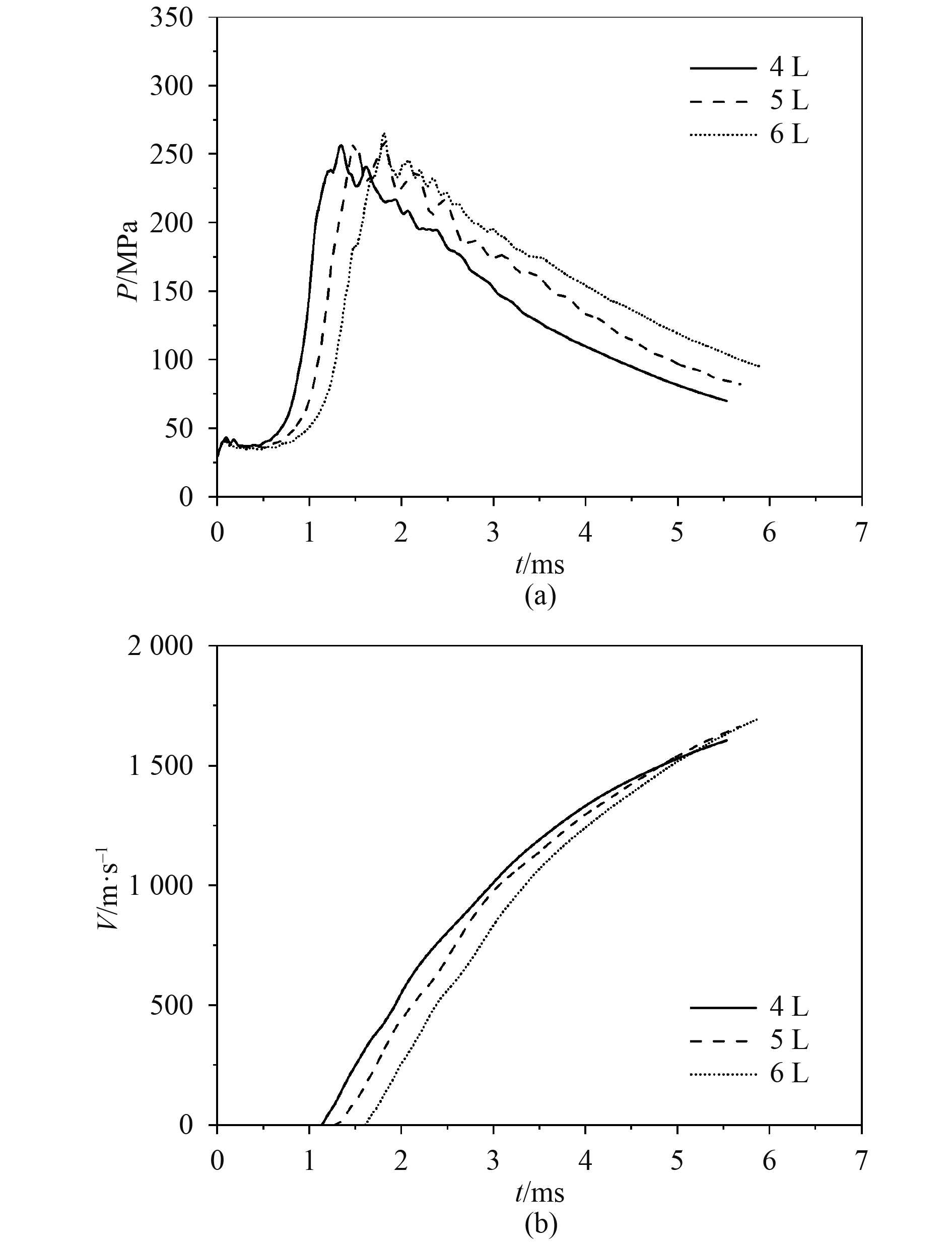
选取3种不同的燃烧室容积(4 L,5 L,6 L)研究燃烧室容积对内弹道性能的影响,同时保持燃烧室内装填气体密度不变,即初始温度和压力等其他条件不变。图5(a)为膛压变化曲线,可以看出,3条曲线表现出相同的趋势:点火后压力逐渐上升,达到最大压力值260 MPa左右后,压力开始下降。扩展燃烧室的容积并没有对压力峰值产生较大影响,仅延长了压力升高到最大值的时刻。从图5(b)可以看出,燃烧室的容积增大时,弹丸加速度衰减减慢,在一定程度上提高弹丸初速。表3为不同燃烧室容积计算结果对比表,3种条件下的效率分别为21.9%,18.8%,16.4%,表明扩展燃烧室的容积增加了装药量,可以在一定程度上提高弹丸初速,但是能量利用率降低,做功能力下降。
|
|
表 3 不同燃烧室容积计算结果对比 Tab.3 The calculation results comparison of different combustion chamber volumes |
|
图 5 不同燃烧室容积对膛压和弹丸速度的影响 Fig. 5 The influence of different chamber volumes on chamber pressure and muzzle velocity |
本文建立45 mm燃烧轻气炮发射过程的仿真计算模型,充分考虑了化学动力学与湍流效应的共同作用,计算结果具有较高的准确度;仿真分析了不同初始温度、初始压力和燃烧室容积对氢氧燃烧和内弹道过程的影响。得到以下结论:
1)膛内氢氧燃烧呈现出湍流火焰特征,随着燃烧火焰的增大,湍流作用加剧,火焰传播速度加快;
2)初始温度对氢氧燃烧过程影响较大,初始温度降低,氢氧发射药总能量增大,膛压增大,压力波动减小,弹丸初速增加;
3)初始压力增大时,发射药总能量增加,膛压增大,弹丸初速增大,实际应用中应该合理地选择发射药气体的初始装填压力,避免膛压过高;
4)保持装填气体密度不变,扩展燃烧室容积可以在一定程度上提高弹丸初速,但是能量利用率降低,做功能力下降。
| [1] |
于子平, 张相炎. 新概念火炮[M]. 北京: 国防工业出版社, 2012.
|
| [2] |
胡静, 张明安, 岳文龙, 等. 内弹道过程中气体工质做功能力计算分析[J]. 火炮发射与控制学报, 2011, (6): 82-85.
|
| [3] |
TIDMAN D A, MASSEY D W, WITHERSPOON F D, et al. Compact light gas gun firings with high pressure gaseous and solid energetic materials - experiments and analysis[C]// 31st JANNAF Combustion Subcommittee Meeting, Sunnyvale, CA, 17-21 Oct, 1994.
|
| [4] |
KRUCZYNSKI D, MASSEY D. Combustion light gas gun technology demonstration[R]. ADA462130, 2007.
|
| [5] |
邓飞, 张相炎. 燃烧轻气炮氢氧燃烧特性详细反应动力学模拟[J]. 兵工学报, 2014, 35(3): 415-420. DENG F, ZHANG X Y. Simulation of hydrogen-oxygen combustion of combustion light gas gun using detailed chemical kinetics model[J]. Acta Armamentarii, 2014, 35(3): 415-420. DOI:10.3969/j.issn.1000-1093.2014.03.019 |
| [6] |
黄滔, 张相炎, 刘宁. 燃烧轻气炮点火对内弹道性能影响的仿真分析[J]. 兵工自动化, 2014, 33(12): 25-28. HUANG T, ZHANG X Y, LING N. Simulation analysis on influence of ignition on internal ballistics of combustion light gas gun[J]. Ordnance Industry Automation, 2014, 33(12): 25-28. DOI:10.7690/bgzdh.2014.01.008 |
| [7] |
ZHOU Fei, LIU Ning, ZHANG Xiangyan, et al. 1D study of the detonation phenomenon and its influence on the interior ballistics of the combustion light gas gun[J]. Defence Technology, 2020, 16(2): 341-347. DOI:10.1016/j.dt.2019.06.009 |
| [8] |
孙从煌, 曲艳东, 刘万里, 等. 点火条件对密闭管道内预混氢气/空气燃爆特性的影响[J]. 爆炸与冲击, 2018, 38(3): 622-631. SUN C H, QU Y D, LIU W L, et al. Influence of different ignition conditions on deflagration characteristics of a premixed mixture of H2 and air in a closed pipe [J]. Explosion and shock waves, 2018, 38(3): 622-631. |
| [9] |
MUELLER M A, KIM T J, YETTER R A, et al. Flow reactor studies and kinetic modeling of the H2/O2 reaction
[J]. International Journal of Chemical Kinetics, 1999, 31(2): 113-125. DOI:10.1002/(SICI)1097-4601(1999)31:2<113::AID-KIN5>3.0.CO;2-0 |
| [10] |
刘玉坪, 肖民, 黄志伟, 等. 基于化学反应动力学的双燃料发动机数值模拟[J]. 舰船科学技术, 2021, 43(6): 122–129. LIU Y P, XIAO M, HUANG Z W, et al. Numerical simulation of dual fuel engine based on chemical reaction mechanism, 2021, 43(6): 122–129. |
 2022, Vol. 44
2022, Vol. 44
