舰船航行时的环境较为复杂,为确保航行的安全性和稳定性,并获得正确的航向,在规定的航线内顺利抵达目的地,需要采取有效的措施,对舰船的航向加以控制。随着对舰船航行安全性要求的不断提升,使得科学操控成为重中之重。大部分舰船采用的是自动舵控制液压舵机的方式,使舰船按照驾驶需要定向航行[1-3]。由于风浪会影响舰船的航向,所以在开发航向自动控制器时,要充分考虑风浪的干扰。借此就风浪干扰条件下舰船航向保持非线性控制系统展开分析。
1 舰船航向控制模型的构建舰船在水面航行的过程中,需要保持航向的正确性,这样才能顺利抵达目的地。由此使得舰船航向控制成为一项非常重要的工作。在具体控制时,舵的转角由自动舵控制系统进行控制,以此来实现控制舰船航向的目标。从控制对象的角度讲,舰船航向控制是以首向角作为控制目标,可将之归入到舰船的操纵性问题中。舰船的动力学运动模型为非线性,为便于舰船自动舵控制系统的设计,对操纵运动做线性处理,在此基础上,考虑非线性的影响。舰船在水面上的运动包括6个自由度,根据这6个自由度,并结合舰船的控制需要便可构建相应的控制模型[4-7]。
2 风浪干扰下舰船航向保持非线性控制系统 2.1 最优控制参数选取将舰船的给定航向设定为
| $ {T_r} = \frac{{{l_n} + \omega _n^{}}}{{{\omega _n}}} \text{。} $ |
阻尼超过1时,这个状态被称为过阻尼状态,输出无超调量,过渡的时间相对较长,预制相关的方程式会出现2个不相等的实根。通常情况下,在实际工程中,阻尼一般采用的都是较大的欠阻尼,该状态下的超调比较小,并且过渡时间也比较短。不仅如此,当初始状态为0时,更加容易获得系统对阶跃响应时的舵角变化速度。若初始状态为0,即给定的航向角与实际航向角一致,并且舰船直线航行时,则实际的舵角为0。舰船采用往复式或转动式舵机时,舵叶由液压缸来推动,接近稳态时,液压储能器、压力控制阀等设备,会确保油缸的压力值在规定允许的范围内。
2.2 基于非线性系统的航向自动控制器舰船的运动模型呈现出典型的非线性特征,基于此在设计舰船航向自动控制器的过程中,可对非线性系统的结构特点加以充分利用,借助反向递推的方法,构造系统相关函数,从而获得控制器。稳定性理论采用状态向量描述,该理论除适用于线性定常系统之外,也适用于多变量的非线性时变系统。由于线性稳定系统中仅存在一个孤立的平衡点,因此,可将这个平衡点本身所具备的稳定性视作为整个线性系统的稳定性。然而,在非线性系统中,平衡点的数量通常都≥1,也就是处在多个平衡点,所以在研究非线性系统的稳定性时,只能以平衡状态作为主要依据。
在对舰船航向自动控制器设计时,需要对非线性项予以适当保留,以免所有的非线性项被全部消除。可以采用非线性控制规律,使舰船在海上航行的实际航向始终跟随期望的参考航向。当输入到系统中的期望参考航向为阶跃函数时,自动控制器将非线性部分进行抵消,在此基础上增加线性化的PID控制,构成具有非线性特征的PID控制系统。抵消非线性误差,是构成线性化PID控制器最为简单且有效的途径之一。舰船的非线性模型如下:
| $ {T_1}{T_2}\psi + {T_3} \cdot K\cdot H(\psi ) = K(\delta + 1) \text{,} $ |
式中:
当非线性因素被对消之后,便能够获得线性系统,此时可以模拟海上的风浪干扰,将海况假定为5级,同时增设白噪声干扰项。为使模拟所得的结果更加准确,改变传递函数,具体而言,就是模拟系统参数的摄动,在此基础上进行仿真,由此得出设计的非线性航向自动控制器具有良好的鲁棒性。
往复式机构的强度分布模型示意图如图1所示。

|
图 1 往复式机构的强度分布模型示意图 Fig. 1 Schematic diagram of the strength distribution model of the reciprocating mechanism |
一般情况下,当舵机转到舵角
舰船需要通过舵机来控制和保持航向,由此使得舵机的特性成为决定控制效果的关键。可以通过下式表示舵机的特性:
| $ TE\cdot \delta + 1 = KE\cdot{\delta _E} \text{。} $ |
式中:
舰船上的舵机有着非线性的特征,具体体现在:受相关因素的限制,操纵舵机时的舵角通常≤±35°;受功率的限制,转舵时的速度基本上不会超过3°/s。基于此,在开展控制系统模拟仿真的过程中,可以采用非线性模块来表示舵角与转舵速度的限制,以增设死区的方法,降低控制器的灵敏度。在海面上,风除了是海浪形成的主要原因之外,还会直接作用于舰船的船体上,风浪对舰船航向控制系统会产生一定程度的影响,这个影响可近似等效为干扰,据此可得到舰船航向PID控制系统的相应情况,风浪干扰下的舰船PID控制系统控制框图如图2所示,其中E为输入,R1,R2,R3为输出。风浪干扰下的舰船PID控制系统中的纵向舵角响应示意图如图3所示,风浪干扰下的舰船PID控制系统中的横向舵角响应示意图如图4所示。

|
图 2 风浪干扰下的舰船PID控制系统控制框图 Fig. 2 Control block diagram of ship PID control system under the disturbance of wind and waves |

|
图 3 风浪干扰下的舰船PID控制系统中的纵向舵角响应示意图 Fig. 3 Schematic diagram of longitudinal rudder angle response in ship PID control system under wind and wave disturbance |
|
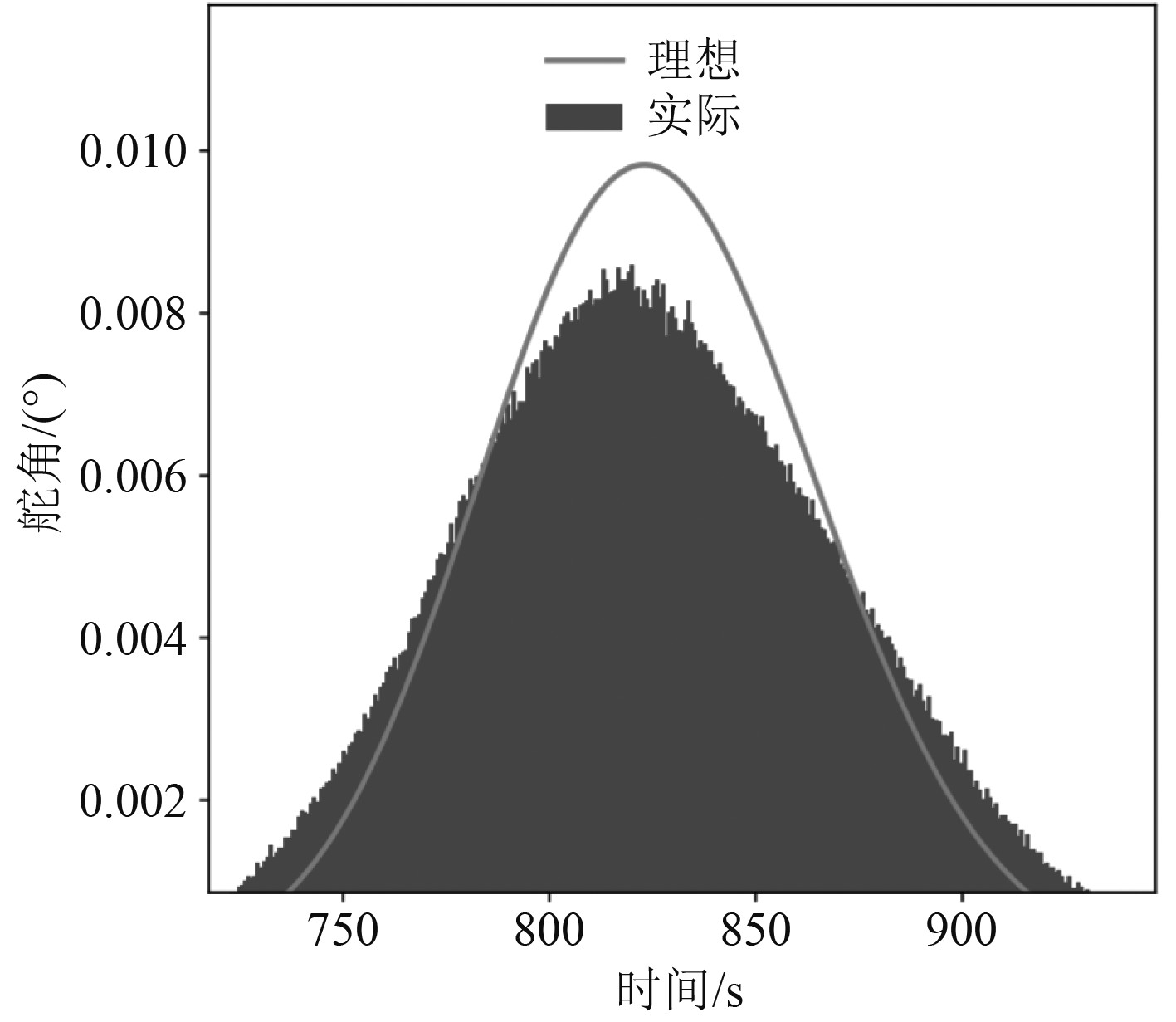
图 4 风浪干扰下的舰船PID控制系统中的横向舵角响应示意图 Fig. 4 Schematic diagram of lateral rudder angle response in ship PID control system under wind and wave disturbance |
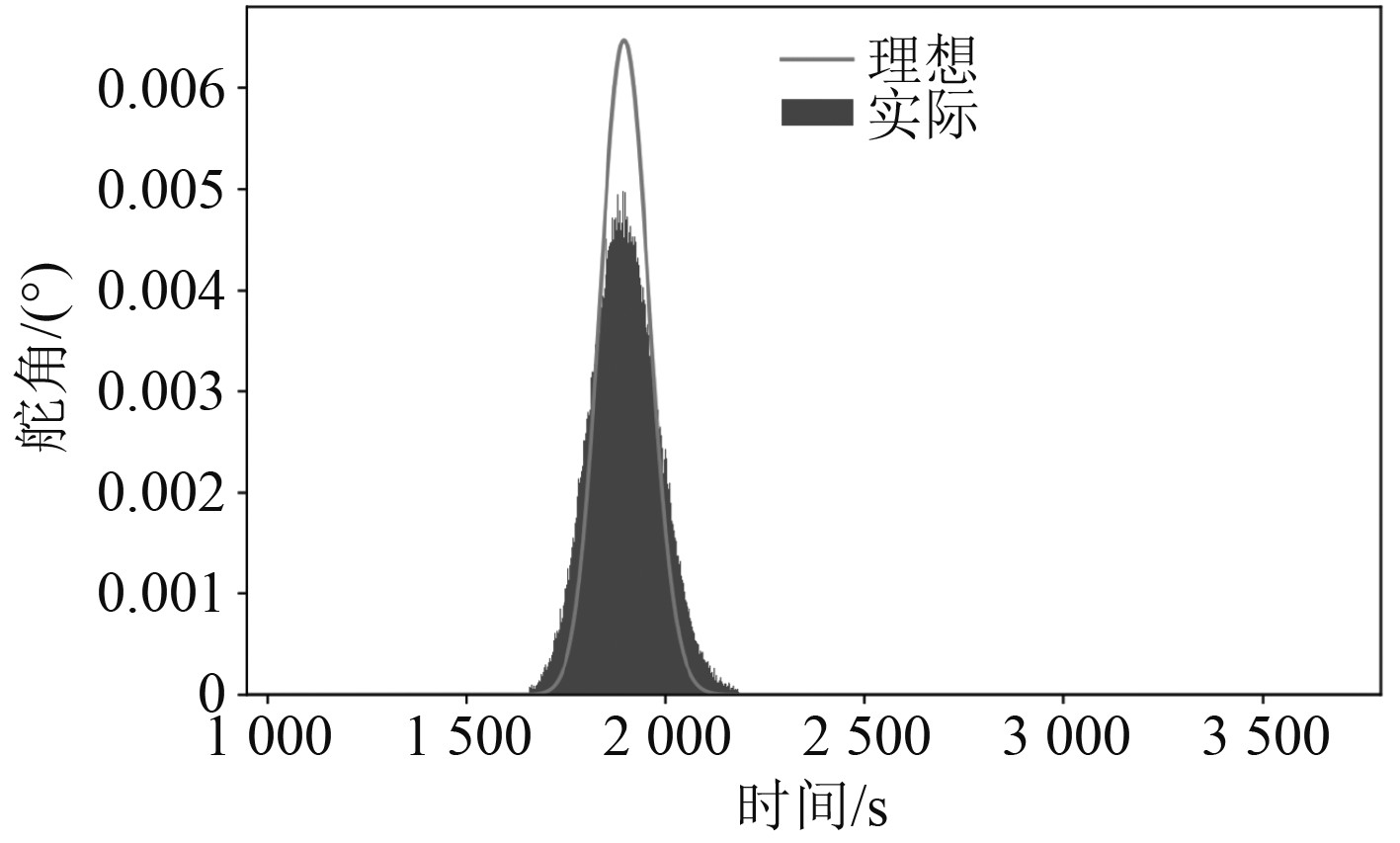
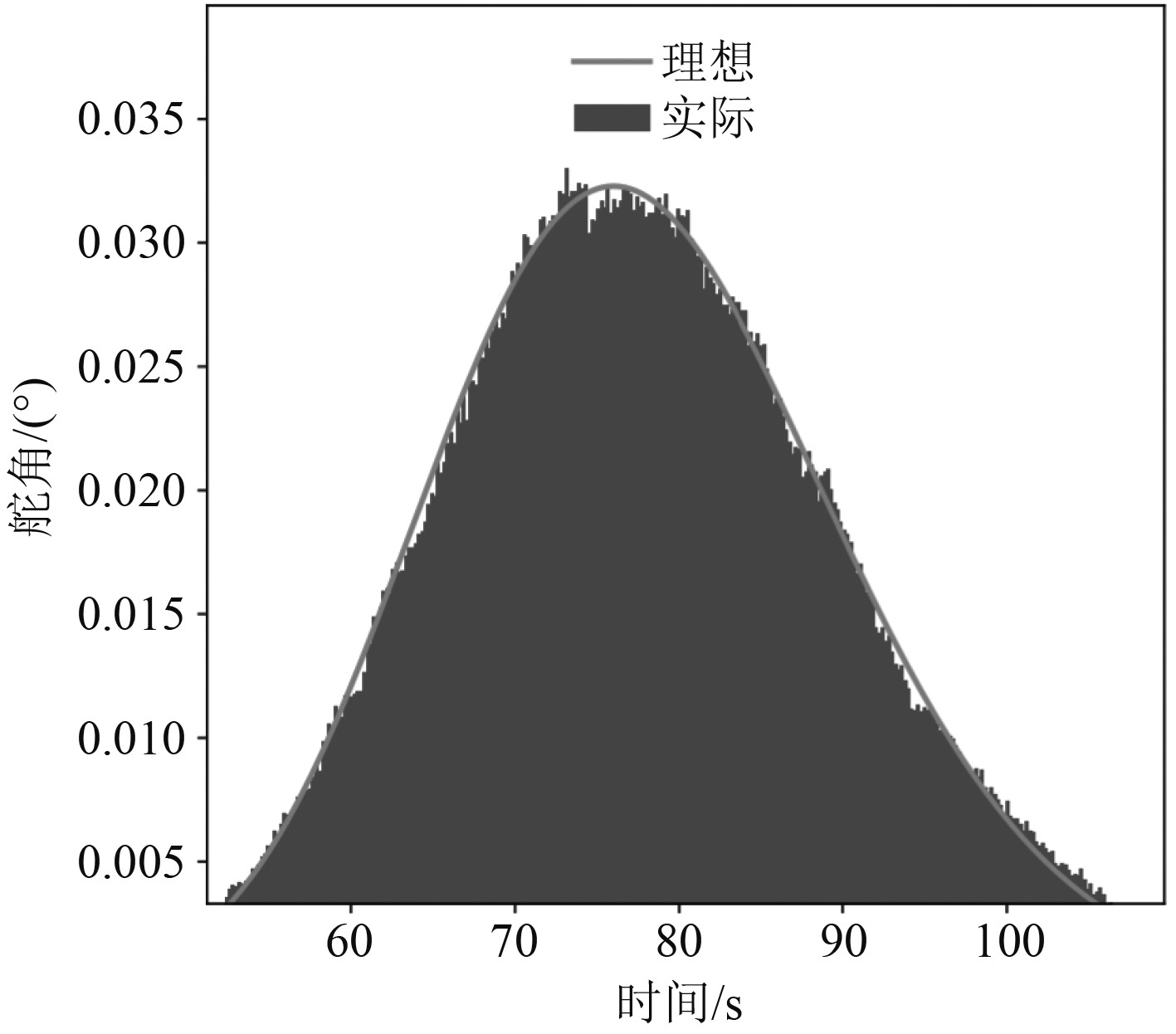
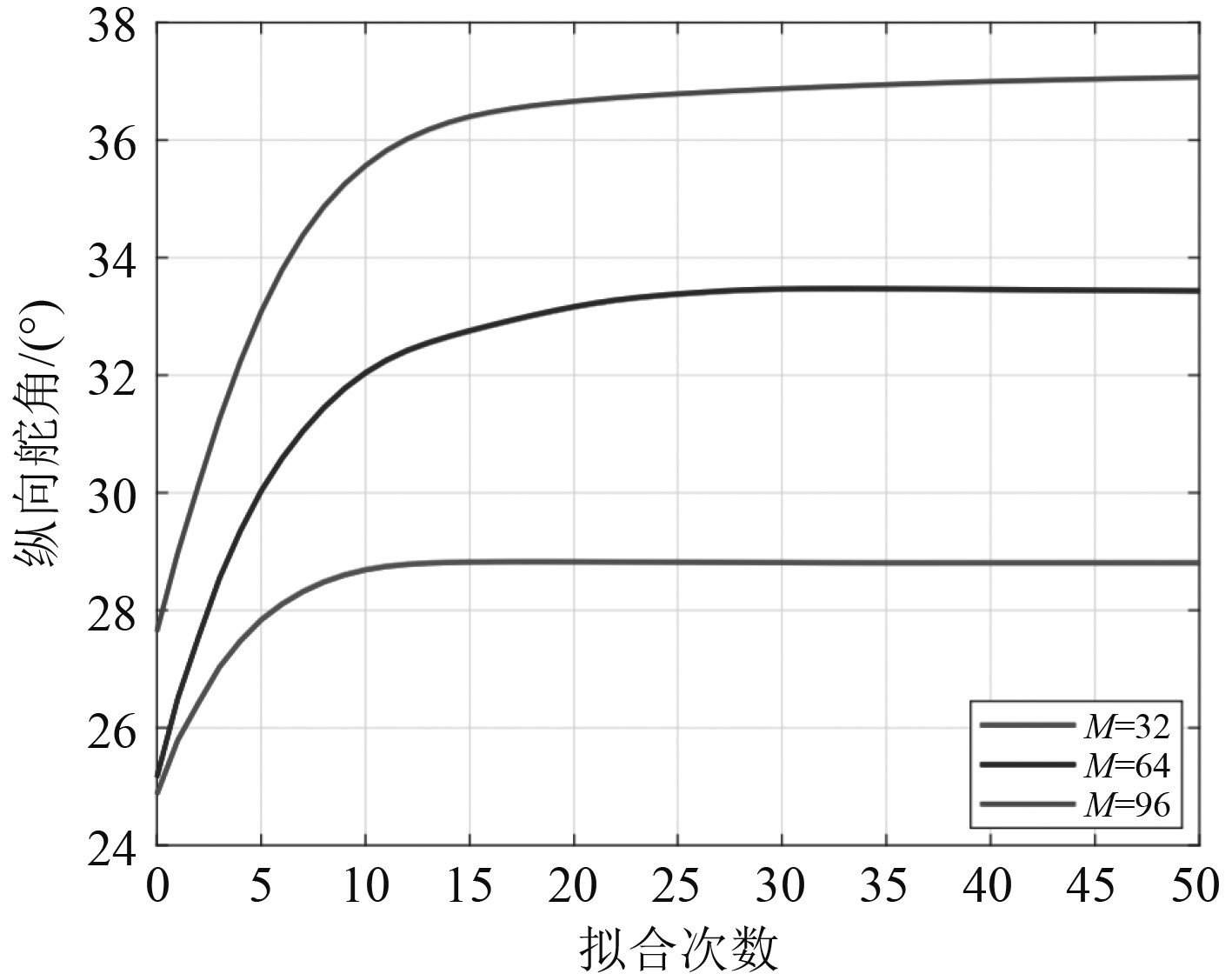
当舰船的舵向角响应呈现为光滑、平顺的状态时,就出现振动迹象,稳定性也比较好。之所以会出现这样的情况,与死区的设置有着直接关系,舵角的波幅与频率随着死区的设置大幅度减少,单位时间内的不稳定性振动相对较少,特别是到控制后期时,表现出来的稳定性更好,仅有非常细小的尖峰出现,因数值不大,可忽略不计。当海上的风浪比较小,可将其对舰船航向保持非线性控制视作为白噪声干扰,其中非线性控制特征值可用M表示。为满足比较的需要,在选取白噪声时,将其最大值选为1.5正旋干扰幅值。引入白噪声干扰后的舰船航向PID控制系统横向舵角响应情况示意图如图5所示。引入白噪声干扰后的舰船航向PID控制系统纵向舵角响应情况示意图如图6所示。实际不同控制参数M下的纵向舵角响应情况示意图如图7所示。
|
图 5 引入白噪声干扰后的舰船航向PID控制系统横向舵角响应情况示意图 Fig. 5 Schematic diagram of lateral rudder angle response of ship heading PID control system after introducing white noise interference |
|
图 6 引入白噪声干扰后的舰船航向PID控制系统纵向舵角响应情况示意图 Fig. 6 Schematic diagram of longitudinal rudder angle response of ship heading PID control system after introducing white noise interference |
|
图 7 实际不同控制参数M下的纵向舵角响应情况示意图 Fig. 7 Schematic diagram of longitudinal rudder angle response under different actual control parameters M |
非线性模块增加后,能够使航向控制系统部分非线性被对消,在系统设计时,通过对λ值的适当调整,并增设可以调节灵敏度的死区单元,可以使操纵舵机时,舵角的变化趋于合理化,舰船的航向也能随之保持平稳。转舵次数及幅度减少,使舵机的能耗随之降低,转舵时的推力损耗也显著减小,达到节约能量的目的。即使加入较强的风浪干扰,自动舵控制系统仍然能够保持稳定的性能,舵机转舵过程中产生的液压波动非常小,符合舵机操纵性能的要求。
3 结 语在开发舰船航向自动控制器的过程中,除了要充分考虑到风浪的干扰之外,还要对非线性系统的构造特点加以合理运用,从而使开发出来的自动控制器能够满足舰船航向保持控制的需要。
| [1] |
刘双. 舰船航向非线性控制的数学模型设计[J]. 舰船科学技术, 2021, 43(18): 73-75. |
| [2] |
王国栋. 非线性Backstepping算法在舰船动力定位系统控制的应用[J]. 舰船科学技术, 2020, 42(6): 112-114. |
| [3] |
王超, 史文森, 郭正东, 等. 基于双轴旋转惯导的舰船航向误差动态评估方法[J]. 中国惯性技术学报, 2020, 28(4): 551-555. |
| [4] |
黄谦, 周红进, 金鑫, 等. 舰船混沌运动的改进自适应Backstepping控制[J]. 指挥控制与仿真, 2020, 42(4): 128-132. DOI:10.3969/j.issn.1673-3819.2020.04.025 |
| [5] |
程春蕊, 毛北行. 一类不确定分数阶舰船运动混沌系统的滑模同步控制[J]. 安徽大学学报(自然科学版), 2019, 45(5): 45-48. |
| [6] |
邓英杰, 张显库, 张国庆. 水面舰船动力定位系统ESO输入饱和控制[J]. 系统工程与电子技术, 2019, 41(5): 1110-1117. |
| [7] |
韩孟孟, 池庆玺, 裴虎城. 一种多站模式下舰船航向航速快速解算方法[J]. 战术导弹技术, 2015(1): 69-72. |
 2022, Vol. 44
2022, Vol. 44
