0 引　言

作为舰船的核心设备，不同机械设备的稳定运行以及设备间的有效合作是确保舰船安全航行的基础^[1]。但舰船中的各类机械设备长时间在劣态环境下运行^[2]，极容易产生故障^[3]，因此研究舰船故障点定位方法对于舰船的安全航行具有显著的应用价值。

周光宇等^[4]在研究设备故障诊断及定位的过程中引入了机器学习算法，利用粗糙集评估样本关键性获取故障特征，在此基础上采用支持向量机完成故障诊断及定位^[4]。但该方法在实际应用过程中所获取的故障特征具有一定主观性，导致最终定位结果产生偏差。赵传宗等^[5]通过小波变换获取故障特征，通过遗传算法完成定位目标。但该方法对于运算过程中的参数选择具有较大依赖性。针对上述方法中存在的问题，研究基于粒子群优化算法的舰船故障点智能定位方法。

1 基子粒子群优化算法的舰船故障点智能定位方法 1.1 舰船故障点智能定位方法架构设计

舰船故障点智能定位方法是通过有效检测舰船内部机械设备运行相关参数，结合模式识别完成舰船故障识别与故障点定位^[6]。在进行舰船故障点智能定位过程中，需检测舰船机械设备运行过程中的振动信号，根据振动信号判断舰船机械设备运行工况是否正常。针对工况异常的振动信号，需挖掘异常振动信号的特征，将舰船设备振动信号特征作为BP神经网络模型的输入，通过粒子群优化算法优质的全局搜索能力，优化BP神经网络模型结构，获取高精度识别与定位结果，由此完成舰船故障识别以及故障点智能定位目的。

1.2 舰船机械设备异常振动信号特征提取

在采集舰船机械设备振动信号并进行检测后，可依照振动信号判断舰船设备运行工况是否正常。针对工况异常的振动信号，采用基于小波包理论的信号特征提取方法进行特征提取，该过程是舰船故障识别与故障点智能定位的基础。若所采集的舰船机械设备异常振动信号样本 $ X $ 内存在 $ n $ 个模式，即 $ X{\text{ = }}\left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\} $ ，其中， ${x_i} = \left\{ {{x_{i1}},{x_{i2}}, \cdots ,{x_{ij}}} \right\}, j = 1,2, \cdots ,m$ ，基于小波包算法提取舰船机械设备异常振动信号特征。

小波包算法基于舰船机械设备异常振动信号自身的特性，变换且判断各频段的信号分辨率^[7]，根据信号的多分辨率转换，实现舰船机械设备异常振动信号的正交分解，并在此基础上进行特征向量提取。在分析舰船机械设备异常振动信号时，将 $ {e_n}\left( x \right) $ 作为特征函数，其需符合标准如下：

$ \left\{ \begin{gathered} {e_{2n + 1}}\left( x \right) = \sum\limits_i {F\left( i \right){e_n}\left( {2x - i} \right)} ，\hfill \\ {e_{2n}}\left( x \right) = \sum\limits_i {G\left( i \right){e_n}\left( {2x - i} \right)} 。\hfill \\ \end{gathered} \right. $

(1)

式中： $ F\left( i \right) $ 与 $ G\left( i \right) $ 均表示正交滤波系数， $ {e_0}\left( x \right) $ 和 $ {e_1}\left( x \right) $ 分别表示尺度函数与小波函数。设定 $ {e_0}\left( x \right) $ 的正交小波包为函数系 $ {\left\{ {e\left( t \right)} \right\}_{t \in Z}} $ ，以尺度函数 $ {e_0}\left( x \right) $ 为基准实施平移与伸缩^[8]，由此构成异常振动信号的小波包空间，描述异常振动信号多分辨率解析式如下：

$ \begin{split} &{\lambda _f}\left( i \right) = \sum\limits_i {{\lambda _i}{F_{n - 2i}}}，\\ &{\lambda _G}\left( i \right) = \sum\limits_i {{\lambda _i}{G_{n - 2i}}} 。\end{split} $

(2)

在此条件下，舰船机械设备异常振动信号 $ z\left( x \right) $ 符合下式：

$ z\left( x \right) = \sum\limits_i {\lambda _n^j{e_{2n}}} \left( {{2^{ - j - 1}}} \right) 。$

(3)

通过分解过程能够得到异常振动信号的2个主要组成部分^[9]，分别是高通滤波与低通滤波处理后的数据信号。异常振动信号在高通滤波处理下于 $ {e_{2n + 1}}{\left( {{2^{ - j - 1}}} \right)_{j \in Z}} $ 上做投影，在低通滤波处理下于 $ {e_{2n}}{\left( {{2^{ - j - 1}}} \right)_{j \in Z}} $ 上做投影。 $ z\left( x \right) $ 的二范数定义为：

$ \left\| z \right\|_2^2 = \left( {\int {{{\left| {z\left( x \right)} \right|}^2}{\rm{d}}x} } \right) \times \theta 。$

(4)

式中， $ \theta $ 表示任意常数值。

提取不同频段内的信号，进行小波包分解系数的重构：

$ \lambda = {\lambda _1} + {\lambda _2} + \ldots + {\lambda _m} 。$

(5)

利用R_j表示各频道信号相应的整体能量，其公式为：

$ {R_j} = \left( {\int {{{\left| {{\lambda _j}\left( t \right)} \right|}^2}dt} } \right) \times \theta = {\left| {{x_{jk}}} \right|^2} 。$

(6)

式中，x_jk表示重构后异常振动信号离散点幅值。

在提取舰船机械设备异常振动信号特征向量时，需以能量元素为基础构建模型，描述所提取的特征向量 $ \sigma $ 为：

$ \sigma = \left\{ {{R_1},{R_2}, \cdots ,{R_m}} \right\} 。$

(7)

利用下式对 $ \sigma $ 进行调整，并实施归一化处理：

$ \left\{ \begin{gathered} \sigma = \frac{1}{R}\left\{ {{R_1},{R_2}, \cdots ,{R_m}} \right\} ，\hfill \\ R = \frac{{\left( {\displaystyle\sum\limits_{j = 1} {{{\left| {{R_j}} \right|}^2}} } \right)}}{2} 。\hfill \\ \end{gathered} \right. $

(8)

考虑所提取的 $ \sigma $ 满足相应的概率分布 $ {p_i}\left( {x,{x_i}} \right) $ ，依照异常振动信号间自熵和互熵间的相关性能够划分特征向量类别。 $ {\tau _i}\left( {{x_j}} \right) $ 表示自熵，即

$ {\tau _i}\left( {{x_j}} \right) = - \sum\limits_{x \in X} {{p_j}\left( {x,{x_j}} \right)}。$

(9)

在此条件下，符合标准 $ {\tau _{ij}}\left( {{x_i},} \right) = {\tau _{ij}}\left( {{x_j}} \right) $ ，能够定义舰船机械设备异常振动信号的互熵，由此实现舰船机械设备异常振动信号特征类别的划分：

$ {\tau _{ij}}\left( {{x_i},{x_j}} \right) = {\tau _{ij}}\left( {{x_j},{x_i}} \right) - \sum\limits_{{x_j} \in {X_j}} {\sum\limits_{x \in {X_j}} {{p_{ij}}\left( {x,{x_i},{x_j}} \right)} } 。$

(10)

将所提取的各类舰船机械设备异常振动信号特征输入BP神经网络内，并利用粒子群优化算法优化BP神经网络，完成舰船机械设备故障识别与定位。

1.3 异常振动信号特征的船舶故障点识别与定位

1）输入层

输入层内输入的是所提取的舰船机械设备异常振动信号特征的分类结果。由于不同的异常振动信号特征数量级差异较为显著，直接采用初始异常振动信号特征数据实施网络训练将导致网络收敛性能下降，因此需在将异常振动信号特征输入网络前，对所输入的异常振动信号特征数据实施归一化处理，公式为：

$ {y_k} = \frac{{{x_k} - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}}。$

(11)

式中， $ {y_k} $ 和 $ {x_k} $ 分别表示归一化处理后的异常振动信号特征数据和初始异常振动信号特征数据， $ {x_{\min }} $ 和 $ {x_{\max }} $ 分别表示初始异常振动信号特征数据内的下限值和上限值。

2）隐含层

隐含层内的节点数量对于最终故障识别与定位的精度产生直接影响：如果节点数量过多，那么网络训练效率下降，且有较大概率陷入局部最优值，由此错过全局最优结果；如果节点数量过少，那么网络无法准确地进行学习，导致最终的训练精度受到限制。因此确定最优隐含层节点数量：

$ h = \sqrt {\left( {m + n} \right)}。$

(12)

式中， $ m $ 和 $ n $ 分别表示输出层和输入层节点数量。

3）输出层

输出层所输出的结果可分为舰船机械设备故障类别和故障点定位结果。

1.4 基于反向粒子群优化算法的神经网络优化

BP神经网络内权值与阈值的设定是影响最终网络性能的主要参数，因此可采用反向粒子群优化算法对这2个参数进行寻优，以此提升BP神经网络性能。采用粒子群优化算法优化BP神经网络过程中，先对一群随机粒子进行初始化处理，其中不同粒子均表示BP神经网络权值与阈值的可能解。各粒子的适应度取决于其位置坐标对应的目标函数值。经由追踪粒子自身所确定的最优解(定义为个体极值，用p_b表示)和种群整体当前所确定的最优解(定义为全局极值，用g_b表示)更新自身。

若BP神经网络最优权值与阈值的搜索空间维数和种群粒子数量分别为 $ K $ 和n，第 $ i $ 个粒子的位置为 $ {x_i} = \left( {{x_{i1}},{x_{i2}}, \cdots ,{x_{iK}}} \right) $ ，而其速度则为 $ {v_i} = \left( {{v_{i1}},{v_{i2}}, \cdots ,{v_{iK}}} \right) $ ，由此可通过下式更新各粒子的速度和位置：

$ v_{ik}^{t + 1} = w \cdot v_{ik}^t + {b_1}\left( {{p_b}_{ik}^t - x_{ik}^t} \right) + {b_2}\left( {{g_b}_{ik}^t - x_{ik}^t} \right) ，$

(13)

$ x_{ik}^{t + 1} = x_{ik}^t + v_{ik}^{t + 1},i = 1,2, \cdots ,n;k = 1,2, \cdots ,K 。$

(14)

式中， $ t $ 和 $ t + 1 $ 分别表示当前进化代数和下一进化代数， $ w $ 和 $ b $ 分别表示惯性权重系数和加速因子， $ {p_b}_{ik}^t $ 和 $ {g_b}_{ik}^t $ 分别表示第 $ i $ 个粒子在最优位置条件下种群当前达到最优位置条件下第 $ k $ 维对应的位置坐标。粒子群优化算法在实际迭代过程中以随机初始种群为初始，在缺乏种群先验信息条件下，初始粒子同最优粒子间距离决定其进化效率。若挑选一个与最优粒子距离较近的初始粒子，则可显著提升算法的进化效率。所以在确定粒子实用度的过程中还需确定其对应个体反向的适应度，经由对比确定同最优粒子距离更新的初始粒子，以此提升BP神经网络优化效率。

2 仿真实验 2.1 故障定位结果

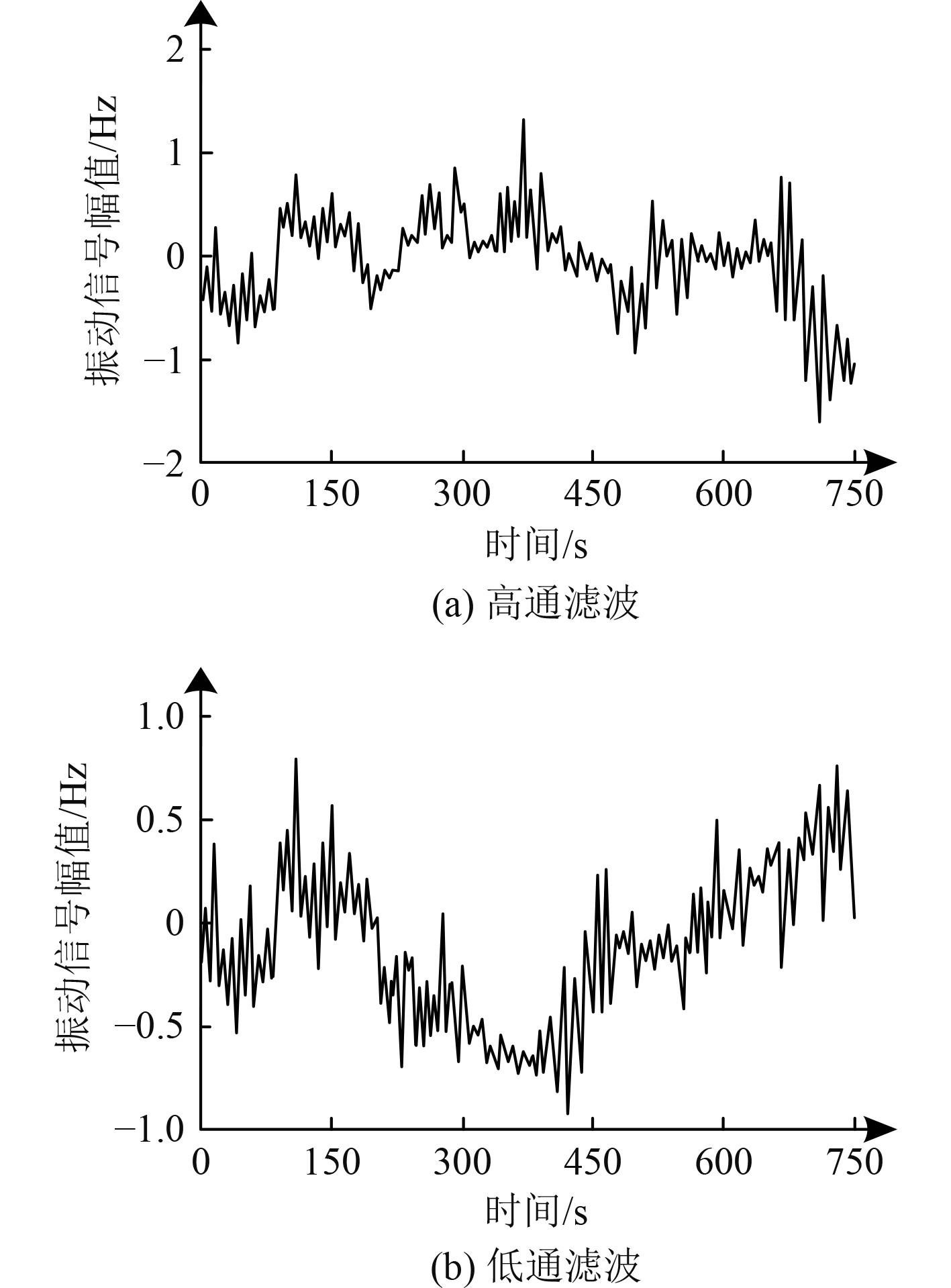
以研究对象内某电机设备为例，采用本文方法对所选电机设备的振动信号进行采集，并在其中提取异常振动信号，利用小波包分解后采集异常振动信号特征，由此获取图1所示的2个通道的特征提取结果。

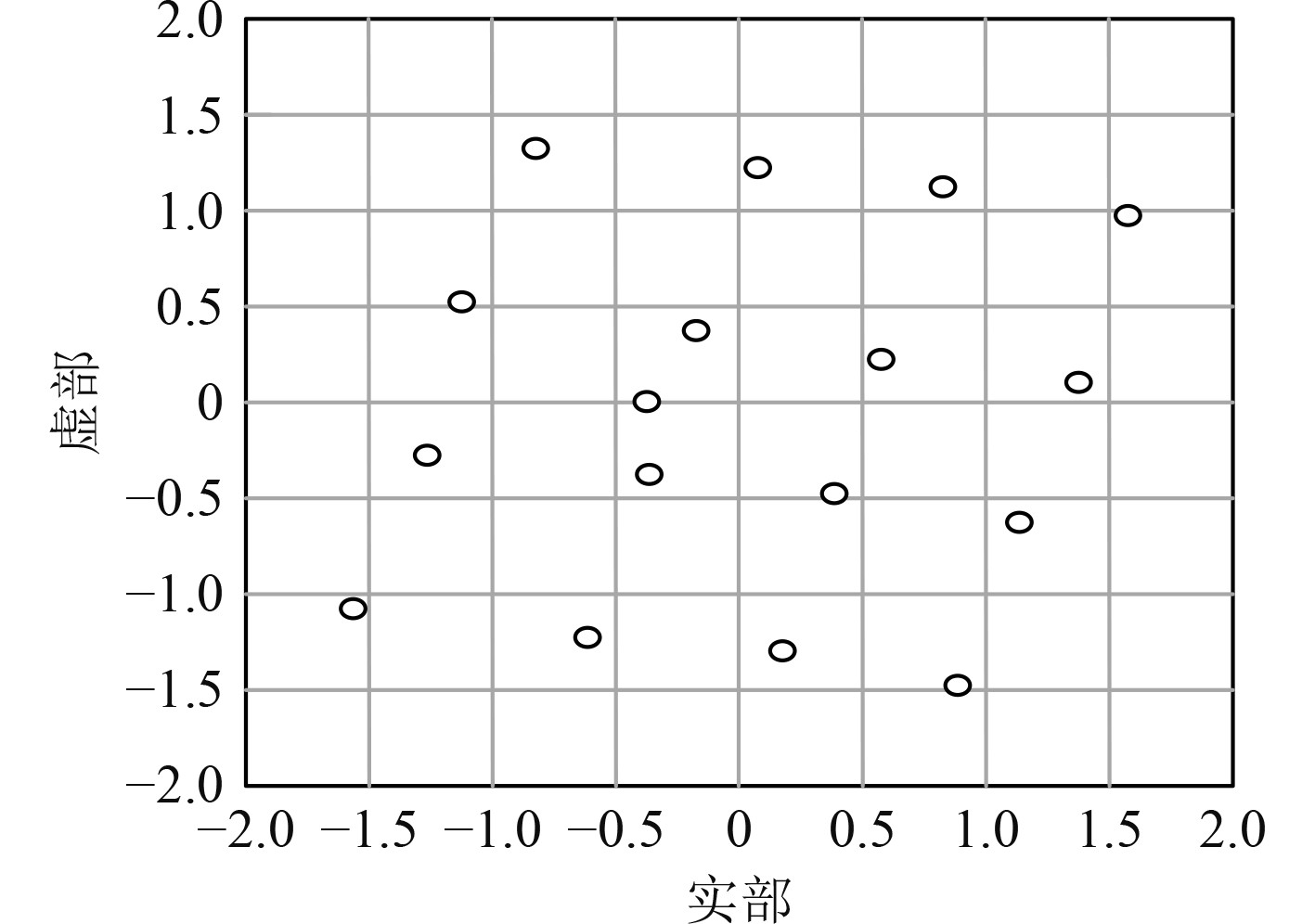
以图1所示的异常振动信号特征提取结果为研究模板数据，采用本文方法进行故障点定位，所得结果如图2所示。可知，通过本文方法定位研究对象机械设备故障点，可有效标注不同故障点位置，由此验证了本文方法的可应用性。

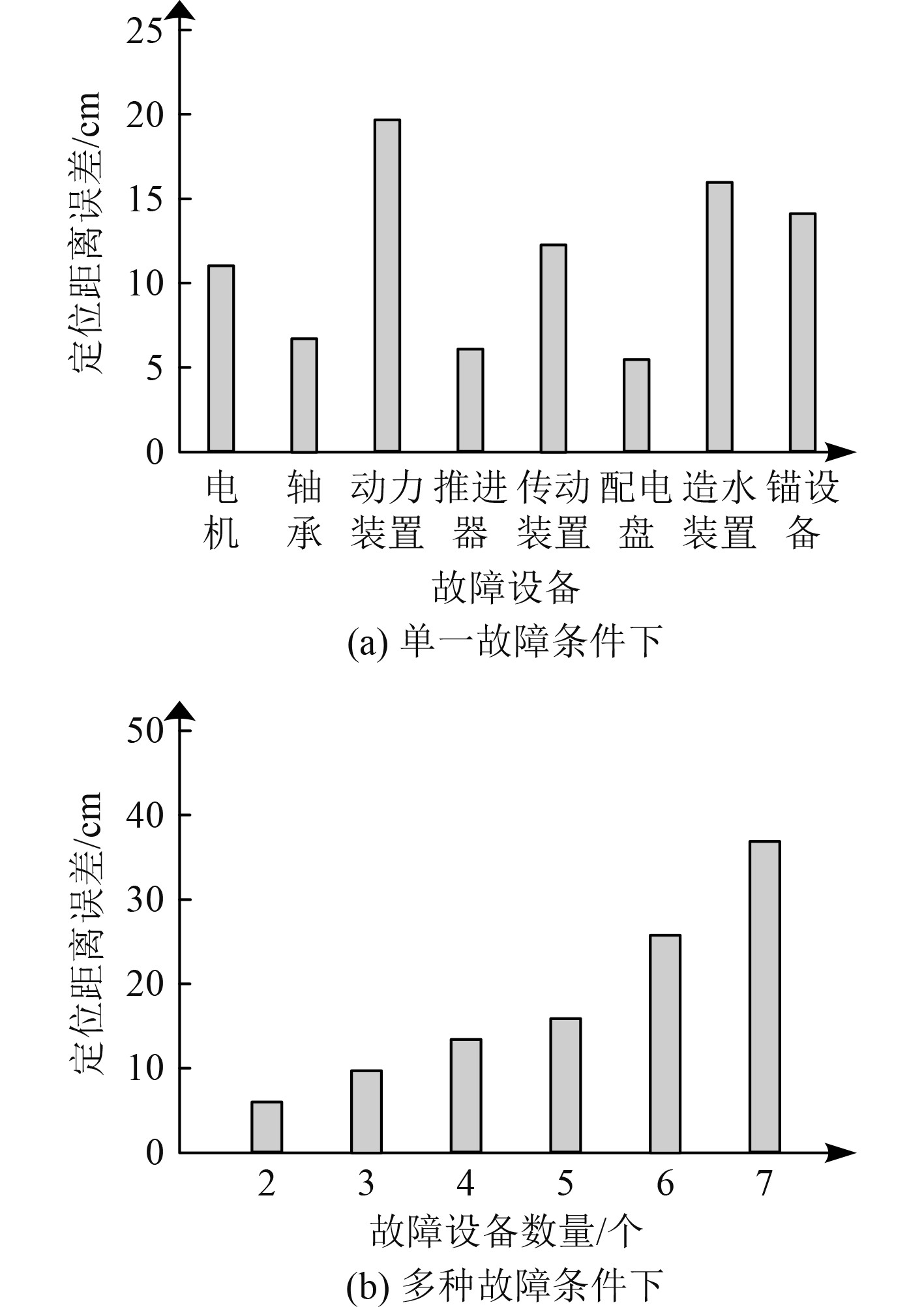
为进一步验证本文方法的故障点定位性能，分别分析单一故障条件下和多种故障共存条件下，本文方法对故障点定位的误差，所得结果如图3所示。可知，在单一故障条件下，本文方法对于故障点的定位误差均控制在20 cm范围内，均值约为10 cm左右。在多种故障条件下，随着故障设备数量的提升，故障点定位误差也逐渐增加，但均控制在40 cm范围内。由此能够说明本文方法较为准确地定位研究对象故障点，对提升研究对象故障维修效率、保障研究对象安全运行产生有利影响。

2.2 故障识别结果

采用本文方法对研究对象机械设备的各类故障进行识别，所得结果如表1所示。可知，本文方法对研究对象各机械设备故障识别结果与其实际故障相同，由此可表明本文方法能够准确识别研究对象各类机械设备故障。

3 结　论

本文研究基于粒子群优化算法的舰船故障点智能定位方法，利用粒子群优化算法优化BP神经网络，识别并定位舰船机械设备故障点。实验结果显示本文方法具有较好的应用效果。