0 引　言

船舶雷达导航系统发射微波脉冲（即电磁波）对海面的目标物体进行照射，然后接收目标物体对电磁波的反射回波，通过分析回波信号并测定其参数，能够实现海上目标物体的成像、识别、检测、定位和跟踪。

船舶雷达导航系统的工作特点包括：

1）导航雷达的辐射波束宽度与回波信号的扩展有关，宽度越宽，雷达回波信号左右扩展越大；

2）雷达成像的目标边缘与噪声信号有关，常见的噪声干扰包括船舶运动、涌浪波动、设备噪声等^[1]；

3）雷达探测受到地球曲率半径影响，距离越远，目标被探测到的区域越小，距离达到一定数量级就会进入船舶导航雷达的盲区。

4）船舶雷达导航系统的工作状态是定向圆周扫描，旋转速度通常大于20 rpm，从而实现一定区域内目标物体的360°覆盖。

由于导航系统在管理港口交通、监视海岸线安全等方面有非常重要的作用，因此针对船舶导航系统的技术开发是业内的研究重点。

本文主要研究船舶导航系统机动目标的高精度跟踪技术，在海上交通和船舶管理时，某些船舶目标的机动性较强，基于该系统能够实现对机动目标的高精度追踪和定位。

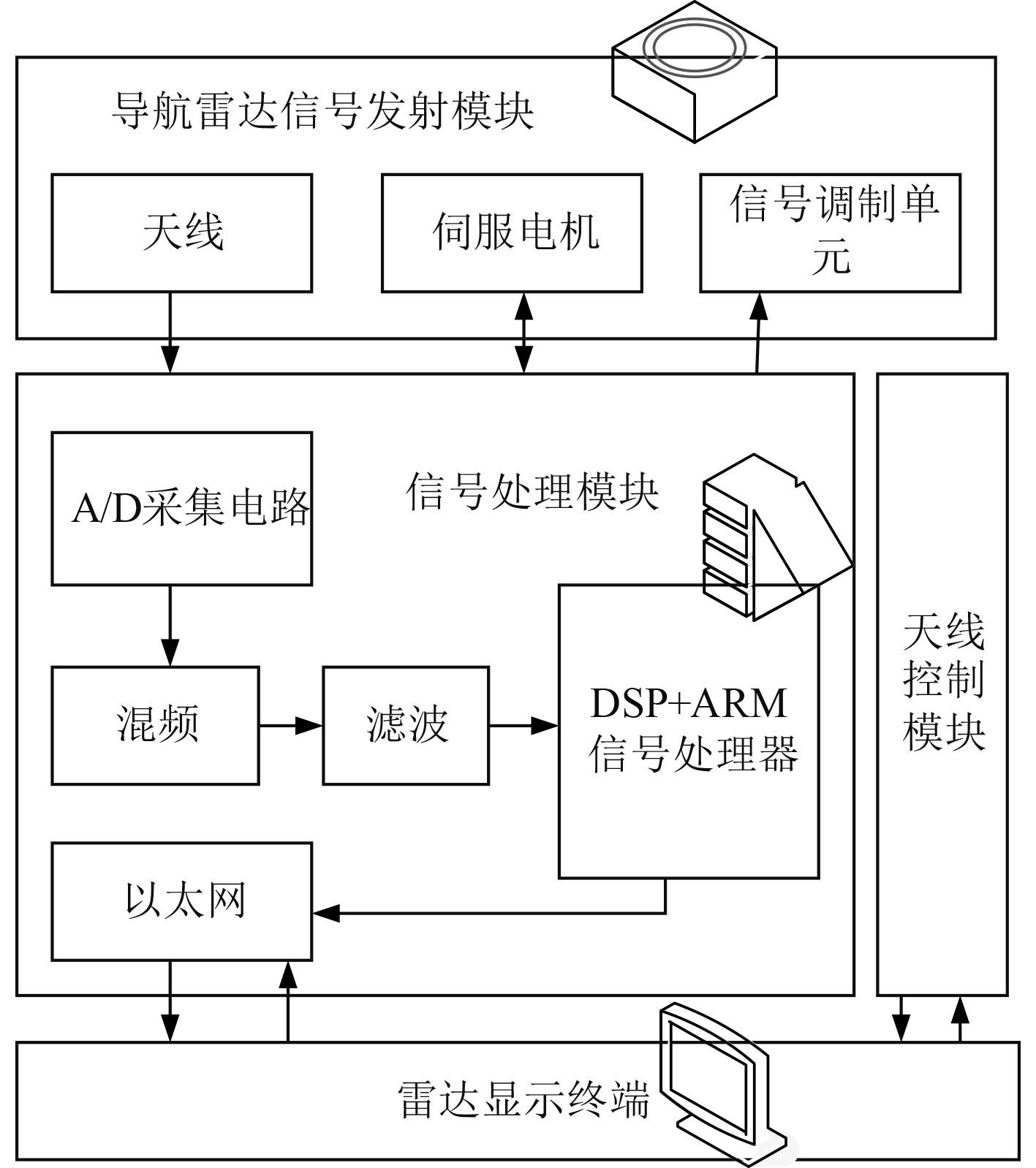
1 船舶雷达导航系统的工作原理

船舶雷达导航系统主要包括雷达信号发射模块、天线控制模块和信号处理模块，原理图如图1所示。

1）信号发射模块

船舶雷达导航系统的电磁波信号周期性发射，信号发射模块包含雷达天线、伺服电机^[2]、信号调制单元等。

2）雷达天线控制模块

其中，雷达导航系统的天线通过串口与伺服电机和嵌入式控制系统相连，具备2种天线控制功能：

①输出雷达天线的控制信号，将信号发送至用户操作界面，用户可对雷达天线的俯仰角、转速等参数进行主动控制。

②雷达天线状态的在线检测，实时接收天线的工作状态信号。

3）信号处理模块

本文研究的雷达导航系统中，信号处理模块采用DSP加ARM的处理器，将来自雷达天线的回波信号发送至模块的采集电路，经过滤波、混频等操作环节后，发送至嵌入式处理器DSP^[3]，在DSP中完成回波信号的处理。

2 船舶导航系统机动目标的高精度跟踪系统设计 2.1 目标跟踪雷达的伺服控制原理

机动目标的实时跟踪技术是本系统的关键，建立船舶导航系统目标跟踪雷达的伺服控制回路，基本原理图如图2所示。

可知，伺服控制回路是一个双闭环反馈控制回路，控制器的输出为雷达转速/角度控制信号，控制器的反馈信号为目标跟踪的误差。

定义某机动目标的运动模型为：

$ {\bar x_n} = {\bar x_i} + \frac{1}{{(n - i)}}\Delta \bar x,\quad i = 1, \cdots ,n - 1 \text{，} $

式中， $ {\bar x_i} $ 为在i时刻的位置， $ \Delta \bar x $ 为目标在雷达扫描周期内的位移，在i时刻雷达采集信号为：

$ f\left( t \right) = {\bar x_i} + \varepsilon \left( t \right) \text{，} $

式中： $ \varepsilon \left( t \right) $ 为噪声信号。

雷达回波信号在控制器中校正、滤波、补偿和放大，滤波后得到机动目标的运动模型为 $ {X_{li}} $ ，则

$ {X_{li}} = {\bar x_i} - k\frac{1}{{(n - i)}}\Delta \bar x,\quad i = 1, \cdots ,n - 1 \text{，} $

得到滤波方程为：

$ \left\{ {\begin{array}{*{20}{l}} {{{\tilde X}_{li}} = \alpha \displaystyle\frac{2}{{n(n + 1)}}\sum\limits_{i = 1}^n {(3i - n - 1)} {x_i}}，\\ {\Delta {{\tilde X}_{li}} = \beta\displaystyle \frac{6}{{n\left( {{n^2} - 1} \right)}}\sum\limits_{i = 1}^n {(2i - n - 1)} {x_i}} 。\end{array}} \right. $

式中： $ \alpha $ 和 $\ \beta $ 为滤波器的系数。

2.2 船舶雷达导航系统下的机动目标位置配准

建立海面机动目标在船舶雷达导航系统下的运动坐标系如图3所示。

假设船舶的航向角为 $ \theta $ ，航速为 $ {v_T} $ ，机动目标的运动速度为 $ \left( {{v_x},{v_y}} \right) $ ，目标相对于雷达的方位角^[4]为 $ {\theta _t} $ ，可解算机动目标的速度方程为：

$ \left\{ {\begin{array}{*{20}{l}} {{v_x} = {v_T}\sin \left( {{\theta _t} - \theta } \right)} ，\\ {{v_y} = {v_T}\cos \left( {{\theta _t} + \theta } \right)} 。\end{array}} \right. $

定义雷达i时刻所在位置坐标为 $ \left( {{\lambda _0},{\varphi _0}} \right) $ ，机动目标在i时刻所处的位置坐标为 $ \left( {{\lambda _t},{\varphi _t}} \right) $ ，将目标的位置坐标投影到地面坐标系O-XYZ下，得到

$ \begin{array}{*{20}{l}} {{X_t} = \left( {{\lambda _t} - {\lambda _0}} \right)\cos {\varphi _t}} ，\\ {{Y_t} = {\varphi _t} - {\varphi _0}} 。\end{array} $

式中： $ {\varphi _t} $ ， $ {\varphi _0} $ 分别为机动目标的航向角和方位角。

将机动目标的位置坐标转换为极坐标形式为：

$ \begin{array}{*{20}{l}} {{R_i} = \sqrt {X_t^2 + Y_t^2} } ，\\ {{\alpha _i} = \arctan \dfrac{{{X_t}}}{{{Y_t}}} - {\varphi _0}} 。\end{array} $

在随动坐标系下观测到机动目标的位置为 $ \left( {{x_0},{y_0},{z_0}} \right) $ ，则基于多雷达的目标位置配准矩阵如下式：

$ {\left( {{x_0},{y_0},{z_0}} \right)^{\rm{T}}} = \left[ \begin{gathered} \cos {\theta _t} \hfill \\ 1 \hfill \\ \sin {\theta _{}} \hfill \\ \end{gathered} \right] \times {\left( {{v_x},{v_y}} \right)^{\rm{T}}} \times \left[ \begin{gathered} \alpha \hfill \\ \beta \hfill \\ \end{gathered} \right] 。$

2.3 船舶雷达导航系统下的机动目标时间配准

时间配准也是船舶雷达导航系统机动目标跟踪的重要环节，由于雷达电磁波的传播速度接近光速，因此可将回波信号的时延忽略。

时间配准针对雷达阵列中不同雷达个体的信号而言，船舶导航系统中往往具有2个以上的雷达阵列，从而提高目标跟踪的精度^[5]。

建立不同雷达单元回波信号的时间关联度如下式：

$ \left| {{k_{r1}} - {k_{r2}}} \right| < C\;\;,j = 0,1,\cdots ,n \text{。} $

其中： $ {k_{r1}} $ 为雷达单元1的回波信号， $ {k_{r2}} $ 为雷达单元2的回波信号；C为时间配准阈值。

雷达信号的时间配准方程为：

$ \left\{ \begin{gathered} f\left( k \right) = f\left( {{t_i}} \right) + {\raise0.7ex\hbox{${\sin \left( {S\left( {{t_i}} \right) \cdot \left( {k - {t_i}} \right)} \right)}$} \mathord{\left/ {\vphantom {{\sin \left( {S\left( {{t_i}} \right) \cdot \left( {k - {t_i}} \right)} \right)} {60}}}\right.} \lower0.7ex\hbox{${60}$}}，\hfill \\ r\left( k \right) = r\left( {{t_i}} \right) + {\raise0.7ex\hbox{${\cos \left( {S\left( {{t_i}} \right) \cdot \left( {k - {t_i}} \right)} \right)}$} \mathord{\left/ {\vphantom {{\cos \left( {S\left( {{t_i}} \right) \cdot \left( {k - {t_i}} \right)} \right)} {60}}}\right.} \lower0.7ex\hbox{${60}$}}。\hfill \\ \end{gathered} \right. $

式中： $ f\left( k \right) $ 为雷达单元1的时间序列信号； $ r\left( k \right) $ 为雷达单元2的时间序列信号； $ S\left( {{t_i}} \right) $ 为雷达扫描周期。

2.4 导航雷达机动目标跟踪过程的信号处理

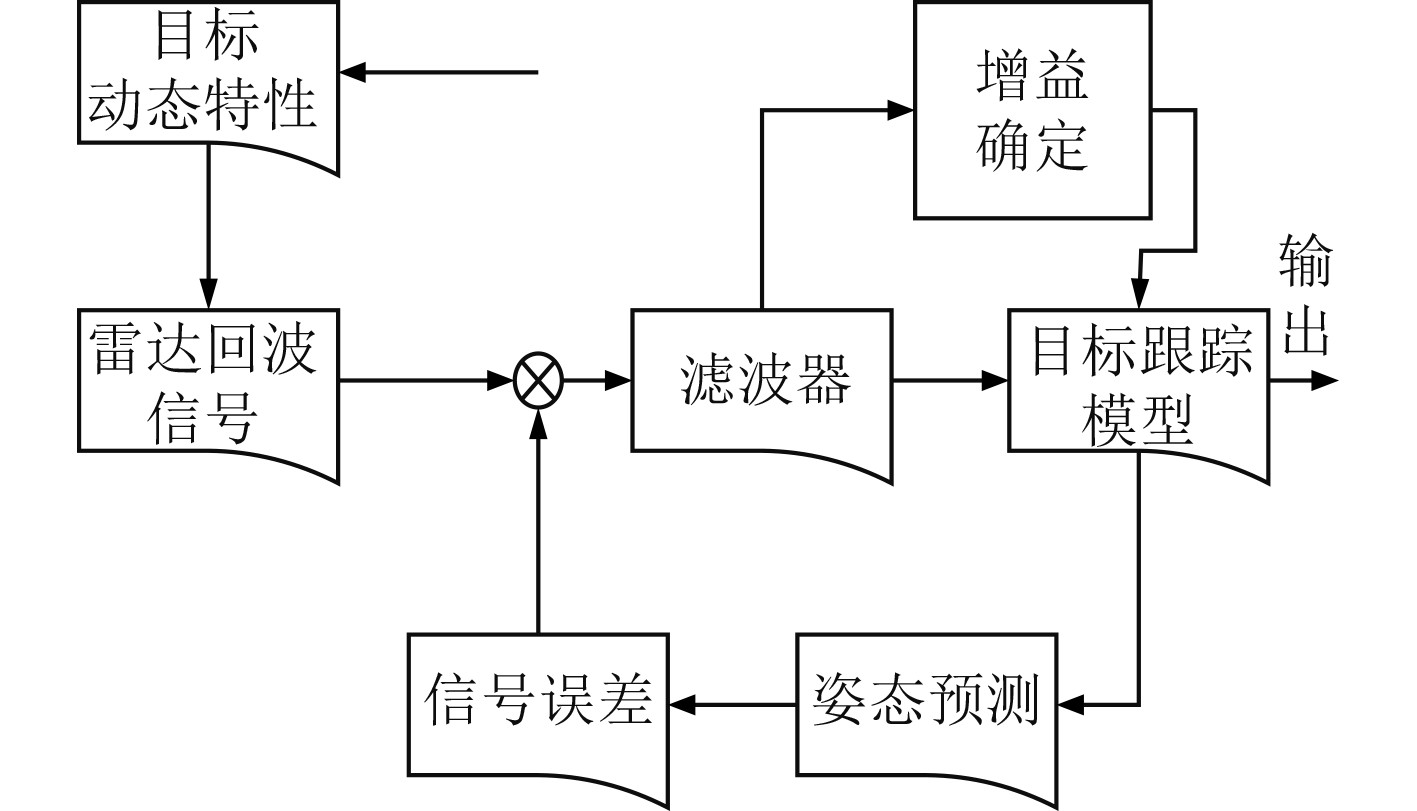
在船舶雷达导航系统中，机动目标跟踪的精度与信号处理密切相关，需要进行自适应滤波，单个机动目标的跟踪原理图如图4所示。

假设船舶导航系统第i个雷达天线发射的信号为：

$ {s_i}(t) = {k_i}(t){e^{j2\text{π} {f_e}t}} \text{。} $

式中： $ {k_i}(t) $ 为基带信号； $ {f_e} $ 为天线的工作频率。雷达天线阵列之间满足：

$ \int {} {k_i}(t){k_j}(t - \tau ){\rm{d}}t = 0 \text{，} $

式中：i，j为整数。

假设导航系统中共有N个雷达天线，天线采集的回波信号可表示为：

$ R = \left\{ {\begin{array}{*{20}{l}} {{\zeta _t}{K_t}\sqrt {\frac{E}{t}} {Q_r} + {n_t}}，&{{S_1}} ，\\ {{n_t}}，&{{S_0}} 。\end{array}} \right. $

式中： $ {\zeta _t} $ 为回波信号的RCS系数^[6]； $ {K_t} $ 为信号增益； $ {n_t} $ 为空信号； $ E $ 为天线功率； $ {Q_r} $ 为阵列增益； $ {S_1} $ 为目标可被探测； $ {S_0} $ 为目标处于盲区。

雷达发射信号的调频如下式：

$ f(t) = \exp \left[ {j2\text{π} \left( {\frac{1}{2}\mu {t^2} + {f_0}t} \right)} \right] \text{，} $

式中： $ \mu $ 为波长； $ {f_0} $ 为调制频率^[7]。

则机动目标k的跟踪模型为：

$ H(k,t) = \sqrt {\frac{{{E^2} \cdot {\xi _t}}}{{{{(4\text{π} )}^3} \cdot {r^4}{E_0}}}} \times \exp \left\{ {2\text{π} \left[ {{f_d}t + \frac{1}{2}r{{\left( {t - {\tau _i}} \right)}^2}} \right]} \right\} \text{。} $

式中： $ {E_0} $ 为功率损耗； $ {f_d} $ 为多普勒频率； $ {\tau _i} $ 为回波信号的时延。

2.5 导航系统的机动目标跟踪系统试验

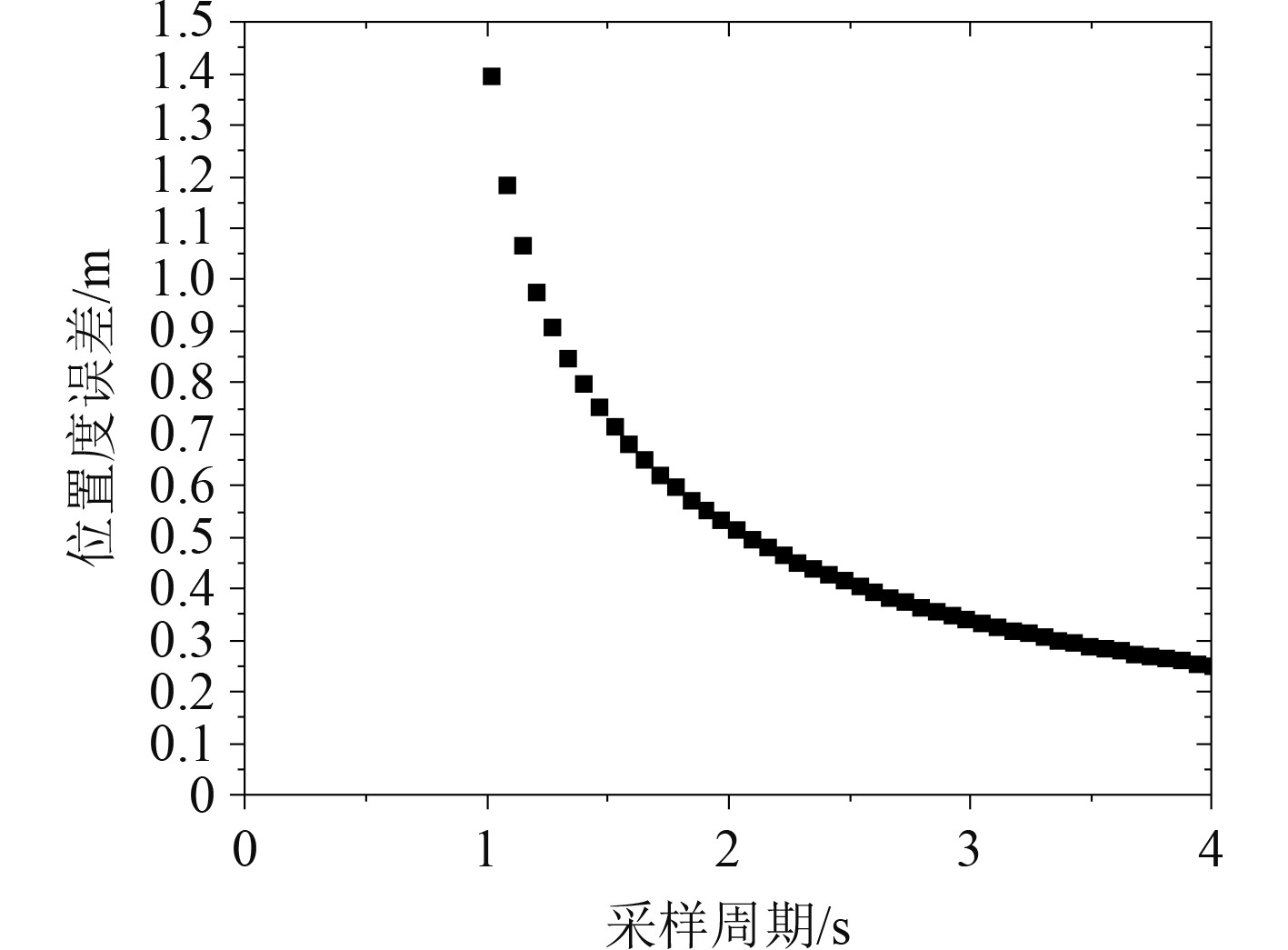
将雷达的采样周期设定为T=4s，机动目标的初始位置设置为随动坐标系下坐标 $ \left( {5,5,5} \right) $ ，采样点数为200个，船舶雷达航行速度为20 kn，计算导航雷达目标跟踪的位置度误差，得到图5所示的误差数据。

图中可见，导航系统的机动目标跟踪误差呈逐渐降低的趋势。

3 结　语

船舶导航系统雷达在机动目标跟踪过程中发挥着重要的作用，本文建立了一种机动目标高精度跟踪系统，从系统的基本架构、运动建模、雷达信号处理和性能测试等方面进行详细研究。