0 引　言

船舶数量的提升，造成水域中船舶密度较大，航道与港口拥挤度成线性趋势变化^[1]。水域中水道繁琐程度较高，且船舶类型颇多，令船舶碰撞危险发生概率增加。通过规划路线，可降低能源消耗^[2-3]，节省成本，有效躲避障碍物，保证船舶航行的安全性^[4]。传统船舶航行路线由专家绘制，专家通过分析风速与天气等因素，手动绘制一条无障碍物的短距离航线，但这种方法费时费力，又容易遗漏关键信息。因此，对船舶航行路线进行精准规划具有重要意义。

曹旺等^[5]以船舶航行安全与平滑度为目标，构建路径规划模型，通过改进NSGA−Ⅲ算法求解该模型，通过在NSGA−Ⅲ算法内添加安全、平滑与修复等算子，该算法可有效规划船舶路径，规划效率高，但该算法仅适用于障碍物为静态状态时的路径规划，当障碍物为动态状态时，则提升碰撞危险。倪生科等^[6]以船舶安全与路径长度等为目标，以非线性规划为规划原则，构建路径规划模型，利用遗传算法求解该模型，以迭代方式获取模型的最佳解，输出最佳路径规划方案，该算法具备一定的可行性^[6]，但该算法未考虑船舶航行的外部环境，路径规划影响因素考虑不全面，容易发生碰撞危险，且遗传算法收敛速度较慢。神经网络利用神经元构建而成，具备较优学习能力，在无规律及存在不确定因素的情况下，具备较优容错性与鲁棒性^[7]，应用效果佳。船舶航行过程中存在很多的不确定性因素，且无规律可循。因此，本文提出一种基于神经网络精准规划船舶航行路线的算法，合理规划航行路线，精准避开障碍物，提升船舶航行安全。

1 精准规划船舶航行路线算法 1.1 基于神经网络的船舶航迹提取 1.1.1 基于神经网络的船舶航迹预测模型

利用2个输入、输出端以及一个隐层建立BP神经网络模型，令船舶航向为ρ，航速为v，经、纬度为 $ \Delta \varphi $ 、 $ \Delta \lambda $ ，将ρ、v作为模型的输入。将 $ \Delta \varphi $ 、 $ \Delta \lambda $ 作为模型的输出，即船舶航迹预测结果，获取船舶路线规划环境^[8]。

令输入层 $ {C_1} $ 与隐层 $ {C_2} $ 间的权重为 $ {w_{ij}} $ ， $ {C_1} $ ， $ {C_2} $ ，输出层 $ {C_3} $ 的神经元编号为i，j，k； $ {C_2} $ 与 $ {C_3} $ 间的权重为 $ {w_{jk}} $ 。

利用BP神经网络预测船舶航迹的步骤如下：

步骤1　初始化 $ {w_{ij}} $ 与 $ {w_{jk}} $ ；

步骤2 将ρ，v， $ \Delta \varphi $ ， $ \Delta \lambda $ 作为训练样本x，输入BP神经网络模型；

步骤3　计算 $ {C_2} $ 内每个神经元输出，公式如下：

$ {g_j} = \frac{{\displaystyle\sum\limits_{i = 1}^2 {{w_{ij}}{x_i}} }}{{1 + {e^{ - x}}}} 。$

(1)

步骤4　计算 $ {C_3} $ 内每个神经元的输出，公式如下：

$ {y_k} = \frac{{\displaystyle\sum\limits_{j = 1}^\varpi {{w_{jk}}{g_j}} }}{{1 + {e^{ - x}}}} ，$

(2)

其中， $ \varpi $ 为 $ {C_3} $ 内神经元数量。

步骤5　调整 $ {w_{jk}} $ ，公式如下：

$ {w_{jk}} = {w_{jk}} + \eta \frac{{\displaystyle\sum\limits_n {{w_{jk}}{g_n}} }}{{1 + {e^{ - x}}}}\left( {{t_k} - {y_k}} \right){g_j} 。$

(3)

其中， $ {t_k} $ 为样本；η为学习率。

步骤6　调整 $ {w_{ij}} $ ，公式如下：

$ {w_{ij}} = {w_{ij}} + \eta \frac{{\displaystyle\sum\limits_m {{w_{mj}}{x_m}} }}{{1 + {e^{ - x}}}}\left[ {\sum\limits_n {{y_n}\left( {1 - {y_n}} \right)\left( {{t_n} - {y_n}} \right){w_{jn}}} } \right]{x_i}。$

(4)

其中，m为训练样本数量；n为样本数量。

步骤7　若符合终止训练条件，输出 $ \Delta \varphi $ 、 $ \Delta \lambda $ ，即航迹预测结果，反之，重复步骤2至步骤6。

1.1.2 基于GA优化的船舶航迹预测模型

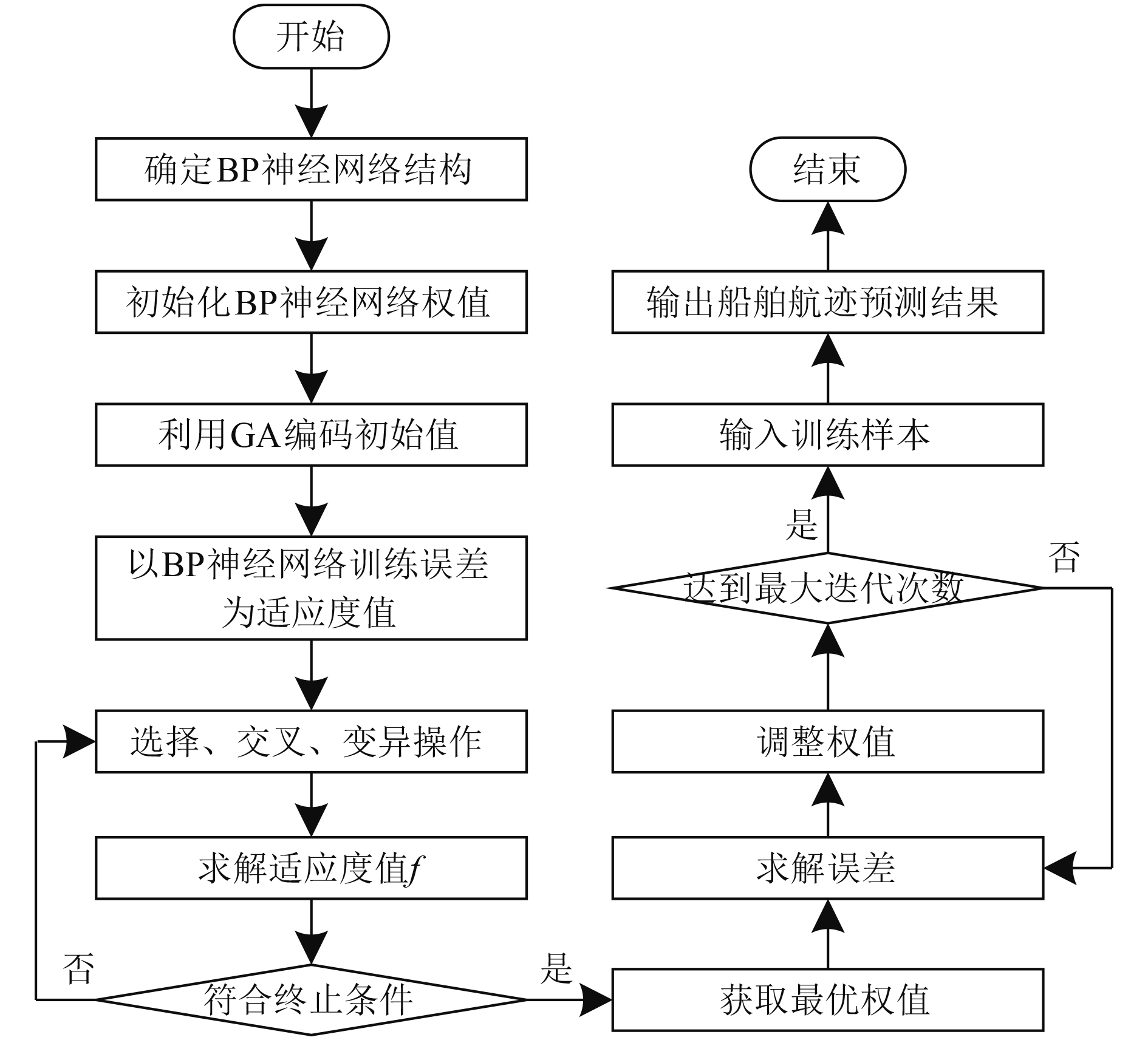
BP神经网络预测船舶航迹时，权值影响航迹预测精度，通过GA优化BP神经网络的权值，提升船舶航迹预测精度，优化流程如图1所示。

令BP网络的每个参数为GA的染色体B，将BP网络的实际与期望输出之差当成B的f，经由全部遗传操作^[9,10]，以迭代方式，获取负符合终止条件的最佳B，即BP网路权值，将其作为BP网络的初始参数，优化BP网络。在优化后的BP网络内输入ρ和v，输出 $ \Delta \varphi $ 和 $ \Delta \lambda $ ，即船舶航迹预测结果，根据船舶航迹预测结果，获取本船舶航行时，水域中其余船舶航迹，获取本船舶航行时的路线规划环境。

1.2 精准规划船舶航行路线算法设计 1.2.1 马尔可夫的船舶航行路线规划的决策过程

船舶航行时下个状态仅和当下状态信息相关，和先前状态无关。在马尔可夫决策过程（Markow decision process，MDP）中，即船舶航行路线规划时，下个状态既与当下状态相关^[11]，又与当下执行的动作相关。在某个状态R时，执行动作b，此时没有办法得到下个状态 $ {H^*} $ ，且与H和b相关，同时无需考虑很早以前的状态与动作，即H与a影响 $ {H^*} $ 。船舶航行的各操作均会影响其航行环境^[12-13]，为此能够由MDP解决船舶航行路线规划问题。

令解决船舶航行路线规划问题的MDP为 $M = \left( {H,B,P,\gamma ,R} \right)$ 。其中，H为船舶航行状态集合， $ {h_\alpha } $ 为时刻α船舶航行状态；B为船舶航行动作集合， $ {b_\beta } $ 为第β个动作；P为H的转移概率，在 $ {h_\alpha } $ 情况下，经过 $ {b_\beta } $ 后， $ {h_\alpha } $ 改变至 $ h' $ 的概率为 $ P_{hh'}^b $ ；后续奖励值对当下船舶航行状态的影响为γ，γ与船舶航行路线规划对于后续奖励的在意程度呈正比，当 $ \gamma = 0 $ 时，说明船舶航行路线规划时仅考虑当下奖励；回报函数为 $R:H \times B \to R$ ，期望奖励为 $ R_{hh'}^b = E\left[ {\mu {r_{\alpha + 1}}\left| {{h_\alpha } = h,{h_{\alpha + 1}} = h',{b_\alpha } = b} \right.} \right] $ ，修正系数为μ，期望为E。

MDP的动态过程是智能体即船舶的初始状态为 $ {h_0} $ ，在B内选择一个 $ {b_0} $ 并执行，依据 $ P_{hh'}^b $ 将智能体转移至下一个 $ {h_1} $ 内，再执行 $ {b_1} $ ， $ {h_1} $ 转移至 $ {h_2} $ ，然后执行 $ {b_2} $ ，反复操作，以全部动作执行完毕为止。每次动作执行后，船舶航行环境均会为当下动作给出立即奖励r。

在船舶航行路线规划策略π时， $ {r_\alpha } $ 没办法确定π的优劣，为此需设置π的长期奖励，由状态值函数 $ {Z^{\text{π}} }\left( h \right) $ 描绘， $ {Z^{\text{π}} }\left( h \right) $ 的计算公式如下：

$ {Z^{\text{π}} }\left( h \right) = {E_{\text{π}} }\left[ {\mu {r_{\alpha + 1}} + \gamma \sum\limits_{k' = 0}^\infty {{\gamma ^{k'}}\mu {r_{\alpha + k' + 2}}\left| {{h_\alpha } = h} \right.} } \right]，$

(5)

其中， $ \gamma \in \left[ {0,1} \right] $ ； $ k' $ 为奖励值编号。

设在某个船舶航行状态时，实施某个动作后，评价该动作的函数为：

$ {Q^{\text{π}} }\left( {h,b} \right) = {E_{\text{π}} }\left[ {\sum\limits_{k' = 0}^\infty {{\gamma ^{k'}}\mu {r_{\alpha + k' + 1}}\left| {{h_\alpha } = h,{b_\alpha } = b} \right.} } \right]。$

(6)

公式（6）代表当下船舶航行状态值和下一状态值间的关系。若下一状态值为已知，则可获取当下船舶航行状态值。计算船舶航行路线规划的MDP，得到船舶航行路线规划的最佳策略网络 $ {{\text{π}} ^*} $ 。

1.2.2 精准规划船舶航行路线算法优化

在α时刻，船舶通过分析当下的其余船舶航迹预测结果，得到该船舶的航行环境状态 $ {H_\alpha } $ ，执行动作 $ {b_\alpha } $ ，再得到一个期望奖励 $ {r_\alpha } $ ，令 ${R_\alpha } = \displaystyle\sum\limits_{k' = 0}^\infty {{\gamma ^{k'}}\mu {r_{\alpha + k' + 1}}}$ 。船舶在航行路线规划策略π内，选取需执行的动作，当下π内H执行b能够得到的回报是 $ {Q^{\text{π}} }\left( {h,b} \right) $ ，当下π内H可得到的回报期望是 $ {Z^{\text{π}} }\left( H \right) $ ，公式如下：

$ \begin{gathered} {Z^{\text{π}} }\left( H \right) = {E_{a \sim {\text{π}} \left( h \right)}}\left[ {{Q^{\text{π}} }\left( {h,b} \right)} \right] ，\hfill \\ {Q^{\text{π}} }\left( {h,b} \right) = E\left[ {{R_\alpha }\left| {{h_\alpha } = h,{b_\alpha } = b,{\text{π}} } \right.} \right] \hfill 。\\ \end{gathered} $

(7)

按照贝尔曼方程，动态递归求解，船舶航行状态动作函数 $ {Q^{\text{π}} }\left( {h,b} \right) $ ，公式如下：

$ {Q^{\text{π}} }\left( {h,b} \right) = {E_{h'}}\left[ {\mu r + \gamma {E_{b' \sim {\text{π}} \left( h \right)}}\left[ {{Q^{\text{π}} }\left( {h',b'} \right)} \right]\left| {h,b,{\text{π}} } \right.} \right]。$

(8)

令优化函数 $ {Q^{\text{π}} }\left( {h,b} \right) = \mathop {\max }\limits_{\text{π}} {Q^{\text{π}} }\left( {h,b} \right) $ ，在确定船舶航行路线规划策略 $b = \mathop {{{arg{\rm{max}}}} }\limits_{a' \in A} {Q^*}\left( {h,b'} \right)$ 后， ${Z^*}\left( h \right) = \mathop {\max }\limits_b {Q^*} \left( {h,b} \right)$ ，此时将 ${Q^{\text{π}} } ({h,b})$ 变更成：

$ {Q^*}\left( {h,b} \right) = {E_{h'}}\left[ {\mu r + \gamma \mathop {\max }\limits_{b'} {Q^*}\left( {h',b'} \right)\left| {h,b} \right.} \right]。$

(9)

通过在深度强化学习内添加优势函数 ${B^{\text{π}} }\left( {h,b} \right) = {Q^{\text{π}} }\left( {h,b} \right) - {Z^{\text{π}} }\left( h \right)$ ，解决深度强化学习不能搜索全部船舶航行状态空间问题。其中 $ {E_{b \sim {\text{π}} \left( h \right)}}\left[ {{B^{\text{π}} }\left( {h,b} \right)} \right] = 0 $ ，说明船舶航行路线精准规划的期望优势值是0，即 $ b < 0 $ ，则b的执行次数，不影响其总奖励，并且b的总奖励始终低于c。

令船舶航行当下状态为方程Z，船舶执行指定b后的状态为方程Q，则通过 $ {B^{\text{π}} }\left( {h,b} \right) = {Q^{\text{π}} }\left( {h,b} \right) - {Z^{\text{π}} }\left( h \right) $ 衡量b的好坏，通过神经网络近似 $ {B^{\text{π}} }\left( {h,b} \right) = {Q^{\text{π}} }\left( {h,b} \right) - {Z^{\text{π}} }\left( h \right) $ ，即深度强化学习神经网络 $ Q\left( {h,b;\theta } \right) $ ，解决决策网络维度高的问题，神经网络参数为θ，利用损失函数 $ L\left( \theta \right) $ 优化θ，公式如下：

$ L\left( \theta \right) = {E_{h,b,r,h'}}\left[ {\left( {\mu r + \gamma \mathop {\max }\limits_{b'} Q\left( {h',b';\theta ,} \right)} \right) - Q\left( {h,b;\theta } \right)} \right] 。$

(10)

可选取船舶航行动作数量为 $ \left| B \right| $ 。

利用优化θ后，可确定深度强化学习神经网络结构，从而近似船舶航行路线规划的最佳策略网络 $ {{\text{π}} ^*} $ ，确定船舶在航行路线规划策略内，选取需执行动作，完成船舶航行路线精准路线规划。

2 实验分析

通过仿真平台测试本文算法精准规划船舶航行路线的效果，在PC机内，利用Python模拟电子海图环境展开仿真验证，并将实验参数应用在真实电子海图环境内，分析本文算法船舶航行路线规划的优劣。

在真实电子海图系统内，随机选择500张电子海图，作为实验样本，随机选取一幅电子海图，该电子海图内共包含2艘船舶，利用本文算法预测这2艘船舶的航迹，结果如图2所示。

根据图2可知，本文算法可有效预测船舶的航迹，且2艘船舶的经、纬度差预测结果与期望结果相差非常小，说明本文算法具备精准的船舶航迹预测结果，为后续精准规划船舶航行路线提供高精度的数据支持。

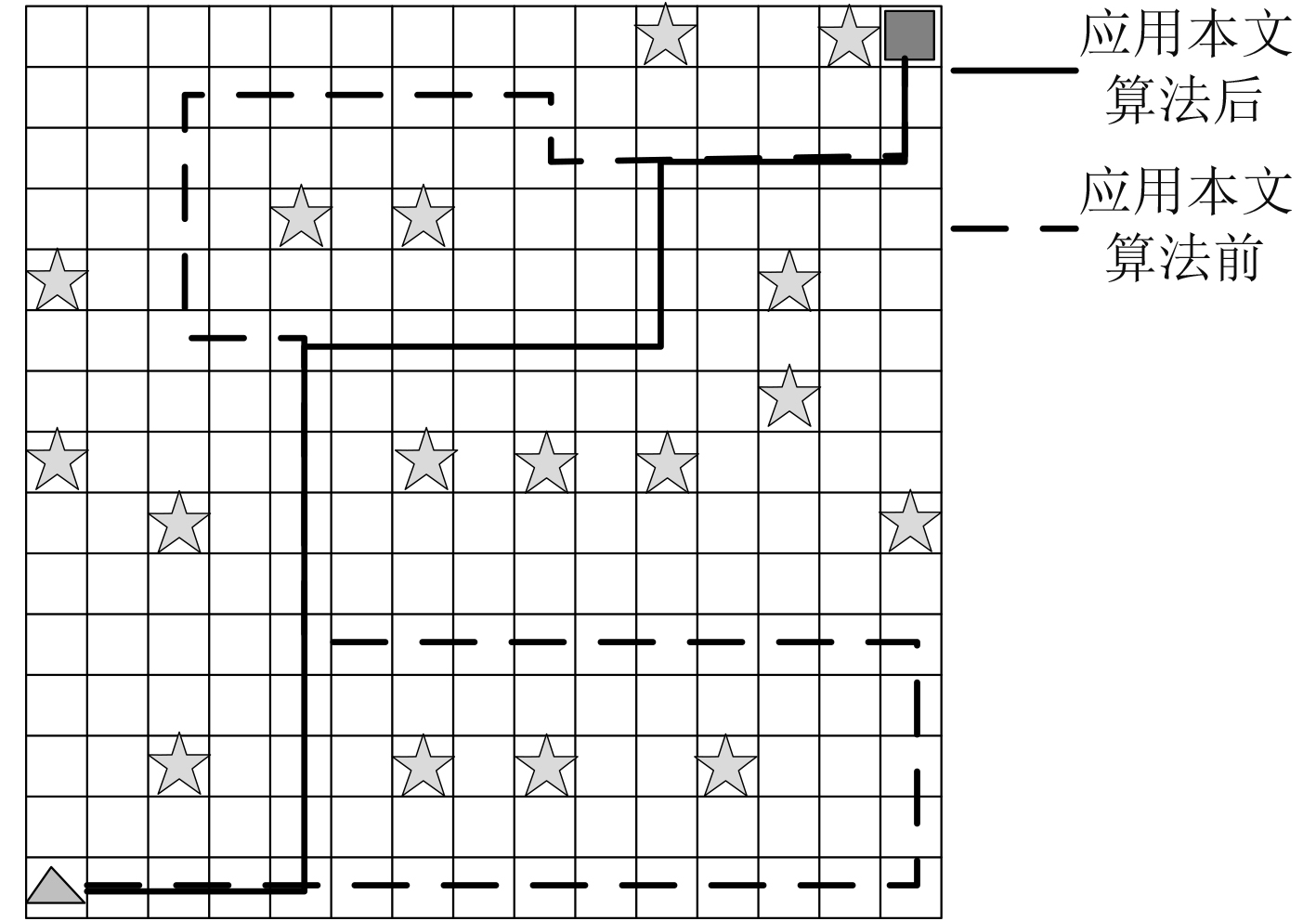
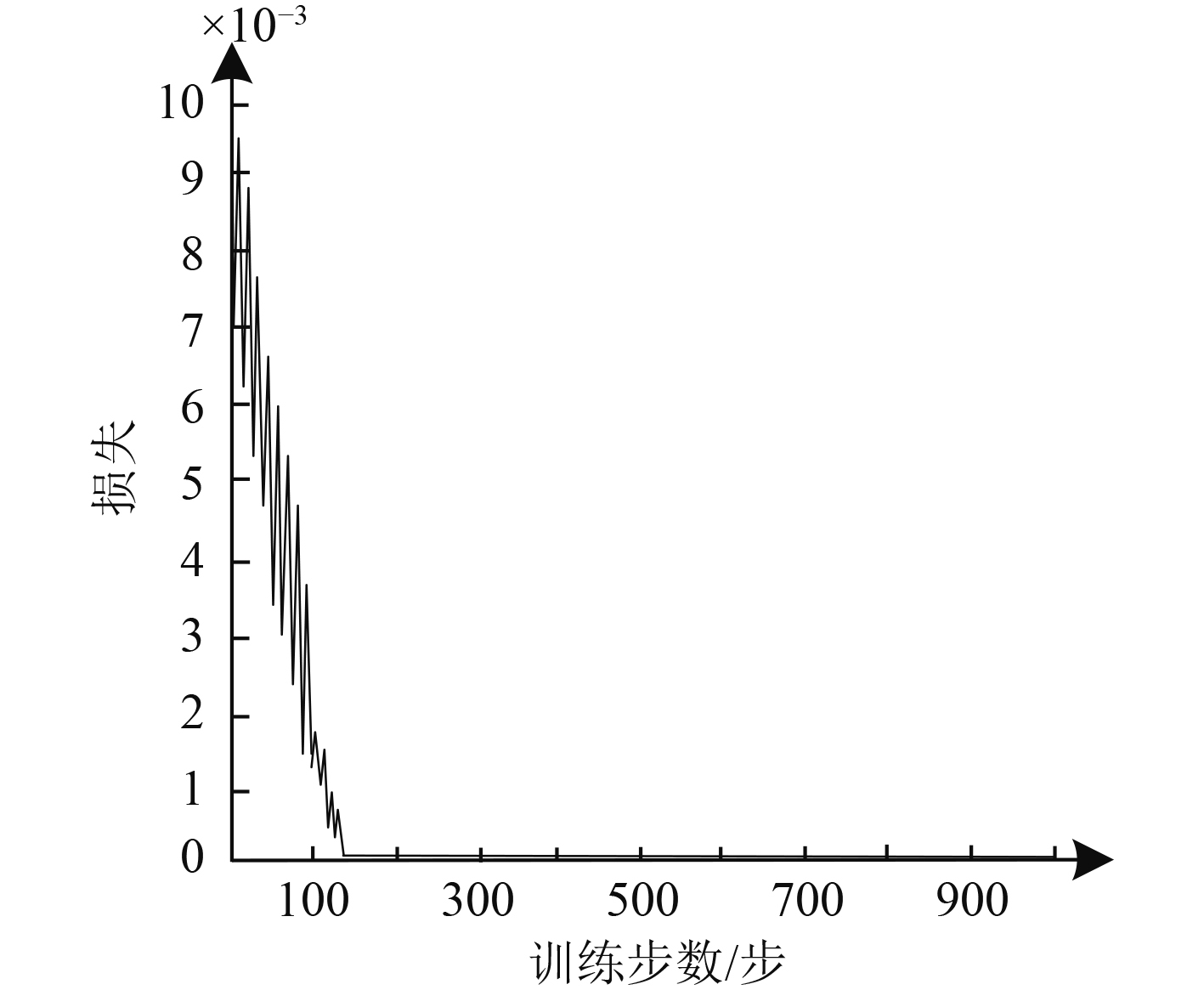
依据500张真实电子海图，生成500张15×15矩阵的电子海图，并在每张电子海图内生成随机障碍，利用五角星代表障碍物，随机选择一张15×15矩阵的电子海图，并在该图内随机生成17个障碍物。利用本文算法根据起始点与目的地，为船舶规划航行路线，规划结果如图3所示；路线规划过程中训练步数和损失间的关系如图4所示。

分析可知，在存在多个障碍物的情况下，应用本文算法后可有效规划船舶航行路线，精准避开障碍物，并与障碍物间存在较大的距离，确保船舶的安全航行，应用本文算法前也可有效避开障碍物，但规划路线长度明显长于应用本文算法后；在规划船舶航行路线时，当训练步数达到140步左右时，本文算法损失值趋于稳定，完成收敛，最终损失值与0较为接近，说明本文算法规划船舶航行路线精度较高。因此，本文算法可精准规划船舶航行路线，精准避开障碍物，缩短航行路线长度。

航行路线规划结果如图5所示。

可知，本文算法可有效规划本船舶的航行路线，精准避开其他船舶，避免出现碰撞危险。

船舶实际航行水域，包含狭窄运河水域与宽广湖泊水域，分析本文算法在2种水域时，会遇、追越与交叉相遇场景下的航行路线规划效果，共规划200次路线，最大航迹点平均距离偏差为50 m，分析结果如表1所示。

可知，在2种水域及3种场景下，本文算法均可有效规划船舶航行路线，碰撞次数均为0次，精准避免发生碰撞危险，最低船舶转向正确概率是98 %，最大航迹点平均距离偏差仅有14.1 m，明显低于最大距离偏差值。实验证明：在不同水域及场景下，本文算法均可精准规划船舶航行路线，确保船舶航行过程中无碰撞危险，提升船舶转向正确概率，降低航迹点平均距离偏差。

3 结　语

为精准避开船舶航行过程中障碍物，缩短航行时间，提出基于神经网络精准规划船舶航行路线的算法。通过预测水域中各船舶航行轨迹，获取本船舶航行环境，合理并精准规划航行路线，避免发生碰撞危险，缩短航行路线，节约航行时间，提升船舶航行的安全性与经济性。