0 引　言

船舶通信网络包括内通和外通，内通以内部各系统的通信、内部指挥、广播、监控报警等任务为主，外通是指船舶与外部环境之间的通信，以船-岸、船-船（艇）等任务为主。船舶的内通和外通网络存在明显的区别，内通以有限通信网络为主，包括Internet通信、总线通信等；外通以无线网络为主，配合无线电、雷达等通信方式。船舶的内部和外部通信网络是密不可分的关系，保证船舶通信网络的质量也是确保船舶正常运行的关键^[1]。

由于海上通信环境及硬件设备的因素，船舶通信网络链路不可避免会发生时延和数据丢包，本文研究的目的在于建立船舶网络丢包率的预测模型，对一定时域内的数据完整性进行预测，从而指导船舶通信网络的链路搭建。

1 最小二乘法与支持向量机理论的基本研究

支持向量机是一种常用的数理统计技术，最初是针对模式识别场景开发而来的，本文基于支持向量机技术进行船舶网络丢包率数据的统计和分析，并搭建网络丢包率预测数学模型。

支持向量机技术通常与最小二乘法结合使用，能够有效提高样本数据的分类和规律提取，其基本原理如下：

假设 $ y $ 为系统的因变量， ${x_1},{x_2},\cdots,{x_n}$ 为自变量，首先建立系统的线性回归方程：

$ y = \frac{{{\alpha _0}}}{2} + {\alpha _1}{x_1} + {\alpha _2}{x_2} + \cdots,{\alpha _n}{x_n} + {\delta _x} \text{，} $

其中， $ {\delta _x} $ 为线性回归方程的随机误差， $ {\delta _x} $ 的方差 $ E\left( {{\delta _x}} \right) = 0 $ 。

系统的每个自变量 ${x_1},{x_2},\cdots,{x_n}$ 又包含n次随时间变化的数据，建立n组样本为：

$ y = \frac{{{\alpha _0}}}{2} + {\alpha _1}{x_{i1}} + {\alpha _2}{x_{i2}} + \cdots,{\alpha _n}{x_{in}} + {\delta _{ix}} \text{，} $

用矩阵的形式表示为：

$ {\boldsymbol{Y}} = \left[ \begin{gathered} {y_1} \hfill \\ {y_2} \hfill \\ \cdots \hfill \\ {y_n} \hfill \\ \end{gathered} \right] \text{，} {\boldsymbol{X}} = {\left[ {\begin{array}{*{20}{c}} 1&{{x_{11}}}&{\cdots}&{{x_{1p}}} \\ 1&{{x_{21}}}&{\cdots}&{{x_{2p}}} \\ {\cdots}&{\cdots}&{\cdots}&{\cdots} \\ 1&{{x_{n1}}}&{}&{{x_{np}}} \end{array}} \right]_p} \text{，} $

基于最小二乘法的回归是通过样本的规律特性对所有系统进行线性预测，定义系统参数 $\alpha = {\left[ {{\alpha _0},{\alpha _1},\cdots,{\alpha _p}} \right]_{}}^{\rm{T}}$ 的线性回归预测值为 ${\boldsymbol{A}} = {\left[ {{\alpha _0},{\alpha _1},\cdots,{\alpha _p}} \right]_{}}^{\rm{T}}$ ，表示为向量形式：

$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\boldsymbol{Y}}} = {\boldsymbol{X}}A \text{，} $

预测偏差用下式计算：

$ e = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\boldsymbol{Y}}} - {\boldsymbol{Y}} \text{，} $

预测偏差越小，证明线性回归模型越贴近实际情况，表示为：

$ {\left| e \right|^2} = {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\boldsymbol{Y}}} - {\boldsymbol{Y}}} \right)^{\rm{T}}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\boldsymbol{Y}}} - {\boldsymbol{Y}}} \right) \to \min \text{，} $

对预测偏差方程求解：

$ \frac{\partial }{{\partial A}}{\left| e \right|^2} = - 2{{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{Y}} + {{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{X}}A = 0 \text{，} $

可以获得数据的最小二乘估计为：

$ {\boldsymbol{Y}} = {\boldsymbol{X}}{\left( {{{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{X}}} \right)^{ - 1}}{{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{Y}} 。$

在最小二乘法的数据基础上，利用支持向量机技术进行数据整理。

样本 ${x_1},{x_2},\cdots,{x_n}$ 为支持向量机SVM分类对象，建立集合 $ S = \left( {{x_i},{y_i}} \right),{x_i} \in {R^{}} $ ，在样本数据中，存在线性函数 $ f\left( x \right) = w{x_i} + b = 0 $ 将样本数据分为两类，定义 $ f\left( x \right) $ 为支持向量机的超平面^[2]。

支持向量机SVM的数据分类误差用下式计算：

$ \Delta \delta = \frac{{w{x_i} + b}}{{\left| w \right|}} 。$

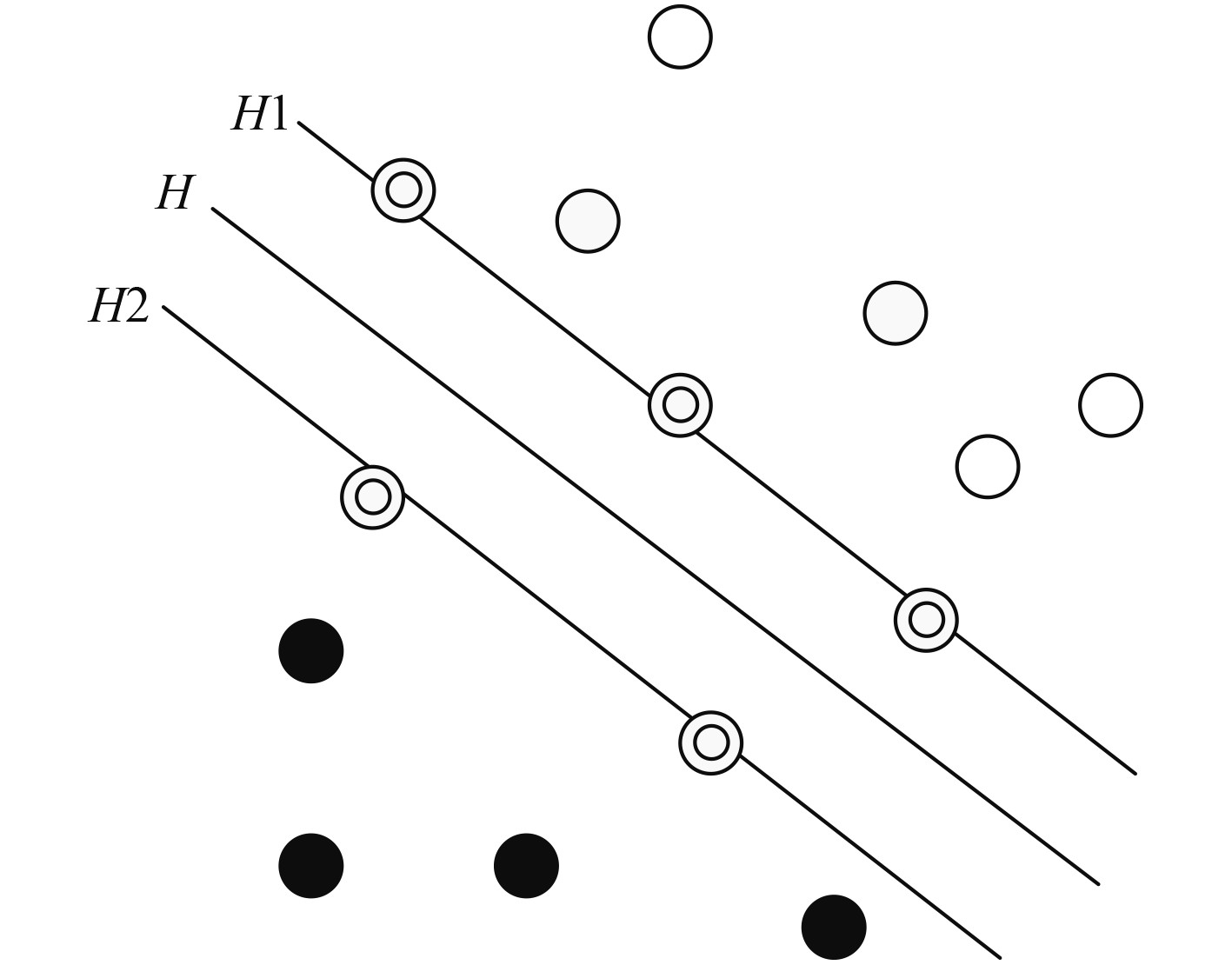
系统样本数据的支持向量机分类示意图如图1所示。

2 基于支持向量机的船舶网络丢包率预测技术 2.1 DSR网络路由协议

网络路由协议对于通信网络的数据传输质量有关键影响，针对海上复杂的通信条件，采用DSR路由协议作为船舶通信的基本路由协议^[3]。

DSR路由协议是一种基于源路由方式的协议，按照源路由节点的需求构成数据链路。与表驱动路由协议不同，DSR路由协议的节点可以不负责网络拓扑信息的维护，因此链路组网的形式更加灵活，具有较高的灵活性。

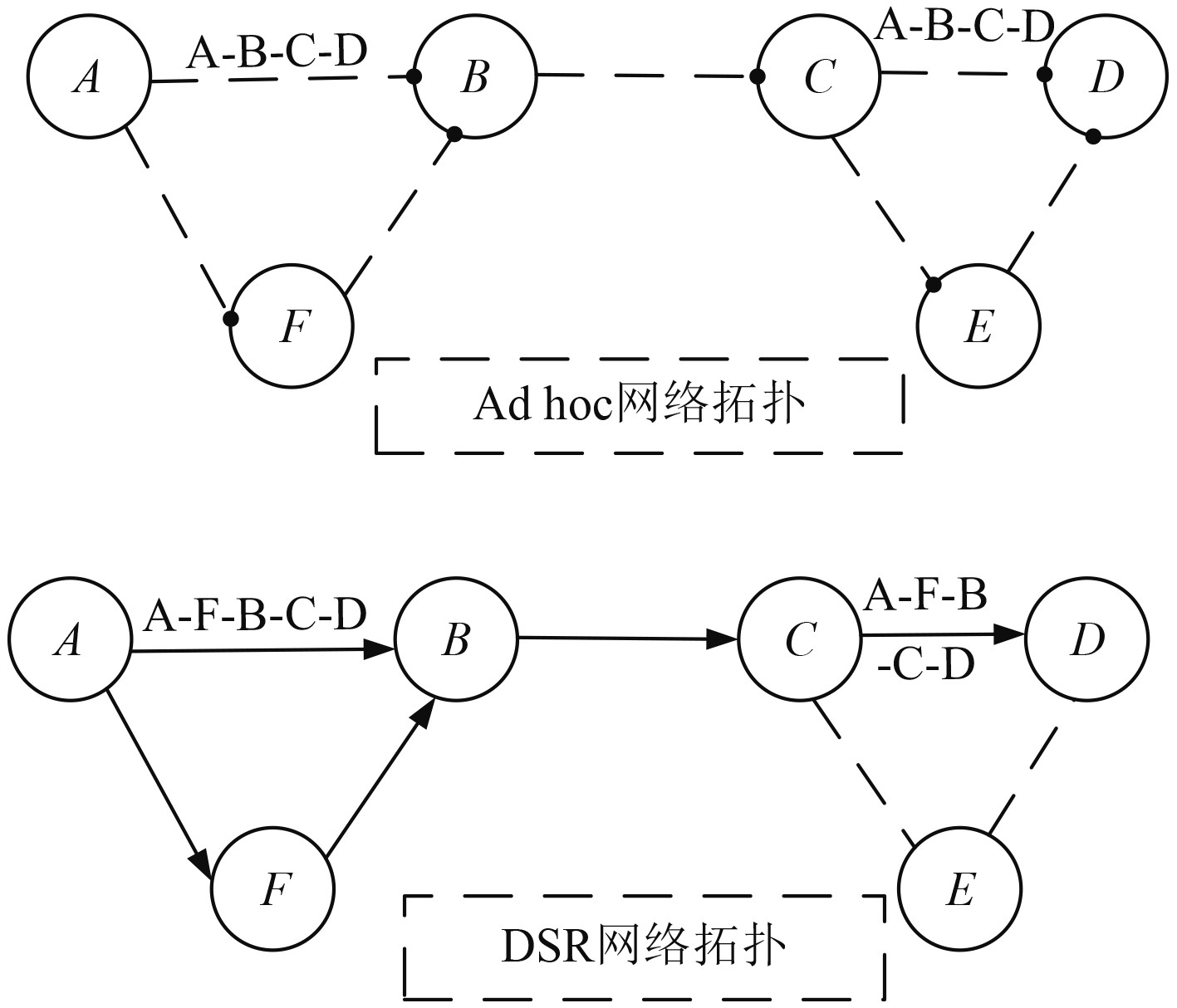
图2为Ad hoc网络拓扑与DSR网络拓扑的结构对比：

如图2，DSR网络拓扑具有路由局部修复功能，当链路A-B中断或其他故障发生时，DSR网络拓扑中的路由A-B-C-D失效，可以在网络中临时构建A-F-B路由代替故障链路，使拓扑变为A-F-B-C-D。

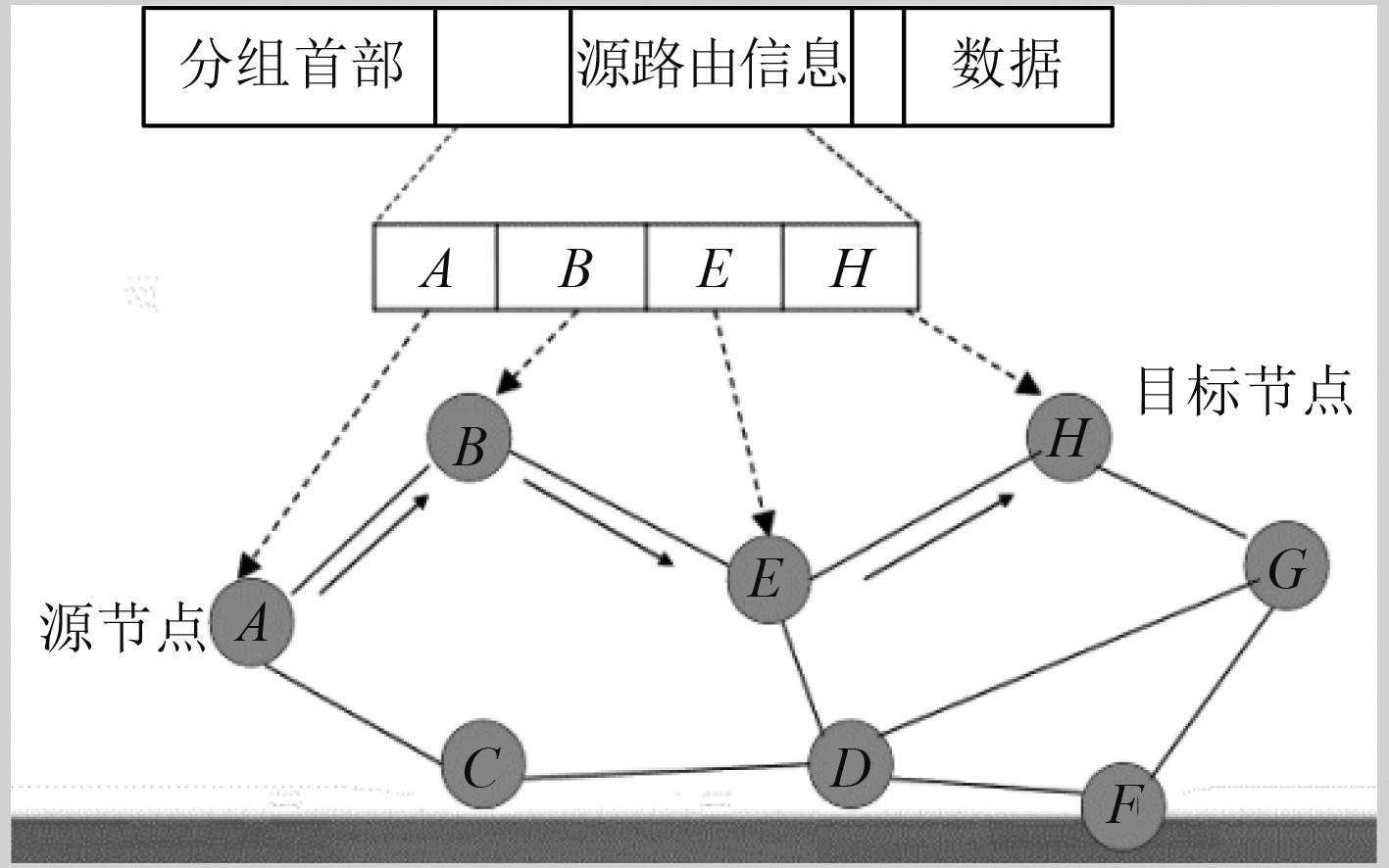
DSR网络路由协议的工作原理如图3所示。

DSR网络路由协议的特点有：

1）分离节点机制

在DSR拓扑网络中，由于数据传输的时延及数据量需求，网络拓扑中的相交节点数量要多于分离节点，DSR中的分离节点随着传输距离的增加而减少，分离节点起到链路冗余设计的功能，当主链路中的节点出现故障无法工作时，分离节点可被激活，并代替故障节点进行数据链路的组建。

2）备份路由机制

备份路由机制同样也是为了提高DSR网络^[3]的可靠性，备份路由往往不唯一，源节点会备份多个路由，一旦某些路由链路出现故障，源节点在发送数据报文时会选择最佳备用路由来发送数据报文。

2.2 基于支持向量机的船舶网络丢包率预测模型

采用支持向量机技术构建船舶网络的丢包率预测模型，主要包括动态预测系数矩阵的建立、预测数学模型的搭建等。

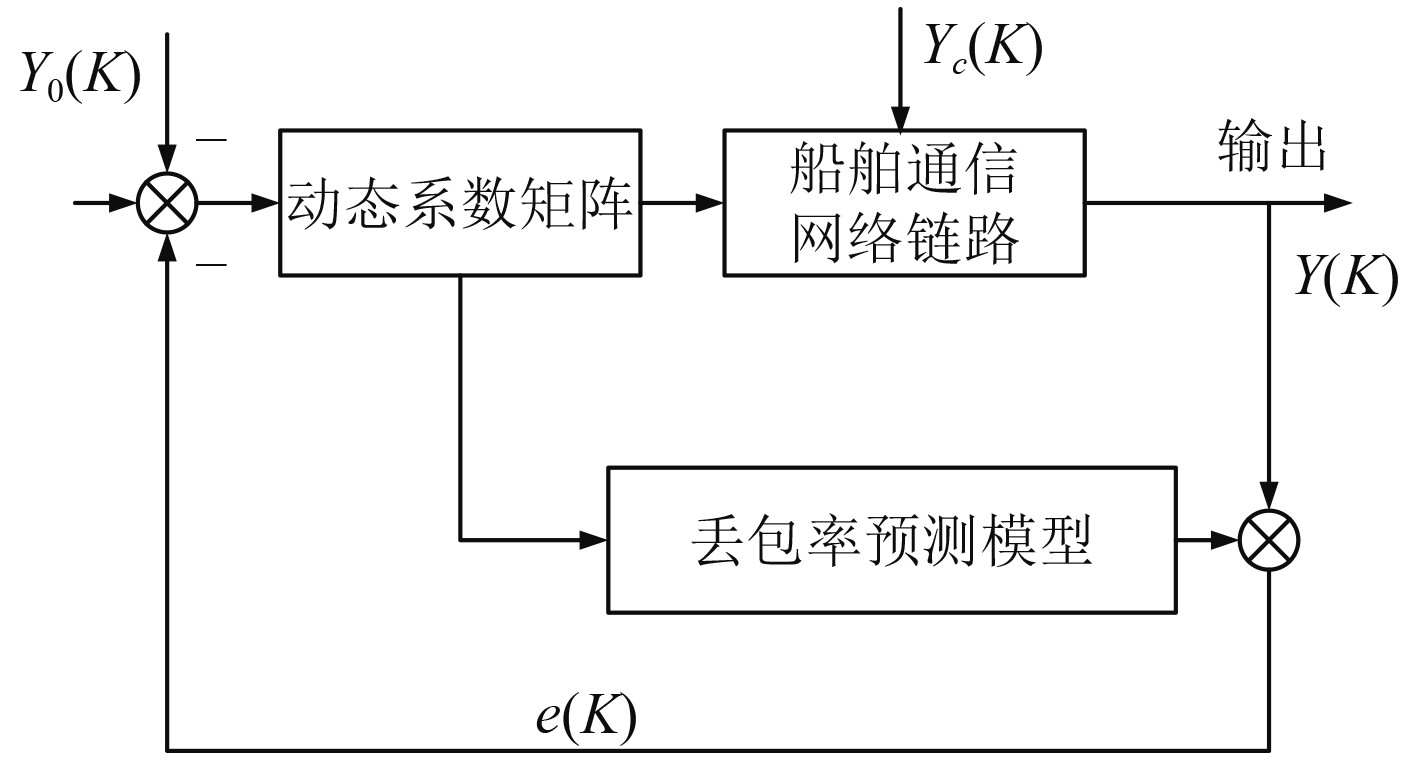
如图4所示， $ {Y_c}\left( K \right) $ 为参考数据， $ {Y_0}\left( K \right) $ 为网络丢包率数据初始值， $ Y\left( K \right) $ 为预测模型的输出， $ e\left( K \right) $ 为预测误差。

假设船舶网络的数据丢包率训练样本为：

$ \left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right),\cdots,\left( {{x_n},{y_n}} \right) \text{，} $

由最小二乘及SVM原理建立系统的预测模型为：

$ y(x) = \sum\limits_{k = 1}^N {{a_k}} \phi {(x)^T}\phi \left( {{x_k}} \right) + b = \sum\limits_{k = 1}^N {{a_k}} K\left( {x,{x_k}} \right) + b \text{，} $

其中， $ \phi (x) $ 为二次回归方程， $ b $ 为0-1之间的实数， $ K\left( {x,{x_k}} \right) $ 计算方法：

$ K\left( {x,{x_k}} \right) = \exp \left\{ { - {{\left| {x - {x_k}} \right|}^2}/2{\sigma ^2}} \right\} \text{，} $

式中 $ \sigma $ 为样本方差。

在DSR网络的节点位置进行m次阶跃响应试验，计算阶跃响应系数^[4]如下：

$ a_i^{} = \frac{{{y_j}(k + i) - {y_0}(k + i)}}{{\Delta {u_j}}},\quad i = 1,2, \cdots ,m \text{，} $

$ \Delta {u_j} $ 为第j次阶跃试验的控制参数，对试验获取的阶跃响应系数 $ a_i^{} $ 进行加权平均，得到：

$ {\bar a_i} = \sum\limits_{j = 1}^m {{q_j}} a_i^j,\quad i = 1,2, \cdots ,m \text{，} $

其中， $ {q_j} $ 为加权系数，满足 $\displaystyle \sum\limits_{j = 1}^m {{q_j}} = 1$ ，最终得到网络丢包率预测模型的动态系数矩阵为：

$ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{a_1}}&0&0&{}&{}&{} \\ {{a_2}}&{{a_1}}&{}&0&{}&{} \\ \cdots&{{a_2}}&{{a_1}}&{}&0&0 \\ {}&\cdots&{{a_2}}&{}&{}&{} \\ {{a_{L + 1}}}&{}&{}&{{a_3}}&0&0 \\ {{a_m}}&{{a_{m - 1}}}&\cdots&{}&{{a_{m - L + 1}}}&{{a_{m - L + 2}}} \end{array}} \right] 。$

2.3 基于支持向量机的船舶网络丢包率预测试验

NS (Network Simulator)是一个性能优异且开源的网络仿真平台，可以完成诸如链路搭建、路由分析、丢包率检测等众多功能，使用NS2.0版本^[5]进行基于支持向量机的船舶网络丢包率预测试验。

为了提高网络试验的真实性，在DSR网络节点之间加入随机的TCP流，并设置网络中的骨干链路具有比较高的带宽。

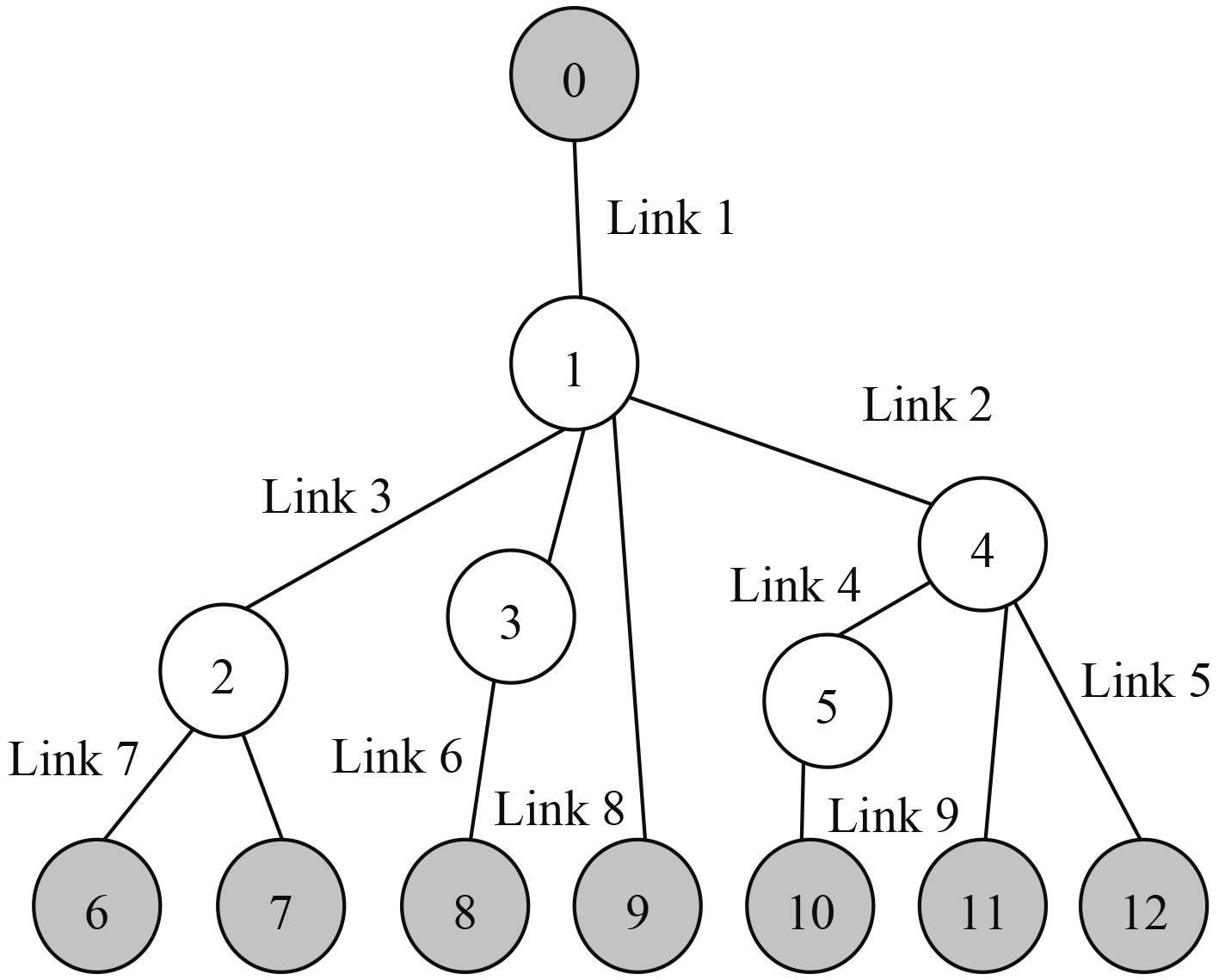
针对船舶通信网络的DSR网络拓扑进行数据丢包率的仿真试验，首先构造一个用于仿真的网络拓扑，如图5所示。

如图，网络中共有节点12个，0节点为源节点，构成链路为link1-link9^[6]。

在NS2仿真平台中设置船舶通信网络的参数如表1所示。

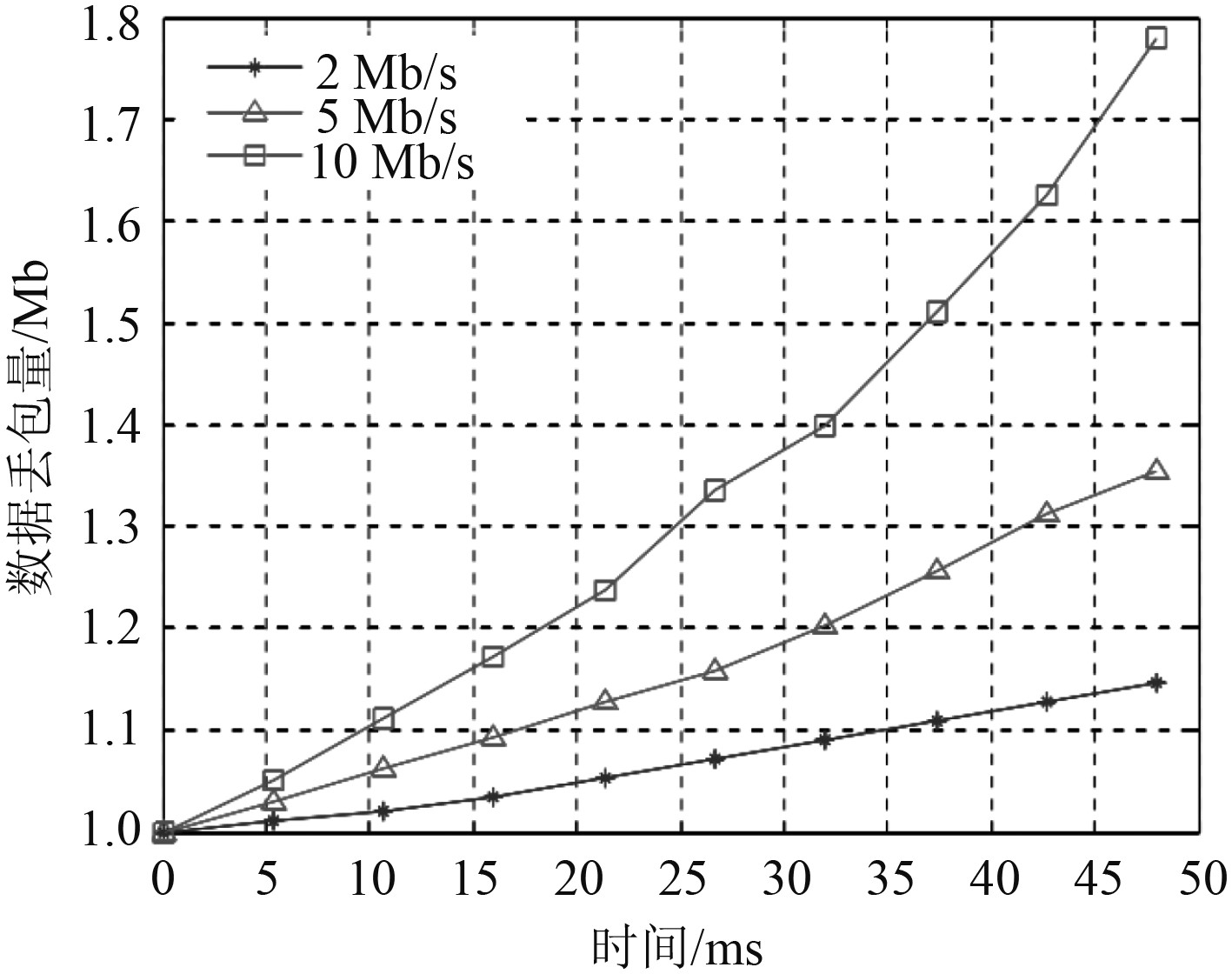
设网络源节点的发包数据量为1000 bytes，速率为 2 Mb/s，5 Mb/s，10 Mb/s，加入网络中的TCP流为200条，速率为0.2 Mb/s。图6分别对比了3种发包速率的网络数据丢包率。

3 结　语

本文结合支持向量机技术建立了船舶网络丢包率预测模型，结合NS2软件平台进行了船舶DSR通信网络的数据丢包率预测，有助于提高船舶通信网络的优化设计。