舰船通信网络是信息传输的核心,大量数据信息在交互过程中主要以数据流量的模式完成,信息的内容、安全性对舰船通信安全存在直接影响。所以,准确估计舰船通信网络流量具有现实意义[1-3]。
目前对网络流量的估计方法不在少数[4-5],曹素娥等[6]主要以聚类分析算法和优化支持向量机为主,需要构建通信网络模型实现流量估计,此类方法仅可使用在小规模网络流量估计问题中。陈浩杰等[7]主要以深度学习方法为主,需要挖掘通信网络流量中的大数据,估计效率也会受到影响。
数据驱动是近几年各大领域都十分关注的数据处理方法,在信号处理问题中,常见的数据驱动技术有小波变换、经验模态分解等。在人工智能方面,常见的数据驱动技术有卷积神经网络、支持向量机,此类方法对大数据问题都有较好的处理效果,处理效率快,且适用于大规模数据处理问题中。本文结合数据驱动技术的优越性,提出基于大数据驱动与分析的舰船通信网络流量智能估计方法,主要使用经验模态分解技术、卷积神经网络对舰船通信网络流量实现精准的智能估计。
1 基于大数据驱动的舰船通信网络流量估计方法 1.1 改进集合经验模态分解的舰船通信网络信号降噪方法为了高精度估计舰船通信网络流量,必须采取有效方法去除舰船通信网络流量的噪声,优化舰船通信网络流量质量[8]。因外界环境所影响,舰船通信网络流量不可避免地存在噪声,导致流量变化不具有平稳性。相关资料显示,经验模态分解方法属于数据驱动方法,可以对舰船通信网络流量这种具有大数据特征的信息进行有效去噪,存在数据驱动价值[9]。
改进集合经验模态分解方法先把存在噪声的舰船通信网络信号x(m)实施集合经验模态分解,获取首次分解的固有模态函数分量v1j(m)。再通过相关系数完成阈值滤波处理,相关系数为:
| $ d\left( j \right) = \sum\limits_{i = 1}^M {x\left( m \right){v_{1j}}\left( m \right)} /\sqrt {\sum\limits_{i = 1}^M {{x^2}\left( m \right)\sum\limits_{i = 1}^M {v_{1j}^2\left( m \right)} } }。$ | (1) |
式中:
相关系数原理显示,在初步去噪阶段,如果舰船通信网络信号信噪比较高,首个相关系数很小,自第2个相关系数开始便会变大,这时需要去掉首阶分量实施信号重构;如果舰船通信网络信号信噪比较小,自首阶至第
将首次分解获取的噪声主导型固有模态函数分量实施二次集合经验模态分解,使用固有模态函数分量v2j(m),获取尺度指数β2j。判断第二次去噪时有效分量主导型固有模态函数分量序数值为:
| $ h_\delta ^* = \max \left\{ {{h_\delta }\left| {{\beta _{2j}} < {\varepsilon _\delta }} \right.} \right\}{v_{2j}}\left( m \right),$ | (2) |
| $ {\varepsilon _\delta } = 0.56{v_{2j}}\left( m \right) - 0.2{\beta _{2j}}{v_{2j}}\left( m \right) 。$ | (3) |
其中:
为分析2次分解的固有模态函数分量的尺度关系,把2次分析获取的有效固有模态函数分量实施重构[12],则
| $ x'\left( m \right) = r\left( m \right){\varepsilon _\delta } + \sum\limits_{j = p}^{{N_1} - 1} {{v_{1j}}\left( m \right){\varepsilon _\delta }} + {s_{{N_1}}}\left( m \right){\varepsilon _\delta }。$ | (4) |
其中:
设置舰船通信网络流量每个属性都属于一种随机事件,通过信息熵判断每个属性相应的流量集中与分散状态,获取舰船通信网络流量的粗粒度描述,构建舰船通信网络流量时间序列图描述属性之间的关系。
去噪后舰船通信网络信号
| $ R\left( S \right) = - x'\left( m \right)\sum\limits_{j = 1}^m {Q_j^2}。$ | (5) |
式中,Qj为属性的某数值出现概率,
信息熵可以充分描述不存在差异的属性中相应的流量数据的集中状态与分散状态,特别是舰船通信网络流量中,数据集中度较高,熵值较小,数据分散度较高,熵值较大。
使用属性1、属性2构建舰船通信网络流量的时间序列图,主要步骤如下:
1)点的描述。把信息熵信息实施归一化,把其数值映射至0~1之间,之后结合映射后数值分解成4种级别,级别信息如表1所示。将源/目的IP、源/目的端口的4个点依次设成
|
|
表 1 映射数值级别 Tab.1 Mapping value level |
2)边的描述。设置
| $ {\varpi ^t}\left( {a,b} \right) = \frac{{{R^t}\left( {{A_{1i}}} \right) - {R^t}\left( {{A_{2i}}} \right)}}{{{R^t}\left( {{B_{1i}}} \right) - {R^t}\left( {{B_{2i}}} \right)}}。$ | (6) |
边权重可描述此边2个端点信息熵在
结合所述方法,在各个时刻采样点中均衍生无向赋权图,整个时间序列中时间序列图。
1.3 基于卷积神经网络的网络流量预测方法将舰船通信网络流量时间序列分解成第2层舰船通信网络信号的近似信号施加序列
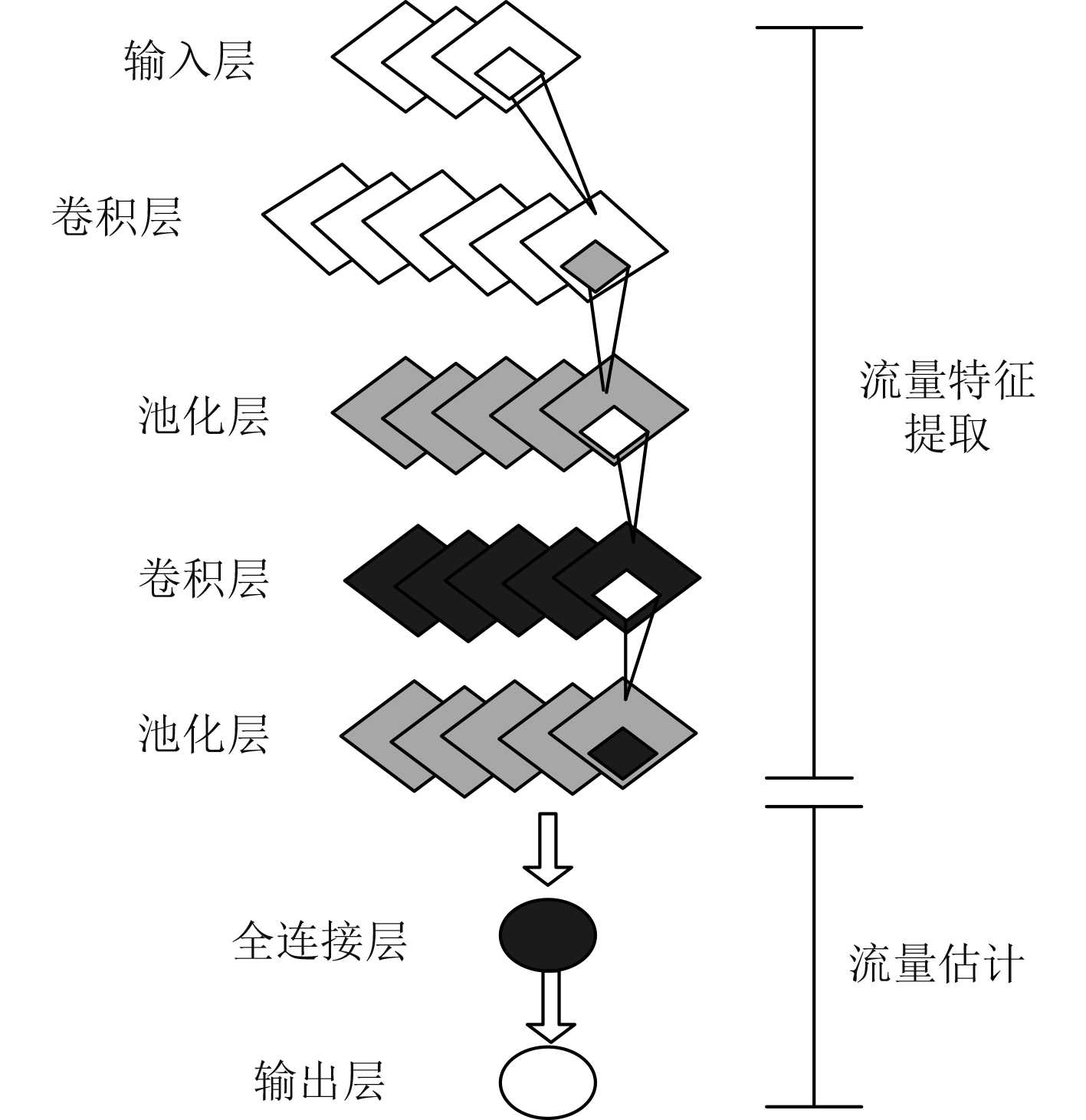
|
图 1 卷积神经网络结构图 Fig. 1 Structure diagram of convolutional neural network |
卷积神经网络输入层的数量如果设置不当,便会增加舰船通信网络流量估计耗时,降低估计精度。为此,使用相关性S(k)这一指标设置卷积神经网络输入层与输出层的具体信息:
| $ S\left( k \right) = \frac{{F\left[ {\left( {{Y_t} - {\lambda _t}} \right)\left( {{Y_{t + h}} - {\lambda _{t + h}}} \right)} \right]}}{{{\theta ^2}}} 。$ | (7) |
式中:
舰船通信网络流量特征提取层神经元的数量设置方法为:
| $ M = \sqrt {n + m} + b 。$ | (8) |
式中:n、m分别为输入神经元数量、输出神经元数量;
差异尺度下的舰船通信网络流量时间序列能够描述流量的随机成分,因为随机成分平稳性较差,使用本文卷积神经网络预测网络流量细节信号的流量信息,将预测值使用小波重构,获取最后的网络流量估计信息:
| $ Y\left( t \right) = \sum\limits_{i = 0}^i {{E_i}\left( t \right)} {\text{ + }}{B_i}\left( t \right) 。$ | (9) |
其中:Ei(t),Bi(t)依次为第
使用某舰船通信链路不同时间粒度的网络流量数据测试本文方法的估计效果,实验中主要使用图2所示的2种流量进行测试。
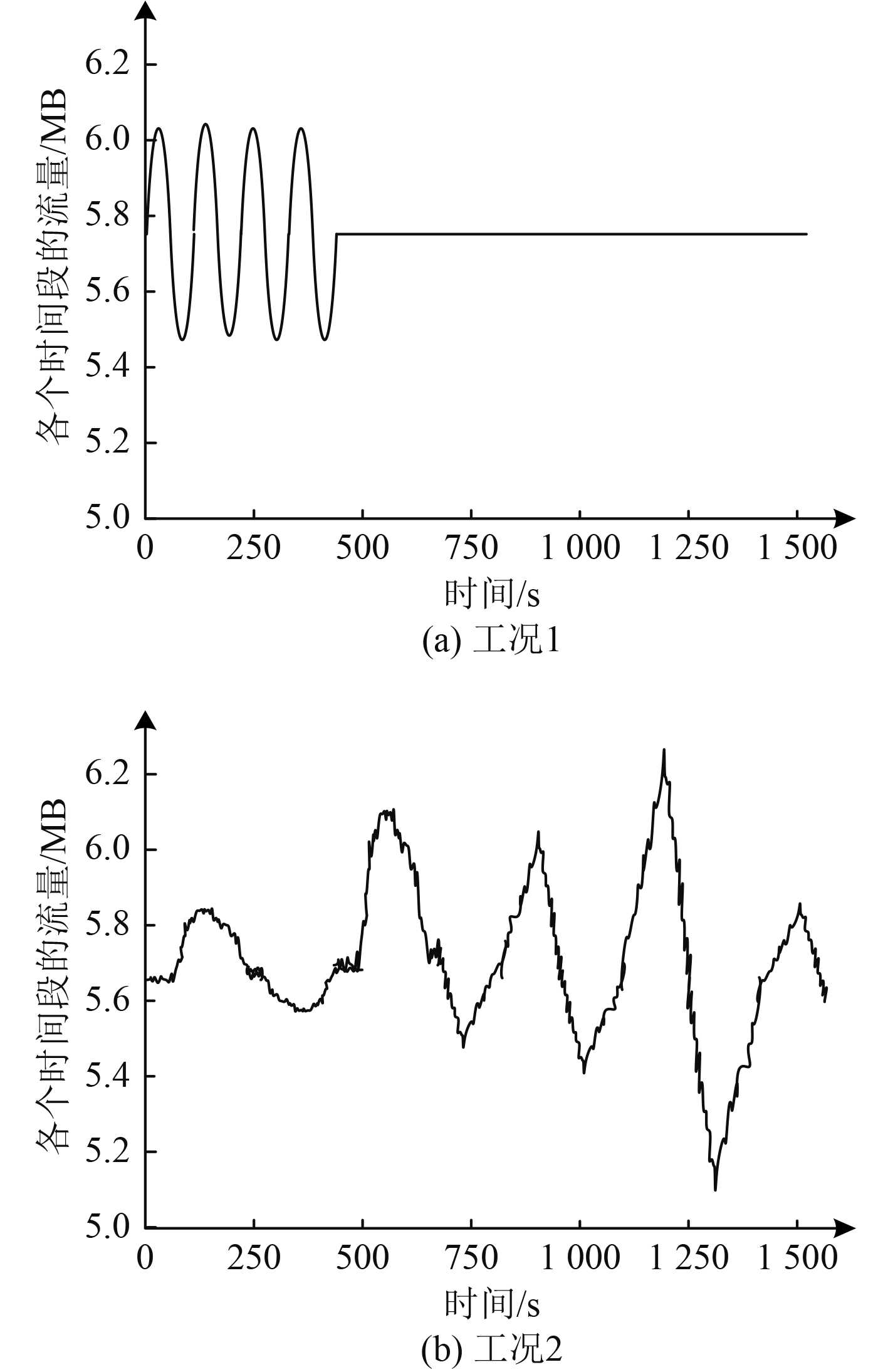
|
图 2 某舰船通信链路不同时间粒度的网络流量数据 Fig. 2 Network traffic data of a ship communication link with different time granularity |
因为流量数据差异显著,为了优化本文方法在估计流量时的收敛效率,将其实施归一化处理,把该舰船通信链路不同时间粒度的网络流量数据归一化至0~1范围内。对2种工况的流量估计结果如图3所示。可知,2种工况中估计结果与实际值偏差极小,基本一致,本文方法可在不同工况中高精度估计舰船通信网络流量。
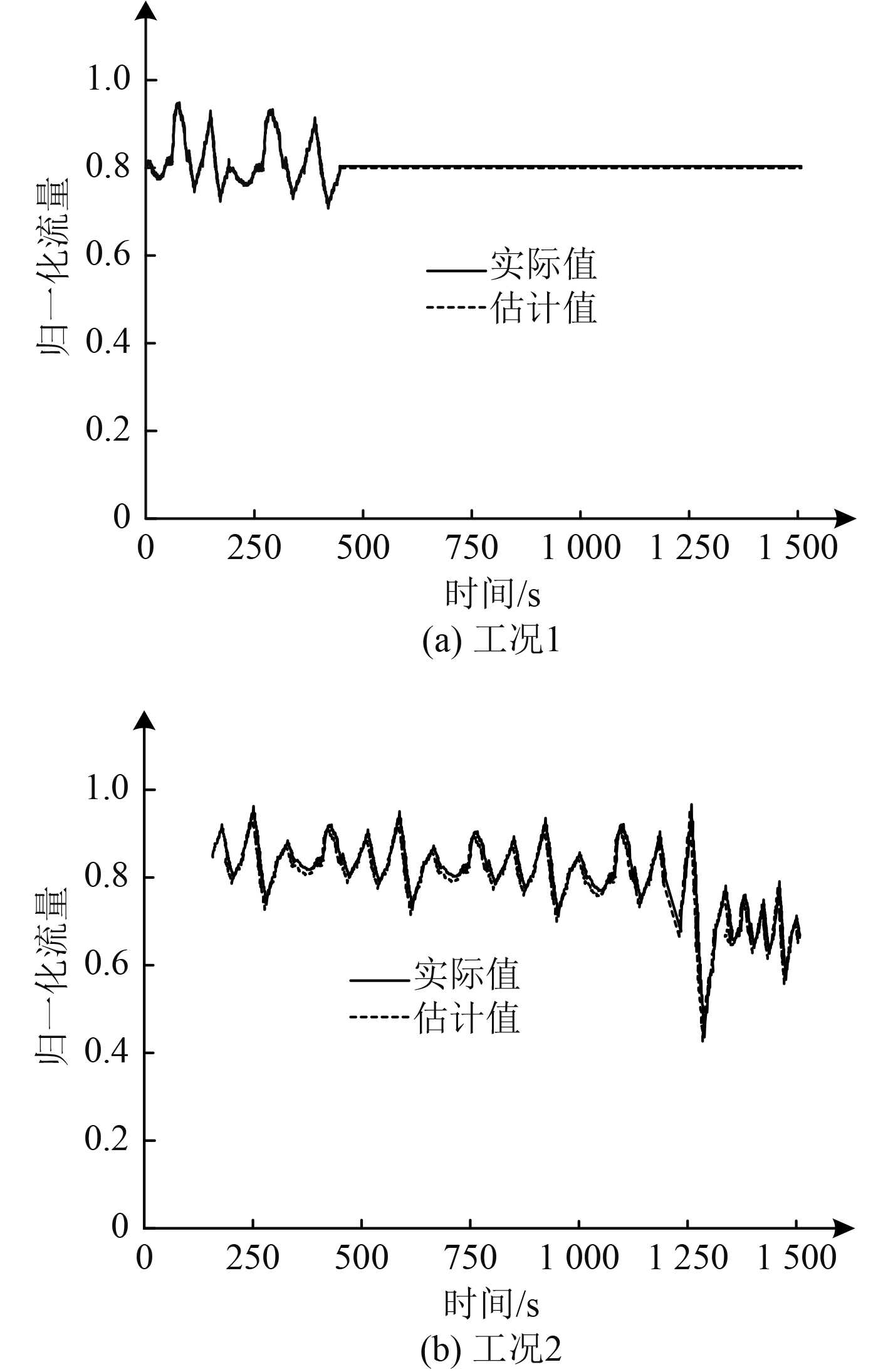
|
图 3 本文方法对舰船通信网络流量估计结果 Fig. 3 This method is used to estimate the traffic of ship communication network |
测试本文方法的抗扰性,在工况1中引入噪声,如图4所示,本文方法对其去噪后的结果如图5所示。从图4和图5可知,加入噪声的舰船通信网络流量信息与原始流量信息存在明显的差异,如果直接进行流量估计,估计误差极大,本文方法处理后的舰船通信网络流量虽然没有与原始舰船通信网络流量信息完全一致,但偏差较小,对流量估计不存在严重影响。由此可见,本文方法具有较好的流量去噪效果,抗扰性较好。
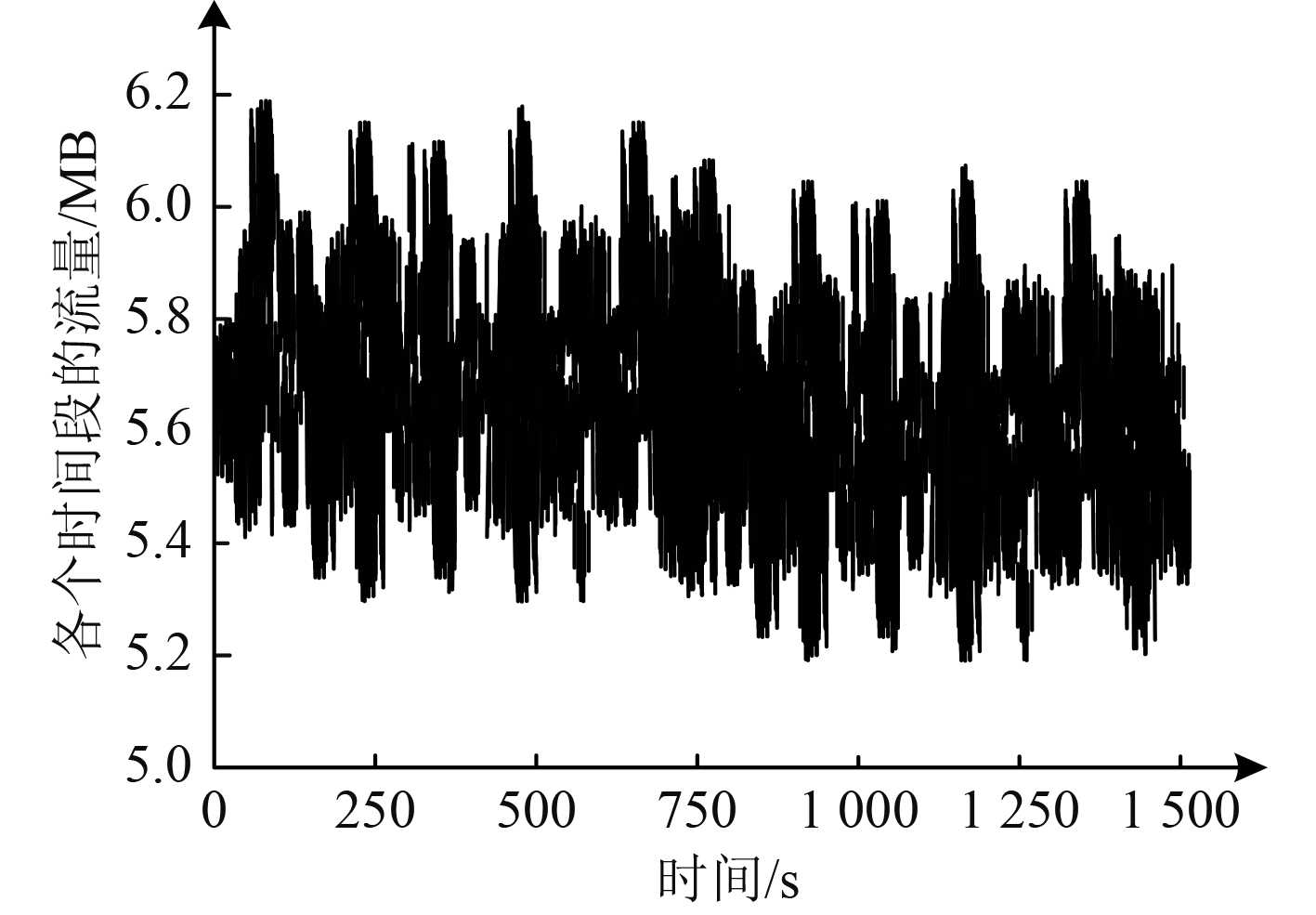
|
图 4 加入噪声的舰船通信网络流量 Fig. 4 Ship communication network traffic with noise |
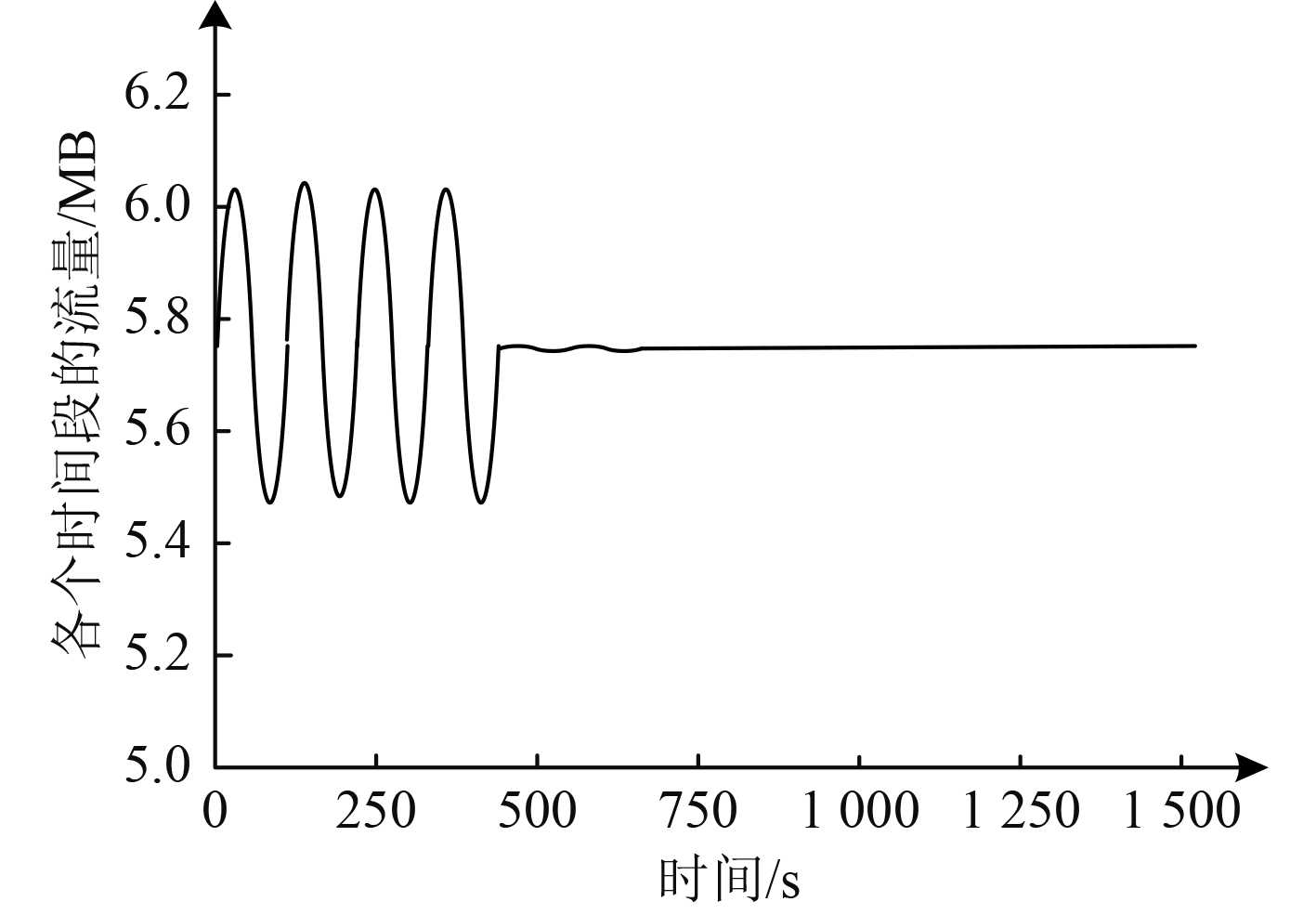
|
图 5 本文方法处理后的舰船通信网络流量 Fig. 5 The ship communication network traffic processed by this method |
本文提出基于大数据驱动与分析的舰船通信网络流量智能估计方法,并在实验中证实了该方法对舰船通信网络流量的估计效果,验证本文方法具有可用性。
| [1] |
徐轶群, 徐弘, 孟令超, 等. 全船无线通信系统网络架构与可靠性研究[J]. 船舶工程, 2021, 43(6): 85-89+95. |
| [2] |
周毅. 智能船舶网络风暴测试及抑制技术[J]. 船海工程, 2021, 50(3): 41-44+48. DOI:10.3963/j.issn.1671-7953.2021.03.011 |
| [3] |
金华标, 肖骁. 基于北斗短报文与4G的内河船载智能终端船岸通信技术[J]. 船海工程, 2021, 50(4): 67-71+76. DOI:10.3963/j.issn.1671-7953.2021.04.015 |
| [4] |
晓敏. 改进灰狼算法优化支持向量机的网络流量预测[J]. 电子测量与仪器学报, 2021, 35(3): 211-217. |
| [5] |
郭佳, 余永斌, 杨晨阳. 基于全注意力机制的多步网络流量预测[J]. 信号处理, 2019, 35(5): 758-767. |
| [6] |
曹素娥, 杨泽民. 基于聚类分析算法和优化支持向量机的无线网络流量预测[J]. 计算机科学, 2020, 47(8): 319-322. |
| [7] |
陈浩杰, 黄锦, 左兴权, 等. 基于宽度&深度学习的基站网络流量预测方法[J]. 郑州大学学报(工学版), 2022, 43(1): 7-13. |
| [8] |
郭芳, 陈蕾, 杨子文. 基于MGU的大规模IP骨干网络实时流量预测[J]. 山东大学学报(工学版), 2019, 49(2): 88-95. |
| [9] |
张杰, 白光伟, 沙鑫磊, 等. 基于时空特征的移动网络流量预测模型[J]. 计算机科学, 2019, 46(12): 108-113. DOI:10.11896/jsjkx.181102207 |
| [10] |
戴宏亮, 罗裕达. 基于蝙蝠算法优化反向传播神经网络模型的无线网络流量预测[J]. 计算机应用, 2021, 41(S1): 185-188. |
| [11] |
许绘香, 曹敏, 马莹莹. 基于大数据分析的非线性网络流量组合预测模型[J]. 沈阳工业大学学报, 2020, 42(6): 670-675. |
| [12] |
李校林, 吴腾. 基于PF-LSTM网络的高效网络流量预测方法[J]. 计算机应用研究, 2019, 36(12): 3833-3836. |
 2022, Vol. 44
2022, Vol. 44
