2. 河南科技职业大学,河南 周口 466000
2. Henan Vocational University of Science and Technology, Zhoukou 466000, China
电子海图在确保船舶航行安全性和降低操纵成本方面具有不可替代的地位,正因如此,使得电子海图成为业内研究的重要内容之一。为使电子海图的作用得以全面发挥,可以在电子海图系统中引入嵌入式技术,并将显示模块的设计作为系统硬件设计的重点,以此来提高电子海图显示的准确性。
1 嵌入式操作系统随着计算机技术的快速发展和完善,使得嵌入式系统的应用越来越广泛,各种嵌入式操作系统也随之出现,常见的有:VxWorks、Windows CE.net、嵌入式Linux等。其中VxWorks是由美国某公司研制开发,这是一款实时性比较强的嵌入式操作系统,它的内核性能比较高,用户开发环境优化,应用领域涉及通信、军事、航空航天等;嵌入式Liux具有开放的源代码,能够同时完成多项任务,它的体积相对较小,性能高,并且免费使用;Windows CE.net是美国微软公司开发的产品,具有32位、多线程、多任务的特点,其体系结构为独立程序语言,兼容API,确保了操作系统的组件化和ROM化,能够适应不同芯片的要求[1-3]。该操作系统采用当前最为流行的模块化设计思路,从而使组合、配置更加方便。通过对上述嵌入式系统的分析,经过比较后,最终决定采用Windows CE.net。
2 基于嵌入式技术的电子海图系统硬件设计 2.1 数据结构本次设计的电子海图系统采用的是军用矢量格式(Military vector chart format,MVCF)电子海图。电子海图的形式相对较多,矢量式海图便是其中之一,数字化信息分类存储,用线段描述图形。比如2个端点可以表示一条直线,多条线段则可近似为一条曲线。由此使得大量的海图可以更加快捷的进行处理,包括缩小、放大、拼接等。除此之外,还可以了解到各种细微的差别,海图中的关键要素能够以分层的方式显示,操作者能按需选择不同层次的信息,并且还能区分各类区域,如警戒区、危险区,船舶进入此类区域后,系统会自动发出报警提示。由于矢量式海图所具备的诸多特点,使其被内业人士称为智能化海图。国际海事组织成员国航道测量局对海图数据库进行批量的更新和维护。根据性质的不同,大体上可将海图内的地理要素细分为以下层次:低洼地带与高层点、陆地方位物、地貌、水系、交通运输桥、火车站、公路、飞机场、管线和垣栅架空索道、电力线、城墙、地面管道、海洋陆地明礁、岸线、滩线等[4-7]。
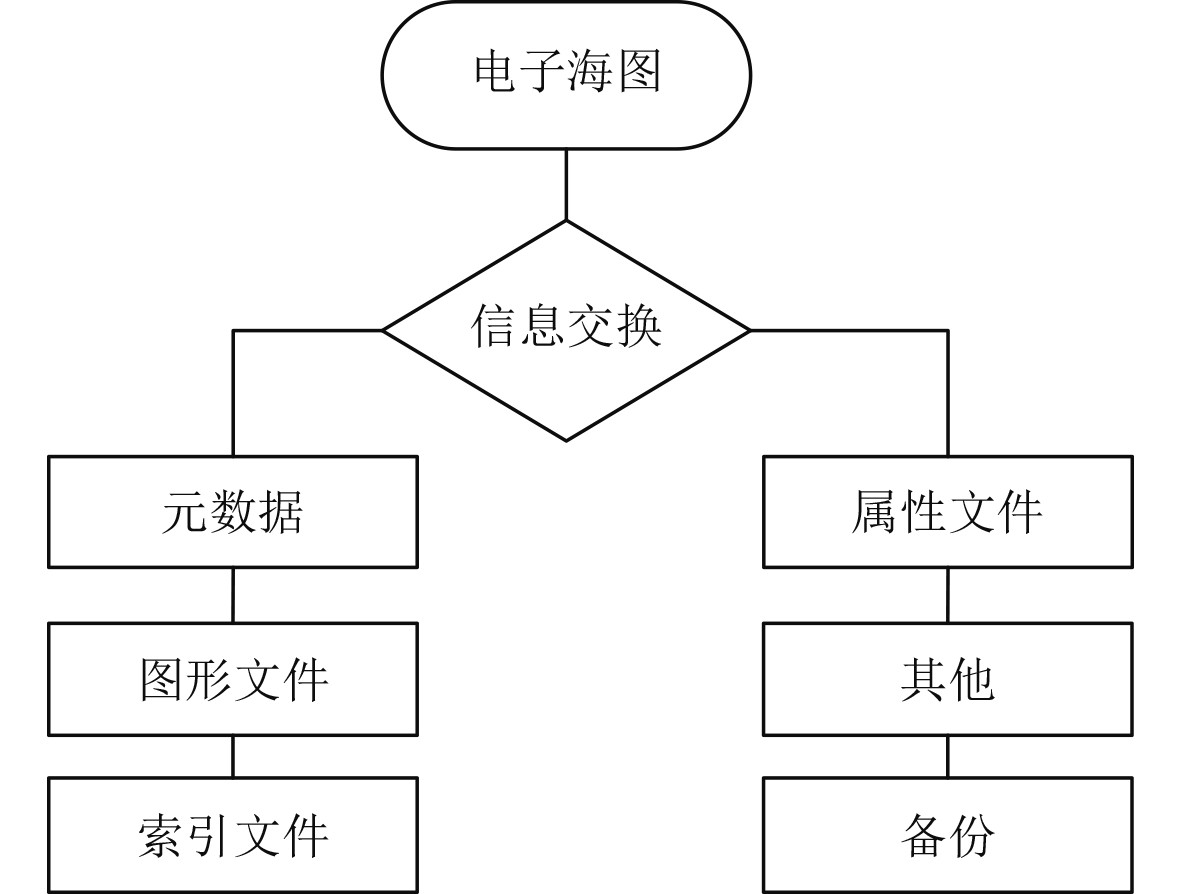
MVCF文件中包含了多个子文件,如元数据、图形、索引、属性等,如图1所示。
|
图 1 军用矢量格式电子海图组织结构示意图 Fig. 1 Organization structure diagram of military vector format electronic chart |
图形文件具有直接存取的特点,其中存储了大量海图要素的坐标位置数据,这些数据能够为船舶海上安全航行提供支撑;不同的数据文件有与之相对应的数据库用于记录和描述各种误差;属性文件采用的是表堆栈结构,即dBase,其中记录的主要内容为海图的各项参数。MVCF海图是一类具有多层次结构的电子海图,其中的每幅海图都包含多种类型的层,不同的MVCF文件,可以通过不同的扩展名加以区分,比如元数据文件的扩展名是.rec,图形文件是.shp,属性文件是.dbf。
2.2 杂波建模仿真在电子海图系统硬件设计的过程中,需要充分考虑杂波对电子海图的干扰,因此需要对杂波进行建模和仿真。在高斯分布杂波模型中,重要的参数包括零频率时杂波的功率谱密度,该参数可以用
| $ S(f)=\frac{P_{c}}{\sqrt{2 {\text π} \sigma_{f}}} \exp \left[\frac{\left(f-\bar f_{d}\right)^{2}}{2 \sigma_{f}^{2}}\right] \text{。} $ |
对于归一化操作而言,以及其他深层次的统计关系,可以用傅里叶变换来描述,基于这一前提,杂波可用高斯型相关函数表示,经过归一化处理后,得到:
| $ R(\tau)=\exp \left(-\alpha \tau^{2}\right) \text{。} $ |
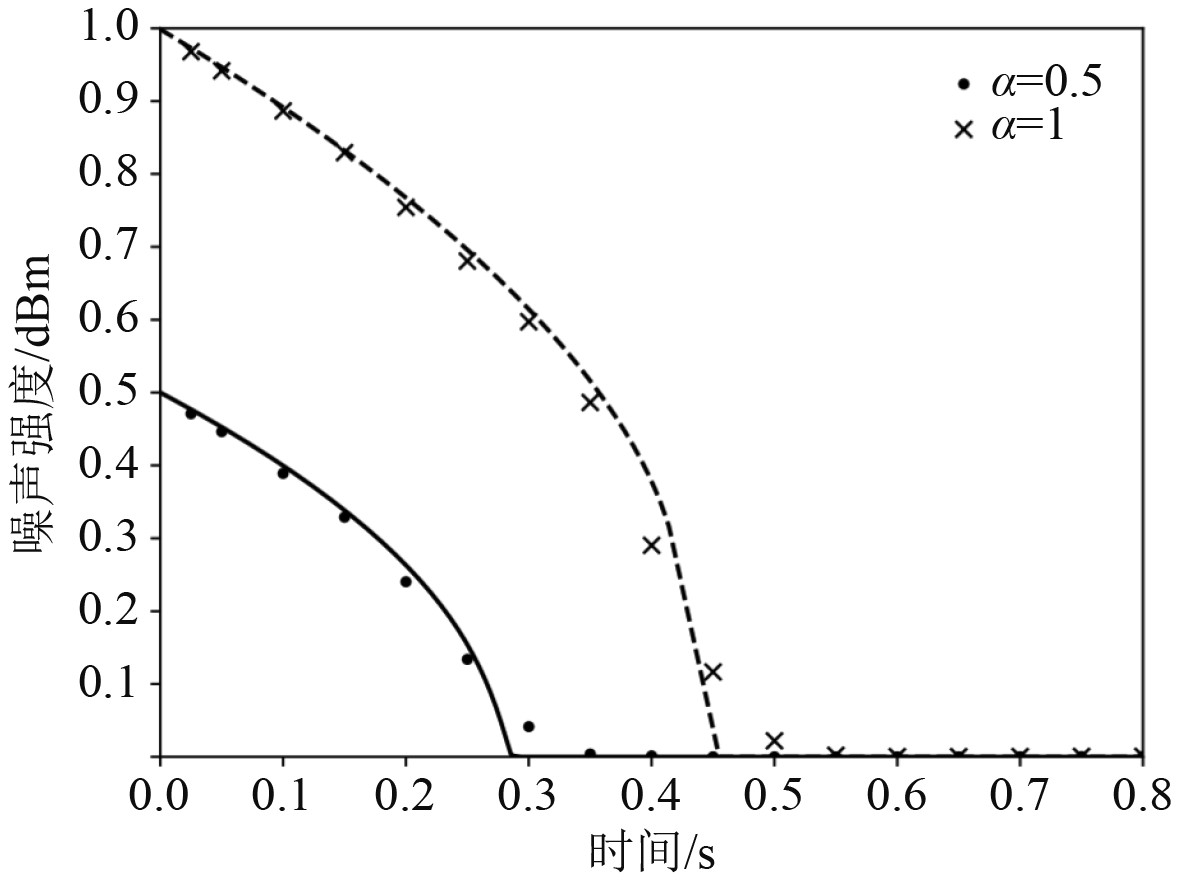
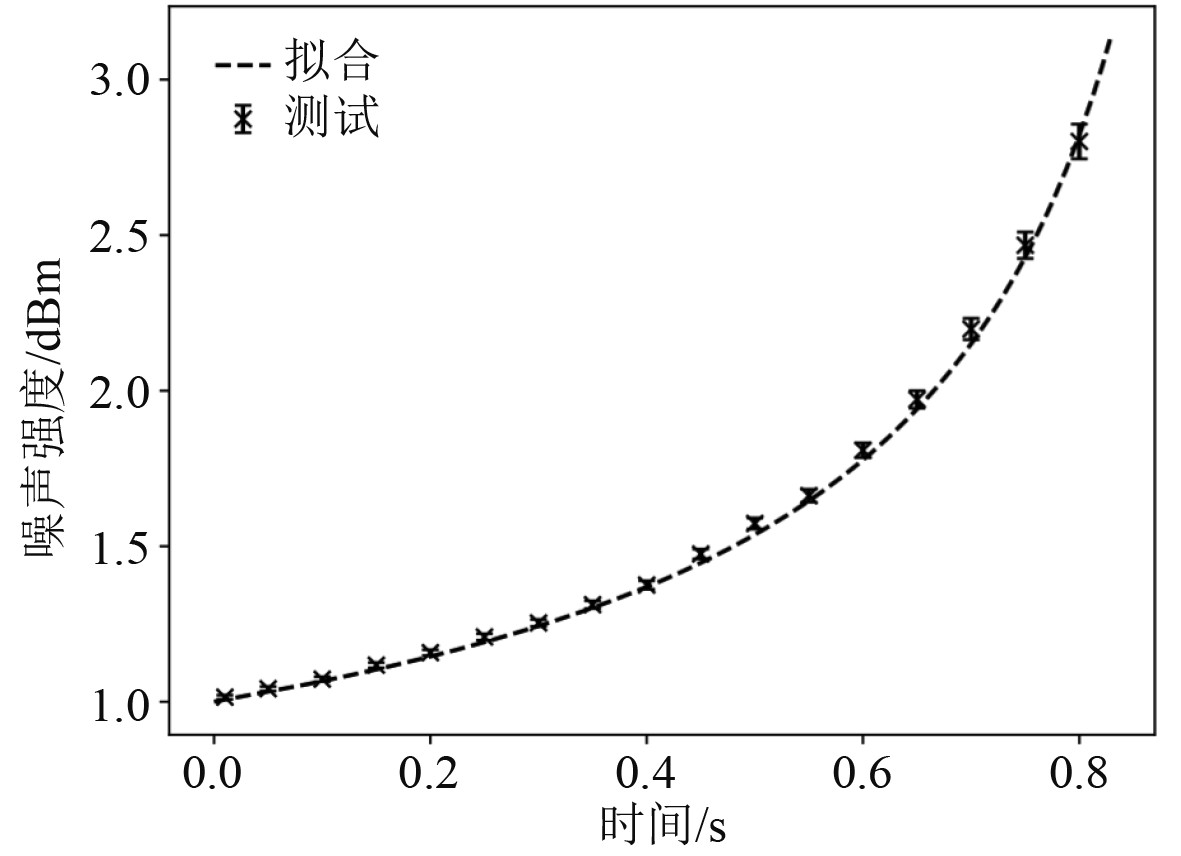
式中,α的值为系统的统计误差离散程度。标准高斯分布的噪声信号示意图如图2所示,传统高斯分布的噪声强度随时间变化图如图3所示。
|
图 2 标准高斯分布的噪声信号示意图 Fig. 2 Schematic diagram of noise signal with standard Gaussian distribution |
|
图 3 传统高斯分布的噪声强度随时间变化图 Fig. 3 A plot of noise intensity versus time for a traditional Gaussian distribution |
瑞利分布的杂波产生模型具有结构简单等特点,在该模型中存在相互独立的高斯白噪声,用线性滤波器处理后,杂波正交分量的功率谱密度可以表示为:
| $ P_{u u}=P_{v v}=\sigma^{2}\left|H\left(e^{j w}\right)^{2}\right| \text{。} $ |
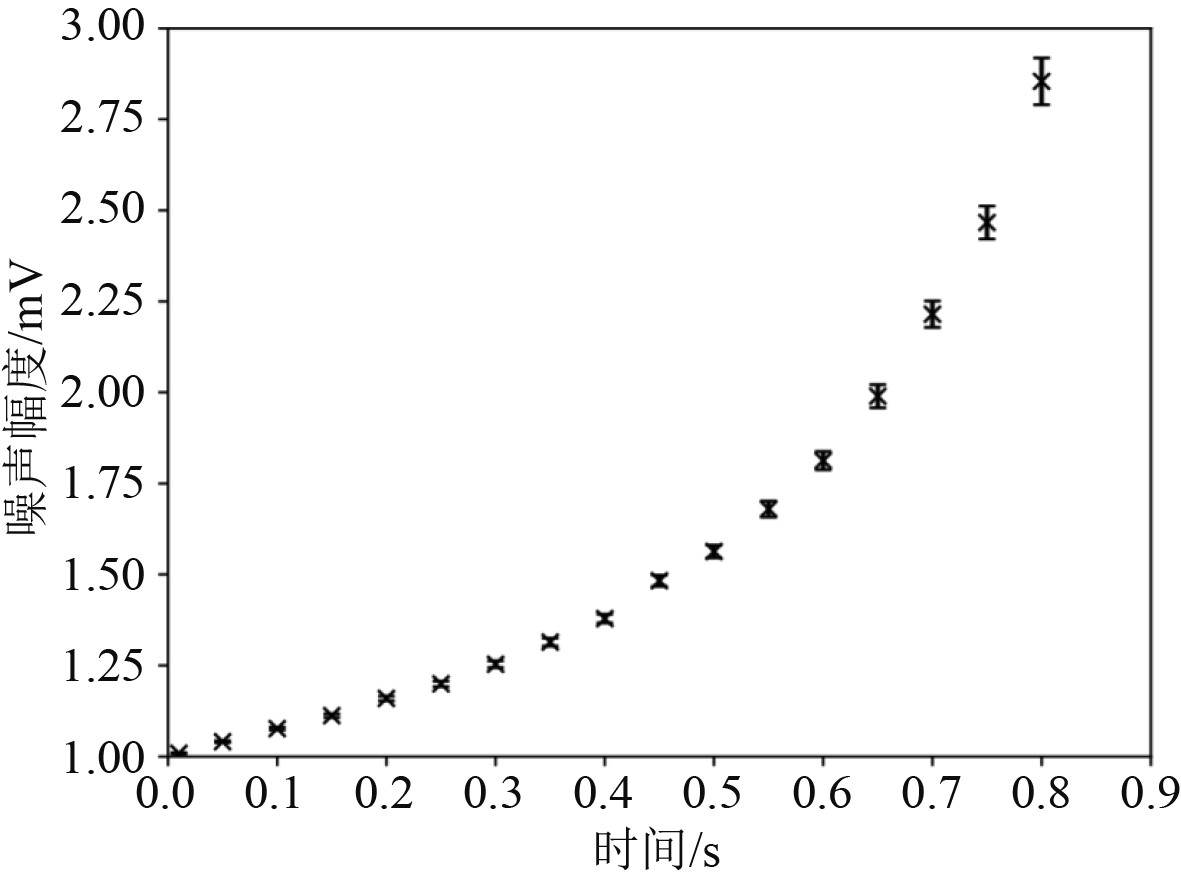
杂波的幅值则可通过瑞利分布来描述,可将杂波的传播速率
|
图 4 瑞利分布模型中的杂波噪声幅度分布情况示意图 Fig. 4 Schematic diagram of clutter noise amplitude distribution in Rayleigh distribution model |
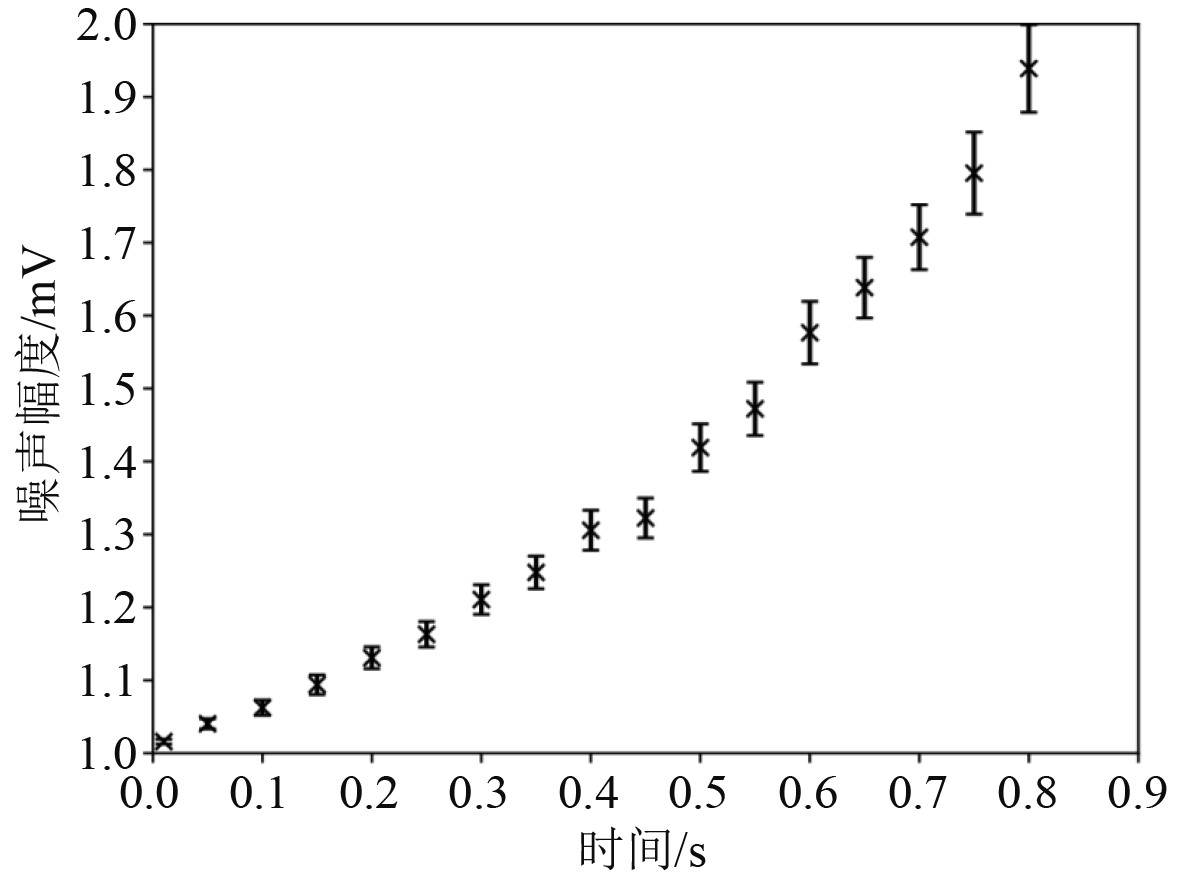
|
图 5 瑞利分布模型中的频谱噪声幅度分布示意图 Fig. 5 Schematic diagram of spectral noise amplitude distribution in Rayleigh distribution model |
在对瑞利模型进行分析的过程种,一般需要采用实时响应函数进行修正,从而可以将各种噪声因素考虑进去,将一维的响应模型变成多维度的模型。在对噪声进行采样分析时,可采用单阶模态对噪声的特征进行识别。首先需要在三维坐标系中建立函数,假设电子海图中船舶的位移向量为:
| $ {\kern 1pt} {\kern 1pt} \left\{ x \right\} = {\left[ {u{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} v{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} w} \right]^{\rm{T}}}{\kern 1pt} \text{,} $ |
航向角度的位移为:
| $ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {{\phi _r}} \right\} = {\left[ {\left\{ {\phi _r^u} \right\}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\phi _r^v} \right\}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\phi _r^w} \right\}} \right]^{\rm{T}}}{\kern 1pt} \text{,} $ |
根据正交向量的可叠加性,综合的船舶位移响应函数可表示为:
| $ \left( {\begin{array}{c} \left\{ u \right\} \\ \left\{ v \right\} \\ \left\{ w \right\} \end{array}} \right) = \sum\limits_{r = 1}^m {{q_r}} \left( {\begin{array}{c} \left\{ {\phi _r^u} \right\}\\ \left\{ {\phi _r^v} \right\}\\ \left\{ {\phi _r^w} \right\} \end{array}} \right) \text{。} $ |
其中,
在高阶的电子海图模型中,需要在各阶的响应函数中加入噪声响应模型,其中噪声模型可以表示为:
| $ \varepsilon = \sum\limits_{r = 1}^m {{q_r}} \psi _r^{{\varepsilon _{}}} \text{。} $ |
通过对位移模型进行求差操作,可以抵消噪声的影响,可表示为:
| $ \Delta \varepsilon = {\varepsilon ^d} - {\varepsilon ^h} \text{。} $ |
在某些特定的情况下,如雷达分辨率较高时,用瑞利模型无法准确描述出海杂波的分布情况,海面的情况越差,如风浪较大、干扰因素多等,杂波的幅值会偏离瑞利分布,此时使用瑞利模型将难以准确描述出杂波的分布。该情况下,可以采用对数正态分布模型来描述海杂波。由于对数正态分布模型本身的动态表示范围非常大,所以在对海杂波建模时,会产生出镜面反射效果。受到观测角度的影响,可能会产生出较大的动态范围。经过大量的实验论证后发现,杂波包络的PDF存在拖尾的迹象。对数正态杂波的时域波形情况及杂波的频谱分别如6和图7所示。
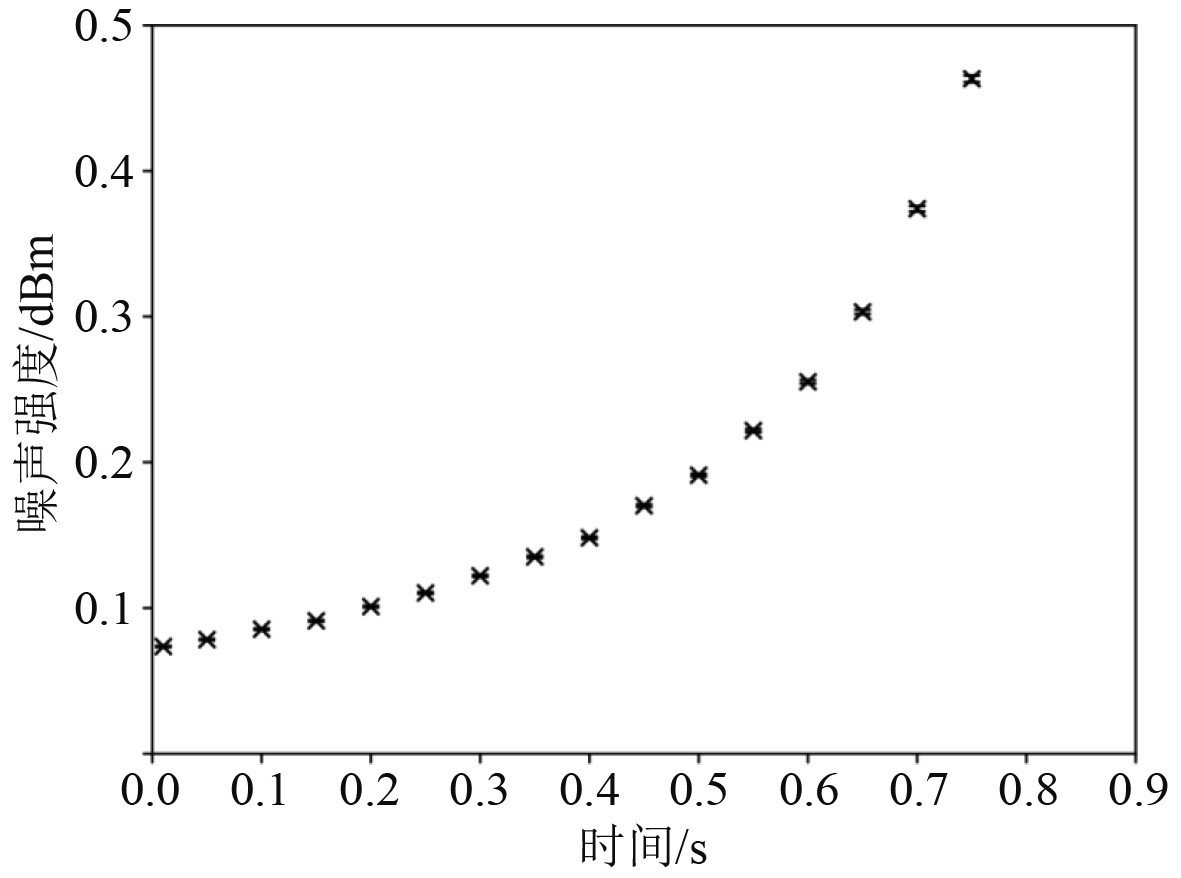
|
图 6 对数正态杂波的时域波形噪声分布情况示意图 Fig. 6 Schematic diagram of the time-domain waveform noise distribution of log-normal clutter |
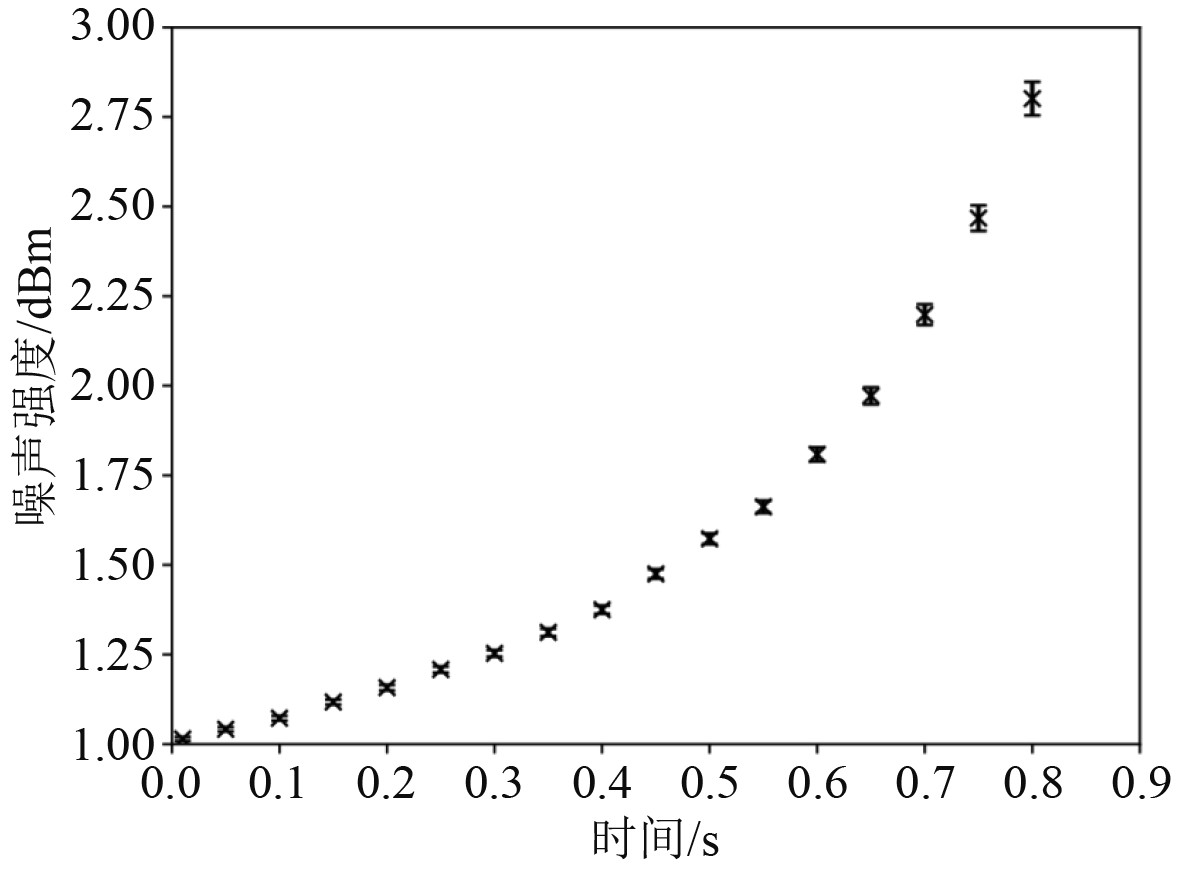
|
图 7 对数正态杂波的频谱噪声情况示意图 Fig. 7 Schematic diagram of spectral noise for log-normal clutter |
在基于嵌入式技术的电子海图系统硬件中,显示模块是必不可少的硬件之一。通过分析电子海图文件后发现,在图形文件中,存储着大量要素的空间数据,要素的位置坐标是以逻辑坐标值进行存储。基于这一前提,可从海图文件中,将相关数据信息读取到屏幕上加以显示,此时便需要运用到显示模块。电子海图坐标系一般为笛卡尔,由于存在非负数,无法进行坐标系变换,即X轴指向右、Y轴指向上,单位为长度0.2 mm的逻辑单位。而普通的坐标系单位为像素,因单位不同,需要对坐标系参数进行转换,即水平方向像素数量为dx个,垂直方向上像素数量为dy个,二者的值与显示设备有关。本次系统开发中,选用的显示屏为液晶屏,尺寸为8.4 in,长宽比为4∶3,设置的分辨率为640×480,由此能够分别计算出dx和dy的数值。当单位转换系数确定之后,需要按照显示窗口转换坐标,由于液晶显示屏内的显示区域有限,所以只能显示海图的局部区域。
对于电子海图而言,除应当具备对图形静态显示的功能之外,还应当可以实时动态的漫游显示图形。若是海图文件生成图形的时间过长,则会对电子海图的使用造成一定程度的影响,因此短时间快速生成图形是电子海图的基本要求,这样才不会影响到海图的显示。在对海图进行绘制的过程中,可以采用预先生成的方法,即需要提前绘制并存储海图,当需要对某个区域显示时,便可将预先绘制好的海图COPY到显示窗口即可。本文中结构最为突出的特点是能够保证电子海图缩放的准确性,这样除了能够使缩放变得更加容易之外,缩放后的显示效果也能得到保障。电子海图在对图形进行缩放显示的过程中,需要先对图形中的数据进行解析,以此为基础,完成显示。
2.4 显示模块设计当电子海图系统的图形显示模块启动时,要先初始化,具体包括:用户界面初始化、变量初始化以及确定显示海图的文件库等。当上述初始化工作全部完成后,便可按照确定好的海图文件库,读取相应的文件,对绘出海图加以显示。本文中的系统为船用电子海图导航系统(Marine electronic chart navigation system,MECNS),当船舶在水面上行驶时,它的位置会不断发生改变,由于电子海图的显示区域有限,所以可能会出现船舶航行时位置不在当前海图中的情况,此时便需要通过换图来保证船舶的位置可能被完全覆盖。当系统程序从GPS接收到相关的导航数据,并获得船舶所处位置的经纬度值,会将当前显示的海图与经纬度的最大值和最小值进行比较,如果当前的海图并不在这一区间范围内,则表明海图无法对船舶当前多处的位置进行覆盖。对此,可将船舶所处位置的经纬度值,与计划航线上海图中经纬度的最大值和最小值作比较,当获得可以覆盖当前船舶位置的海图时,获取其名称,并在液晶屏幕上对该海图加以显示。
当船舶在水面上正常航行时,电子海图系统的导航模块将接收到航海数据,并在更新数据后重新发出相应的消息,此时显示模块将会对船舶所处位置的新坐标进行获取,并对窗口显示的船舶位置加以更新,船舶的标志会始终位于电子海图的中心。当船舶的位置发生改变后,在显示区域内绘制出船舶所处区域中央的海图区域,此时的船舶位置仍然处在海图的中心,这样能够为船舶驾驶人员观察船周围的情况提供便利。
3 结 语电子海图以其自身所具备的诸多作用,成为船舶航行中不可或缺的重要工具,为最大限度发挥出电子海图的作用,可以在硬件系统开发设计中引入嵌入式技术,并将显示模块的设计作为重点,使电子海图能够更加清晰、准确地显示出相关信息,为船舶的安全航行提供保障。
| [1] |
王玉玺, 丁琰, 肖冲冲. MapInfo数字海图向MVCF数字海图的转换方法研究[J]. 舰船电子工程, 2019, 39(1): 83-84,97. DOI:10.3969/j.issn.1672-9730.2019.01.020 |
| [2] |
郝江凌, 单雄飞, 赵丽宁, 等. 电子海图导航系统的研究进展与未来趋势[J]. 大连海事大学学报, 2021, 47(3): 1-7. |
| [3] |
李荣川, 陈宁. 基于电子海图的船舶路径规划模拟器开发[J]. 机电设备, 2021, 38(4): 9-14. |
| [4] |
王百勇, 张艳华, 贾俊乾. 基于深度学习理论下电子海图与雷达图像船舶感知信息融合[J]. 现代雷达, 2021, 43(5): 44-50. |
| [5] |
陈明. Douglas-Peucker算法在电子海图岛屿轮廓提取的应用[J]. 电子技术, 2020, 49(5): 36-37. |
| [6] |
张大恒, 张英俊, 张闯. 基于Faster R-CNN的电子海图和雷达图像的数据融合[J]. 系统工程与电子技术, 2020, 42(6): 1267-1273. |
| [7] |
叶美芬, 陈育才. 基于OGR库的S-57标准电子海图到Shapefile格式的转换[J]. 测绘地理信息, 2020, 45(1): 91-94. |
 2022, Vol. 44
2022, Vol. 44
