0 引　言

船舶在风浪条件下航行或者停泊时，受到海风作用力和海浪作用力的影响，船体会产生沿船体坐标系的直线运动和绕坐标轴的转动，在这些六自由度运动形式中，船体的横摇、纵摇和垂荡运动产生的频次和造成的影响最明显，可能使船体的稳性下降，严重时会发生倾覆等事故。尤其是横摇运动，当横摇运动发生的幅值超过了船体的平衡位置，船舶就有可能失稳。因此，提升船舶在风浪条件下的抗倾覆是船舶设计过程需要重点考虑的因素^[1]。

船舶的稳性是指当船舶受到外力或力矩影响时，船舶在发生倾斜等运动后具备的恢复至平衡位置的能力。稳性设计是评估船舶设计质量的重要因素。通常，船舶的稳性设计包括静稳性设计和动态稳性设计2种，本文主要研究船舶的动态稳性设计。

通过建立船舶运动坐标系及运动模型，结合可控减摇水舱技术，开发一种船舶稳性控制系统，并对系统的功能原理进行介绍，结合试验台进行了稳性控制系统的性能仿真。

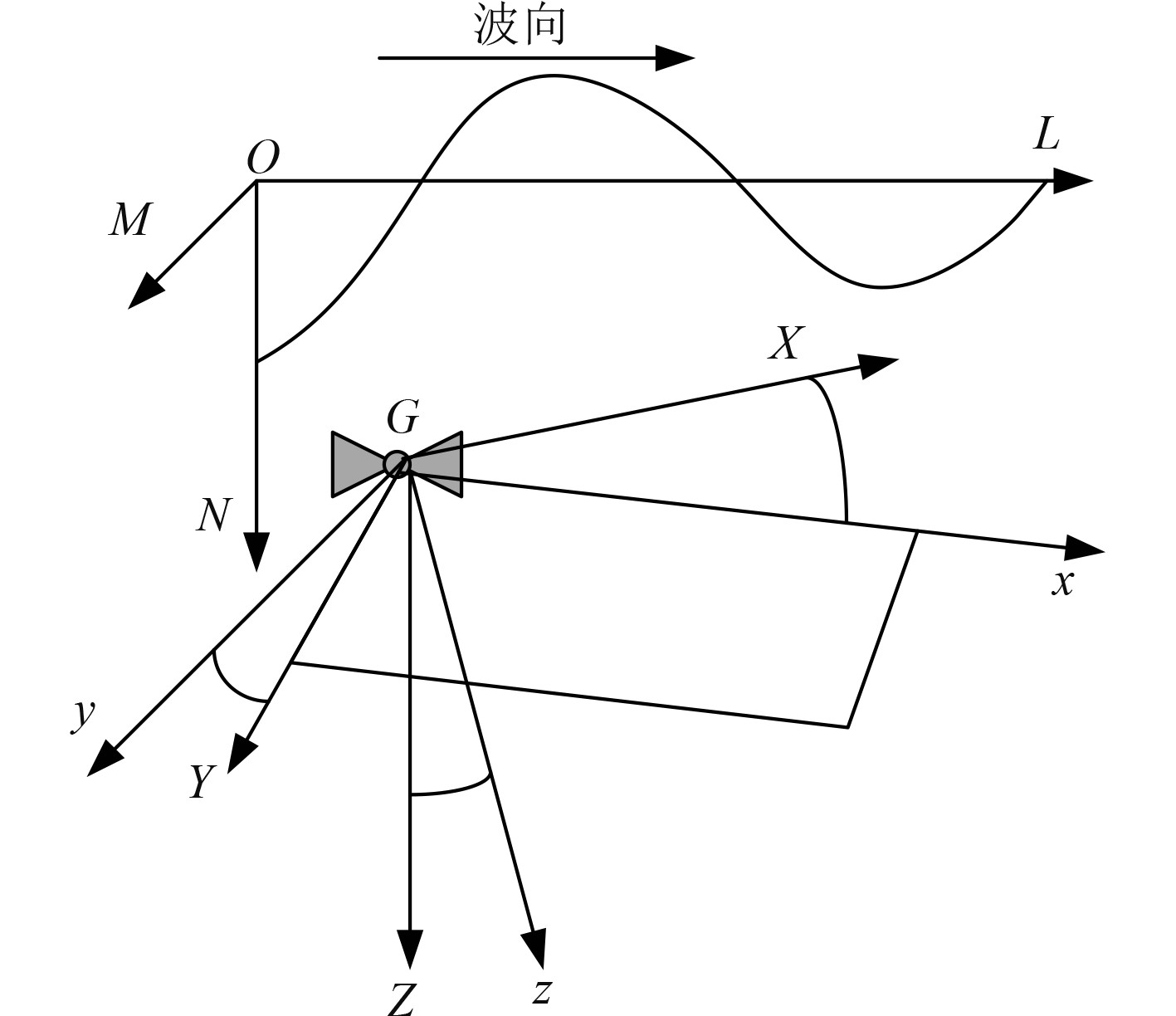
1 船舶稳性运动坐标系及波浪载荷的建模

在建立船舶稳性运动坐标系时，将坐标系分为以下3种：

1）固定坐标系O-LMN，坐标系原点位于静止水面上，ON轴竖直向下，OL轴指向波浪正向，固定坐标系用来描述波浪；

2）运动坐标系O-XYZ，以船舶的重心G为坐标系原点，OX轴平行于甲板面指向船舷；

3）参考坐标系o-xyz；该坐标系以船舶的航行速度随船一起运动，描述船舶自身运动。

建立船舶稳性运动坐标系如图1所示。

假定船舶横倾角度为 $ \varphi $ ，在该稳性运动坐标系下，运动坐标系和参考坐标系的转换关系为：

$ \begin{gathered} X = x ，\hfill \\ Y = y\cos \varphi - z\sin \varphi ，\hfill \\ Z = y\sin \varphi + z\cos \varphi ，\hfill \\ \end{gathered} $

其矩阵形式为：

$ \left[ {\begin{array}{*{20}{l}} X \\ Y \\ Z \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \varphi }&{ - \sin \varphi } \\ 0&{\sin \varphi }&{\cos \varphi } \end{array}} \right]\left[ {\begin{array}{*{20}{l}} x \\ y \\ z \end{array}} \right] \text{，} $

假定船舶的横倾角为 $ \varphi $ ，纵倾角为 $ \theta $ ，航向角为 $ \beta $ ，则固定坐标系与参考坐标系的转换关系为：

$ \left[ {\begin{array}{*{20}{l}} l \\ m \\ n \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\cos \theta \cos \beta }&{ - \cos \varphi \sin \beta }&{\cos \varphi } \\ {\cos \theta \sin \beta }&{\cos \varphi \cos \beta }&{\cos \beta } \\ { - \sin \theta }&{\sin \varphi \cos \theta }&{\cos \varphi \cos \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{l}} x \\ y \\ z \end{array}} \right] \text{，} $

结合稳性运动坐标系，建立舰船的运动模型为：

$ \left\{ {\begin{array}{*{20}{c}} {\left( {{J_0} + \Delta {J_{}}} \right)w + 2\kappa w + \dfrac{1}{2}Dh\theta = {T_0}} ，\\ {M\dfrac{{{\rm{d}}v}}{{{\rm{d}}t}}\sin \theta + M\dfrac{{{\rm{d}}u}}{{\rm{d}}t}\cos \theta = {F_0}} 。\end{array}} \right. $

式中： $ {J_0} $ 为舰船横摇转动惯量^[2]； $ \Delta J $ 为附加转动惯量； $ h $ 为吃水深度； $ {T_0} $ 为倾覆力矩和； $ {F_0} $ 为扰动合力； $ \kappa $ 为舰船运动的阻尼系数^[3]； $ D $ 为船舷宽度； $ \theta $ 为纵倾角度； $ v $ ， $ u $ 分别为船舶沿参考坐标系ox，oy轴的运动速度。

船舶的横摇周期为：

$ t = \sqrt 2 \text{π} \sqrt {\frac{{v + \Delta v}}{{D\sin \theta }}} 。$

建立海浪的波面方程为：

$ f\left( t \right) = {\theta _m} - B\sin \left( {{w_o}t + {\varphi _0}} \right) \text{。} $

式中： $ B $ 为海浪的高度（波峰到波谷的距离）； $ {w_o} $ 为海浪的频率值； $ {\varphi _0} $ 为海浪的初始相位角； $ {\theta _m} $ 为最大波面倾角，用下式计算：

$ {\theta _m} = \frac{{2\text{π}\zeta }}{\lambda } \text{。} $

式中： $ \zeta $ 为最大相位角。

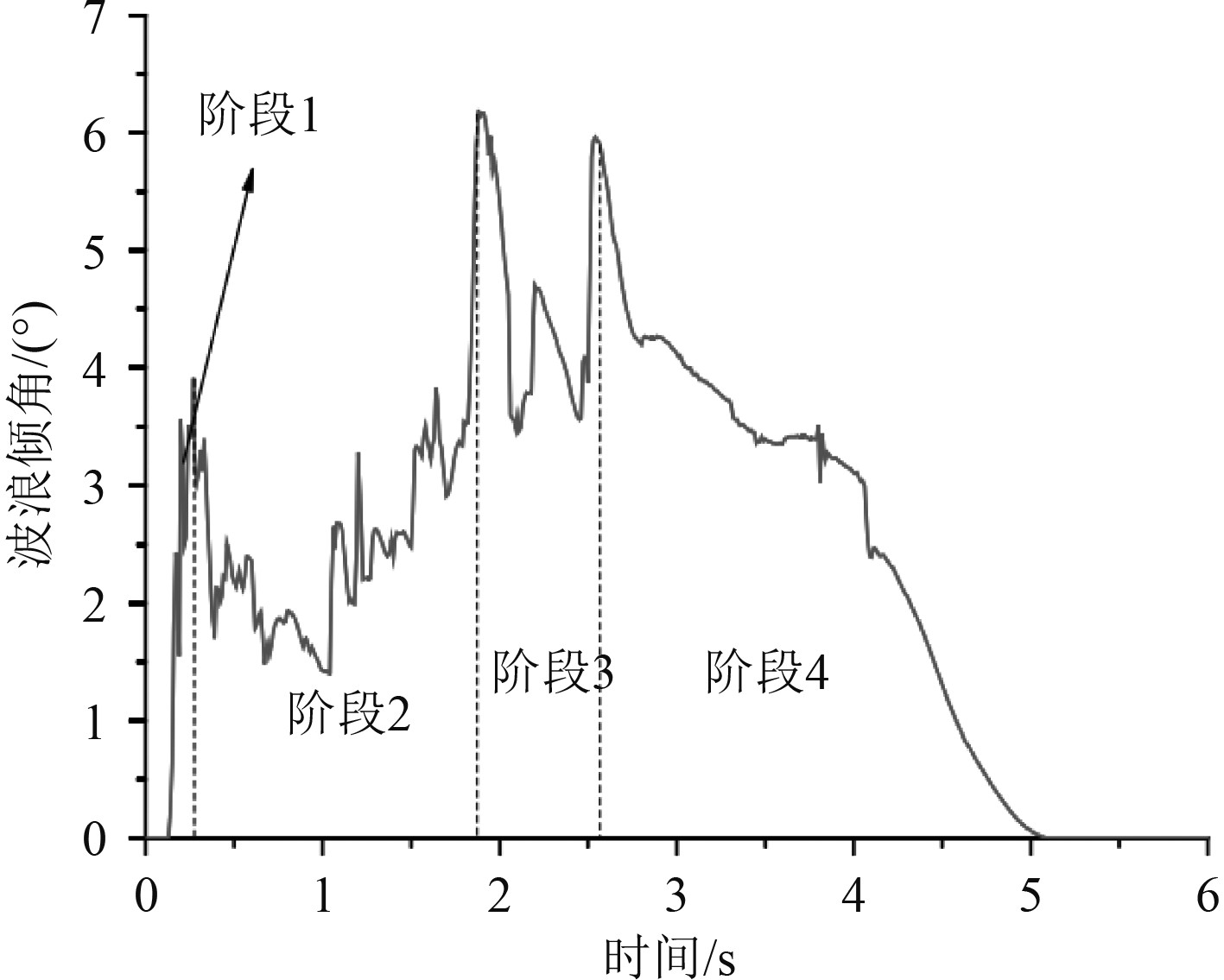
实际情况下，海浪的波面倾角在一个周期内具有非线性变化，0～5 s周期内海浪的波面倾角曲线如图2所示。

2 船舶稳性控制系统设计 2.1 船舶稳性控制原理介绍

通常，船舶的稳性设计主要有增大阻尼系数、降低船体固有频率、降低扰动力或力矩等3种方法：

1）增大阻尼系数

增大阻尼系数是比较常用的稳性设计方法，阻尼越大，初始运动发生时所需要的能量阈值越大，当外界的扰动力和扰动力矩较小时，船体由于阻尼较大，基本不产生相对运动。

2）降低船体固有频率

降低船体固有频率的主要目的是与波浪的扰动频率避开，防止因为频率接近产生共振，使船体发生大幅度的运动。尽管降低船体固有频率，能够有效防止船舶的振动，但是这种做法在船舶设计过程中会造成成本的升高。

3）降低扰动力或力矩

这种方式的原理是施加一个与扰动力矩相反的力矩，直接减小扰动力和力矩，常用的减摇水舱等技术均属于该类方法。

减摇水舱基于双共振原理，在船舶发生周期性摇动时，水舱内的水也同样发生周期性摇动，当相位角相差180°时，周期性摇动相互抵消，实现船减摇。

图3为船舶减摇水舱与扰动力矩的相位图。

2.2 船舶稳性控制系统硬件组成

利用减摇水舱建立一种可控的船舶稳性控制系统，在船舶横向和纵向布置多个减摇水舱，每个减摇水舱装有液位传感器和倾角传感器，可以实时采集船舶减摇水舱内的液位与倾角。传感器采集的数据通过A/D接口发送至稳性控制系统的处理核心，同时采集船舶当前的海浪环境，输出最佳的液位控制信号。

在每个减摇水舱中还配置了液位开关和液压阀^[4]，防止水舱的液位过高，对其他部件造成冲击。

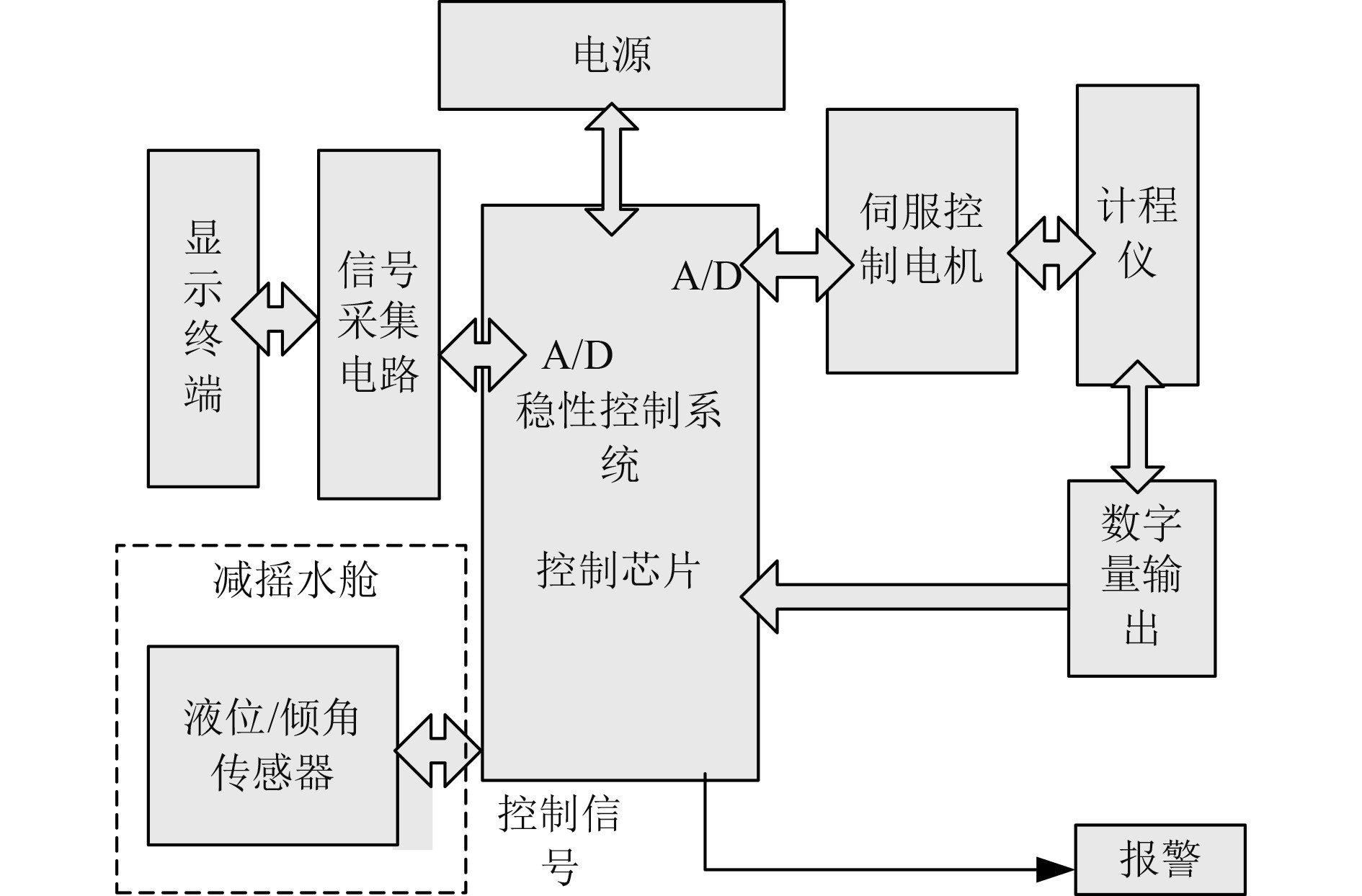
船舶稳性控制系统的硬件原理如图4所示。

如图所示，船舶稳性控制系统除了包括减摇水舱外，还包括电源、伺服驱动电机、控制芯片、信号采集电路、显示终端、输入输出接口等。

1）伺服驱动电机

伺服驱动电机是接收到舰船的稳定控制信号后，驱动减摇水舱产生运动，从而保证船变得稳定性。在船舶稳定控制系统中使用的伺服驱动电机型号为ECMA-B2。

2）控制芯片

嵌入式芯片是系统的核心，采用TI公司生产的TMS320LF240系列芯片，该芯片工作频率为40 MHz，外围接口包括JTAG仿真接口、EEPROM 接口等，可保证船舶稳定控制系统的传感器数据处理、减摇设备的运动控制。

3）信号采集电路

在稳定控制系统中，为了保证减摇水舱运动控制的敏捷性，必须要同时采集大量的传感器信号、电机信号、船舶的位置信号等。

该船舶稳性控制系统的特点：

1）远程控制功能

稳性控制系统能够通过无线网络实现远程控制，在系统的减摇水舱底部安装有水泵和控制阀，远程输入控制信号就可以实现水舱的充水和放水，满足减摇的要求；

2）分布式控制

系统的控制器硬件相对简单，有足够的输入输出端口，可同时对多个水舱进行分布式控制，因此该稳性控制系统具有较高的适应性，用户可以根据需求定义船体减摇水舱的个数；

3）智能控制

系统控制实现了智能化。

3 船舶稳性控制系统仿真 3.1 稳性控制试验台设计

由于船舶在海浪中的运动是一种复杂的动力学组合，试验台在进行设计时必须要满足相似性要求，分别如下：

1）几何相似性

是指试验台的尺寸设计必须与实际船舶存在合理的尺寸关系，尺度比为固定的常数，如下：

$ \delta=\frac{L_{H}}{L_{{K}}} \text{。} $

式中： $ L_{H } $ 为实际船舶的任意特征尺度； $ {L_K} $ 为试验台对应的特征尺度^[6]。

2）运动相似性

横摇运动的船舶存在非线性特征，试验台设计时必须要保证2种运动体系的相似性，保证系统的斯特鲁哈参数 $ {\xi _h} $ 一致，如下：

$ {\xi _h} = \frac{{{V_H}{T_H}}}{{{L_H}}} = \frac{{{V_K}{T_K}}}{{{L_K}}} \text{。} $

式中： $ {V_H} $ / $ {V_K} $ 为速度； $ {T_H} $ / $ {T_K} $ 为时间。

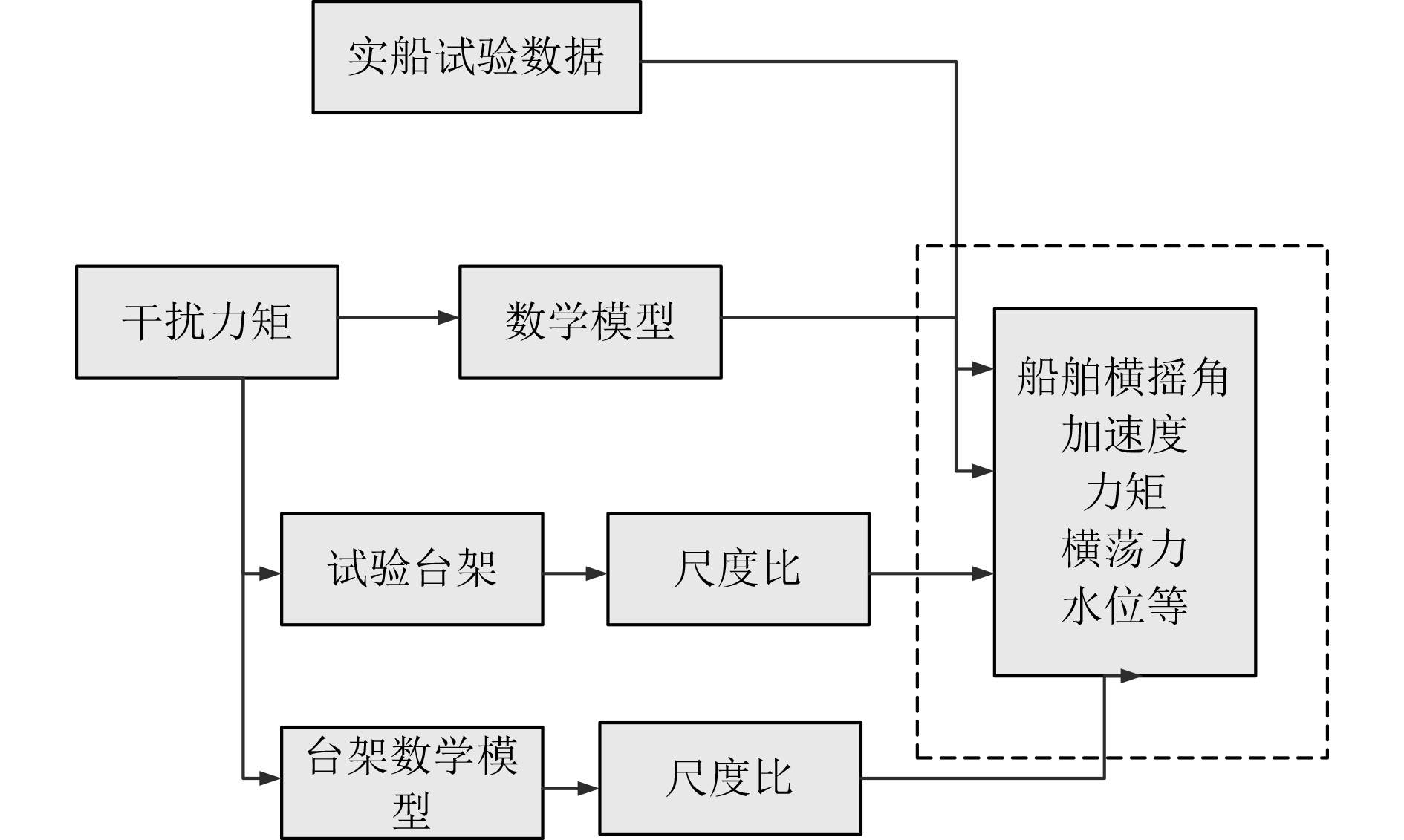
仿真试验台的工作原理如图5所示。

3.2 船舶稳性控制仿真试验

采用的稳性控制试验台上位机基于微型计算机，计算机内核CPU硬件为coreI5-5200，数据采集板卡为AX5412H，数据采集板与上位机平台具有良好的交互性^[7]。

试验台的输入信号为幅值60 mm的正弦干扰信号，波浪的频率为：

$ f = \sqrt 2 \text{π} \sqrt {\frac{1}{{D\sin \theta }}} = 100\;{\rm{H}}{\rm{z}} \text{。} $

初始纵倾角 $ \theta = 4.5 $ °，船舷宽度D为15 m，船的升力系数 $ \delta = 0.36 $ ，在仿真平台进行稳性控制试验，图6为输入激励（曲线C）与船舶实际横摇角度（曲线B）的关系曲线。

4 结　语

船舶的静态和动态稳定性对于船舶航行安全有重要意义，由于船舶在海浪作用下的运动是一种复杂的非线性运动，本文通过建立运动/参考/静止坐标系，客观描述船舶的横摇运动，并建立了波浪干扰模型。基于减摇水舱技术，开发了船舶稳性控制系统，从原理、软件/硬件设计、系统仿真等方面分别进行了阐述。