2. 中国人民解放军32382部队,湖北 武汉 430311
2. No.32382 Unit of PLA, Wuhan 430311, China
舰船的船体一般由低合金钢或铝合金制造,螺旋桨则由铜合金制造,在海水中不同金属具有不同的化学性质,所以会产生不同的电极电位,一旦舰船不同金属间发生电连接,在海水中将会产生腐蚀电流[1-3]。为了保护舰船免受腐蚀,普遍会在舰船设计和制造中采取防腐措施。腐蚀电流和防腐措施引起的电流共同作用产生舰船静电场[4]。
当前对舰船静电场的建模方法主要有边界元法、有限元法及离散偶极子源法,其中发展起来并且投入使用的方法是边界元法和离散偶极子源法。如英国的Frazer-Nash Consultancy Company和美国的Ultra Electronics limited Company均采用边界元方法对舰船腐蚀防护模型进行评估,并且预测相应的水下电磁信号;陈聪利用偶极子源法建立了舰船腐蚀静电场模型[5-7]。
对舰船的实测结果显示,电场各频段的能量并不均衡,静电场能量最大、衰减小,能够在海水中进行较远距离的传播,且有明显的信号特征,成为舰船目标的暴露源、水中兵器的攻击源,极易被敌方装有电场引信的水中武器攻击[8-10]。为了增强舰船的隐身性能,提高其生存力,就必须了解静电场的水下传播规律。因此通过三维边界元法建立舰船腐蚀静电场模型,研究其水下电场传播规律则非常必要。但国内外对舰船静电场的研究主要集中于深度换算和电场补偿方面,有关舰船静电场水下传播规律的研究鲜见报道。
1 舰船腐蚀静电场边界元模型 1.1 模型建立利用Comsol仿真软件建立潜艇空间直角坐标系下的几何模型,设定船尾向船首为X轴正方向,龙骨向左舷为Y轴正方向,垂直于水面竖直向上为Z轴正方向,该坐标系的三轴符合右手螺旋法则。舰船未执行作战任务时主要停靠于港口,船体两侧容易被港口码头磨损导致涂层脱落,在模型中设定两处破损(总破损率为2%)对称分布于潜艇两侧。潜艇外围建立400 m×300 m×200 m的长方体代表无限海水域,采用Comsol仿真软件对潜艇表面和海水域进行网格剖分,潜艇剖分结果如图1所示。
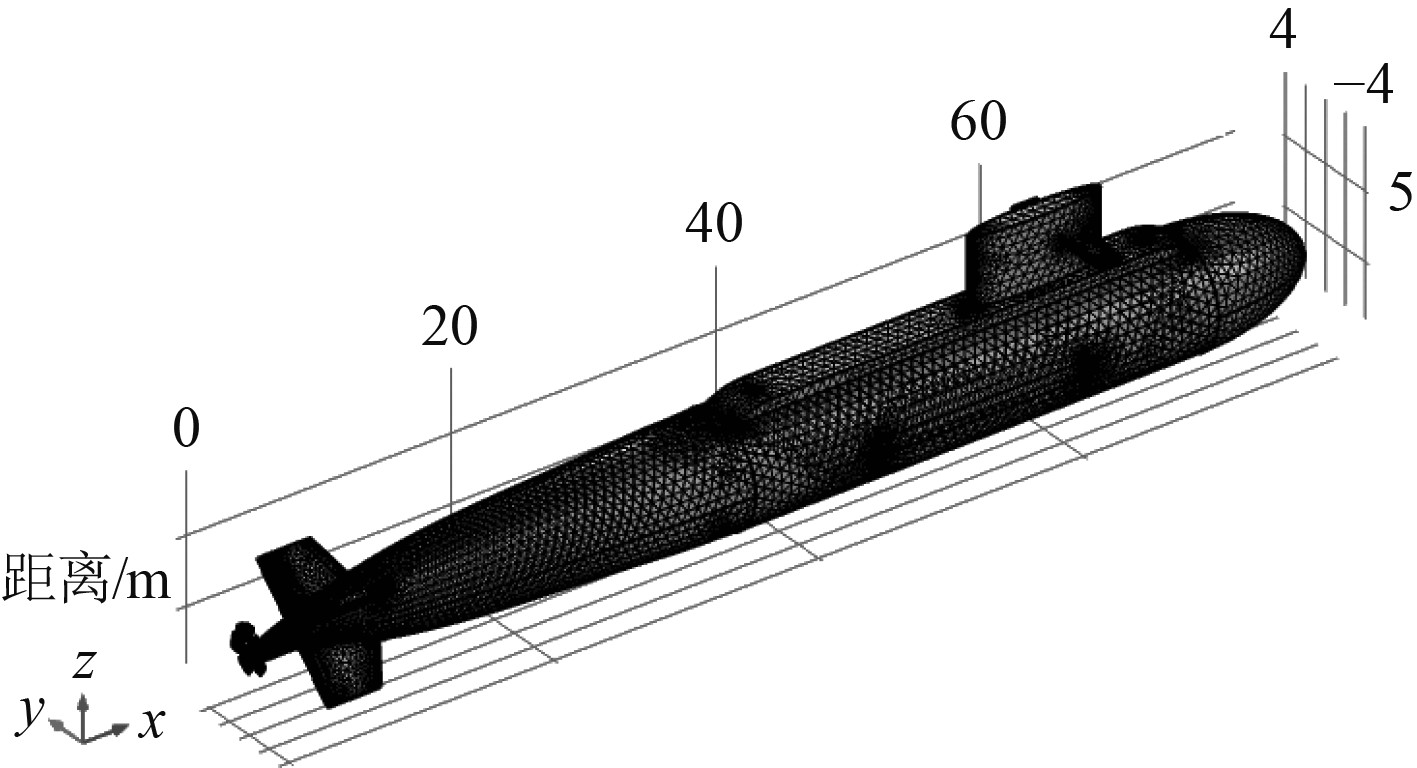
|
图 1 潜艇边界元模型 Fig. 1 Boundary element model of submarine |
在模型中将潜艇螺旋桨和涂层破损处视为裸露金属浸泡于海水中,而将船体及舵视为被涂层完整包覆[11]。潜艇周围海水中电位满足拉普拉斯方程[12-14]:
| $ {\nabla ^2}\phi {\text{ = }}\frac{{{\partial ^2}\phi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\phi }}{{\partial {y^2}}} + \frac{{{\partial ^2}\phi }}{{\partial {z^2}}} = 0 。$ | (1) |
海水中的电流密度矢量J与电位
| $ {\boldsymbol J}=- \sigma \nabla \phi ,$ | (2) |
式中:
当潜艇的运动状态和周围海域环境比较稳定时,艇壳表面电化学腐蚀速度可以认为是恒定的,所以由电化学产生的腐蚀电流也是不变的。恒定电场满足下式:
| $ {\boldsymbol J}= \sigma {\boldsymbol E}。$ | (3) |
式中:J为电流密度,A/m2;E为电场强度,V/m。
1.2 边界条件将实验测得的921A钢和B10铜合金的极化曲线作为模型的边界条件,整个模型的求解域及边界条件设定如下:1)无限空区域中充满均匀海水介质,电导率
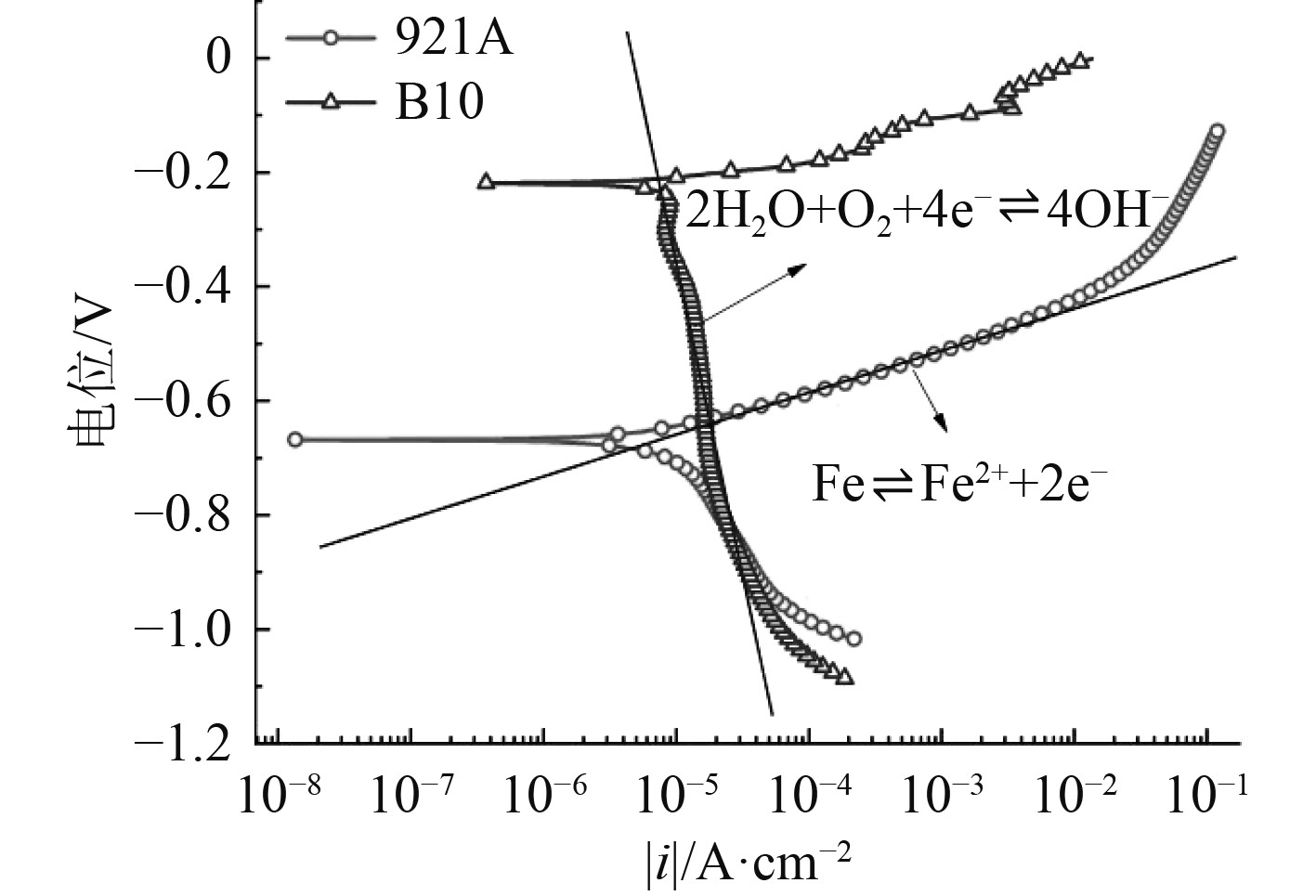
|
图 2 921A钢和B10铜合金的实测极化曲线 Fig. 2 Polarization curves of 921A steel and B10 copper alloy |
假设潜艇位于深海环境中,忽略海床及泥沙对静电场分布的影响,海水深度为1 500 m,下潜深度为50 m,通过仿真得到空间不同位置处潜艇静电场分布情况。为了解静电场随着距离变化的传播规律,分别选取水平方向(XOY面)、垂直方向(ZOX面)和斜45°方向(45°斜面,与Y轴正方向和Z轴负方向夹角45°)进行观测,对电场三分量EX,Ey和EZ随距离的变化规律进行分析。
为观测潜艇静电场,选择潜艇正下方20 m处,以点(−80 m, 0 m, −20 m)为起点和点(160 m, 0 m, −20 m)为终点的路径作为观测对象,潜艇正下方20 m处水平面上电场三分量分布如图3所示,潜艇正下方20 m处水平路径上电场三分量线分布如图4所示。对照图3和图4分析可知,EX和EZ关于ZOX平面对称分布,EZ沿着X轴正方向分别有一个正峰值和一个负峰值,正峰值在螺旋桨附近区域,而负峰值出现在艇体中部。EX正峰值出现在螺旋桨后侧区域,而负峰值出现在螺旋桨附近区域,在艇首区域出现一个小的正峰值。Ey关于ZOX平面呈反对称分布,在螺旋桨位置和艇体中部两侧区域电场各出现一次最大值和一次最小值,正峰值和负峰值大小基本一致。

|
图 3 Z=−20m 平面上舰船静电场分布 Fig. 3 Ship electrostatic filed distribution on the Z=−20m plane |
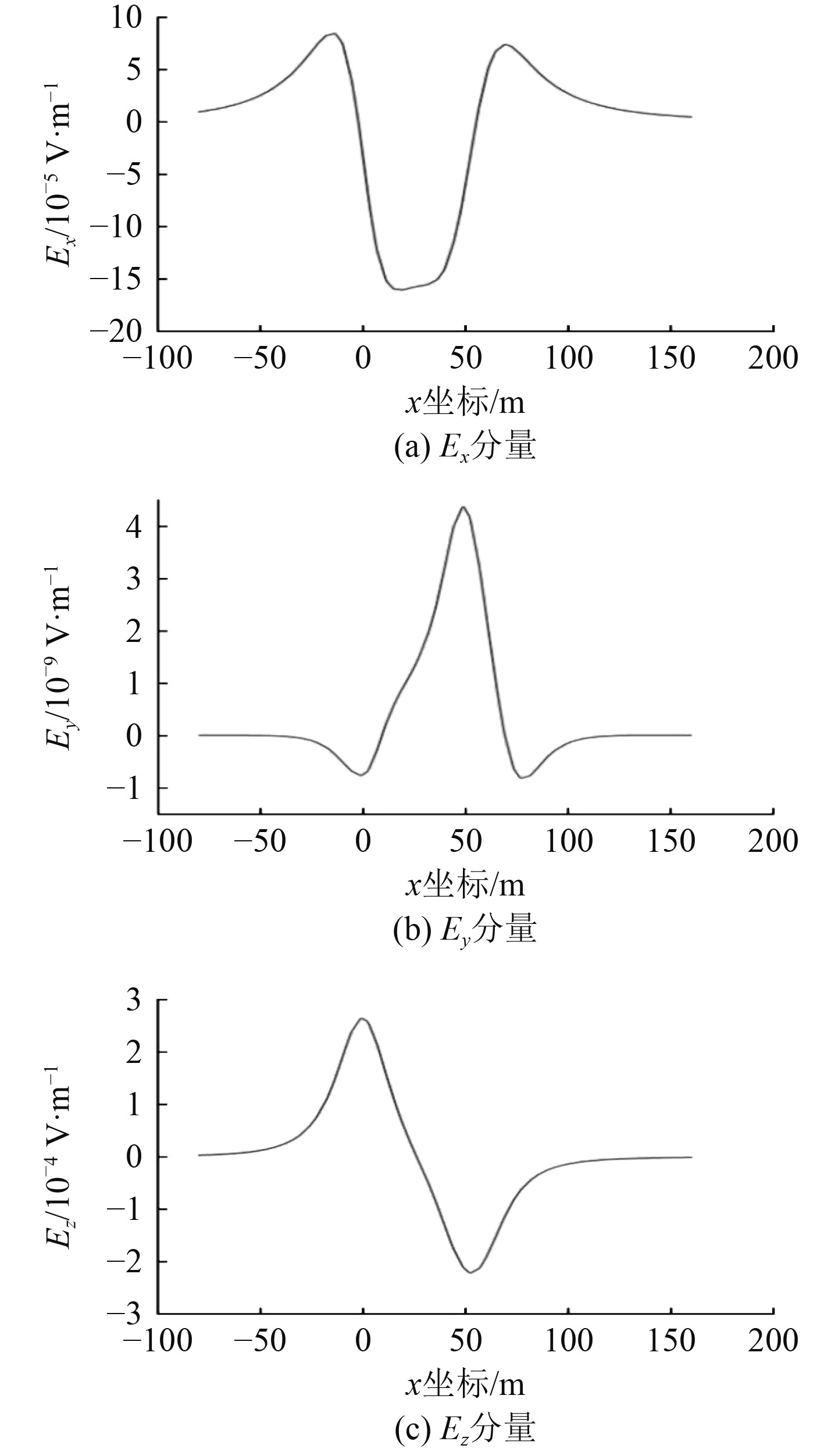
|
图 4 Z=−20m平面上指定路径电场线分布 Fig. 4 Electric filed line distribution of specified path on the Z=−20m plane |
为了更加直观的分析静电场随距离变化的传播规律,在XOY面、ZOX面和45°斜面3个观测面,分别选取水下以X=-80 m为起点和X=160 m为终点,距离艇体由10~1 200 m的路径选取32个点作为观测对象,其中在距离10~150 m之间,每间隔10 m均匀取点,在150~1 200 m之间,每间隔60 m均匀取点,电场三分量随距离的变化规律如图5所示。由图可知,不同观测平面上的电场三分量变化规律基本一致。电场三分量量值随着场点和艇体之间距离的增加不断减小,当场点与艇体距离200 m以内时,电场量值衰减迅速;场点与艇体距离200~1 200 m时,电场量值衰减缓慢,与舰船极低频电场衰减规律吻合。在XOY水平面上,Ex和Ey变化基本同步且量值远大于Ez,在ZOX垂直面上,Ex和Ez变化基本同步且远大于Ey,在45°斜面上,电场三分量变化基本同步且量值基本相等。在3个观测面上同时选取Ex作为研究对象,在不同观测面上其电场衰减量级均达到105数量级。
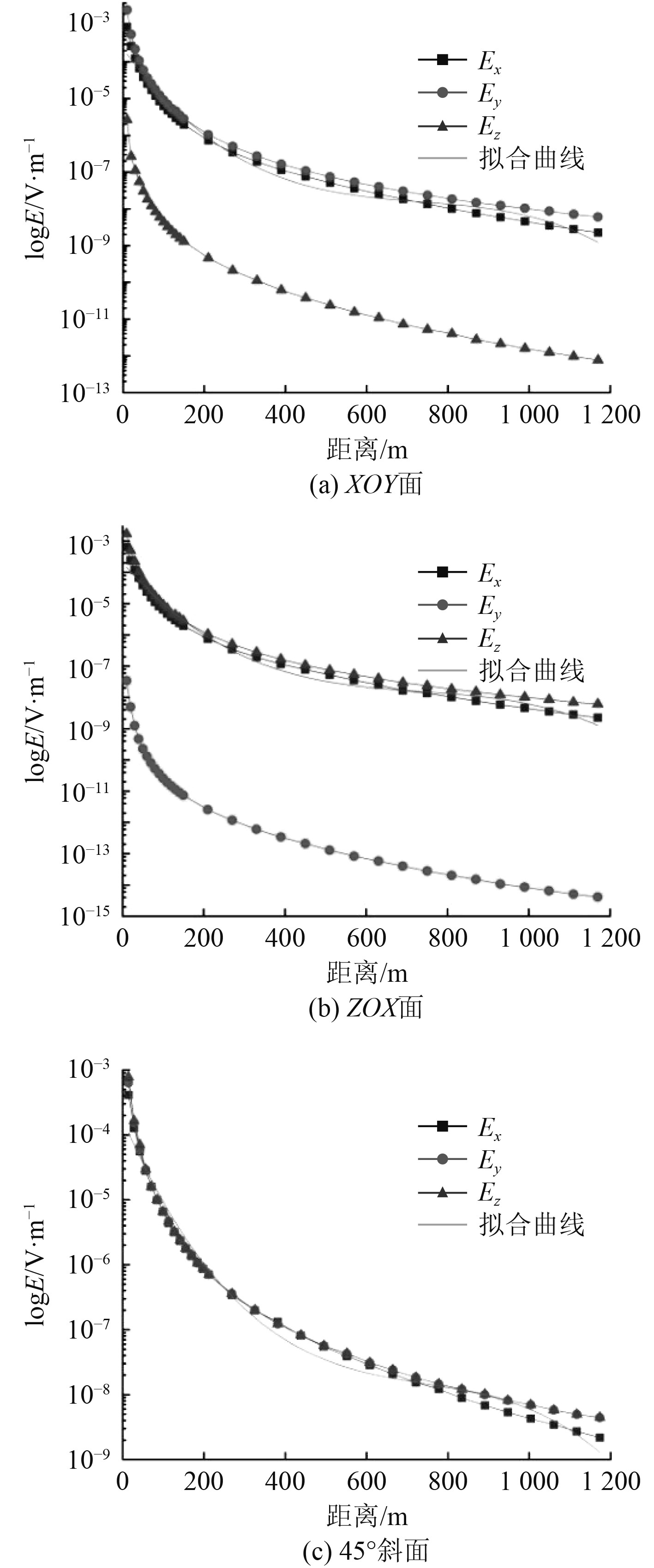
|
图 5 不同观测面电场三分量大小 Fig. 5 Three-component of electric field indifferent observation surfaces |
舰船静电场的影响因素较多,静电场空间变化规律会随着外界环境的改变产生一定的变化,在实际情况下的舰船静电场较边界元模型更加复杂,对舰船静电场的仿真研究中对模型进行了简化,在边界元建模中,对条件进行理想化假设。
结合边界元模型和仿真结果,得出以下结论:
1)在3个观测面上得到的电场三分量信号中,Ex分量因量值较大,在远距离信号检测中更容易被电场传感器检测,因此在今后的舰船定位研究中,应重点利用量值大、衰减小的舰船静电场Ex分量;
2)电场三分量在距离艇体200 m以内时衰减迅速,距离超过200 m时衰减缓慢,与舰船极低频电场衰减规律吻合;
3)在3个观测面上对电场Ex分量传播规律曲线进行拟合,拟合曲线方程及拟合系数如表1所示。由图5和表1可知,拟合曲线和电场变化规律曲线可以较好的拟合,且由电场信号的衰减曲线可知在距离艇体1 000 m以上时,静电场信号微弱容易被噪声所覆盖。
|
|
表 1 拟合曲线方程及拟合系数 Tab.1 Fitting line equation and fitting coefficient |
水下电场信号是舰船的重要信号特征,对舰船建模可以实现其水下电场预测。本文采用边界元法对潜艇建立腐蚀电场模型,研究了水下20 m平面上静电场三分量的变化规律,得出3个方向上静电场三分量随距离的传播规律。通过对仿真结果分析可知,静电场三分量在3个方向上具有相似的变化规律,电场在近场有较大衰减,随着距离的增加衰减变慢。在距离潜艇1 000 m以上时,静电场信号微弱,容易被海洋噪声所覆盖。本文的建模方法为舰船静电场的水下电场预测提供了思路,为下一步利用静电场对舰船实现定位奠定了基础。
| [1] |
姜润翔, 陈新刚, 张伽伟. 舰船电场及其应用[M]. 北京: 国防工业出版社, 2019.
|
| [2] |
何芳, 王向军, 张建春. 舰船腐蚀电场建模及补偿最优解验证[J]. 国防科技大学学报, 2019, 41(6): 118-125. DOI:10.11887/j.cn.201906018 |
| [3] |
刘胜道. 舰船水下电场的测试技术与电偶极子模型研究[D]. 武汉: 海军工程大学, 2002.
|
| [4] |
JEFFREY I. Electromagnetic signature modeling and reduction[J]. The Newal Architect, 1999(8): 22-23. |
| [5] |
陈聪, 李定国, 龚沈光. 舰船静态电场深度换算方法[J]. 哈尔滨工程大学学报, 2009, 30(6): 719-722. DOI:10.3969/j.issn.1006-7043.2009.06.024 |
| [6] |
徐庆林, 王向军, 张建春, 等. 温度对舰船阴极保护和腐蚀静电场的影响[J]. 国防科技大学学报, 2019, 41(4): 182-189. DOI:10.11887/j.cn.201904026 |
| [7] |
DYMARKOWSKI K, UCZCIWEK J. The extremely low frequency electromagnetic signature of the electric field of the ship[C]//Conference Proceding. UDT Europe, 2001: 1-6.
|
| [8] |
SCHAEFER D, ZION S, DOOSE J, et al. Numerical simulation of UEP signatures with propeller-induced ULF modulations in marritime ICCPsystem[C]//Marelec Marine Electromagnetics Conference, San Diego, 2011.
|
| [9] |
喻浩. 舰船电场和低频电磁场防护措施[J]. 舰船科学技术, 2000, 22(3): 37-39. |
| [10] |
张华, 王向军, 单潮龙, 等. 基于目标静电场的水中兵器制导方法研究[J]. 电子学报, 2013, 41(3): 470-474. DOI:10.3969/j.issn.0372-2112.2013.03.009 |
| [11] |
曹寓. 舰船水下腐蚀静电场有限元仿真分析[J]. 舰船科学技术, 2015, 37(7): 69-72. DOI:10.3404/j.issn.1672-7649.2015.07.016 |
| [12] |
陈聪, 李定国, 龚沈光. 基于拉式方程的舰船静态电场深度换算[J]. 电子学报, 2010, 38(9): 2025-2029. |
| [13] |
LAN Z G, WANG X T, HOU B R, et al. Simulation of sacrificial anode protection for steel platform using boundary element method.[J]. Engineering Analysis with Boundary Elements, 2012, 36(5): 903-906. DOI:10.1016/j.enganabound.2011.07.018 |
| [14] |
姜润翔, 胡英娣, 龚沈光. 基于点电源的传播静态电场深度换算方法研究[J]. 电波科学学报, 2014, 29(4): 685-693. |
 2022, Vol. 44
2022, Vol. 44
