2. 中国人民解放军 91388部队,广东 湛江 524022;
3. 国防科技大学 智能科学学院,湖南 长沙 410073;
4. 中国船舶集团有限公司第七一〇研究所,湖北 宜昌 443003
2. No. 91388 Unit of PLA, Zhanjiang 524022, China;
3. College of Intelligent Science, National University of Defense Technology, Changsha 410073, China;
4. The 710 Research Institute of CSSC, Yichang 443003, China
声波是目前海洋中唯一能够远距离传播的能量辐射形式,如果水下航行器的辐射噪声过大,既容易被对方水声探测设备发现,又会干扰己方所搭载的水声探测设备性能,平台振动还会影响惯导装置导航精度。良好的声隐身性能是保证水下航行器隐蔽性的关键,也是衡量水下航行器作战能力的重要指标,因而受到各国海军的高度重视。
目前,国内水下UUV大多采用高精度惯性陀螺仪和计程仪组合导航的方式实现水下自主导航与定位。其中,高精度导航系统常采用“激光惯导+计程仪”组合导航模式,两者之间的相对安装位置精度要求极高。激光惯性导航陀螺仪内部含有机械抖动器,抖动器在工作时需产生一定的抖动频率来消除陀螺仪的闭锁现象。在三轴方向上分别设有3个陀螺,相应地配套有3个机械抖动器,产生的固有频率,一般在300~500 Hz之间。如图1所示,UUV惯导系统除有典型的线谱特征外,还会伴随产生一定带宽的激振力。而该频带正好与声呐设备探测声波的频带相重叠,3根线谱在自噪声能量中占比较高,对声呐设备探测性能影响极大。此外,某一个方向的抖动幅度不对称会使陀螺仪产生累积偏置误差,导致陀螺仪输出精度降低,严重时将导致陀螺仪输出波形完全失真,严重影响导航性能。

|
图 1 陀螺仪在某方向上的抖动振动信号 Fig. 1 The jitter vibration signal of the gyroscope in a certain direction |
综上所述,亟需在保证导航精度的前提下,对UUV惯导系统的多线谱振动开展抑制技术研究工作。
1 国内外研究现状当前惯导系统的减振设计为满足导航精度,普遍将隔振系统固有频率设计较低(50 Hz左右)。通过合理设计减振器,虽然惯性姿态解算的精度略有下降,但该精度仍可满足应用环境下的需求。然而,UUV惯导系统的减振设计需考虑导航仪振动引起的壳体振动与声辐射,对导航仪隔振的要求更高,采用传统的隔振措施已难以满足高效减振要求。
弹性超结构/超材料理论与技术是在承载结构上采取措施,通过弹性波带隙来抑制振动或降低振动传递,无需将隔振频率设计得过低,为导航系统高效减隔振提供了新的技术途径。
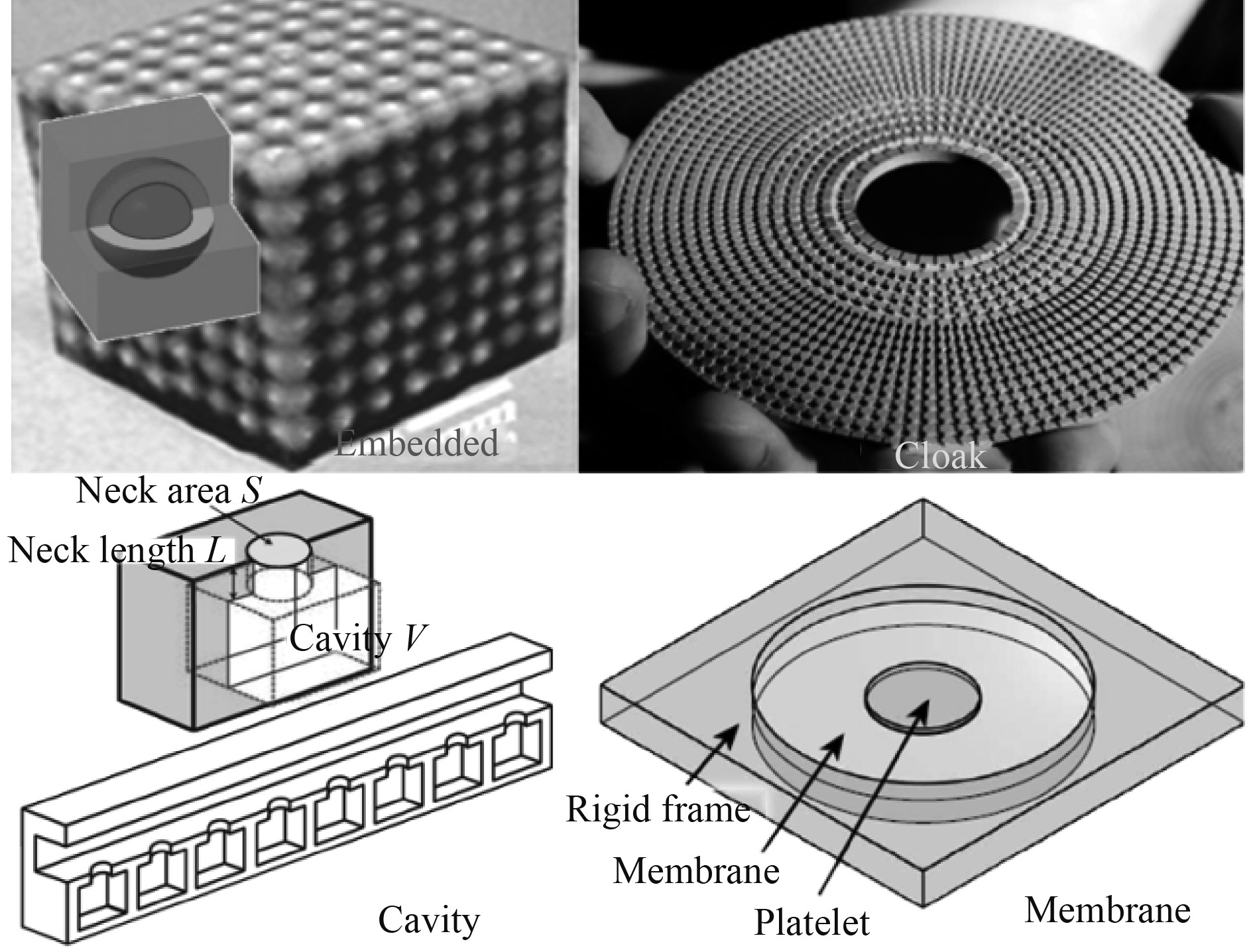
弹性超结构又称弹性超材料(见图2),是具有超常声波/弹性波调控特性的人工复合结构/材料,通常是周期结构,是近年来的前沿交叉热点领域[1]。当前,国内外对弹性超结构的研究主要集中于线性弹性超结构,其基本物理特性已得到大量揭示[2]。
|
图 2 典型弹性超结构 Fig. 2 Typical elastic superstructure |
2000年,Liu等[3]提出局域共振声子晶体,利用小尺寸晶格实现了低频弹性波带隙,为低频小尺寸的弹性波抑制开辟了新的途径。局域共振机理不仅可以实现等效负质量密度[4],还可以实现负模量超常特性[5],也可同时实现等效负质量密度和负模量(即“双负”)。
2004年,Jensen等[6]提出了“弹性超结构”的概念。弹性超结构的弹性波抑制/衰减机理主要是局域共振引起的低频带隙和增强超阻尼效应。
带隙是能带结构中无本征波解的频率范围,能高效抑制结构振动。低频带隙是弹性超结构最典型的特征。2000年以来,大量文献应用局域共振原理设计弹性超结构产生高效的低频弹性波抑制效果[7]。当多个带隙的频率相互靠近时,结合在一起的带宽会增加,即带隙相邻耦合,它是线性弹性超结构中拓展带隙宽度的主要机理。
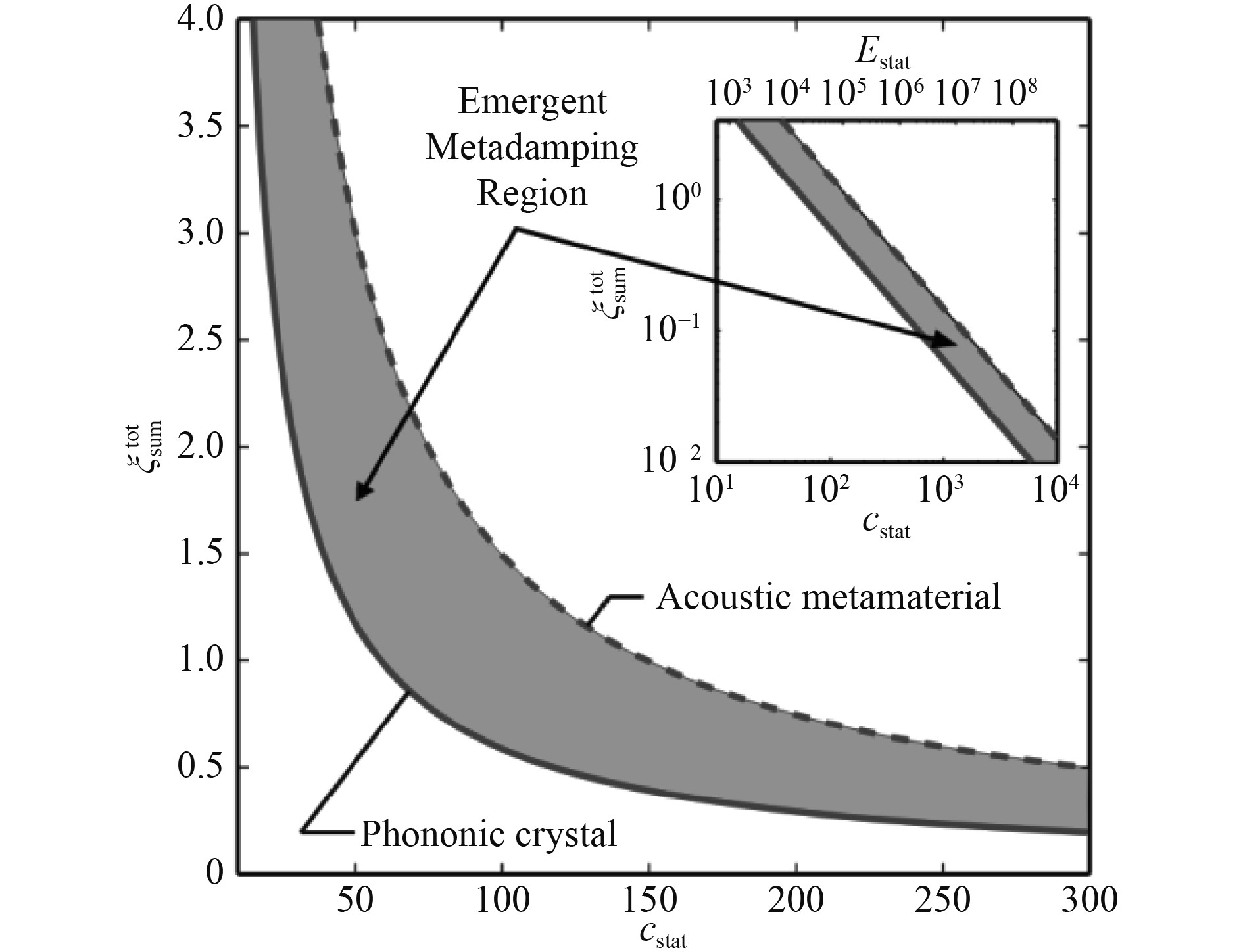
超结构还能产生超阻尼效果。相比Bragg型声子晶体,局域共振弹性超结构在亚波长频段具有更高的阻尼效应(见图3),据此提出了超阻尼的概念[8]。Chen等[9]采用超阻尼实现了宽带振动抑制,Fang等[10]也研究了多共振耦合对超材料阻尼的增强作用。
|
图 3 局域共振弹性超结构与布拉格型声子晶体的阻尼特性 Fig. 3 Local resonance elastic superstructure and damping characteristics of Bragg-type phononic crystals |
本文研究对象中的导航仪基座是类似于厚度较大的板壳结构。自2010年至今,大量研究设计了基于局域共振的超材料板壳结构,典型模型如图4所示,将局域共振单元周期性地安装在壁板结构上。基于周期性局域共振单元产生的带隙和超阻尼效应,可将板壳结构低频振动降低20~40 dB。

|
图 4 典型超材料板壳结构模型 Fig. 4 Typical metamaterial plate and shell structure model |
弹性超结构可以用局域共振和Bragg散射形成的带隙和增强耗散作用使弹性波快速衰减,高效抑制给定频带内的结构振动与声辐射,是UUV惯导系统多线谱振动抑制的理想手段。
2 研究思路借助计算机仿真技术,结合分析研究,应用弹性超结构/超材料理论与技术,针对本文研究的UUV惯导系统承载结构采取减振降噪措施,通过弹性波带隙来抑制振动或降低振动传递,进而无需将隔振频率设计得过低,以便保证导航精度。在此前提下,显著隔离UUV导航系统的振动噪声,有效降低辐射噪声,并减少自噪声对探测性能的影响。
3 具体方案与仿真计算结果本文研究的惯性导航系统所在的舱段模型如图5所示。连接板上固定的方块即为惯性导航部件,该部件固定连接在两侧的基座上,基座端部固定连接在UUV壳体上。根据建模计算,原系统的一阶共振频率为100 Hz左右,几乎无阻尼效果,因此隔振效果差。受UUV壳体尺寸限制,难以在导航系统上附加大量减振单元,因此采取了2种减振降噪措施:基于弹性超结构的减振基座和导航系统减振设计方案。

|
图 5 惯性导航舱段结构 Fig. 5 Inertial navigation module structure |
1)基于弹性超结构的减振基座设计方案
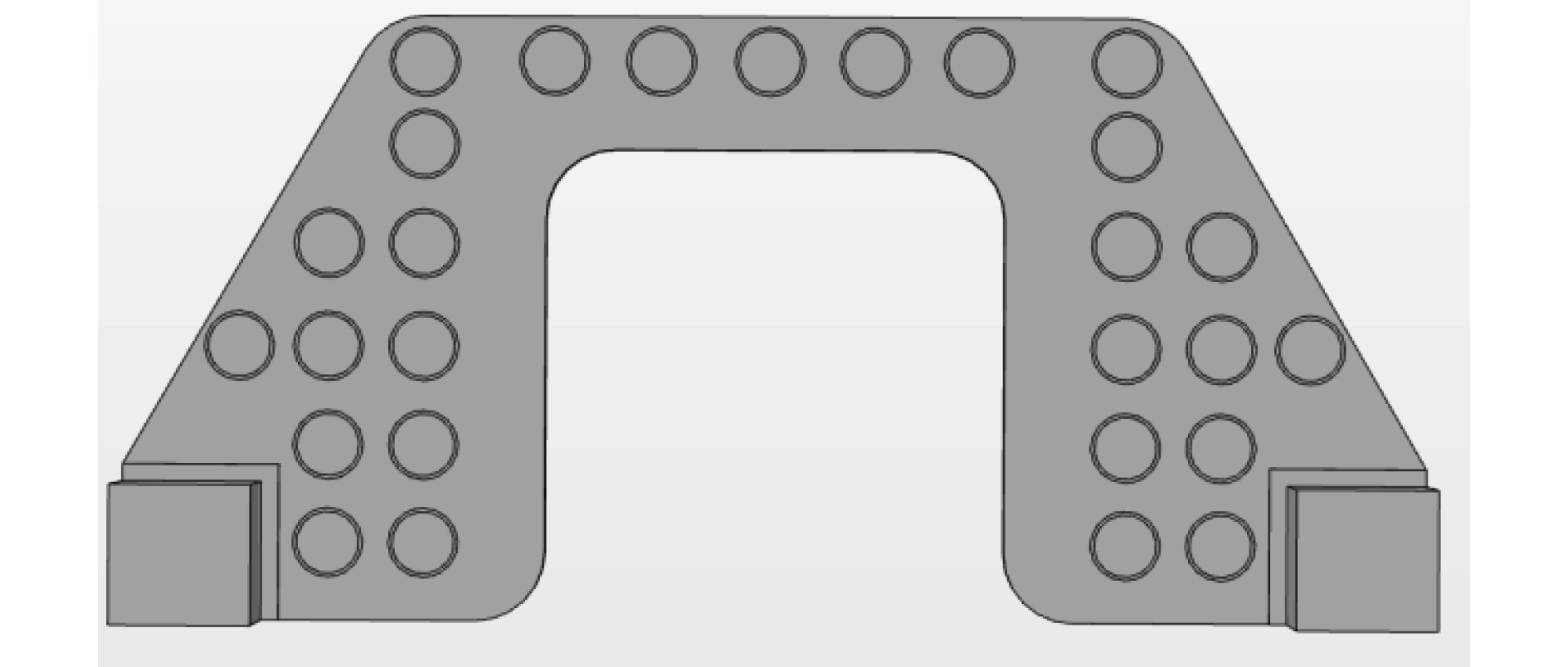
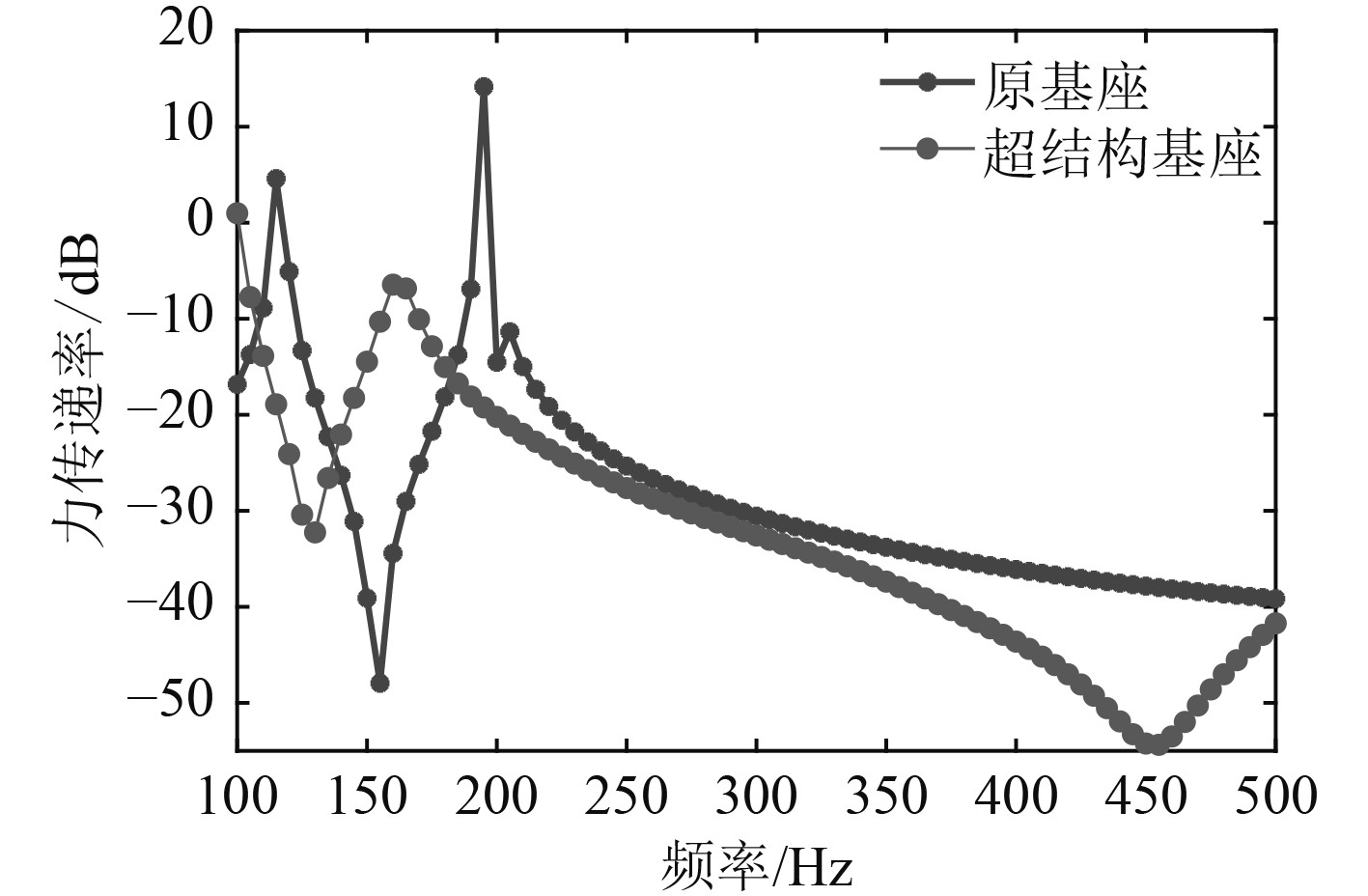
基于局域共振产生的带隙和超阻尼原理,在基座没有承载的基板面上,开出一系列通孔,并周期性地安置局域共振单元,布置方案如图6 所示,其中通孔中的圆环为橡胶圈,里面的圆柱作为振子。共振单元的频率并不完全相同,典型的振动模态如图7所示。通过计算机仿真计算得到的减振效果如图8所示。计算结果表明,加入局域共振单元后,振动峰值显著降低,说明加入共振单元可以增加结构阻尼效果,抑制宽频振动。此外,通过优化设计结构刚度、局域共振单元的参数,可以显著增加300~500Hz频段上基座本身产生的隔离效果。
|
图 6 基于弹性超结构的新型基座初步设计方案 Fig. 6 Preliminary design scheme of new base based on elastic superstructure |

|
图 7 新型基座的振动模态图 Fig. 7 Vibration mode diagram of the new base |
|
图 8 基座减振效果初步计算图 Fig. 8 Preliminary calculation diagram of base damping effect |
2)基于弹性超结构的导航系统减振设计方案
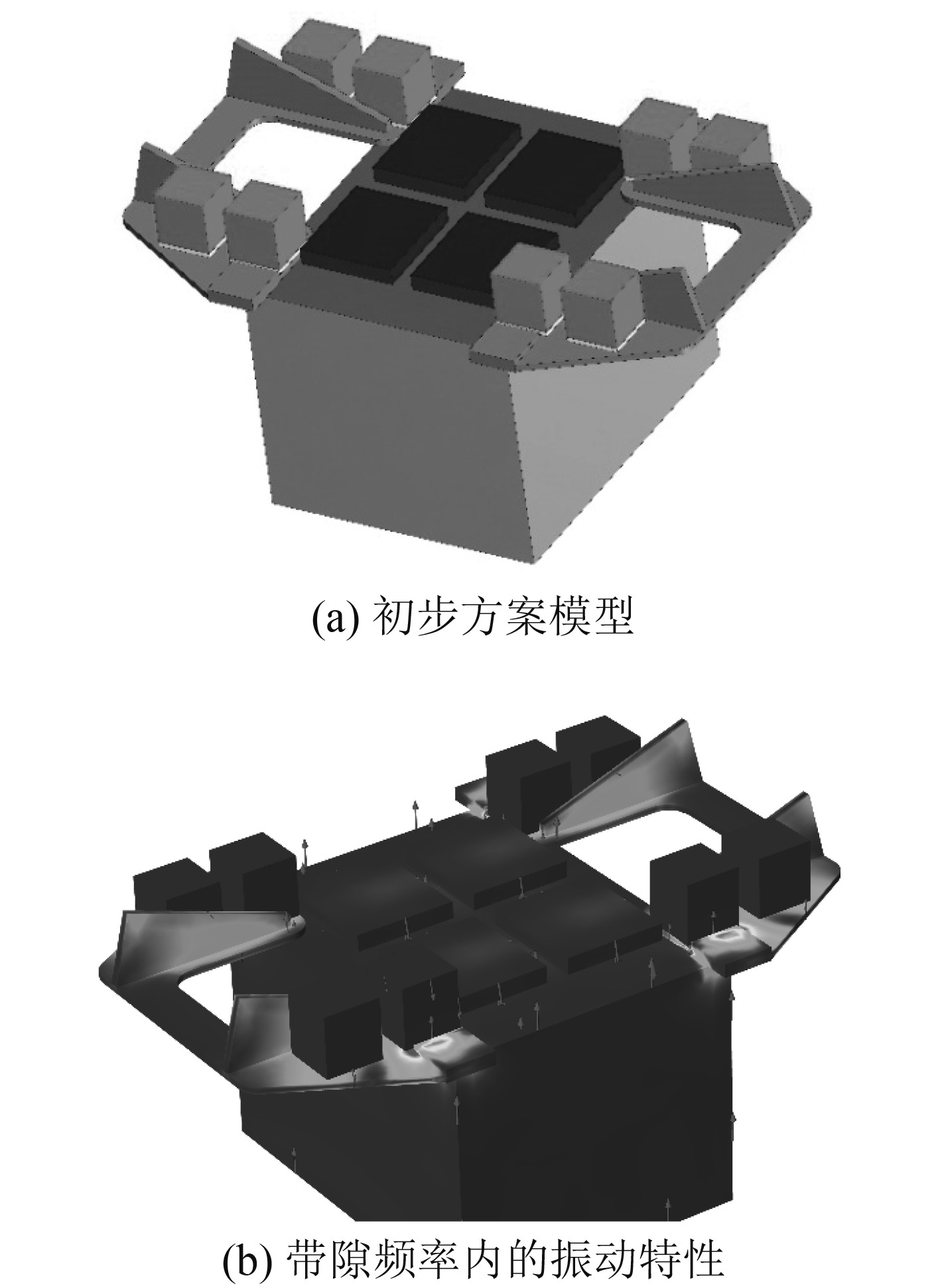
根据实际舱体空间,设计了基于共振型超结构的惯性导航陀螺仪系统减振方案,如图9(a)所示。图中安装在基座和设备底部的质量块即为可产生局域共振带隙的共振单元。进而,开展了数值仿真计算,研究系统振动特性,分析陀螺仪振动引起的基座固定安装部位反作用力频谱。通过反作用力即可定量估计陀螺仪振动对艇体振动的影响。将振动传递率定义为反作用力与激励力的比值。在仿真中,输入力施加在导航设备的上表面上。
|
图 9 基于共振型超结构的初步减振设计方案及数值计算 Fig. 9 Preliminary Design Scheme and Numerical Calculation of Vibration Reduction Based on Resonant Superstructure |
由图9(b)可知,在带隙频率内,局域共振单元会对导航设备和基座产生反向作用力,从而降低陀螺仪振动向艇体的传递,而且也降低了陀螺仪本身的振动幅值。研究初步对比了不同参数组的力传递率频谱,如图10所示。计算结果表明,恰当设计结构和材料参数能够使局域共振带隙范围(图10(a)中的阴影部分)超过350~420 Hz范围,实现对陀螺仪线谱频带的全覆盖。如图10(b)所示,通过恰当设计材料参数,可使带隙覆盖范围内的力传递率衰减达到8~17 dB。对3根线谱的力传递率衰减量分别为8 dB,17 dB,10 dB。

|
图 10 研究方案的有限元计算结果 Fig. 10 Finite element calculation results of the research proposal |
本初步设计方案是没有采取系统优化的结果,进一步优化结构和材料参数有望进一步降低带隙内的振动传递率。
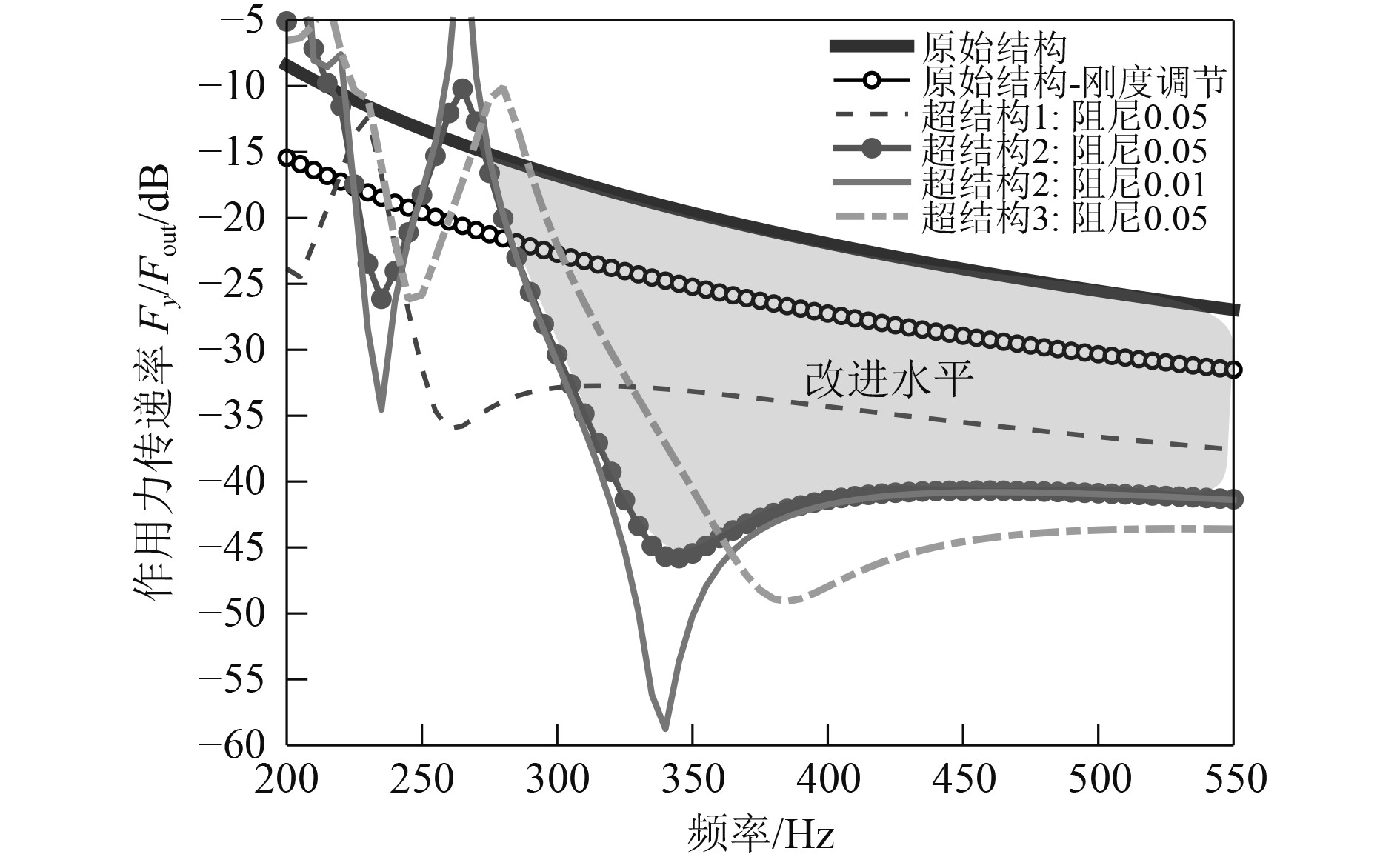
进一步,适度降低基座的结构刚度,通过仿真计算对比超结构设计方案的力传递率,结果如图11 所示。分析表明,降低刚度后,整个系统的隔振水平都会提升,通过优化共振单元的频率可以在300~500 Hz内产生带隙,显著降低力传递率。此外,共振单元的阻尼对带隙谷值有显著影响,阻尼越小,减振效果越好。通过当前初步方案的优化设计,相比现役方案,可以将3根线谱的力传递率衰减量分别提高25~30 dB,21 dB,17 dB,实现了高效振动抑制。
|
图 11 将基座结构刚度降低约50%后超结构设计方案的力传递率 Fig. 11 The force transmission rate of the superstructure design scheme after reducing the rigidity of the base structure by about 50% |
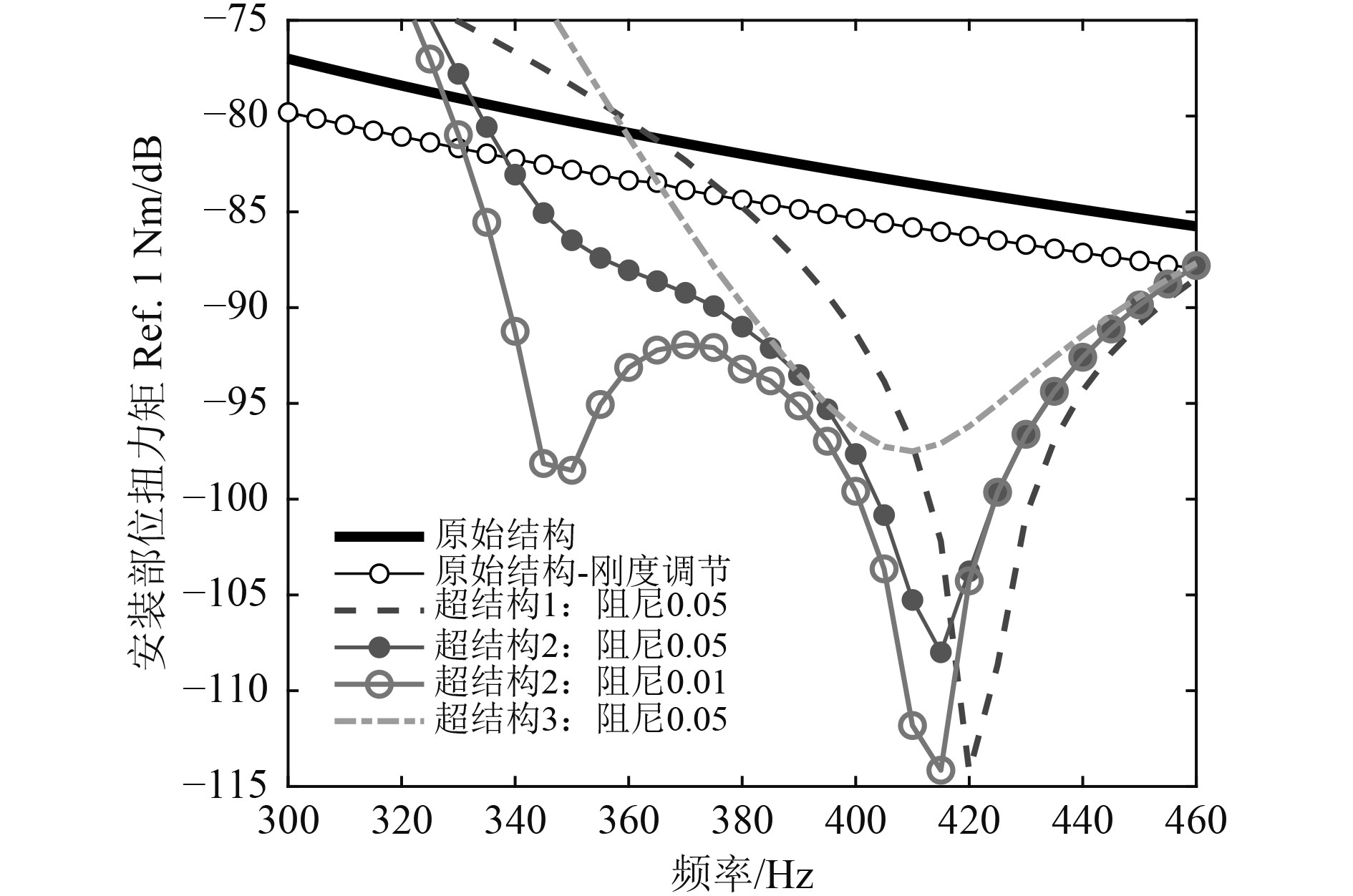
进一步,分析上述设计方案中,在陀螺仪表面采用力激励,传递至艇体安装部位的扭转力矩量级,如图12 所示。在阻尼最小的情况下,相比现役方案,可将3根线谱的扭转力矩量级分别降低18 dB,11 dB,21 dB。
|
图 12 将基座结构刚度降低约50%后超结构方案中传递至艇体的扭转力矩量级 Fig. 12 The magnitude of the torsional moment transmitted to the hull in the superstructure scheme after the rigidity of the base structure is reduced by about 50% |
进一步优化超结构设计方法、结构和材料参数有望进一步提升减振效果,从而降低由陀螺仪引起振动噪声。
计算结果表明,本文提出的基于超结构的惯性导航陀螺仪多线谱抑制方案完全可行,通过优化设计可达到预期效果。
4 结 语针对UUV惯性系统产生的多根线谱振动噪声,开展了基于弹性超结构的多线谱振动噪声抑制技术研究。在保证导航精度的前提下,对UUV惯导系统承载结构,提出了基于超结构的系统减振和陀螺仪隔振基座设计方案,并开展了多线谱抑制优化设计计算机仿真,实现对多线谱的有效抑制。验证了基于超结构的惯性导航陀螺仪多线谱抑制方案的可行性,为下一步基于弹性超结构的导航系统新型隔振基座设计、导航系统减振设计、多线谱抑制优化设计及相应的系统制备、集成、试验验证奠定了基础。
| [1] |
LIU Z, ZHANG X, MAO Y, et al. Locally resonant sonic materials[J]. Science, 2000, 289(5485): 1734-1736. DOI:10.1126/science.289.5485.1734 |
| [2] |
LIU Z, CHAN C T, SHENG P. Analytic model of phononic crystals with local resonances[J]. Physical Review B, 2005, 71(1): 14103. DOI:10.1103/PhysRevB.71.014103 |
| [3] |
FANG N, XI D, XU J, et al. Ultrasonic metamaterials with negative modulus[J]. Nature Materials, 2006, 5(6): 452-456. DOI:10.1038/nmat1644 |
| [4] |
LI J, CHAN C T. Double-negative acoustic metamaterial[J]. Physical Review E, 2004, 70(5): 55602. DOI:10.1103/PhysRevE.70.055602 |
| [5] |
ZHU R, LIU X N, HU G K, et al. A chiral elastic metamaterial beam for broadband vibration suppression[J]. Journal of Sound and Vibration, 2014, 333(10): 2759-2773. DOI:10.1016/j.jsv.2014.01.009 |
| [6] |
刘攀, 刘和平, 张琛. 激光陀螺捷联惯组减振系统动力学特性研究[J]. 光学与光电技术, 2011, 9(5): 70-74. |
| [7] |
XU X, BARNHART M V, LI X, et al. Tailoring vibration suppression bands with hierarchical metamaterials containing local resonators[J]. Journal of Sound and Vibration, 2019, 442: 237-248. DOI:10.1016/j.jsv.2018.10.065 |
| [8] |
XIAO Y, WEN J, WANG G, et al. Theoretical and experimental study of locally resonant and bragg band gaps in flexural beams carrying periodic arrays of beam-like resonators[J]. Journal of Vibration and Acoustics, 2013, 135(4): 41006. DOI:10.1115/1.4024214 |
| [9] |
XIAO Y, WEN J, WEN X. Flexural wave band gaps in locally resonant thin plates with periodically attached spring–mass resonators[J]. Journal of Physics D Applied Physics, 2012, 45(19): 195401. DOI:10.1088/0022-3727/45/19/195401 |
| [10] |
HUSSEIN M I, FRAZIER M J. Metadamping: An emergent phenomenon in dissipative metamaterials[J]. Journal of Sound and Vibration, 2013, 332(20): 4767-4774. DOI:10.1016/j.jsv.2013.04.041 |
 2022, Vol. 44
2022, Vol. 44
