2. 中国舰船研究院,北京 100101
2. China Ship Research and Development Academy, Beijing 100192, China
离心泵类设备被广泛应用于舰船动力及其他系统,随着舰船噪声水平的不断降低,离心泵类系统在实际使用过程中,除应满足设计功能外,还需兼顾舰船整体声学性能。为降低系统对舰船噪声的影响,一方面可以通过不断优化设计、提升建造工艺来降低系统本身的振动噪声;另一方面则需要提高声学故障诊断能力,及时发现并消除因噪声控制措施失效产生的声学故障[1-2]。然而由于舰船离心泵类系统振动噪声数据难以采集,导致可用样本较少,因而传统故障诊断方法难以适用。
为了满足小样本条件下复杂系统故障诊断需求,20世纪80年代,Judea pearl[3]首次提出贝叶斯网络,随后该方法成为研究热点,多用于专家系统,成为表示不确定知识和推理问题的流行方法。在诸多学者的研究基础上,Cai等[4]提出了故障预测贝叶斯网络模型的概念。在故障诊断时常常根据故障特征结合经验给出诊断结论,利用此类信息及检测信号建立的贝叶斯网络被称为诊断贝叶斯网络(DBN)[5]。国内外学者基于贝叶斯网络模型开展了大量故障诊断方面的研究,并取得丰硕成果。邹树梁等[6]基于故障树和贝叶斯网络建立了液压举升机故障诊断模型,可实现故障点的快速诊断。张皓宇等[7]基于FMEA,FTA,BN提出了一种舰艇机电装备故障分析方法,并应用于工程实践。
本文基于典型离心泵系统结构组成及振动传递机理确定贝叶斯网络结构,通过模拟试验获取数据样本,在对数据样本开展分析基础上确定贝叶斯网络各节点参数,从而建立离心泵类系统声学故障诊断贝叶斯网络模型,并以实验数据对该诊断模型的有效性进行了验证。结果表明,该网络模型计算量小、诊断准确率高,可以实现舰船离心泵类系统声学故障诊断。
1 理论基础贝叶斯网络又称信度网络,是贝叶斯方法的扩展,是目前不确定知识表达和推理领域最有效的理论模型之一。一个贝叶斯网络是一个有向无环图,由代表变量节点及连接这些节点的有向边构成。节点代表随机变量,节点间的有向边代表相互关系(由父节点指向子节点),用条件概率表达相互关系强度,没有父节点的用先验概率表示。
假设对于
| $ P\left( {F|E} \right) = \frac{{P\left( {F \cap E} \right)}}{{P\left( E \right)}},$ | (1) |
式中
而全概率公式为:
| $ P\left( E \right) = \sum\limits_i {P\left( {E|{F_i}} \right)} P\left( {{F_i}} \right),$ | (2) |
将式(2)代入式(1),得到贝叶斯公式:
| $ P\left( {{F_j}|E} \right) = \frac{{P\left( {E|{F_j}} \right)P\left( {{F_j}} \right)}}{{\sum\limits_i {P\left( {E|{F_i}} \right)} P\left( {{F_i}} \right)}}。$ | (3) |
图1诊断贝叶斯网络中故障节点为事件节点,变量类型为布尔型,即取值为0或1,代表发生故障与未发生故障2种情况。对于如上网络
|
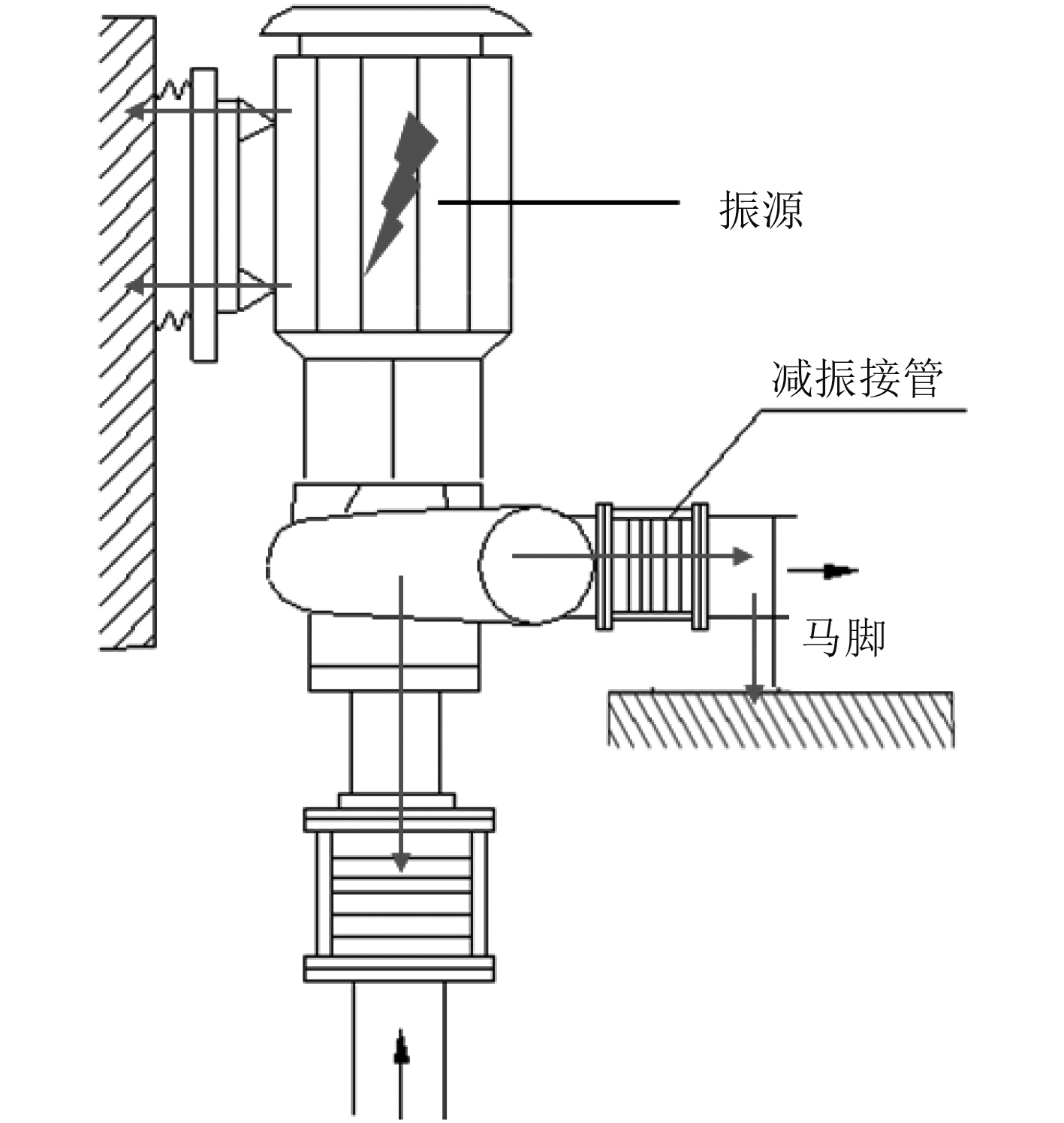
图 1 离心泵系统振动传递路径示意图 Fig. 1 Vibration path of propeller pump system |
| $ P\left( x \right) = {\prod _{i \in V}}P\left( {{x_i}|{x_{pa(i)}}} \right)。$ | (4) |
式中:
因此,对于图中任意随机变量,联合概率可以通过连乘所有条件概率得到:
| $ P\left( {{x_1}, \cdot \cdot \cdot ,{x_k}} \right) = P\left( {{x_k}|{x_1}, \cdot \cdot \cdot ,{x_{k - 1}}} \right) \cdot \cdot \cdot P\left( {{x_2}|{x_1}} \right)P\left( {{x_1}} \right)。$ | (5) |
根据国内船舶建造过程中出现的声学质量问题统计结果,管路专业问题占比超过60%,是建造阶段声学质量问题的重点。其中造成管路声学质量问题的主要原因是管路干涉、管卡损坏、管路支架与设备距离不符合要求等原因造成的减振降噪措施失效。因此本文以典型离心泵系统为例,重点研究离心泵系统减振元器件失效故障,并以评价隔振元器件隔振效果的隔振量为证据节点,开展基于贝叶斯网络的舰船离心泵类系统建造阶段声学故障诊断方法研究。
|
|
表 1 诊断贝叶斯网络模型节点内容 Tab.1 Node content of diagnosis model |
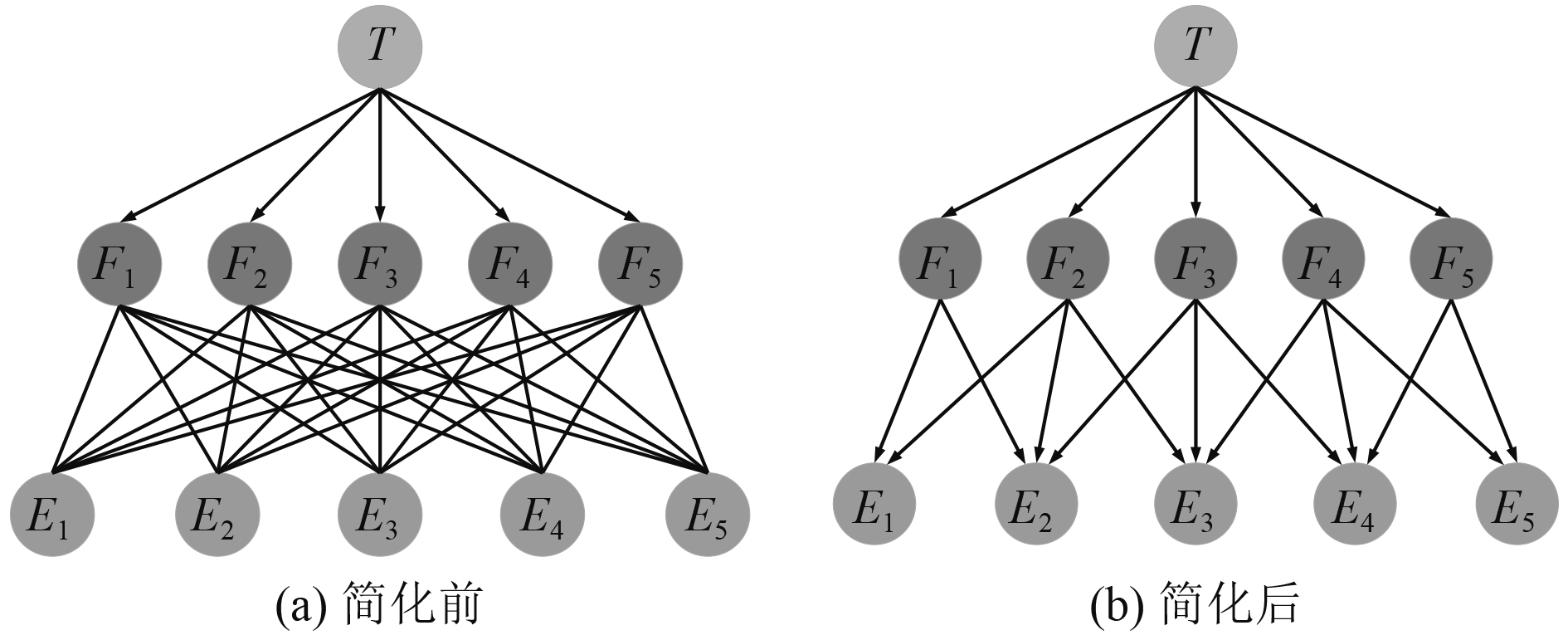
构建诊断贝叶斯网络模型结构,需要确定网络结构以及各节点的条件概率两部分。离心泵类系统诊断贝叶斯网络中各故障节点为父节点,证据节点为子节点,具体结构如图2(a)所示。该网络拓扑结构复杂,简化网络结构,对该离心泵系统振动传递路径进行分析,主要包括:1)设备振动经机脚-基座传递至船体;2)减振接管后向进水管、出水管方向传播;3)管路振动经支吊架传递至船体[8],振动传递示意图见图1。因此可以根据振动传递关系对网络拓扑结构进行简化,将振动传动关系较弱的节点之间的有向边省略。由图1可知,进口管路支吊架只与进口管路与进口一级马脚具有振动传递关系,因此在图2(a)中只保留E1与F1,F2之间的有向边。按照以上简化原则将图2(a)贝叶斯诊断网络进行简化,简化结果如图2(b)所示。
|
图 2 诊断贝叶斯网络结构 Fig. 2 Construction of nodes |
确定诊断贝叶斯网络结构后,需确定各故障节点的先验概率。实际应用中通常使用不同故障发生频率代替先验概率,如ASHRAE项目中关于不同故障发生频率的调查结果[9]。由于离心泵类系统声学故障数据样本较少,且选取的5个证据节点结构上相互独立,5个故障节点之间没有耦合关系。因此基于以上分析做出2点假设:1)5个故障相互独立;2)5个故障发生概率相同,因此将全部故障的先验概率设置为0.2,如表2所示。后续随机组故障数据积累对以上概率进行更新。
|
|
表 2 贝叶斯网络故障节点先验概率 Tab.2 Prior probability of net |
在传统贝叶斯网络中需确定
1)在离心泵类系统正常运行工况下获取进口支吊架、出口支吊架、进口挠性接管、出口挠性接管、机脚基座的隔振量,如表3所示。将4次测试值进行能量平均,作为基准值,在理想状态下,所观测变量E应与基准值的偏差为0,但由于误差影响,实测数据与基准值之间存在偏差,因此针对隔振量设置正常状态区间为
|
|
表 3 正常工况下各减振元器件隔振量(10 Hz~8 kHz) Tab.3 Vibration level difference of components in normal condition(10 Hz~8 kHz) |
2)设置5个故障工况,获取了31组数据样本,随机选取26组试验数据作为贝叶斯网络训练样本,其余5组作为模型验证样本。对训练样本数据进行统计,将证据节点偏离频率作为条件概率,以F1故障为例,通过将进口支吊架隔振器上下刚性连接模拟声短路故障。该故障模拟试验共进行8组,其中5组试验出现E1小于基准值正常状态区间,因此P(E1减小|F1)为0.625。考虑到意外事件发生的可能性,避免运算过程中出现分母为0的情况,将统计结果为0的条件概率修正为0.001。根据以上统计方法得到表4中各证据节点条件概率。
|
|
表 4 诊断贝叶斯网络证据节点条件概率 Tab.4 Conditional probability of evidence node of net |
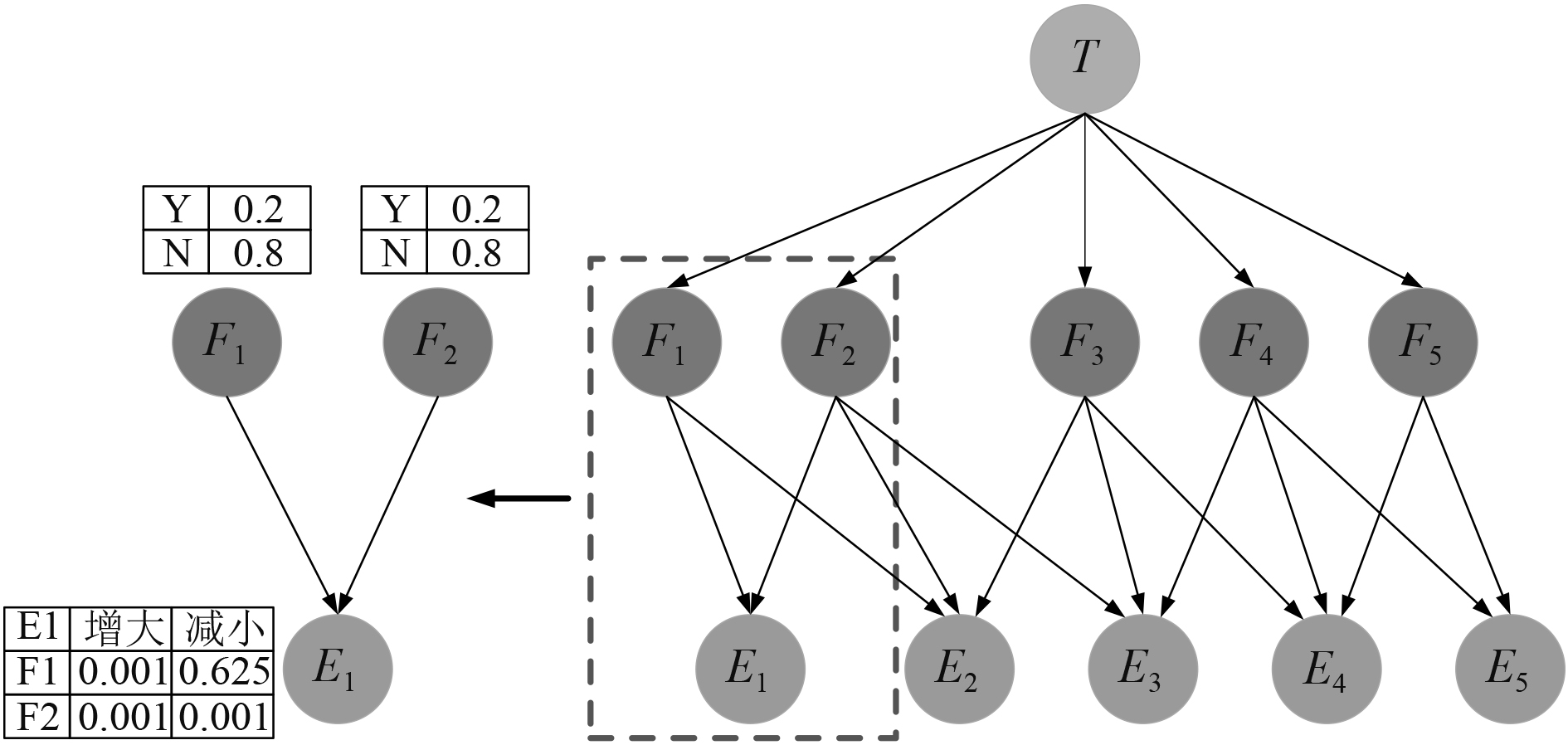
以上完成了贝叶斯网络的参数设置,以E1为例,由表2可知故障F1和F2发生的先验概率为0.2此处用Y表示。由表3可知,当故障F1发生的条件下,进口支吊架隔振量(E1)增大的概率为0.001,减小的概率为0.625;故障F2发生的条件下,E1增大的概率为0.001,减小的概率为0.001。将故障节点的先验概率及故障节点与证据节点的条件概率代入诊断贝叶斯网络结构中,得到贝叶斯网络如图3所示。
|
图 3 贝叶斯网络 Fig. 3 Bayesian network |
为验证模型有效性,将5组模型验证样本数据作为输入对诊断贝叶斯网络进行验证。通过贝叶斯理论,可根据式(3)计算后验概率,如果获取了
|
|
表 5 诊断贝叶斯网络输入量 Tab.5 Input of net |
将表5中各证据节点数据情况代入诊断贝叶斯网络,计算得到各故障发生的后验概率,当后验概率≥0.8认为故障发生。由表6可知,样本1计算结果显示F1故障后验概率为0.994,因此诊断样本1故障为F1故障,其余4组样本数据诊断结果见表6。结果显示该网络对5组实验数据的诊断结果均正确。
|
|
表 6 各故障节点后验概率 Tab.6 Posterior probability of failed nodes |
本文以舰船离心泵系统为研究对象,针对建造阶段此类系统常见声学故障,以各减振元器件隔振量作为观测值,提出一种基于贝叶斯网络的舰船离心泵类系统建造阶段声学故障诊断模型。并通过定量试验对该模型的有效性进行验证,结论如下:
1)通过振动传递路径分析,排除贝叶斯网络中关联度较低的有向边,优化了网络拓扑结构。
2)在故障样本有限的情况下,通过模拟试验获取样本数据,基于统计获取网络模型所需的26个条件概率。
3)通过随机选取的5组模型验证样本数据对本文提出的网络模型进行验证,结果显示该方法的诊断结果与实际故障相吻合,验证了贝叶斯网络在舰船离心泵类系统建造阶段声学故障诊断领域应用的可行性。
| [1] |
O'MARA D, GEAR G, MCMAHON D. Automated self-noise monitoring and acoustic fault detection[C]// UDT Korea, 2002.
|
| [2] |
章林柯, 何琳, 江涌. 基于MIMO模型的潜艇声学故障预报研究[J]. 武汉理工大学学报, 2008, 32(2): 320-322+326. |
| [3] |
PEARL J. Bayesian networks: A model of self-activated memory for evidential reasoning[J]. Proceeding of Cognitive Science Society, 1985, 1985. |
| [4] |
CAI Z , SUN S , SI S , et al. Research of failure prediction Bayesian network model[C]// International Conference on Industrial Engineering & Engineering Management. IEEE, 2009.
|
| [5] |
李前舸. 基于诊断贝叶斯网络的螺杆式冷水机组故障检测与诊断研究[D]. 上海: 上海交通大学, 2020.
|
| [6] |
邹树梁, 陈树强. 基于故障树分析和贝叶斯网络方法的液压举升机构故障诊断[J]. 南华大学学报:自然科学版, 2021, 35(4): 6. |
| [7] |
张皓宇, 付锦洲, 魏曙寰. 基于贝叶斯网络的舰艇机电装备故障分析方法研究[J]. 装备制造技术, 2020(12): 5. |
| [8] |
张义忠, 张华栋, 计方, 等. 船舶典型通海电动泵管路系统建造声学故障模式初探[J], 舰船科学技术, 2021, 43(S1): 7–12.
|
| [9] |
陈东超. 基于贝叶斯网络的汽轮发电机组故障诊断方法及应用研究[D]. 北京: 华北电力大学, 2018.
|
| [10] |
张连文, 郭海鹏. 贝叶斯网引论[M]. 北京: 科学出版社, 2006: 41–45.
|
 2022, Vol. 44
2022, Vol. 44
