2. 重庆大学 机械传动国家重点实验室,重庆 400044;
3. 重庆红江机械有限责任公司,重庆 402160;
4. 重庆大学 弘深学院机械实验班,重庆 400044
2. State Key Laboratory of Mechanical Transmission, Chongqing University, 400044 Chongqing, China;
3. Chongqing Hongjiang Machinery Co. Ltd., Chongqing 402160, China;
4. Hongshen Honors School, Chongqing University, Chongqing 400044, China
低速机共轨式电控燃油喷射技术是提高柴油机工作效率、节能减排的关键技术,系统中电磁阀的响应速度和稳定开关直接影响着喷油效果。常浩和刘鹏等[1-2]对车用机油泵电磁阀的温度场进行了研究,以电磁阀作为热源,给出电磁阀内部温度场分布。研究人员主要研究了车用电磁阀电磁有限元计算及换热分析,对船用低速机喷射系统电磁阀研究较少,电磁阀线圈散热和重油管路散热为低速机电控喷油器电磁阀组件的主要热源,该电磁阀换热相对于车用电磁阀换热更加复杂。
本文以某型船用低速机电控喷油器为研究对象,在确定电磁阀三维结构并且满足其工作性能的基础上,采用Fluent共轭耦合换热计算模型,将电磁阀线圈和重油作为热源,分析重油、线圈和冷却油换热对电磁阀温度场的影响。通过对电磁阀共轭耦合流动换热计算和分析,为低速机电控喷油器电磁阀的设计提供指导。
1 电磁阀结构电控式喷油器电磁阀组件结构简图如图1所示,其主要结构包括重油管路、密封垫圈、电磁阀、润滑油管路、喷油器体、复位弹簧、衔铁、控制阀芯等,喷油器电控系统中电磁阀控制着针阀的启闭,对燃油雾化质量起着关键作用。电磁阀安装在喷油器体内部,通电后电磁阀线圈本身产生热量,流经喷油器体的重油温度大于200℃,重油通过针阀器体导热和辐射散热,使电磁阀的温度升高。若电磁阀温度过高,则导致电磁阀失效,喷油器无法正常工作。在电磁阀四周设计有润滑冷却管路,通过冷却油的流动完成换热,带走电磁阀组件中的热量,维持电磁阀正常工作所需的稳定温度。

|
图 1 电磁阀组件剖面图 Fig. 1 Component section of solenoid valve |
电磁阀的换热形式遵循基本的传热学理论,其换热形式分为电磁阀表面与润滑油的热对流,喷油器体表面与重油、冷却油的热对流、喷油器体的导热及重油辐射能量[2]。本文研究的电磁阀可简化为轴对称的圆柱结构,对于该稳定状态下电磁阀的导热微分方程[3]为:
| $ \frac{1}{r}\times \frac{\partial }{\partial r}\left(kr\frac{\partial T}{\partial r}\right)+\frac{1}{{r}^{2}}\times \frac{\partial }{\partial \phi }\left(k\frac{\partial T}{\partial \phi }\right) +\frac{\partial }{\partial z}\left(k\frac{\partial T}{\partial z}\right)+\varnothing =0。$ | (2.1) |
式中:r为半径,m;
对于针阀体与流体间的对流传热,可用牛顿冷却公式[3]表示为:
| $ {q}={h}({T}_{\infty }-{T}_{s})。$ | (2.2) |
式中:q为热流密度,W/m2;h为对流换热系数,W/(m2·k);
高温重油和电磁阀通过电磁波辐射传输能量,由波尔兹曼定律可以得出其热流密度公式[3]为:
| $ {E}=\mathrm{\epsilon }\mathrm{\sigma }{T}_{s}^{4}。$ | (2.3) |
式中:
电磁阀共轭换热计算过程既要考虑流体的连续性问题,也要遵守换热过程的能量守恒问题,计算流体力学流动换热求解的动量微分方程和能量微分方程表达式[4]分别为:
| $ \frac{\partial }{\partial t}\rho {u}_{i}+\frac{\partial }{\partial {x}_{i}}\rho {u}_{i}{u}_{j}=-\frac{\partial p}{\partial {x}_{i}}+\frac{\partial }{\partial {x}_{i}}\mu \left(\frac{\partial {u}_{i}}{\partial {x}_{i}}+\frac{\partial {u}_{i}}{\partial {x}_{j}}\right)+{F}_{i},$ | (2.4) |
| $ \frac{\partial }{\partial t}\mathrm{\rho }{E}+\frac{\partial }{\partial {x}_{i}}{u}_{i}\left(\rho E+p\right)=\frac{\partial }{\partial {x}_{i}}k\frac{\partial T}{\partial {x}_{i}}。$ | (2.5) |
式中:ρ为密度,kg/m3;u为速度,m/s;p为压力,Pa;Fi为体积力,N;μ为等效动力粘度,kg/m·s;E为质量平均变量参数,kg;T为热力学温度,K。
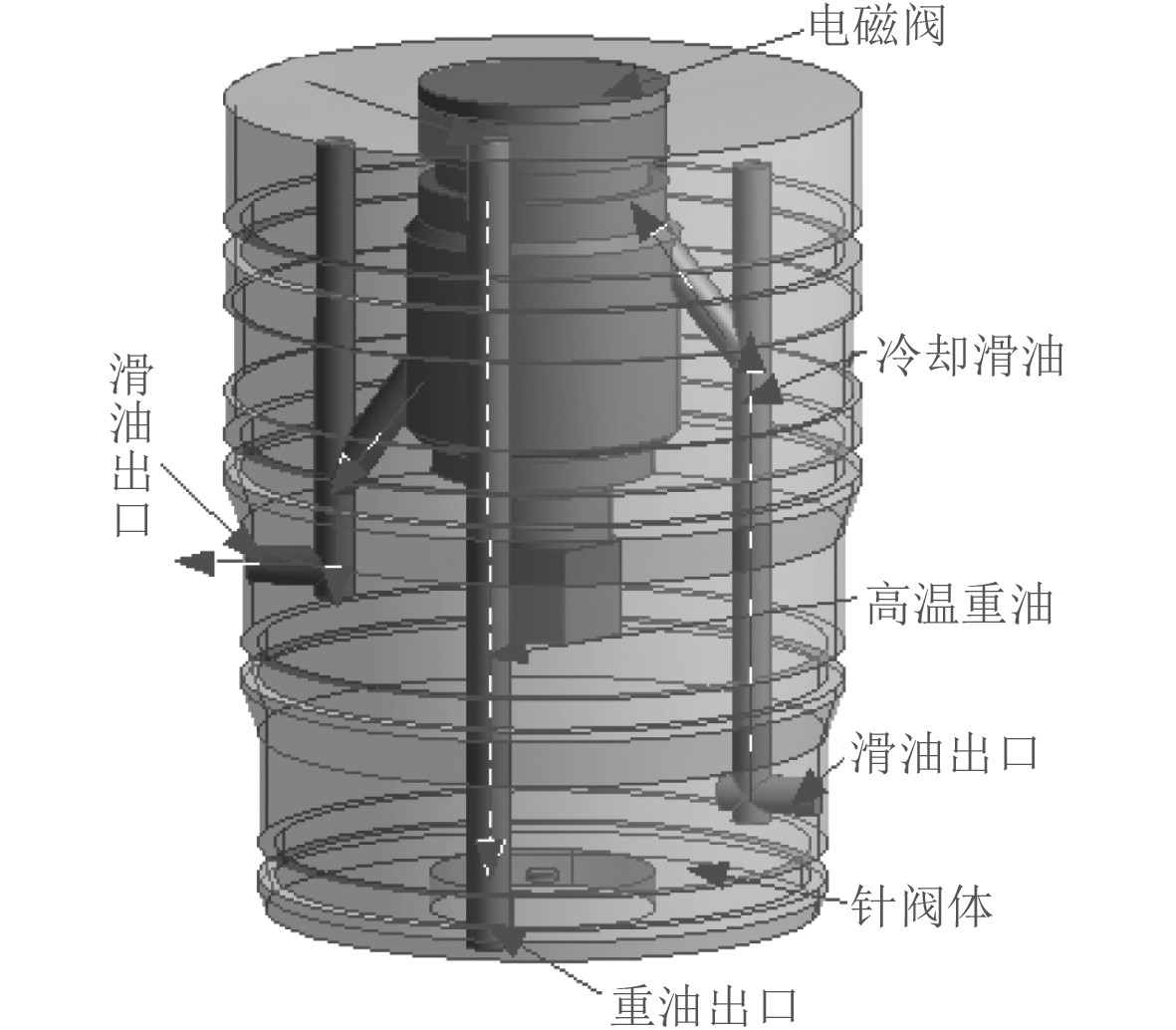
3 共轭耦合计算 3.1 仿真模型喷油器电磁阀组件中存在较多的螺钉、沉头孔以及微小导圆角区域等,为了便于网格的划分,保证计算网格的质量,因此对模型进行简化,删除对计算无影响的特征[5]。采用SCDM软件填充功能抽取计算流域,其整个计算流域如图2所示,共轭换热模型主要包括针阀特金属固体、电磁阀、冷却润滑油、高温重油区域,图中虚线分别为冷却滑油和高温重油流动方向。
|
图 2 计算模型 Fig. 2 Computational model |
基于简化的电磁阀冷却仿真模型,采用Meshing进行网格划分。求解采用四面体网格与边界层的方式进行网格离散,为保证流体网格和固体网格交界面节点一一对应,将模型4个部分拓扑成为一个组,电磁阀网格尺寸设置为1 mm,针阀体网格尺寸设置为1.5 mm,流体区域网格尺寸设置为0.5 mm,边界膨胀层设置为3层,最大层的厚度为0.4 mm,最终网格总数量约为302万,网格平均质量约为0.78,模型网格如图3所示。

|
图 3 模型网格 Fig. 3 Model mesh |
共轭换热计算的边界条件及材料属性如表1所示。
|
|
表 1 材料属性及边界 Tab.1 Material properties and boundaries |
Fluent提供了丰富的湍流模型,如标准k-ε模型、RNG k-ε模型、低雷诺数Wilcox模型、低雷诺数Menter、代数雷诺应力模型、微分雷诺应力模型、微分雷诺通量模型及LES模型、DES模型等[6-7]。针对燃油系统电磁阀冷却仿真的问题,采用SST k-ω模型[8]进行计算分析,该湍流模型包含修正的湍流粘性公式,并且考虑了湍流剪切应力产生的效应,考虑了湍流剪切应力的SST k-ω模型不会对涡流粘度造成过度预测,对设置近壁面参数计算敏感,计算结果准确度高。
4 共轭换热分析在Fluent完成边界和材料的相关设置,分析所用重油和润滑油均为不可压缩流体,且流速较低,故选择基于压力求解器。压力-速度求解方法选择Fluent中的Coupled Pseudo Transient方法,监测冷却润滑油、重油的进出口流量及温度,其计算结果如表2所示,冷却油进口流量均为5.270 5 L/min,进口温度为55.0℃,出口温度为78.7℃。重油在进出口流量为3.0 L/min的工况下,进口温度为200℃,出口温度为198.8℃。
|
|
表 2 流域计算结果 Tab.2 Fluid calculation results |
图4(a)为冷却滑油的速度云图,由图可知,在靠近壁面和流道封闭端的流速接近0 m/s,整个滑油的流体域最大流速约为13.69 m/s。图4(b)为计算稳定下的滑油温度分布情况,从图中可以明显的看出进口区域的温度比较低,换热完成后在出口附近流体的温度稍高,在滑油封闭端不流通的区域温度最高约为135℃。

|
图 4 滑油计算云图 Fig. 4 Calculation results of lubricating oil |
电磁阀组件换热部分主要包括重油流动换热、润滑油换热、电磁阀线圈散热,针阀体表面散热。共轭换热计算结果如表3所示。
|
|
表 3 共轭换热温度结果 Tab.3 Conjugate heat transfer temperature results |
冷却润滑油的最高温为135.08℃,重油的平均温度为199.27℃,针阀体平均温度为97.83℃,电磁阀最高温度为93.42℃,平均温度为74.22℃。在表1的边界条件下,要求电磁阀的最高温度低于180℃,电磁阀保持正常的工作状况。
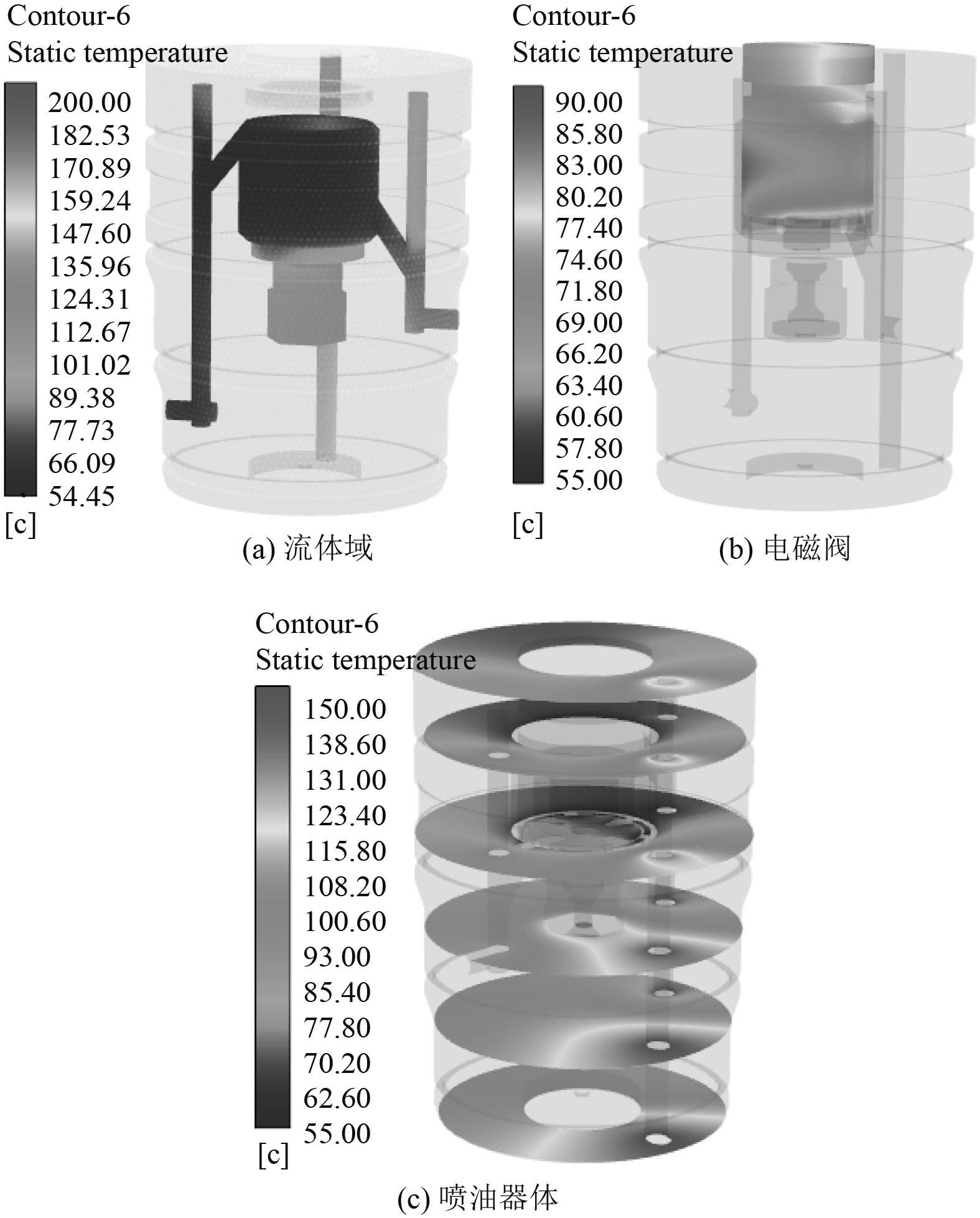
图5(a)为流体域的温度分布情况,从图中可以看出滑油从进口到出口温度在逐渐升高,在衔铁位置腔体部分的流体温度约130℃,重油管路从进口到出口的温度逐渐降低。图5(b)为电磁阀的温度分布云图,在靠近润滑油进口区域阀体表面温度较低,在电磁阀顶端靠近重油管附近的温度约为85℃。图5(c)为针阀体纵向多个截面云图分布情况,从图中可以看出针阀体从上往下的温度分布趋势越来越高,同一截面在靠近重油的区域温度较高,针阀体靠近重油管壁处的最高温度约为140℃,从电磁阀和针阀体的温度分布来看,电磁阀的温度主要受高温重油的影响。
|
图 5 共轭换热计算云图 Fig. 5 Cloud of conjugate heat transfer calculation |
本文通过Ansys Fluent共轭耦合换热计算,分析了电磁阀的流动换热特性,获得流域流场情况以及各区域的温度分布情况,结论如下:
1) 滑油流动方向温度不断升高,重油在流动方向温度下降,电磁阀靠近重油附近温度逐渐升高。
2) 电磁阀的温升来源线圈和重油散热,受重油的影响较大。
3) 电磁阀最高温度93.42℃,远小于极限温度,换热效果较好,其结构满足工作性能要求。
4) 流固热共轭耦合换热分析,为船用低速机喷油器电磁阀设计提供指导。
| [1] |
常浩. 一种汽车机油泵电磁阀的稳态温度场分析[D]. 上海: 上海交通大学, 2015
|
| [2] |
刘鹏. 电控燃油喷射系统复合磁路高速电磁阀设计与特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2018
|
| [3] |
杨世铭, 陶文铨. 传热学[M]. 北京: 北京高等教育出版社, 2006
|
| [4] |
张师帅. 计算流体动力学及其应用[M]. 武汉: 华中科技大学出版社, 2010: 5-8.
|
| [5] |
陈继涛, 宋海燕. 基于Fluent的柴油机冷却环道流动特性分析[J]. 液压与气动, 2019(10): 44-49. DOI:10.11832/j.issn.1000-4858.2019.10.008 |
| [6] |
王福军. 计算流体动力学分析CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004.
|
| [7] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. Aiaa Journal, 1994, 32(8): 1598-1605. |
| [8] |
刘友宏, 丁玉林, 常正则, 等. 发动机矢量喷管作动器电磁阀非稳态热分析[J]. 科学技术与工程, 2016(16): 285-289. DOI:10.3969/j.issn.1671-1815.2016.16.049 |
 2022, Vol. 44
2022, Vol. 44

