永磁同步电机(PMSM),以其效率高、功率因数高、惯性低、高功率密度、结构简单、可靠性高及低噪声等优点,被广泛作为船舶电力推进电机。直接转矩控制(DTC)作为船舶电力推进的核心技术之一,使用2个Bang-Bang控制器分别控制磁链幅值和转矩,响应速度快,对系统参数变动和外部的干扰具有很强的鲁棒性。但是,其存在较大的磁链和转矩脉动,逆变器的开关频率不稳定,系统难以在低转速下精确控制,并因此产生高频噪声。同时,由于风、浪、流的影响,螺旋桨负载受到的干扰具有不确定性,传统的采用DTC直接转矩控制会因参数变化和外部扰动加大电动机的转矩脉动,影响系统性能和稳定运行。
在外界干扰的情况下,滑模变结构控制系统鲁棒性强,响应速度快,本文采用二阶滑模控制中超螺旋算法分别设计了转矩和磁链控制器,替代传统的Bang-Bang开关控制,建立了船舶电力推进调速系统的仿真模型,仿真结果表明相比传统DTC,采用基于滑模控制的DTC交流调速系统时的电磁转矩波动幅值较小,具有较好的动态性能和抗扰动能力,可以满足船用推进电动机动态控制性能的需要。
1 直接转矩控制分析图1中,
|
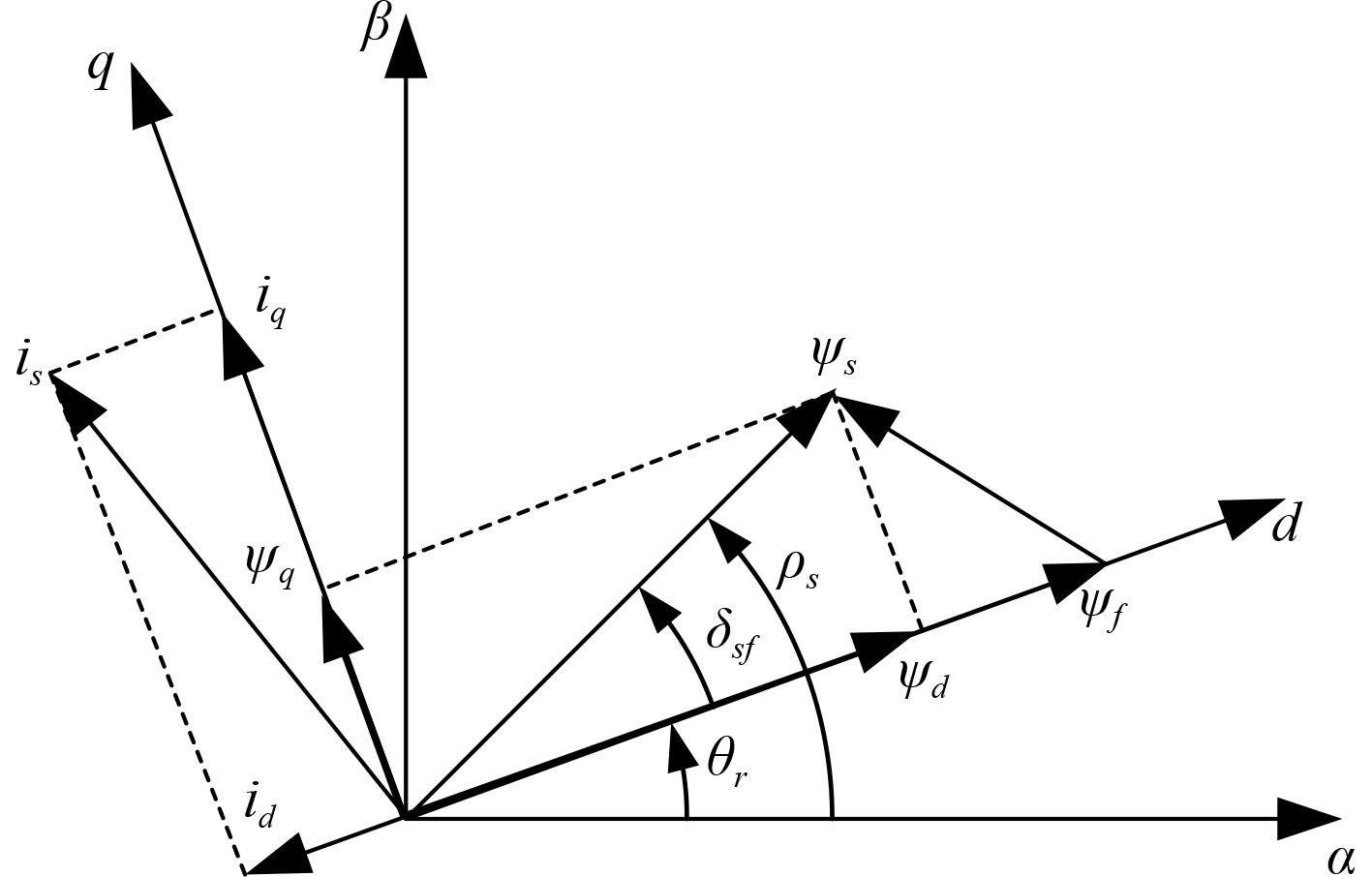
图 1 PMSM矢量关系图 Fig. 1 PMSM vector diagram |
根据图1中的向量关系可得:
| $ \left\{ \begin{gathered} {\psi _d} = \left| {{\psi _s}} \right|\cos {\delta _{sf}},\hfill \\ {\psi _q} = \left| {{\psi _s}} \right|\sin {\delta _{sf}},\hfill \\ \end{gathered} \right. $ | (1) |
永磁同步电机在d-q坐标系下的定子磁链方程为:
| $ \left\{ \begin{gathered} {\psi _d} = {\psi _f} + {L_d}{i_d},\hfill \\ {\psi _q} = {L_q}{i_q}。\hfill \\ \end{gathered} \right. $ | (2) |
其中:Ld和Lq为d,q轴的同步电感。
根据坐标变换原理对PMSM数学模型进行解耦计算得到d-q坐标系下,永磁同步电机的转矩方程为:
| $ {T_e} = 1.5{p_n}[{\psi _f}{i_q} + ({L_d} - {L_q})]{i_d}{i_q},$ | (3) |
将式(1)和式(2)代入得:
| $ {T_e} = \frac{3}{2}\frac{{{p_n}}}{{{L_d}}}\left| {{\psi _s}} \right|{\psi _f}\sin {\delta _{sf}} + \frac{3}{4}\frac{{{p_n}({L_d} - {L_q})}}{{{L_d}{L_q}}}{\left| {{\psi _s}} \right|^2}\sin 2{\delta _{sf}},$ | (4) |
其中,pn为极对数,由式(4)可以看出电磁转矩包含由电机的定子转子之间的磁场相互作用产生的电磁转矩和由电机的凸极结构产生的磁阻转矩两部分。对于三相表贴式PMSM而言,Ld=Lq=Ls,此时式(4)可以表示为:
| $ {T_e} = \frac{3}{2}\frac{{{p_n}}}{{{L_s}}}\left| {{\psi _s}} \right|{\psi _f}\sin {\delta _{sf}}。$ | (5) |
在PMSM中
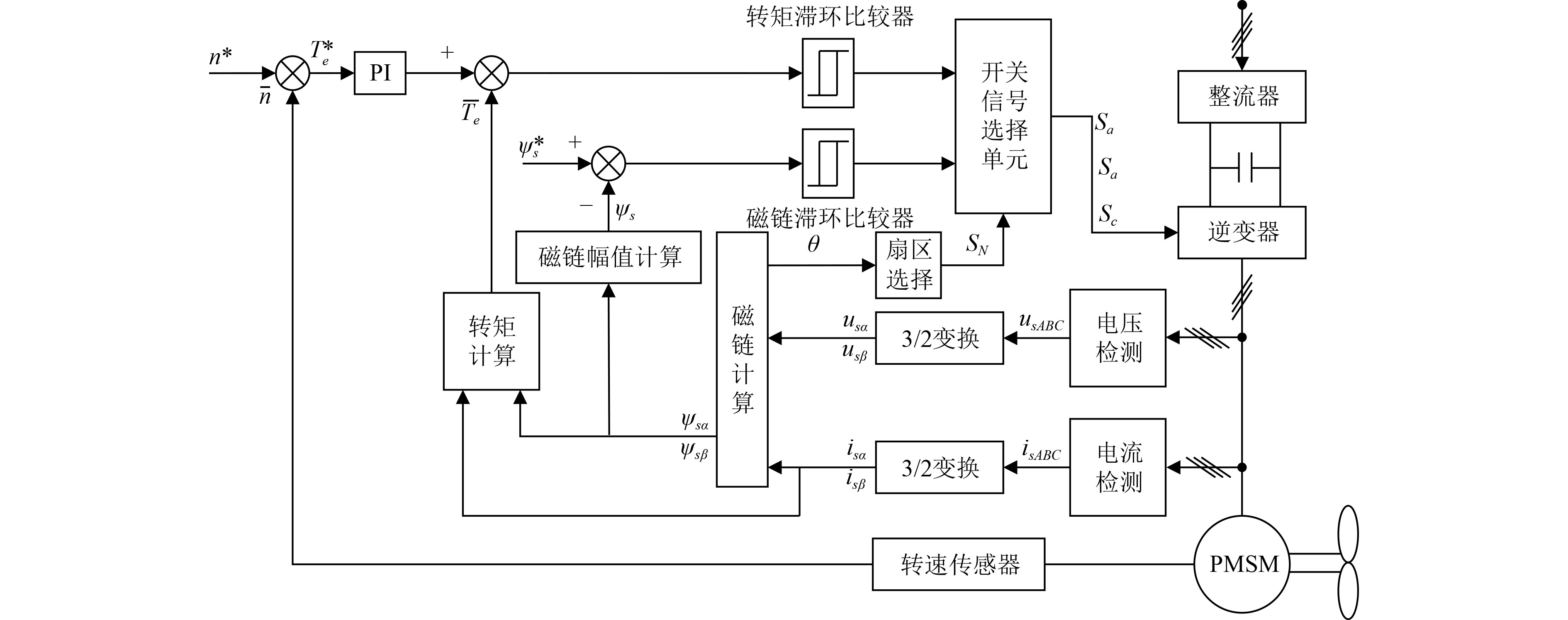
如图2所示,传统直接转矩控制系统是将转矩滞环比较器和磁链滞环比较器的输出扇区值与计算的扇区值一起送入到开关表,得出一组脉冲控制信号,进而控制逆变器开关的接通和断开,从而控制永磁同步电机的转速。
|
图 2 传统直接转矩控制系统框图 Fig. 2 The system block diagram of traditional PMSM-DTC |
考虑到电机的复杂耦合性以及高难度的控制,通常采用二阶滑模进行电机的转速控制,常见的二阶滑模控制方法有螺旋算法(Twisting)、超螺旋算法(Super-Twisting)、次优算法(Sub-Optimal)和漂移算法(Drift)等。而只有超螺旋算法不需要很难得到的
一般的动态系统:
| $ \left\{ \begin{gathered} \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = a(x,t) + b(x,t)u ,\hfill \\ y = c(x,t) 。\hfill \\ \end{gathered} \right. $ | (6) |
其中:x为状态量,u控制输入量,y是输出被控量,a,b,c为未知函数。对于这个系统来说,控制问题就是选择一个合适的控制量
| $ \left\{ \begin{gathered} u = - {K_p}{\left| y \right|^r}{\rm{sgn}} (y) + {u_1},\hfill \\ \frac{{{\rm{d}}{u_1}}}{{{\rm{d}}t}} = - {K_i}{\rm{sgn}} (y)。\hfill \\ \end{gathered} \right. $ | (7) |
其中Kp和Ki为正增益,r是一个正常数且0<r≤0.5,滑动变量s=y。可以看出,滑动变量s的导数信息没有在超螺旋算法中体现。超螺旋算法在滑动面上收敛和稳定的充要条件是增益足够大,即
| $ \left\{ \begin{gathered} {K_p} > \frac{{{A_M}}}{{{B_m}}},\hfill \\ {K_i} \geqslant \frac{{4{A_M}}}{{B_m^2}} \cdot \frac{{{B_M}({K_p} + {A_M})}}{{{B_m}({K_p} - {A_M})}}。\hfill \\ \end{gathered} \right. $ | (8) |
式中,
| $ \frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{t^2}}} = A(x,t) + B(x,t)\frac{{{\rm{d}}u}}{{{\rm{d}}t}}。$ | (9) |
根据式(5),连续对电机电磁转矩进行求导,得到转矩和负载角变化的表达式为:
| $ \frac{{{\rm{d}}{T_e}}}{{{\rm{d}}t}} = \frac{3}{2}\frac{{{p_n}}}{{{L_s}}}\left| {{\psi _s}} \right|{\psi _f}\cos {\delta _{sf}}\frac{{{\rm{d}}{\delta _{sf}}}}{{{\rm{d}}t}},$ | (10) |
| $ \frac{{{{\rm{d}}^2}{T_e}}}{{{\rm{d}}{t^2}}} =\frac{{ - 3p\left| {{\psi _s}} \right|{\psi _f}\sin {\delta _{sf}}}}{{2{L_s}\Delta {T^2}}} + \frac{{3p\left| {{\psi _s}} \right|{\psi _f}\cos {\delta _{sf}}}}{{2{L_s}\Delta T}} \cdot \frac{{{\rm{d}}\Delta {\delta _{sf}}}}{{{\rm{d}}t}}。$ | (11) |
式中
| $ A = \frac{{ - 3p\left| {{\psi _s}} \right|{\psi _f}\sin {\delta _{sf}}}}{{2{L_s}\Delta {T^2}}},$ | (12) |
| $ B = \frac{{3p\left| {{\psi _s}} \right|{\psi _f}\cos {\delta _{sf}}}}{{2{L_s}\Delta T}}。$ | (13) |
其中
| $ {s_T} = T_e^* - {T_e},$ | (14) |
此时转矩控制器的表达式为:
| $ \left\{ \begin{gathered} u_d^* = {K_p}{\left| {{s_T}} \right|^r}{\rm{sgn}} ({s_T}) + {u_{sq}},\hfill \\ \frac{{\rm{d}}}{{{\rm{d}}t}}{u_{sq}} = {K_i}{\rm{sgn}} ({s_T})。\hfill \\ \end{gathered} \right. $ | (15) |
同理,由永磁电机矢量坐标系,可知
| $ \frac{{{\rm{d}}{\psi _s}}}{{{\rm{d}}t}} = {u_d} - {R_s}{i_d},$ | (16) |
| $ \frac{{{{\rm{d}}^2}{\psi _s}}}{{{\rm{d}}{t^2}}} = \frac{{R_s^2}}{{{L_s}}}{i_d} - {\omega _r}{R_s}{i_q} - \frac{{{R_s}}}{{{L_s}}}{u_d} + {\dot u_d}。$ | (17) |
式中:
| $ {s_\psi } = \psi _s^* - {\psi _s},$ | (18) |
此时磁链控制器的表达式为:
| $ \left\{ \begin{gathered} u_d^* = {K_p}{\left| {{s_\psi }} \right|^r}{\rm{sgn}} ({s_\psi }) + {u_{sd}},\hfill \\ \frac{{\rm{d}}}{{{\rm{d}}t}}{u_{sd}} = {K_i}{\rm{sgn}} ({s_\psi })。\hfill \\ \end{gathered} \right. $ | (19) |
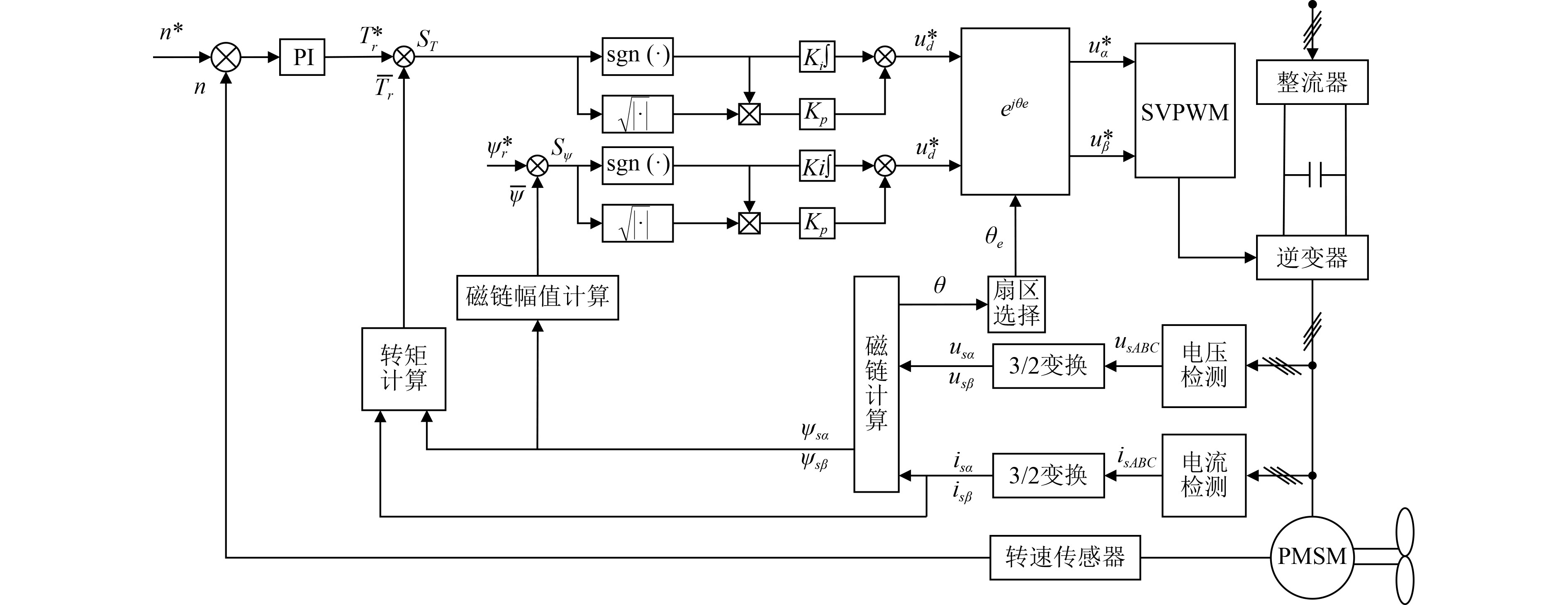
根据上述分析,构建基于滑模控制的DTC控制系统框图如图3所示。与传统DTC相比,用滑模控制器取代了传统的Bang-Bang控制器,还包含了SVPWM算法。
|
图 3 基于滑模控制的直接转矩控制系统图 Fig. 3 The system block diagram of PMSM-DTC based on sliding mode control |
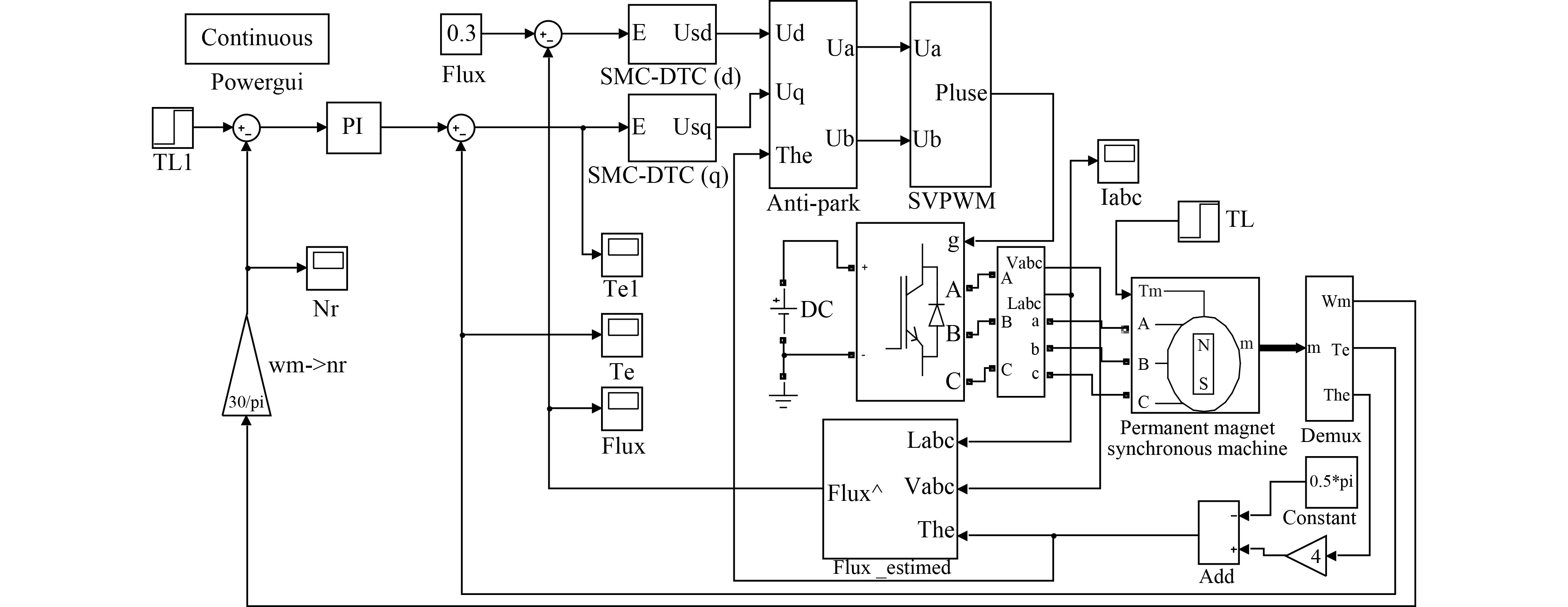
根据上文分析,基于Matlab/Simulink设计相应的仿真程序,如图4~图7所示。
|
图 4 基于滑模控制的DTC仿真程序 Fig. 4 DTC simulation program based on sliding mode control |
|
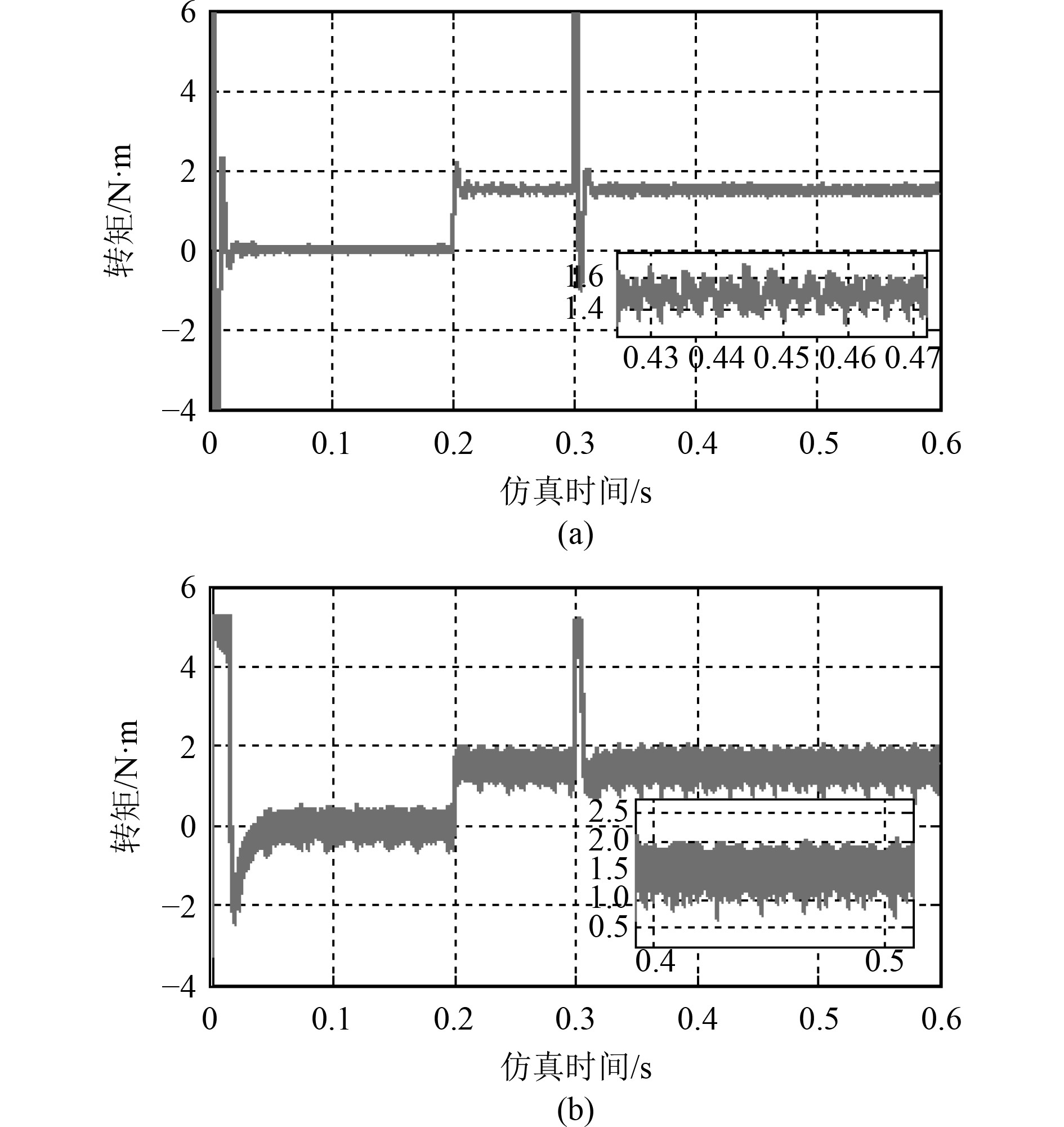
图 7 实际转矩变化曲线 Fig. 7 Actual torque curve |
仿真时,逆变器直流侧的直流电压为311 V,磁链参考设定值为0.3 Wb,数值求解算法采用定步长ode23tb算法,转矩滞环控制器的开关切换点为[0.1,−0.1],输出为[1 0],磁链滞环控制器的开关切换点为[0.002,−0.002],输出为[1 0],电机极对数pn为4,定子电感Ls为8.5 mH,定子电阻R为1.2 Ω,转子磁链
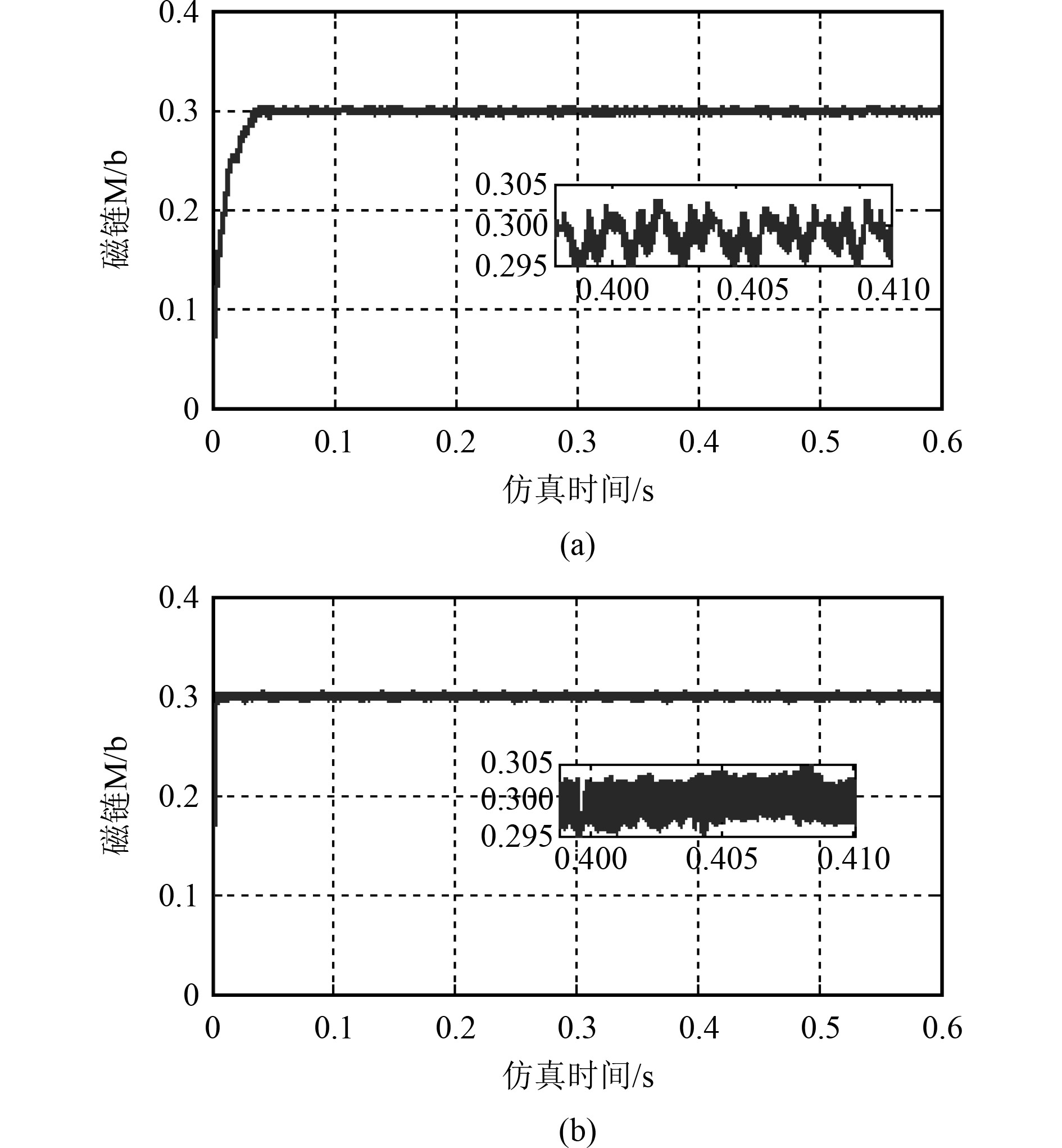
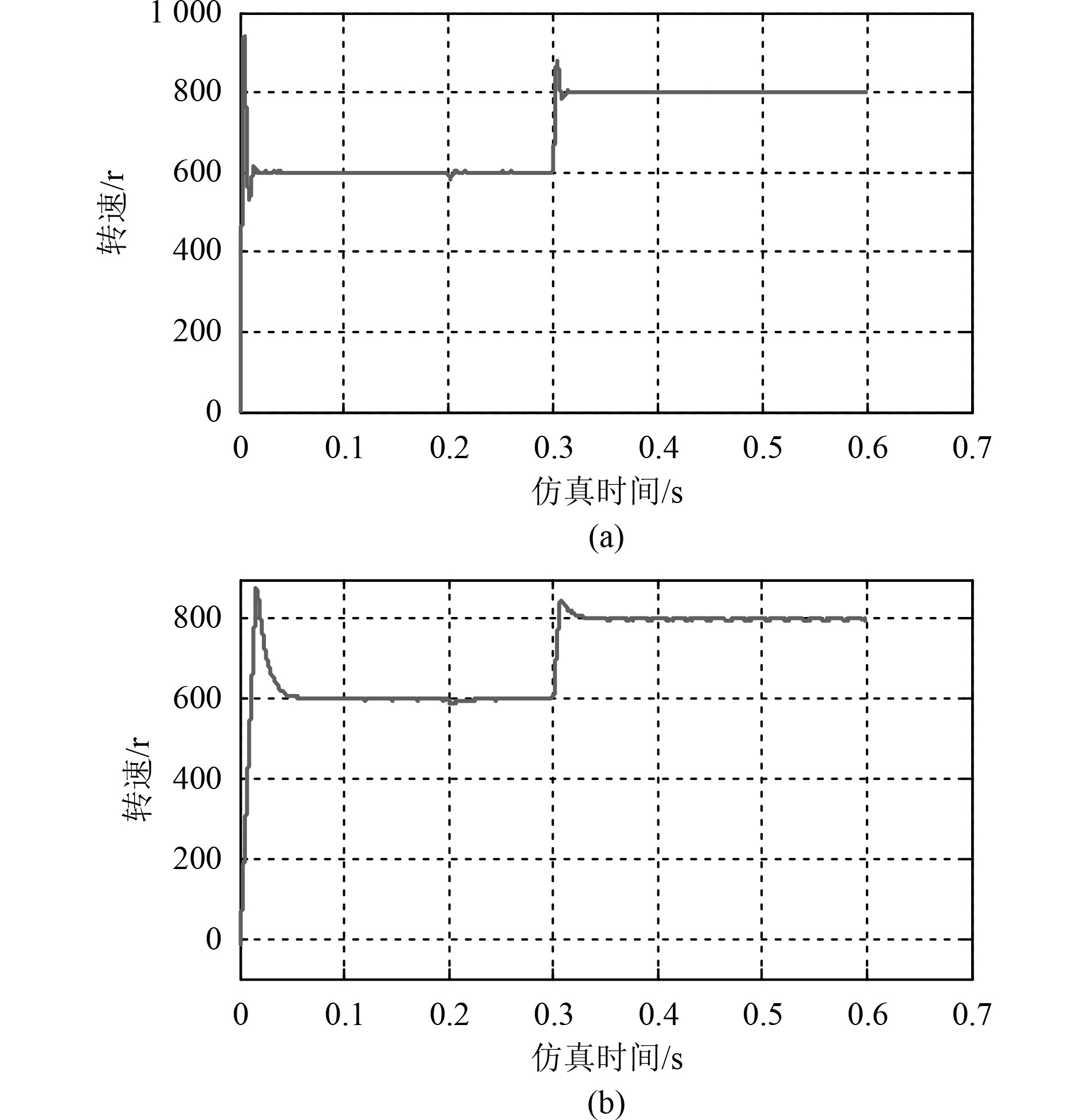
为了方便对比分析,传统DTC系统的仿真设置与滑模控制的DTC仿真过程相同,仿真开始时模拟船舶推进电机空载起动,初始转速设定为600 r/min,0.2 s时模拟螺旋桨负载突加为1.5 N·m,0.3 s时模拟转速突然增加到800 r/min,得到各参数在整个过程中的响应曲线如图5~图7所示。其中图5(a)、图6(a)和图7(a)为基于滑模控制的DTC参数响应曲线,图5(b)、图6(b)和图7(b)为传统DTC控制响应曲线。
|
图 5 实际定子磁链变化曲线 Fig. 5 Actual stator flux curve |
|
图 6 实际转速变化曲线 Fig. 6 Actual speed curve |
1)从图5可以看出,在整个仿真过程中,2种控制方式的定子磁链相轨迹都为符合理论的圆形,都可以稳定在参考值上,但基于滑模控制的DTC相对于传统DTC,具有更小的磁链脉动,而且,波动频率相对小,这对降低电磁转矩脉动必然产生有利的作用。
2)从图6可以看出,当电机由零速上升到600 r/min参考转速时,以及在带载时,转速由600 r/min增加到800 r/min时,在2种控制方式下,电机都有一定的转速超调量,但基于滑模控制的DTC与传统DTC相比具有更快的动态响应,而且转速稳定后非常稳定平滑,几乎无波动。
3)从图7可以看出,在加速及突加负载等整个仿真过程中,基于滑模控制的DTC与传统DTC相比,动态响应时间更快,而且当状态稳定后,传统DTC控制较基于滑模的DTC控制的电机电磁转矩波动幅值大而且频率较快,从而说明基于滑模控制的DTC控制相对于传统DTC具有更好的动态性能和抗扰动能力,具有良好的船舶推进电机的控制性能。
4 结 语目前,吊舱推进器成为船舶电力推进技术的发展亮点,而永磁同步电动机作为吊舱推进器主电机的最佳选择,开展永磁同步推进电机控制系统的研究,对于船舶推进系统的设计和应用意义重大。本文在分析传统DTC的基础上,提出基于滑模控制的DTC控制系统,并从理论上证明了基于二阶滑模控制的超螺旋算法在永磁同步电机电磁转矩及磁链控制中的收敛性。基于Matlab/Simulink建立了永磁同步推进电机传统DTC系统和基于滑模控制的DTC系统的仿真程序,通过仿真对比证明了基于滑模控制的DTC系统的优越性,对永磁同步推进电机控制系统的设计具有一定的参考价值。
| [1] |
陈睿炜. 永磁同步电机在舰船推进系统中的滑模控制研究[J]. 舰船科学技术, 2017, 39(7A): 82-84. CHEN Rui-wei. Sliding mode control of permanent magnet synchronous motor in ship propulsion system[J]. Ship Science and Technology, 2017, 39(7A): 82-84. |
| [2] |
袁雷. 现代永磁同步电机控制原理及MATLAB仿真[M]. 北京: 北京航空航天大学出版社, 2016.
|
| [3] |
高键, 吴祥瑞. 基于滑模控制的船舶电力推进调速系统仿真[J]. 舰船科学技术, 2018, 40(1): 104-107. GAO Jian, WU Xiang-rui. Propulsion control system simulation based sliding mode control of ship electric[J]. Ship Science and Technology, 2018, 40(1): 104-107. DOI:10.3404/j.issn.1672-7649.2018.01.018 |
| [4] |
池飞飞. 船用永磁同步电机直接转矩控制仿真研究[D]. 武汉: 武汉理工大学, 2013. CHI Fei-fei. Research on simulation of the direct torque control for PMSM In marine electrical propulsion [D]. Wuhan: Wuhan University of Technology, 2013. |
| [5] |
张庆超, 马瑞卿, 皇甫宜耿, 等. 电机转速环节Super-Twisting算法二阶滑模控制律设计与研究[J]. 西北工业大学学报, 2016, 34(4): 669-676. ZHANG Qing-chao, MA Rui-qing, HUANGFU Yi-geng. Second order sliding mode control based on super-twisting algorithm for the speed outer loop of motors[J]. Journal of Northwestern Poly technical University, 2016, 34(4): 669-676. |
| [6] |
刘恩东, 高岚, 罗永吉, 等. 船舶电力推进系统VC与DTC调速控制策略建模与仿真研究[J]. 舰船科学技术, 2017, 39(5): 88-93. LIU En-dong, GAO Lan, LUO Yong-ji. Research on modeling & simulation analysis of marine electric propulsion system of VC/DTC speed control strategy[J]. Ship Science and Technology, 2017, 39(5): 88-93. DOI:10.3404/j.issn.1672-7619.2017.05.017 |
 2022, Vol. 44
2022, Vol. 44
