水下航行器可通过释放、控制无人机的方式,接收来自海面上的视频数据。为实现对无人机的控制并进行高速信息传输,水下航行器可与无人机之间保持430~440 MHz频段或中心频率433 MHz的双向近距离通信。目前实现水下航行器与无人机之间的双向通信,仍存在两大问题有待解决:一是由于漂浮线缆距离水下航行器较远,信号在传输线中的损耗较大,天线仅能以较小的功率与无人机进行双向通信;二是半波振子天线在海面环境中感抗明显,造成了发射功率的失配损耗。
针对问题一,可以采用光纤与信号放大器代替传统传输线减少信号的损耗并对其进行放大,但由于体积和供电限制,改善程度有限。针对问题二,在小功率的基础上,如何降低前端天线功率的失配损耗,成为目前研究的重点。半波振子天线的失配损耗,是由缩短效应导致的[1]。解决天线失配损耗的方法主要有2种:一是通过匹配网络使天线阻抗特性处于谐振状态;二是通过对天线进行适当截短,抵消感抗。在高频段、小功率的情况下,为避免匹配网络带来的额外能量泄露,采用方法二对天线进行优化。
在理想条件下,半波振子天线会与对应波长的电磁波产生谐振。但在实际环境中,振子辐射会引起电流衰减,使得振子上电流相速减小,进而导致振子上电磁波波长缩短;振子的实际直径使得天线末端分布电容增大,使得天线末端不处于电磁波的波节位置,等效于振子长度增加。所以,在实际应用中,要严格按照计算出的对称振子天线的缩短长度对其进行缩短优化。目前对于天线缩短效应的研究,均处于自由空间中,对天线处于非自由空间介质中的缩短效应未做推导[1-2]。
通过使用感应电动势法在对称振子天线表面进行坡印廷矢量的积分,提出缩短长度与介质相关的观点,并推出非自由空间中的缩短长度计算公式;基于非自由空间中的缩短长度计算公式,提出了一种改进后的对称振子天线优化方法。在海面漂浮线缆中的双向通信天线中,对该方法进行了应用与验证,降低了海面天线因阻抗不匹配带来的功率损耗。
1 自由空间中缩短长度的计算天线在自由空间中缩短长度的公式为[1]:
| $ \Delta {{l = }}\frac{{42.54L}}{{60{\text{π}} \ln \dfrac{\lambda }{{{\text{π}} d}}}} 。$ | (1) |
式中:42.54为半波对称振子天线在自由空间中的感抗值;
本文探究自由空间中的缩短效应公式(1)在非自由空间中的适用性问题,若其不适用于非自由空间中,提出非自由空间中的缩短长度计算公式。
2 非自由空间中缩短效应分析天线阻抗表达式如下式:
| $ {X_{{\text{in}}}} = {R_m} + {X_m},$ | (2) |
其中
令
| $G = - 2\cos \left( {\dfrac{{kL}}{2}} \right)\dfrac{{\cos \left( {kr} \right)}}{r} + \dfrac{{\cos \left( {k{R_1}} \right)}}{{{R_1}}} + \dfrac{{\cos \left( {k{R_2}} \right)}}{{{R_2}}},$ |
式中:
| $ \begin{split} {X_m} =& \frac{\eta }{{4{\text{π}} }}\int_{ - \frac{L}{2}}^0 {\sin \left[ {k\left( {\frac{L}{2} + z} \right)} \right] \times G{\rm{d}}z} + \\ & \frac{\eta }{{4{\text{π}} }}\int_0^{\frac{L}{2}} {\sin \left[ {k\left( {\frac{L}{2} - z} \right)} \right]} \times G{\rm{d}}z 。\end{split} $ | (3) |
其中
为表达简洁,将式(3)中关于天线长度的积分用
| $ \begin{split} M =& \int_{ - \frac{L}{2}}^0 {\sin \left[ {k\left( {\frac{L}{2} + z} \right)} \right] \times G{\rm{d}}z } + \\ & \int_0^{\frac{L}{2}} {\sin \left[ {k\left( {\frac{L}{2} - z} \right)} \right]} \times G{\rm{d}}z 。\end{split} $ | (4) |
得到天线阻抗虚部的简略表达式,如下式:
| $ {X_m} = \frac{\eta }{{4{\text{π}} }}M ,$ | (8) |
式中:
| $ \eta = \sqrt {\frac{\mu }{\varepsilon }} 。$ | (9) |
振子处于谐振状态时,输入电抗应当为0。根据感应电动势法可以求出,振子单臂缩短长度
| $ \begin{split}\Delta X=&30\;\mathrm{sin}\;2\alpha \left(\dfrac{L}{2}\text-\Delta \text{l}\right)\times\\ &\left(0.57721+\mathrm{ln}\alpha \dfrac{L}{2}+ci2\alpha L-2ci\alpha L-2\mathrm{ln}\dfrac{L}{d}\right)。\end{split} $ | (10) |
式中:0.57721为欧拉常数,
令
| $ \Delta l = \dfrac{{{X_m}L}}{{60{\text{π}} \ln \dfrac{\lambda }{{{\text{π}} d}}}} = \dfrac{{\sqrt {\dfrac{\mu }{\varepsilon }} ML}}{{240{{\text{π}} ^2}\ln \dfrac{c}{{{\text{π}} df\sqrt \varepsilon }}}} 。$ | (11) |
由式(8)可以得知,天线的缩短长度与所处介质环境有关,不能通过式(1)进行非自由空间中天线缩短长度的计算。
在非自由空间介质中,结合式(1)和式(3),可以推出振子感抗与天线长度的关系式如下:
| $ \Delta {{l = }}\frac{{{X_{{m}}}L}}{{60{\text{π}} \ln \dfrac{\lambda }{{{\text{π}} d}}}} ,$ | (12) |
得到对称振子天线具体的单臂缩短长度。
将对称振子天线的双臂分别缩短
在海面上的漂浮线缆中,电磁环境复杂,使用经典电磁学难以求得天线在实际环境中的阻抗[3-5]。借助将计算机技术与经典电磁学结合兴起的计算电磁学可以解决此类问题[6-8]。
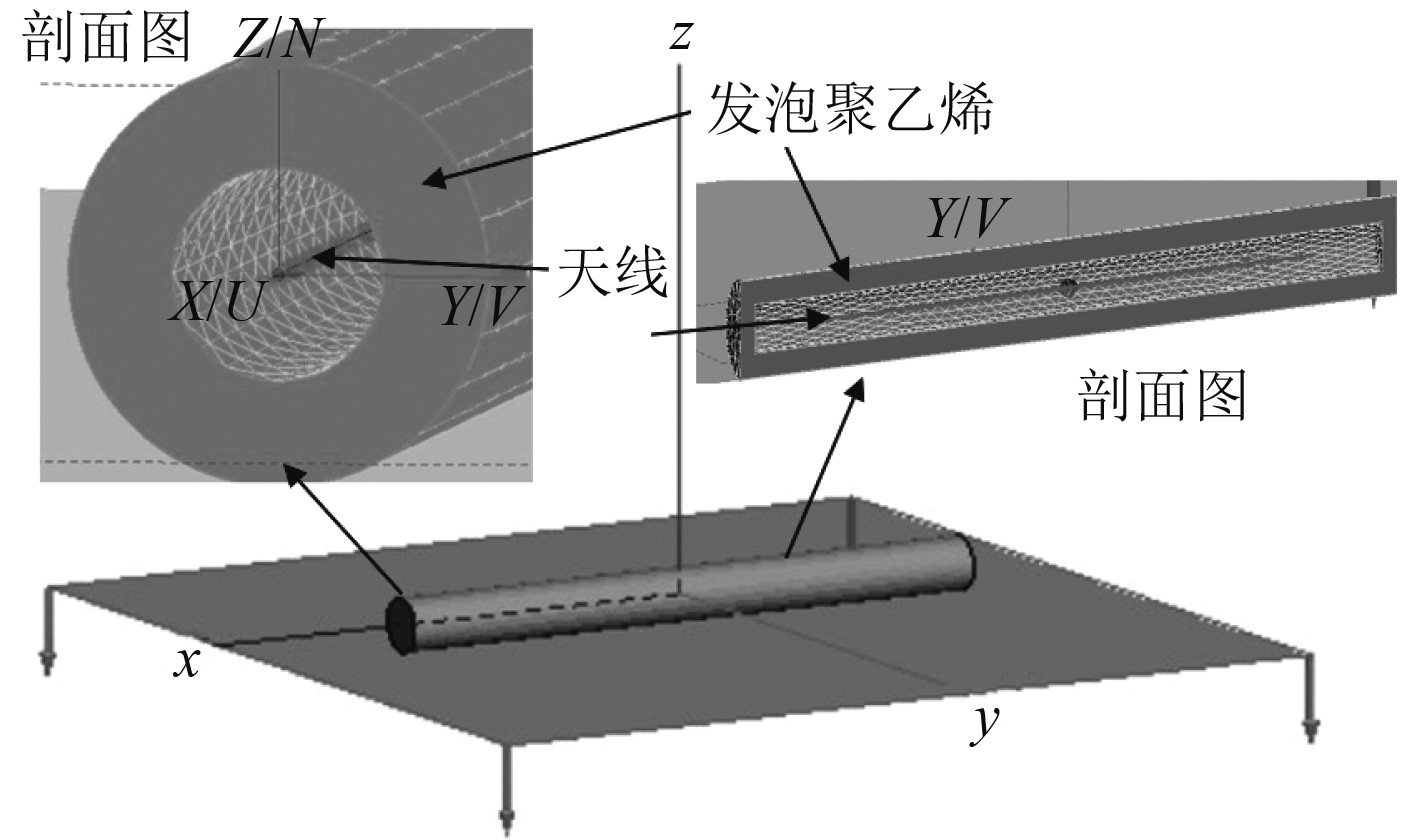
在FEKO电磁仿真软件中,建立海面上漂浮的漂浮线缆仿真电磁模型。漂浮线缆的主要材质为发泡度70%的聚乙烯泡沫,相对介电常数为1.2[9]。图1为海面上漂浮线缆的仿真电磁模型。天线位于漂浮线缆内部。在海面上漂浮线缆电磁环境中进行求解可得,直径1 mm、中心频率在433 MHz的半波振子感抗
|
图 1 空气-发泡聚乙烯-海水分层电磁模型 Fig. 1 Air-foamed polyethylene-seawater layered electromagnetic model |
|
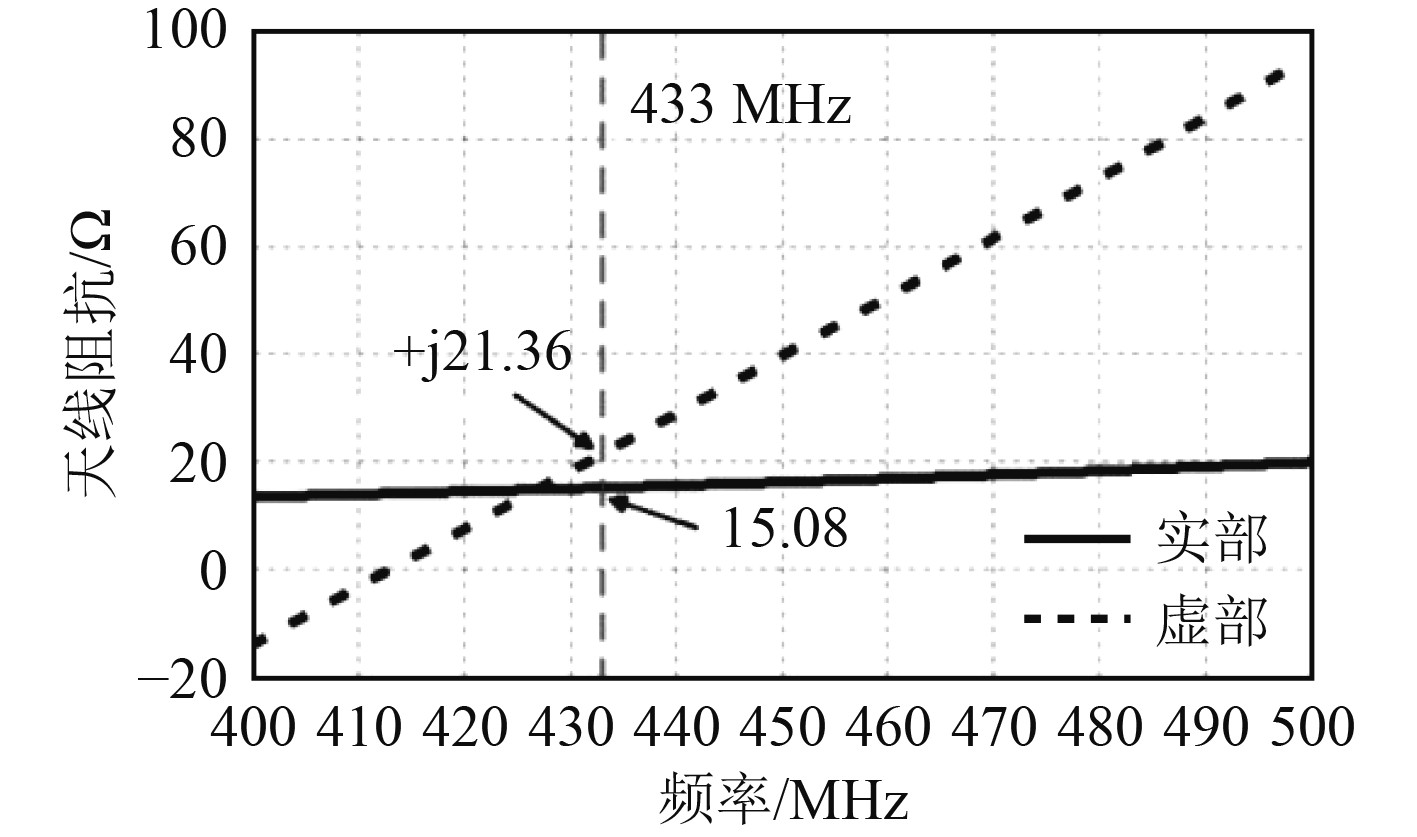
图 2 半波振子在分层电磁模型中的阻抗特性 Fig. 2 Impedance characteristics of a half-wave oscillator in the layered electromagnetic model |
如图2所示,半波振子在理想谐振频点处的阻抗特性为感性,为了对天线进行优化,需要对天线进行适当截短。
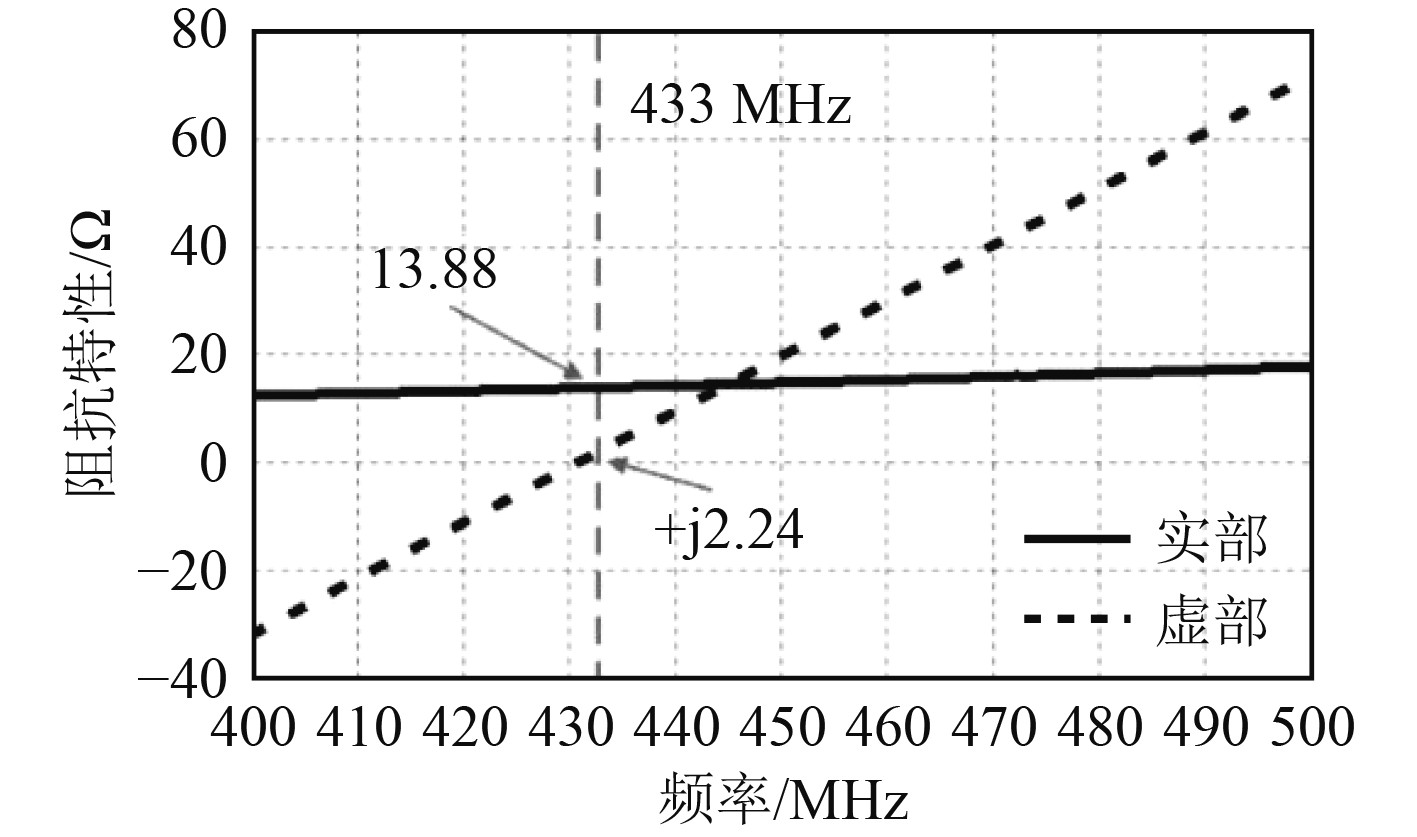
图3为在分层电磁模型中进行截短
|
图 3 缩短后对半波振子天线在分层电磁环境中的阻抗特性 Fig. 3 Impedance characteristics of the optimized symmetric oscillator in the stratified electromagnetic environment |
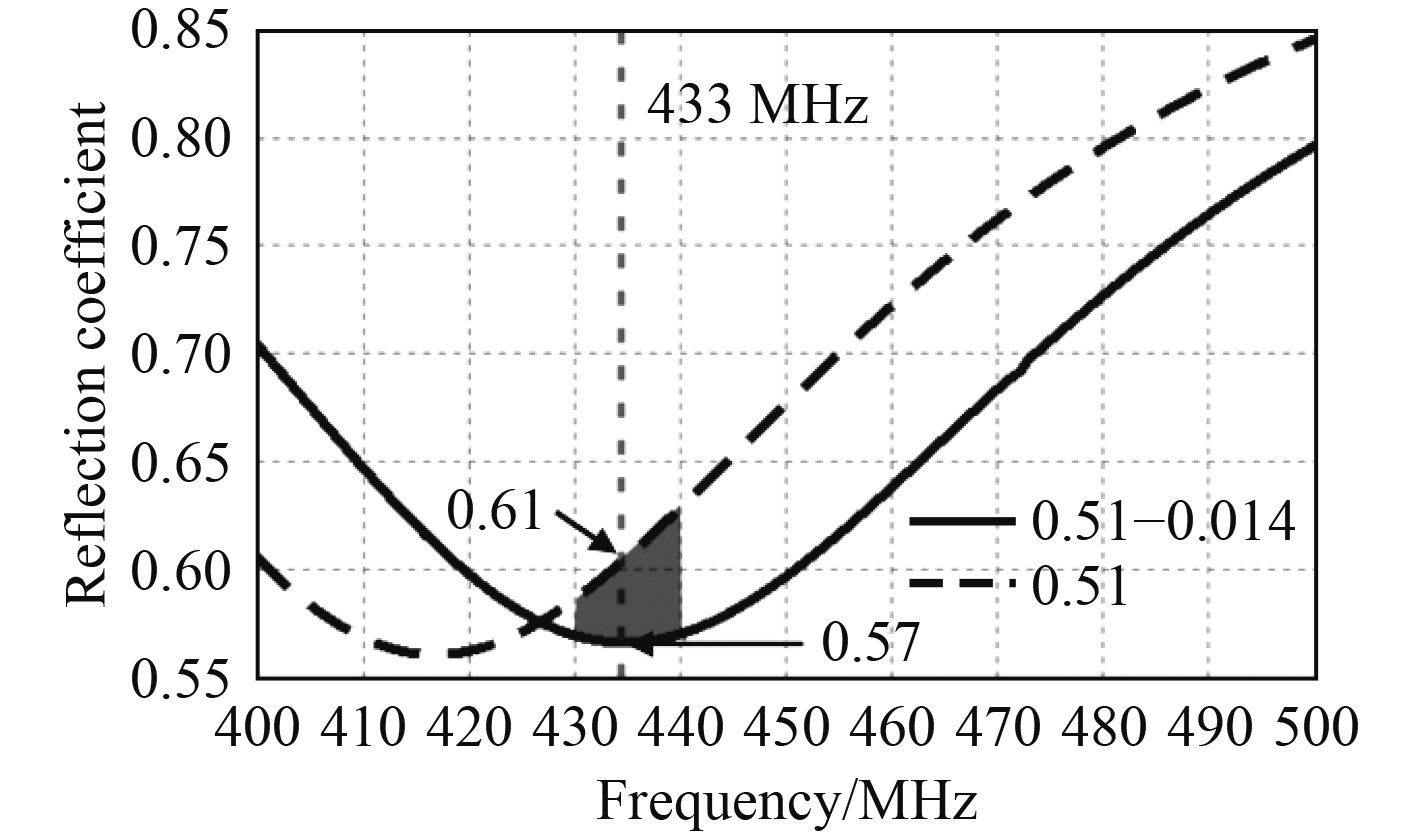
图4表示在400~500 MHz频段半波对称振子天线及缩短后天线在空气-发泡聚乙烯-海水分层模型中的反射系数对比。选定433 MHz作为天线波长的基准频率,图例中0.5l表示原天线长度的半波振子,0.51−0.014表示缩短
|
图 4 半波振子天线缩短长度与反射系数的关系 Fig. 4 The relation between the fine-tuning length of half-wave oscillator antenna and reflection coefficient |
由图4可以看出,半波振子天线的谐振频率在工作环境中偏移到了416 MHz;缩短
在实验阶段,根据相似原理搭建出海面环境天线测试平台[10]。平台可用于对比不同长度的对称振子天线,对天线接收信号的幅度进行测试。根据天线的互易原理,天线接收信号能力的提升同样代表了天线在相同环境中发信能力的提升。发信端固定发射频率为433 MHz,信号幅度10 dBm,测试结果为多次测量后的平均值。
优化前后的对称振子天线接收信号幅度对比结果如表1所示。
|
|
表 1 缩短前后的对称振子天线在模拟工作环境中接收信号幅度对比结果 Tab.1 Comparison results of signal amplitudes received by symmetric oscillators in a simulated working environment before and after optimization |
缩短前后的天线在模拟海面环境中阻抗特性测试结果分别如图5和图6所示。
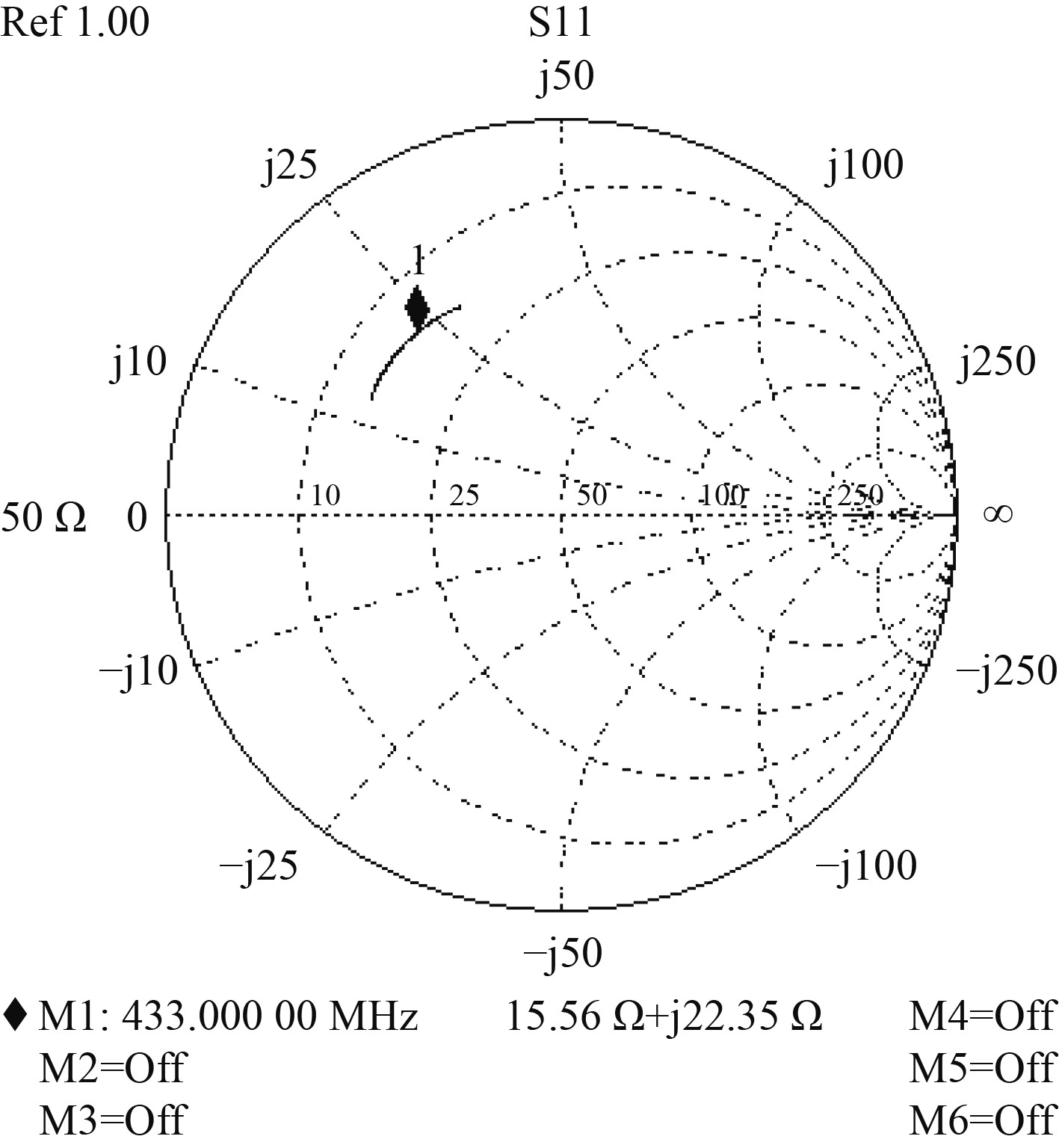
|
图 5 缩短前天线在工作环境中阻抗特性 Fig. 5 Impedance characteristics of the antenna in a simulated working environment before optimization |
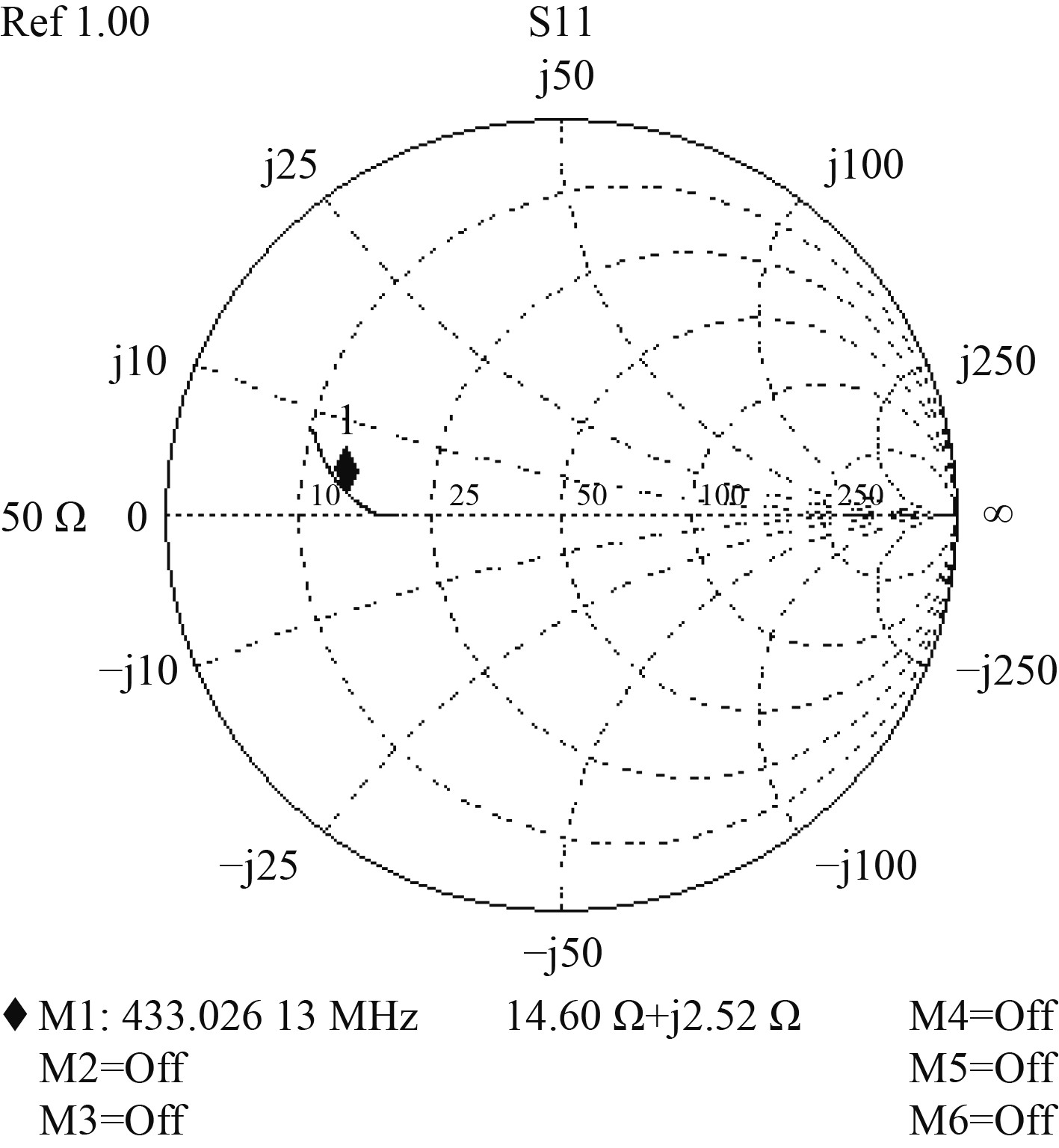
|
图 6 缩短后天线在工作环境中阻抗特性 Fig. 6 Impedance characteristics of the optimized antenna in a simulated working environment |
从图5和图6可以看出,实测天线在工作环境中的阻抗特性与其在仿真环境中近似,优化后的天线阻抗特性为14.60 Ω+j2.52 Ω,相比较于原天线的阻抗特性15.56 Ω+j22.35 Ω,优化后的天线更接近谐振状态。通过非自由空间中的缩短长度公式,求出振子在分层电磁模型中的缩短长度,对天线进行优化,可以使得天线在工作频率处于谐振状态,降低天线在工作频点的失配损耗,有效提高天线的通信能力。
4 结 语在非自由空间中,天线缩短长度较自由空间中有明显区别。通过感性电动势法求出了不同介质中天线感抗对缩短长度的影响,进而对天线进行优化。在空气-发泡聚乙烯(漂浮线缆)-海水空间分层电磁模型中,对缩短后天线的优化效果进行了验证。使用网络分析仪、信号发生器、频谱仪对优化前后的天线特性和接收信号能力进行了对比测试,结果表明:通过非自由空间中的缩短长度计算公式,计算出天线在不同介质中所对应的最佳缩短长度,可以使得天线在工作频率达到谐振状态,有效提高天线在工作环境中的信号收发能力;降低了水下航行器与无人机进行短距离双向通信时,因失配造成的功率损耗。
本文提出的基于非自由空间中缩短效应的天线优化方法及天线缩短长度的计算公式,为降低对称振子天线在实际工作环境中的实验误差做出了贡献;基于跨介质缩短效应,对漂浮线缆中的对称振子天线进行了优化,为水下航行器在安全深度与空中平台进行双向通信提供了基本保障。
| [1] |
李小腊. 箔条与箔片模型的散射特性研究[D]. 西安: 西安电子科技大学, 2015.
|
| [2] |
杨坤龙, 刘鑫, 周坚, 等. 一种坐标轴型箔条的设计与散射特性研究[J]. 电波科学学报, 2020, 35(4): 571-584. |
| [3] |
杨坤, 杜度. 国外对潜通信技术发展研究[J]. 舰船科学技术, 2018, 40(1): 153-157. DOI:10.3404/j.issn.1672-7649.2018.01.028 |
| [4] |
LUCAS E J. Signal transmission through seawater for MHz frequencies and medium distances (0–30 m) using ionic current waves[J]. Underwater Technology, 2019, 36(3).
|
| [5] |
SERCEL. Patent issued for tension monitoring method and system for towed antenna [J]. Journal of Engineering, 2019.
|
| [6] |
王俊, 王世练. 电磁波在水-空气两层媒质中的传播 特性研究[J]. 舰船电子工程, 2019, 39(10): 227-231. DOI:10.3969/j.issn.1672-9730.2019.10.051 |
| [7] |
陈聪, 周骏, 龚沈光. 海水中电磁波传播特性的研究[J]. 海军工程大学学报, 2004(2): 61-64. DOI:10.3969/j.issn.1009-3486.2004.02.016 |
| [8] |
ZHANG Xiao-bin, LIU Cong, ZHANG Xing-yi, et al. Quantitative observation of attenuation coefficient of electromagnetic wave propagation in haze incorporating charged aerosol[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2020, 257. |
| [9] |
MORADIAN M, AZDAST T, DONIAVI A. Investigating the effect of foam properties on the attenuation of coaxial cables with foamed polyethylene dielectric[J]. Polymers for Advanced Technologies, 2020, 31(12).
|
| [10] |
WANG Shi-yu, LI Li-hua, ZHANG Ya-lun, WANG Yong-bin. Application analysis of similarity principle in the design of the underwater receiving antenna[J]. Progress In Electromagnetics Research M, 2020, 95: 189−197.
|
 2022, Vol. 44
2022, Vol. 44
