2. 中国科学院机器人与智能制造创新研究院, 辽宁 沈阳 110169;
3. 中国科学院大学, 北京 100049
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
水下直升机(AUH)(见图1)是一种圆碟形的新概念自主水下机器人(AUV),具有在海底节点间往返作业、自由起降的作业模式[1]。AUH圆碟形的外形使其具有灵活的首向机动性,但同时也为AUH首向点镇定控制带来了困难,为了保证AUH稳定的开展水下作业,需要设计高性能的首向控制器[2]。

|
图 1 水下直升机 Fig. 1 Autonomous Underwater Helicopters |
AUV具有强耦合性、高度非线性和参数不确定性等动力学特性,很难获得精确的动力学模型[3]。同时,AUH首向的灵活性,也使其容易受到海流、执行机构不对称等未知扰动的影响,产生振荡和超调。因此,基于精确模型的控制方法,如状态反馈线性化和模型预测控制等在实际应用中往往难以达到理想的效果。为了应对模型参数的不确定性和未知外部扰动的影响,反步控制[4-5]和滑模控制(sliding mode control,SMC)[6-7]等鲁棒控制方法得到了广泛的关注。其中,滑模控制因其设计简洁和便于应用等特点,获得了广泛的研究和应用[8]。但是,上述方法的设计仍然依赖于被控对象的模型。
PID控制是一种典型的无模型控制,其主要问题是被控对象参数变化时控制器需要重新整定,控制快速性和精确性的平衡较为依赖于经验。基于数据驱动的无模型控制方法依据被控对象的输入/输出测量数据设计控制器[9],这极大地简化了控制器设计。无模型自适应控制(model-free adaptive control,MFAC)通过引入伪偏导数(pseudo-partial derivative ,PPD)概念,在闭环系统的动态操作点建立等效的动态线性化模型,替代控制对象的非线性模型。其具有所需I/O数据量小、控制器参数较少、控制器设计简洁的特点[10],适合于AUH的运动控制。目前MFAC已经在海洋机器人控制领域得到了一些成功应用[11-13]。
现有的传统MFAC存在控制系统收敛速度慢、超调量大等问题,这是由于固有的动态线性化误差导致的。SMC根据系统期望的动态特性来设计系统的滑模面,具有响应速度快、对参数变化和扰动不敏感、实现简单等特点。将MFAC与SMC方法相结合构建无模型自适应滑模控制器(简称MFASMC),可以实现两者的优势互补。近年来,对两者结合的方案已经有了一些研究,MFASMC被用于处理自主式四轮车自动泊车[14]、组合航天器控制[15]、摄像头稳定平台的控制[16]和半潜船吊舱推进电机控制[17]等问题。但上述研究中且尚未见对被控对象参数大范围变化时控制器的适应性开展深入研究。
具体到圆碟形AUV的首向控制问题,文献[18]使用广义预测控制器实现圆碟形AUV的姿态控制。文献[19]设计了PID控制器实现圆碟形AUV的姿态控制。但从两者的试验结果看,首向控制均出现了较为明显的超调和振荡。
本文提出了一种改进的无模型参数自适应滑模控制(MFASMC-VL)方法,并将其应用于存在模型参数失配和外部未知扰动的AUH首向点镇定控制。首先利用动态线性化方法建立被控对象在当前工作点的全格式动态线性化(full form dynamic linearization,FFDL)数据模型,在此模型基础上设计无抖振离散滑模首向控制器(DSMC),实现AUH首向无模型控制。并通过引入自适应权重因子,在被控对象参数大范围变化情况下有效的抑制了首向超调和振荡,改善了控制效果。通过数字仿真和湖上试验验证了所提方法的可行性和有效性。
1 动力学模型及问题描述 1.1 AUH动力学模型AUH的六自由度动力学模型可由如下的矩阵方程描述:
| $ {\boldsymbol{M\dot v}} + {\boldsymbol{C}}({\boldsymbol{\nu }}){\boldsymbol{\nu }} + {\boldsymbol{D}}({\boldsymbol{\nu }}){\boldsymbol{\nu }} + {\boldsymbol{g}}({{\boldsymbol{\eta }}_2}) = {{\boldsymbol{\tau }}_c} + \Delta {\boldsymbol{f}}。$ | (1) |
其中:
AUH的六自由度运动学模型可由如下的矩阵方程描述:
| $ {\boldsymbol{\dot \eta }} = {\boldsymbol{J}}({{\boldsymbol{\eta }}_2}){\boldsymbol{\nu }}。$ | (2) |
其中:
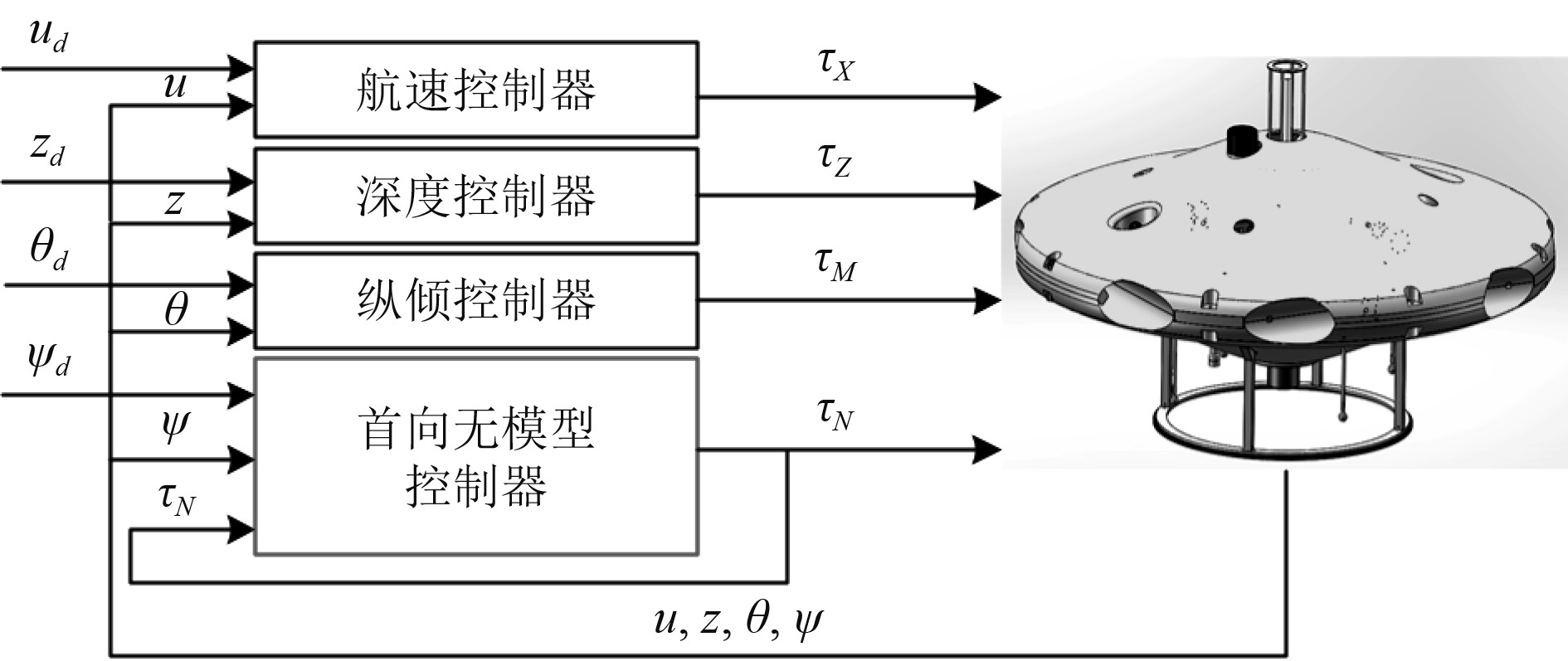
考虑AUH低速航行且姿态变化不大,可以将各向运动解耦,分别设计控制器控制AUH的前向速度、深度、纵倾角和首向角,其控制架构如图2所示。
|
图 2 水下直升机控制架构 Fig. 2 Control architecture for AUH |
其中
本文研究AUH首向无模型控制的目的是:设计仅依赖于首向控制力矩输入
基于FFDL[10]数据模型设计控制器,被控的离散非线性单输入单输出系统描述如下:
| $ \begin{split} &y(t + 1) = f(y(t), \cdots ,y(t - {n_y}), \\ &u(t), \cdots ,u(t - {n_u})) 。\end{split} $ | (3) |
其中:
定义向量
| $ \begin{split} & {{\boldsymbol{H}}_{{L_y},{L_u}}}(k) = [y(k), \cdots ,y(k - {L_y} + 1), \\ &u(k), \cdots ,u(k - {L_u} + 1){]^{\rm{T}}}。\end{split} $ | (4) |
当
定义
式(3)满足如下的假设:
1)对于各变量都存在连续偏导数;
2)满足广义Lipchitz条件,即对
| $ \begin{split} {{\boldsymbol{\varPhi }}_{f,{L_y},{L_u}}}(k) =& [{\phi _1}(k), \cdots ,{\phi _{{L_y}}}(k),{\phi _{{L_y} + 1}}(k), \cdots , \\ &{\phi _{{L_y} + {L_u}}}(k){]^{\rm{T}}} \in {{\boldsymbol{R}}^{{L_y} + {L_u}}},\end{split} $ | (5) |
可以使式(3)转换为FFDL数据模型:
| $ \Delta y(k + 1) = {\boldsymbol{\varPhi }}_{f,{L_y},{L_u}}^{\rm{T}}(k)\Delta {{\boldsymbol{H}}_{{L_y},{L_u}}}(k),$ | (6) |
且伪梯度
设计PG的估计准则函数如式(7)所示,其中
| $ \begin{split} J({{\boldsymbol{\varPhi }}_{f,{L_y},{L_u}}}(k)) =& {\left| {\Delta y(k) - {\boldsymbol{\varPhi }}_{f,{L_y},{L_u}}^{\rm{T}}(k)\Delta {{\boldsymbol{H}}_{{L_y},{L_u}}}(k - 1)} \right|^2} +\\ &\mu {\left\| {{{\boldsymbol{\varPhi }}_{f,{L_y},{L_u}}}(k) - {{{\boldsymbol{\hat \varPhi }}}_{f,{L_y},{L_u}}}(k - 1)} \right\|^2} ,\end{split} $ | (7) |
对式(7)求极值,则可得PG的估计算法如下式:
| $ \begin{split} {{{\boldsymbol{\hat \varPhi }}}_{f,{L_y},{L_u}}}(k) =& {{{\boldsymbol{\hat \Phi }}}_{f,{L_y},{L_u}}}(k - 1) + \frac{{\eta \Delta {{\boldsymbol{H}}_{{L_y},{L_u}}}(k - 1)}}{{\mu + {{\left\| {\Delta {{\boldsymbol{H}}_{{L_y},{L_u}}}(k - 1)} \right\|}^2}}}(\Delta y(k) - \\ & {\boldsymbol{\hat \varPhi }}_{f,{L_y},{L_u}}^T(k - 1)\Delta {{\boldsymbol{H}}_{{L_y},{L_u}}}(k - 1)),\\[-10pt] \end{split} $ | (8) |
其中,
对于模型(6),设计滑模面如下式:
| $ s(k) = {k_1}\Delta y(k) + {k_2}e(k) 。$ | (9) |
其中
将式(6)写为下式:
| $ \begin{split} \Delta y(k + 1) =& \sum\nolimits_{i\; = \;1}^{{L_y}} {{{\hat \phi }_i}(k)\Delta y(k - i + 1)} + {{\hat \phi }_{{L_y} + 1}}(k)\Delta u(k) +\\ &\sum\nolimits_{i\; = \;{L_y} + 2}^{{L_y} + {L_u}} {{{\hat \phi }_i}(k)\Delta u(k + {L_y} - i + 1)} ,\\[-15pt] \end{split} $ | (10) |
设计滑模趋近律[20]为:
| $ s(k + 1) = s(k) - {q_1}h \cdot s(k) - {q_2}h \cdot {\text{si}}{{\text{g}}^\alpha }(s(k)) 。$ | (11) |
其中:
将式(9)和式(10)代入(11),可推导得到如下的控制输入增量:
| $ \begin{split} \Delta u(k) =& - \frac{1}{{({k_1} + {k_2}){{\hat \phi }_{{L_y} + 1}}(k)}}[{k_2}(y(k) - r(k + 1)) + \\ &({k_1} + {k_2})(\sum\nolimits_{i\; = \;1}^{{L_y}} {{{\hat \phi }_i}(k)\Delta y(k - i + 1)} + \\ & \sum\nolimits_{i\; = \;{L_y} + 2}^{{L_y} + {L_u}} {{{\hat \phi }_i}(k)\Delta u(k + {L_y} - i + 1)} ) + \\ &({q_1}h - 1)s(k) + {q_2}h \cdot {\text{si}}{{\text{g}}^\alpha }(s(k))] 。\end{split} $ | (12) |
加入可调权重因子
| $ \begin{split} \Delta u(k) =& \frac{{ - {{\hat \phi }_{{L_y} + 1}}(k)}}{{\lambda + ({k_1} + {k_2})\hat \phi _{{L_y} + 1}^2(k)}}[{k_2}(y(k) - r(k + 1) + \\ & ({k_1} + {k_2})(\sum\nolimits_{i\; = \;1}^{{L_y}} {{{\hat \phi }_i}(k)\Delta y(k - i + 1)} + \\ & \sum\nolimits_{i\; = \;{L_y} + 2}^{{L_y} + {L_u}} {{{\hat \phi }_i}(k)\Delta u(k + {L_y} - i + 1)} ) +\\ & ({q_1}h - 1)s(k) + {q_2}h \cdot {\text{si}}{{\text{g}}^\alpha }(s(k))] 。\end{split} $ | (13) |
合适的权重因子
| $ u(k) = {F_f} \cdot u(k - 1) + \Delta u(k)。$ | (14) |
其中
注意到伪偏导数
通过引入自适应权重因子
| $ \begin{split} \Delta u(k) =& \frac{{ - {{\hat \phi }_{{L_y} + 1}}(k)}}{{{\lambda _v} + ({k_1} + {k_2})\hat \phi _{{L_y} + 1}^2(k)}}[{k_2}(y(k) - r(k + 1) + \\ & ({k_1} + {k_2})(\sum\nolimits_{i\; = \;1}^{{L_y}} {{{\hat \phi }_i}(k)\Delta y(k - i + 1)} + \\ & \sum\nolimits_{i\; = \;{L_y} + 2}^{{L_y} + {L_u}} {{{\hat \phi }_i}(k)\Delta u(k + {L_y} - i + 1)} ) + \\ & ({q_1}h - 1)s(k) + {q_2}h \cdot {\text{si}}{{\text{g}}^\alpha }(s(k))] 。\\ {\lambda _v} =& \left\{ {\begin{array}{*{20}{c}} {{\lambda _{\max }},\hat \phi _{{L_y} + 1}^{}(k) > \hat \phi _{{L_y} + 1,\max }^{}},\\ {{\lambda _{std}},\hat \phi _{{L_y} + 1,\min }^{} \leqslant \hat \phi _{{L_y} + 1}^{}(k) \leqslant \hat \phi _{{L_y} + 1,\max }^{}}。\\ {{\lambda _{\min }},\hat \phi _{{L_y} + 1}^{}(k) < \hat \phi _{{L_y} + 1,\min }^{}} 。\end{array}} \right. \end{split} $ | (15) |
MFASMC-VL控制器结构如图3所示,控制输入计算流程如下:
1)确定伪阶数
| $ \begin{split} \Delta {{\boldsymbol{H}}_{{L_y},{L_u}}}(k) =& [\Delta y(k), \cdots ,\Delta y(k - {L_y} + 1), \\ &\Delta u(k), \cdots ,\Delta u(k - {L_u} + 1){]^{\rm{T}}} 。\end{split} $ | (16) |
2)使用式(8)估计伪梯度PG。
3)由式(15)计算控制输入增量
4)计算控制输入
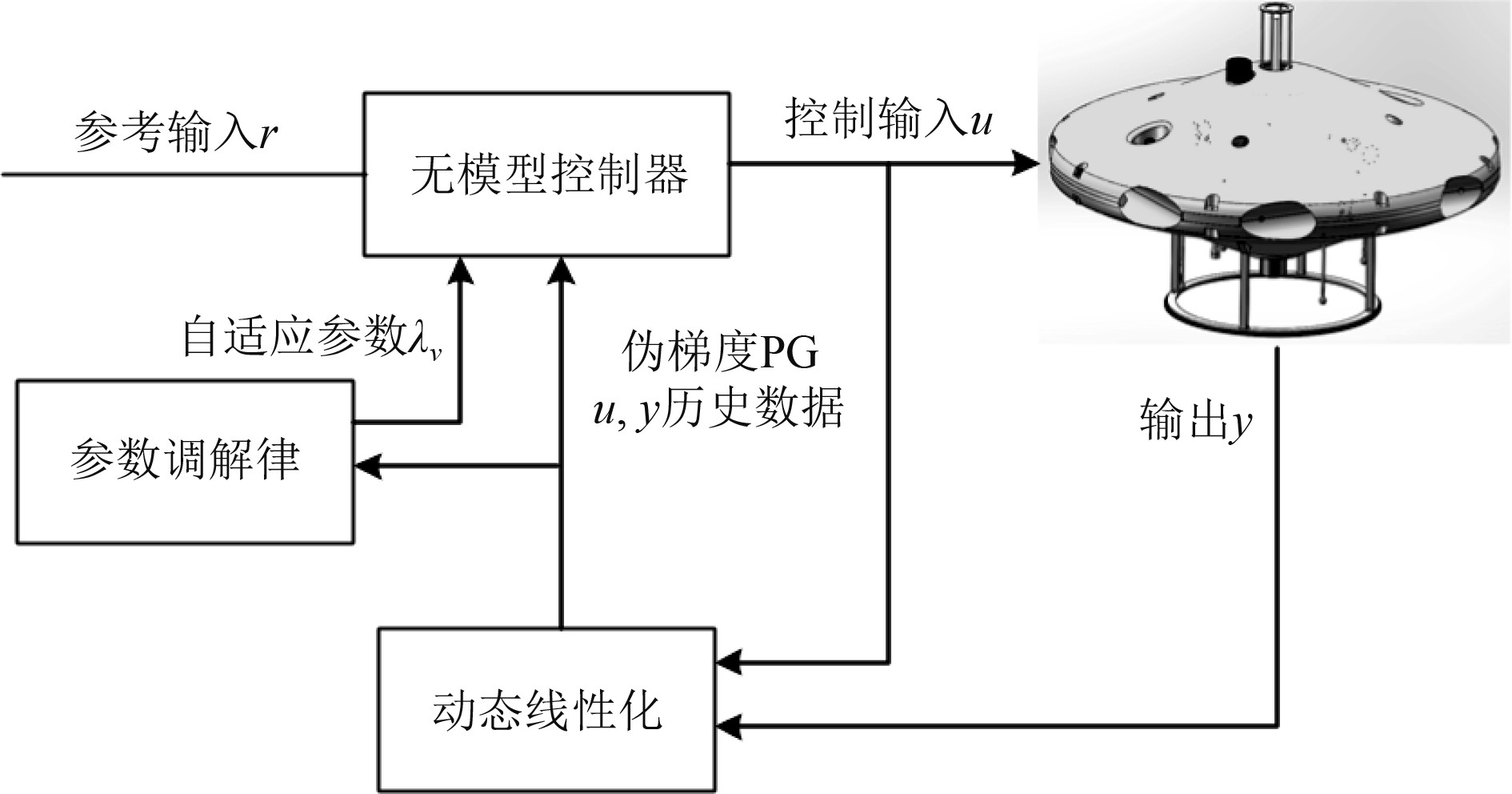
|
图 3 MFASMC-VL控制器结构图 Fig. 3 Architecture for MFASMC-VL |
为验证本文提出的MFASMC-VL控制器应用于AUH首向控制的有效性,设计了多个场景的仿真试验。被控对象采用AUH的六自由度水动力模型[21]。控制周期选择为0.5s,与AUH实际的控制周期一致。MFASMC-VL伪阶数选为
在试验中使用的DSMC和MFASMC-VL控制器,均在名义模型下对控制参数进行了整定,并且将带遗忘因子的MFASMC简称为MFASMC-FF。FFDL数据模型的初始值取
|
|
表 1 MFASMC-FF和MFASMC-VL主要参数 Tab.1 Main parameter of MFASMC-FF and MFASMC-VL |
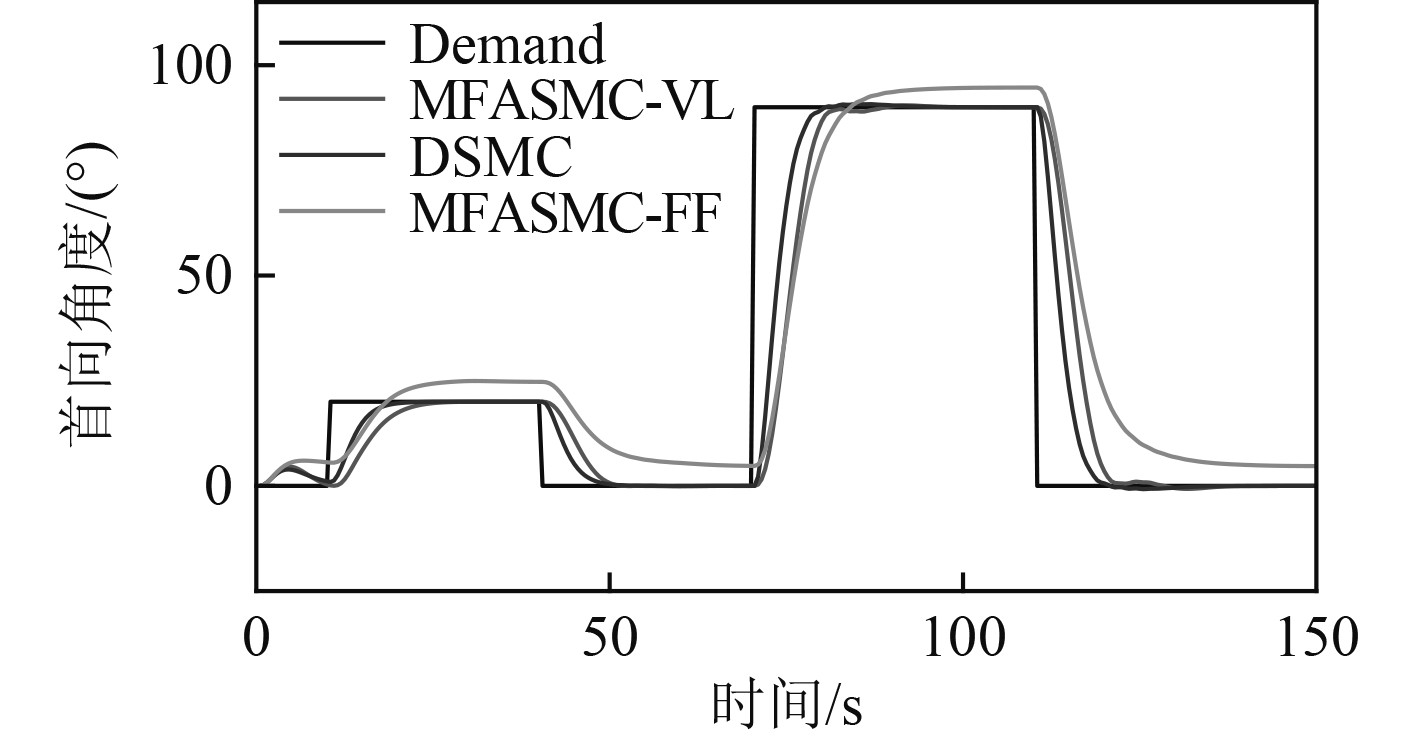
|
图 4 首向阶跃响应曲线(1 kn,2 Nm常值扰动) Fig. 4 Heading step response curve (1 kn, 2 Nm constant disturbance) |
|
|
表 2 控制器阶跃响应性能指标(1 kn,2 Nm常值扰动) Tab.2 Performance index of controller step response (1 kn, 2 Nm constant disturbance) |
可知,MFASMC-FF存在约4.7°的稳态误差,即该方法无法消除常值扰动的影响,这对与AUH的首向控制来说是不可接受的,为使分析结果更加清晰,后续不再讨论该方法。DSMC和MFASMC-VL在20°和90°阶跃转向中表现相当,MFASMC-VL的响应速度稍慢,在90°阶跃转向中的调节时间稍长。但DSMC在90°阶跃转向中产生了0.9%的超调,而MFASMC-VL控制器的超调仅为0.5%。
为了进一步分析控制器性能,考虑被控对象模型参数变化的情况。如AUH更换了安装的载荷设备,会引起AUH的质量惯性矩
|
|
表 3 控制器阶跃响应性能指标(1 kn,2 Nm常值扰动,主要参数减小80%) Tab.3 Performance index of controller step response (1 kn, 2 Nm constant disturbance, main parameters reduced by 80%) |
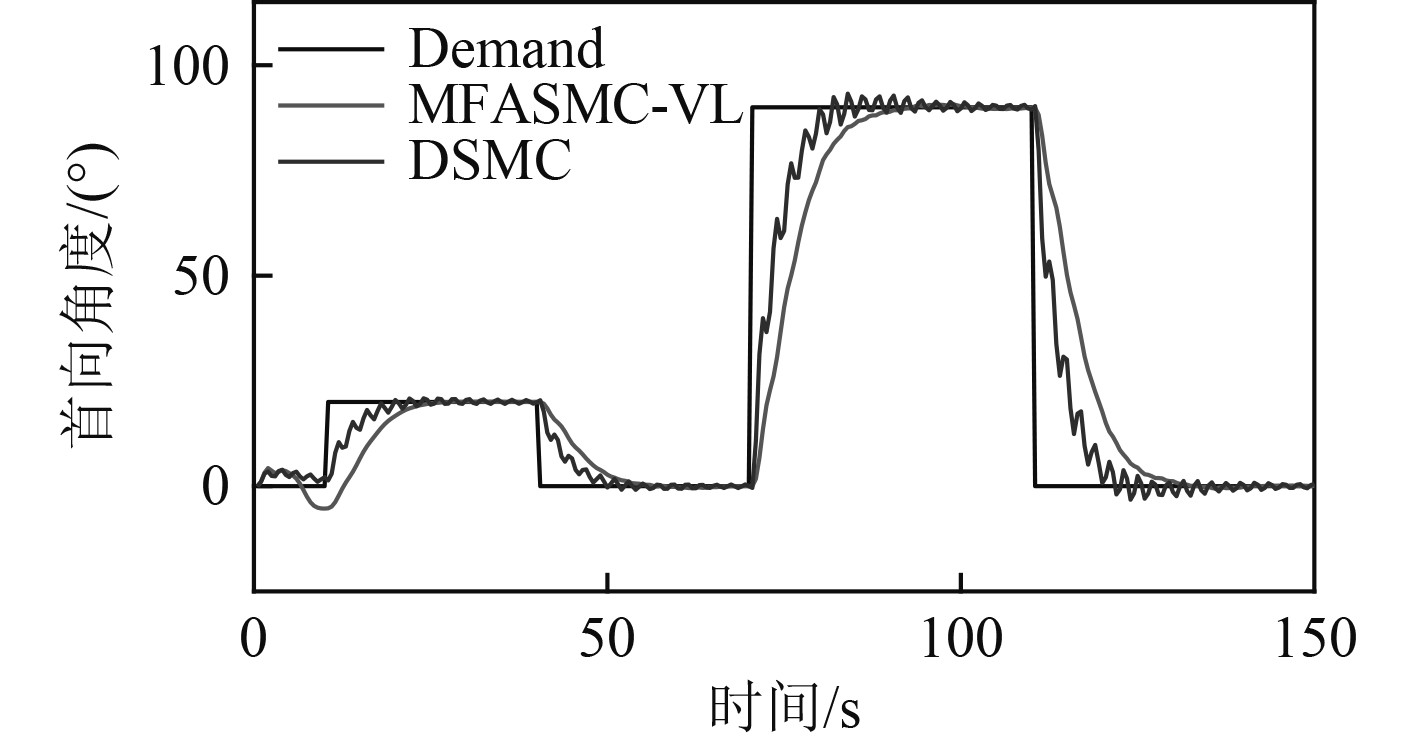
|
图 5 首向阶跃响应曲线(1 kn,2N m常值扰动,主要参数减小80%) Fig. 5 Heading step response curve (1 kn, 2 Nm constant disturbance, main parameters reduced by 80%) |
|
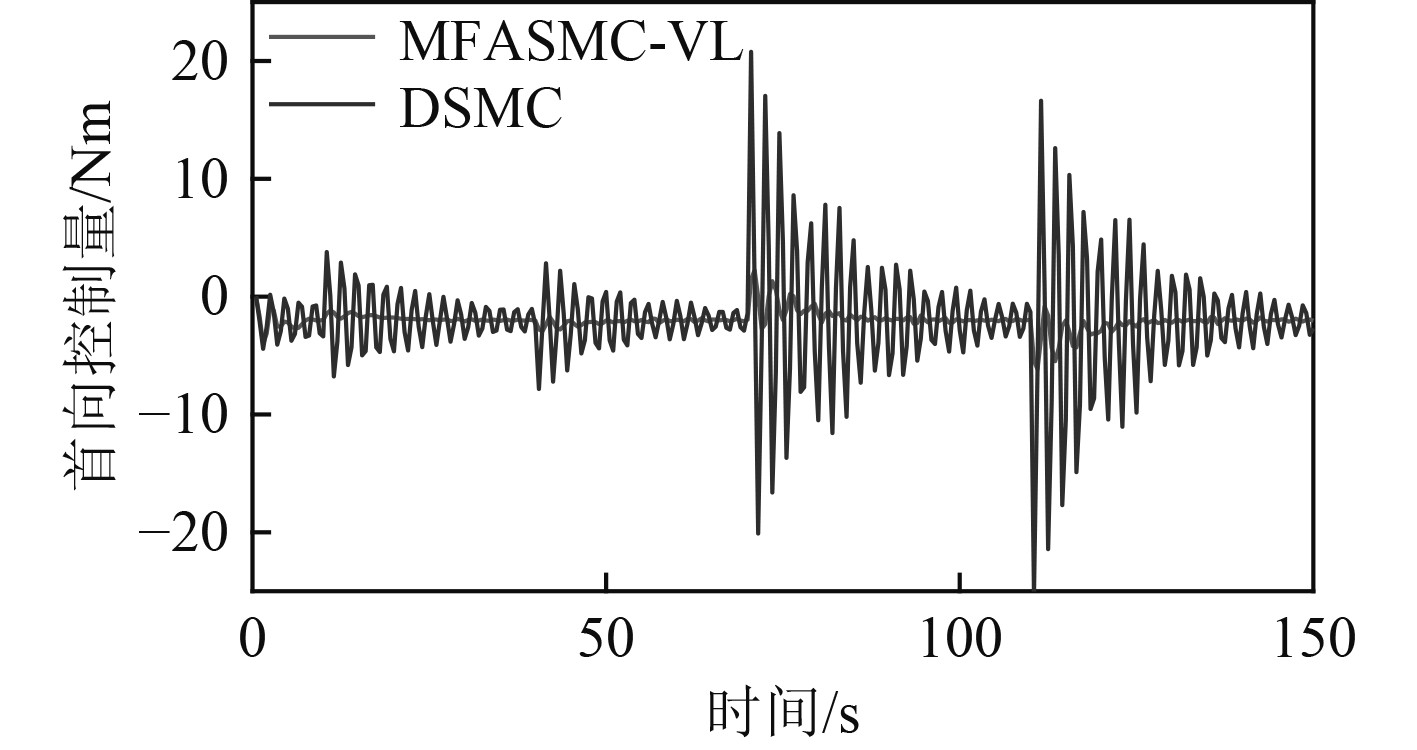
图 6 控制输入曲线(1 kn,2 Nm常值扰动,主要参数减小80%) Fig. 6 Control input curve (1 kn, 2 Nm constant disturbance, main parameters reduced by 80%) |
通过分析图5响应曲线和表3性能指标,可以发现DSMC由于模型参数失配的影响,其首向输出出现了明显的抖振,输出存在最大4.3%的超调,调节时间明显增大。而MFASMC-VL的输出响应平滑,保持了小于1%的超调和较短的调节时间。同时,DSMC的控制输入也出现了大幅度的抖振,控制输入峰峰值达到了40.9 Nm,而MFASMC-VL的控制输入相对平滑,峰峰值仅为6.2 Nm,这显然会降低执行机构的损耗和能源消耗。
综上数据表明,本文提出的MFASMC-VL方法可以有效的使AUH首向稳定平滑的收敛到目标值,并能有效处理外部扰动和适应被控对象参数的大范围变化,在不同场景下均保持了小于1%的超调和较为一致的调节时间。
3.2 湖上试验与分析为了进一步验证MFASMC-VL方法的有效性,在AUH的湖上试验中,将MFASMC-VL应用于AUH的首向控制。试验内容包括悬停状态下的定首向控制和声学信息导引下的首向跟踪。
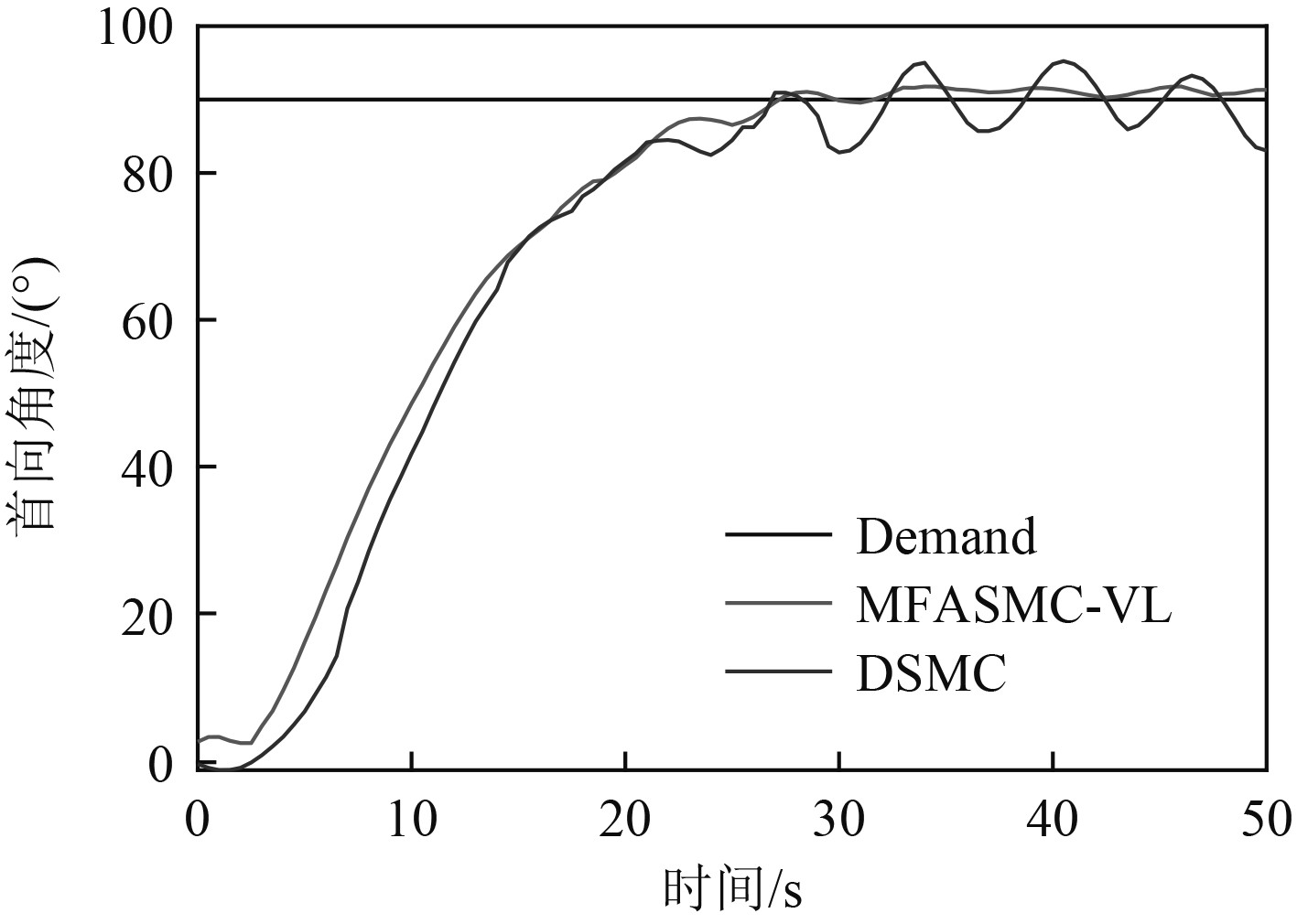
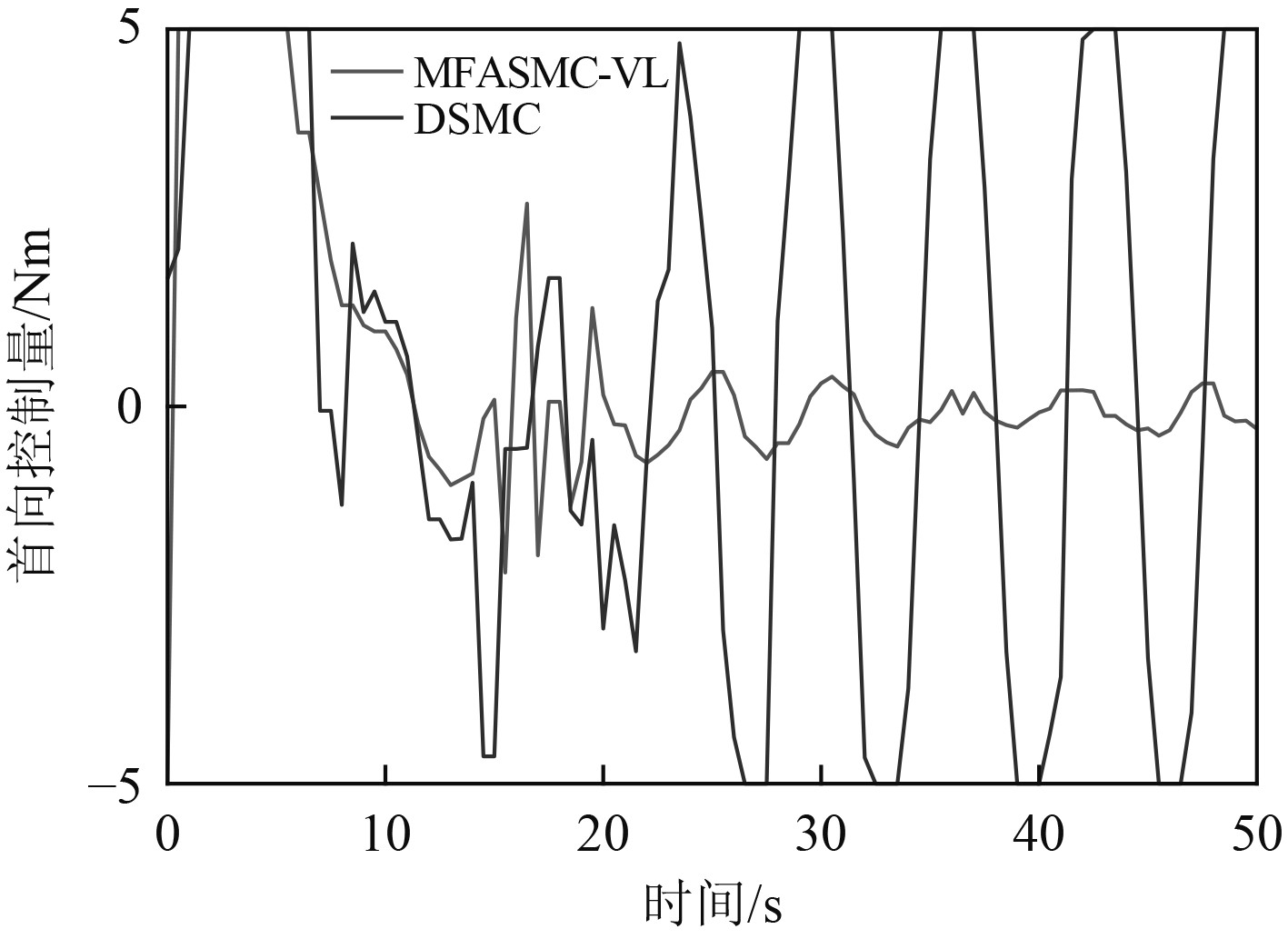
AUH在定深悬停状态下的首向90 º阶跃响应曲线和控制输入如图7和图8所示,可见MFASMC-VL与DSMC的响应速度基本相当。DSMC的首向输出存在明显的振荡,振荡峰峰值9.5º。MFASMC-VL的首向输出在稳态下仅有小幅度的波动,波动峰峰值1.5 º。同时,DSMC的控制输入在首向接近目标值时出现了大幅度的抖振。湖试中对AUH的首向控制力矩做了5 Nm的限幅处理,DSMC的控制输入在限幅值间反复振荡。MFASMC-VL的控制输入相对平滑,获得了更好的控制效果。
|
图 7 首向阶跃响应曲线(悬停) Fig. 7 Heading step response curve (hovering) |
|
图 8 控制输入曲线(悬停, 限幅5 Nm) Fig. 8 Heading step response curve (hovering) |
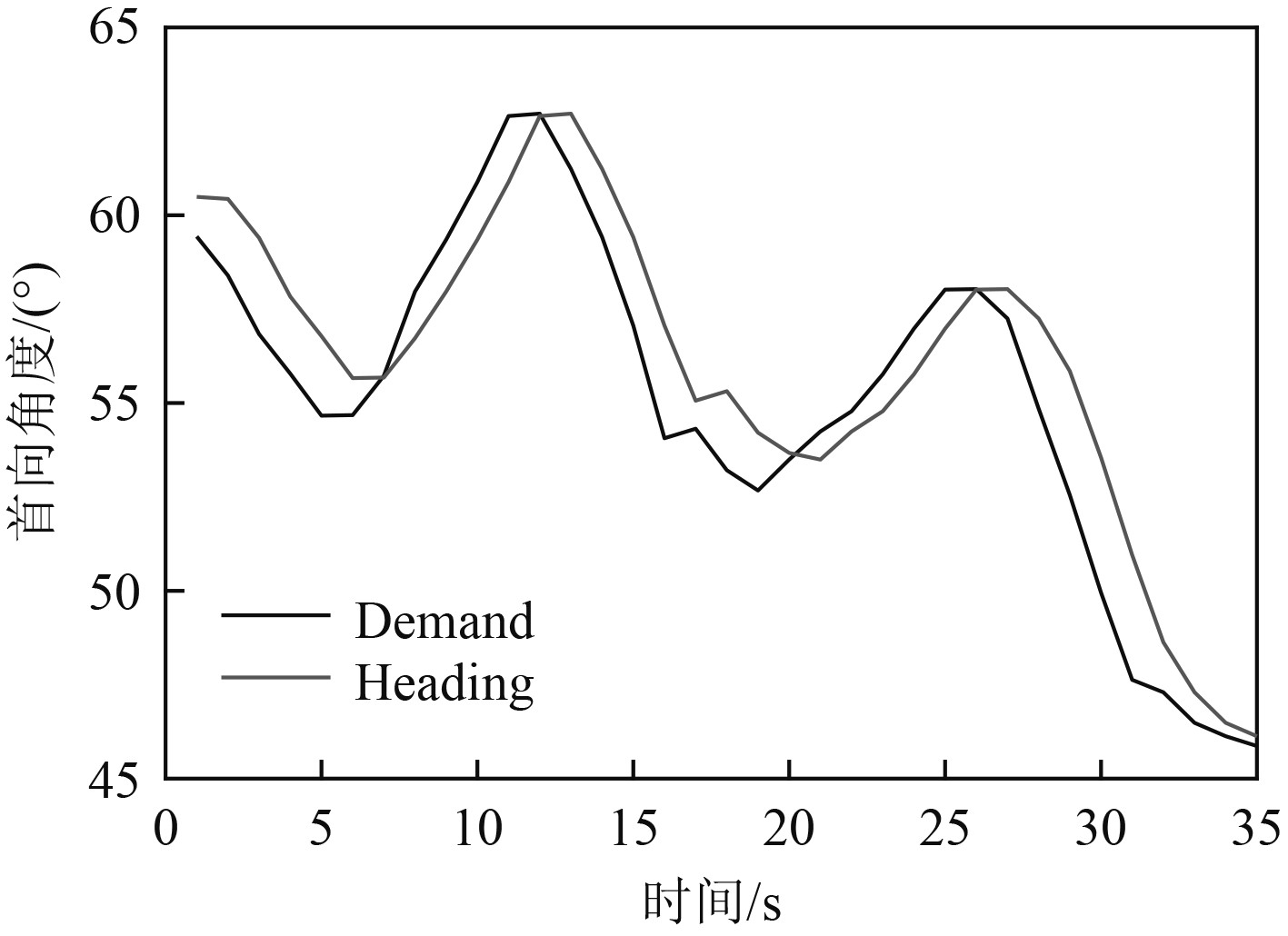
AUH在湖试中的航行任务是根据声学定位设备给出的相对方位角调整航向,以到达布置在水下的基站,航行过程中的巡航速度为1 kn。图9为AUH跟踪目标首向的曲线,其中黑色曲线为首向参考量,灰色曲线为AUH的首向跟踪曲线,从图9中可见AUH很好的跟踪了目标首向,过程中跟踪均方误差为1.7 º。
|
图 9 首向跟踪曲线 Fig. 9 Heading tracking curve |
本文研究了圆碟形AUV水下直升机的首向无模型控制问题,采用了一种无模型自适应控制与无抖振滑模控制结合的无模型自适应滑模控制器,并提出了一种参数自适应的无模型滑模控制方法。仿真对比试验表明,在被控对象参数大范围变化和存在外部扰动的情况下,无模型参数自适应滑模控方法调节时间与无抖振滑模控制相当,同时有效抑制了输出超调和振荡。将无模型参数自适应滑模控应用于水下直升机首向控制,通过湖上航行试验进一步证明了方法的有效性和可行性。
后续将进一步深入研究无模型参数自适应滑模控制器的参数对控制效果的影响机制,设计更为优化的控制器参数在线调整律。
| [1] |
JI D X, CHEN C W, CHEN Y. Autonomous underwater helicopters AUV with disc-shaped design for deepwater agility[J]. Sea Technology, 2018, 59(8): 25-27. |
| [2] |
LIN Y, HUANG Y, ZHU H, et al. Simulation study on the hydrodynamic resistance and stability of a disk-shaped autonomous underwater helicopter[J]. Ocean Engineering, 2021, 219: 108385. DOI:10.1016/j.oceaneng.2020.108385 |
| [3] |
杨超, 张铭钧, 吴珍臻, 等. 作业型水下机器人纵、横倾姿态自适应区域控制方法[J]. 机器人, 2021, 43(2): 224-233. YANG Chao, ZHANG Mingjun, WU Zhenzhen, et al. Adaptive region control method of the pitch and roll attitudes for operating autonomous underwater vehicle[J]. ROBOT, 2021, 43(2): 224-233. |
| [4] |
WANG J Q, WANG C, WEI Y J, et al. Three-dimensional path following of an underactuated AUV based on neuro-adaptive command filtered backstepping control[J]. IEEE Access, 2018(6): 74355-74365. DOI:10.1109/ACCESS.2018.2883081 |
| [5] |
GHARESI N, EBRAHIMI Z, FOROUZANDEH A, et al. Extended state observer-based backstepping control for depth tracking of the underactuated AUV[C]//2017 5th International Conference on Control, Instrumentation, and Automation. Shiraz, Iran: IEEE, 2017: 354-358.
|
| [6] |
TANAKITKORN K, WILSON P A, TURNOCK S R, et al. Sliding mode heading control of an overactuated, hover-capable autonomous underwater vehicle with experimental verification[J]. Journal of Field Robotics, 2018, 35(3): 396-415. DOI:10.1002/rob.21766 |
| [7] |
ZHANG Y Y, GAO L E, LIU W D, et al. Research on control method of AUV terminal sliding mode variable structure[C]//2017 International Conference on Robotics and Automation Sciences. Hong Kong, China: IEEE, 2017: 88-93.
|
| [8] |
MAT-NOH M, MOHD-MOKHTAR R, ARSHAD M R, et al.. Review of sliding mode control application in autonomous underwater vehicles[J]. Indian Journal of Geo-Marine Sciences, 2019, 48(7): 973-984. |
| [9] |
HOU Z, H G, LEWIS F L. Data-Driven Control and Learning Systems[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5): 4070-4075. DOI:10.1109/TIE.2017.2653767 |
| [10] |
侯忠生, 金尚泰. 无模型自适应控制: 理论与应用[M].北京: 科学出版社, 2013.
|
| [11] |
LIAO Y L, DU T P, JIANG Q Q. Model-free adaptive control method with variable forgetting factor for unmanned surface vehicle control[J]. Applied Ocean Research, 2019, 93. |
| [12] |
LI H, HE B, YIN Q, et al. Fuzzy optimized MFAC based on ADRC in AUV heading control[J]. Electronics, 2019. 8(6).
|
| [13] |
LI X, REN C, MA S, et al. Compensated model-free adaptive tracking control scheme for autonomous underwater vehicles via extended state observer[J]. Ocean Engineering, 2020, 217: 107976. DOI:10.1016/j.oceaneng.2020.107976 |
| [14] |
XU D Z, SHI Y, JI Z C. Model-free adaptive discrete-time integral sliding-mode-constrained-control for autonomous 4WMV parking systems[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 834-843. DOI:10.1109/TIE.2017.2739680 |
| [15] |
GAO H, MA G F, LV Y Y, et al. Forecasting-based data-driven model-free adaptive sliding mode attitude control of combined spacecraft[J]. Aerospace Science and Technology, 2019, 86: 364-374. DOI:10.1016/j.ast.2019.01.004 |
| [16] |
WANG W, RANA J M. Model-free-adaptive-based data-driven method for three-axis gimbal control[J]. Measurement & Control, 2020, 53(7-8): 1512-1517. |
| [17] |
姚文龙, 王加利, 庞震, 等. 吊舱推进电机的无模型自适应滑模矢量控制[J]. 交通运输工程学报, 2020, 20(3): 72-79. YAO Wen-long, WANG Jia-li, PANG zhen, et al. Model-free adaptive sliding mode vector control for podded propulsion motor[J]. Journal of Traffic and Transportation Engineering, 2020, 20(3): 72-79. |
| [18] |
王天. 新型碟形水下机器人及其航姿预测控制系统研究[D]. 哈尔滨: 哈尔滨工程大学, 2013. WANG Tian. Researches on a novel disk-like underwater robot and attitude predictive control[D]. Harbin: Harbin Engineering University, 2013. . |
| [19] |
WANG Z K, LIU X, HUANG H c, et al.. Development of an Autonomous Underwater Helicopter with high maneuverability[J]. Applied Sciences-Basel, 2019, 9(19): 19. |
| [20] |
DU H, YU X, CHEN M Z Q, et al. Chattering-free discrete-time sliding mode control[J]. Automatica, 2016, 68: 87-91. DOI:10.1016/j.automatica.2016.01.047 |
| [21] |
CHEN C W, WANG T X, FENG Z, et al. Simulation research on water-entry impact force of an autonomous underwater helicopter[J]. Journal of Marine Science and Technology, 2020, 25(4): 1166-1181. DOI:10.1007/s00773-020-00707-8 |
 2022, Vol. 44
2022, Vol. 44

