随着全球能源消费的日益上涨,天然气因其热值高、二氧化碳排放低,已成为替代煤炭、石油等传统化石能源的最佳选择[1],其需求不断增长,有关液化天然气的产业链持续发展[2]。对液化天然气(liquefied natural gas,LNG)的储存、运输和利用过程的优化具有重要意义。其中换热器是液化天然气进行汽化过程中的关键部件,针对换热器的优化研究价值较高[3]。
换热器内部由许多微细流道构成。研究发现,流体在微细流道内的流动与换热特性明显好于常规尺度条件下的流动与换热性能[4],但尺度微小化也会造成较大的压降和阻力[5]。在实际应用中,需将LNG加压至临界压力以上,以达到超临界态,再经接收站汽化才能满足需求[6]。与普通流体相比,超临界流体具有密度大、黏度小、扩散速度快、导热系数高等优点[7],在微细流道内流动产生的压降和阻力相比于普通流体大幅度降低,能够获得更好的流动与换热性能[8]。有相关的文献表明,Z型和S型弯曲流道可以提高换热器的换热性能,而在弯曲角度为15°时获得了较好的流动换热性能[9];结构形状为错列S形翅片的微通道能在保证良好的传热性能时获得较低的阻力压降[10]。通过改变流道形状和流道结构来提高换热性能和降低压降,是近年来针对换热器研究的主要方向之一[11]。本文设计螺旋形微细流道,并重点对单根螺旋形流道内超临界LNG的流动和换热性能进行计算和讨论。
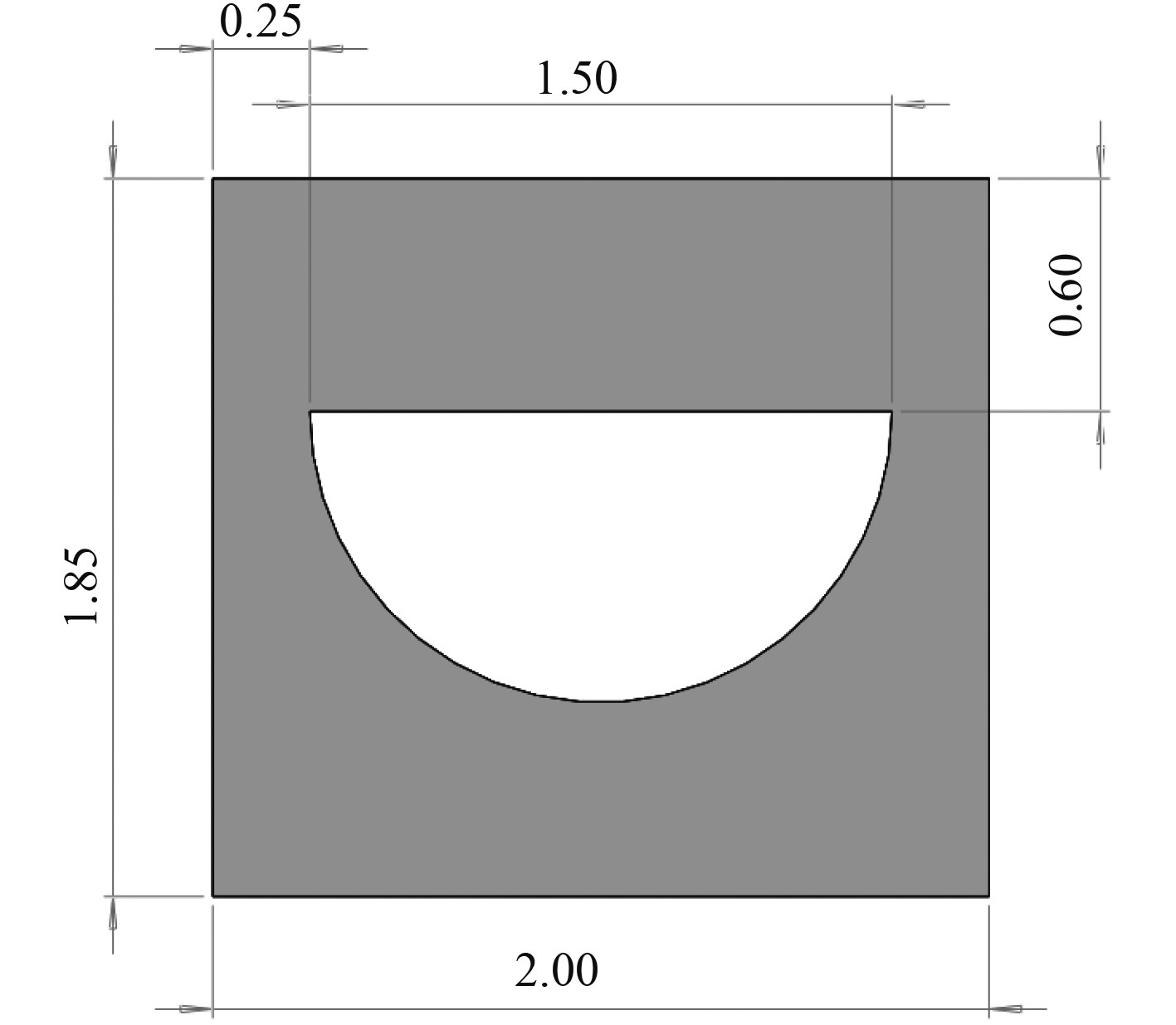
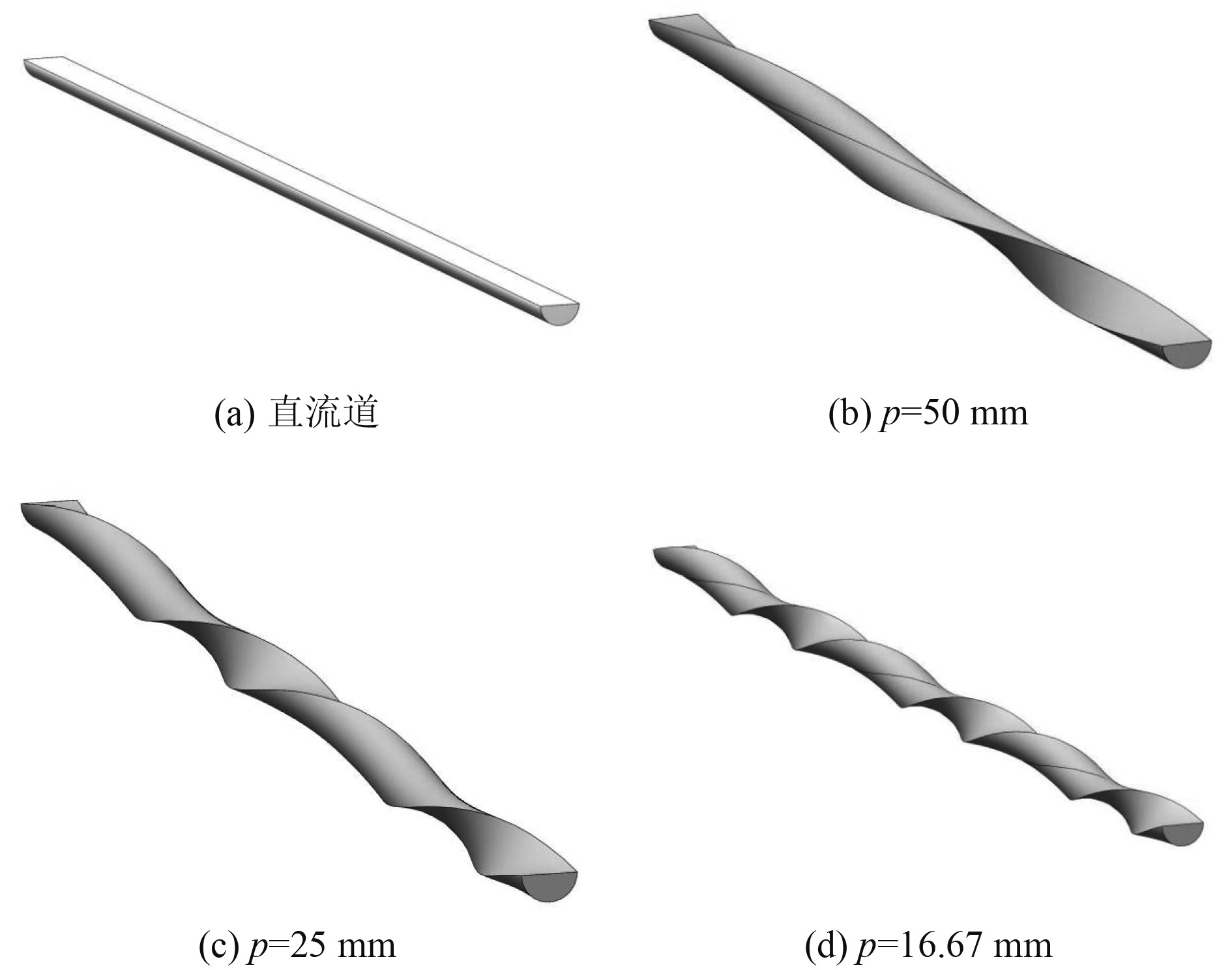
1 模型介绍改进的原型为横截面为2.0 mm×1.85 mm的矩形、纵向长度为50 mm的单个长方体流道,矩形截面分为内外2个区域,内部为超临界LNG流道,外部为导热固体壁面,流道区域为半径为0.75 mm的半圆形,横截面如图1所示。设计不同于常用直管形式的螺旋形微细流道,螺旋形旋转一圈所前进的纵向距离为螺距p,直流道、p=50 mm、p=25 mm、p=16.67 mm(每50 mm旋转3周)的流体域模型分别如图2所示。
|
图 1 流道横截面 Fig. 1 Cross section of flow channel |
|
图 2 不同形状的流体域模型 Fig. 2 Fluid domain models with different shapes |
对超临界LNG在螺旋形流道中的流动换热情况进行了数值仿真计算。计算时采用稳态计算,湍流模型为k-ω模型,并开启能量模型,边界条件为质量入口和压力出口,上下壁面施加恒定热流密度。
2.2 热物性参数通过对文献[12]采用的热物性曲线图进行拟合,取得热物性参数多项式如下:
ρ=865.759−6.751T+0.0396786T2−9.93909×10−5T3,121≤T<233.65;ρ=5606.645−53.738T+0.176T2−1.94134×10−4T3,233.65≤T<384.791。
Cp=−29299.31+585.69T−3.57T2+7.39546×10−3T3,162.12≤T<200.618;Cp=780505.89−11103.73T+52.66T2−8.27359×10−2T3,200.618≤T<218.679;Cp=15131340.31−269079.85T+1790.33T2−5.28T3+5.8255×10−3T4,218.679≤T<236.74;Cp=−367428.36+4796.08T−20.25T2+2.80547×10−2T3,236.74≤T<260.504;Cp=169650.39−1620.37T+5.29T2−5.78818×10−3T3,260.504≤T<303.992;Cp=37704.89−285.23T+0.778489T2−7.11777×10−4T3,303.992≤T<361.74;Cp=3152.65,361.74≤T<385。
λ=0.34317−1.268×10−3T−7.43911×10−7T2+4.035×10−9T3,121≤T<233.413;λ=2.333486−2.4318×10−2T+8.63542×10−5T2−1.02523×10−7T3,233.413≤T<284.268;λ=0.350815−2.69×10−3T+7.60346×10−6T2−6.82556×10−9T3,284.268≤T<384.791。
μ=1.283575×10−3−2.1655×10−5T+1.49×10−7T2−1.75047×10−10T3+5.77234×10−13T4,121≤T<258.84;μ=1.52655×10−5,258.84≤T<367.918;μ=−5.813×10−5+1.99×10−7T ,367.918≤T<374.572;μ=1.65929×10−5,374.572≤T<384.791。
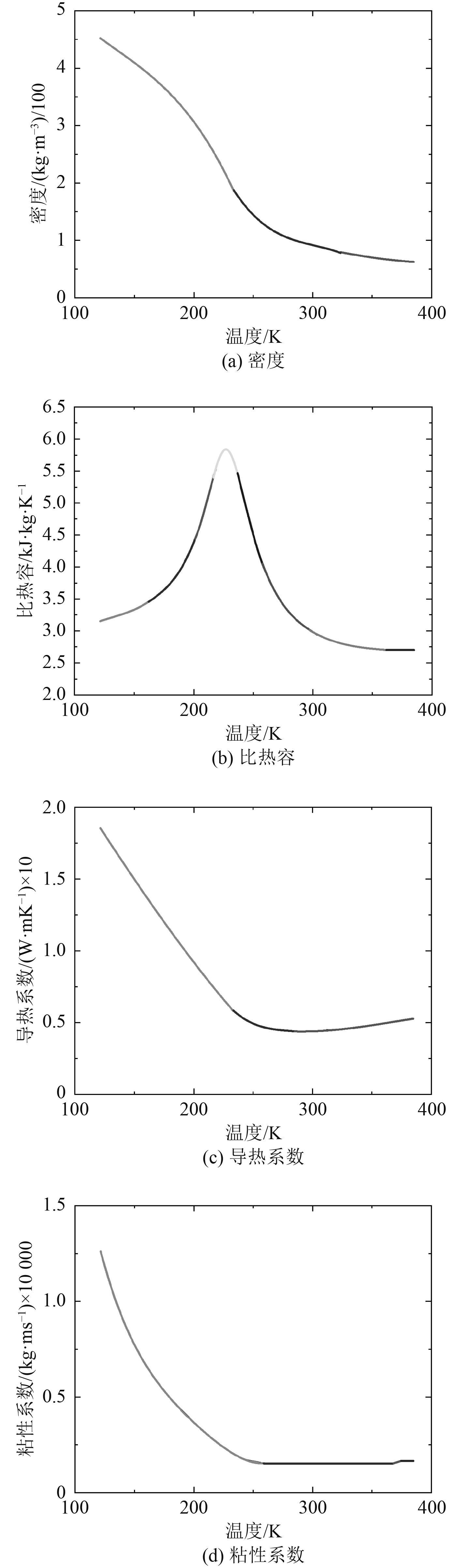
多项式拟合后的物性参数如图3所示。
|
图 3 多项式拟合后的物性参数 Fig. 3 Physical parameters after polynomial fitting |
通过以上多项式编写udf,运用udf在相同条件下对相同尺寸的直流道模型进行CFD计算,以验证结果。
2.3 计算方法验证通过努赛尔数Nu来表示对流换热强烈程度,其计算公式如下:
| $ Nu = \frac{{h{D_h}}}{\lambda }。$ | (1) |
其中:水力直径Dh为4倍的最小自由流通面积与湿周之比;λ为导热系数;h为对流换热系数,h由以下公式得出:
| $ h = \frac{{{q_w}}}{{{T_{wall}} - {T_b}}} = \frac{{{q_w}}}{{{T_{wall}} - ({T_{out}} + {T_{in}})/2}}。$ | (2) |
其中:qw为壁面热流密度;Twall为壁面温度;Tin为入口温度;Tout为出口温度。
选择欧拉数来表示的压力损失,计算公式如下:
| $ Eu = \frac{{\Delta P}}{{\rho {u^2}}} 。$ | (3) |
其中:ΔP为压力差;ρ为密度;u为流速。
计算时采用的直流道网格如图4所示。

|
图 4 260 mm直流道网格 Fig. 4 260 mm straight channel grid |
文献[12]中260 mm直流道在流入的质量通量为325 kg/m2s时,Eu数为8.1401。计算得出,Eu数为8.2604,与文献结果误差在2%以内。
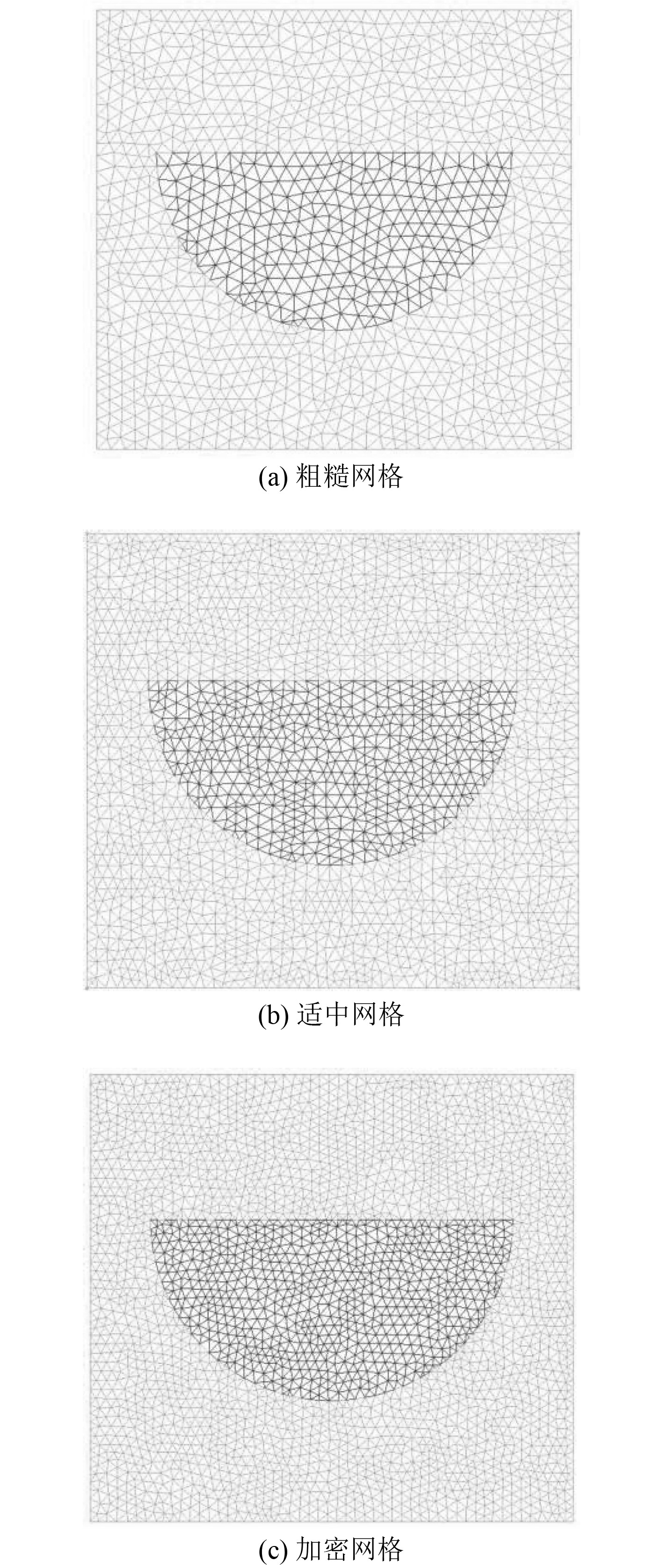
2.4 网格收敛性验证以p=25 mm螺旋形模型为对象,分别划分粗糙网格、适中网格和加密网格3种流体计算网格,各划分方案对应的网格总量为1000万、2000万和4000万单元。
3种网格量的y+值都主要分布在0.1~1之间,不同网格量的入口处网格如图5所示。
|
图 5 50 mm螺旋形流道不同网格量方案入口处网格 Fig. 5 Inlet grid of different grid amount schemes for 50 mm spiral channel |
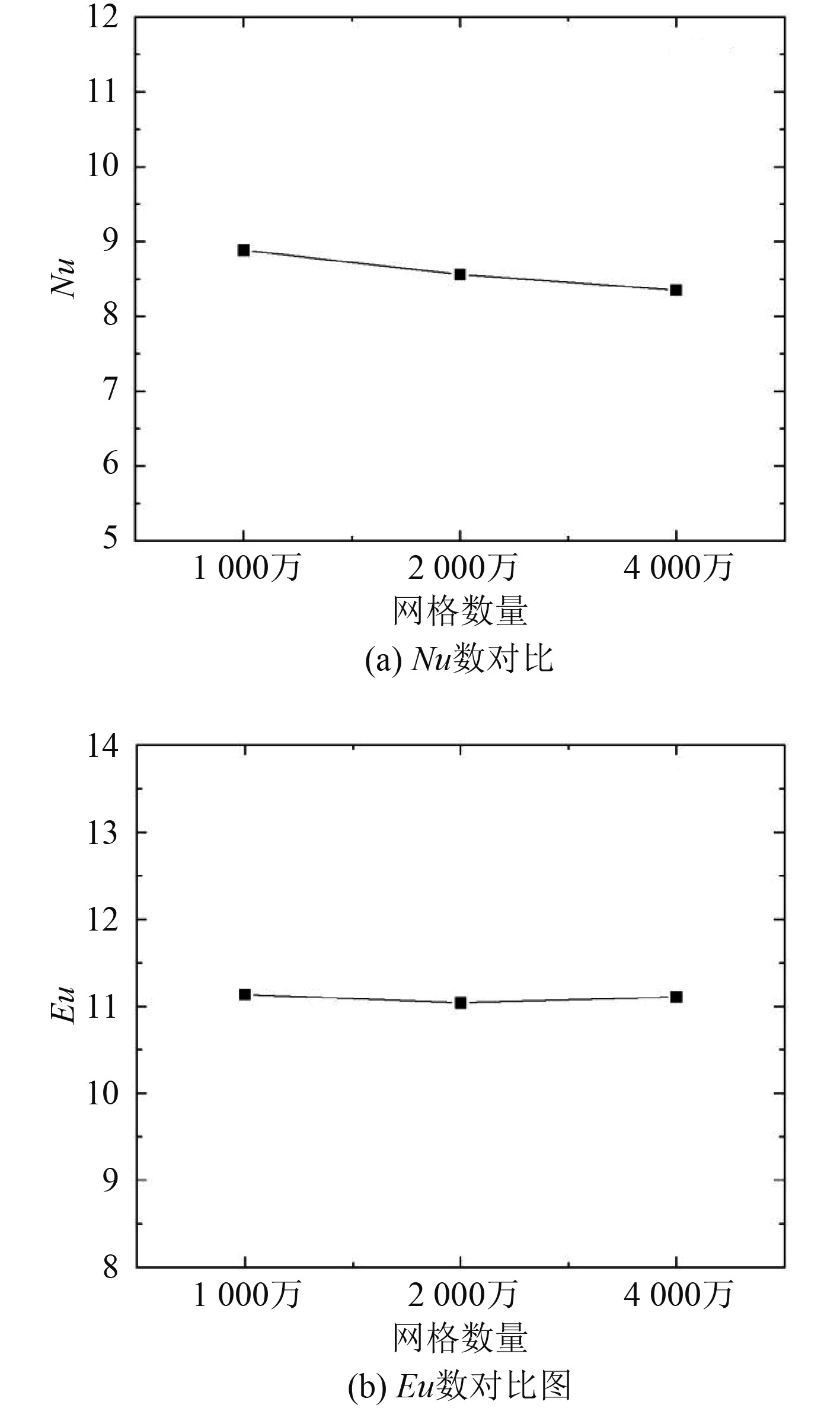
不同网格量情况下计算得到的Nu和Eu数对比如图6所示。
|
图 6 不同网格数量Nu和Eu数对比图 Fig. 6 Comparison of Nu and Eu with different grid numbers |
由图6可知,分别用以上3种网格量计算时,计算结果相差较小,采用适中网格能够满足精度要求。
3 不同形状下换热流动情况对比分别对直流道,p=50 mm,p=25 mm,p=16.67 mm的微细流道在入口质量通量为325 kg/m2s、压强为10.5 Mpa、上下壁面施加恒定为30 000 W/m2热流密度情况下进行CFD计算。
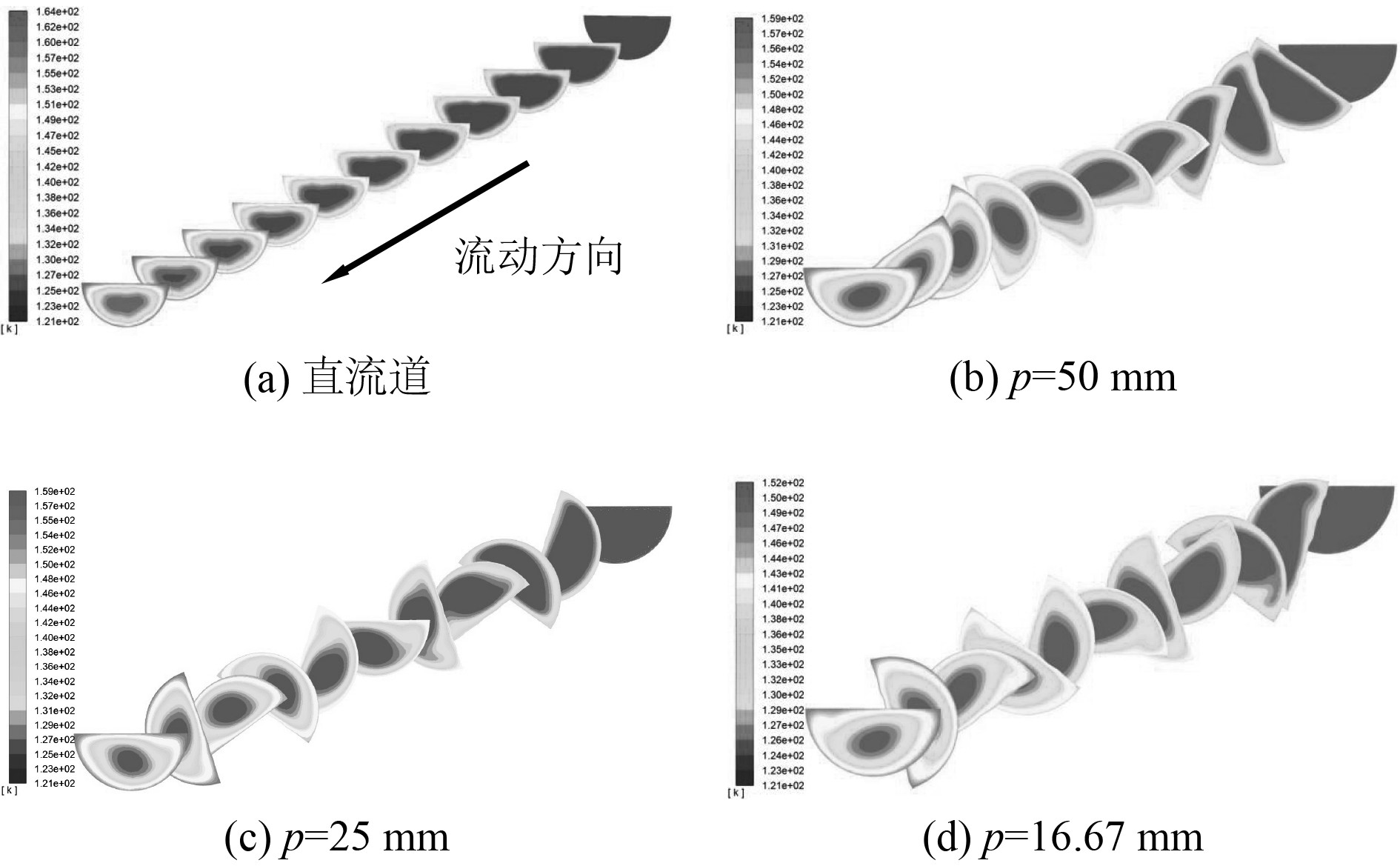
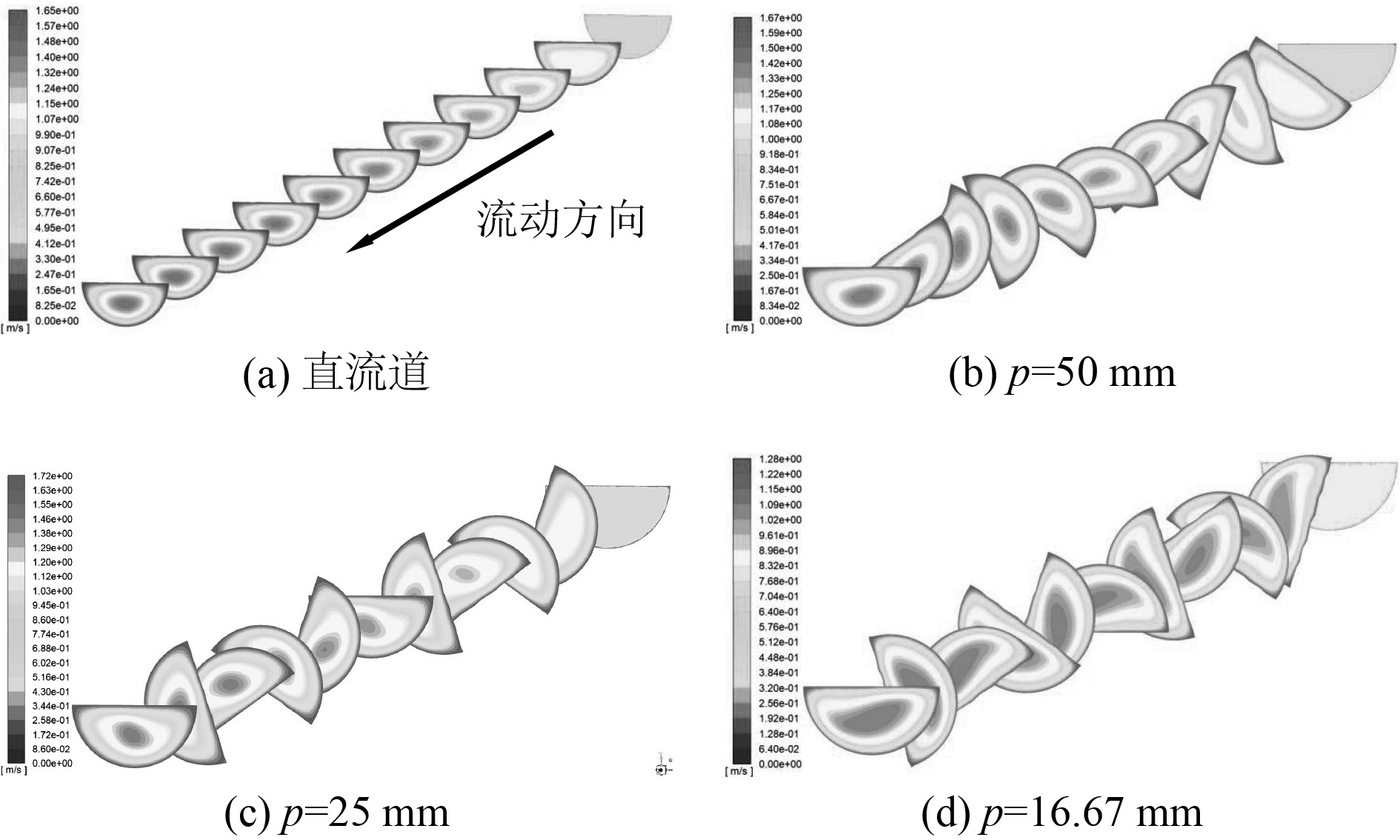
每隔5 mm取一个横截面,不同形状下的温度云图如图7所示,速度云图如图8所示。图中右上端为流道入口,左下端为流道出口,其余横截面依次排列。
|
图 7 不同螺距情况下的温度云图 Fig. 7 Contours of temperature under different pitch |
|
图 8 不同螺距情况下的速度云图 Fig. 8 Contours of velocity under different pitch |
通过云图可以看出,LNG的温度和速度都随着流动方向而增大,流道中心的LNG温度较低流速较快,直流道、p=50 mm流道和p=25 mm流道内的流动较稳定,而p=16.67 mm的流道内的流动情况变差。
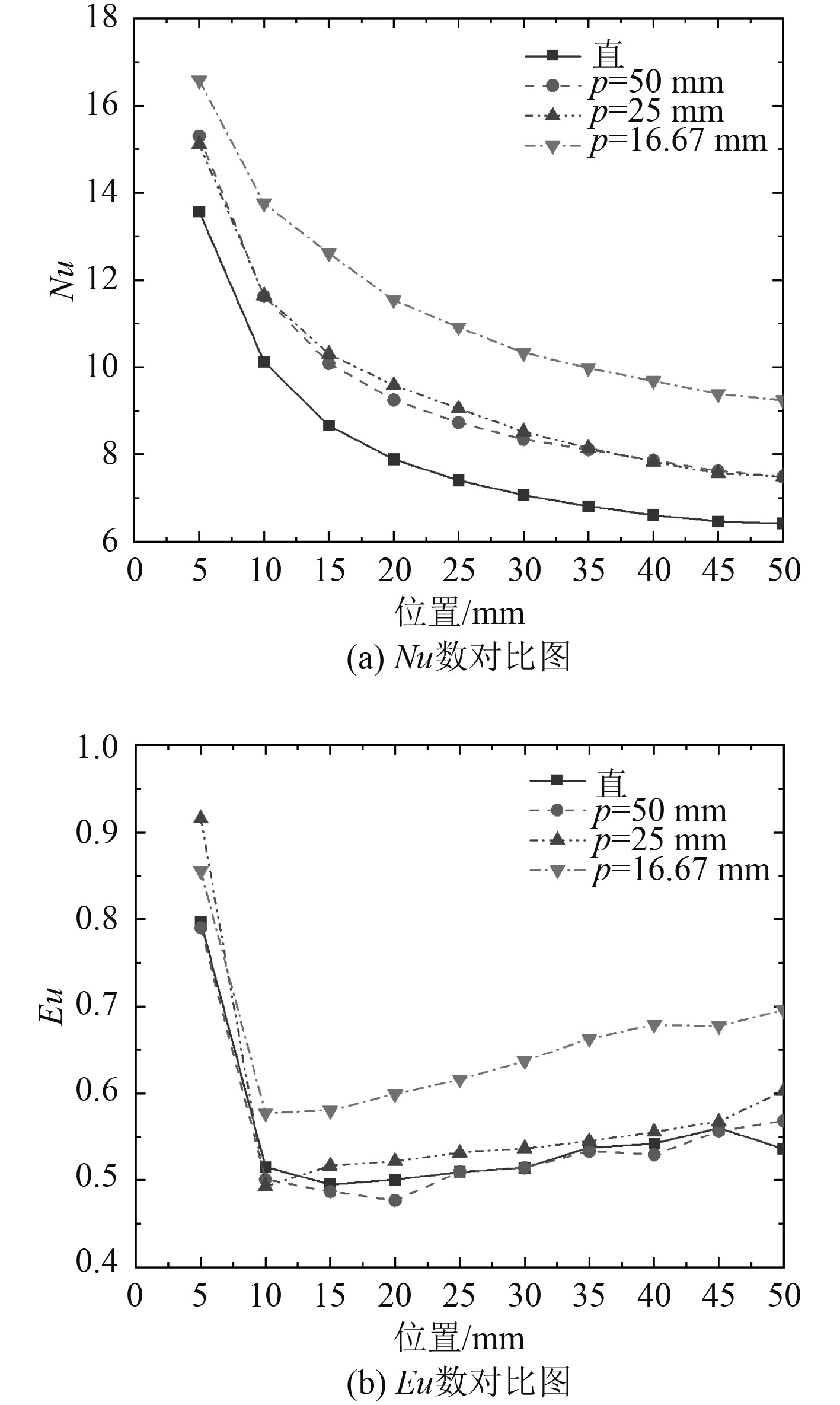
Nu数与Eu数对比如图9所示。
|
图 9 不同几何形状局部Nu数和Eu数对比 Fig. 9 Comparison of local Nu and Eu numbers in different geometric shapes |
由Nu数对比图可知,随着旋转角度的增大,换热效果也随之增强。其中,螺距为50 mm和25 mm的微细流道的换热效果明显强于直流道,而16.67 mm螺距微细流道的换热效果也明显强于螺距为50 mm和25 mm的流道。但是通过Eu数对比图可以看出直、50 mm螺距、25 mm螺距流道的流动性能相差较小,而螺距为16.67 mm的流道的压力损失则明显增大。
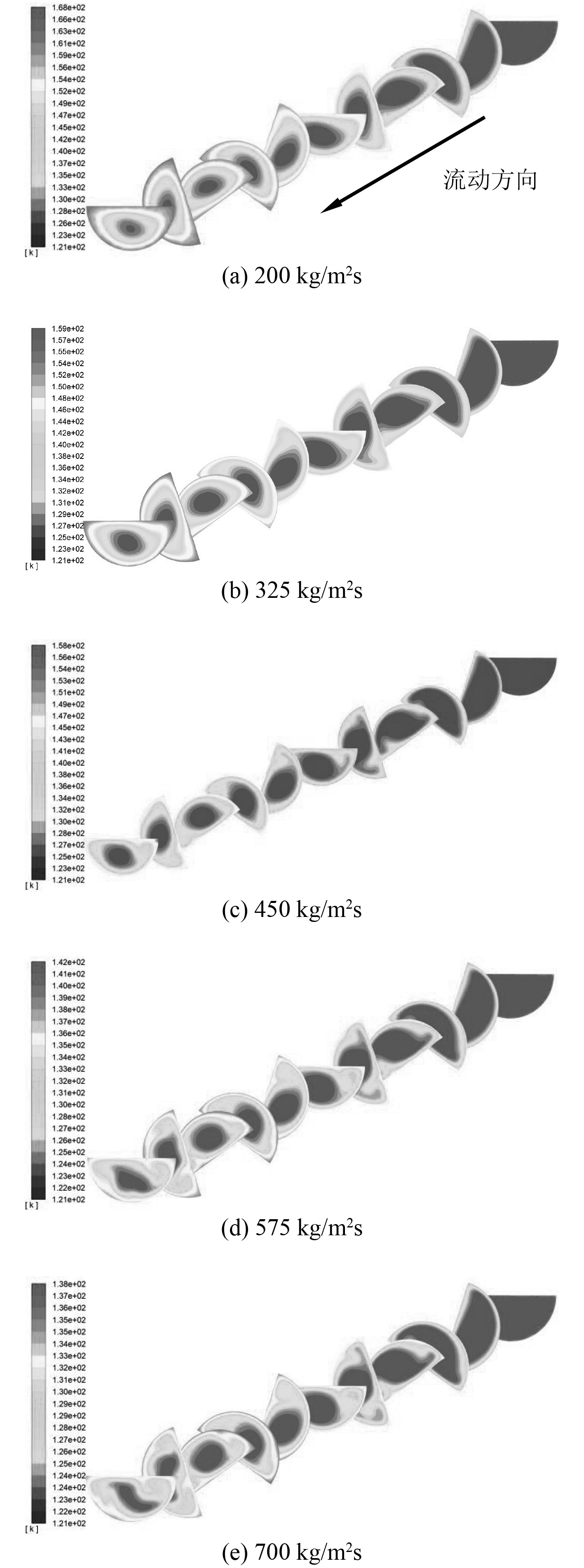
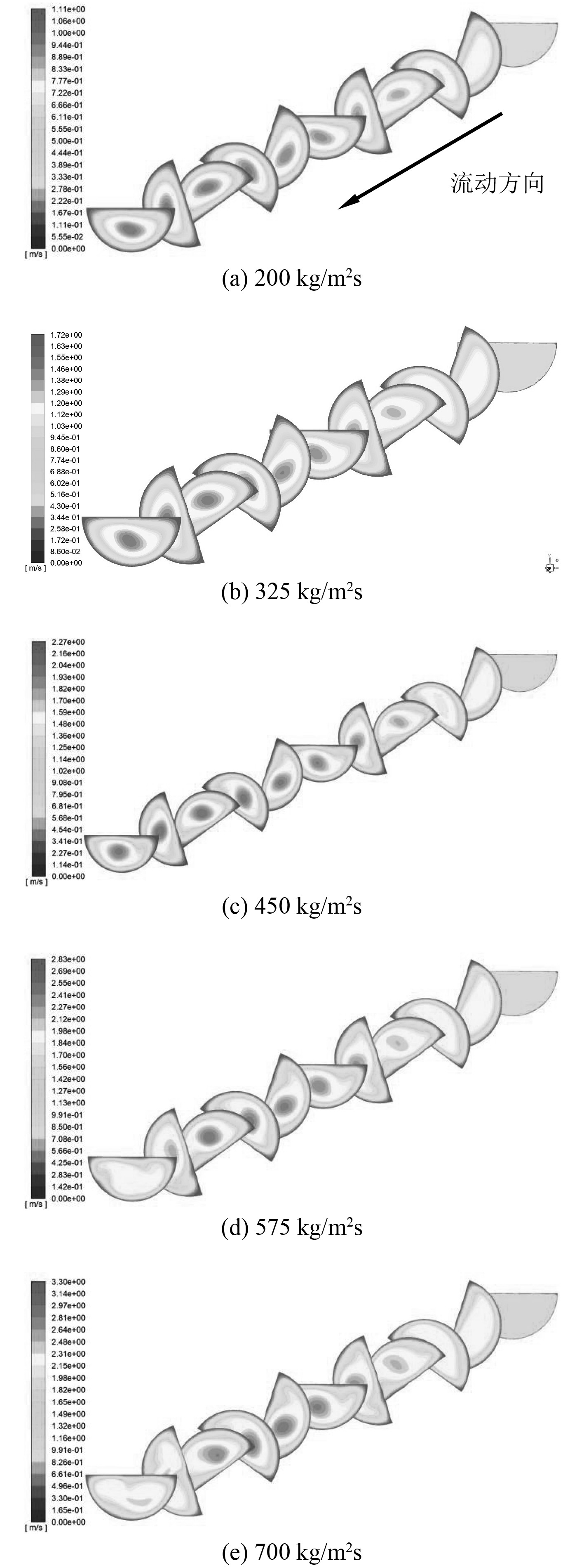
4 不同流速下换热流动情况对比对p=25 mm的微细流道在入口质量通量分别为200 kg/m2s,325 kg/m2s,450 kg/m2s,575 kg/m2s,700 kg/m2s,压强为10.5 MPa,上下壁面施加恒定为30000 W/m2热流密度情况下进行CFD计算,得到不同流速情况下温度云图如图10所示,速度云图如图11所示。
|
图 10 不同质量通量情况下的温度云图 Fig. 10 Contours of temperature under different mass fluxes |
|
图 11 不同质量通量情况下的速度云图 Fig. 11 Contours of velocity under different mass fluxes |
由图10和图11可知,质量通量为200 kg/m2s,325 kg/m2s时,流动较稳定,当质量通量超过450 kg/m2s时流动变得紊乱。
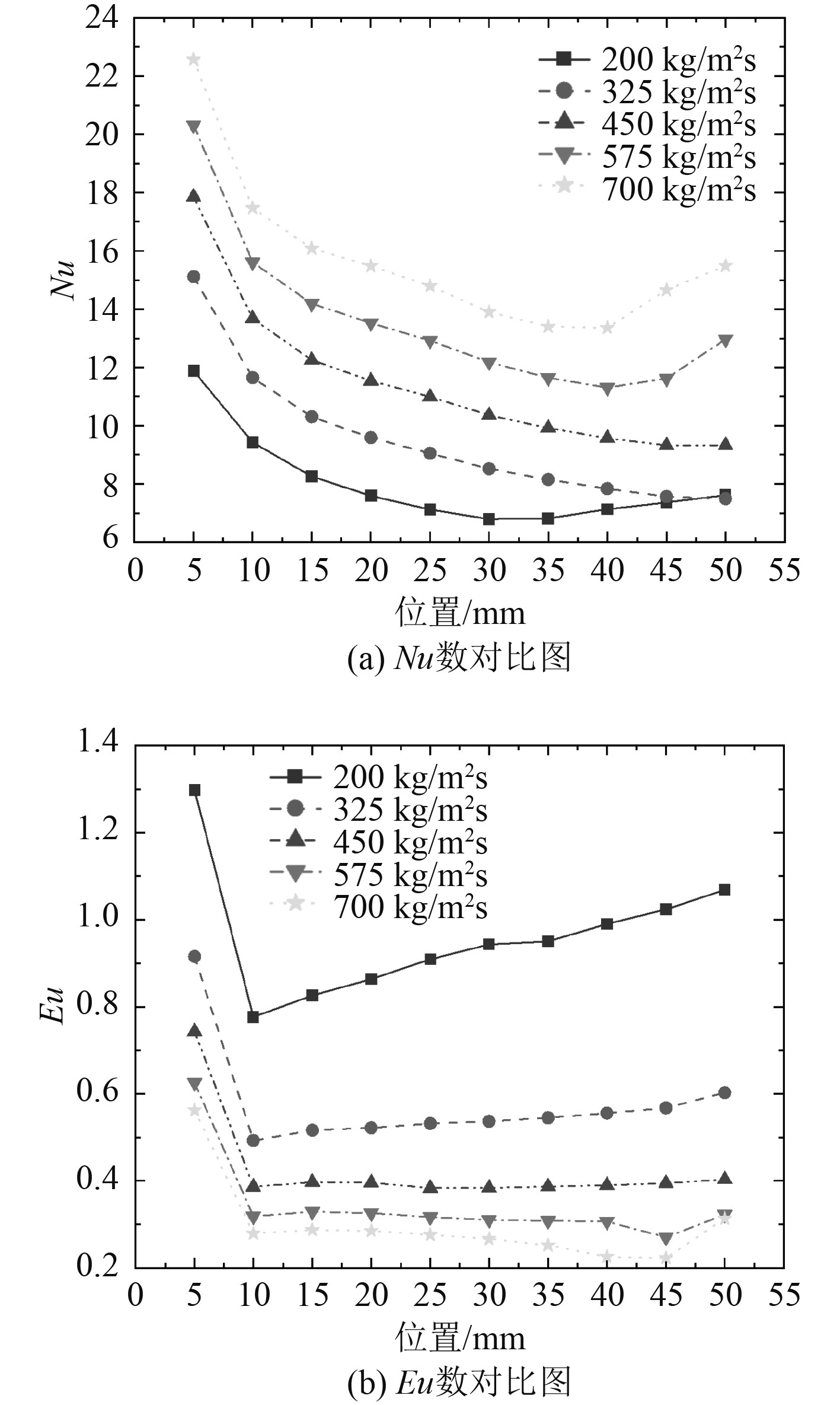
不同质量通量条件下Nu数与Eu数对比如图12所示。
|
图 12 不同质量通量时局部Nu数和Eu数对比 Fig. 12 Comparison of local Nu and Eu numbers at different mass fluxes |
由图12可知,随着质量通量的增大,Nu数增大,而Eu数减小,换热和流动性能都有提升,但质量通量超过450 kg/m2s后,流动性能的提升空间较小。
综上所述,超临界LNG的质量通量不宜超过450 kg/m2s。
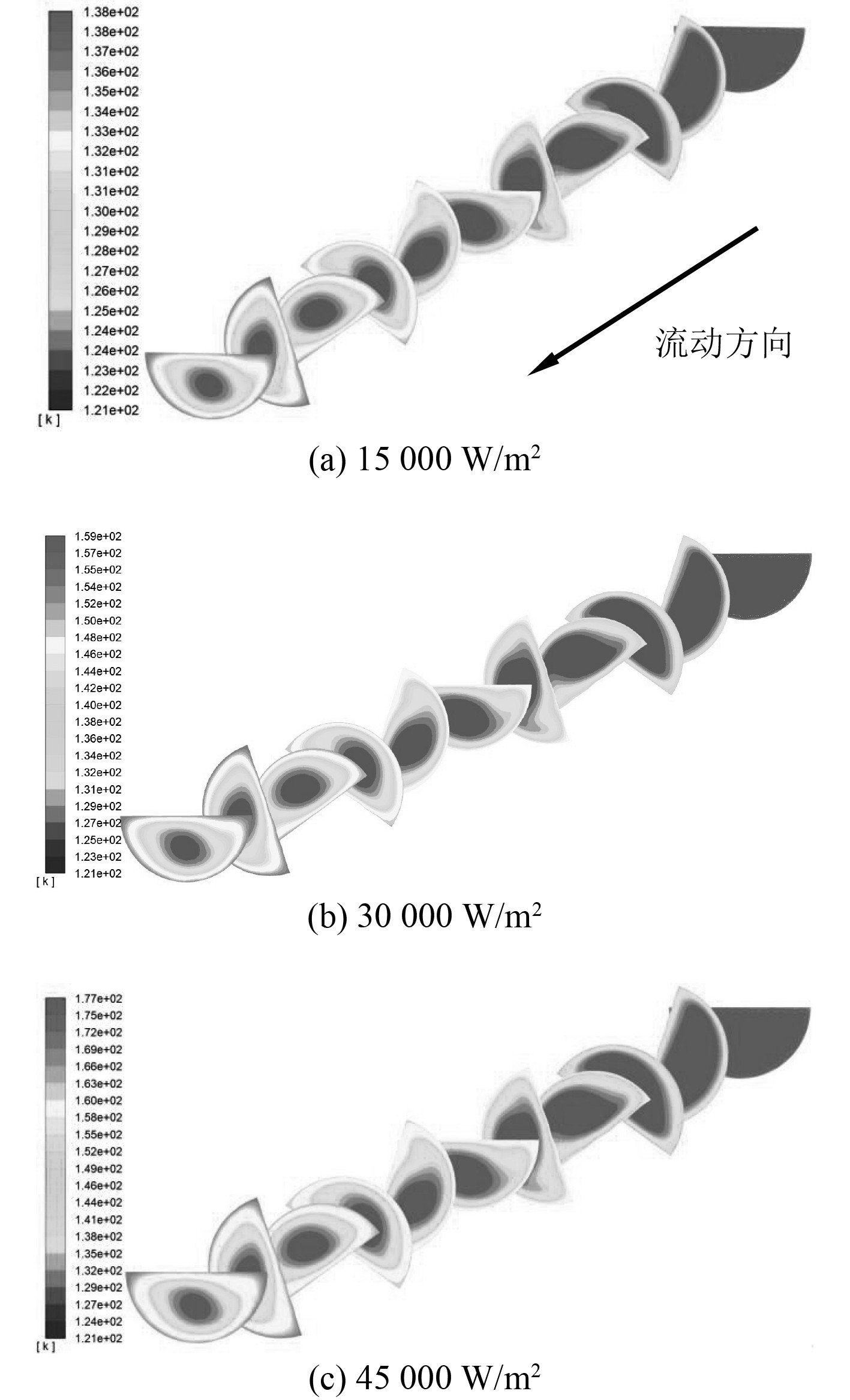
5 不同热流密度下换热流动情况对比不同上下壁面热流密度情况下,温度云图如图13所示,速度云图如图14所示。
|
图 13 不同热流密度情况下的温度云图 Fig. 13 Contours of temperature under different heat flux |
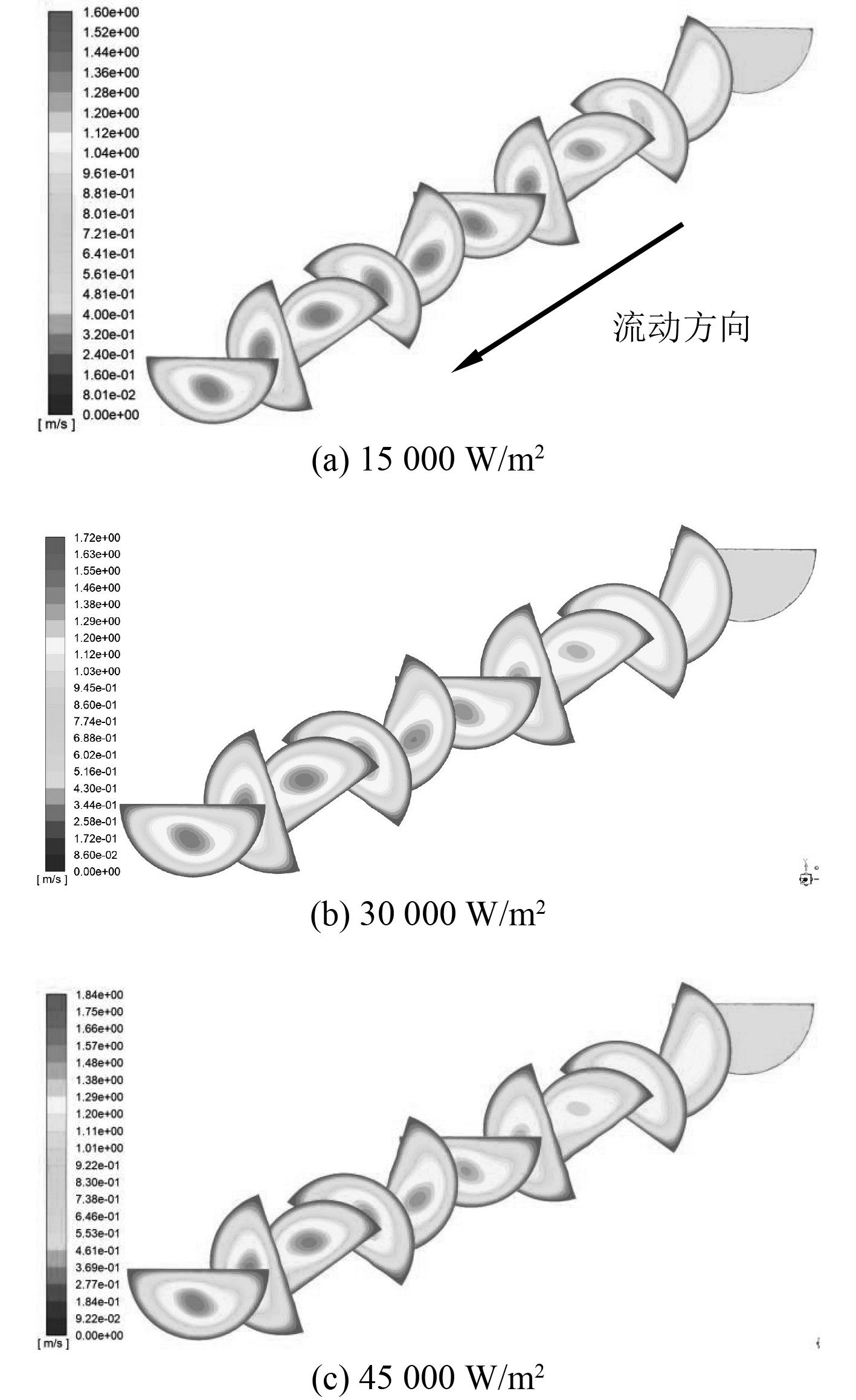
|
图 14 不同热流密度情况下的速度云图 Fig. 14 Contours of velocity under different heat flux |
对25 mm螺距的微细流道在入口质量通量为325 kg/m2s,压强为10.5 MPa,上下壁面分别施加恒定为15000 W/m2,30000 W/m2,45000 W/m2热流密度情况下进行CFD计算,得到Nu数与Eu数对比图如图15所示。
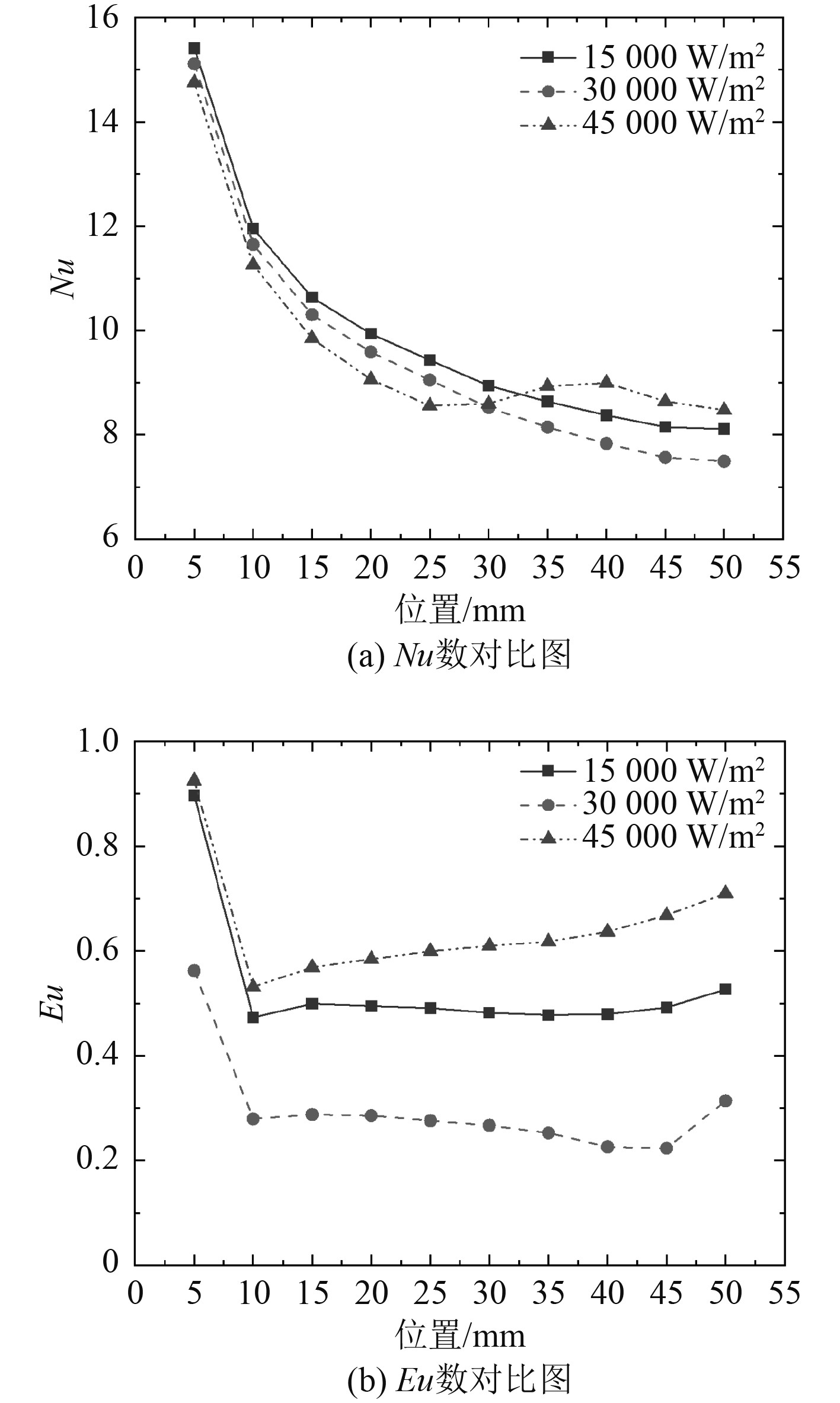
|
图 15 不同热流密度时局部Nu数和Eu数对比 Fig. 15 Comparison of local Nu number and Eu number under different heat flux |
由图15可知,不同热流密度情况下换热性能较接近,而热流密度为30 000 W/m2时,流动性能最佳。
6 结 语通过对单根螺旋形微细流道内的超临界LNG的流动情况进行计算,对比了不同螺距流道在不同流速、不同上下壁面热流密度时的流动换热性能,得出以下结论:
1)随着螺旋程度的加大,换热性能改善而流动性能下降,流道半径为0.75 mm条件下,选择螺距为50 mm或25 mm可以获得更好的换热性能而对流动性能的影响较小;
2)螺旋形微流道内,随着流速的加快,换热性能和流动性能都有提升,但流速较快时,流动性能提升有限,流动变得紊乱,且温度变化较小无法满足汽化的条件。
3)随着上下壁面热流密度的增大,换热性能变化较小而流动性能先改善后变差,本文模型选择热流密度为30 000 w/m2最佳。
综上所述,与直流道相比,选择螺距不低于25 mm的螺旋形流道可以改善换热性能而对流动性能的影响较小。另外合理选择流速和上下壁面热流密度也可以改善螺旋形流道的流动换热性能。
| [1] |
A YOUSEFI, M BIROUK. Investigation of natural gas energy fraction and injection timing on the performance and emissions of a dual-fuel engine with pre-combustion chamber under low engine load[J]. Applied Energy, 2017, 189: 492−505,
|
| [2] |
谷家扬, 魏世松, 景宝金, 等. 紧凑高效微通道换热器流动与换热特性研究进展[J]. 江苏科技大学学报(自然科学版), 2020, 34(6): 42-49. |
| [3] |
赵星霖, 王平阳, 黄佳卉. 带有横向微槽道的超临界LNG紧凑式换热器换热强化模拟研究[J]. 低温工程, 2020(6): 1-8. DOI:10.3969/j.issn.1000-6516.2020.06.001 |
| [4] |
胡芳. 印刷电路板式换热器流动与传热特性研究[D]. 南京: 南京航空航天大学, 2012.
|
| [5] |
李成文. 微小通道内气体流动特性的实验研究[D]. 北京: 北京交通大学, 2010.
|
| [6] |
孙宝坤. 螺旋管汽化器超临界LNG流动与换热特性研究[D]. 武汉: 武汉工程大学, 2018.
|
| [7] |
YOON Y B. A new formulation of variable turbulent Prandtl number for heat transfer to supercritical fluids[J]. International Journal of Heat and Mass Transfer, 2016, 92: 792-806.
|
| [8] |
钟艳. 微槽道两相流传热特性研究[D]. 广州: 华南理工大学, 2012.
|
| [9] |
贾丹丹, 赵忠超, 张永, 等. 超临界LNG在印刷板式汽化器微细流道内的流动与换热性能数值研究[J]. 船舶工程, 2017, 39(5): 35-40. |
| [10] |
宋丹, 蒋庆峰, 冯国增, 等. 超临界LNG在错列S形翅片微通道的流动传热特性研究[J]. 低温与超导, 2021, 49(1): 16-21. |
| [11] |
周依檬. 超临界LNG在印刷板式换热器内流动与换热特性数值仿真研究[D]. 镇江: 江苏科技大学, 2019.
|
| [12] |
ZHAO Zhongchao, ZHAO Kai, JIA Dandan, et al. Numerical investigation on the flow and heat transfer characteristics of supercritical liquefied natural gas in an airfoil fin printed circuit heat exchanger[J]. Energies, 2017, 10(11): 1828.
|
 2022, Vol. 44
2022, Vol. 44

