2. 上海交通大学 船舶海洋与建筑工程学院,上海 200240;
3. 上海交通大学 海洋装备研究院,上海 200240
2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China;
3. Institute of Marine Equipment, Shanghai Jiaotong University, Shanghai 200240, China
冰海结构物受风、海浪、温度、海冰等多种外界因素共同作用。平整冰在结构物水线面处产生的推挤载荷对结构物安全影响重大[1],国内外不少结构物的安全事故均源自于海冰推挤[2]。20世纪70年代,渤海多个平台曾被海冰推倒[3];同一时期,波斯尼亚湾也发生过多起与海冰相关的事故[4]。为避免类似事故发生,冰海结构物常在水线面处加设与图1结构类似的抗冰锥以减少海冰推移所产生的推挤载荷[5]。
抗冰结构物的设计离不开冰载荷预报,冰载荷预报方法主要有公式法、试验法和数值模拟法。Croasdale曾在1980年基于弹性地基梁理论提出用于计算平整冰与宽大斜面间相互作用力的二维模型。随后,Croasdale等[6]在该模型基础上,提出了计算锥体冰载荷的三维模型。除Croasdale公式外,可用于计算锥体冰载荷的公式还有Ralston公式、Kato公式、Hirayama-Obara公式等[7]。但是,冰载荷公式在使用时均需遵循特定条件,结果准确性受对象、环境等因素影响,同时也难以计算复杂表面结构物的冰载荷。
试验法则是浮冰与冰海结构物作用关系研究中最准确的预报方法,其可分为模型试验和现场观测。关湃等[8]、武海斌等[9]、XU等[10]、陈晓东等[11]都曾在其研究中使用过该方法,且得到较为准确的冰载荷结果与碎冰现象。但是,模型试验中尺度效应的存在、模型冰属性不统一等问题,现场测量中成本巨大、耗时长、难以重复等问题,使得试验法难以作为抗冰结构物设计初期的研究手段[12]。
数值模拟法以研究成本低、可重复性高、模型易替换等优点逐步被研究人员重视。其中,有限元法与光滑粒子流体动力学(SPH)法是较为常用的2种模拟方法。Song等[13,14]通过有限元法探究平整冰与漂浮式风机的相互作用力。为处理网格大变形问题,研究者们通常将有限元法与侵蚀算法相结合,当单元达到失效准则时将被删去,以发生网格畸变。但是,该方法违背了质量守恒,只能计算冰载荷中推挤载荷部分,无法再现破碎冰的载荷与堆积形态。同时,当应变率过高时,有限元法还会出现网格畸变等问题。为解决上述问题,Obisesan等[15]、齐雅薇等[16]、卞光夫等[17]通过SPH法对平整冰推挤冰海结构物过程进行了模拟,结果表明,SPH法虽能解决网格畸变等问题,但存在计算资源需求大、计算效率低、边界条件定义困难等问题。
为更高效、准确地模拟平整冰推挤冰海结构物过程,学者们不断将新方法引入浮冰与冰海结构物作用关系的研究中。Chen等[18]将FEM-SPH耦合算法运用到锥体与平整冰相互作用的模拟中,以期寻求模拟碎冰堆积现象的新方法,但其仅对FEM-SPH耦合算法进行了初步介绍,并未对冰推挤载荷、破碎冰堆积现象等因素进行深入研究。
本文分别采用FEM-SPH耦合算法与有限元法模拟平整冰推挤不同水线面直径抗冰锥过程,展现FEM-SPH耦合算法相较有限元法在破碎冰研究方面的优势,探讨FEM-SPH耦合算法中水线面直径取值对冰载荷中平整冰推挤载荷与破碎冰堆积形态的影响,为海上平台结构物与平整冰相互作用的数值研究提供理论参考与实践经验。
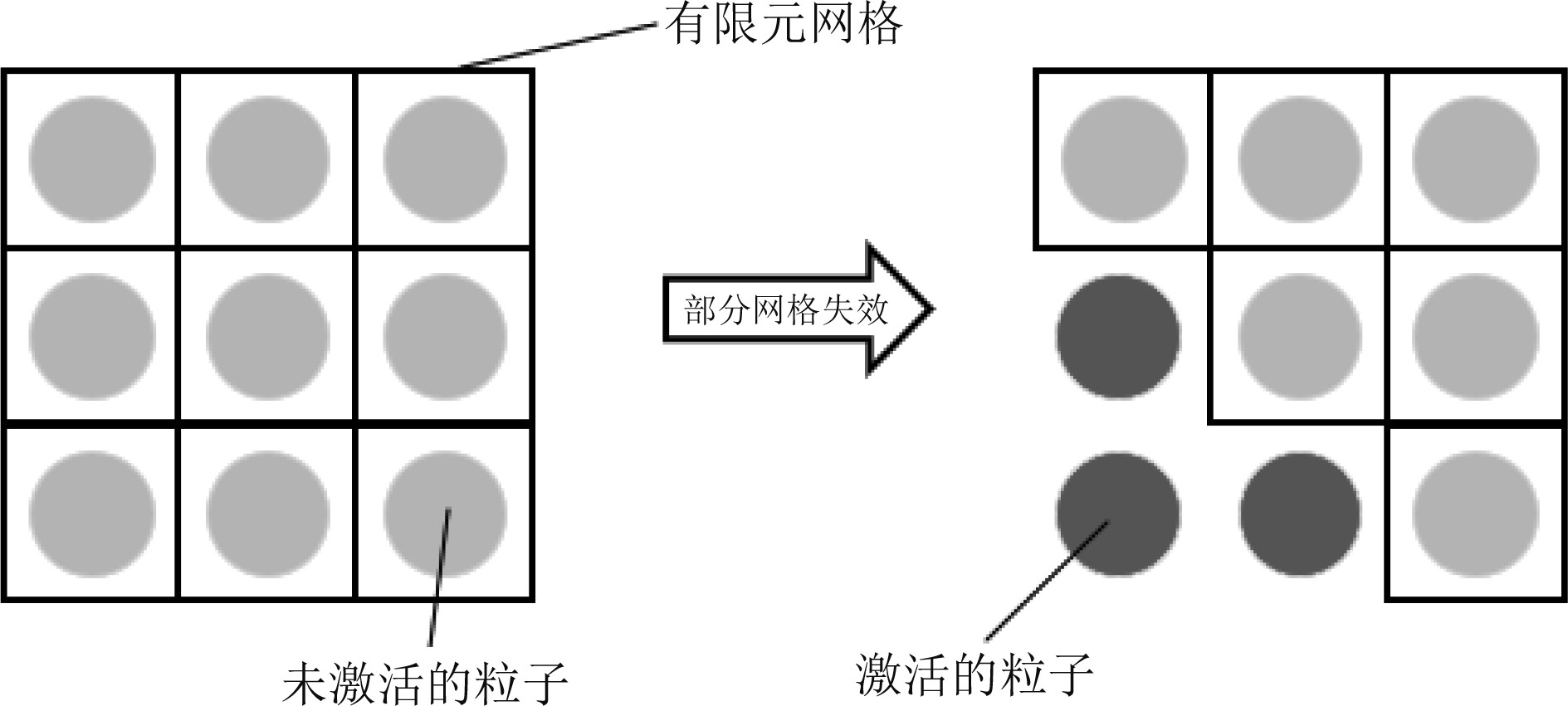
1 基础理论 1.1 FEM-SPH耦合算法FEM-SPH耦合算法将有限元法(FEM)与光滑粒子流体动力学(SPH)法相结合。在有限元网格失效后生成的光滑粒子将遵守质量守恒原则,以SPH法计算原理继续参与后续计算,模拟出碎冰或其他碎片飞散、堆积效果。FEM-SPH耦合算法在保证计算效率的同时,避免了有限元法存在的网格畸变等问题。单元转化过程如图1所示。
|
图 1 FEM-SPH耦合算法单元转化示意图 Fig. 1 Transformation process of units in FEM-SPH coupling algorithm |
以等效塑性应变为失效准则,当有限元网格未达到预定的等效塑性应变时,网格中的SPH粒子将处于未激活状态并与之耦合。未激活的粒子将不参与计算。当有限元网格形变达到预定等效塑性应变时,单元将被删去,一个或多个粒子将被激活并参与后续计算。激活的粒子将继承原单元的质量、速度、位置等物理属性。
1.2 Croasdale理论模型为计算斜面结构物在冰区所受冰载荷,Croasdale等基于弹性地基梁假定,提出了二维斜面冰载荷计算模型。后经改进,得到能用于计算三维锥体冰载荷的理论公式,即Croasdale理论模型[7]。曲月霞等[20]的模型试验对该公式准确性进行了验证。计算倒锥体时具体公式如下:
| $ \mathrm{F}={C}_{1}D{\sigma }_{f}{\left(\frac{{\rho }_{w}g{h}^{5}}{E}\right)}^{\frac{1}{4}}\left(1+\frac{{{\text{π}} }^{2}{I}_{c}}{4D}\right)+{C}_{2}Dzh({\rho }_{w}-{\rho }_{i})g 。$ | (1) |
其中:
| $ {C}_{1}=0.68\frac{\mathrm{sin}\alpha +\mu \mathrm{cos}\alpha }{\mathrm{cos}\alpha -\mu \mathrm{sin}\alpha },$ | (2) |
| $ {C}_{2}=\left(\mathrm{sin}\alpha +\mu \mathrm{cos}\alpha \right)\left(\frac{\mathrm{sin}\alpha +\mu \mathrm{cos}\alpha }{\mathrm{cos}\alpha -\mu \mathrm{sin}\alpha }+\frac{\mathrm{cos}\alpha }{\mathrm{sin}\alpha }\right),$ | (3) |
| $ {I}_{c}={\left(\frac{E{h}^{3}}{12{\rho }_{w}g\left(1-{\upsilon }^{2}\right)}\right)}^{\frac{1}{4}} 。$ | (4) |
式中:
式(1)结果分别由平整冰破碎力与碎冰堆积力组成。此次模拟目标为计算抗冰锥所受推挤载荷,不涉及碎冰堆积力,故只使用公式前半部分。抗冰锥在数值模拟过程中与有限元冰排间作用力理论计算公式为:
| $ {F}={C}_{1}D{\sigma }_{f}{\left(\frac{{\rho }_{w}g{h}^{5}}{E}\right)}^{\frac{1}{4}}\left(1+\frac{{\text{π}}^{2}{I}_{c}}{4D}\right) 。$ | (5) |
参考刘璐等[20]文献中数值模型,对平整冰碰撞抗冰锥过程进行仿真,平整冰尺寸选取30 m×20 m×0.5 m,抗冰锥与平整冰模型如图2所示。其中,抗冰锥采用壳单元进行网格划分,网格平均尺寸为0.2 m,仿真模型相关几何参数如表1所示。
|
|
表 1 抗冰锥相关参数 Tab.1 Parameters of ice cone |

|
图 2 仿真模型 Fig. 2 Simulation model |
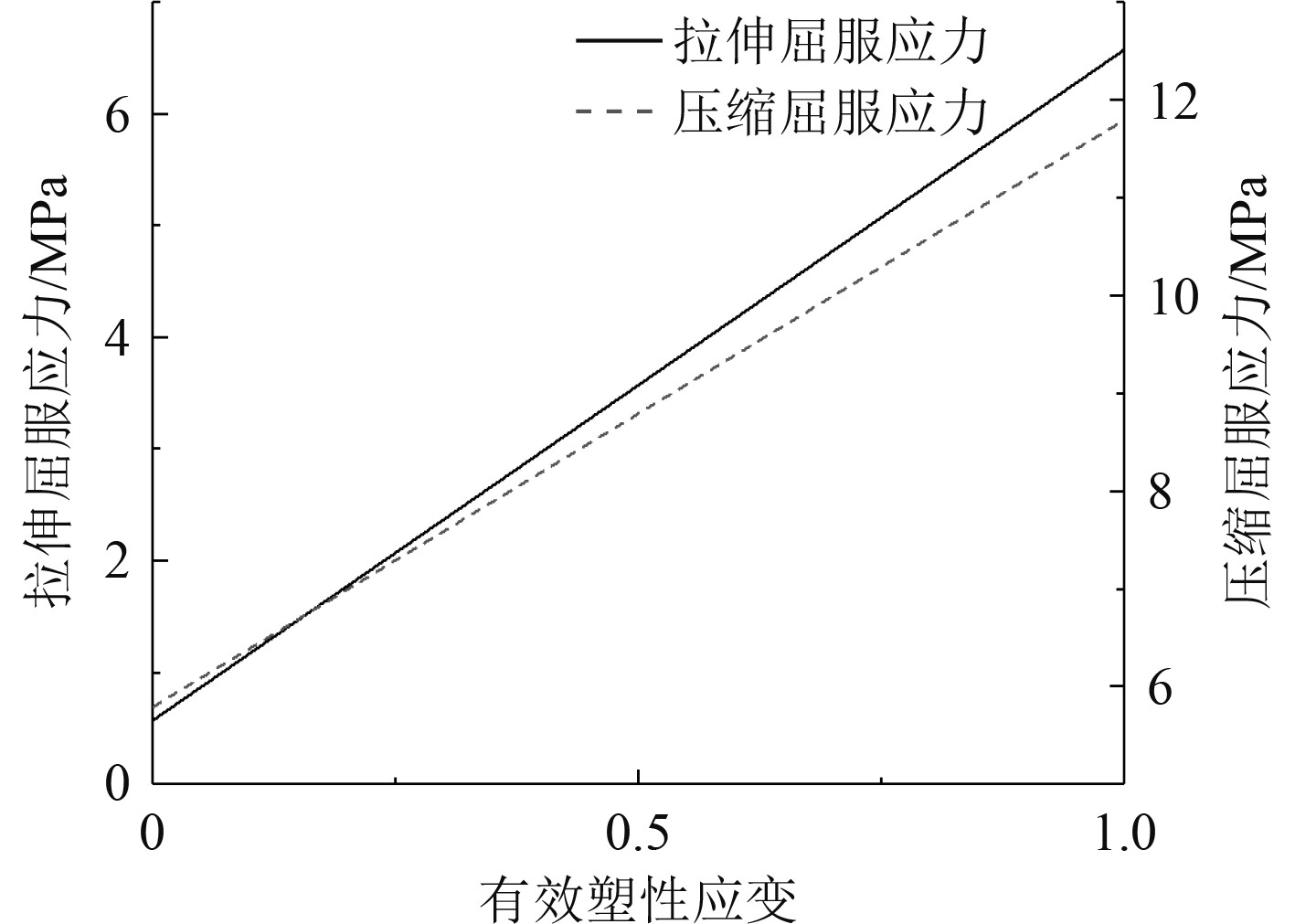
冰的材料模型选取Ls-dyna中的各向同性弹塑性材料,该材料能模拟冰在拉伸和压缩过程中力学特性的差异,材料准确性已在文献[21]中得到验证。材料模型的相关参数如表2所示,材料本构曲线如图3所示。在压缩过程中,材料模型的压缩塑性应变曲线随应变率一同改变。以应变率
|
|
表 2 冰材料模型相关参数 Tab.2 Parameters of ice material |
|
图 3
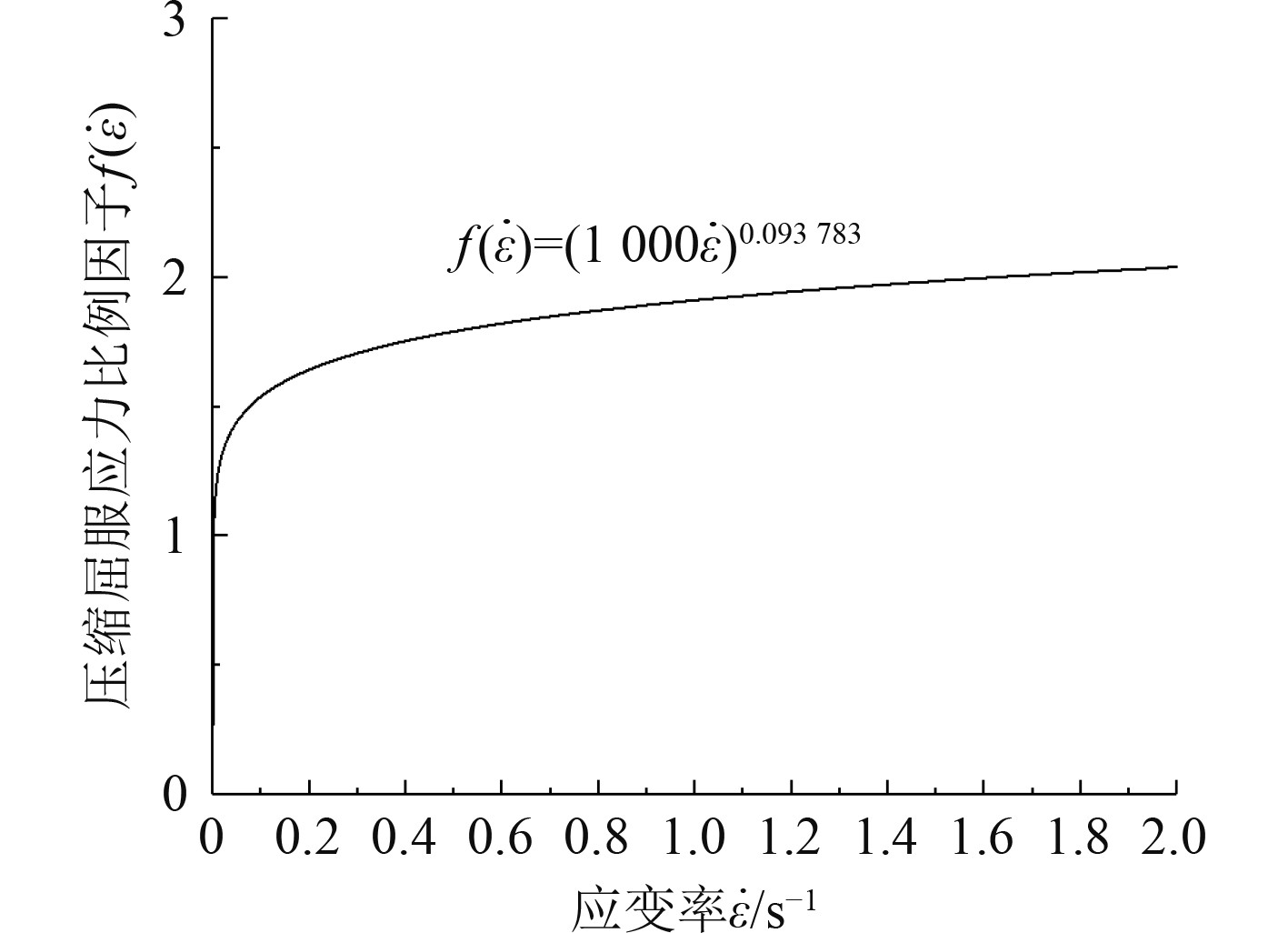
应变率
|
|
图 4 压缩屈服应力比例因子-应变率曲线 Fig. 4 Relationship between strain rates and compressive yield stress scale factors |
FEM-SPH耦合算法与有限元法在有限元部分设置相同,有限元冰排面向抗冰锥的一边自由,其余三边均刚性固定,以抗冰锥为主动面,平整冰为从动面,建立两者间接触关系。FEM-SPH耦合算法中,除抗冰锥与平整冰间接触外,还需建立抗冰锥与SPH粒子、SPH粒子与SPH粒子间的接触关系。因上述接触关系的建立均独立进行,推挤载荷可从仿真结果中直接读取。
除固体间相互作用力,SPH粒子还受浮力与阻尼力影响。SPH粒子所受浮力由下式实现:
| $ {F}_{b}=\left\{\begin{array}{l} 0{z}_{p}\geqslant 0,\\ {\rho }_{w}g\times \dfrac{4}{3}{\text{π}} {r}^{3}{z}_{p} < 0。\end{array}\right. $ | (6) |
式中:
水所产生的阻尼力方向与粒子速度方向相反,其数值计算公式为:
| $ {F}_{d}={c}_{d}\times \frac{1}{2}{\rho }_{w}{v}^{2}\times \mathrm{\pi }{r}^{2}。$ | (7) |
其中,
为验证数值模型正确性,需进行网格无关性分析。为将FEM-SPH耦合算法与有限元法进行对比,仅对两者都能得到的推挤载荷进行对比研究。
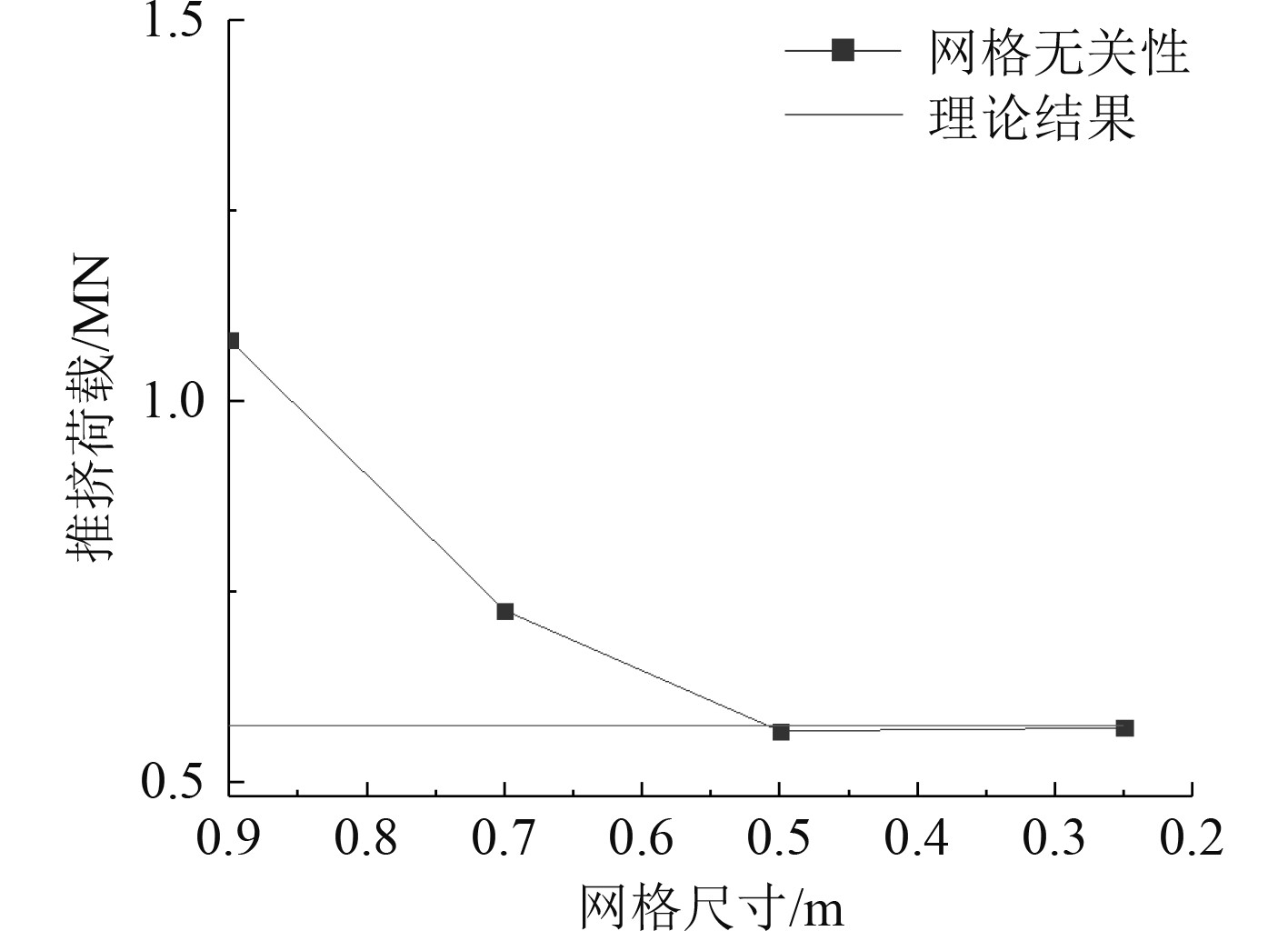
选取水平尺寸为0.25~1 m等多个不同尺寸的网格建模并计算。选取推挤载荷趋于稳定时段的峰值求得平均值,最终结果如图5所示。
|
图 5 平均推挤载荷与网格尺寸关系 Fig. 5 Relationship between mean pushing load and grid size |
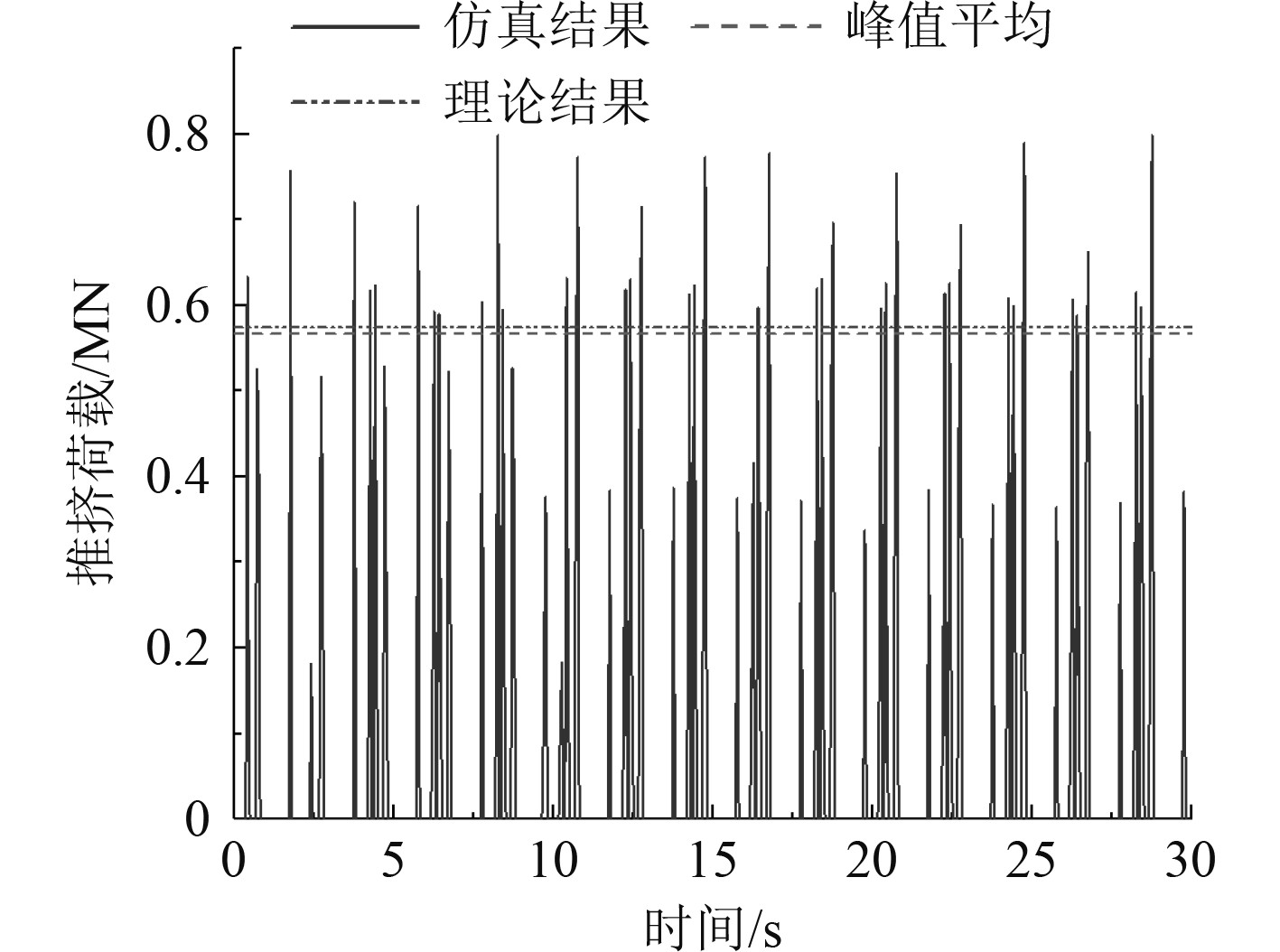
随网格细化,冰载荷逐渐收敛。0.25~0.5 m网格的数值模型计算结果与经验公式结果相近。如图6所示,推挤载荷的时历图呈现周期性的加载、卸载过程,其载荷的变化对应着实际冰破坏过程中冰的“挤压—弯曲—破坏”这一循环过程。当网格尺寸取值为0.5 m时,推挤过程趋于稳定时的平均峰值为0.567 MN,与理论结果0.574 MN间相对误差仅为1.22%。因此,FEM-SPH耦合算法模拟平整冰推移抗冰锥过程具有较高可信度。
|
图 6 0.5m网格尺寸仿真结果 Fig. 6 Simulation result when grid size equals to 0.5m |
从计算时间,几何因素及模拟精度等多方面角度考虑,后续仿真均选用0.5 m尺寸网格建立平整冰模型。
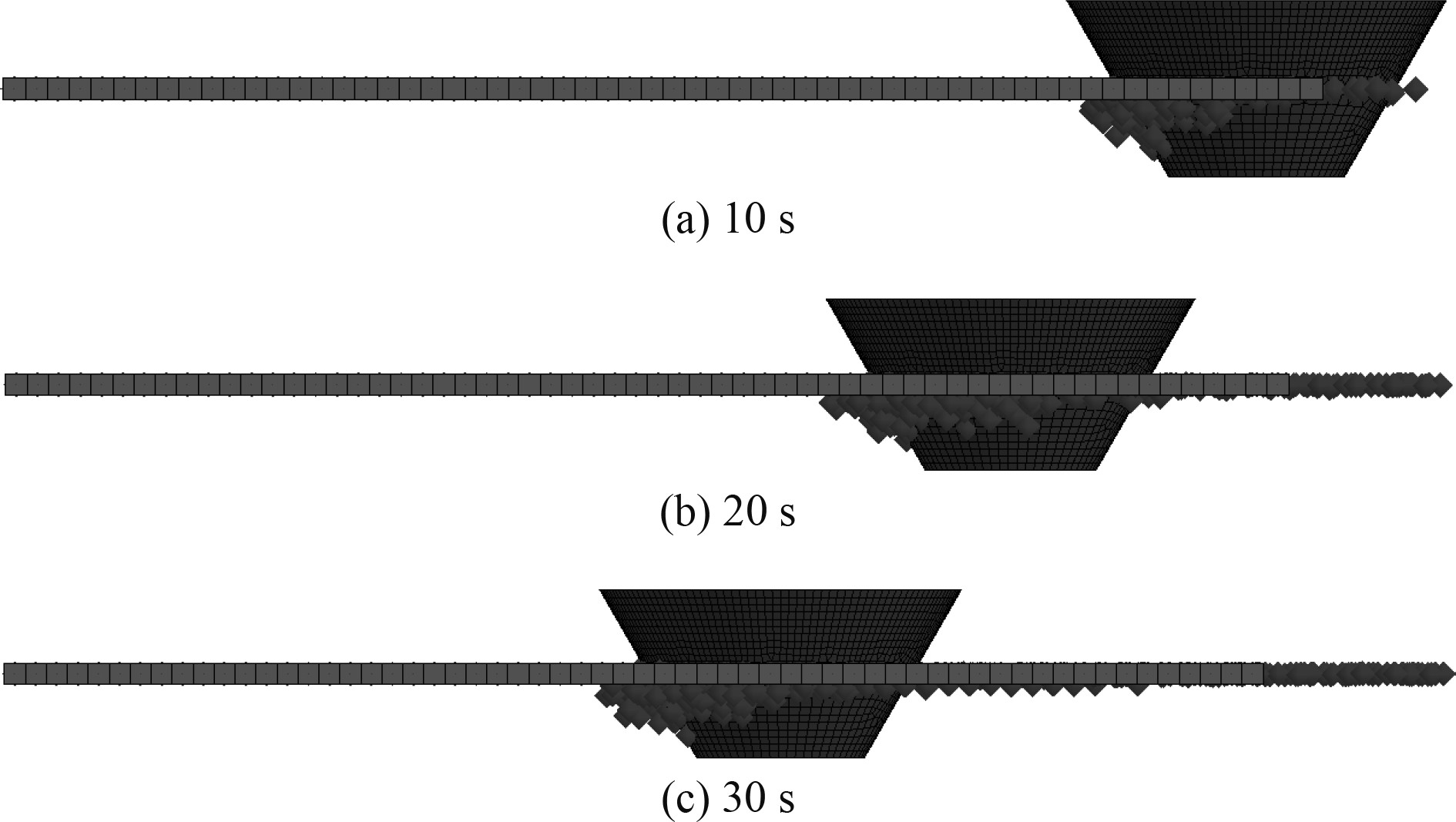
3.2 模拟结果分析平整冰模型中有限元单元达到预定失效条件时,该单元将从计算过程中删除,随后,一个继承原单元网格所有物理属性的SPH粒子将在原处激活。激活后的SPH粒子将作为碎冰继续参与后续计算,与平整冰、抗冰锥以及其他SPH粒子发生碰撞,产生碎冰堆积现象。该过程如图7所示。
|
图 7 仿真结果 Fig. 7 Simulation result |
从图中可知,有限元网格在抗冰锥与平整冰的作用过程中不断失效,其中SPH粒子随对应有限元单元失效而被激活、参与计算。激活后的SPH粒子最初于水面附近聚集,随后在浮力、重力、其他物体间相互作用力共同作用下,粒子沿抗冰锥表面向其下方与后方滑动。由于阻尼力、浮力、摩擦力的存在,最终粒子在达到一定深度后上浮,并在抗冰锥后方水线面处漂浮、静止。上述堆积现象证明了FEM-SPH耦合算法模拟碎冰运动、堆积现象的可行性。
3.3 水线面直径对堆积现象影响保持其他参数不变,对拥有不同水线面直径的抗冰锥进行推挤过程的模拟。测量各算例中碎冰粒子所能达到的平均深度与碎冰宽度,统计得到表3。其中,平均深度指算例趋于稳定时,同一时刻下不再向下方移动的粒子到水线距离的平均值。
|
|
表 3 不同水线面直径下冰堆积情况 Tab.3 Parameters of rushing ice accumulation from ice cones with different diameters |
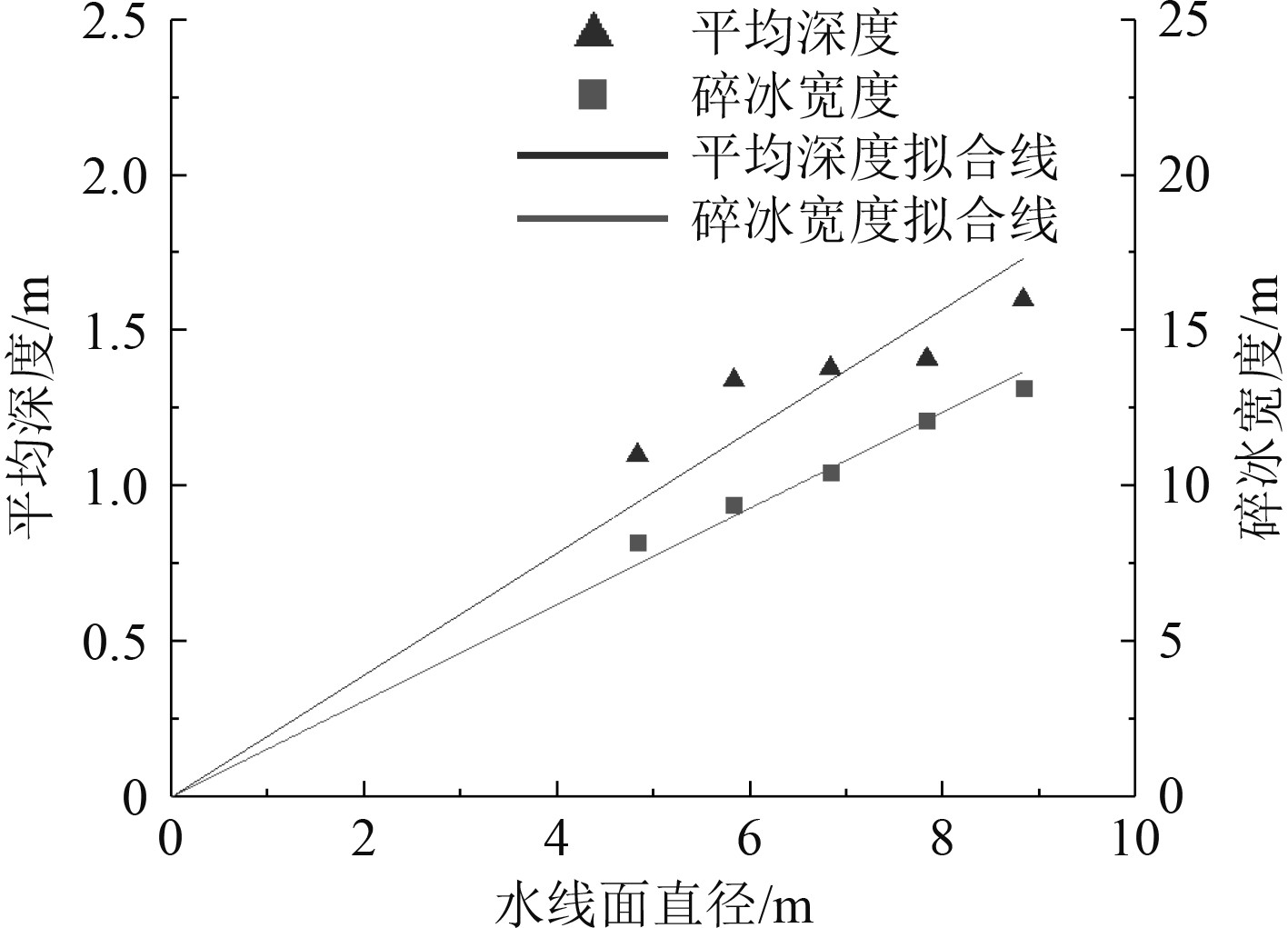
为更加直观观察水线面直径与平均深度、碎冰宽度之间关系,对数值进行拟合,最终结果如图8所示,其中2条拟合线均通过原点。
|
图 8 冰堆积参数拟合图 Fig. 8 Fitting curves of parameters from crushing ice accumulation |
2条拟合曲线相关系数r均不低于0.99,且决定系数R2均达到0.99。上述数据说明,在误差允许范围内,碎冰平均深度与碎冰宽度均与抗冰锥的水线面直径呈正比关系。
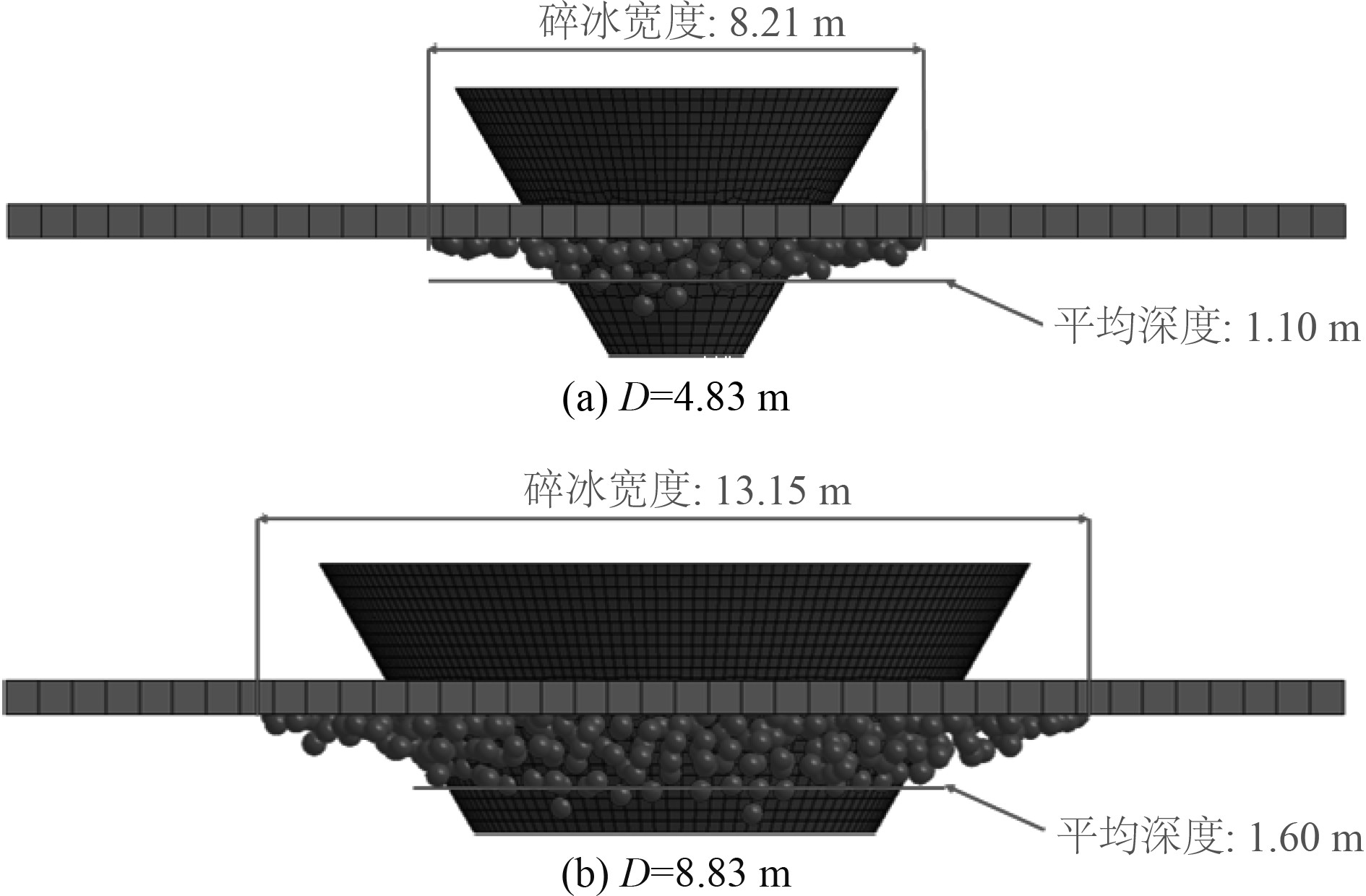
选取水线面直径最大和最小的2个算例进行冰堆积现象的对比,两者在结果均趋于稳定时的图像如图9所示。
|
图 9 不同水线面直径主视图 Fig. 9 Main view of ice cone with different diameters |
随着水线面直径增大,同深度碎冰数量增多,堆积现象加剧。直径为4.83 m的算例中,红线处至水线面距离为1.10 m,同一时刻,水线面直径8.83 m的抗冰锥则为1.60 m。通过对比可知,除碎冰平均深度增加外,平均深度处的粒子数量也将随水线面直径增大而增多。
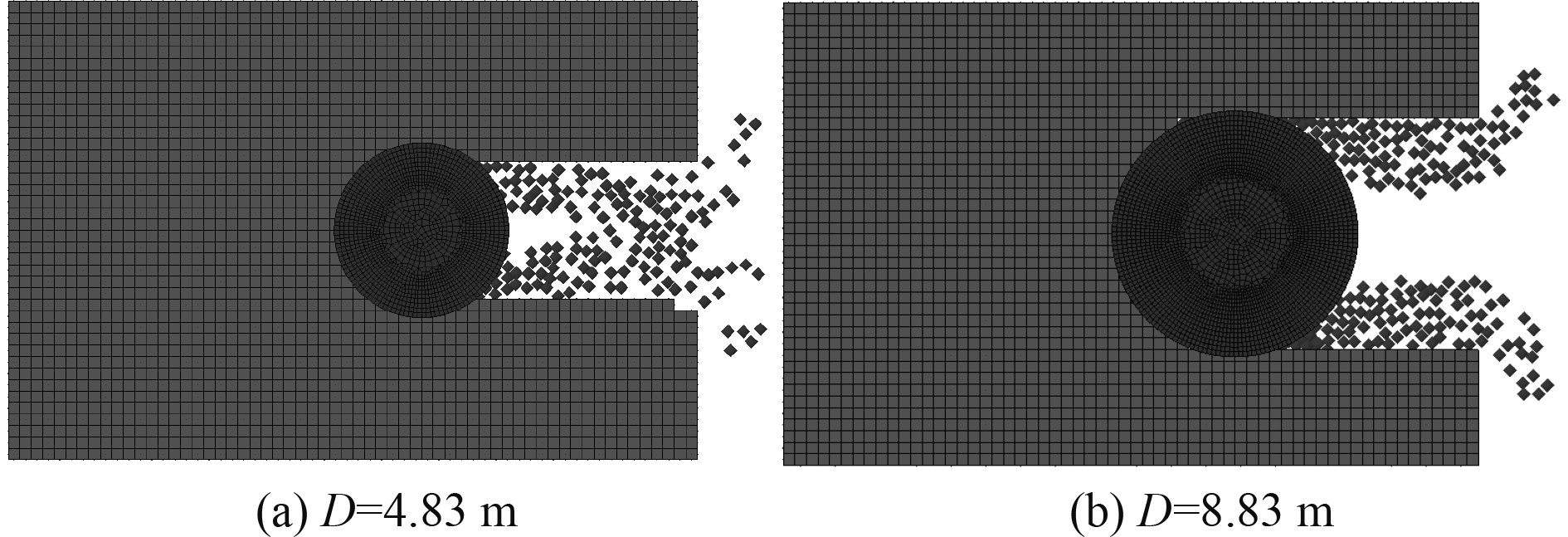
抗冰锥主视图中粒子最大扩散宽度,即图中所示碎冰宽度也将随水线面直径增大而增大。小水线面直径算例的结果图中,碎冰宽度仅为8.21 m,而大水线面直径算例中该距离则达到了13.15 m。当粒子到达一定高度后,将沿锥体侧面向后滑动,最后以平衡态漂浮于抗冰锥后方,形成碎冰通道,如图10所示。
|
图 10 不同水线面直径俯视图 Fig. 10 Top view of ice cone with different diameters |
在运动过程中,相较水线面直径较小的抗冰锥,水线面直径较大的抗冰锥更易在后方形成明显的通道。前者因直径较小,碎冰在到达抗冰锥后方时因横向速度不足而逐渐静止,与之后的粒子发生大量的二次碰撞,向通道中心移动,从而无法形成明显通道。通道的形成会使抗冰锥后方形成几乎没有浮冰的安全区。在抗冰锥的设计中,需适当增加结构物的直径,以减少结构物后方漂浮的碎冰量,避免浮冰对其他结构发生过多的冲击作用。
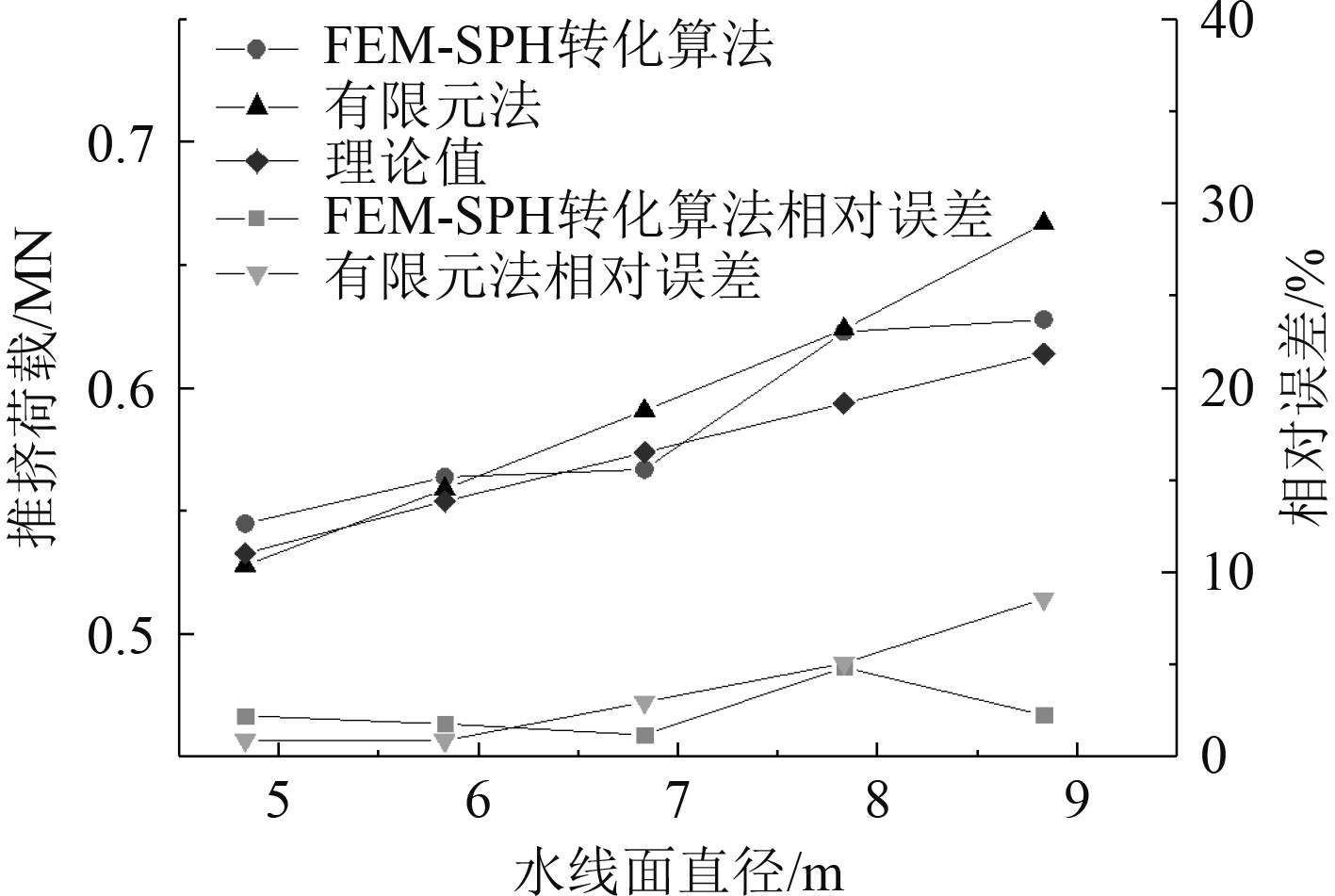
3.4 水线面直径对作用力影响为更好分析水线面直径对冰载荷造成的影响,对比FEM-SPH耦合算法与有限元法间区别,分别通过FEM-SPH耦合算法与有限元法模拟得到不同水线面直径时平整冰推挤抗冰锥产生的推挤载荷,并计算与Croasdale理论模型结果的差异,分析结果如图11所示。
|
图 11 水线面直径与推挤载荷关系曲线 Fig. 11 Relationship between diameters of ice cone and pushing load |
水线面直径增加将导致抗冰锥与平整冰接触面积增加。因此,水线面直径较大的抗冰锥在平整冰中前行时,与相同情况下水线面直径更小的抗冰锥相比,破坏平整冰这一过程所需的能量将更大,抗冰锥与平整冰间相互作用力也将更大。无论是FEM-SPH耦合算法还是传统有限元法,与Croasdale理论模型计算所得值相比,两者与理论结果间变化趋势一致。FEM-SPH耦合算法与有限元法计算结果与经验公式间误差均小于10%,在误差允许范围内,两者都能准确预报平整冰推挤载荷。但是,忽略破碎冰存在的有限元法计算结果的可靠性不及考虑更全面的FEM-SPH耦合算法。同时,随着在碎冰方面研究的推进,相比传统的有限元法,研究破碎冰载荷、再现碎冰堆积形态的FEM-SPH耦合算法将更具研究意义。
4 结 语本文基于FEM-SPH耦合算法建立抗冰锥与平整冰相互作用数值模型,将计算结果与Croasdale理论公式进行对比,验证数值模型的准确性。建立不同水线面直径抗冰锥与平整冰相互作用的模型,分析水线面直径对抗冰锥破冰过程中碎冰堆积现象和冰载荷影响。最后将其与有限元法结果进行比较,展现了FEM-SPH耦合算法在再现碎冰堆积现象方面的优势。
相较于只能计算某种规则几何体冰载荷平均值的理论公式,FEM-SPH耦合算法能够计算冰排在推挤过程中的动态载荷,再现冰排对结构物的加载、卸载过程。同时,FEM-SPH耦合算法在实际使用中还能计算复杂表面结构物所受冰载荷。因此FEM-SPH耦合算法相较理论公式更具泛用性与使用意义。
FEM-SPH耦合算法与有限元法模拟的抗冰锥冰载荷均随着水线面直径增加而增大,计算结果均与Croasdale理论公式接近。其中FEM-SPH耦合算法的精度略优于有限元法。
除较高的预报精度外,FEM-SPH耦合算法还能模拟平整冰推挤抗冰锥时的碎冰堆积现象,再现破碎冰的运动状态。而碎冰在推挤过程中所能达到的平均深度和碎冰宽度也均与抗冰锥的水线面直径呈良好的正比关系。相较有限元法,FEM-SPH耦合算法对于浮冰与冰海结构物作用关系的研究更具意义。
| [1] |
PAQUETTE E, THOMAS G B. Ice crushing forces on offshore structures: Global effective pressures and the ISO 19906 design equation[J]. Cold Regions Science and Technology, 2017, 142: 23-68. |
| [2] |
NECCI A, TARANTOLA S, VAMANU B, et al. Lessons learned from offshore oil and gas incidents in the Arctic and other ice-prone seas[J]. Ocean Engineering, 2019, 185: 12-26. DOI:10.1016/j.oceaneng.2019.05.021 |
| [3] |
张方俭. 海冰作用力在渤海海洋工程设计中的意义[J]. 海洋工程, 1987(2): 58-65. |
| [4] |
季顺迎. 渤海海冰数值模拟及其工程应用[D]. 大连: 大连理工大学, 2001.
|
| [5] |
季春群. 抗冰结构物的设计探讨[J]. 中国海洋平台, 1993, 2: 51-54. |
| [6] |
CROASDALE K R, CAMMAERT A B. An improved method for the calculation of ice loads on sloping structures in first-year ice[J]. Hydrotechnical Construction, 1994, 28(3): 174-179. DOI:10.1007/BF01545935 |
| [7] |
吴桐. 大连港长兴岛30万吨级原油码头工程破冰锥体应用[D]. 大连: 大连理工大学, 2018.
|
| [8] |
关湃, 黄焱, 万军, 等. 基于模型试验的导管架平台抗冰锥体优化设计[J]. 中国海洋平台, 2017, 32(4): 7-13. DOI:10.3969/j.issn.1001-4500.2017.04.002 |
| [9] |
武海斌, 黄焱, 李伟. 大直径单桩风机基础冰荷载模型试验研究[J]. 海洋工程, 2018, 36(2): 83-91. |
| [10] |
XU Ning, YUE Qianjin, BI Xiangjun, et al. Experimental study of dynamic conical ice force[J]. Cold Regions Science and Technology, 2015, 120: 21-29. DOI:10.1016/j.coldregions.2015.08.010 |
| [11] |
陈晓东, 王安良, 季顺迎. 海冰在单轴压缩下的韧-脆转化机理及破坏模式[J]. 中国科学: 物理学 力学 天文学. 2018, 48(12): 24-35.
|
| [12] |
高明帅. 破冰船在破冰过程中的运动数值仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [13] |
SONG Ming, SHI Wei, REN Zheng-ru, et al. Numerical study of the interaction between level ice and wind turbine tower for estimation of ice crushing loads on structure[J]. Journal of Marine Science and Engineering, 2019, 7(12): 439. DOI:10.3390/jmse7120439 |
| [14] |
ZHOU Li, DING Shi-feng, SONG Ming, et al. A simulation of non-simultaneous ice crushing force for wind turbine towers with large slopes[J]. Energies. 2019, 12(13): 2608.
|
| [15] |
ABAYOMI O, SRINIVAS S. Efficient response modelling for performance characterisation and risk assessment of ship-iceberg collisions[J]. Applied Ocean Research. 2018, 74: 127−141.
|
| [16] |
齐雅薇. 基于SPH方法的船—冰相互作用仿真分析研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [17] |
卞光夫. 基于SPH-FEM耦合算法的海冰-海洋结构物相互作用过程研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [18] |
CHEN Zhe, HE Yan-ping, HUANG Chao, et al. Numerical simulation of sloping structure-level ice interaction based on SPH-FEM conversion algorithm[C]// Proceedings of the Thirtieth (2020) International Ocean and Polar Engineering Conference. Shanghai, China, October 11-16, 2020.
|
| [19] |
曲月霞, 王永学, 李志军, 等. 作用于正倒锥结构上冰力物理模拟试验研究[J]. 大连理工大学学报, 2001(2): 231-236. DOI:10.3321/j.issn:1000-8608.2001.02.023 |
| [20] |
刘璐, 尹振宇, 季顺迎. 船舶与海洋平台结构冰载荷的高性能扩展多面体离散元方法[J]. 力学学报, 2019, 51(6): 1720-1739. |
| [21] |
Mahmud Sharif Sazidy. Development of velocity dependent ice flexural failure mode and application to safe speed methodology for polar ships[D]. Newfoundland: Faculty of Engineering and Applied Science Memorial University of Newfoundland, 2015.
|
 2022, Vol. 44
2022, Vol. 44

