近年来,海难事故有相当一部分是由于疲劳失效引起的船舶结构断裂导致的。研究表明船舶结构发生的总体破坏通常为多轴载荷作用下的低周疲劳破坏与累积塑性破坏耦合作用的结果[1-2]。在实际的海况中,船舶往往承受的是多轴非比例载荷的作用,因此,考虑累积塑性的船体裂纹板双轴非比例低周疲劳研究对于保障船舶结构的安全有效性具有重要意义。
20世纪中叶,塑性损伤的概念就被相关学者提出,但并没有引起重视。国外学者Coffin[3]指出累积塑性应变会对金属结构造成额外的损伤,并可能导致疲劳寿命缩短。Satyadevi[4]在研究断裂准则时指出分析低周疲劳寿命必须考虑累积塑性的影响。Kang[5]对SS304不锈钢进行了一系列实验,提出了考虑累积塑性影响的疲劳失效模型预测疲劳寿命。国内学者黄震球等[6]通过大量的理论验证与实验结果分析,进一步强调了累积塑性破坏在船舶总体结构分析中起关键性的作用。任慧龙等[7]指出当累积塑性变形超过某一限定值后,船舶局部结构会引发裂纹的萌生、扩展并最终导致总体断裂破坏。杨平等[8]发现船体缺口板缺口附近存在明显的累积塑性变形,并基于数值仿真建立裂纹萌生寿命预测模型。因此,对船体裂纹板双轴非比例低周疲劳载荷下累积塑性的数值分析势在必行。
本文通过对双轴非比例载荷下裂纹尖端的弹塑性分析,从理论上探究裂纹尖端低周疲劳的累积塑性变化机理。选用Abaqus有限元分析软件对裂纹板进行数值分析,探究在不同相位差、应力比、双轴应力比下累积塑性与低周疲劳的相互作用关系。
1 理论分析双轴低周疲劳载荷作用下船体裂纹板本构关系结合弹性理论、塑性理论求得。考虑增量物理方程[9]和塑性流动规则与可塑性表面的关系,其表达式如下:
| $ \Delta {\varepsilon _{ij}} = \frac{{1 + \upsilon }}{E}\Delta {\sigma _{ij}} - \frac{\upsilon }{E}\Delta {\sigma _{kk}}{\delta _{ij}} + \frac{3}{2}\frac{{2f(\Delta {\sigma _{eq}}/2)}}{{\Delta {\sigma _{eq}}}}{S_{ij}},$ | (1) |
其中,Δεij和Δσij为应变和应力张量分量的增量,E为杨氏模量,ʋ为泊松比,ΔSij和Δσeq通过下式计算获得:
| $ \left\{ {\begin{array}{*{20}{c}} {\Delta {S_{ij}}{\text{ = }}\Delta {\sigma _{ij}} - \dfrac{1}{3}\Delta {\sigma _{kk}}{\delta _{ij}}} ,\\ {\Delta {\sigma _{eq}}{\text{ = }}\sqrt {\dfrac{3}{2}\Delta {S_{ij}}\Delta {S_{ij}}} } 。\end{array}} \right. $ | (2) |
根据Chaboche模型[10]中有关累积塑性应变的微分关系,在n+1个载荷循环中累积塑性应变为:
| $ d{\varepsilon _{p,n + 1}} = {\left( {\frac{{{f_1}}}{Z}} \right)^n} = \sqrt {\frac{2}{3}d\varepsilon _{n + 1}^p:d\varepsilon _{n + 1}^p} 。$ | (3) |
其中:dεp,n+1为第n+1个循环后裂纹尖端等效塑性应变增量,可以根据Newton-Raphson迭代法[11]通过n+1个载荷循环后裂纹板裂纹尖端应力-应变关系来获得。
依次更新相应的参数,可以求得在第i个循环的塑性应变增量。因此,双轴低周疲劳载荷下裂纹板裂纹尖端在n+1个载荷循环的塑性应变增量Δεp可以表示为:
| $ \Delta {\varepsilon _{p,n + 1}} = = \sum\limits_{i = 1}^{n + 1} {d{\varepsilon _{p,n + 1}}} = {\sum\limits_i^{n + 1} {\left\langle {\frac{{{f_1}}}{Z}} \right\rangle } ^n} = \sum\limits_i^{n + 1} {\sqrt {\frac{2}{3}d\varepsilon _i^p:d\varepsilon _i^p} },$ | (4) |
根据文献[12],双轴非比例低周疲劳载荷下裂纹板等效塑性应变结合X轴和 Y 轴向的累积塑性应变分量Δɛp,x 和 Δɛp,y获得,表示如下:
| $ \begin{split}\Delta {\varepsilon _{p,eq}} =& \frac{{\Delta {\varepsilon _{p,x}}}}{{\left( {1 - {\nu ^2}} \right)}}\times\\ &\sqrt {\left[ {1 + {\nu ^2} - \nu } \right]\left[ {1 + {{\left( {\frac{{\Delta {\varepsilon _{p,y}}}}{{\Delta {\varepsilon _p}_{,x}}}} \right)}^2}} \right] - \left[ {1 + {\nu ^2} - 4\nu } \right]\frac{{\Delta {\varepsilon _{p,y}}}}{{\Delta {\varepsilon _{p,x}}}}} \end{split}。$ | (5) |
根据式(4)获得的累积塑性应变作为双轴非比例低周疲劳载荷下裂纹板在X轴和Y轴方向的塑性变形分量代入式(5),即可获得在双轴非比例低周疲劳载荷下裂纹板在相应载荷循环后裂纹尖端等效塑性应变。
2 数值分析 2.1 数值模型选用Abaqus软件对在双轴非比例载荷作用下裂纹板进行数值计算。首先,对裂纹板的初始裂纹进行定义,将裂纹表面绑定在裂纹长度为8 mm处,在预制裂纹周围区域采用插件设置为0.05 mm×0.05 mm的细化网格,采用过渡网格对过渡区域进行网格划分。在预制裂纹处建立中心对称边界条件,设置其载荷频率为1 Hz下σx和σy的拉-拉加载方式,结合静态隐式分析步,进行周期为60 s的船体板双轴低周疲劳响应计算分析。
Chaboche本构模型能够较好地表征结构构件在裂纹尖端区域的累积塑性现象,经过一系列有限元计算及修正优化,确定Chaboche模型系数如表1所示。
|
|
表 1 塑性本构模型的材料参数值 Tab.1 Material parameter values of plastic constitutive model |
采用双轴非比例拉伸载荷加载,在载荷设计中以水平应力分量σx和垂直应力分量σy作为基准。通过控制变量法,考虑应力比R、双轴应力比λ和相位差φ等3种不同因素影响。
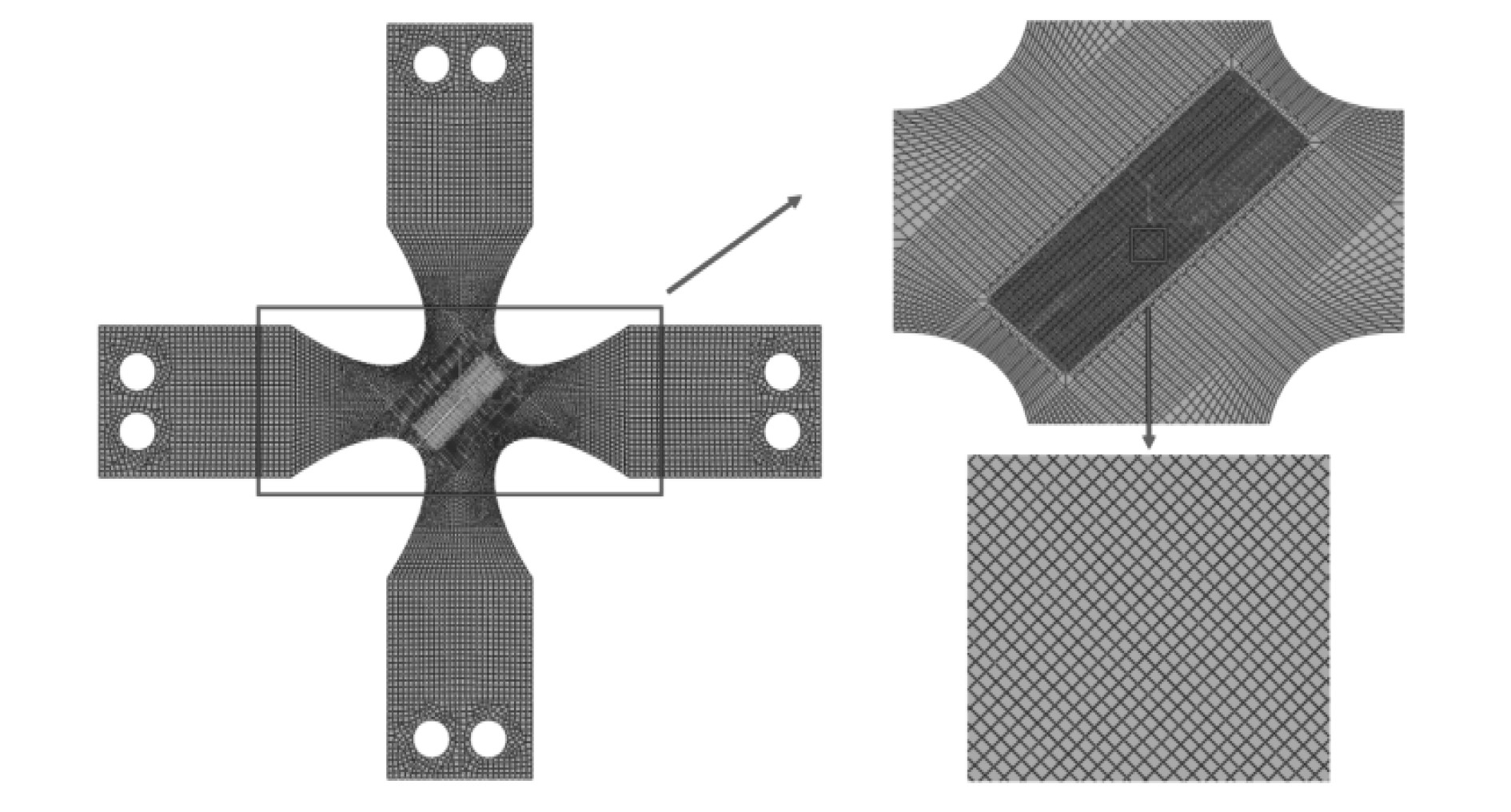
|
图 1 裂纹板数值计算模型 Fig. 1 Numerical calculation model of cracked plate |
通过Abaqus中Chaboche本构模型对十字型船体裂纹板进行有限元数值仿真分析,得到不同相位差φ、双轴应力比λ和应力比R下裂纹尖端应力应变曲线。
2.2.1.1 相位差φ的影响在不同相位差条件下,水平载荷分量与垂直载荷分量不同于等比例载荷下同步变大或减小,不同相位差所对应的加载路径如图2所示。
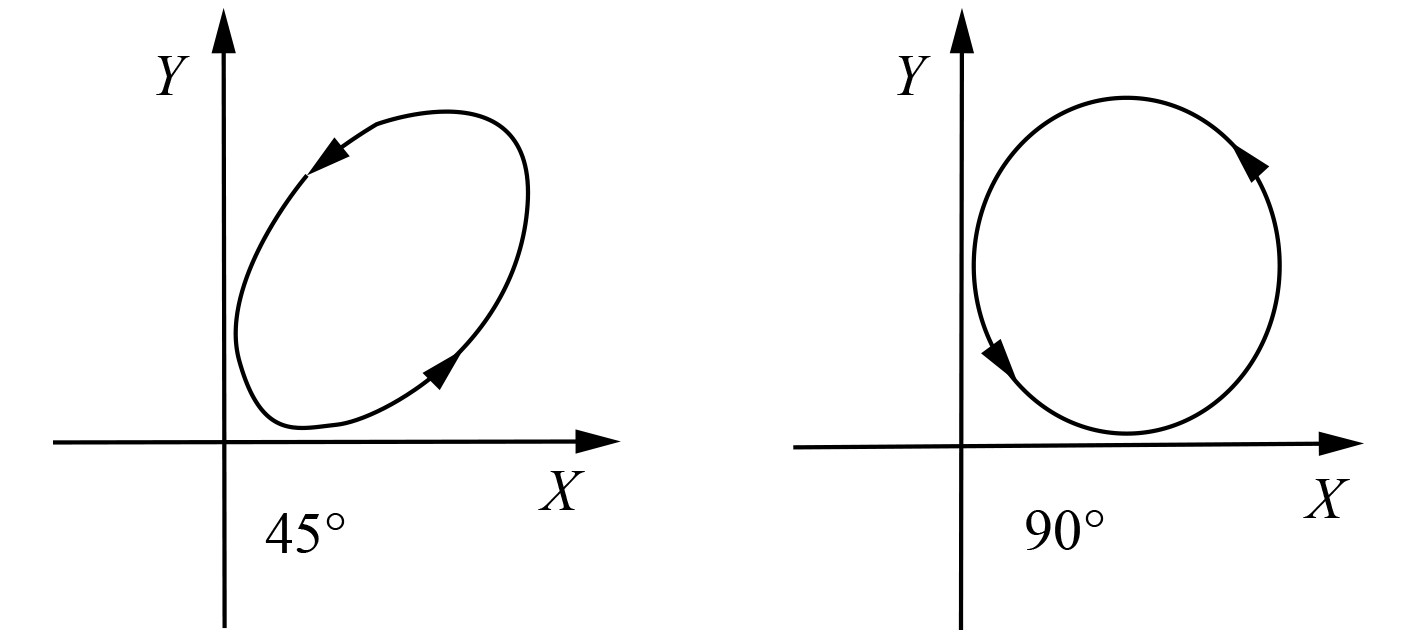
|
图 2 不同相位差下载荷路径 Fig. 2 Load paths under different phase differences |
由图3可知,随着相位差φ的增加,应力应变水平缓慢增加,迟滞曲线的应力水平稳定上升,应变水平也逐渐升高。由此可知,裂纹尖端的应力应变水平与相位差呈正相关。

|
图 3 不同相位差作用下裂纹板应力应变迟滞回线 Fig. 3 Stress-strain hysteresis loop of cracked plate under different phase differences |
从图4可以看出,随着双轴应力比λ的增加,应力应变范围逐渐变小。由此可知,裂纹尖端的应力应变水平与预制裂纹垂直方向的载荷幅值呈正相关,平行方向的载荷值对应力应变水平影响较小。
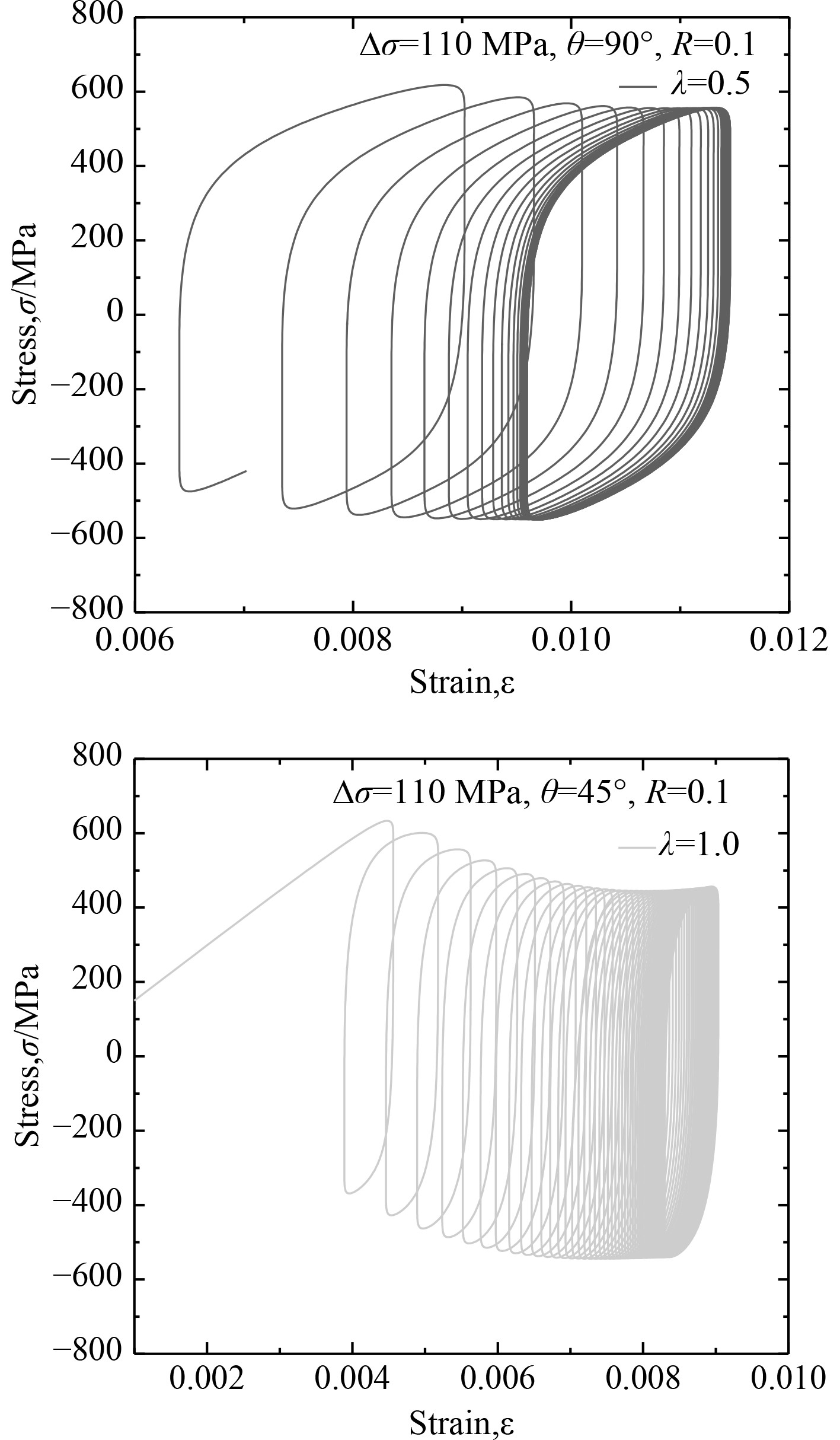
|
图 4 不同双轴应力比作用下的应力应变迟滞回线 Fig. 4 Stress-strain hysteresis loop under different biaxial stress ratios |
在探究不同应力比R时,为保证单一变量,固定最大应力σmax值,改变最小应力σmin的值,得到如图5所示不同应力比下的迟滞回线。
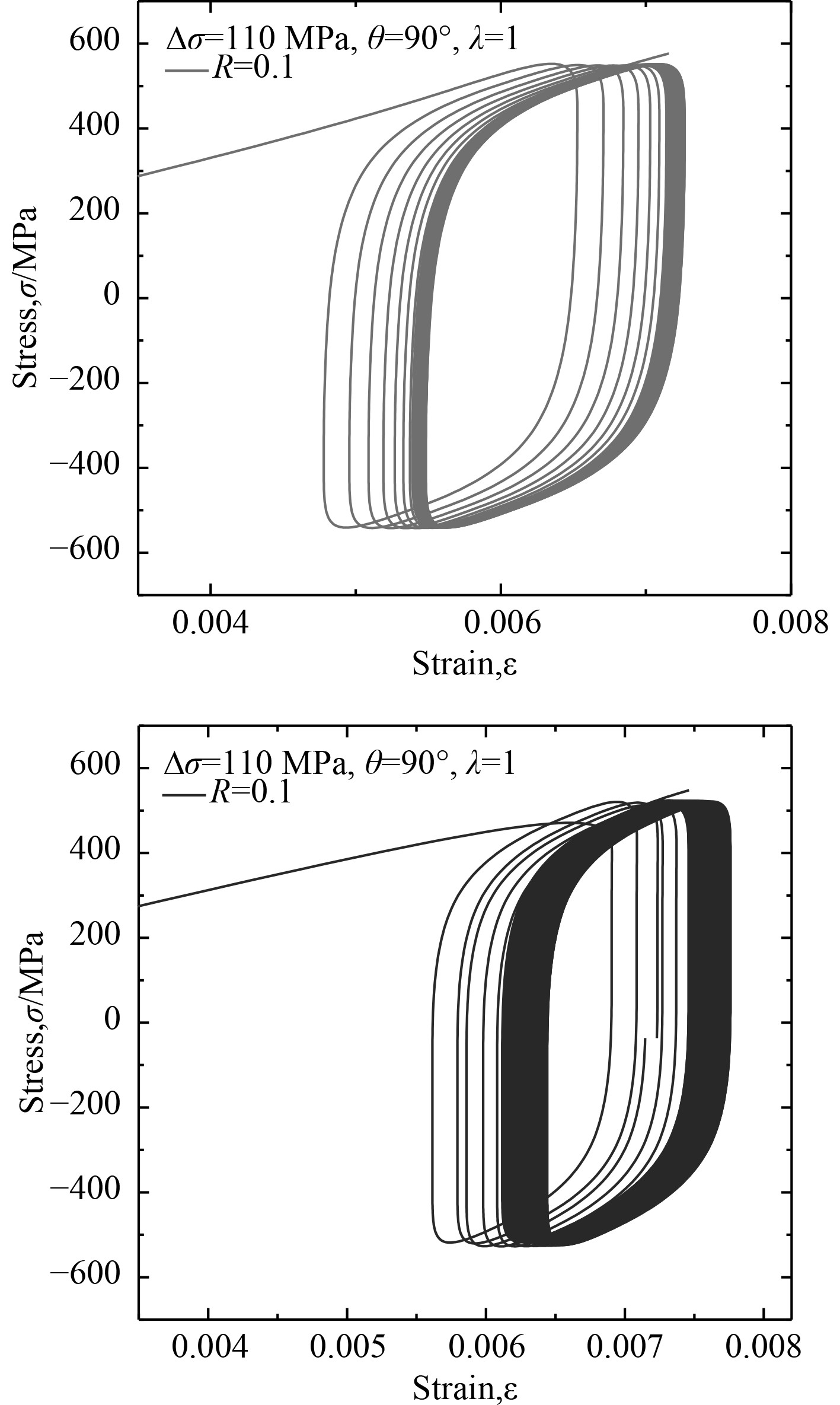
|
图 5 不同应力比作用下的应力应变迟滞回线 Fig. 5 Stress-strain hysteresis loop under different stress ratios |
由图5可知,裂纹尖端迟滞回线的应变水平随着应力比R的增加而增加。应力比越大,对应的平均载荷应力值也更大,引起的应变水平更高。
2.2.2 裂纹尖端应力应变云图选取相位差为0°和180°进行有限元计算,得到如图6所示的应力应变云图。从图6(a)和图6(c)的应力云图可以看出船体裂纹板裂纹尖端处的应力随着相位差的增加而增加。从图6(b)和图6(d)的应变云图发现船体裂纹板的应变随着相位差的增加而增加,并且在初始的循环过程中,累积递增塑性应变增长的速度较快,随着循环周期的持续,逐渐趋于稳定。因此,双轴非比例低周疲劳载荷下船体裂纹板累积塑性变形所引起的附加破坏应该需要考虑。

|
图 6 不同相位差下裂纹尖端应力应变云图 Fig. 6 Stress-strain contours of crack tip at different phase differences |
为了探究双轴非比例载荷作用下低周疲劳和累积塑性相互作用,对有限元模型在不同相位差φ、双轴应力比λ和应力比R下进行了双轴拉-拉有限元计算。
图7表明在双轴非比例载荷作用下累积塑性应变随着相位差φ、双轴应力比λ和应力比R的增加而增加,且变化的规律是急速增加后再趋于稳定。说明在双轴非比例低周疲劳拉-拉载荷分析中,相位差φ、双轴应力比λ和应力比R对船体裂纹板的累积递增塑性应变有着较大的影响。

|
图 7 不同非比例低周疲劳载荷下累积塑性应变与循环次数关系曲线 Fig. 7 Relationship between accumulative plastic strain and cycle times under different non-proportional low-cycle fatigue loads |
根据低周疲劳累积塑性数值计算获得在不同应力比、双轴应力比以及不同相位差载荷下,裂纹尖端累积塑性应变及变化率随循环次数的对应关系如图8和图9所示。
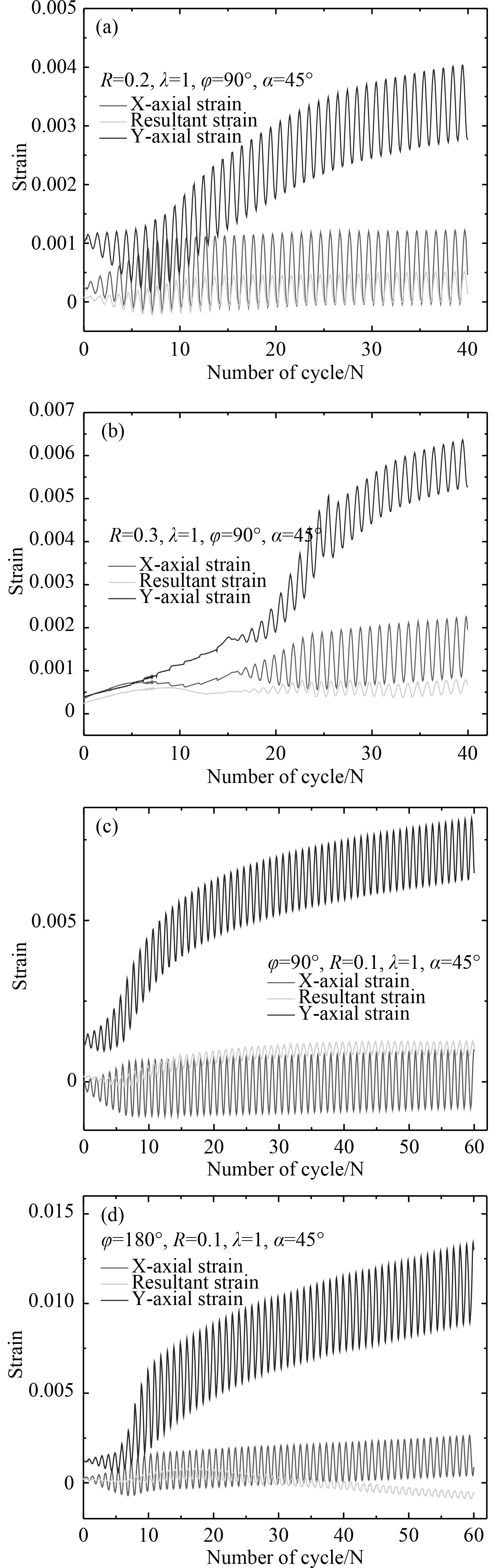
|
图 8 不同非比例低周疲劳载荷条件下裂纹板塑性应变累积变化关系曲线 Fig. 8 Accumulative variation curves of plastic strain of cracked plates under different non-proportional low-cycle fatigue loads |

|
图 9 不同非比例低周疲劳载荷条件下裂纹板塑性应变累积率变化关系曲线 Fig. 9 Variation curves of plastic strain accumulation rates of cracked plates under different non-proportional low-cycle fatigue loads |
从图8可以看出,在相同相位差和应力比、不同双轴应力比的循环载荷作用下,结构构件预制裂纹区域存在明显的累积塑性变形现象,其合应变随着循环周期次数的增加逐渐增大,而双轴应力比越大时,结构构件的合应变相对减小。这是由于在进行双轴拉伸-拉伸数值仿真计算时,选用的有限元模型其预制裂纹距水平方向偏离45°夹角,随着双轴应力比增加,其有限元模型施加载荷的主应力方向逐渐偏向于裂纹的平行方向,导致响应的应变水平越来越低,从而延缓其应变值。可以看出结构构件预制裂纹区域的累积塑性应变随着双轴应力比的增大而逐渐减小,双轴应力比越高,结构构件累积塑性变形越小,即进入累积塑性变形加速发展阶段也越慢。但含有相位差的累积塑性应变始终小于无相位差的等比例累积塑性应变,表明相位差的引入,导致结构构件预制裂纹处的累积塑性变形在初始阶段累积会有一定的延缓。
由图9可知,累积塑性应变率在不同因素的影响下表现出了较好的一致性。累积塑性应变率由最开始不稳定到逐渐浮动减低直至非零的稳定值。图9(a)表明在双轴非比例载荷作用下,裂纹尖端的累积塑性应变随着应力比的增加呈正相关。图9(b)中不同双轴应力比的累积率与循环次数的关系呈下降趋势。根据图9(c)可以看出在不同相位差下曲线由最低值达到峰值后缓慢降低至非零稳定值,在趋于稳定的情况下,累积塑性应变率随着相位差的增加而逐渐增大。
3 结 语1)通过数值仿真计算不同相位差φ、双轴应力比λ和应力比R对双轴非比例载荷作用下应力应变迟滞回线的影响。可以发现在不同应力比和相位差下,迟滞回线应变水平随着变量的增加而向单调增大,应力水平则单调减小。对于不同双轴应力比,随着双轴应力比增加,应力应变水平都随变量增大而减小。
2)在双轴非比例载荷下低周疲劳累积塑性数值计算中,十字型模型的累积塑性随着循环周期的增加而增加,其累积塑性应变由初期变化后,稳定至非零值,并且,不同的相位差、双轴应力比和应力比对累积塑性应变都有影响。
3)在双轴应力比及相位差恒定的情况下,随着应力比R的增加,累积塑性应变及累积塑性应变率单调增加;而当双轴应力比不同时,可以发现累积塑性应变先增大后缓慢减小,并且裂纹尖端的累积塑性现象与主应力密切相关。此外,随着相位差的增加对累积塑性应变值也有一定影响。
| [1] |
黄震球. 关于海船船体总强度准则的一个新见解[J]. 武汉造船(武汉造船工程学会会刊), 1993(6): 8-12. |
| [2] |
黄震球. 船舶强度研究中的几个问题[J]. 武汉造船, 1999(3): 3-7. |
| [3] |
COFFIN L F. The deformation and Fracture of a ductile metal under superimposed cyclic and monotonic strain[J]. Achievement of high fatigue resistance in metals and alloys, ASTM, 1970, STP-467,53-76. |
| [4] |
SATYADEVI A, SIVAKUMAR S M. A new failure criterion for materials exhibitingratcheting during very low cycle fatigue[J]. Materials and Science Engineering, 2007, 452-453.
|
| [5] |
KANG G Z, LIU Y J. Uniaxial ratcheting and low cycle fatigue failure of the steel with cyclic stabilizing or softening feature[J]. Materials and Science Engineering, 2008, 472: 258-268. DOI:10.1016/j.msea.2007.03.029 |
| [6] |
黄震球, 陈齐树, 骆子夜, 等. 循环面内压缩载荷下方板的非弹性变形性能[J]. 华中理工大学学报, 1996(3): 39-42. |
| [7] |
任慧龙, 李陈峰. 基于递增塑性破坏的船体极限强度分析研究[C]//2007年船舶力学学术会议暨《船舶力学》创刊十周年纪念学术会议, 中国宁夏银川, 2007.
|
| [8] |
DENG J L, YANG P, CHEN Y. Low-cycle fatigue crack initiation life of hull-notched plate considering short crack effect and accumulative plastic damage[J]. Applied Ocean Research, 2017, 68: 65-76. DOI:10.1016/j.apor.2017.08.003 |
| [9] |
J. SZUSTA, A. Seweryn. Low-cycle fatigue model of damage accumulation-The strain approach[J]. Engineering Fracture Mechanics, 2010, 77: 1604-1616. DOI:10.1016/j.engfracmech.2010.04.014 |
| [10] |
TONG J, ZHAO LG, LIN B. Ratcheting strain as a driving force for fatigue crack growth[J]. International Jounal of Fatigue, 2013, 46: 49-57. DOI:10.1016/j.ijfatigue.2012.01.003 |
| [11] |
BUDIANSKY B, HUTCHINSON JW. Analysis of crack closure in fatigue crack growth[J]. Journal of Applied Mechanics, Transcation of ASME, 1978, 45: 67-76. DOI:10.1115/1.3424275 |
| [12] |
STEPHANIE A, KULAWINSKI D, SEBASTIAN H, etal. Biaxial in-phase and out-of-phase cyclic deformation and fatigue behavior of an austenitic TRIP steel[J]. International Journal of Fatigue, 2014, 67: 12133.
|
 2022, Vol. 44
2022, Vol. 44

